Belirli İntegralin Özellikleri
Aşağıda bahsedeceğimiz belirli integral özelliklerinin belirli integralin alan anlamı akılda tutularak incelenmesi bu özelliklerin anlaşılmasını kolaylaştıracaktır.
Fonksiyon İşlemleri
Sabit Çarpım
Bir fonksiyonun sabit bir değerle çarpımının integrali, fonksiyonun integralinin sabit değerle çarpımına eşittir. Bir diğer deyişle, bir fonksiyon sabit bir \( k \) sayısı ile çarpıldığında \( x \) ekseni ile arasında kalan alan da aynı oranda büyür/küçülür.
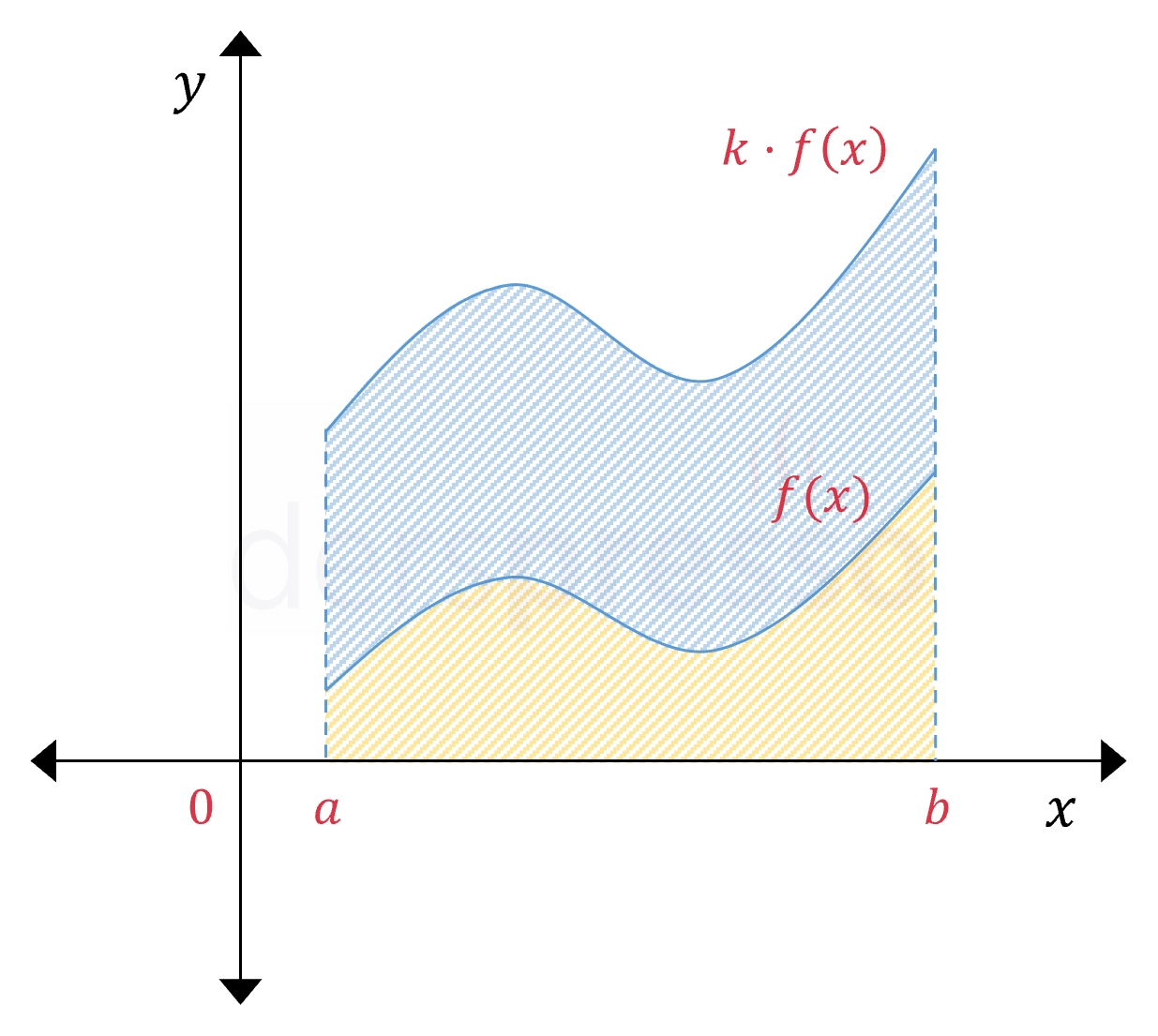
\( k \in \mathbb{R} \) olmak üzere,
\( \displaystyle\int_a^b {k \cdot f(x)\ dx} = k \cdot \displaystyle\int_a^b {f(x)\ dx} \)
\( \displaystyle\int_0^2 {5x^2\ dx} = 5\displaystyle\int_0^2 {x^2\ dx} \)
İSPATI GÖSTER
Verilen belirli integralin limit tanımını yazalım.
\( \displaystyle\int_a^b {k \cdot f(x)\ dx} = \lim_{n \to \infty} \displaystyle\sum_{i = 1}^{n}{k \cdot f(x_i^*) \cdot \Delta x} \)
Toplam sembolü işlem kurallarına göre toplam sembolünün içindeki ifadenin sabit bir çarpanı toplam sembolünün dışına çarpan olarak çıkarılabilir.
\( = \lim_{n \to \infty} k \cdot \displaystyle\sum_{i = 1}^{n}{f(x_i^*) \cdot \Delta x} \)
Limit işlem kurallarına göre limit tanımlı bir ifadenin sabit bir sayı ile çarpımının limiti, ifadenin limitinin sabit sayı ile çarpımına eşittir.
\( = k \cdot \lim_{n \to \infty} \displaystyle\sum_{i = 1}^{n}{f(x_i^*) \cdot \Delta x} \)
Bu limit ifadesi \( f(x) \) fonksiyonunun \( [a, b] \) aralığındaki belirli integralidir.
\( = k \cdot \displaystyle\int_a^b {f(x)\ dx} \)
Fonksiyonların Toplamı/Farkı
İki fonksiyonun toplamının/farkının integrali, integrallerinin toplamına/farkına eşittir. Bir diğer deyişle, iki fonksiyonun toplamı/farkı olan fonksiyonun \( x \) ekseni ile arasında kalan alan, fonksiyonların ayrı ayrı \( x \) ekseni ile aralarında kalan alanların toplamına/farkına eşittir.
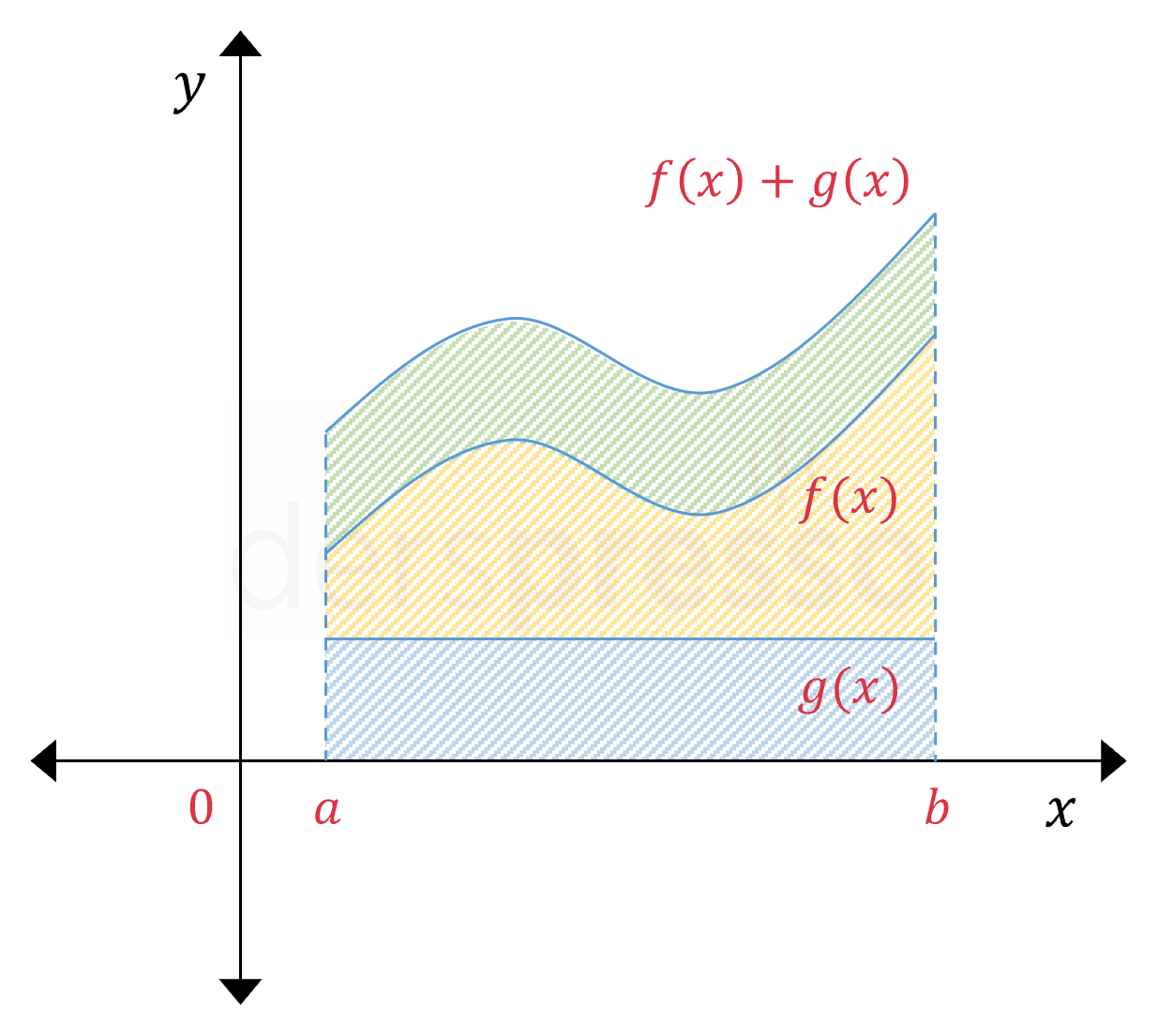
\( \displaystyle\int_a^b {(f(x) \pm g(x))\ dx} = \displaystyle\int_a^b {f(x)\ dx} \pm \displaystyle\int_a^b {g(x) dx}\ \)
\( \displaystyle\int_1^4 {(x^2 + 2^x)\ dx} = \displaystyle\int_1^4 {x^2\ dx} + \displaystyle\int_1^4 {2^x\ dx} \)
İSPATI GÖSTER
Verilen belirli integralin limit tanımını yazalım.
\( \displaystyle\int_a^b {(f(x) \pm g(x))\ dx} = \lim_{n \to \infty} \displaystyle\sum_{i = 1}^{n}{(f(x_i^*) \pm g(x_i^*)) \cdot \Delta x} \)
Toplam sembolü işlem kurallarına göre toplam sembolü ifadedeki terimlere dağıtılabilir.
\( = \lim_{n \to \infty} (\displaystyle\sum_{i = 1}^{n}{f(x_i^*) \cdot \Delta x} \pm \displaystyle\sum_{i = 1}^{n}{g(x_i^*) \cdot \Delta x}) \)
Limit işlem kurallarına göre limiti tanımlı iki ifadenin toplamının/farkının limiti, ifadelerin ayrı ayrı limitlerinin toplamına/farkına eşittir.
\( = \lim_{n \to \infty} \displaystyle\sum_{i = 1}^{n}{f(x_i^*) \cdot \Delta x} \pm \lim_{n \to \infty} \displaystyle\sum_{i = 1}^{n}{g(x_i^*) \cdot \Delta x} \)
Bu limit ifadeleri sırasıyla \( f(x) \) ve \( g(x) \) fonksiyonlarının \( [a, b] \) aralığındaki belirli integralidir.
\( = \displaystyle\int_a^b {f(x)\ dx} \pm \displaystyle\int_a^b {g(x)\ dx} \)
Aralık İşlemleri
Sınırların Yer Değiştirmesi
Bir integralin alt ve üst sınırları kendi aralarında yer değiştirirse (\( [a, b] \to [b, a] \)) integral değeri işaret değiştirir.
\( \displaystyle\int_{\textcolor{red}{b}}^{\textcolor{blue}{a}} {f(x)\ dx} = -\displaystyle\int_{\textcolor{blue}{a}}^{\textcolor{red}{b}} {f(x)\ dx} \)
\( \displaystyle\int_0^{\pi} {\sin{x}\ dx} = -\displaystyle\int_{\pi}^0 {\sin{x}\ dx} \)
İSPATI GÖSTER
Verilen belirli integralin limit tanımını yazalım.
\( \displaystyle\int_b^a {f(x)\ dx} = \lim_{n \to \infty} \displaystyle\sum_{i = 1}^{n}{f(x_i^*) \cdot \Delta x} \)
\( \Delta x \) üst ve alt sınır değerlerinin farkının aralık sayısına bölümüne eşittir.
\( \Delta x = \dfrac{a - b}{n} \)
\( = \lim_{n \to \infty} \displaystyle\sum_{i = 1}^{n}{f(x_i^*) \cdot \dfrac{a - b}{n}} \)
\( a - b = -(b - a) \) yazalım.
\( = \lim_{n \to \infty} \displaystyle\sum_{i = 1}^{n}{f(x_i^*) \cdot \dfrac{-(b - a)}{n}} \)
Toplam sembolü işlem kurallarına göre toplam sembolünün içindeki \( -1 \) çarpanı toplam sembolünün dışına çarpan olarak çıkarılabilir.
\( = \lim_{n \to \infty} -\displaystyle\sum_{i = 1}^{n}{f(x_i^*) \cdot \dfrac{b - a}{n}} \)
Limit işlem kurallarına göre limit tanımlı bir ifadenin sabit bir sayı ile çarpımının limiti, ifadenin limitinin sabit sayı ile çarpımına eşittir.
\( = -\lim_{n \to \infty} \displaystyle\sum_{i = 1}^{n}{f(x_i^*) \cdot \dfrac{b - a}{n}} \)
\( \Delta x = \frac{b - a}{n} \) olduğunda bu limit ifadesi \( f(x) \) fonksiyonunun üst sınır değeri \( b \) ve alt sınır değeri \( a \) olmak üzere \( [a, b] \) aralığındaki belirli integralidir.
\( = -\displaystyle\int_a^b {f(x)\ dx} \)
Aralıkların Birleşimi
Aynı kapalı ve sürekli aralıkta bulunan \( a \), \( b \) ve \( c \) noktaları için, \( [a, c] \) arasındaki integral değeri, \( [a, b] \) ve \( [b, c] \) arasındaki integral değerlerinin toplamına eşittir. Bir diğer deyişle, bir fonksiyonun iki farklı aralıkta \( x \) ekseni ile arasında kalan alanların toplamı, bu aralıkların birleşimi olan aralıkta \( x \) ekseni ile arasında kalan alana eşittir.
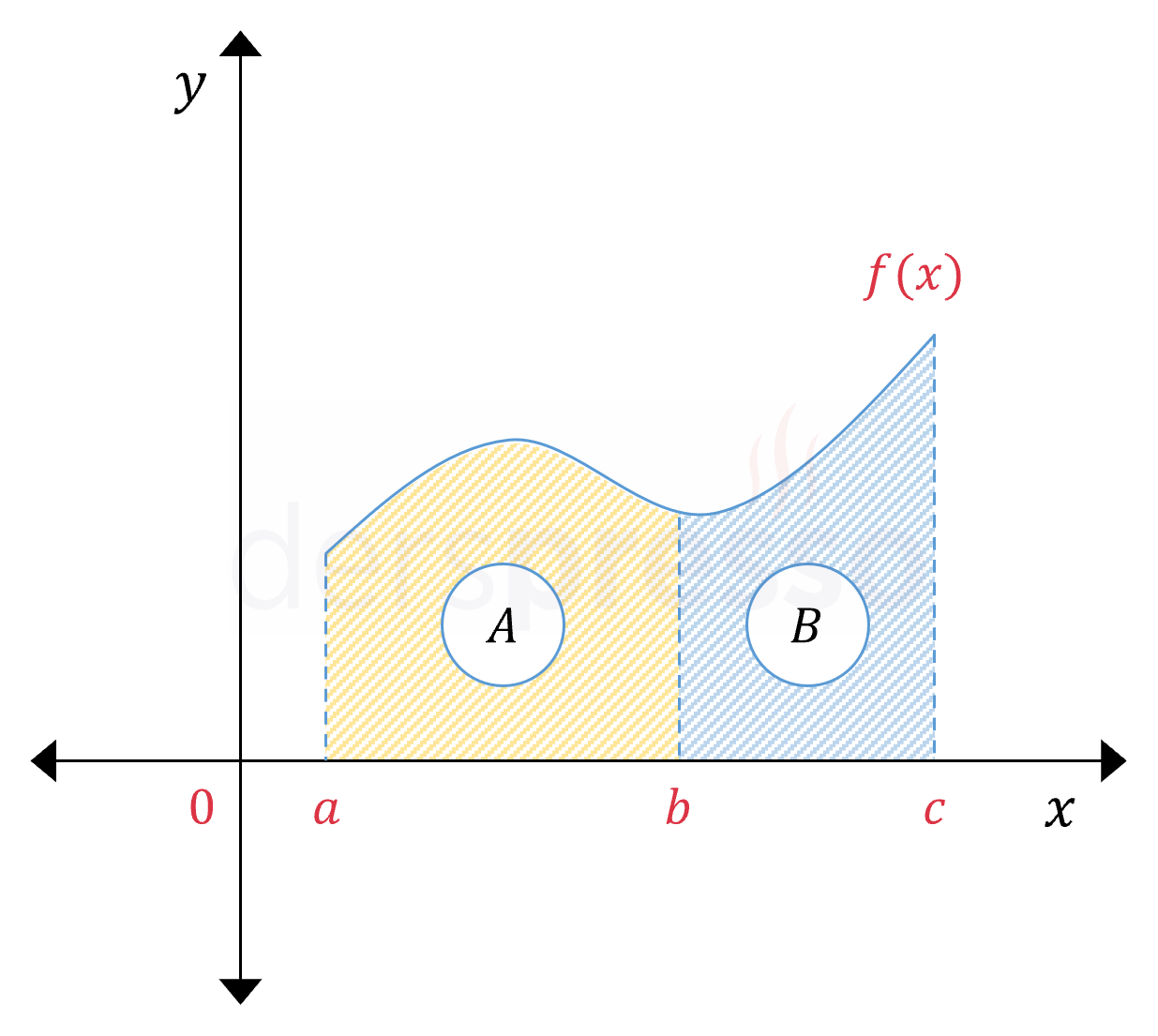
\( \displaystyle\int_a^c {f(x)\ dx} = \displaystyle\int_a^b {f(x)\ dx} + \displaystyle\int_b^c {f(x)\ dx} \)
\( \displaystyle\int_{-4}^4 {x^2\ dx} = \displaystyle\int_{-4}^0 {x^2\ dx} + \displaystyle\int_0^4 {x^2\ dx} \)
İSPATI GÖSTER
Belirli integralin limit tanımındaki \( \Delta x \), aralığın üst ve alt sınırlarının farkının aralığın bölündüğü alt aralık sayısına bölümüne eşittir.
\( \displaystyle\int_b^a {f(x)\ dx} = \lim_{n \to \infty} \displaystyle\sum_{i = 1}^{n}{f(x_i^*) \cdot \Delta x} \)
\( \Delta x = \dfrac{b - a}{n} \)
Verilen belirli integralin limit tanımını \( \Delta x \) ifadesinin açılımı ile yazalım.
\( \displaystyle\int_a^c {f(x)\ dx} = \lim_{n \to \infty} \displaystyle\sum_{i = 1}^{n}{f(x_i^*) \cdot \dfrac{b - a}{n}} + \lim_{n \to \infty} \displaystyle\sum_{i = 1}^{n}{f(x_i^*) \cdot \dfrac{c - b}{n}} \)
Limit işlem kurallarına göre iki limit ifadesinin toplamını ifadelerin toplamının limiti şeklinde yazabiliriz.
\( = \lim_{n \to \infty} [\displaystyle\sum_{i = 1}^{n}{f(x_i^*) \cdot \dfrac{b - a}{n}} + \displaystyle\sum_{i = 1}^{n}{f(x_i^*) \cdot \dfrac{c - b}{n}}] \)
Toplam sembolü işlem kurallarına göre değişkenleri ve sınır değerleri aynı olan iki toplam sembolü arasındaki toplama işlemini tek bir toplam sembolü altında birleştirebiliriz.
\( = \lim_{n \to \infty} \displaystyle\sum_{i = 1}^{n}{(f(x_i^*) \cdot \dfrac{b - a}{n} + f(x_i^*) \cdot \dfrac{c - b}{n})} \)
İfadeyi \( f(x_i^*) \) parantezine alalım.
\( = \lim_{n \to \infty} \displaystyle\sum_{i = 1}^{n}{f(x_i^*) \cdot (\dfrac{b - a}{n} + \dfrac{c - b}{n})} \)
\( = \lim_{n \to \infty} \displaystyle\sum_{i = 1}^{n}{f(x_i^*) \cdot \dfrac{b - a + c - b}{n}} \)
\( = \lim_{n \to \infty} \displaystyle\sum_{i = 1}^{n}{f(x_i^*) \cdot \dfrac{c - a}{n}} \)
Bu limit ifadesi \( f(x) \) fonksiyonunun \( [a, c] \) aralığındaki belirli integralidir.
\( = \displaystyle\int_a^c {f(x)\ dx} \)
Sıfır Genişlik
Bir integralin alt ve üst sınırları aynı ise integral değeri sıfır olur. Bir diğer deyişle, genişliği sıfır olan bir şeklin alanı da sıfırdır.
\( \displaystyle\int_a^a {f(x)\ dx} = 0 \)
\( \displaystyle\int_3^3 {e^x\ dx} = 0 \)
İSPATI GÖSTER
Belirli integralin limit tanımındaki \( \Delta x \), aralığın üst ve alt sınırlarının farkının aralığın bölündüğü alt aralık sayısına bölümüne eşittir.
\( \displaystyle\int_a^b {f(x)\ dx} = \lim_{n \to \infty} \displaystyle\sum_{i = 1}^{n}{f(x_i^*) \cdot \Delta x} \)
\( \Delta x = \dfrac{b - a}{n} \)
Verilen belirli integralin limit tanımını \( \Delta x \) ifadesinin açılımı ile yazalım.
\( \displaystyle\int_a^a {f(x)\ dx} = \lim_{n \to \infty} \displaystyle\sum_{i = 1}^{n}{f(x_i^*) \cdot \dfrac{a - a}{n}} \)
\( = \lim_{n \to \infty} \displaystyle\sum_{i = 1}^{n}{f(x_i^*) \cdot 0} \)
\( = \lim_{n \to \infty} \displaystyle\sum_{i = 1}^{n}{0} \)
\( = \lim_{n \to \infty} 0 = 0 \)
Karşılaştırma
Bir fonksiyon bir \( [a, b] \) aralığında sıfırdan büyükse (ya da sıfıra eşitse) bu aralıktaki belirli integrali (\( x \) ekseni ile arasındaki alan) de sıfırdan büyüktür (ya da sıfıra eşittir).
\( [a, b] \) aralığında \( f(x) \ge 0 \) ise,
\( \displaystyle\int_a^b {f(x)\ dx} \ge 0 \)
İSPATI GÖSTER
Riemann toplam formülünü yazalım.
\( \displaystyle\sum_{i = 1}^{n}{f(x_i^*) \cdot \Delta x} \)
\( \Delta x \) üst ve alt sınır değerlerinin farkının aralık sayısına bölümüne eşittir.
\( \Delta x = \dfrac{b - a}{n} \)
\( [a, b] \) aralığında \( f(x) \ge 0 \) olduğu verildiğine göre tüm alt aralıklarda da \( f(x_i^*) \ge 0 \) olur.
\( a \le b \) olduğu için \( \Delta x \ge 0 \) olur.
Buna göre sıfırdan büyük ya da sıfıra eşit çarpanların toplamı da sıfırdan büyük ya da sıfıra eşit olur.
\( \displaystyle\sum_{i = 1}^{n}{f(x_i^*) \cdot \Delta x} \ge 0 \)
İki tarafın limitini alalım.
\( \lim_{n \to \infty} \displaystyle\sum_{i = 1}^{n}{f(x_i^*) \cdot \Delta x} \ge \lim_{n \to \infty} 0 \)
Sağ taraftaki limit ifadesi sıfıra eşittir.
\( \lim_{n \to \infty} \displaystyle\sum_{i = 1}^{n}{f(x_i^*) \cdot \Delta x} \ge 0 \)
Sol taraftaki limit ifadesi belirli integralin tanımıdır.
\( \displaystyle\int_a^b {f(x)\ dx} \ge 0 \)
Bir \( f \) fonksiyonu bir \( [a, b] \) aralığında diğer bir \( g \) fonksiyonundan büyükse (ya da ona eşitse) bu aralıktaki belirli integrali \( g \) fonksiyonunun belirli integralinden büyüktür (ya da ona eşittir).
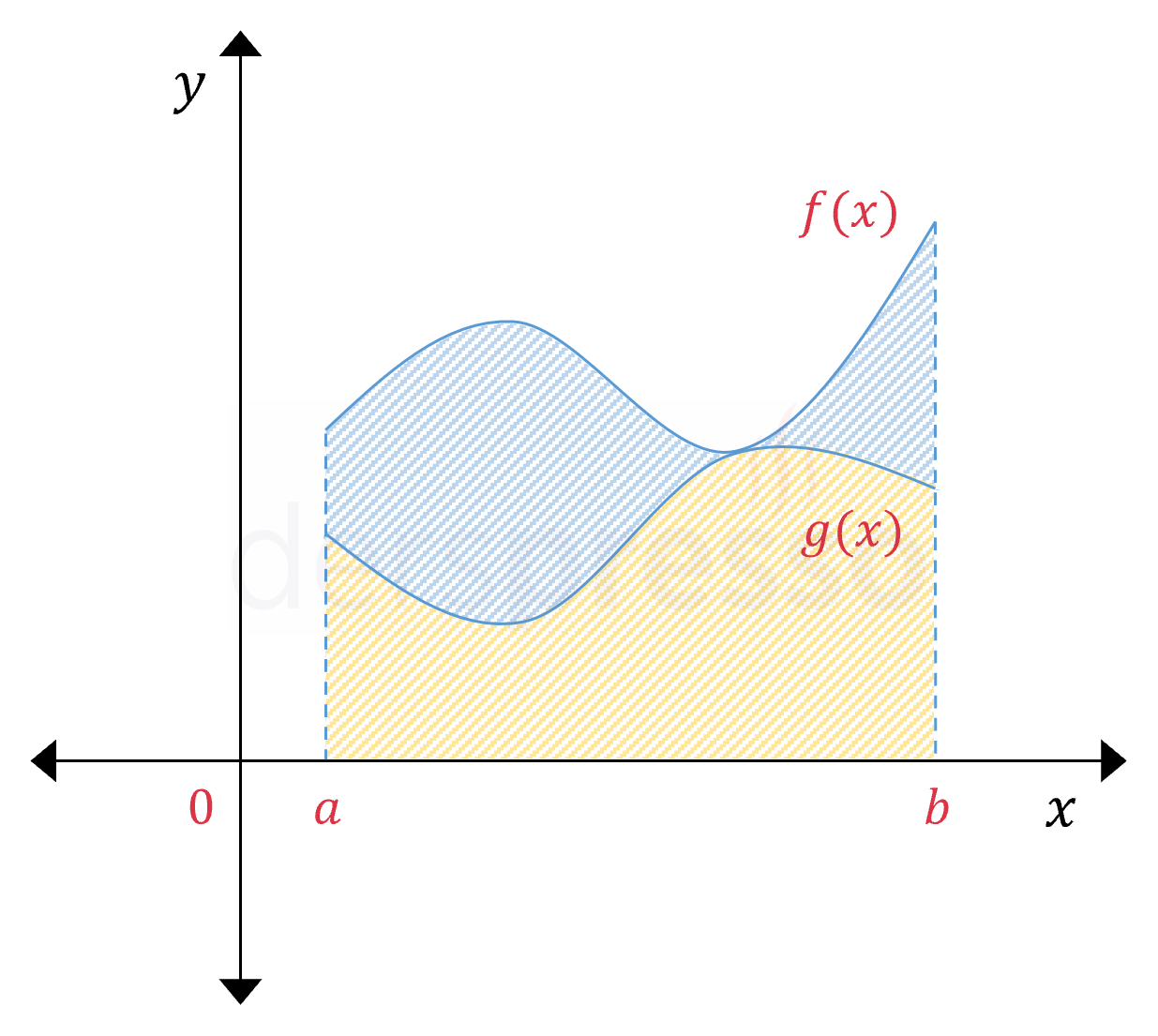
\( [a, b] \) aralığında \( f(x) \ge g(x) \) ise,
\( \displaystyle\int_a^b {f(x)\ dx} \ge \displaystyle\int_a^b {g(x)\ dx} \)
İSPATI GÖSTER
\( [a, b] \) aralığında aşağıdaki ilişki verilmiştir.
\( f(x) \ge g(x) \)
Sağ taraftaki ifadeyi eşitsizliğin sol tarafına alalım.
\( f(x) - g(x) \ge 0 \)
Yukarıda ispatını verdiğimiz birinci karşılaştırma özelliğine göre yukarıdaki ifadeyi aşağıdaki şekilde yazabiliriz.
\( \displaystyle\int_a^b {(f(x) - g(x))\ dx} \ge 0 \)
Yukarıda ispatını verdiğimiz fonksiyonların toplamı/farkı özelliğine göre iki fonksiyonun farkının integrali, integrallerinin farkına eşittir.
\( \displaystyle\int_a^b {f(x)\ dx} - \displaystyle\int_a^b {g(x)\ dx} \ge 0 \)
Sol taraftaki ikinci terimi eşitsizliğin sağ tarafına alalım.
\( \displaystyle\int_a^b {f(x)\ dx} \ge \displaystyle\int_a^b {g(x)\ dx} \)
Bir \( f \) fonksiyonu bir \( [a, b] \) aralığında \( m \) ve \( M \) değerlerinin arasında kalıyorsa bu aralıktaki belirli integrali de yükseklikleri bu iki değer olan iki dikdörtgenin alanları arasında kalır.
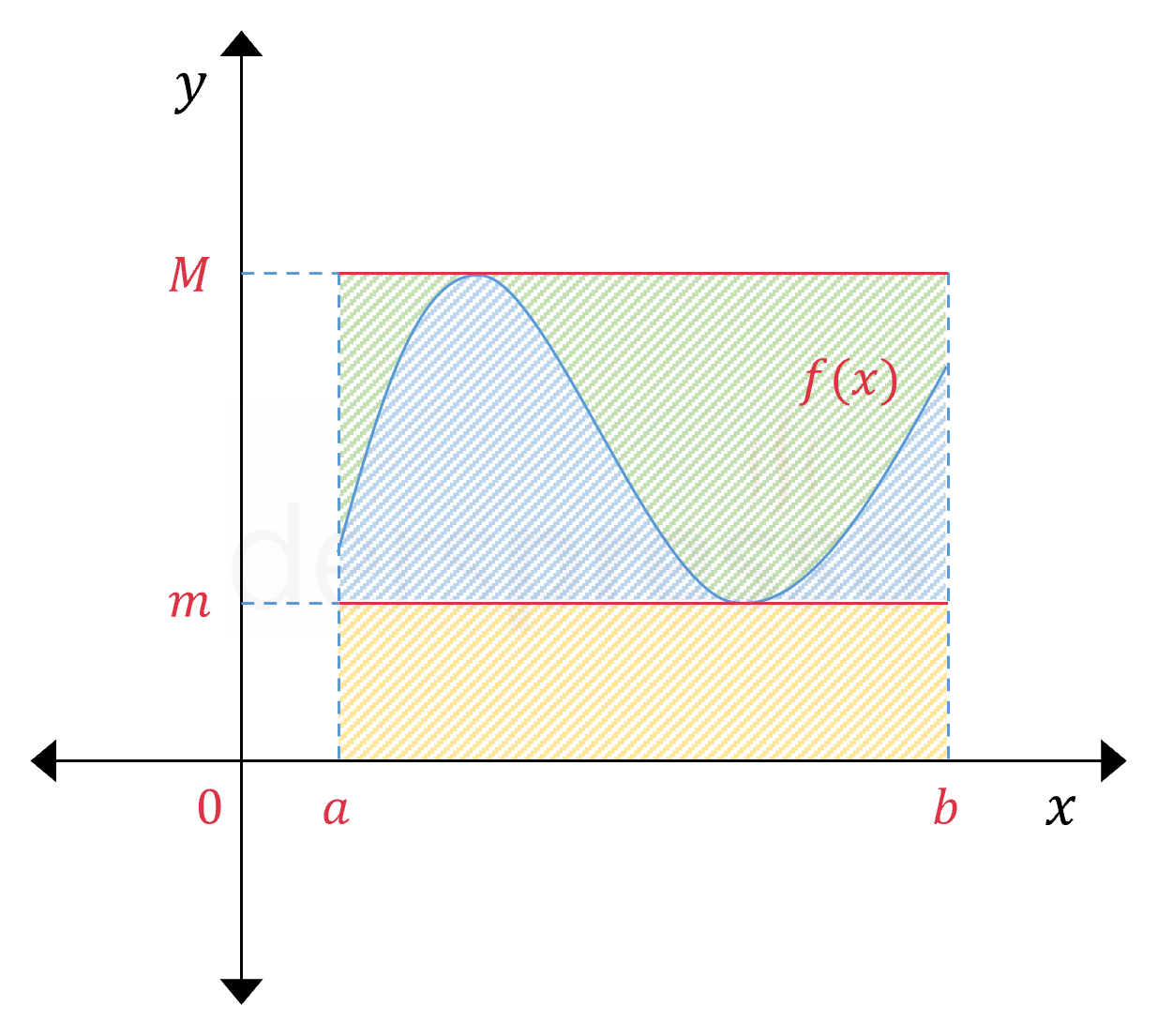
\( [a, b] \) aralığında \( m \le f(x) \le M \) ise,
\( m \cdot (b - a) \le \displaystyle\int_a^b {f(x)\ dx} \le M \cdot (b - a) \)
Dönüşümler
Öteleme
Bir fonksiyonun \( [a, b] \) aralığındaki belirli integral değeri, fonksiyon \( x \) ekseni boyunca \( k \) birim sağa ötelendiğinde \( [a + k, b + k] \) aralığındaki belirli integral değerine, fonksiyon \( k \) birim sola ötelendiğinde ise \( [a - k, b - k] \) aralığındaki belirli integral değerine eşittir.
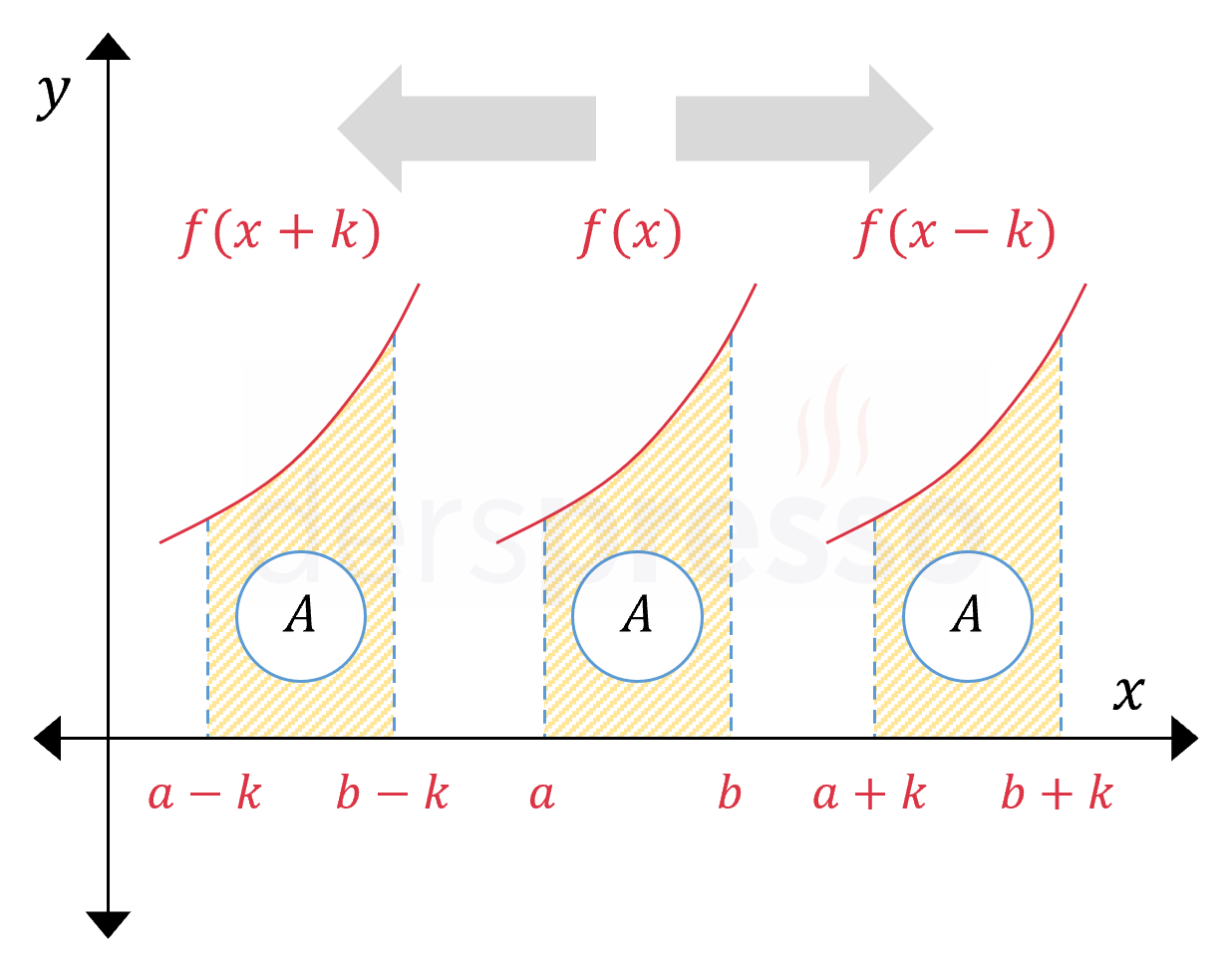
\( k \in \mathbb{R}, \quad k \gt 0 \) olmak üzere,
\( \displaystyle\int_a^b {f(x)\ dx} = \displaystyle\int_{a+k}^{b+k} {f(x - k)\ dx} \)
\( \displaystyle\int_a^b {f(x)\ dx} = \displaystyle\int_{a-k}^{b-k} {f(x + k)\ dx} \)
\( \displaystyle\int_{\frac{\pi}{2}}^{\pi} {\sin{x}\ dx} = \displaystyle\int_{\frac{3\pi}{2}}^{2\pi} {\sin(x - \pi)\ dx} \)
\( \displaystyle\int_7^9 {e^x\ dx} = \displaystyle\int_3^5 {e^{x+4}\ dx} \)
İSPATI GÖSTER
\( \displaystyle\int_{a+k}^{b+k} {f(x - k)\ dx} \)
Yukarıdaki ifadeye değişken değiştirme yöntemini uygulayalım.
\( u = x - k \)
\( du = dx \)
Bu değişkenleri integral ifadesinde yerine koyalım.
\( = \displaystyle\int_{u(a + k)}^{u(b + k)} {f(u)\ du} \)
\( u \) değişkenine göre alacağımız integralin sınır değerlerini bulalım.
\( u(a + k) = (a + k) - k = a \)
\( u(b + k) = (b + k) - k = b \)
\( = \displaystyle\int_a^b {f(u)\ du} \)
\( \displaystyle\int_{a-k}^{b-k} {f(x + k)\ dx} \)
Yukarıdaki ifadeye değişken değiştirme yöntemini uygulayalım.
\( u = x + k \)
\( du = dx \)
Bu değişkenleri integral ifadesinde yerine koyalım.
\( = \displaystyle\int_{u(a - k)}^{u(b - k)} {f(u)\ du} \)
\( u \) değişkenine göre alacağımız integralin sınır değerlerini bulalım.
\( u(a - k) = (a - k) + k = a \)
\( u(b - k) = (b - k) + k = b \)
\( = \displaystyle\int_a^b {f(u)\ du} \)
Yansıma
Bir fonksiyonun \( y \) eksenine göre yansımasını kullanarak aşağıdaki iki eşitliği yazabiliriz.
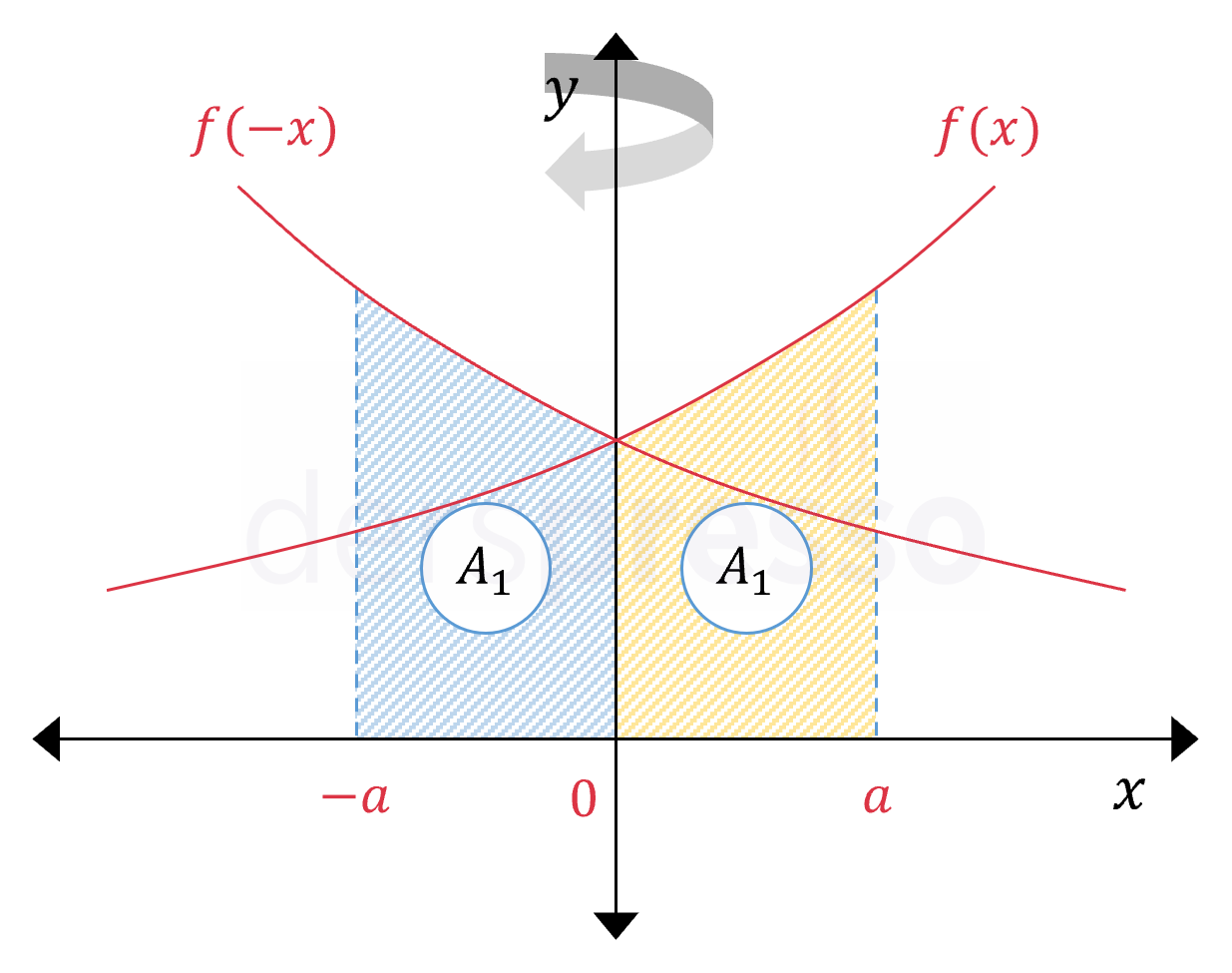
\( \displaystyle\int_0^a {f(x)\ dx} = \displaystyle\int_{-a}^0 {f(-x)\ dx} \)
\( \displaystyle\int_0^a {f(x)\ dx} = \displaystyle\int_0^a {f(a - x)\ dx} \)
\( \displaystyle\int_0^4 {x^3\ dx} = \displaystyle\int_{-4}^0 {(-x)^3\ dx} \)
\( \displaystyle\int_0^{\frac{\pi}{2}} {\cos{x}\ dx} = \displaystyle\int_0^{\frac{\pi}{2}} {\cos(\frac{\pi}{2} - x)\ dx} \)
İSPATI GÖSTER
Birinci eşitlik:
\( \displaystyle\int_{-a}^0 {f(-x)\ dx} \)
Yukarıdaki ifadeye değişken değiştirme yöntemini uygulayalım.
\( u = -x \Longrightarrow x = -u \)
\( du = -dx \Longrightarrow dx = -du \)
Bu değişkenleri integral ifadesinde yerine koyalım.
\( = \displaystyle\int_{u(-a)}^{u(0)} {f(u)\ (-du)} \)
\( = -\displaystyle\int_{u(-a)}^{u(0)} {f(u)\ du} \)
\( u \) değişkenine göre alacağımız integralin sınır değerlerini bulalım.
\( u(-a) = -(-a) = a \)
\( u(0) = -0 = 0 \)
\( = -\displaystyle\int_a^0 {f(u)\ du} \)
Bir integralin alt ve üst sınırları kendi aralarında yer değiştirirse integral değeri işaret değiştirir.
\( = \displaystyle\int_0^a {f(u)\ du} \)
İkinci eşitlik:
Yukarıda eşitliğini gösterdiğimiz belirli integraldeki fonksiyonu yukarıda ispatını verdiğimiz yöntemle \( a \) birim sağa öteleyelim.
\( \displaystyle\int_{-a}^0 {f(-x)\ dx} \)
\( = \displaystyle\int_{-a+a}^{0+a} {f(-(x - a))\ dx} \)
\( = \displaystyle\int_0^a {f(a - x)\ dx} \)
Öteleme kuralını kullanarak yansıma kuralını belirli integralin alt sınırının sıfır olmadığı duruma da uygulayabiliriz.
\( \displaystyle\int_a^b {f(x)\ dx} = \displaystyle\int_a^b {f(a + b - x)\ dx} \)
\( \displaystyle\int_3^5 {2^x\ dx} = \displaystyle\int_3^5 {2^{8-x}\ dx} \)
İSPATI GÖSTER
\( \displaystyle\int_a^b {f(a + b - x)\ dx} \)
Yukarıda ispatını verdiğimiz yöntemle \( a \) birim sola öteleme uygulayalım.
\( = \displaystyle\int_{a-a}^{b-a} {f(a + b - (x + a))\ dx} \)
\( = \displaystyle\int_0^{b-a} {f(b - x)\ dx} \)
Yukarıda ispatını verdiğimiz \( y \) eksenine göre yansıma özelliğini kullanalım.
\( = \displaystyle\int_{-(b-a)}^0 {f(b - (-x))\ dx} \)
\( = \displaystyle\int_{a-b}^0 {f(x + b)\ dx} \)
Yukarıda ispatını verdiğimiz yöntemle \( b \) birim sağa öteleme uygulayalım.
\( = \displaystyle\int_{a-b+b}^{0+b} {f((x - b) + b)\ dx} \)
\( = \displaystyle\int_a^b {f(x)\ dx} \)
Çift ve Tek Fonksiyonlar
Çift Fonksiyonlar
Çift fonksiyonlar \( y \) eksenine göre simetrik oldukları için, bir çift fonksiyonun \( [-a, 0] \) ve \( [0, a] \) aralıklarındaki integralleri birbirine eşittir. Bunun bir sonucu olarak bir çift fonksiyonun \( [-a, a] \) aralığındaki integrali \( [-a, 0] \) ve \( [0, a] \) aralıklarındaki integrallerinin iki katına eşittir.
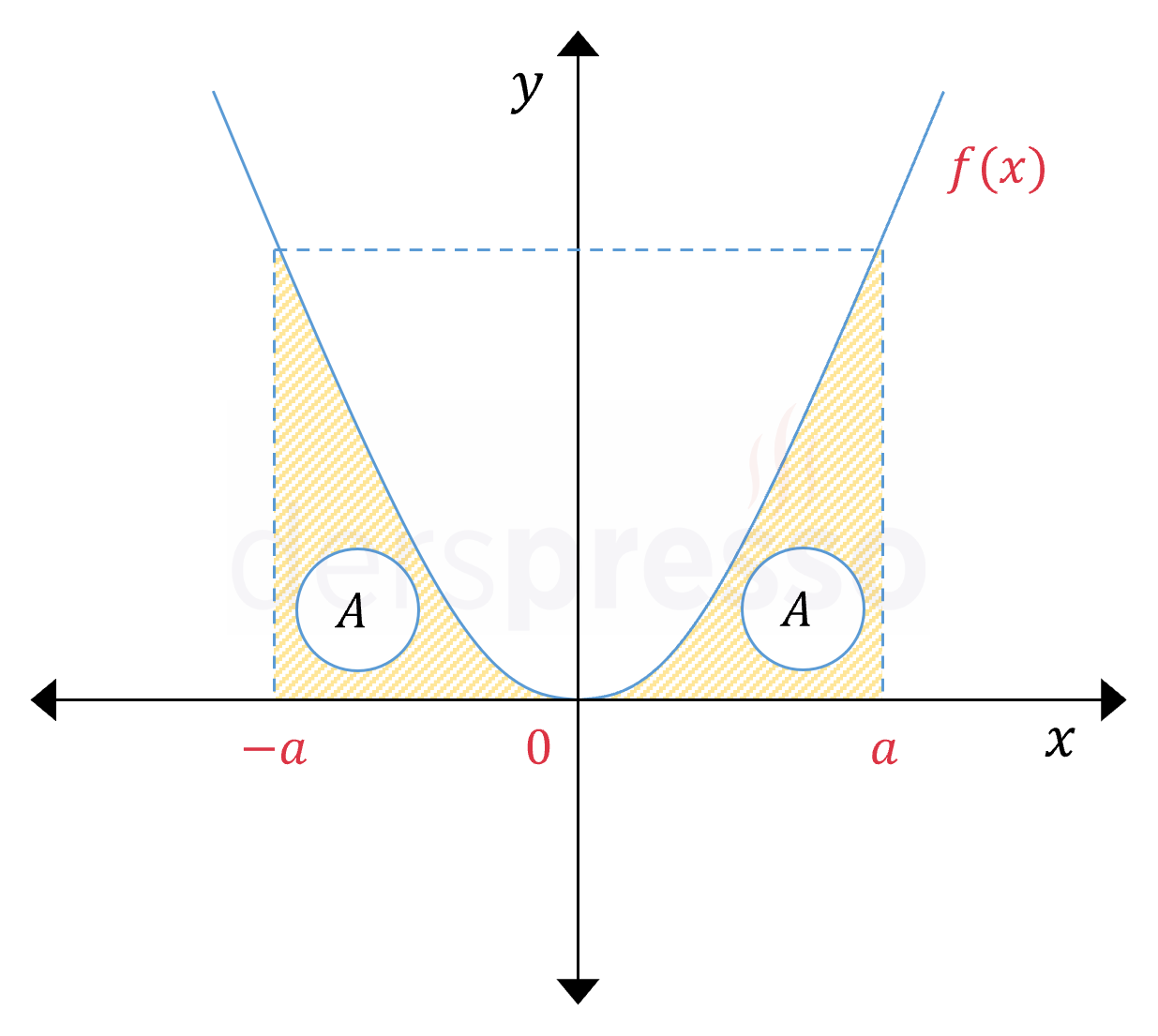
\( f \) çift fonksiyon olmak üzere,
\( \displaystyle\int_{-a}^0 {f(x)\ dx} = \displaystyle\int_0^a {f(x)\ dx} \)
\( \displaystyle\int_{-a}^a {f(x)\ dx} = 2\displaystyle\int_{-a}^0 {f(x)\ dx} = 2\displaystyle\int_0^a {f(x)\ dx} \)
\( \displaystyle\int_{0}^\pi {\cos{x} \cdot x^2\ dx} = A \) ise,
\( \displaystyle\int_{-\pi}^0 {\cos{x} \cdot x^2\ dx} = A \)
\( \displaystyle\int_{-\pi}^\pi {\cos{x} \cdot x^2\ dx} = 2A \)
Tek Fonksiyonlar
Tek fonksiyonlar orijine göre simetrik oldukları için, bir tek fonksiyonun \( [-a, 0] \) ve \( [0, a] \) aralıklarındaki integralleri birbirinin ters işaretlisidir. Bunun bir sonucu olarak bir tek fonksiyonun \( [-a, a] \) aralığındaki integrali sıfıra eşittir.
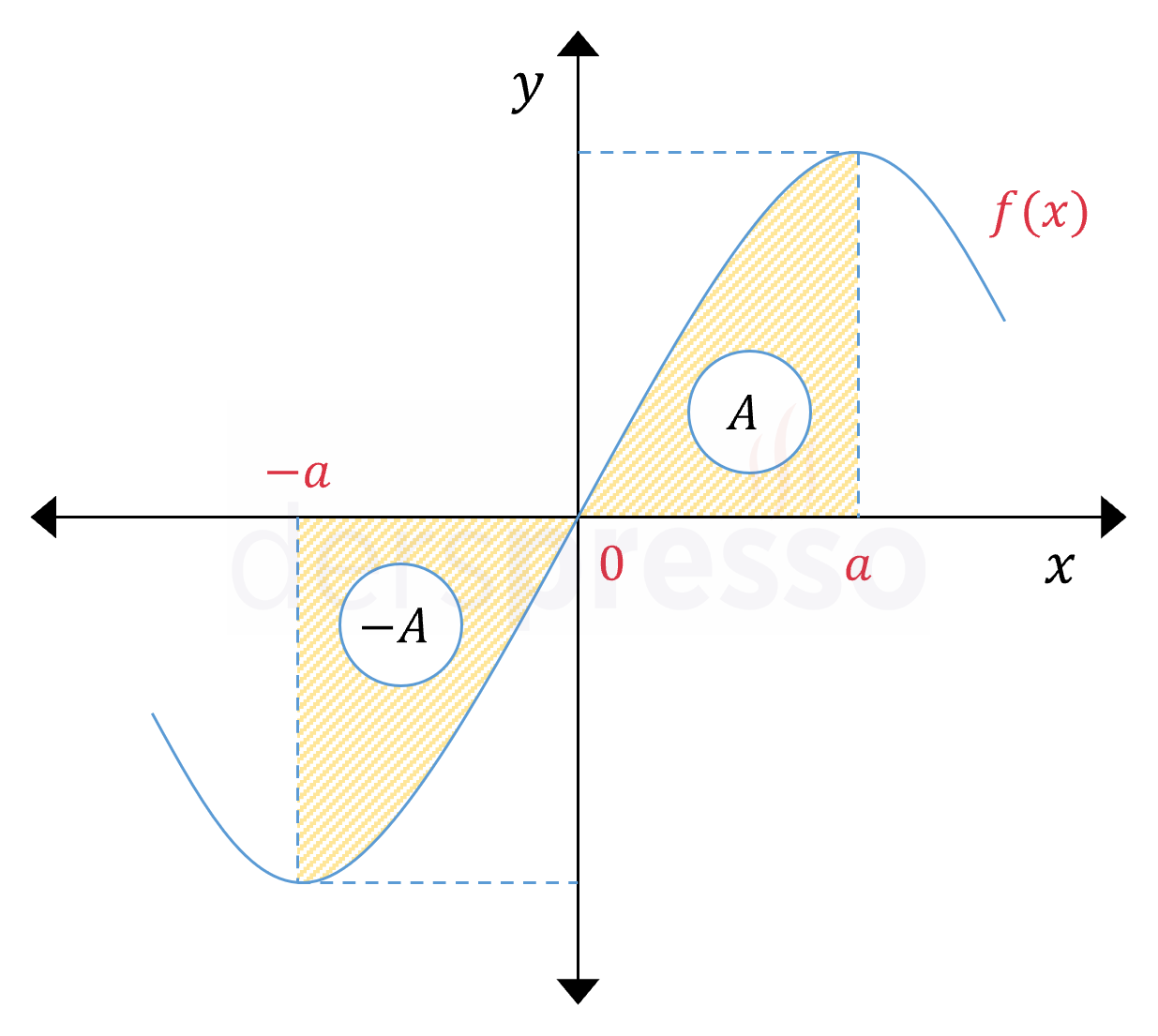
\( f \) tek fonksiyon olmak üzere,
\( \displaystyle\int_{-a}^0 {f(x)\ dx} = -\displaystyle\int_0^a {f(x)\ dx} \)
\( \displaystyle\int_{-a}^a {f(x)\ dx} = 0 \)
\( \displaystyle\int_{-\pi}^\pi {\sin{x} \cdot \abs{x}\ dx} = 0 \)
\( f \) ve \( g \) integrallenebilir fonksiyonlar olmak üzere,
\( \displaystyle\int_1^3 {f(x)\ dx} = 5 \)
\( \displaystyle\int_1^6 {f(x)\ dx} = 9 \)
\( \displaystyle\int_1^6 {g(x)\ dx} = 14 \)
olduğuna göre, aşağıdaki integralleri hesaplayınız.
(a) \( \displaystyle\int_6^1 {g(x)\ dx} \)
(b) \( \displaystyle\int_3^6 {f(x)\ dx} \)
(c) \( \displaystyle\int_1^6 [3f(x) - g(x)] \ dx \)
Çözümü Göster(a) seçeneği:
Bir integralin alt ve üst sınırları kendi aralarında yer değiştirirse integral değeri işaret değiştirir.
\( \displaystyle\int_6^1 {g(x)\ dx} = -\displaystyle\int_1^6 {g(x)\ dx} \)
\( = -14 \)
(b) seçeneği:
Belirli integralin aralıkların birleşimi özelliğini kullanalım.
\( \underbrace{\displaystyle\int_1^6 {f(x)\ dx}}_\text{9} = \underbrace{\displaystyle\int_1^3 {f(x)\ dx}}_\text{5} + \displaystyle\int_3^6 {f(x)\ dx} \)
\( \displaystyle\int_3^6 {f(x)\ dx} = 4 \)
(c) seçeneği:
İki fonksiyonun toplamının/farkının integrali, integrallerinin toplamına/farkına eşittir.
\( \displaystyle\int_1^6 [3f(x) - g(x)]\ dx = \displaystyle\int_1^6 {3f(x)\ dx} - \displaystyle\int_1^6 {g(x)\ dx} \)
Bir fonksiyonun sabit bir değerle çarpımının integrali, fonksiyonun integralinin sabit değerle çarpımına eşittir.
\( = 3\underbrace{\displaystyle\int_1^6 {f(x)\ dx}}_\text{9} - \underbrace{\displaystyle\int_1^6 {g(x)\ dx}}_\text{14} \)
\( = 3 \cdot 9 - 14 = 13 \)
\( \displaystyle\int_0^5 f(x)\ dx = A \) olduğuna göre,
\( \displaystyle\int_{-5}^0 (2f(x + 5) + 3)\ dx \) integralinin sonucu \( A \) cinsinden kaçtır?
Çözümü Göster\( \displaystyle\int_{-5}^0 (2f(x + 5) + 3)\ dx \)
İntegral ifadesine toplama ve sabit çarpma kurallarını uygulayalım.
\( = 2\displaystyle\int_{-5}^0 f(x + 5)\ dx + \displaystyle\int_{-5}^0 3\ dx \)
Birinci integral ifadesini 5 birim sağa öteleyelim.
\( = 2\displaystyle\int_0^5 f(x)\ dx + \displaystyle\int_{-5}^0 3\ dx \)
İfadelerin integralini alalım.
Birinci integral ifadesi \( A \)'ya eşittir.
\( = 2A + (3x)_{-5}^0 \)
\( = 2A + (3(0) - 3(-5)) \)
\( = 2A + 15 \) bulunur.
\( \displaystyle\int_{\ln{2} - \pi}^{\pi - \ln{2}} (x^5 + \sin{x} + x)\ dx \) integralinin sonucu kaçtır?
Çözümü Gösterİntegrali alınan terimlerin tümü birer tek fonksiyondur, dolayısıyla bu terimlerin toplamı da bir tek fonksiyon olur.
Ayrıca integralin sınır değerleri birbirinin ters işaretlisidir.
\( \ln{2} - \pi = -(\pi - \ln{2}) \)
Tek fonksiyonlar orijine göre simetrik oldukları için herhangi bir \( [-a, a] \) aralığındaki belirli integral değerleri sıfır olur.
\( \displaystyle\int_{-(\pi - \ln{2})}^{\pi - \ln{2}} (x^5 + \sin{x} + x)\ dx = 0 \)
\( \displaystyle\int_{-2}^5 f(x)\ dx = 5 \)
\( \displaystyle\int_{1}^5 (2 + f(x))\ dx = 12 \) olduğuna göre,
\( \displaystyle\int_{-2}^1 f(x)\ dx \) kaçtır?
Çözümü GösterAralıkların birleşimi özelliğini kullanalım.
\( \displaystyle\int_{-2}^5 f(x)\ dx = 5 \)
\( \displaystyle\int_{-2}^1 f(x)\ dx + \displaystyle\int_1^5 f(x)\ dx = 5 \)
İntegralin toplama işlem özelliğini kullanalım.
\( \displaystyle\int_1^5 (2 + f(x))\ dx = 12 \)
\( \displaystyle\int_1^5 2\ dx + \displaystyle\int_1^5 f(x)\ dx = 12 \)
\( (2x)|_1^5 + \displaystyle\int_1^5 f(x)\ dx = 12 \)
\( (2 \cdot 5 - 2 \cdot 1) + \displaystyle\int_1^5 f(x)\ dx = 12 \)
\( \displaystyle\int_1^5 f(x)\ dx = 4 \)
Bu değeri yukarıdaki eşitlikte yerine yazalım.
\( \displaystyle\int_{-2}^1 f(x)\ dx + 4 = 5 \)
\( \displaystyle\int_{-2}^1 f(x)\ dx = 1 \) bulunur.
\( \displaystyle\int_{-6}^{-4}{3f(x)}\ dx = 27 \) ve \( \displaystyle\int_{-6}^{2}{f(x)}\ dx = 13 \) olduğuna göre,
\( \displaystyle\int_{-4}^{2}{f(x)}\ dx \) integralinin değeri kaçtır?
Çözümü GösterBelirli integralde aralıkların birleşimi kuralı aşağıdaki gibidir.
\( \displaystyle\int_a^c {f(x)\ dx} = \displaystyle\int_a^b {f(x)\ dx} + \displaystyle\int_b^c {f(x)\ dx} \)
\( \displaystyle\int_{-6}^2{f(x)}\ dx = \displaystyle\int_{-6}^{-4}{f(x)}\ dx + \displaystyle\int_{-4}^2{f(x)}\ dx\ \)
\( \displaystyle\int_{-6}^{-4}{3f(x)}\ dx = 27 \)
\( 3\displaystyle\int_{-6}^{-4}{f(x)}\ dx = 27 \)
\( \displaystyle\int_{-6}^{-4}{f(x)}\ dx = 9 \)
Soruda verilen ve bulduğumuz değerleri yerlerine koyalım.
\( 13 = 9 + \displaystyle\int_{-4}^2{f(x)}\ dx \)
\( \displaystyle\int_{-4}^2{f(x)}\ dx = 13 - 9 \)
\( = 4 \) olarak bulunur.
\( f \) fonksiyonu orijine göre simetrik bir fonksiyondur.
\( \displaystyle\int_{-1}^4 f(x)\ dx = 6 \)
\( \displaystyle\int_{-4}^0 f(x)\ dx = 4 \) olduğuna göre,
\( \displaystyle\int_0^1 f(x)\ dx \) integralinin sonucu kaçtır?
Çözümü Göster\( f \) fonksiyonu orijine göre simetrik olduğuna göre tek fonksiyondur.
Buna göre \( f \) fonksiyonunun belirli integrali ile ilgili aşağıdaki iki kural geçerlidir.
\( \displaystyle\int_{-a}^0 {f(x)\ dx} = -\displaystyle\int_0^a {f(x)\ dx} \)
\( \displaystyle\int_{-a}^a {f(x)\ dx} = 0 \)
\( \displaystyle\int_{-4}^0 f(x)\ dx = 4 \) ise,
\( \displaystyle\int_0^4 f(x)\ dx = -4 \)
Soruda verilen birinci integrali ifadesini aralıkların birleşimi kuralı ile iki aralığın toplamı şeklinde yazalım.
\( \displaystyle\int_{-1}^4 f(x)\ dx = \displaystyle\int_{-1}^1 f(x)\ dx + \displaystyle\int_1^4 f(x)\ dx = 6 \)
\( \displaystyle\int_{-1}^1 f(x)\ dx = 0 \) olduğuna göre,
\( \displaystyle\int_1^4 f(x)\ dx = 6 \)
Aralıkların toplamı özelliğini kullanalım.
\( \displaystyle\int_0^4 f(x)\ dx = \displaystyle\int_0^1 f(x)\ dx + \displaystyle\int_1^4 f(x)\ dx \)
\( -4 = \displaystyle\int_0^1 f(x)\ dx + 6 \)
\( \displaystyle\int_0^1 f(x)\ dx = -10 \) bulunur.
\( f \) tek ve \( g \) çift fonksiyondur.
\( \displaystyle\int_0^5 g(x)\ dx = 12 \) olduğuna göre,
\( \displaystyle\int_{-5}^5 (3f(x) + 4g(x))\ dx \) integralinin sonucu kaçtır?
Çözümü Gösterİntegral toplama ve sabit çarpım kurallarını kullanarak ifadeyi iki integral işleminin toplamı şeklinde yazalım.
\( \displaystyle\int_{-5}^5 (3f(x) + 4g(x))\ dx = 3\displaystyle\int_{-5}^5 f(x)\ dx + 4\displaystyle\int_{-5}^5 g(x)\ dx \)
Tek fonksiyonlar orijine göre simetrik oldukları için herhangi bir \( [-a, a] \) aralığındaki belirli integral değerleri sıfır olur, dolayısıyla ilk ifadenin değeri sıfırdır.
\( g \) çift fonksiyon olduğu için \( [-5, 0] \) aralığındaki belirli integral değeri \( [0, 5] \) aralığındaki değerine eşittir.
\( \displaystyle\int_{-5}^5 g(x)\ dx = 2\displaystyle\int_0^5 g(x)\ dx = 24 \)
Buna göre sorudaki ifadenin değerini bulalım.
\( 3 \cdot 0 + 4 \cdot 24 = 96 \) bulunur.
\( \displaystyle\int_{\frac{\pi}{4}}^{-\frac{\pi}{4}} \sin{x}(\cos{x} + 1)\ dx \) integralinin sonucu kaçtır?
Çözümü Gösterİntegrali alınan ifadeyi düzenleyelim.
\( \displaystyle\int_{\frac{\pi}{4}}^{-\frac{\pi}{4}} (\sin{x}\cos{x} + \sin{x})\ dx \)
\( \sin{x}\cos{x} \) terimi tek ve çift iki fonksiyonun çarpımından oluştuğu için tek fonksiyondur.
\( \sin{x} \) terimi de tek fonksiyondur.
İki tek fonksiyonun toplamından oluşan fonksiyon tek fonksiyon olduğu için integrali alınan ifade tek fonksiyondur.
Tek fonksiyonlar orijine göre simetrik oldukları için herhangi bir \( [-a, a] \) aralığındaki belirli integral değerleri sıfır olur.
İntegral işleminde sınır değerleri birbirinin ters işaretlisi olduğu için ifadenin integral değeri 0 olur.
\( f(x) \) ve \( g'(x) \) tek fonksiyonlardır.
\( f(0) = 0 \) ve \( f(4) = 10 \) olduğuna göre,
\( \displaystyle\int_{-4}^4 (f'(x) - g'(x))\ dx \) integralinin sonucu kaçtır?
Çözümü Göster\( \displaystyle\int_{-4}^4 (f'(x) - g'(x))\ dx = \displaystyle\int_{-4}^4 f'(x)\ dx - \displaystyle\int_{-4}^4 g'(x)\ dx \)
Bir tek fonksiyonun sınır değerleri birbirinin ters işaretlisi olan integralinin değeri 0'a eşittir.
Buna göre \( g'(x) \) tek fonksiyon olduğu için ikinci terim 0'a eşittir.
\( = \displaystyle\int_{-4}^4 f'(x)\ dx - 0 \)
Bir tek fonksiyonun türevi çift fonksiyondur.
Buna göre \( f(x) \) tek fonksiyon olduğu için türevi çift fonksiyondur.
Çift fonksiyonlar \( y \) eksenine göre simetrik oldukları için \( [-a, 0] \) ve \( [0, a] \) aralıklarındaki belirli integral değerleri birbirine eşittir.
\( = 2\displaystyle\int_0^4 f'(x)\ dx \)
İfadenin integralini alalım.
\( = 2(f(x))|_0^4 \)
\( = 2(f(4) - f(0)) = 2(10 - 0) = 20 \) bulunur.
\( \displaystyle\int_{-3}^3 {\ln{\dfrac{5 + x}{5 - x}} \cdot e^{x^{4}}\ dx} \) integralini hesaplayınız.
Çözümü Gösterİntegrali alınan ifadeyi bir fonksiyon olarak tanımlayalım.
\( f(x) = \ln{\dfrac{5 + x}{5 - x}} \cdot e^{x^4} \)
\( = (\ln(5 + x) - \ln(5 - x)) \cdot e^{x^4} \)
Fonksiyonun tek/çift fonksiyon olma durumunu anlamak için \( f(-x) \) fonksiyonunu bulalım.
\( f(-x) = (\ln(5 + (-x)) - \ln(5 - (-x))) \cdot e^{(-x)^4} \)
\( = (\ln(5 - x) - \ln(5 + x)) \cdot e^{x^4} \)
\( = -(\ln(5 + x) - \ln(5 - x)) \cdot e^{x^4} \)
\( = -f(x) \)
\( f(-x) = -f(x) \) olduğu için \( f \) fonksiyonu bir tek fonksiyondur.
Bir tek fonksiyonun \( [-a, a] \) aralığındaki belirli integrali sıfıra eşittir.
\( \displaystyle\int_{-3}^3 {\ln{\dfrac{5 + x}{5 - x}} \cdot e^{x^{4}}\ dx} = 0 \)
\( \displaystyle\int_{-\pi}^\pi {\dfrac{\sin{x}}{1 + x^4}\ dx} \) integralini hesaplayınız.
Çözümü Göster\( \sin{x} \) bir tek fonksiyondur.
\( 1 + x^4 \) bir çift fonksiyondur.
Bir tek fonksiyonun çift fonksiyona bölümü tek fonksiyon olur.
Bir tek fonksiyonun \( [-a, a] \) aralığındaki belirli integrali sıfıra eşittir.
\( \displaystyle\int_{-\pi}^\pi {\dfrac{\sin{x}}{1 + x^4}\ dx} = 0 \)
\( 3\displaystyle\int_3^5 f(x) \ dx + 7\displaystyle\int_5^7 f(x) \ dx = 27 \)
\( \displaystyle\int_1^3 f(x + 2) \ dx = -12 \)
Yukarıda verilenlere göre \( \displaystyle\int_7^3 f(x)\ dx \) değerini bulunuz.
Çözümü GösterBir integral ifadesine aşağıdaki şekilde öteleme uygulayabiliriz.
\( \displaystyle\int_a^b {f(x)\ dx} = \displaystyle\int_{a+k}^{b+k} {f(x - k)\ dx} \)
\( k = 2 \) verelim.
\( \displaystyle\int_1^3 f(x + 2) \ dx = -12 \)
\( \displaystyle\int_{1 + 2}^{3 + 2} f((x - 2) + 2) \ dx = -12 \)
\( \displaystyle\int_3^5 f(x) \ dx = -12 \)
Soruda verilen ilk eşitlikte bu değeri yerine koyalım.
\( 3\displaystyle\int_3^5 f(x) \ dx + 7\displaystyle\int_5^7 f(x) \ dx = 27 \)
\( 3(-12) + 7\displaystyle\int_5^7 f(x) \ dx = 27 \)
\( 7\displaystyle\int_5^7 f(x) \ dx = 63 \)
\( \displaystyle\int_5^7 f(x) \ dx = 9 \)
Değeri sorulan ifadeye sınırların yer değiştirmesi kuralını uygulayalım.
\( \displaystyle\int_7^3 f(x)\ dx = -\displaystyle\int_3^7 f(x)\ dx \)
Aralıkların birleşimi kuralını uygulayalım.
\( = -(\displaystyle\int_3^5 f(x)\ dx + \displaystyle\int_5^7 f(x)\ dx) \)
Yukarıda bulduğumuz değerleri yerine koyalım.
\( = -(-12 + 9) \)
\( = 3 \) bulunur.
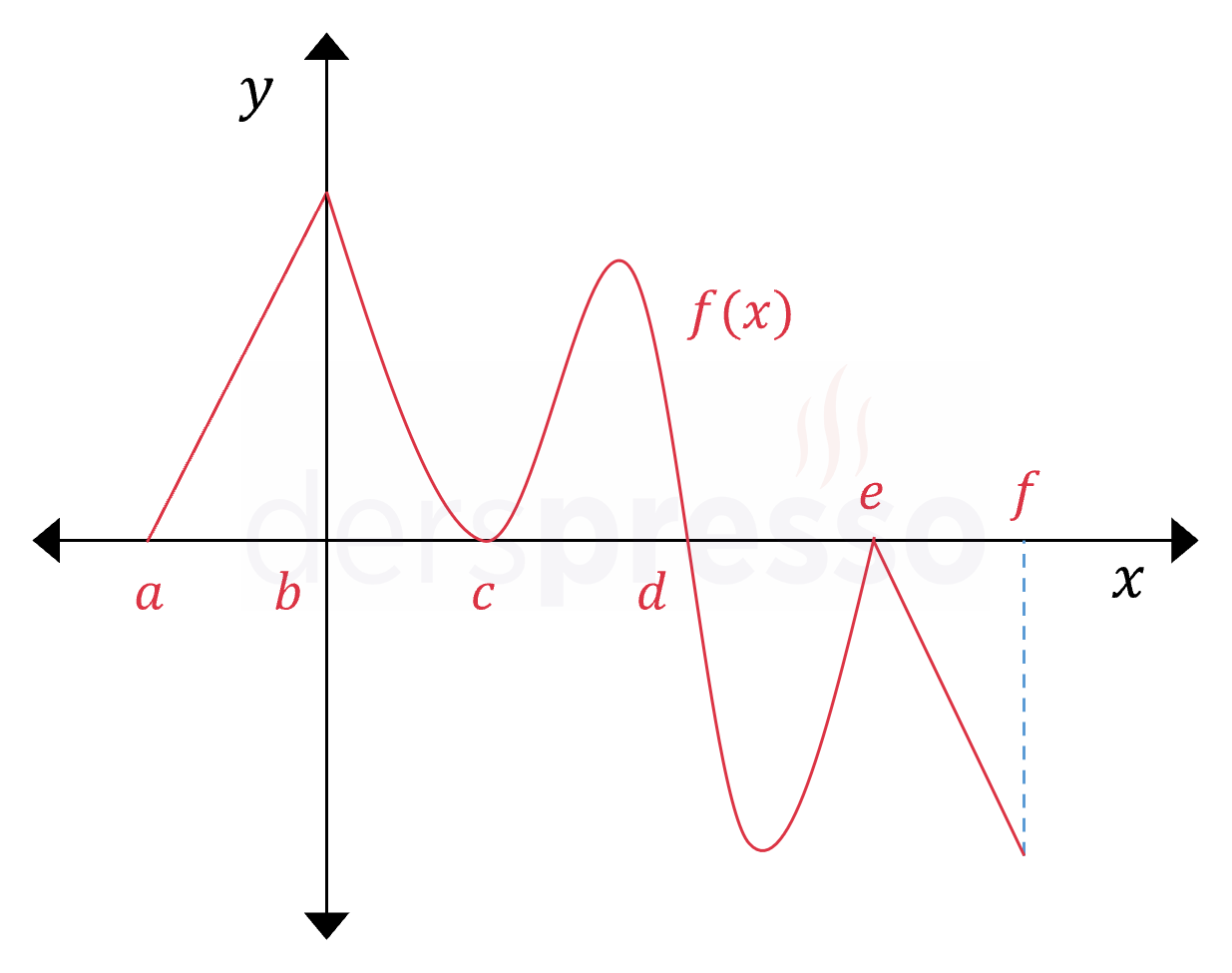
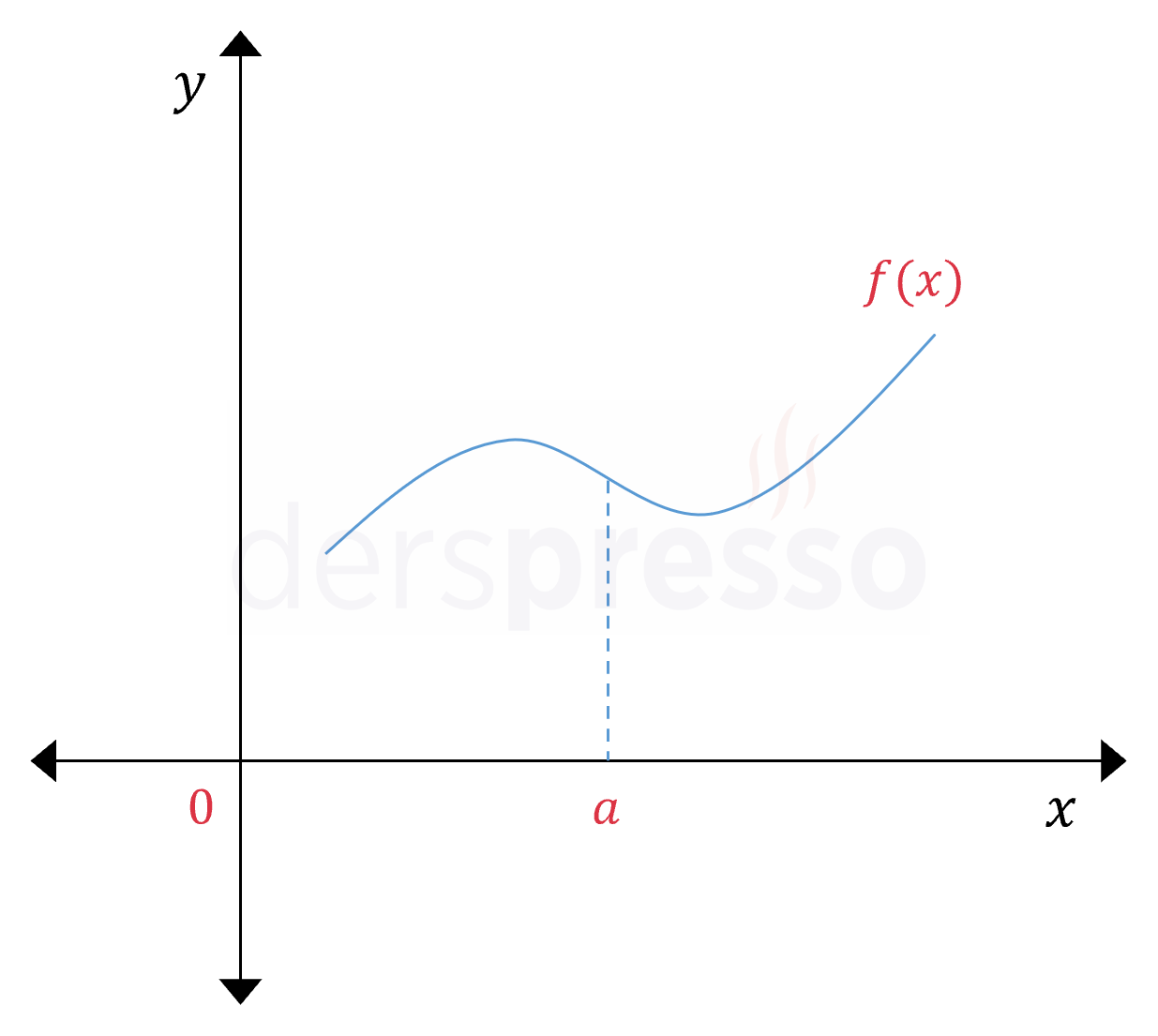
Yukarıda \( y = f(x) \) grafiği verilmiştir.
\( g(x) = \displaystyle\int_a^x f(x)\ dx \) integralinin değerinin en büyük olduğu \( x \) değeri şekildeki harflerden hangisidir?
Çözümü Göster\( g(x) \) fonksiyonu belirli bir \( x \) değeri için \( f \) fonksiyonunun \( [a, x] \) aralığındaki belirli integral değerini vermektedir.
Belirli integral değeri fonksiyon grafiğinin \( x \) ekseninin üstünde kaldığı aralıklarda pozitif, altında kalıdığı aralıklarda negatiftir.
Buna göre \( g(x) \) fonksiyonu \( [a, d] \) aralığında artandır.
\( \displaystyle\int_a^d f(x)\ dx \gt 0 \)
\( g(x) \) fonksiyonu \( [d, f] \) aralığında azalandır.
\( \displaystyle\int_d^f f(x)\ dx \lt 0 \)
\( d \) noktasına kadar alan artan \( g(x) \) fonksiyon değeri \( d \) noktasından sonra azalmaya başladığı için fonksiyon en büyük değerini \( x = d \) noktasında alır.
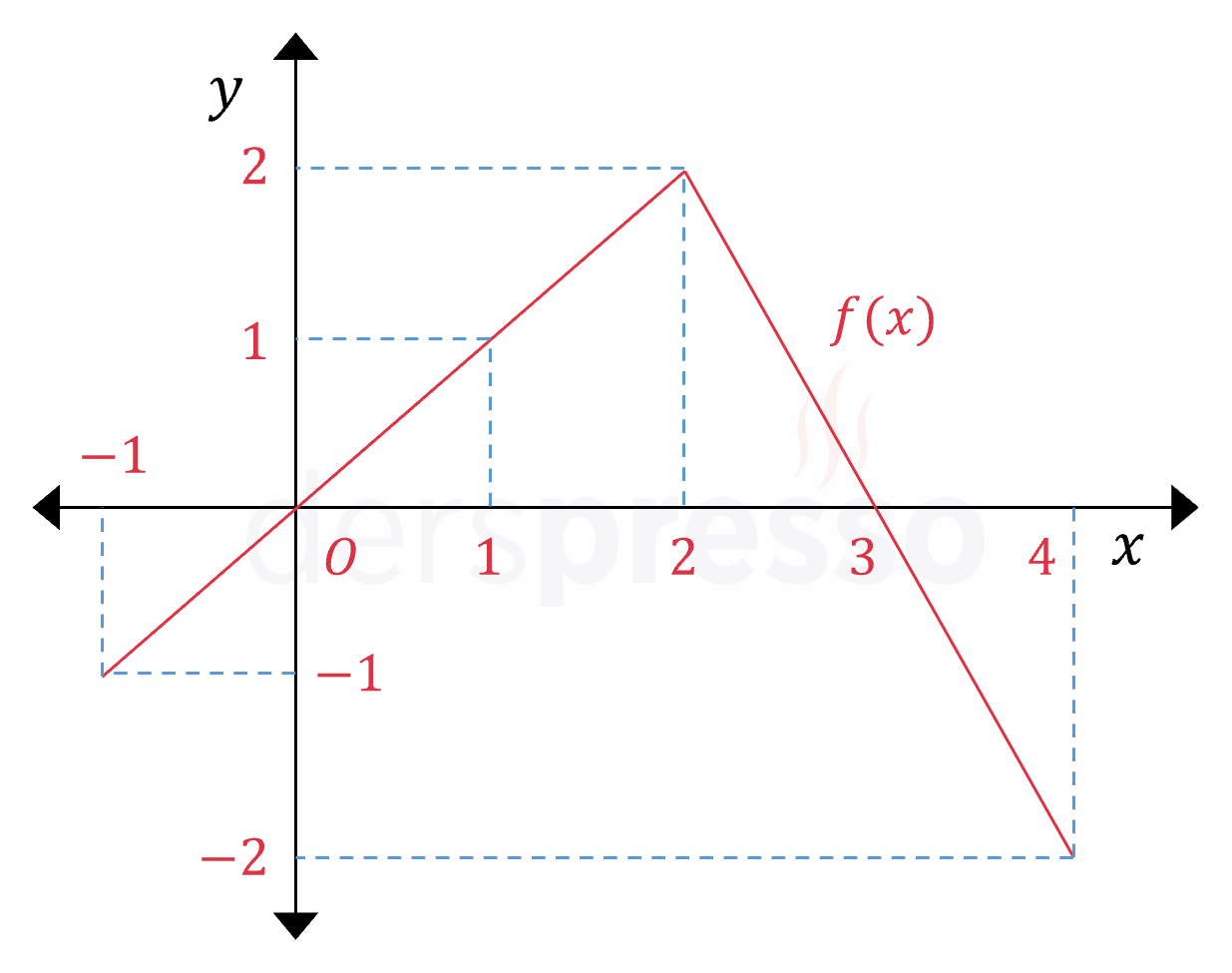
Yukarıda \( f \) fonksiyonunun \( [-1, 4] \) aralığındaki grafiği verilmiştir.
\( g(x) = \displaystyle\int_{-1}^x f(t)\ dt \) olduğuna göre, \( g(x) \)'in en büyük değere sahip olduğu \( x \) değeri kaçtır?
Çözümü GösterBir fonksiyonun belirli bir aralıktaki belirli integrali fonksiyonun grafiğinin \( x \) ekseni ile arasında kalan net alanı verir.
\( f \) fonksiyonunun değeri \( [-1, 0) \) ve \( (3, 4] \) aralıklarında negatif, \( (0, 3) \) aralığında pozitiftir.
Buna göre \( f \) fonksiyonunun bu aralıklardaki belirli integrali de sırasıyla negatif ve pozitif işaretlidir.
\( g \) fonksiyonu belirli bir \( x \) değeri için \( f \) fonksiyonunun \( [-1, x] \) aralığındaki belirli integralini, yani \( x \) ekseni ile arasında kalan net alanını verir.
\( g \) fonksiyonu en büyük değerini \( f \) fonksiyonunun pozitif değer aldığı en son nokta olan \( x = 3 \) noktasında alır.
\( g(x) \) fonksiyonu \( [-1, 3] \) aralığında türevlenebilir bir fonksiyondur.
\( \displaystyle\int_{-1}^3 2g(x)\ dx + \displaystyle\int_{-1}^0 3g(x)\ dx = 26 \)
\( \displaystyle\int_0^3 2g(x)\ dx + \displaystyle\int_3^{-1} g(x)\ dx = 19 \) ise,
\( \displaystyle\int_{-1}^0 g(x)\ dx \) ifadesinin değerini bulunuz.
Çözümü GösterVerilen ifadelere değişkenler atayalım.
\( \displaystyle\int_0^3 g(x)\ dx = A \)
\( \displaystyle\int_{-1}^0 g(x)\ dx = B \)
\( \displaystyle\int_{-1}^3 g(x)\ dx = A + B \)
Bir integralin alt ve üst sınırları kendi aralarında yer değiştirirse integral değeri işaret değiştirir.
\( \displaystyle\int_3^{-1} g(x)\ dx = -(A + B) \)
\( g(x) \) fonksiyonu \( [-1, 3] \) aralığında türevlenebilir olduğu için ardışık aralıklarda belirli integralleri birleştirme özelliğini kullanabiliriz.
Verilen eşitliklerde \( A \) ve \( B \)'yi yerlerine yazalım.
İntegral içindeki sabit çarpanları integral dışına alabiliriz.
\( 2(A + B) + 3B = 2A + 5B = 26 \)
\( 2A - (A + B) = A - B = 19 \)
İkinci denklemi 2 ile genişletip birinci denklemden taraf tarafa çıkaralım.
\( 7B = -12 \)
\( B = -\dfrac{12}{7} \) bulunur.
\( 0 \lt a \lt b \lt c \lt d \) olmak üzere,
Aşağıdaki \( f(x) \) fonksiyonu için bazı aralıklardaki belirli integral değerleri verilmiştir.
\( \displaystyle\int_0^d f(x)\ dx = 2 \)
\( \displaystyle\int_a^c f(x)\ dx = 1 \)
\( \displaystyle\int_a^d f(x)\ dx = -7 \)
\( \displaystyle\int_b^d f(x)\ dx = -1 \)
Buna göre \( (0, d) \) aralığında \( f(x) \) fonksiyonunun \( x \) ekseni ile arasında kalan toplam alan nedir?
Çözümü GösterBelirli integralin aralıkların birleşimi kuralını kullanarak her aralıktaki belirli integral değerini bulalım.
\( (a, d) \) aralığını iki aralığa bölelim.
\( \displaystyle\int_a^d f(x)\ dx = \displaystyle\int_a^c f(x)\ dx + \displaystyle\int_c^d f(x)\ dx \)
\( -7 = 1 + \displaystyle\int_c^d f(x)\ dx \)
\( \displaystyle\int_c^d f(x)\ dx = -8 \)
Buna göre fonksiyonun \( (c, d) \) aralığındaki belirli integral değeri -8'dir.
\( (b, d) \) aralığını iki aralığa bölelim.
\( \displaystyle\int_b^d f(x)\ dx = \displaystyle\int_b^c f(x)\ dx + \displaystyle\int_c^d f(x)\ dx \)
\( -1 = \displaystyle\int_b^c f(x)\ dx + (-8) \)
\( \displaystyle\int_b^c f(x)\ dx = 7 \)
Buna göre fonksiyonun \( (b, c) \) aralığındaki belirli integral değeri 7'dir.
\( (a, c) \) aralığını iki aralığa bölelim.
\( \displaystyle\int_a^c f(x)\ dx = \displaystyle\int_a^b f(x)\ dx + \displaystyle\int_b^c f(x)\ dx \)
\( 1 = \displaystyle\int_a^b f(x)\ dx + 7 \)
\( \displaystyle\int_a^b f(x)\ dx = -6 \)
Buna göre fonksiyonun \( (a, b) \) aralığındaki belirli integral değeri -6'dır.
\( (0, d) \) aralığını iki aralığa bölelim.
\( \displaystyle\int_0^d f(x)\ dx = \displaystyle\int_0^a f(x)\ dx + \displaystyle\int_a^d f(x)\ dx \)
\( 2 = \displaystyle\int_0^a f(x)\ dx + (-7) \)
\( \displaystyle\int_0^a f(x)\ dx = 9 \)
Buna göre fonksiyonun \( (0, a) \) aralığındaki belirli integral değeri 9'dur.
Özetle fonksiyonun \( (0, a), (a, b), (b, c), (c, d) \) aralıklarındaki belirli integral değerleri sırasıyla 9, -6, 7 ve -8 olur.
Fonksiyonun \( (0, d) \) aralığında \( x \) ekseni ile arasında kalan alan bu belirli integral değerlerinin mutlak değerlerinin toplamına eşittir.
\( A = 9 + 6 + 7 + 8 = 30 \) bulunur.
\( f(x) \) sürekli ve çift bir fonksiyon olmak üzere,
\( \displaystyle\int_{-5}^{5}{f(x)}\ dx = 36 \)
\( \displaystyle\int_{-1}^{2}{f(x)}\ dx = 12 \)
\( \displaystyle\int_{1}^{2}{f(x)}\ dx = 5 \) eşitlikleri veriliyor.
Buna göre \( \displaystyle\int_{2}^{5}{f(x)}\ dx \) integrali kaça eşittir?
Çözümü GösterÇift fonksiyonlar \( y \) eksenine göre simetrik olduğu için \( y \) eksenine göre simetrik olan aralıklardaki belirli integral değerleri birbirine eşittir.
\( \displaystyle\int_{-a}^{0}{f(x)}\ dx = \displaystyle\int_{0}^{a}{f(x)}\ dx = A \)
\( \displaystyle\int_{-a}^{a}{f(x)}\ dx = 2A \)
Bu bilgiden yararlanarak \( \displaystyle\int_{-5}^{5}{f(x)}\ dx \) integralini parçalayalım.
\( \displaystyle\int_{-5}^{5}{f(x)}\ dx = \displaystyle\int_{-5}^{0}{f(x)}\ dx + \displaystyle\int_{0}^{5}{f(x)}\ dx \)
\( = 2\displaystyle\int_{0}^{5}{f(x)}\ dx = 2\displaystyle\int_{-5}^{0}{f(x)}\ dx \)
\( 36 = 2\displaystyle\int_{0}^{5}{f(x)}\ dx \)
\( \displaystyle\int_{0}^{5}{f(x)}\ dx = 18 \)
Belirli integralde aralıkların birleşimi kuralı aşağıdaki gibidir.
\( \displaystyle\int_a^c {f(x)\ dx} = \displaystyle\int_a^b {f(x)\ dx} + \displaystyle\int_b^c {f(x)\ dx} \)
Yukarıdaki formülü \( \displaystyle\int_{-1}^{2}{f(x)}\ dx \) fonksiyonuna uygulayalım.
\( \displaystyle\int_{-1}^{2}{f(x)}\ dx = \displaystyle\int_{-1}^{1}{f(x)}\ dx + \displaystyle\int_{1}^{2}{f(x)}\ dx \)
\( 12 = \displaystyle\int_{-1}^{1}{f(x)}\ dx + 5 \)
\( \displaystyle\int_{-1}^{1}{f(x)}\ dx = 7 \)
\( f(x) \) fonksiyonunun çift olma özelliğini tekrar kullanalım.
\( \displaystyle\int_{-1}^{1}{f(x)}\ dx = 2\displaystyle\int_{0}^{1}{f(x)}\ dx \)
\( \displaystyle\int_{0}^{1}{f(x)}\ dx = \dfrac{7}{2} \)
Soruda istenen integrali bulmak için \( \displaystyle\int_{0}^{5}{f(x)}\ dx \) integralini aralıkların birleşim kuralı ile 3 parçaya ayıralım.
\( \displaystyle\int_{0}^{5}{f(x)}\ dx = \displaystyle\int_{0}^{1}{f(x)}\ dx + \displaystyle\int_{1}^{2}{f(x)}\ dx + \displaystyle\int_{2}^{5}{f(x)}\ dx \)
\( 18 = \dfrac{7}{2} + 5 + \displaystyle\int_{2}^{5}{f(x)}\ dx \)
\( \displaystyle\int_{2}^{5}{f(x)}\ dx = \dfrac{19}{2} \) olarak bulunur.
\( f \) sürekli bir çift fonksiyon olmak üzere,
\( \displaystyle\int_{-3}^{-2} f(x)\ dx = 7 \)
\( \displaystyle\int_4^5 f(x - 1)\ dx = -4 \) eşitlikleri veriliyor.
Buna göre \( \displaystyle\int_2^4 f(6 - x)\ dx \) integrali kaça eşittir?
Çözümü Göster\( f \) çift fonksiyon olduğu için aşağıdaki eşitlik yazılabilir.
\( \displaystyle\int_{-3}^{-2} f(x)\ dx = \displaystyle\int_2^3 f(x)\ dx = 7 \)
Bir integral ifadesine aşağıdaki şekilde öteleme dönüşümü uygulayabiliriz.
\( \displaystyle\int_a^b f(x)\ dx = \displaystyle\int_{a + k}^{b + k} f(x - k)\ dx \)
Bu dönüşümü verilen ikinci integral ifadesine uygulayalım.
\( \displaystyle\int_4^5 f(x - 1)\ dx = \displaystyle\int_{4 - 1}^{5 - 1} f((x + 1) - 1)\ dx \)
\( = \displaystyle\int_3^4 f(x)\ dx = -4 \)
Bir integral ifadesine aşağıdaki şekilde yansıma dönüşümü uygulayabiliriz.
\( \displaystyle\int_a^b f(x)\ dx = \displaystyle\int_a^b f(a + b - x)\ dx \)
\( \displaystyle\int_2^4 f(6 - x)\ dx = \displaystyle\int_2^4 f(2 + 4 - x)\ dx \)
\( = \displaystyle\int_2^4 f(x)\ dx \)
Buna göre soruda \( \displaystyle\int_2^4 f(x)\ dx \) ifadesinin değeri sorulmuş.
\( \displaystyle\int_2^4 f(6 - x)\ dx = \displaystyle\int_2^4 f(x)\ dx \)
İfadeye aralıkların birleşimi kuralını uygulayalım.
\( = \displaystyle\int_2^3 f(x)\ dx + \displaystyle\int_3^4 f(x)\ dx \)
İfadelerin yukarıda bulduğumuz değerlerini yazalım.
\( = \displaystyle\int_{-3}^{-2} f(x)\ dx + \displaystyle\int_4^5 f(x - 1)\ dx \)
\( = 7 + (-4) = 3 \) bulunur.
\( a \lt b \) olmak üzere,
\( \displaystyle\int_a^b (x^2 - 7x)\ dx \) ifadesinin en küçük değerini alması için \( a \) ve \( b \) kaç olmalıdır?
Çözümü Göster\( f(x) = x^2 - 7x = x(x - 7) \)
\( f(x) \) fonksiyonunun grafiği aşağıda verilmiştir.

\( f(x) \) fonksiyonu \( (-\infty, 0) \) ve \( (7, \infty) \) aralıklarında pozitif, \( (0, 7) \) aralığında negatif değer alır.
Fonksiyonun değerinin pozitif olduğu aralıklarda belirli integrali de pozitif, negatif olduğu aralıklarda belirli integrali de negatiftir.
Verilen belirli integralin en küçük değerini alması için, \( a \) ve \( b \) değerleri grafiğin \( x \) ekseninin altında kaldığı en geniş aralığı kapsayacak şekilde seçilmelidir.
Buna göre \( a \) ve \( b \) değerleri şekildeki turuncu bölgeyi kapsayacak şekilde \( a = 0 \), \( b = 7 \) olmalıdır.