Trigonometrik Fonksiyonların İntegrali
Bu bölümde trigonometrik ve ters trigonometrik fonksiyonların integralini inceleyeceğiz. Önceki bölümde belirttiğimiz gibi, belirli bir integral alma kuralının ispatı olarak integral işleminin sonucunun türevinin orijinal fonksiyonu verip vermediği kontrol edilebilir.
Trigonometrik Fonksiyonlar
İntegrali altı trigonometrik fonksiyon olan ifadeler aşağıdaki gibidir.
\( \displaystyle\int {\cos{x}\ dx} = \sin{x} + C \)
\( \displaystyle\int {\sin{x}\ dx} = -\cos{x} + C \)
\( \displaystyle\int {\sec^2{x}\ dx} = \tan{x} + C \)
\( \displaystyle\int {\csc^2{x}\ dx} = -\cot{x} + C \)
\( \displaystyle\int {\sec{x}\tan{x}\ dx} = \sec{x} + C \)
\( \displaystyle\int {\csc{x}\cot{x}\ dx} = -\csc{x} + C \)
Diğer dört trigonometrik fonksiyonun integralleri aşağıdaki gibidir.
\( \displaystyle\int {\tan{x}\ dx} = \ln{\abs{\sec{x}}} + C \)
İSPATI GÖSTER
\( \displaystyle\int {\tan{x}\ dx} = \displaystyle\int {\dfrac{\sin{x}}{\cos{x}}\ dx} \)
Değişken değiştirme uygulayalım.
\( u = \cos{x} \)
Her iki tarafın diferansiyelini alalım.
\( du = -\sin{x}\ dx \)
\( \sin{x}\ dx = -du \)
İntegral ifadesinde bu değişkenleri yerine koyalım.
\( = \displaystyle\int {-\dfrac{du}{u}} = -\displaystyle\int {\dfrac{du}{u}} \)
İntegral işleminin sonucu doğal logaritma fonksiyonudur.
\( = -\ln{\abs{u}} + C \)
\( u \) değişkeni yerine karşılığını yazalım.
\( = -\ln{\abs{\cos{x}}} + C \)
Negatif işaretini logaritma içine üs olarak alalım.
\( = \ln{\abs{(\cos{x})^{-1}}} + C \)
\( = \ln{\abs{\sec{x}}} + C \)
\( \displaystyle\int {\cot{x}\ dx} = \ln{\abs{\sin{x}}} + C \)
İSPATI GÖSTER
\( \displaystyle\int {\cot{x}\ dx} = \displaystyle\int {\dfrac{\cos{x}}{\sin{x}}\ dx} \)
Değişken değiştirme uygulayalım.
\( u = \sin{x} \)
Her iki tarafın diferansiyelini alalım.
\( du = \cos{x}\ dx \)
İntegral ifadesinde bu değişkenleri yerine koyalım.
\( = \displaystyle\int {\dfrac{du}{u}} \)
İntegral işleminin sonucu doğal logaritma fonksiyonudur.
\( = \ln{\abs{u}} + C \)
\( u \) değişkeni yerine karşılığını yazalım.
\( = \ln{\abs{\sin{x}}} + C \)
\( \displaystyle\int {\sec{x}\ dx} = \ln{\abs{\sec{x} + \tan{x}}} + C \)
İSPATI GÖSTER
\( \displaystyle\int {\sec{x}\ dx} \)
Payı ve paydayı \( \sec{x} + \tan{x} \) ile çarpalım.
\( = \displaystyle\int {\dfrac{\sec{x}(\sec{x} + \tan{x})}{\sec{x} + \tan{x}}\ dx} \)
\( = \displaystyle\int {\dfrac{\sec^2{x} + \sec{x}\tan{x}}{\sec{x} + \tan{x}}\ dx} \)
Değişken değiştirme uygulayalım.
\( u = \sec{x} + \tan{x} \)
Her iki tarafın diferansiyelini alalım.
\( du = \sec{x}\tan{x}\ dx + \sec^2{x}\ dx \)
\( = (\sec^2{x} + \sec{x}\tan{x})\ dx \)
Bu ifade paydaki ifadeye eşittir.
İntegral ifadesinde bu değişkenleri yerine koyalım.
\( = \displaystyle\int {\dfrac{du}{u}} \)
İntegral işleminin sonucu doğal logaritma fonksiyonudur.
\( = \ln{\abs{u}} + C \)
\( u \) değişkeni yerine karşılığını yazalım.
\( = \ln{\abs{\sec{x} + \tan{x}}} + C \)
\( \displaystyle\int {\csc{x}\ dx} = -\ln{\abs{\csc{x} + \cot{x}}} + C \)
İSPATI GÖSTER
\( \displaystyle\int {\csc{x}\ dx} \)
Payı ve paydayı \( \csc{x} + \cot{x} \) ile çarpalım.
\( = \displaystyle\int {\dfrac{\csc{x}(\csc{x} + \cot{x})}{\csc{x} + \cot{x}}\ dx} \)
\( = \displaystyle\int {\dfrac{\csc^2{x} + \csc{x}\cot{x}}{\csc{x} + \cot{x}}\ dx} \)
Değişken değiştirme uygulayalım.
\( u = \csc{x} + \cot{x} \)
Her iki tarafın diferansiyelini alalım.
\( du = -\csc{x}\cot{x}\ dx - \csc^2{x}\ dx \)
\( = -(\csc^2{x} + \csc{x}\cot{x})\ dx \)
\( (\csc^2{x} + \csc{x}\cot{x})\ dx = -du \)
Bu ifade paydaki ifadeye eşittir.
İntegral ifadesinde bu değişkenleri yerine koyalım.
\( = \displaystyle\int {\dfrac{-du}{u}} = -\displaystyle\int {\dfrac{du}{u}} \)
İntegral işleminin sonucu doğal logaritma fonksiyonudur.
\( = -\ln{\abs{u}} + C \)
\( u \) değişkeni yerine karşılığını yazalım.
\( = -\ln{\abs{\csc{x} + \cot{x}}} + C \)
Ters Trigonometrik Fonksiyonlar
İntegrali ters sinüs fonksiyonu olan ifadeler aşağıda verilmiştir.
\( \displaystyle\int {\dfrac{dx}{\sqrt{1 - x^2}}} = \arcsin{x} + C \)
\( \displaystyle\int {\dfrac{dx}{\sqrt{a^2 - x^2}}} = \arcsin{\frac{x}{a}} + C \)
\( \displaystyle\int {\dfrac{dx}{\sqrt{9 - x^2}}} = \arcsin{\frac{x}{3}} + C \)
\( \displaystyle\int {\dfrac{dx}{\sqrt{9 - 4x^2}}} = \dfrac{1}{2}\arcsin{\frac{2x}{3}} + C \)
İSPATI GÖSTER
Ters sinüs fonksiyonunun türevini hatırlayalım.
\( f(x) = \arcsin{x} \) ise,
\( f'(x) = \dfrac{1}{\sqrt{1 - x^2}} \)
\( y = \arcsin{\frac{x}{a}} \) olarak tanımlayalım.
İki tarafın türevini alalım.
\( y' = (\arcsin{\frac{x}{a}})' \)
Eşitliğin sağ tarafına zincir kuralını uygulayalım.
\( = \dfrac{1}{\sqrt{1 - (\frac{x}{a})^2}} \cdot (\dfrac{x}{a})' \)
\( = \dfrac{1}{\sqrt{1 - \frac{x^2}{a^2}}} \cdot \dfrac{1}{a} \)
\( = \dfrac{1}{\sqrt{\frac{a^2 - x^2}{a^2}}} \cdot \dfrac{1}{a} \)
\( = \dfrac{1}{\frac{1}{a}\sqrt{a^2 - x^2}} \cdot \dfrac{1}{a} \)
\( \frac{1}{a} \) ifadeleri sadeleşir.
Buna göre \( y' \) aşağıdaki gibi olur.
\( y' = \dfrac{1}{\sqrt{a^2 - x^2}} \)
İki tarafın integralini alalım.
\( \displaystyle\int {\dfrac{dx}{\sqrt{a^2 - x^2}}} = \displaystyle\int {y'\ dx} \)
\( = \arcsin{\frac{x}{a}} + C \)
İntegrali ters kosinüs fonksiyonu olan ifadeler aşağıda verilmiştir.
\( \displaystyle\int {-\dfrac{dx}{\sqrt{1 - x^2}}} = \arccos{x} + C \)
\( \displaystyle\int {-\dfrac{dx}{\sqrt{a^2 - x^2}}} = \arccos{\frac{x}{a}} + C \)
\( \displaystyle\int {-\dfrac{dx}{\sqrt{16 - x^2}}} = \arccos{\frac{x}{4}} + C \)
\( \displaystyle\int {-\dfrac{dx}{\sqrt{16 - 25x^2}}} = \dfrac{1}{5}\arccos{\frac{5x}{4}} + C \)
İSPATI GÖSTER
Ters kosinüs fonksiyonunun türevini hatırlayalım.
\( f(x) = \arccos{x} \) ise,
\( f'(x) = -\dfrac{1}{\sqrt{1 - x^2}} \)
\( y = \arccos{\frac{x}{a}} \) olarak tanımlayalım.
İki tarafın türevini alalım.
\( y' = (\arccos{\frac{x}{a}})' \)
Eşitliğin sağ tarafına zincir kuralını uygulayalım.
\( = -\dfrac{1}{\sqrt{1 - (\frac{x}{a})^2}} \cdot (\dfrac{x}{a})' \)
\( = -\dfrac{1}{\sqrt{1 - \frac{x^2}{a^2}}} \cdot \dfrac{1}{a} \)
\( = -\dfrac{1}{\sqrt{\frac{a^2 - x^2}{a^2}}} \cdot \dfrac{1}{a} \)
\( = -\dfrac{1}{\frac{1}{a}\sqrt{a^2 - x^2}} \cdot \dfrac{1}{a} \)
\( \frac{1}{a} \) ifadeleri sadeleşir.
Buna göre \( y' \) aşağıdaki gibi olur.
\( y' = -\dfrac{1}{\sqrt{a^2 - x^2}} \)
İki tarafın integralini alalım.
\( \displaystyle\int {-\dfrac{dx}{\sqrt{a^2 - x^2}}} = \displaystyle\int {y'\ dx} \)
\( = \arccos{\frac{x}{a}} + C \)
İntegrali ters tanjant fonksiyonu olan ifadeler aşağıda verilmiştir.
\( \displaystyle\int {\dfrac{dx}{1 + x^2}} = \arctan{x} + C \)
\( \displaystyle\int {\dfrac{dx}{a^2 + x^2}} = \dfrac{1}{a}\arctan{\frac{x}{a}} + C \)
\( \displaystyle\int {\dfrac{dx}{16 + x^2}} = \dfrac{1}{4}\arctan{\frac{x}{4}} + C \)
\( \displaystyle\int {\dfrac{dx}{16 + 9x^2}} = \dfrac{1}{12}\arctan{\frac{3x}{4}} + C \)
İSPATI GÖSTER
Ters tanjant fonksiyonunun türevini hatırlayalım.
\( f(x) = \arctan{x} \) ise,
\( f'(x) = \dfrac{1}{1 + x^2} \)
\( y = \arctan{\frac{x}{a}} \) olarak tanımlayalım.
İki tarafın türevini alalım.
\( y' = (\arctan{\frac{x}{a}})' \)
Eşitliğin sağ tarafına zincir kuralını uygulayalım.
\( = \dfrac{1}{1 + (\frac{x}{a})^2} \cdot (\dfrac{x}{a})' \)
\( = \dfrac{1}{1 + \frac{x^2}{a^2}} \cdot \dfrac{1}{a} \)
\( = \dfrac{1}{\frac{a^2 + x^2}{a^2}} \cdot \dfrac{1}{a} \)
\( = \dfrac{a^2}{a^2 + x^2} \cdot \dfrac{1}{a} \)
\( a \) ifadeleri sadeleşir.
Buna göre \( y' \) aşağıdaki gibi olur.
\( y' = \dfrac{a}{a^2 + x^2} \)
\( \dfrac{y'}{a} = \dfrac{1}{a^2 + x^2} \)
İki tarafın integralini alalım.
\( \displaystyle\int {\dfrac{1}{a^2 + x^2}} = \displaystyle\int {y'\ dx} \)
\( = \arctan{\frac{x}{a}} + C \)
İntegrali ters kotanjant fonksiyonu olan ifadeler aşağıda verilmiştir.
\( \displaystyle\int {-\dfrac{dx}{1 + x^2}} = \arccot{x} + C \)
\( \displaystyle\int {-\dfrac{dx}{a^2 + x^2}} = \dfrac{1}{a}\arccot{\frac{x}{a}} + C \)
\( \displaystyle\int {-\dfrac{dx}{9 + x^2}} = \dfrac{1}{3}\arccot{\frac{x}{3}} + C \)
\( \displaystyle\int {-\dfrac{dx}{9 + 4x^2}} = \dfrac{1}{6}\arccot{\frac{2x}{3}} + C \)
İntegrali ters sekant fonksiyonu olan ifadeler aşağıda verilmiştir.
\( \displaystyle\int {\dfrac{dx}{x\sqrt{x^2 - 1}}} = \arcsec{x} + C \)
\( \displaystyle\int {\dfrac{dx}{x\sqrt{x^2 - a^2}}} = \dfrac{1}{a}\arcsec{\frac{x}{a}} + C \)
\( \displaystyle\int {\dfrac{dx}{x\sqrt{x^2 - 25}}} = \dfrac{1}{5}\arcsec{\frac{x}{5}} + C \)
\( \displaystyle\int {\dfrac{dx}{x\sqrt{9x^2 - 25}}} = \dfrac{1}{5}\arcsec{\frac{3x}{5}} + C \)
İntegrali ters kosekant fonksiyonu olan ifadeler aşağıda verilmiştir.
\( \displaystyle\int {-\dfrac{dx}{x\sqrt{x^2 - 1}}} = \arccsc{x} + C \)
\( \displaystyle\int {-\dfrac{dx}{x\sqrt{x^2 - a^2}}} = \dfrac{1}{a}\arccsc{\frac{x}{a}} + C \)
\( \displaystyle\int {-\dfrac{dx}{x\sqrt{x^2 - 16}}} = \dfrac{1}{4}\arccsc{\frac{x}{4}} + C \)
\( \displaystyle\int {-\dfrac{dx}{x\sqrt{9x^2 - 16}}} = \dfrac{1}{4}\arccsc{\frac{3x}{4}} + C \)
Aşağıdaki integrallerin sonuçlarını bulunuz.
(a) \( \displaystyle\int {5\cos(7x)\ dx} \)
(b) \( \displaystyle\int {4\sin(10x)\ dx} \)
(c) \( \displaystyle\int {15\sec^2(5x - 4)\ dx} \)
Çözümü Göster(a) seçeneği:
\( \displaystyle\int {5\cos(7x)\ dx} \)
İfadenin integralini alalım.
\( = \dfrac{5}{7}\sin(7x) + C \)
(b) seçeneği:
\( \displaystyle\int {4\sin(10x)\ dx} \)
İfadenin integralini alalım
\( = -\dfrac{4}{10}\cos(10x) + C \)
\( = -\dfrac{2}{5}\cos(10x) + C \)
(c) seçeneği:
\( \displaystyle\int {15\sec^2(5x - 4)\ dx} \)
İfadenin integralini alalım.
\( = \dfrac{15}{5}\tan(5x - 4) + C \)
\( = 3\tan(5x - 4) + C \)
Aşağıdaki integrallerin sonuçlarını bulunuz.
(a) \( \displaystyle\int \left( \sin(7x) - \dfrac{1}{5}\cos{\frac{13x}{5}} \right)\ dx \)
(b) \( \displaystyle\int \left( 5\cos(2x) + 6\sin{\frac{3x}{2}} \right)\ dx \)
(c) \( \displaystyle\int \left( \dfrac{5}{6}\cos{\dfrac{2x}{3}} - \dfrac{6}{7}\sin{\dfrac{3x}{4}} \right)\ dx \)
Çözümü Göster(a) seçeneği:
\( \displaystyle\int \left( \sin(7x) - \dfrac{1}{5}\cos{\frac{13x}{5}} \right)\ dx \)
Terimlerin ayrı ayrı integralini alalım.
\( = \dfrac{-\cos(7x)}{7} - \dfrac{1}{5} \cdot \dfrac{\sin{\frac{13x}{5}}}{\frac{13}{5}} + C \)
\( = -\dfrac{1}{7}\cos(7x) - \dfrac{1}{13}\sin{\dfrac{13x}{5}} + C \)
(b) seçeneği:
\( \displaystyle\int \left( 5\cos(2x) + 6\sin{\frac{3x}{2}} \right)\ dx \)
Terimlerin ayrı ayrı integralini alalım.
\( = 5 \cdot \dfrac{\sin(2x)}{2} + 6 \cdot \dfrac{-\cos{\frac{3x}{2}}}{\frac{3}{2}} + C \)
\( = \dfrac{5}{2}\sin(2x) - 4\cos{\dfrac{3x}{2}} + C \)
(c) seçeneği:
\( \displaystyle\int \left( \dfrac{5}{6}\cos{\dfrac{2x}{3}} - \dfrac{6}{7}\sin{\dfrac{3x}{4}} \right)\ dx \)
Terimlerin ayrı ayrı integralini alalım.
\( = \dfrac{5}{6} \cdot \dfrac{\sin{\frac{2x}{3}}}{\frac{2}{3}} - \dfrac{6}{7} \cdot \dfrac{-\cos{\frac{3x}{4}}}{\frac{3}{4}} + C \)
\( = \dfrac{5}{4}\sin{\dfrac{2x}{3}} + \dfrac{8}{7}\cos{\dfrac{3x}{4}} + C \)
\( \displaystyle\int (5 + 5\tan^2{x})\ dx \) integralinin sonucu nedir?
Çözümü GösterVerilen ifadeyi 5 parantezine alalım.
\( 5\displaystyle\int (1 + \tan^2{x})\ dx \)
\( 1 + \tan^2{x} = \sec^2{x} \) özdeşliğini kullanalım.
\( = 5\displaystyle\int {\sec^2{x}\ dx} \)
Elde ettiğimiz ifadenin integralini alalım.
\( = 5\tan{x} + C \)
\( \displaystyle\int 6\sin{\frac{x}{2}}\cos{\frac{x}{2}}\ dx \) integralinin sonucu nedir?
Çözümü GösterSinüs iki kat açı formülünü kullanalım.
\( \sin{x} = 2\sin{\dfrac{x}{2}}\cos{\dfrac{x}{2}} \)
\( \displaystyle\int 6\sin{\frac{x}{2}}\cos{\frac{x}{2}}\ dx = \displaystyle\int 3\sin{x}\ dx \)
İfadenin integralini alalım.
\( = -3\cos{x} + C \)
\( \displaystyle\int_0^{\frac{\pi}{4}} {\cos(2x + \frac{\pi}{2})\ dx} \) integralinin sonucu nedir?
Çözümü GösterAşağıdaki şekilde değişken değiştirme uygulayalım.
\( u = 2x + \dfrac{\pi}{2} \)
\( du = 2\ dx \)
\( \Longrightarrow \dfrac{du}{2} = dx \)
\( u \) değişkeni için integralin sınır değerlerini bulalım.
\( u(0) = 2(0) + \dfrac{\pi}{2} = \dfrac{\pi}{2} \)
\( u(\dfrac{\pi}{4}) = 2 \cdot \dfrac{\pi}{4} + \dfrac{\pi}{2} = \pi \)
\( x \) değişkenlerinin \( u \) karşılıklarını yazalım.
\( \displaystyle\int_0^{\frac{\pi}{4}} {\cos(2x + \frac{\pi}{2})\ dx} = \displaystyle\int_{\frac{\pi}{2}}^{\pi} {\cos{u} \cdot\ \dfrac{du}{2}} \)
\( = \dfrac{1}{2}\displaystyle\int_{\frac{\pi}{2}}^{\pi} {\cos{u}\ du} \)
İfadenin integralini alalım.
\( = \dfrac{1}{2}(\sin{u})|_{\frac{\pi}{2}}^{\pi} \)
\( = \dfrac{1}{2}(\sin{\pi} - \sin{\frac{\pi}{2}}) \)
\( = \dfrac{1}{2}(0 - 1) \)
\( = -\dfrac{1}{2} \) bulunur.
\( \displaystyle\int{(4\cos{x} - 1)^2\ dx} \) integralinin sonucu nedir?
Çözümü GösterParantez karesi ifadesinin açılımını yazalım.
\( \displaystyle\int{(4\cos{x} - 1)^2\ dx} = \displaystyle\int (16\cos^2{x} - 8\cos{x} + 1)\ dx \)
Birinci terimde kosinüs iki kat açı formülünü kullanalım.
\( \cos^2{x} = \dfrac{\cos(2x) + 1}{2} \)
\( = \displaystyle\int (16 \cdot \dfrac{\cos(2x) + 1}{2} - 8\cos{x} + 1)\ dx \)
\( = \displaystyle\int (8\cos(2x) + 8 - 8\cos{x} + 1)\ dx \)
\( = \displaystyle\int (8\cos(2x) - 8\cos{x} + 9)\ dx \)
Terimlerin ayrı ayrı integralini alalım.
\( = 4\sin(2x) - 8\sin{x} + 9x + C \)
\( \displaystyle\int {\dfrac{3 + 4\cos^4{x}}{\cos^2{x}}\ dx} \) integralinin sonucu nedir?
Çözümü Gösterİfadeyi iki kesrin toplamı şeklinde yazalım.
\( \displaystyle\int \left( \dfrac{3}{\cos^2{x}} + \dfrac{4\cos^4{x}}{\cos^2{x}} \right)\ dx \)
\( = \displaystyle\int \left( \dfrac{3}{\cos^2{x}} + 4\cos^2{x} \right)\ dx \)
Birinci ifadeyi sekant cinsinden yazalım.
İkinci ifadede kosinüs iki kat açı formülünü kullanalım.
\( \cos^2{x} = \dfrac{\cos(2x) + 1}{2} \)
\( = \displaystyle\int \left( 3\sec^2{x} + 4 \cdot \dfrac{\cos(2x) + 1}{2} \right)\ dx \)
\( = \displaystyle\int (3\sec^2{x} + 2\cos(2x) + 2)\ dx \)
Terimlerin ayrı ayrı integralini alalım.
\( = 3\tan{x} + 2 \cdot \dfrac{1}{2}\sin(2x) + 2x + C \)
\( = 3\tan{x} + \sin(2x) + 2x + C \)
\( \displaystyle\int {14\sin^5{x}\sin(2x)\ dx} \) integralinin sonucu nedir?
Çözümü GösterSinüs iki kat açı formülünü kullanalım.
\( \sin(2x) = 2\sin{x}\cos{x} \)
\( \displaystyle\int {14\sin^5{x}(2\sin{x}\cos{x})\ dx} \)
\( = 28\displaystyle\int {\sin^6{x}\cos{x}\ dx} \)
Aşağıdaki şekilde değişken değiştirelim.
\( u = \sin{x} \)
\( du = \cos{x}\ dx \)
Son ifadede bu değişkenleri yerine koyalım.
\( = 28\displaystyle\int {u^6\ du} \)
Elde ettiğimiz ifadenin integralini alalım.
\( = 28 \cdot \dfrac{u^7}{7} + C \)
\( = 4u^7 + C \)
İfadede \( u \) değişkeni yerine \( x \) cinsinden karşılığını yazdığımızda verilen ifadenin integralini buluruz.
\( = 4\sin^7{x} + C \)
\( \displaystyle\int {\tan^2{x}\ dx} \) integralinin sonucu nedir?
Çözümü Göster1. yöntem:
Tanjant fonksiyonunu sinüs ve kosinüs cinsinden yazalım.
\( \displaystyle\int {\left( \dfrac{\sin{x}}{\cos{x}} \right)^2\ dx} \)
\( = \displaystyle\int {\dfrac{\sin^2{x}}{\cos^2{x}}\ dx} \)
Paydaki ifadede Pisagor özdeşliğini kullanalım.
\( = \displaystyle\int {\dfrac{1 - \cos^2{x}}{\cos^2{x}}\ dx} \)
\( = \displaystyle\int {\left( \dfrac{1}{\cos^2{x}} - \dfrac{\cos^2{x}}{\cos^2{x}} \right)\ dx} \)
\( = \displaystyle\int {(\sec^2{x} - 1)\ dx} \)
\( = \displaystyle\int {\sec^2{x}\ dx} - \displaystyle\int {1\ dx} \)
Terimlerin ayrı ayrı integralini alalım.
\( = \tan{x} - x + C \)
2. yöntem:
İfadeye 1 ekleyip çıkaralım.
\( \displaystyle\int {(\tan^2{x} + 1 - 1)\ dx} \)
\( \tan^2{x} + 1 = \sec^2{x} \) özdeşliğini kullanalım.
\( = \displaystyle\int {(\sec^2{x} - 1)\ dx} \)
\( = \displaystyle\int {\sec^2{x}\ dx} - \displaystyle\int {1\ dx} \)
Terimlerin ayrı ayrı integralini alalım.
\( = \tan{x} - x + C \)
\( \displaystyle\int {\sqrt[5]{\sin^2{x}\cos^5{x}}\ dx} \) integralinin sonucu nedir?
Çözümü Gösterİfadeyi düzenleyelim.
\( \displaystyle\int {\sqrt[5]{\sin^2{x}\cos^5{x}}\ dx} = \displaystyle\int {\sqrt[5]{\sin^2{x}}\cos{x}\ dx} \)
\( = \displaystyle\int {(\sin{x})^{\frac{2}{5}}\cos{x}\ dx} \)
Aşağıdaki şekilde değişken değiştirelim.
\( u = \sin{x} \)
\( du = \cos{x}\ dx \)
Son ifadede bu değişkenleri yerine koyalım.
\( = \displaystyle\int {u^{\frac{2}{5}}\ du} \)
Elde ettiğimiz ifadenin integralini alalım.
\( = \dfrac{u^{\frac{7}{5}}}{\frac{7}{5}} + C \)
\( = \dfrac{5\sqrt[5]{u^7}}{7} + C \)
İfadede \( u \) değişkeni yerine \( x \) cinsinden karşılığını yazdığımızda verilen ifadenin integralini buluruz.
\( = \dfrac{5\sqrt[5]{\sin^7{x}}}{7} + C \)
\( \displaystyle\int {\dfrac{10\tan^4{x}}{\cos^2{x}}\ dx} \) integralinin sonucu nedir?
Çözümü Gösterİfadeyi düzenleyelim.
\( \displaystyle\int {\dfrac{10\tan^4{x}}{\cos^2{x}}\ dx} = 10\displaystyle\int {\tan^4{x}\sec^2{x}\ dx} \)
Aşağıdaki şekilde değişken değiştirme uygulayalım.
\( u = \tan{x} \)
\( du = \sec^2{x}\ dx \)
Son ifadede bu değişkenleri yerine koyalım.
\( = 10\displaystyle\int {u^4\ du} \)
İfadenin integralini alalım.
\( = 10 \cdot \dfrac{u^5}{5} + C \)
\( = 2u^5 + C \)
\( u \) değişkenini tekrar \( x \) cinsinden yazalım.
\( = 2\tan^5{x} + C \)
\( \displaystyle\int_0^{3\pi} \cos(2x)\ dx + \displaystyle\int_0^{3\pi} 2\sin^2{x}\ dx \) integralinin sonucu nedir?
Çözümü Gösterİki kat açı formülü ile birinci ifadeyi düzenleyelim.
\( \cos(2x) = 1 - 2\sin^2{x} \)
\( \displaystyle\int_0^{3\pi} (1 - 2\sin^2{x})\ dx + \displaystyle\int_0^{3\pi} 2\sin^2{x}\ dx \)
İki integral işleminin sınır değerleri eşit olduğu için toplama kuralını kullanarak iki ifadeyi tek integral işleminde birleştirebiliriz.
\( = \displaystyle\int_0^{3\pi} (1 - 2\sin^2{x} + 2\sin^2{x})\ dx \)
\( = \displaystyle\int_0^{3\pi} 1\ dx \)
İfadenin integralini alalım.
\( = (x)|_0^{3\pi} = 3\pi - 0 = 3\pi \) bulunur.
\( \displaystyle\int {5\csc^2{x}\cos{x}\ dx} \) integralinin sonucu nedir?
Çözümü GösterKosekant fonksiyonunu sinüs cinsinden yazalım.
\( 5\displaystyle\int {\dfrac{1}{\sin^2{x}}\cos{x}\ dx} \)
\( = 5\displaystyle\int {\dfrac{1}{\sin{x}} \cdot \dfrac{\cos{x}}{\sin{x}}\ dx} \)
\( = 5\displaystyle\int {\csc{x}\cot{x}\ dx} \)
Elde ettiğimiz ifadenin integralini alalım.
\( = -5\csc{x} + C \)
\( \displaystyle\int {\dfrac{\sin^9{x}}{\cos^{11}{x}}\ dx} \) integralinin sonucu nedir?
Çözümü Gösterİfadeyi düzenleyelim.
\( \displaystyle\int {\dfrac{\sin^9{x}}{\cos^{11}{x}}\ dx} = \displaystyle\int {\dfrac{\sin^9{x}}{\cos^9{x}} \cdot \dfrac{1}{\cos^2{x}}\ dx} \)
\( = \displaystyle\int {\tan^9{x}\sec^2{x}\ dx} \)
Aşağıdaki şekilde değişken değiştirme uygulayalım.
\( u = \tan{x} \)
\( du = \sec^2{x}\ dx \)
Son ifadede bu değişkenleri yerine koyalım.
\( = \displaystyle\int {u^9\ du} \)
İfadenin integralini alalım.
\( = \dfrac{u^{10}}{10} + C \)
\( u \) değişkenini tekrar \( x \) cinsinden yazalım.
\( = \dfrac{\tan^{10}{x}}{10} + C \)
\( \displaystyle\int {3x^2\sin{x^3}\cos{x^3}\ dx} \) integralinin sonucu nedir?
Çözümü GösterAşağıdaki şekilde değişken değiştirelim.
\( u = \sin{x^3} \)
\( du = 3x^2\cos{x^3}\ dx \)
Verilen ifadede bu değişkenleri yerine koyalım.
\( = \displaystyle\int {u\ du} \)
Elde ettiğimiz ifadenin integralini alalım.
\( = \dfrac{u^2}{2} + C \)
İfadede \( u \) değişkeni yerine \( x \) cinsinden karşılığını yazdığımızda verilen ifadenin integralini buluruz.
\( = \dfrac{\sin^2{x^3}}{2} + C \)
\( \displaystyle\int_0^{\frac{\pi}{4}} (5\sec{x} + 4\cos{x})^2\ dx \) integralinin sonucu nedir?
Çözümü Göster\( \displaystyle\int_0^{\frac{\pi}{4}} (5\sec{x} + 4\cos{x})^2\ dx \)
İntegral içerisindeki ifadenin açılımını yazalım.
\( = \displaystyle\int_0^{\frac{\pi}{4}} (25\sec^2{x} + 40\sec{x}\cos{x} + 16\cos^2{x})\ dx \)
\( \sec{x}\cos{x} = 1 \)
\( = \displaystyle\int_0^{\frac{\pi}{4}} (25\sec^2{x} + 40 + 16\cos^2{x})\ dx \)
Üçüncü terimde kosinüs iki kat açı formülünü kullanalım.
\( \cos^2{x} = \dfrac{\cos(2x) + 1}{2} \)
\( = \displaystyle\int_0^{\frac{\pi}{4}} \left( 25\sec^2{x} + 40 + 16 \cdot \dfrac{\cos(2x) + 1}{2} \right)\ dx \)
\( = \displaystyle\int_0^{\frac{\pi}{4}} (25\sec^2{x} + 48 + 8\cos(2x))\ dx \)
Terimlerin ayrı ayrı integralini alalım.
\( = (25\tan{x} + 48x + 8 \cdot \dfrac{1}{2}\sin(2x))|_0^{\frac{\pi}{4}} \)
\( = (25\tan{x} + 48x + 4\sin(2x))|_0^{\frac{\pi}{4}} \)
\( = (25\tan{\frac{\pi}{4}} + 48 \cdot \dfrac{\pi}{4} + 4\sin(2 \cdot \frac{\pi}{4})) - (25\tan{0} + 48 \cdot 0 + 4\sin(2 \cdot 0)) \)
\( = (25 \cdot 1 + 12\pi + 4 \cdot 1) - (25 \cdot 0 + 48 \cdot 0 + 4 \cdot 0) \)
\( = 25 + 12\pi + 4 - 0 \)
\( = 12\pi + 29 \)
\( \displaystyle\int{\dfrac{\cos{x}}{\cos(2x) - 1} \ dx} \) integralinin sonucu nedir?
Çözümü GösterKosinüs iki kat açı formülü ile paydadaki ifadeyi düzenleyelim.
\( \displaystyle\int{\dfrac{\cos{x}}{\cos(2x) - 1} \ dx} = \displaystyle\int {\dfrac{\cos{x}}{1 - 2\sin^2{x} - 1}\ dx} \)
\( = -\dfrac{1}{2}\displaystyle\int {\dfrac{\cos{x}}{\sin^2{x}}\ dx} \)
Aşağıdaki şekilde değişken değiştirme uygulayalım.
\( u = \sin{x} \)
\( du = \cos{x}\ dx \)
Verilen ifadede bu değişkenleri yerine koyalım.
\( = -\dfrac{1}{2}\displaystyle\int {\dfrac{1}{u^2}\ du} = -\dfrac{1}{2}\displaystyle\int{u^{-2}\ du} \)
İfadenin integralini alalım.
\( = -\dfrac{1}{2} \cdot \dfrac{u^{-1}}{-1} + C \)
\( = \dfrac{1}{2u} + C \)
İfadede \( u \) değişkeni yerine \( x \) cinsinden karşılığını yazdığımızda verilen ifadenin integralini buluruz.
\( = \dfrac{1}{2\sin{x}} + C \)
\( = \dfrac{1}{2}\csc{x} + C \)
\( \displaystyle\int {\cos^2{x}\csc^2{x}\ dx} \) integralinin sonucu nedir?
Çözümü GösterKosinüs ve kosekant ifadelerini sinüs cinsinden yazalım.
\( \cos^2{x} = 1 - \sin^2{x} \)
\( \csc^2{x} = \dfrac{1}{\sin^2{x}} \)
\( \displaystyle\int {\cos^2{x}\csc^2{x}\ dx} = \displaystyle\int {(1 - \sin^2{x})\dfrac{1}{\sin^2{x}}\ dx} \)
\( = \displaystyle\int {\dfrac{1 - \sin^2{x}}{\sin^2{x}}\ dx} \)
\( = \displaystyle\int \left( \dfrac{1}{\sin^2{x}} - 1 \right)\ dx \)
\( = \displaystyle\int {(\csc^2{x} - 1)\ dx} \)
Terimlerin ayrı ayrı integralini alalım.
\( = -\cot{x} - x + C \)
\( \displaystyle\int {\dfrac{1}{1 + \sin{x}}\ dx} \) integralinin sonucu nedir?
Çözümü GösterPayı ve paydayı, paydanın eşleniği ile çarpalım.
\( = \displaystyle\int {\dfrac{1}{1 + \sin{x}} \cdot \dfrac{1 - \sin{x}}{1 - \sin{x}}\ dx} \)
\( = \displaystyle\int {\dfrac{1 - \sin{x}}{1 - \sin^2{x}}\ dx} \)
Pisagor özdeşliğini kullanalım.
\( = \displaystyle\int {\dfrac{1 - \sin{x}}{\cos^2{x}}\ dx} \)
İfadeyi iki kesrin toplamı şeklinde yazalım.
\( \displaystyle\int \left( \dfrac{1}{\cos^2{x}} - \dfrac{\sin{x}}{\cos^2{x}} \right)\ dx \)
\( \displaystyle\int \left( \dfrac{1}{\cos^2{x}} - \dfrac{\sin{x}}{\cos{x}} \cdot \dfrac{1}{\cos{x}} \right)\ dx \)
Elde ettiğimiz ifadeyi sekant ve tanjant cinsinden yazalım.
\( = \displaystyle\int (\sec^2{x} - \tan{x}\sec{x})\ dx \)
Terimlerin ayrı ayrı integralini alalım.
\( = \tan{x} - \sec{x} + C \)
\( \displaystyle\int {\dfrac{8\sqrt[5]{\tan^3{x}}}{\cos^2{x}}\ dx} \) integralinin sonucu nedir?
Çözümü Gösterİfadeyi düzenleyelim.
\( 8\displaystyle\int {\sqrt[5]{\tan^3{x}} \cdot \dfrac{1}{\cos^2{x}}}\ dx \)
İkinci ifadeyi sekant cinsinden yazalım.
\( = 8\displaystyle\int {\sqrt[5]{\tan^3{x}}\sec^2{x}\ dx} \)
\( = 8\displaystyle\int {(\tan{x})^{\frac{3}{5}}\sec^2{x}\ dx} \)
Aşağıdaki şekilde değişken değiştirelim.
\( u = \tan{x} \)
\( du = \sec^2{x}\ dx \)
Son ifadede bu değişkenleri yerine koyalım.
\( = 8\displaystyle\int {u^{\frac{3}{5}}\ du} \)
Elde ettiğimiz ifadenin integralini alalım.
\( = 8 \cdot \dfrac{u^{\frac{8}{5}}}{\frac{8}{5}} + C \)
\( = 5u^{\frac{8}{5}} + C \)
\( = 5\sqrt[5]{u^8} + C \)
İfadede \( u \) değişkeni yerine \( x \) cinsinden karşılığını yazdığımızda verilen ifadenin integralini buluruz.
\( = 5\sqrt[5]{\tan^8{x}} + C \)
\( \displaystyle\int {\dfrac{1}{\sqrt{x - 2}\sqrt{4 - x}}\ dx} \) integralinin sonucu nedir?
Çözümü Gösterİfadeyi düzenleyelim.
\( \displaystyle\int {\dfrac{1}{\sqrt{x - 2}\sqrt{4 - x}}\ dx} = \displaystyle\int {\dfrac{1}{\sqrt{(x - 2)(4 - x)}}\ dx} \)
\( = \displaystyle\int {\dfrac{1}{\sqrt{-x^2 + 6x - 8}}\ dx} \)
Kök içindeki ifadeyi tam kareye tamamlamak için 9 çıkarıp ekleyelim.
\( = \displaystyle\int {\dfrac{1}{\sqrt{-x^2 + 6x - 9 + 9 - 8}}\ dx} \)
\( = \displaystyle\int {\dfrac{1}{\sqrt{-(x^2 - 6x + 9) + 1}}\ dx} \)
\( = \displaystyle\int {\dfrac{1}{\sqrt{1 - (x - 3)^2}}\ dx} \)
İfadenin integralini alalım.
\( = \arcsin(x - 3) + C \)
\( \displaystyle\int_{0}^{50\pi} \sqrt{\sin^2{x} + \cos(2x)}\ dx \) integralinin sonucu nedir?
Çözümü Gösterİki kat açı formülünü kullanarak ifadeyi düzenleyelim.
\( \cos(2x) = \cos^2{x} - \sin^2{x} \)
\( \displaystyle\int_0^{50\pi} \sqrt{\sin^2{x} + \cos^2{x} - \sin^2{x}}\ dx \)
\( \displaystyle\int_0^{50\pi} \sqrt{1 - \sin^2{x}}\ dx \)
Pisagor özdeşliğini kullanalım.
\( = \displaystyle\int_0^{50\pi} \sqrt{\cos^2(x)}\ dx \)
\( = \displaystyle\int_0^{50\pi} \abs{\cos{x}}\ dx \)
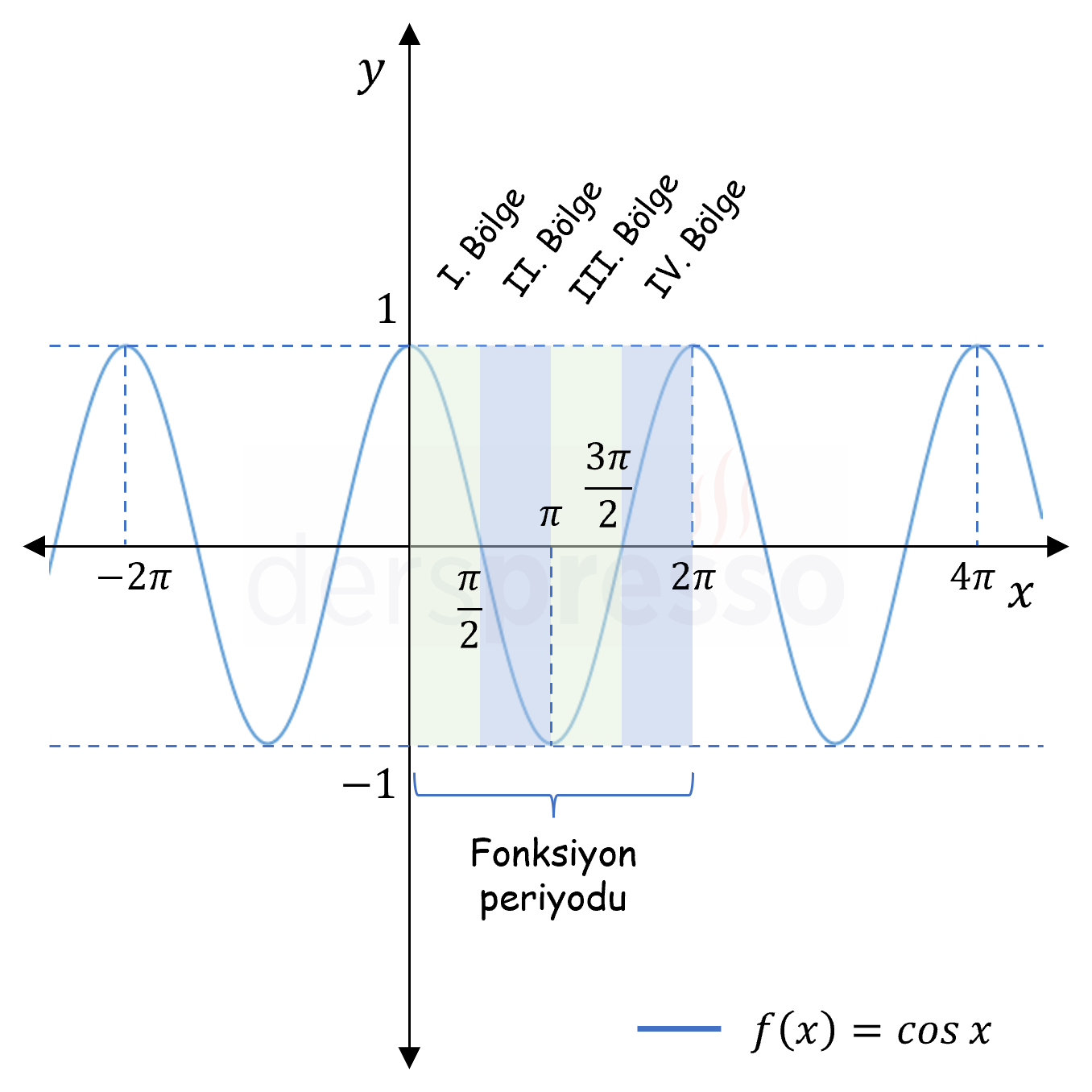
Kosinüs fonksiyonunun grafiğini ve \( x \) ekseni ile arasında kalan alanı düşündüğümüzde grafiğin \( x \) ekseninin üzerinde kaldığı \( [0, \frac{\pi}{2}] \) ve \( [\frac{3\pi}{2}, 2\pi] \) aralıklarındaki belirli integral değerleri birbirine eşittir. Grafiğin \( x \) ekseninin altında kaldığı \( [\frac{\pi}{2}, \pi] \) ve \( [\pi, \frac{3\pi}{2}] \) aralıklarında ise belirli integral aynı değerlerin negatifine eşittir.
Buna göre kosinüs fonksiyonunun mutlak değerinin \( [0, 2\pi] \) aralığındaki değeri \( [0, \frac{\pi}{2}] \) aralığındaki değerinin 4 katıdır.
Kosinüs fonksiyonu periyodik olduğu ve periyodu \( 2\pi \) olduğu için \( [0, 50\pi] \) aralığında aynı grafik 25 kez tekrarlanır.
Buna göre ifadeyi aşağıdaki şekilde yazabiliriz.
\( = \displaystyle\int_0^{50\pi} \abs{\cos{x}}\ dx = 25 \cdot 4\displaystyle\int_0^{\frac{\pi}{2}} \cos{x}\ dx \)
İfadenin integralini alalım.
\( = 100(\sin{x})_0^{\frac{\pi}{2}} \)
\( = 100(\sin{\frac{\pi}{2}} - \sin{0}) \)
\( = 100(1 - 0) = 100 \) bulunur.