İki Eğri Arasında Kalan Alan
Belirli integrali kullanarak bir eğrinin eksenlerle arasında kalan alanı bulabildiğimiz gibi, iki eğri arasında kalan alanı da bulabiliriz. Aşağıdaki şekilde \( f \) ve \( g \) eğrileri arasında kalan alan taralı şekilde gösterilmiştir.
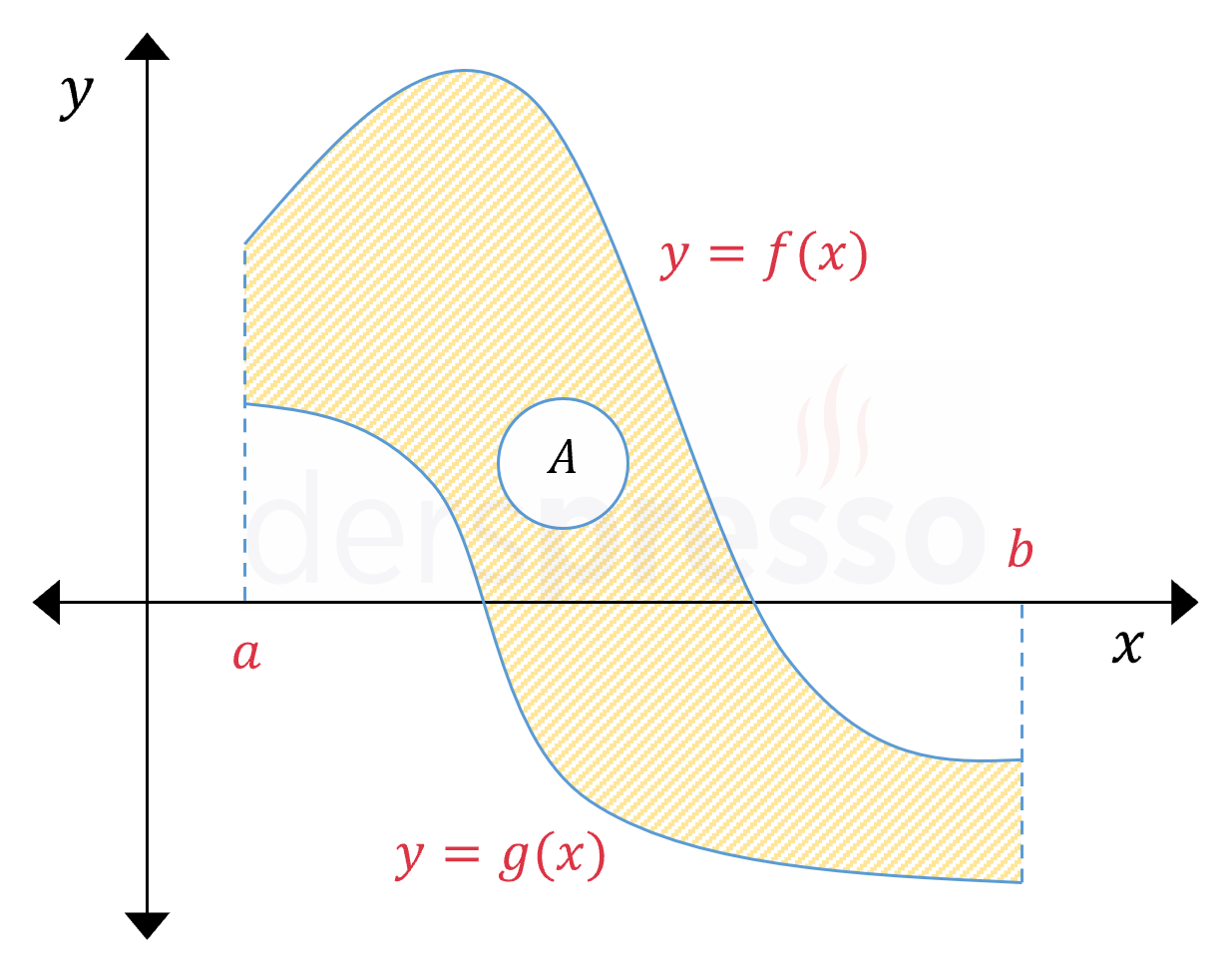
Belirli bir aralıkta iki eğri arasında kalan alan, üstteki eğri ile alttaki eğrinin farkının bu aralıktaki belirli integraline eşittir.
\( f \) ve \( g \) \( [a, b] \) aralığında sürekli fonksiyonlar,
Bu aralıkta \( f(x) \ge g(x) \) olmak üzere,
\( A = \displaystyle\int_a^b {(f(x) - g(x))\ dx} \)
İSPATI GÖSTER
\( f(x) \ge g(x) \) olmak koşuluyla, iki fonksiyonun \( x \) eksenine göre durumu üç farklı şekilde olabilir.
- İki fonksiyon da \( x \) ekseninin üstünde
- Sadece \( f \) fonksiyonu \( x \) ekseninin üstünde
- İki fonksiyon da \( x \) ekseninin altında
Bu üç durum aşağıdaki grafikte sırasıyla \( [a, c] \), \( [c, d] \) ve \( [d, b] \) aralıklarına karşılık gelmektedir.
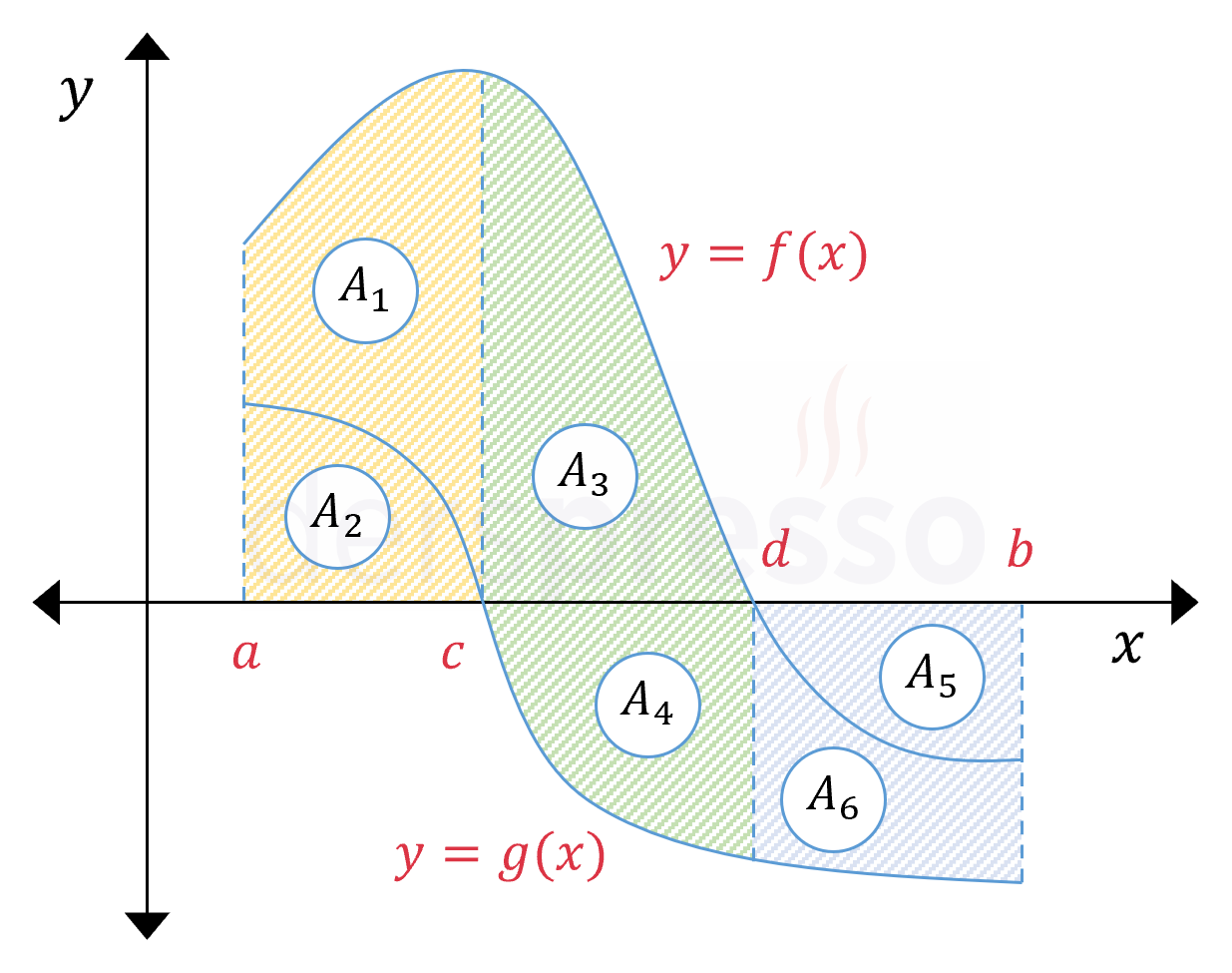
\( \displaystyle\int_a^b {(f(x) - g(x))\ dx} \)
Yukarıdaki iki eğri arasında kalan alan formülünün bu üç durum için de geçerli olduğunu gösterelim.
İki fonksiyon da \( x \) ekseninin üstünde: \( [a, c] \) aralığı
Grafiğe göre iki eğri arasında kalan alan \( A_1 \) olur.
Fonksiyonların bu aralıktaki integral değerlerini bulalım.
\( \displaystyle\int_a^c {f(x)\ dx} = A_1 + A_2 \)
\( \displaystyle\int_a^c {g(x)\ dx} = A_2 \)
Buna göre bu aralıkta iki fonksiyonun farkının integrali iki eğri arasında kalan alanı verir.
\( \displaystyle\int_a^c {(f(x) - g(x))\ dx} = A_1 + A_2 - A_2 = A_1 \)
Sadece \( f \) fonksiyonu \( x \) ekseninin üstünde: \( [c, d] \) aralığı
Grafiğe göre iki eğri arasında kalan alan \( A_3 + A_4 \) olur.
Fonksiyonların bu aralıktaki integral değerlerini bulalım.
\( \displaystyle\int_c^d {f(x)\ dx} = A_3 \)
\( \displaystyle\int_c^d {g(x)\ dx} = -A_4 \)
Buna göre bu aralıkta iki fonksiyonun farkının integrali iki eğri arasında kalan alanı verir.
\( \displaystyle\int_c^d {(f(x) - g(x))\ dx} = A_3 - (-A_4) = A_3 + A_4 \)
İki fonksiyon da \( x \) ekseninin altında: \( [d, b] \) aralığı
Grafiğe göre iki eğri arasında kalan alan \( A_6 \) olur.
Fonksiyonların bu aralıktaki integral değerlerini bulalım.
\( \displaystyle\int_d^b {f(x)\ dx} = -A_5 \)
\( \displaystyle\int_d^b {g(x)\ dx} = -A_5 + (-A_6) = -A_5 - A_6 \)
Buna göre bu aralıkta iki fonksiyonun farkının integrali iki eğri arasında kalan alanı verir.
\( \displaystyle\int_d^b {(f(x) - g(x))\ dx} = -A_5 - (-A_5 - A_6) = A_6 \)
Her üç farklı aralık tipinde de fonksiyonların farkının integralinin eğrilerin arasında kalan alanı verdiğini göstermiş olduk.
İki eğri arasında kalan alanı bulmak için grafiği üstte kalan fonksiyondan altta kalan fonksiyon çıkarılmalıdır. Aşağıdaki örnekteki gibi farklı aralıklarda farklı eğrinin üstte kaldığı durumda, her zaman üstteki eğriden alttaki eğri çıkarılacak şekilde integral işlemi alt aralıklara bölünür.
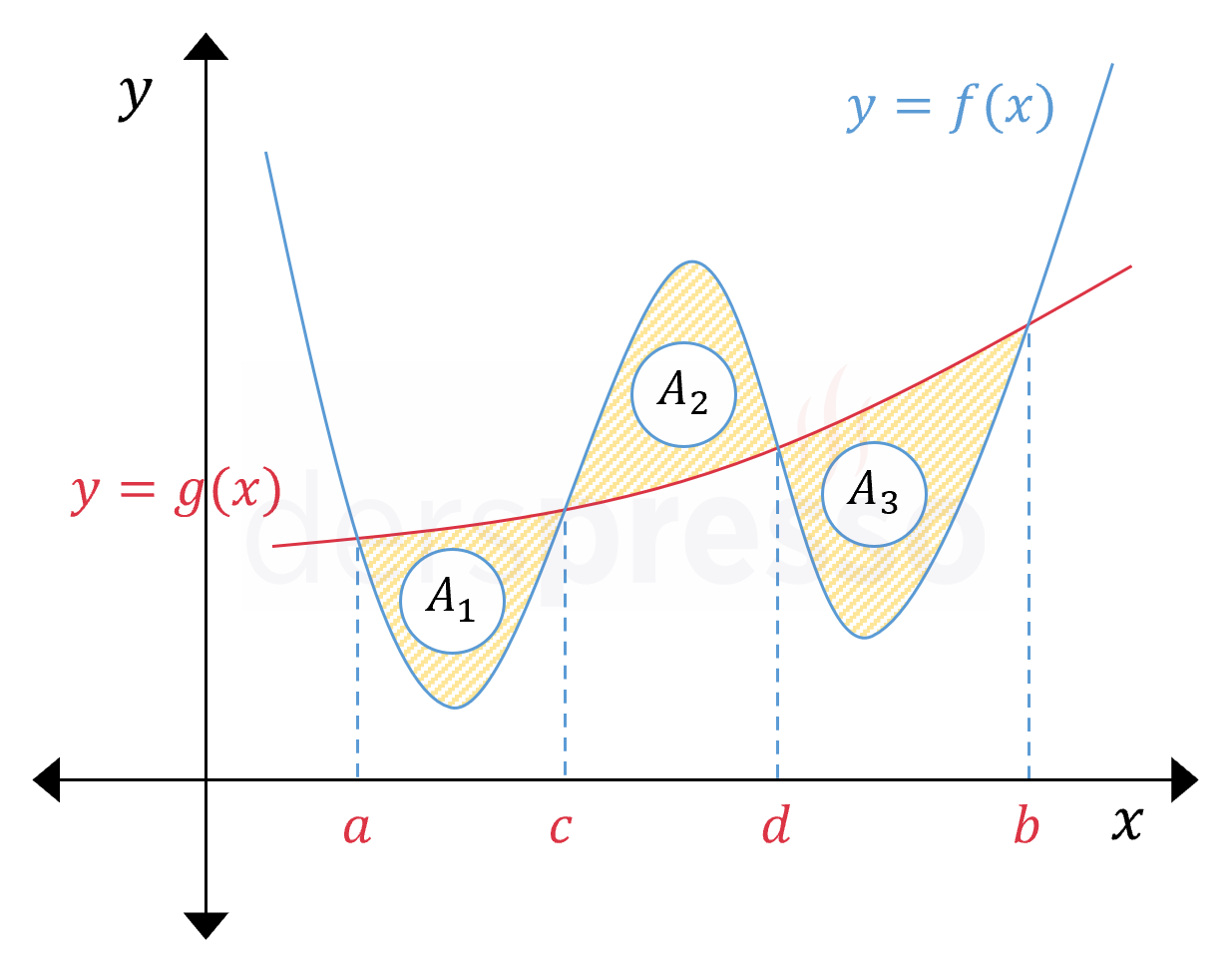
\( A_1 = \displaystyle\int_a^c {(g(x) - f(x))\ dx} \)
\( A_2 = \displaystyle\int_c^d {(f(x) - g(x))\ dx} \)
\( A_3 = \displaystyle\int_d^b {(g(x) - f(x))\ dx} \)
İki eğri arasında kalan alanı bulmak için bir integrali yukarıdaki gibi alt integrallere bölerken kullanmamız gereken sınır noktaları, iki eğrinin birbiriyle kesişim noktalardır. Bu noktalar \( f(x) = g(x) \) denkleminin tek katlı kökleridir. Çift katlı köklerde ise eğriler yine kesişirler ama üstteki eğri üstte, alttaki eğri de altta kalmaya devam eder.
Alternatif olarak, tüm \( [a, b] \) aralığı için bu alanı tek işlemde farkın mutlak değerini alarak bulabiliriz.
\( A = A_1 + A_2 + A_3 \) olmak üzere,
\( A = \displaystyle\int_a^b {\abs{f(x) - g(x)}\ dx} \)
Denklemleri \( y \) cinsinden verilmiş iki eğri arasında kalan alan da, \( y \) eksenine göre üstte (sağda) kalan fonksiyonun altta (solda) kalan fonksiyondan farkının belirli integraline eşittir.

\( [a, b] \) aralığında \( f(y) \ge g(y) \) olmak üzere,
\( A = \displaystyle\int_a^b {(f(y) - g(y))\ dy} \)
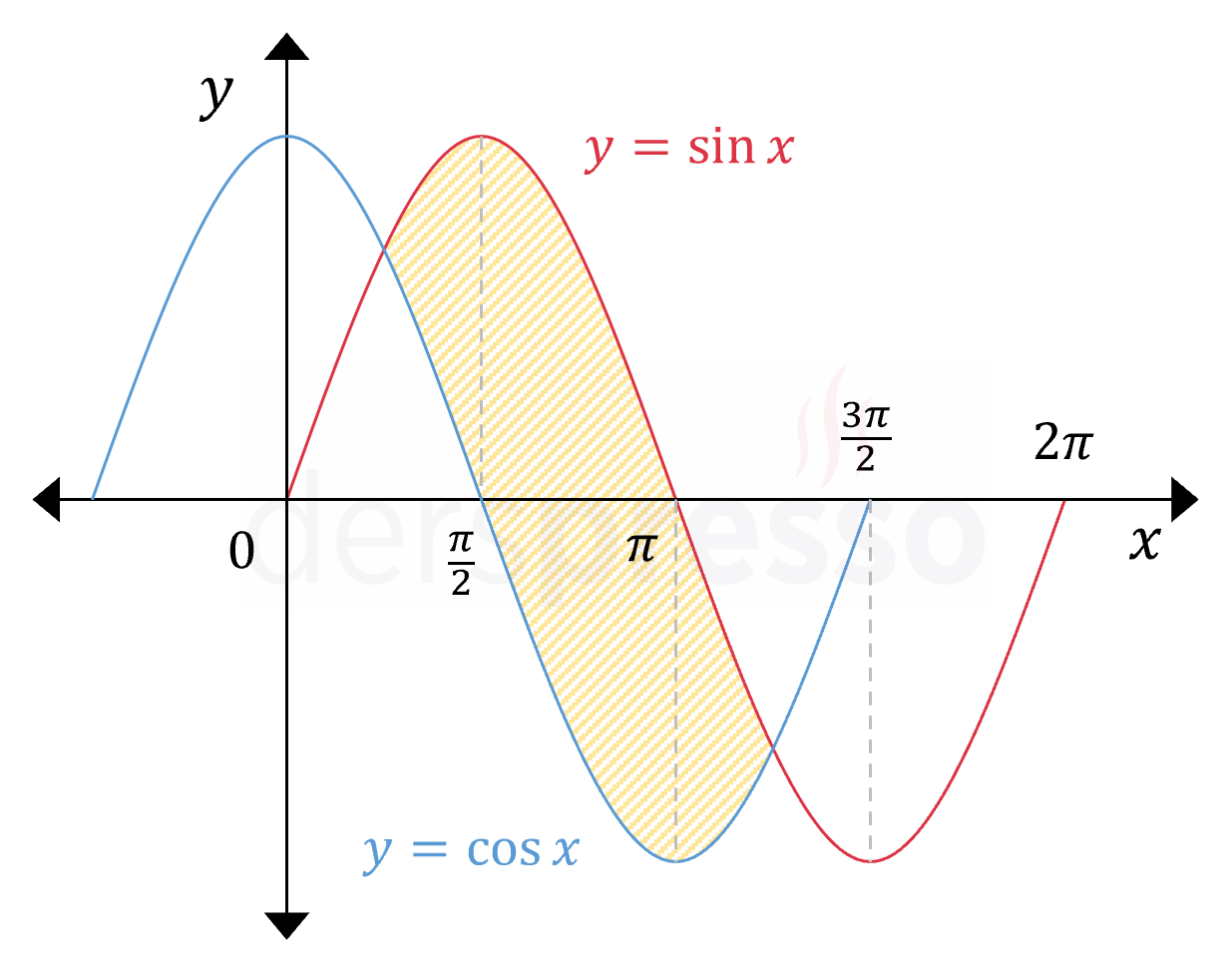
Şekildeki sinüs ve kosinüs eğrileri arasında kalan taralı bölgenin alanı nedir?
Çözümü GösterTaralı alan iki eğrinin kesişim noktaları arasındaki aralıkta üstteki sinüs eğrisi ile alttaki kosinüs eğrisi arasında kalan bölgeye karşılık gelir.
İki denklemi ortak çözerek kesişim noktalarının apsis değerlerini bulalım.
\( \sin{x} = \cos{x} \)
\( \tan{x} = 1 \)
Tanjant fonksiyonu \( [0, 2\pi] \) aralığında \( x \in \{\frac{\pi}{4}, \frac{5\pi}{4}\} \) noktalarında 1 değerini alır.
Buna göre taralı alanı aşağıdaki şekildeki aralıkta iki eğri arasında kalan alan şeklinde ifade edebiliriz.
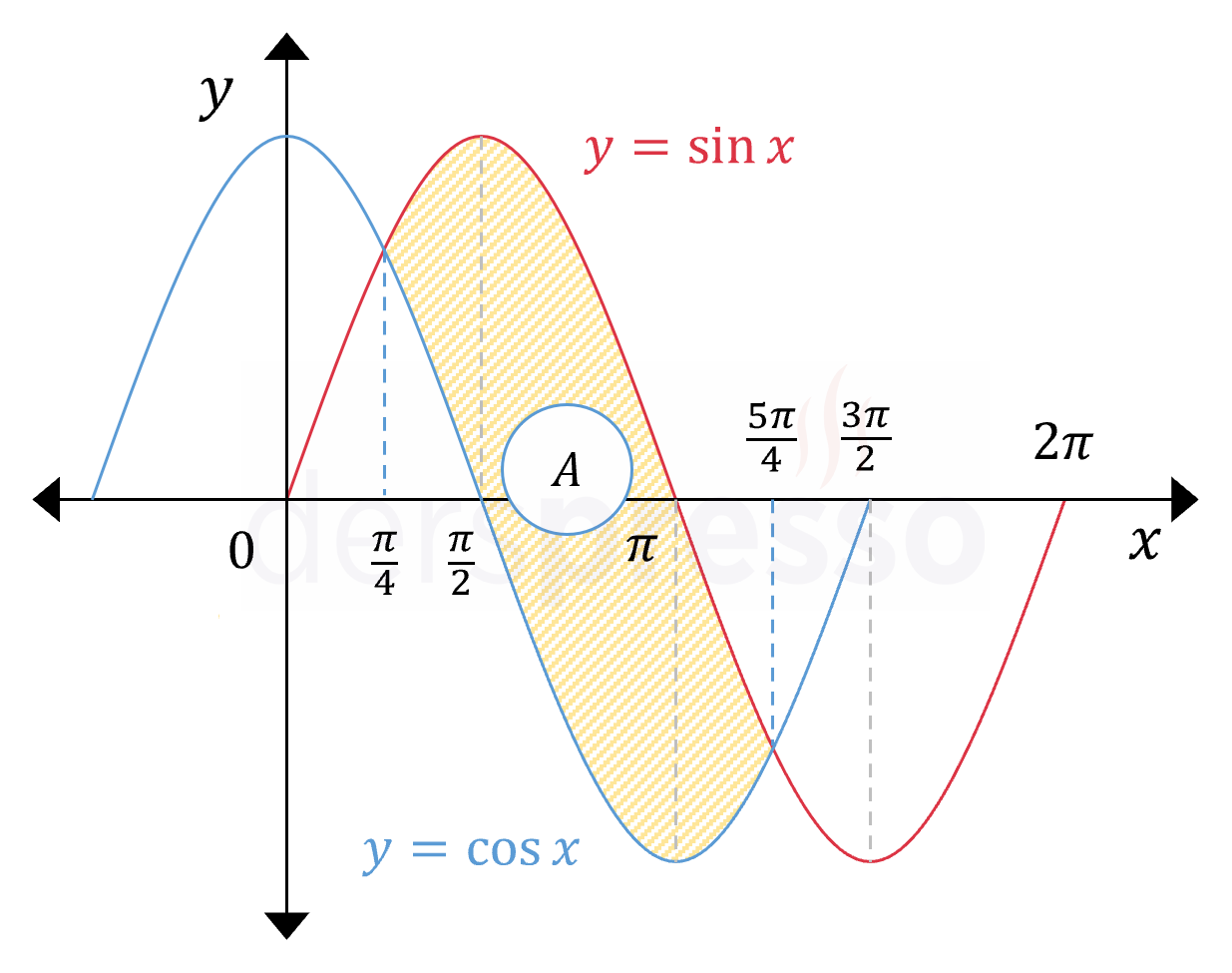
\( A = \displaystyle\int_{\frac{\pi}{4}}^{\frac{5\pi}{4}} (\sin{x} - \cos{x})\ dx \)
İfadenin integralini alalım.
\( = (-\cos{x} - \sin{x})|_{\frac{\pi}{4}}^{\frac{5\pi}{4}} \)
Sınır değerlerini yerine koyarak belirli integral değerini bulalım.
\( = (-\cos{\frac{5\pi}{4}} - \sin{\frac{5\pi}{4}}) - (-\cos{\frac{\pi}{4}} - \sin{\frac{\pi}{4}}) \)
\( = (\frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2}) - (-\frac{\sqrt{2}}{2} - \frac{\sqrt{2}}{2}) \)
\( = 2\sqrt{2} \) bulunur.

Şekildeki üç doğrunun oluşturduğu \( ABC \) üçgeninin alanını integral kullanarak bulunuz.
Çözümü GösterÖnce doğruların kesişim noktalarını bulalım.
\( A \) noktasında kesişen iki doğruyu ortak çözelim.
\( 2x + 2 = x - 1 \)
\( x = -3 \)
Buna göre \( A \) noktasının apsis değeri \( -3 \)'tür.
\( B \) noktasında kesişen iki doğruyu ortak çözelim.
\( 2x + 2 = -x + 5 \)
\( x = 1 \)
Buna göre \( B \) noktasının apsis değeri \( 1 \)'dir.
\( C \) noktasında kesişen iki doğruyu ortak çözelim.
\( -x + 5 = x - 1 \)
\( x = 3 \)
Buna göre \( C \) noktasının apsis değeri \( 3 \)'tür.
Bu noktaların apsis değerleri aşağıdaki şekilde işaretlenmiştir.

\( ABC \) üçgeninin alanını \( ABD \) ve \( BCD \) üçgenlerinin alanlarının toplamı şeklinde hesaplayabiliriz.
\( ABD \) üçgeninin alanı \( [-3, 1] \) aralığında \( y = 2x + 2 \) ve \( y = x - 1 \) doğruları arasında kalan alana karşılık gelir.
\( A(ABD) = \displaystyle\int_{-3}^1 ((2x + 2) - (x - 1))\ dx \)
\( = \displaystyle\int_{-3}^1 (x + 3)\ dx \)
İfadenin integralini alalım.
\( = (\frac{x^2}{2} + 3x)_{-3}^1 \)
\( = (\frac{1^2}{2} + 3(1)) - (\frac{(-3)^2}{2} + 3(-3)) \)
\( = 8 \)
\( BCD \) üçgeninin alanı \( [1, 3] \) aralığında \( y = -x + 5 \) ve \( y = x - 1 \) doğruları arasında kalan alana karşılık gelir.
\( A(ABD) = \displaystyle\int_1^3 ((-x + 5) - (x - 1))\ dx \)
\( = \displaystyle\int_1^3 (-2x + 6)\ dx \)
İfadenin integralini alalım.
\( = (-x^2 + 6x)_1^3 \)
\( = (-3^2 + 6(3)) - (-1^2 + 6(1)) \)
\( = 4 \)
\( ABC \) üçgeninin alanı bu iki üçgenin alanları toplamına eşittir.
\( A(ABC) = 8 + 4 = 12 \) bulunur.
\( y = x^2 - 2x - 4 \) fonksiyonu ile \( y = x \) doğrusu arasında kalan bölgenin alanı kaç birimkaredir?
Çözümü GösterParabol ve doğrunun kesişim noktalarını bulmak için iki denklemi ortak çözelim.
\( x^2 - 2x - 4 = x \)
\( x^2 - 3x - 4 = 0 \)
\( (x + 1)(x - 4) = 0 \)
Buna göre parabol ve doğru apsisi \( x = -1 \) ve \( x = 4 \) olan noktalarda kesişirler.
İki grafik arasında kalan alanı bulmak için \( [-1, 4] \) aralığında üstte kalan denklemin altta kalan denklemden farkının belirli integralini almalıyız.
Grafikler parabol ve doğruya ait olduğu için kesişim noktaları arasındaki aralıkta sadece biri üstte kalır, dolayısıyla \( [-1, 4] \) aralığında tek belirli integral ile alanı hesaplayabiliriz.
Parabolün başkatsayısı pozitif olduğu için kolları yukarı yönlüdür, dolayısıyla kesişim noktaları arasında doğru parabolün üstünde kalır.
Bu çıkarımlarımızı iki denklemin grafiğini çizerek de teyit edebiliriz.
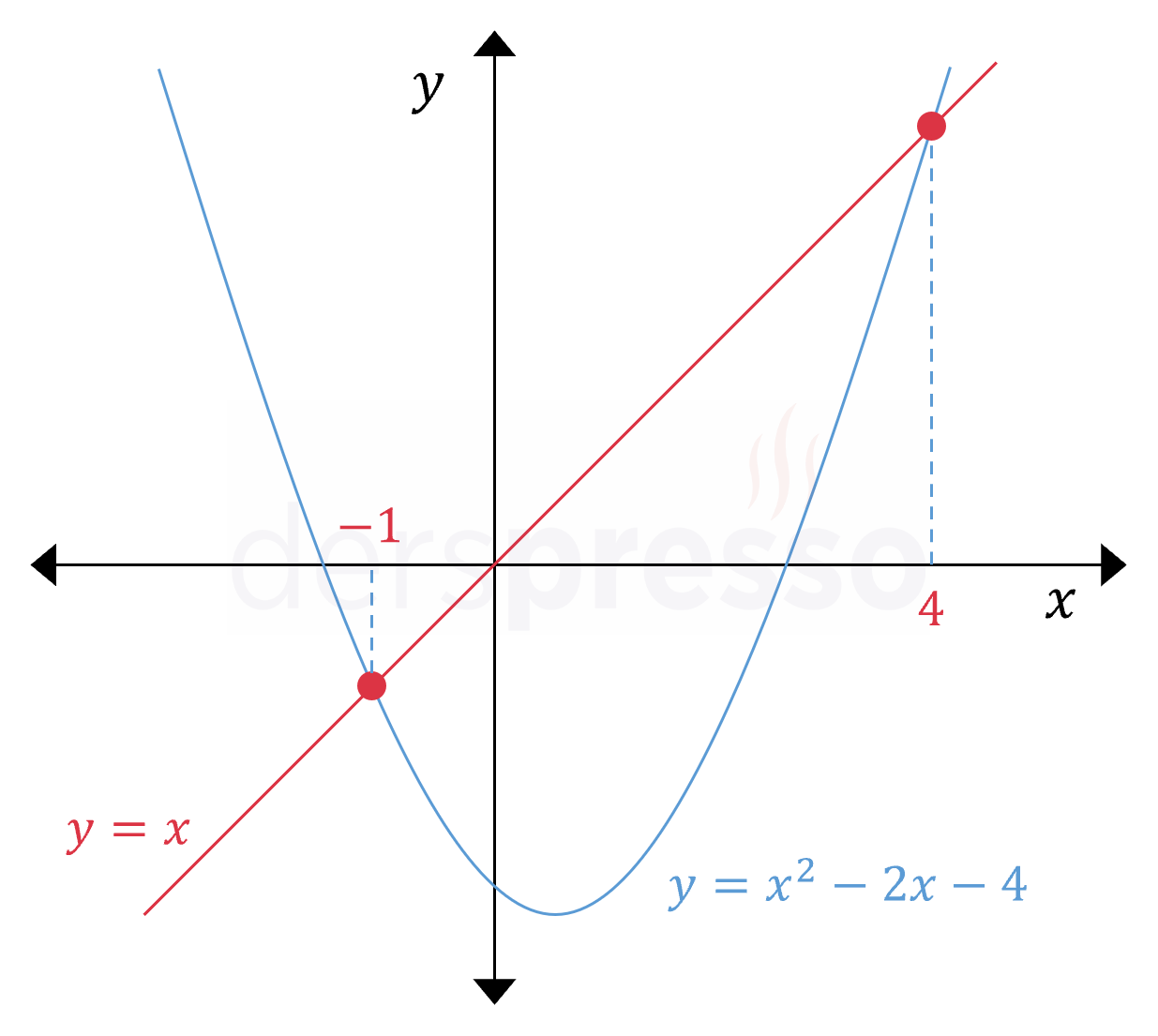
Doğru denkleminin parabol denkleminden farkının integralini alalım.
\( \displaystyle\int_{-1}^4 (x - (x^2 - 2x - 4))\ dx \)
\( = \displaystyle\int_{-1}^4 (-x^2 + 3x + 4)\ dx \)
İfadenin integralini alalım.
\( = (-\dfrac{x^3}{3} + \dfrac{3x^2}{2} + 4x)|_{-1}^4 \)
\( = (-\dfrac{4^3}{3} + \dfrac{3(4)^2}{2} + 4(4)) - (-\dfrac{(-1)^3}{3} + \dfrac{3(-1)^2}{2} + 4(-1)) \)
\( = -\dfrac{64}{3} + 24 + 16 - \dfrac{1}{3} - \dfrac{3}{2} + 4 \)
\( = 44 - \dfrac{139}{6} = \dfrac{125}{6} \) bulunur.
\( x = y^2 \) parabolü ve \( x = y + 2 \) doğrusu tarafından sınırlanan bölgenin alanını bulunuz.
Çözümü GösterParabol ve doğrunun kesişim noktalarını bulmak için iki denklemi ortak çözelim.
\( y^2 = y + 2 \)
\( y^2 - y - 2 = 0 \)
\( (y + 1)(y - 2) = 0 \)
Buna göre parabol ve doğru ordinatı \( y = -1 \) ve \( y = 2 \) olan noktalarda kesişirler.
Parabolün ve doğrunun grafikleri aşağıdaki şekildeki gibi olur.
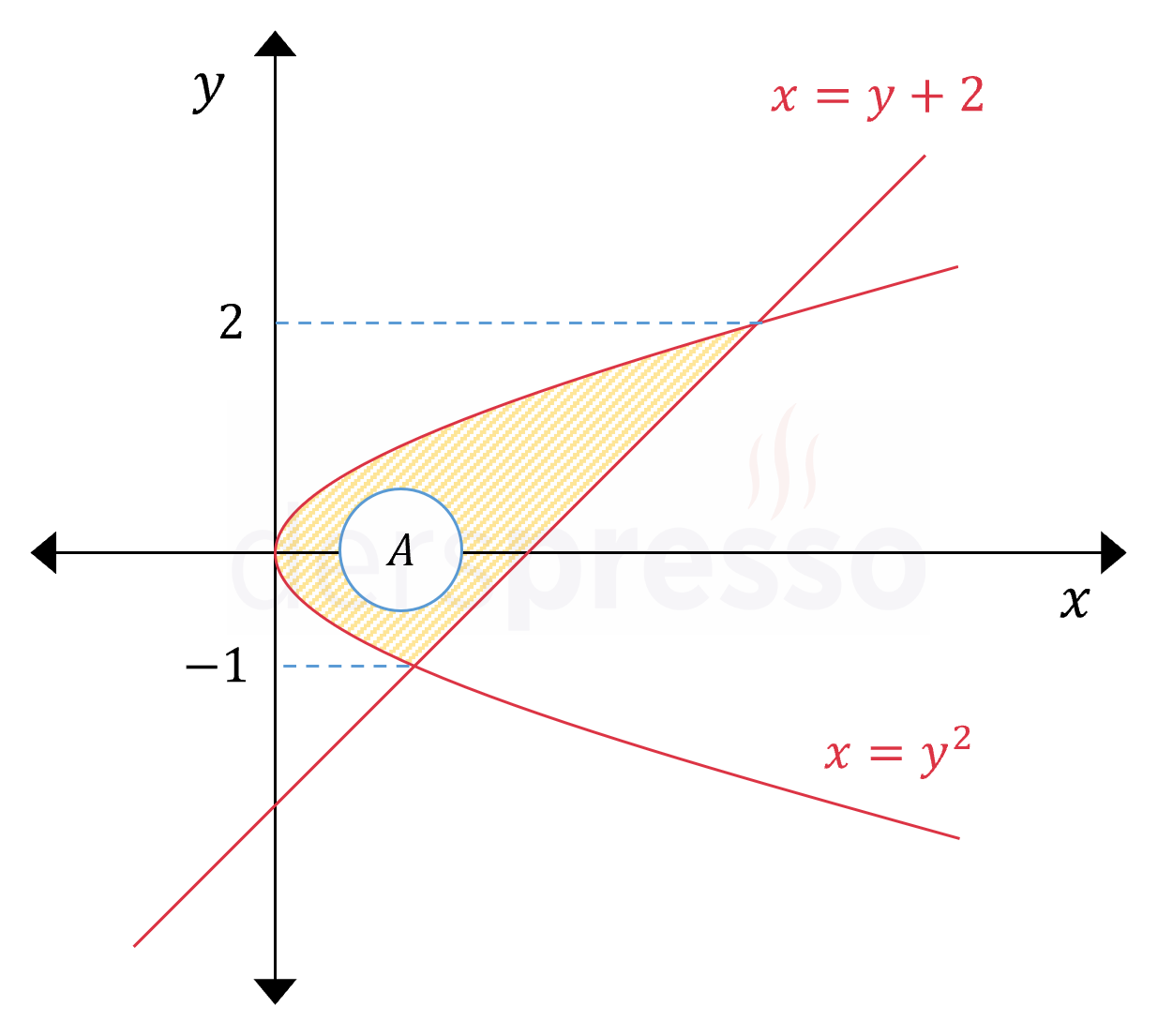
Denklemleri \( y \) cinsinden verilmiş parabol ve doğru arasında kalan alan, \( y \) eksenine göre sağda kalan fonksiyonun solda kalan fonksiyondan farkının kesişim noktaları arasındaki belirli integraline eşittir.
Grafikten görebileceğimiz gibi \( x = y + 2 \) doğrusu bu aralıkta \( x = y^2 \) parabolünün sağında kalır.
\( A = \displaystyle\int_{-1}^2 (y + 2 - y^2)\ dy \)
\( = (\dfrac{y^2}{2} + 2y - \dfrac{y^3}{3})|_{-1}^2 \)
\( = (\dfrac{2^2}{2} + 2(2) - \dfrac{2^3}{3}) - (\dfrac{(-1)^2}{2} + 2(-1) - \dfrac{(-1)^3}{3}) \)
\( = (2 + 4 - \dfrac{8}{3}) - (\dfrac{1}{2} - 2 + \dfrac{1}{3}) \)
\( = \dfrac{9}{2} \) bulunur.
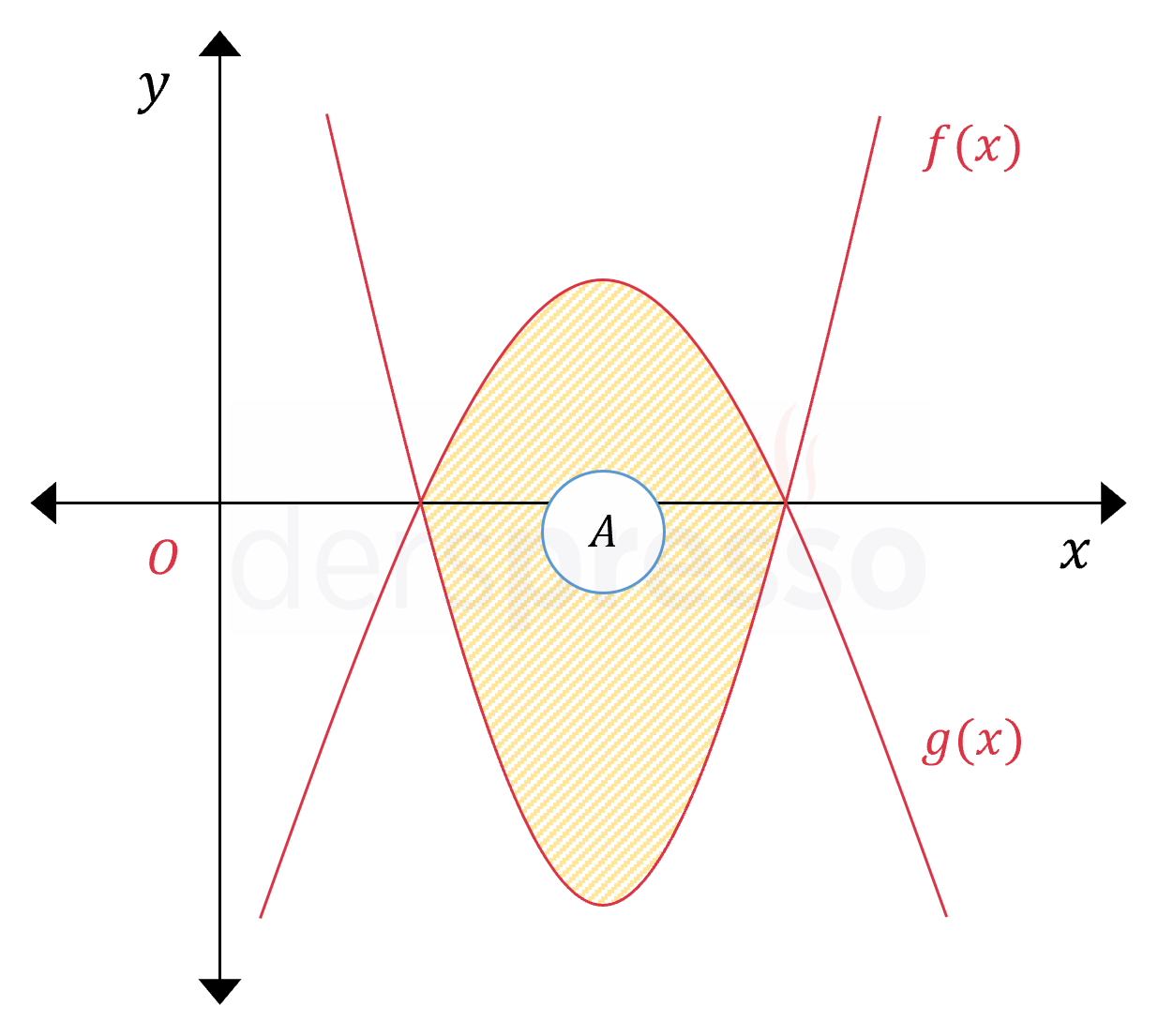
Yukarıda \( f(x) = 2x^2 - 14x + 20 \) ve \( g(x) = -x^2 + 7x - 10 \) parabollerinin grafikleri verilmiştir. Buna göre taralı bölgenin alanı kaç birimkaredir?
Çözümü Göster\( f \) fonksiyonunun \( x \) eksenini kestiği noktaları bulalım.
\( f(x) = 2(x - 2)(x - 5) \)
\( f \) fonksiyonu \( x \) eksenini \( x = 2 \) ve \( x = 5 \) apsisli noktalarda keser.
\( g \) fonksiyonunun \( x \) eksenini kestiği noktaları bulalım.
\( g(x) = -(x - 2)(x - 5) \)
\( g \) fonksiyonu \( x \) eksenini \( x = 2 \) ve \( x = 5 \) apsisli noktalarda keser.
İki fonksiyon \( x \) eksenini aynı noktalarda kestiği için kesişim noktaları \( x \) ekseni üzerindedir.
Taralı bölgenin alanı \( [2, 5] \) aralığında \( f \) ve \( g \) eğrilerinin arasında kalan alana eşittir.
Bu alan grafiği bu aralıkta üstte kalan \( g \) fonksiyonunun \( f \) fonksiyonundan farkının belirli integraline eşittir.
\( A = \displaystyle\int_2^5(g(x) - f(x))\ dx \)
\( = \displaystyle\int_2^5(-x^2 + 7x - 10 - (2x^2 - 14x + 20))\ dx \)
\( = \displaystyle\int_2^5(-3x^2 + 21x - 30)\ dx \)
İfadenin integralini alalım.
\( = (-x^3 + \dfrac{21x^2}{2} - 30x)|_2^5 \)
\( = (-5^3 + \dfrac{21(5)^2}{2} - 30(5)) - (-2^3 + \dfrac{21(2)^2}{2} - 30(2)) \)
\( = (-125 + \dfrac{525}{2} - 150) - (-8 + 42 - 60) \)
\( = \dfrac{27}{2} \) olarak bulunur.
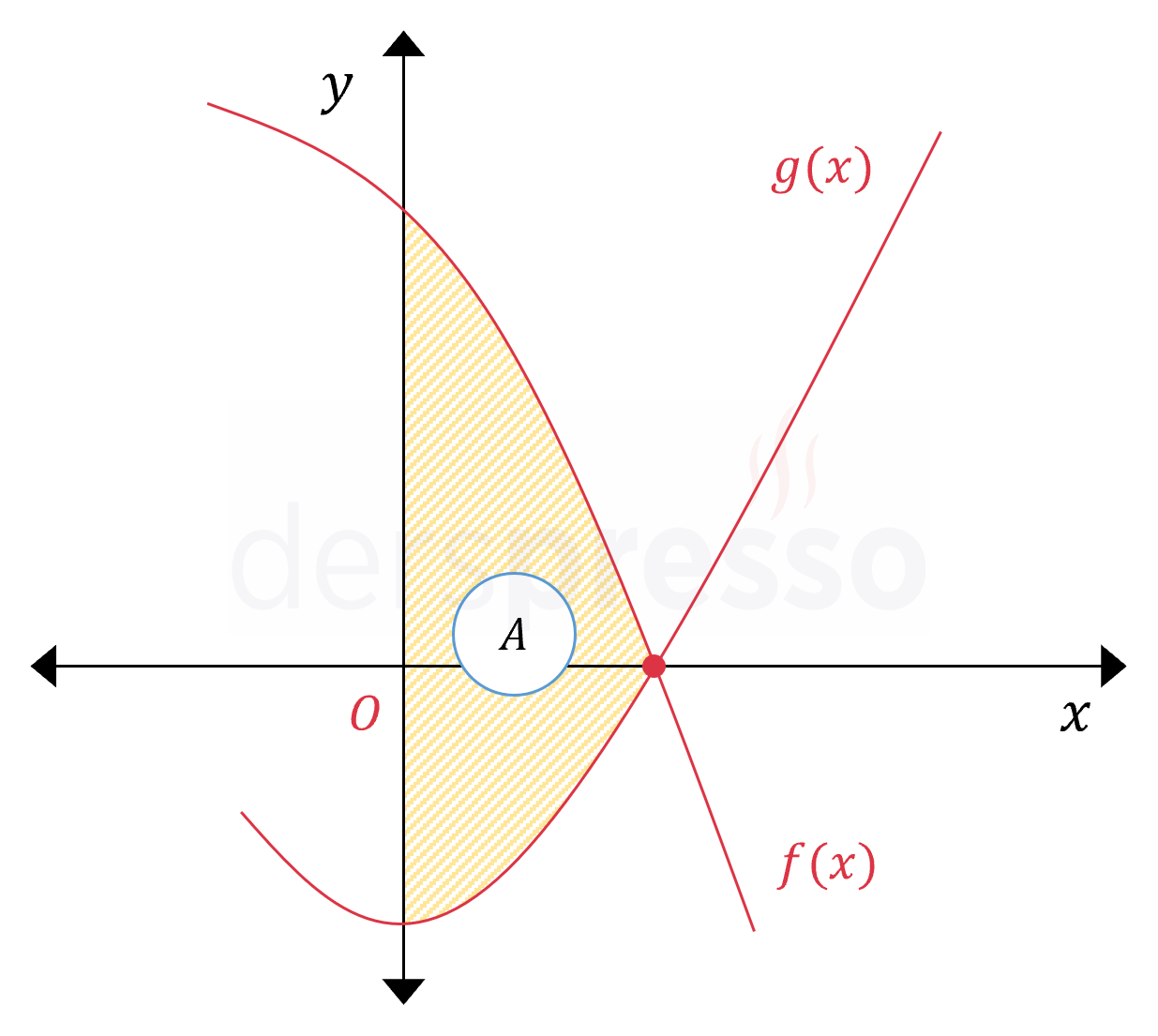
Yukarıda \( f(x) = 6 - 6e^{2x - 1} \) ve \( g(x) = 3x^2 - \frac{3}{4} \) eğrilerinin grafikleri verilmiştir. Buna göre taralı bölgenin alanı kaç birimkaredir?
Çözümü Gösterİki eğrinin \( x \) ekseni üzerinde kesiştikleri noktanın koordinatlarını bulmak için denklemlerden birinin \( x \) eksenini kestiği noktayı bulalım.
\( f(x) = 6 - 6e^{2x - 1} = 0 \)
\( 6e^{2x - 1} = 6 \)
\( e^{2x - 1} = 1 \)
\( 2x - 1 = 0 \)
\( x = \dfrac{1}{2} \)
Bu durumda fonksiyonların \( x \) ekseni üzerindeki kesişim noktasının koordinatları \( (\frac{1}{2}, 0) \) olur.
Taralı bölgenin alanı üstte kalan \( f \) fonksiyonu ile altta kalan \( g \) fonksiyonunun farkının \( [0, \frac{1}{2}] \) aralığındaki belirli integraline eşittir.
\( A = \displaystyle\int_0^{\frac{1}{2}}{(f(x) - g(x))\ dx} \)
\( = \displaystyle\int_0^{\frac{1}{2}}(6 - 6e^{2x - 1} - (3x^2 - \dfrac{3}{4}))\ dx \)
\( = \displaystyle\int_0^{\frac{1}{2}}(-6e^{2x - 1} - 3x^2 + \dfrac{27}{4})\ dx \)
İfadenin integralini alalım.
\( = (-3e^{2x - 1} - x^3 + \dfrac{27x}{4})|_0^{\frac{1}{2}} \)
\( = (-3e^{2 \cdot \frac{1}{2} - 1} - (\dfrac{1}{2})^3 + \dfrac{27 \cdot \frac{1}{2}}{4}) - (-3e^{2(0) - 1} - 0^3 + \dfrac{27(0)}{4}) \)
\( = -3e^0 - \dfrac{1}{8} + \dfrac{27}{8} + 3e^{-1} + 0 \)
\( = \dfrac{1}{4} + \dfrac{3}{e} \) bulunur.

Yukarıda \( f(x) = x^2 - 3x + 4 \) parabolü ile \( g(x) = -3x + 8 \) doğrusunun grafikleri verilmiştir. Buna göre taralı bölgenin alanı kaç birimkaredir?
Çözümü Göster\( f \) ve \( g \) fonksiyonlarının kesişim noktalarını bulmak için iki denklemi ortak çözelim.
\( f(x) = g(x) \)
\( x^2 - 3x + 4 = -3x + 8 \)
\( x^2 - 4 = 0 \)
\( (x - 2)(x + 2) = 0 \)
Buna göre iki fonksiyon \( x = -2 \) ve \( x = 2 \) apsisli noktalarda kesişir.
Taralı bölgenin alanı \( [-2, 2] \) aralığında \( f \) ve \( g \) eğrilerinin arasında kalan alana eşittir.
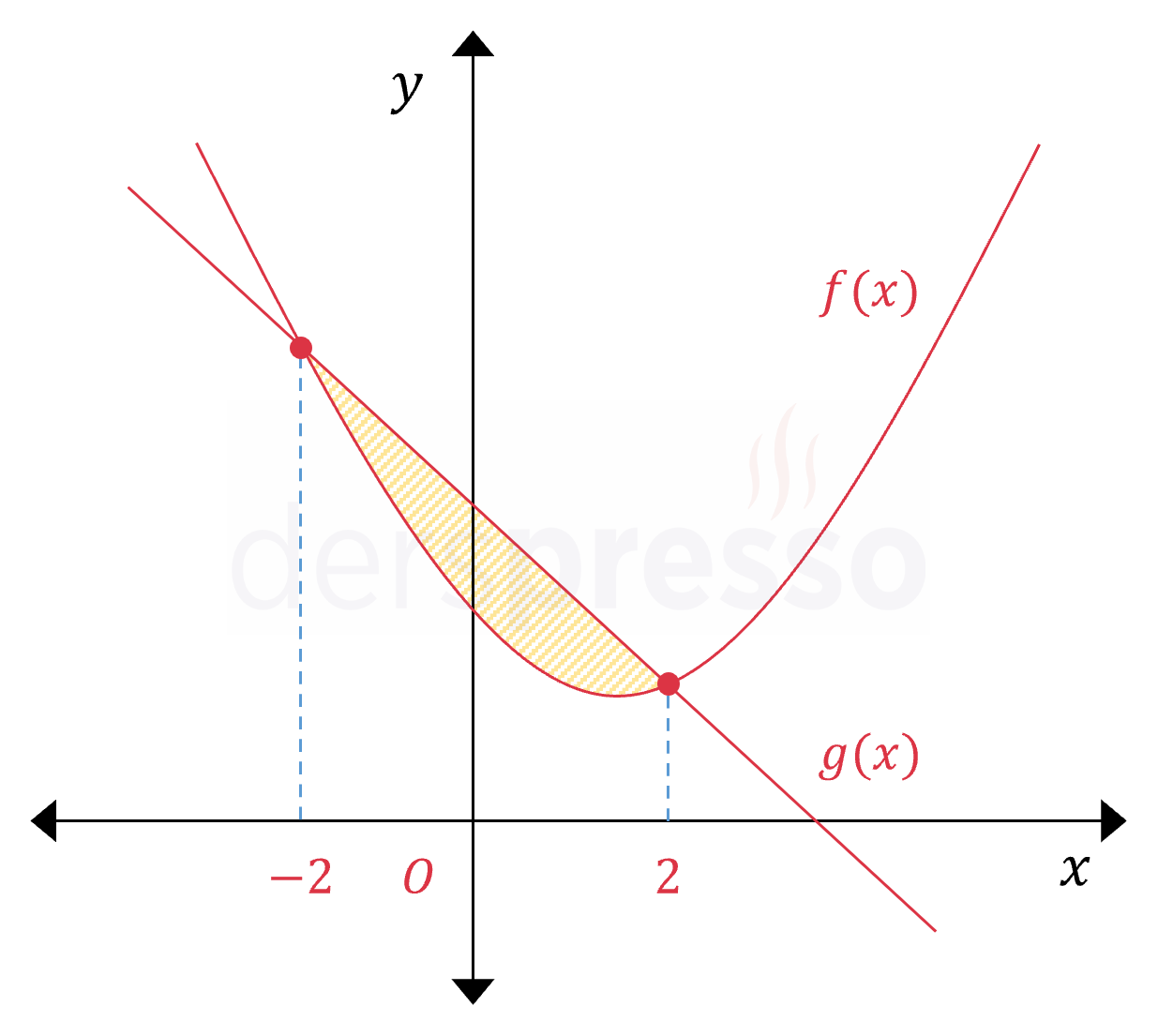
Bu alan grafiği bu aralıkta üstte kalan \( g \) fonksiyonunun \( f \) fonksiyonundan farkının belirli integraline eşittir.
\( A = \displaystyle\int_{-2}^2(g(x) - f(x))\ dx \)
\( = \displaystyle\int_{-2}^2(-3x + 8 - (x^2 - 3x + 4))\ dx \)
\( = \displaystyle\int_{-2}^2(-x^2 + 4)\ dx \)
İfadenin integralini alalım.
\( = (\dfrac{-x^3}{3} + 4x)|_{-2}^2 \)
\( = (\dfrac{-2^3}{3} + 4(2)) - (\dfrac{-(-2)^3}{3} + 4(-2)) \)
\( = (\dfrac{-8}{3} + 8) - (\dfrac{8}{3} - 8) \)
\( = \dfrac{32}{3} \) olarak bulunur.
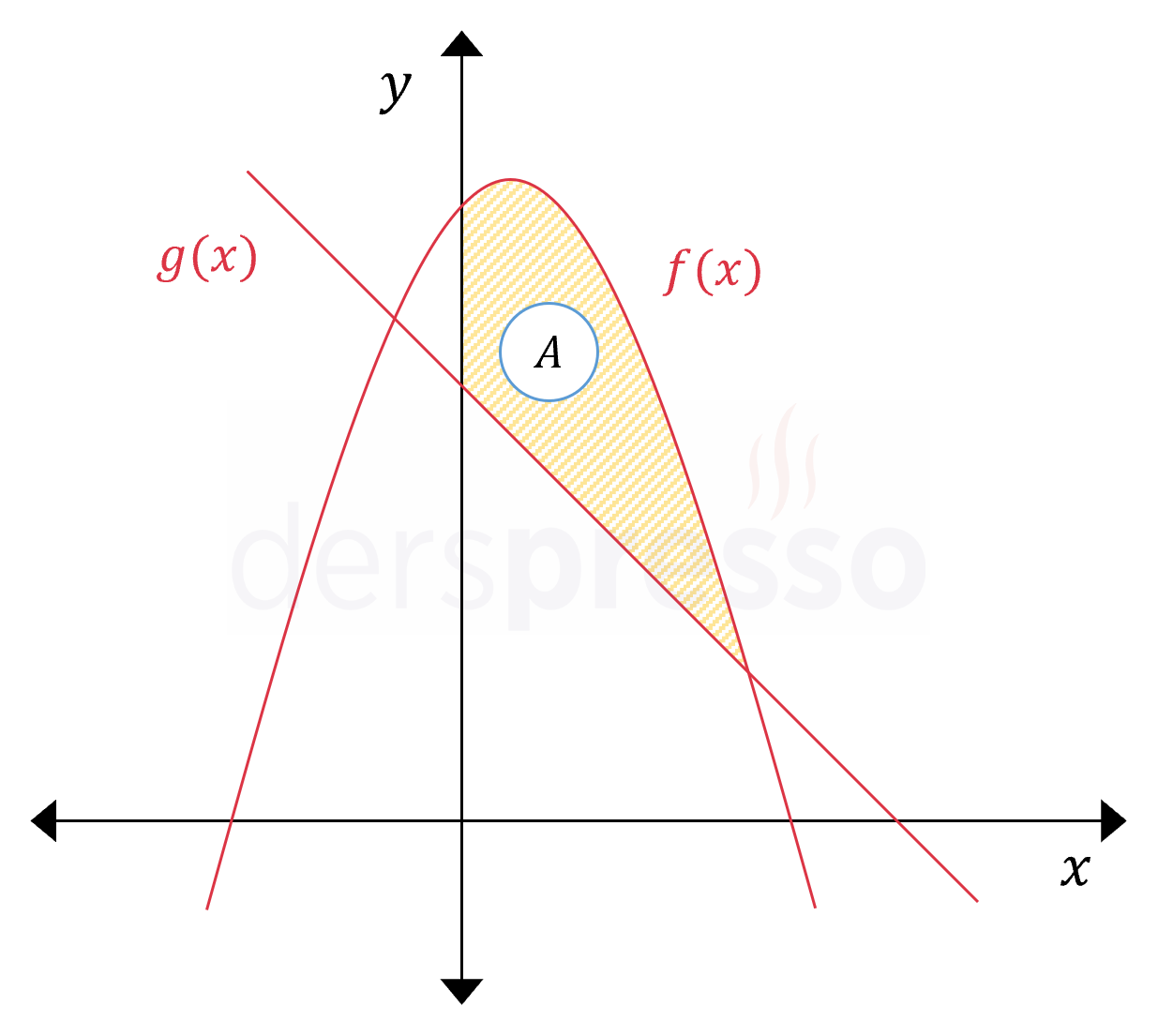
Yukarıda \( f(x) = -x^2 + x + 8 \) ve \( g(x) = 5 - x \) fonksiyonlarının grafikleri verilmiştir. Buna göre taralı bölgenin alanı kaç birimkaredir?
Çözümü Göster\( f \) ve \( g \) fonksiyonlarının kesişim noktalarını bulmak için iki denklemi ortak çözelim.
\( f(x) = g(x) \)
\( -x^2 + x + 8 = 5 - x \)
\( x^2 - 2x - 3 = 0 \)
\( (x + 1)(x - 3) = 0 \)
Buna göre iki fonksiyon \( x = -1 \) ve \( x = 3 \) apsisli noktalarda kesişir.
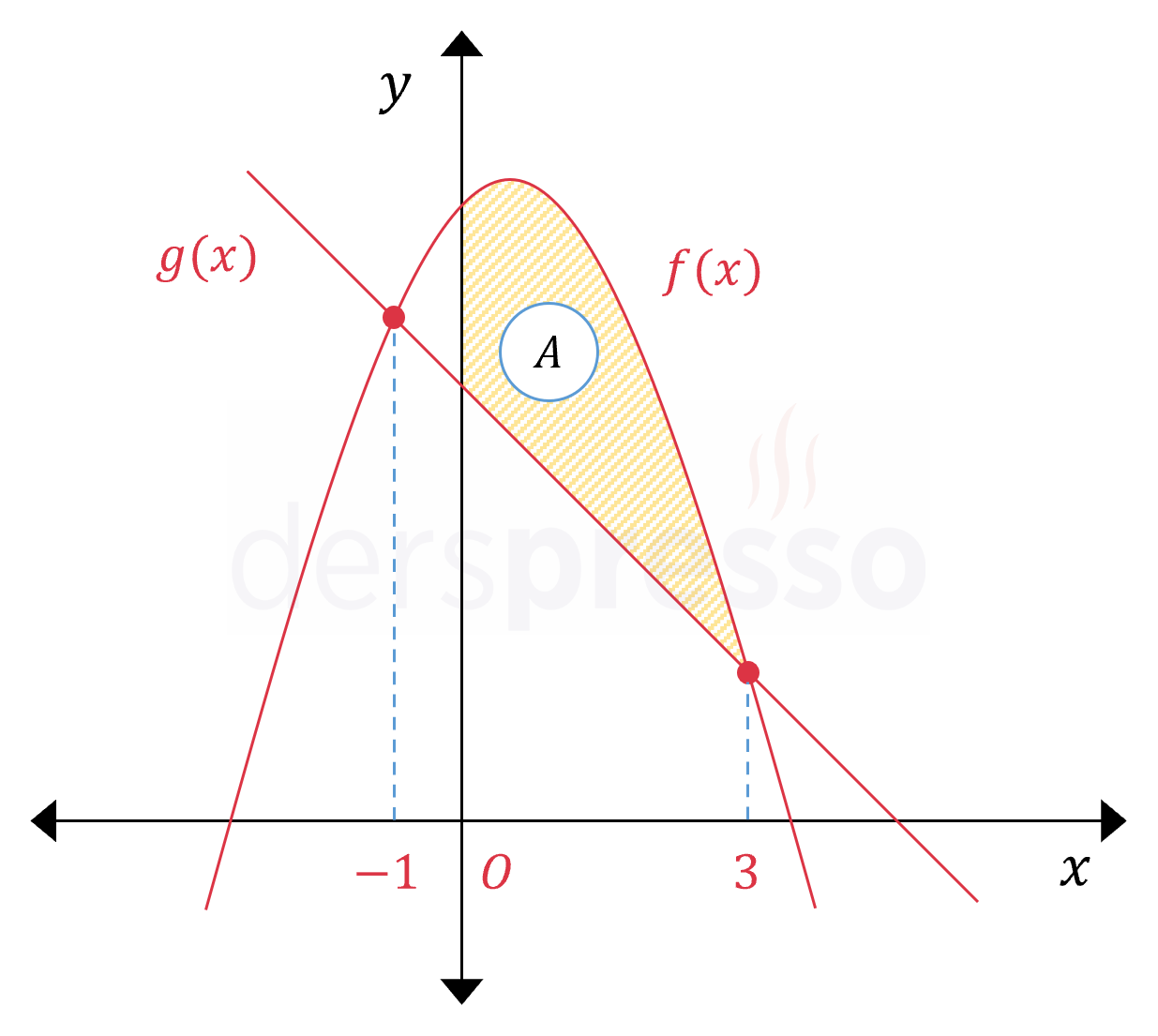
Taralı bölgenin alanı \( [0, 3] \) aralığında \( f \) ve \( g \) eğrilerinin arasında kalan alana eşittir.
Bu alan grafiği bu aralıkta üstte kalan \( f \) fonksiyonunun \( g \) fonksiyonundan farkının belirli integraline eşittir.
\( A = \displaystyle\int_0^3(f(x) - g(x))\ dx \)
\( = \displaystyle\int_0^3(-x^2 + x + 8 - (5 - x))\ dx \)
\( = \displaystyle\int_0^3(-x^2 + 2x + 3)\ dx \)
İfadenin integralini alalım.
\( = (\dfrac{-x^3}{3} + x^2 + 3x)|_0^3 \)
\( = (\dfrac{-3^3}{3} + 3^2 + 3(3)) - (\dfrac{-0^3}{3} + 0^2 + 3(0)) \)
\( = (-9 + 9 + 9) - (0) \)
\( = 9 \) olarak bulunur.
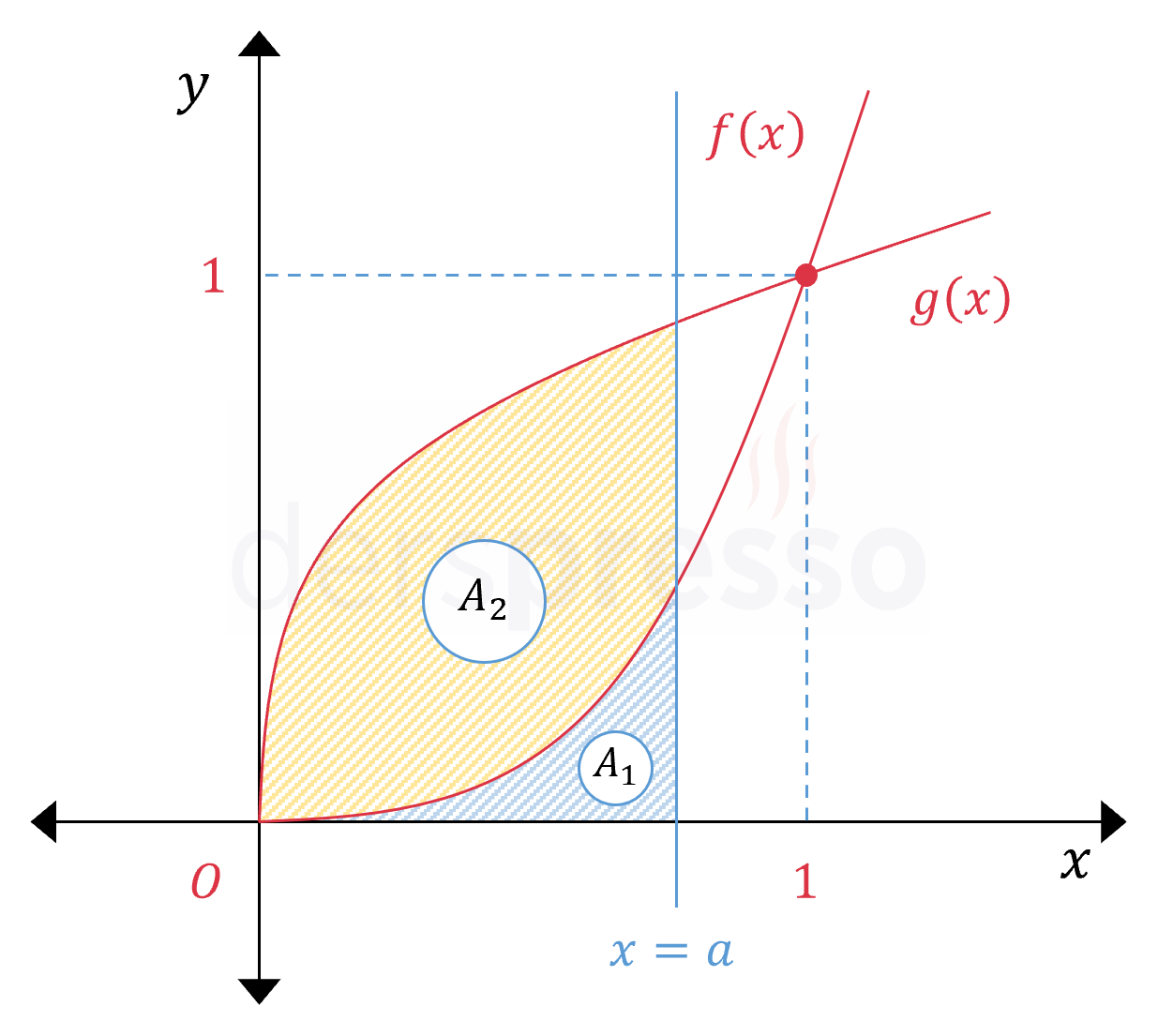
\( 0 \lt a \le 1 \) olmak üzere,
Yukarıdaki şekilde \( f(x) = x^2 \) ve \( g(x) = \sqrt{x} \) eğrileri ve \( x = a \) doğrusu verilmiştir.
Taralı \( A_2 \) alanı \( A_1 \) alanının 4 katına eşit olduğuna göre, \( a \) değeri kaçtır?
Çözümü Gösterİki taralı bölge için integral alan formüllerini yazalım.
\( A_1 \) alanı \( [0, a] \) aralığında \( f(x) \) eğrisi ile \( x \) ekseni arasında kalan alana karşılık gelir.
\( A_1 = \displaystyle\int_0^a x^2\ dx \)
İfadenin integralini alalım.
\( = (\dfrac{x^3}{3})|_0^a \)
\( = \dfrac{a^3}{3} - \dfrac{0^3}{3} \)
\( = \dfrac{a^3}{3} \)
\( A_2 \) alanı \( [0, a] \) aralığında \( g(x) \) eğrisi ile \( f(x)\) eğrisi arasında kalan alana karşılık gelir.
\( A_2 = \displaystyle\int_0^a (g(x) - f(x))\ dx \)
\( = \displaystyle\int_0^a (\sqrt{x} - x^2)\ dx \)
İfadenin integralini alalım.
\( = (\dfrac{2\sqrt{x^3}}{3} - \dfrac{x^3}{3})|_0^a \)
\( = (\dfrac{2\sqrt{a^3}}{3} - \dfrac{a^3}{3}) - (\dfrac{2\sqrt[2]{0^3}}{3} - \dfrac{0^3}{3}) \)
\( = \dfrac{2\sqrt{a^3}}{3} - \dfrac{a^3}{3} \)
\( A_2 \) alanı \( A_1 \) alanının 4 katına eşittir.
\( 4A_1 = A_2 \)
\( 4 \cdot \dfrac{a^3}{3} = \dfrac{2\sqrt{a^3}}{3} - \dfrac{a^3}{3} \)
\( \dfrac{5a^3}{3} = \dfrac{2\sqrt{a^3}}{3} \)
\( a^{\frac{3}{2}} = \dfrac{2}{5} \)
\( a = \sqrt[3]{\dfrac{4}{25}}\) bulunur.
\( y = 7e^x \), \( y = 3 - 2e^x \) ve \( y \) ekseni arasında kalan bölgenin alanı nedir?
Çözümü GösterFonksiyonların kesişim noktalarının apsis değerlerini bulmak için iki denklemi ortak çözelim.
\( 7e^x = 3 - 2e^x \)
\( 9e^x = 3 \)
\( e^x = \dfrac{1}{3} = 3^{-1} \)
\( x = \ln{3^{-1}} = -\ln{3} \lt 0 \)
\( y \) ekseni denklemi \( x = 0 \) olan doğrudur. Bu yüzden istenen alanı bulmak için integral \( [-\ln{3}, 0] \) aralığında alınmalıdır.
\( y = 7e^x \) fonksiyonu artan, \( y = 3 - 2e^x \) fonksiyonu azalan olduğu için, iki fonksiyonun kesiştiği \( x = -\ln{3} \) noktası ile \( x = 0 \) doğrusu arasında birinci fonksiyon üstte olur, dolayısıyla birinci fonksiyonun ikinci fonksiyondan farkının integralini almalıyız.
\( \displaystyle\int_{-\ln{3}}^0 (7e^x - (3 - 2e^x))\ dx \)
\( = \displaystyle\int_{-\ln{3}}^0 (9e^x - 3)\ dx \)
İfadenin integralini alalım.
\( = (9e^x - 3x)|_{-\ln{3}}^0 \)
\( = (9e^0 - 3(0)) - (9e^{-\ln{3}} - 3(-\ln{3})) \)
\( = 9 - (9e^{\ln{3^{-1}}} + 3\ln{3}) \)
\( = 9 - 9 \cdot 3^{-1} - 3\ln{3} \)
\( = 6 - 3\ln{3} \) bulunur.
\( y = 2x^2 - 3ax + a \) ve \( y = -x^2 + 3ax + a \) parabolleri arasındaki alan 32 birimdir.
Buna göre \( a \)'nın alabileceği değerler nedir?
Çözümü GösterParabollerin kesişim noktalarının apsis değerlerini bulmak için iki denklemi ortak çözelim.
\( 2x^2 - 3ax + a = -x^2 + 3ax + a \)
\( 3x^2 - 6ax = 0 \)
\( 3x(x - 2a) = 0 \)
Denklemin çözüm kümesi her bir çarpanı sıfır yapan değerlerden oluşur.
\( x = 0 \) ya da \( x = 2a \)
Parabollerin arasında kalan alan, kesişim noktaları arasındaki aralıkta grafiği üstte olan parabolün denkleminin altta olan parabolün denkleminden farkının integraline eşittir.
Pozitif ve negatif başkatsayılı iki parabolün kesişim noktaları arasında negatif başkatsayılı parabol daha üsttedir, dolayısıyla negatif başkatsayılı denklemden pozitif başkatsayılı denklemi çıkarmalıyız.
İntegral işlemi apsis değeri daha küçük olan noktadan daha büyük olana alınmalıdır. \( 2a \) sayısının işaretini bilmediğimiz için integrali \( [0, 2a] \) aralığında alıp sonucun mutlak değerini alabiliriz.
\( \displaystyle\int_0^{2a} (-x^2 + 3ax + a - (2x^2 - 3ax + a))\ dx \)
\( = \displaystyle\int_0^{2a} (6ax - 3x^2)\ dx \)
İfadenin integralini alalım.
\( = (3ax^2 - x^3)|_0^{2a} \)
\( = (3a(2a)^2 - (2a)^3) - (3a(0)^2 - 0^3) \)
\( = 12a^3 - 8a^3 - 0 = 4a^3 \)
Bulduğumuz integral değerinin mutlak değerini 32'ye eşitleyelim.
\( \abs{4a^3} = 32 \)
\( 4a^3 = 32 \) ya da \( 4a^3 = -32 \)
\( a \in \{2, -2\} \) bulunur.
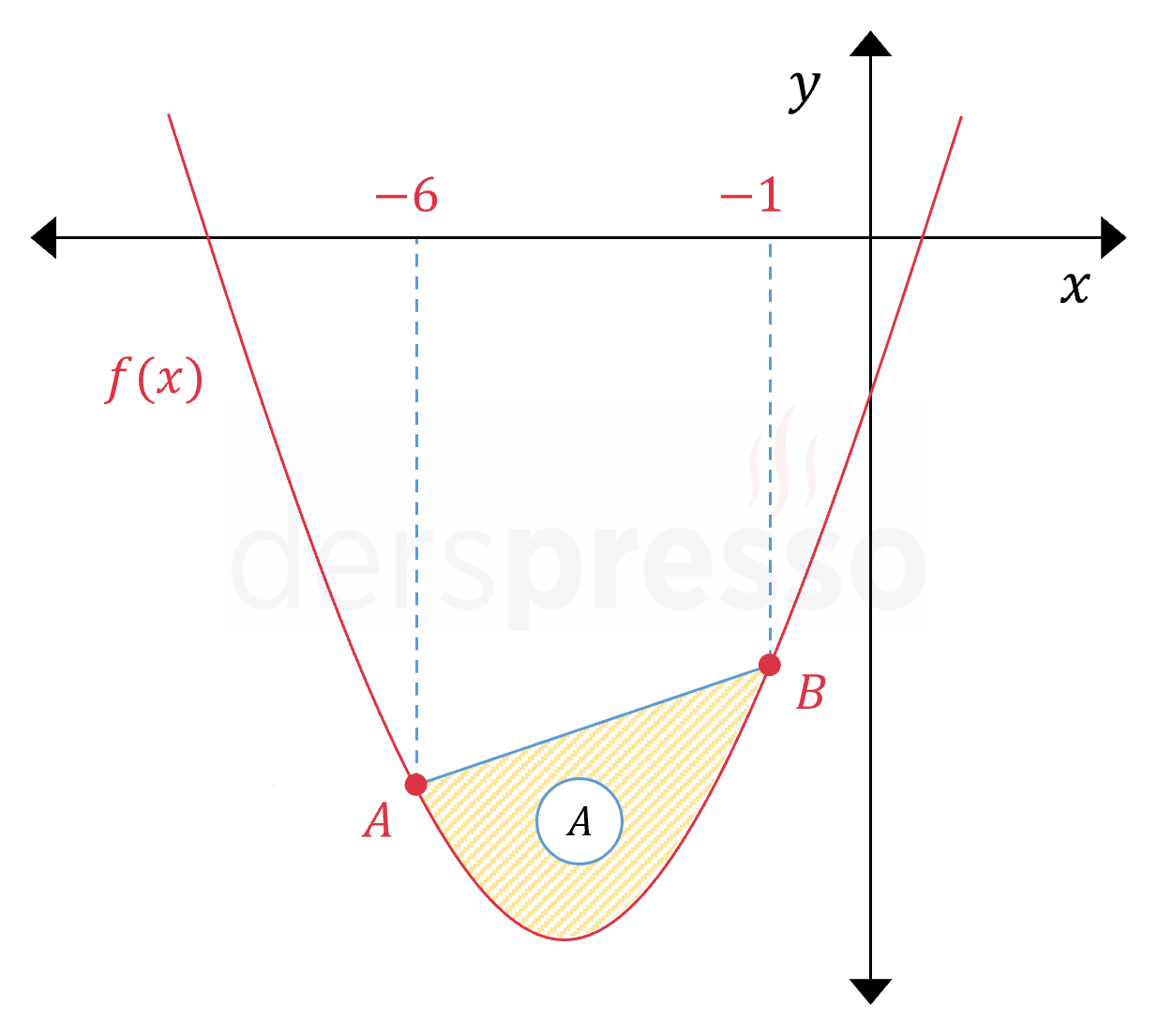
Yukarıda \( f(x) = x^2 + 8x - 4 \) parabolü ile \( [AB] \) doğru parçası verilmiştir. \( A \) ve \( B \) noktalarının apsisleri sırasıyla -6 ve -1 olduğuna göre, taralı bölgenin alanı kaç birimkaredir?
Çözümü Göster\( A \) ve \( B \) noktalarının ordinat değerlerini bulalım.
\( f(-6) = (-6)^2 + 8(-6) - 4 = -16 \)
\( A(-6, -16) \)
\( f(-1) = (-1)^2 + 8(-1) - 4 = -11 \)
\( B(-1, -11) \)
Bu iki noktanın koordinatlarını kullanarak \( [AB] \) doğru parçasının denklemini bulalım.
\( \dfrac{y - y_2}{x - x_2} = \dfrac{y_2 - y_1}{x_2 - x_1} \)
\( \dfrac{y - (-11)}{x - (-1)} = \dfrac{(-11) - (-16)}{(-1) - (-6)} \)
\( \dfrac{y + 11}{x + 1} = \dfrac{5}{5} \)
\( y = x - 10 \)
Belirli bir aralıkta iki fonksiyon arasında kalan alan, üstteki fonksiyon ile alttaki fonksiyonun farkının bu aralıktaki belirli integraline eşittir.
Taralı bölgenin alanını bulmak için \( [-6, -1] \) aralığında üstte olan \( y = x - 10 \) doğru denklemi ile alttaki \( f(x) \) parabol denkleminin farkının belirli integralini alalım.
\( A = \displaystyle\int_{-6}^{-1}((x - 10) - (x^2 + 8x - 4))\ dx \)
\( = \displaystyle\int_{-6}^{-1}(-x^2 - 7x - 6)\ dx \)
İfadenin integralini alalım.
\( = (\dfrac{-x^3}{3} - \dfrac{7x^2}{2} - 6x)|_{-6}^{-1} \)
\( = (\dfrac{-(-1)^3}{3} - \dfrac{7(-1)^2}{2} - 6(-1)) - (\dfrac{-(-6)^3}{3} - \dfrac{7(-6)^2}{2} - 6(-6)) \)
\( = (\dfrac{1}{3} - \dfrac{7}{2} + 6) - (72 - 126 + 36) \)
\( = \dfrac{125}{6} \) birimkare olarak bulunur.
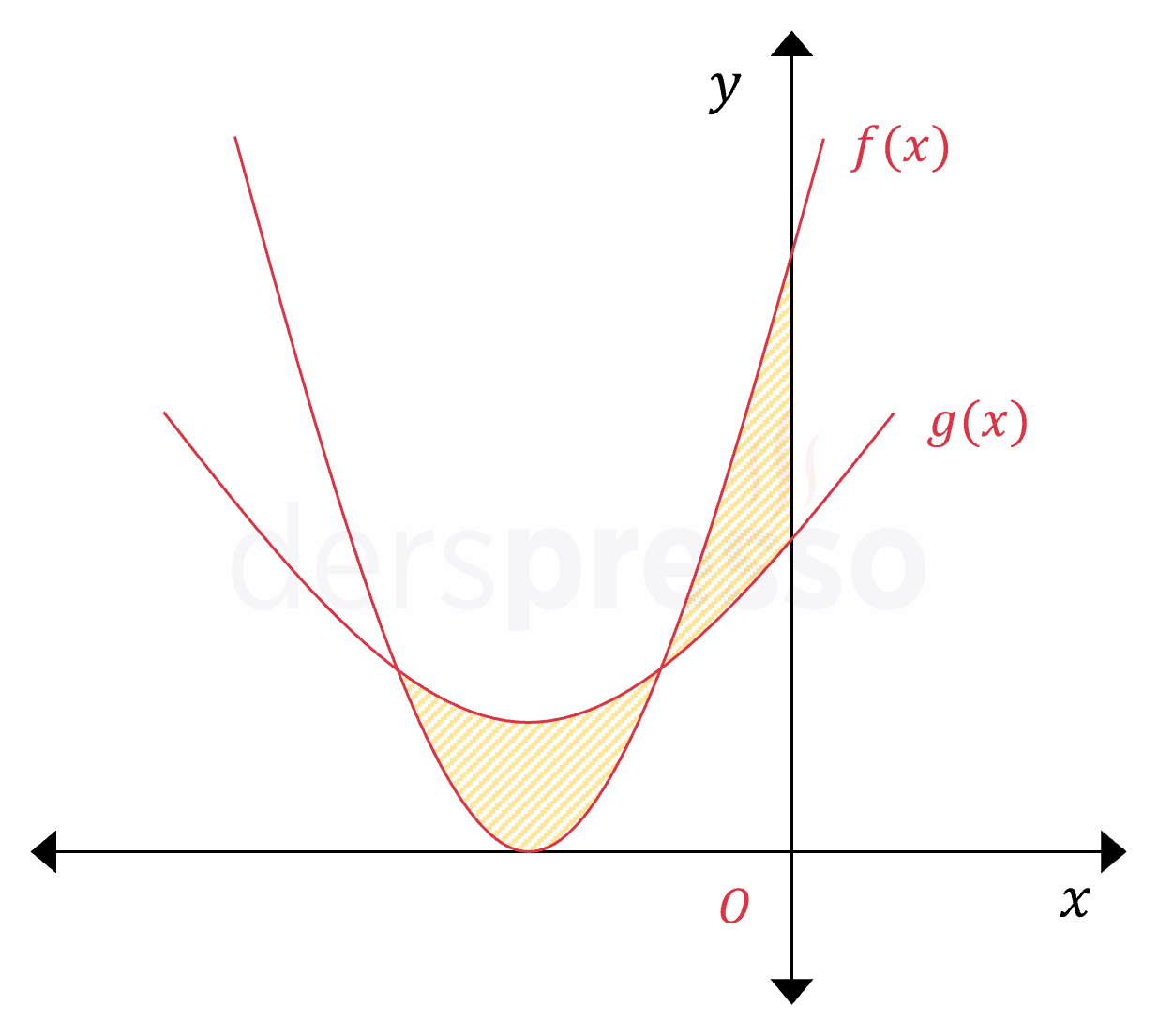
Yukarıda \( f(x) = 2(x + 3)^2 \) ve \( g(x) = \dfrac{x^2}{2} + 3x + 6 \) parabollerinin grafikleri verilmiştir. Buna göre taralı bölgenin alanı kaç birimkaredir?
Çözümü Göster\( f \) ve \( g \) fonksiyonlarının kesişim noktalarını bulmak için iki denklemi ortak çözelim.
\( f(x) = g(x) \)
\( 2(x + 3)^2 = \dfrac{x^2}{2} + 3x + 6 \)
\( 2(x^2 + 6x + 9) = \dfrac{x^2}{2} + 3x + 6 \)
\( 4x^2 + 24x + 36 = x^2 + 6x + 12 \)
\( 3x^2 + 18x + 24 = 0 \)
\( 3(x + 4)(x + 2) = 0 \)
Buna göre iki fonksiyon \( x = -4 \) ve \( x = -2 \) apsisli noktalarda kesişir.
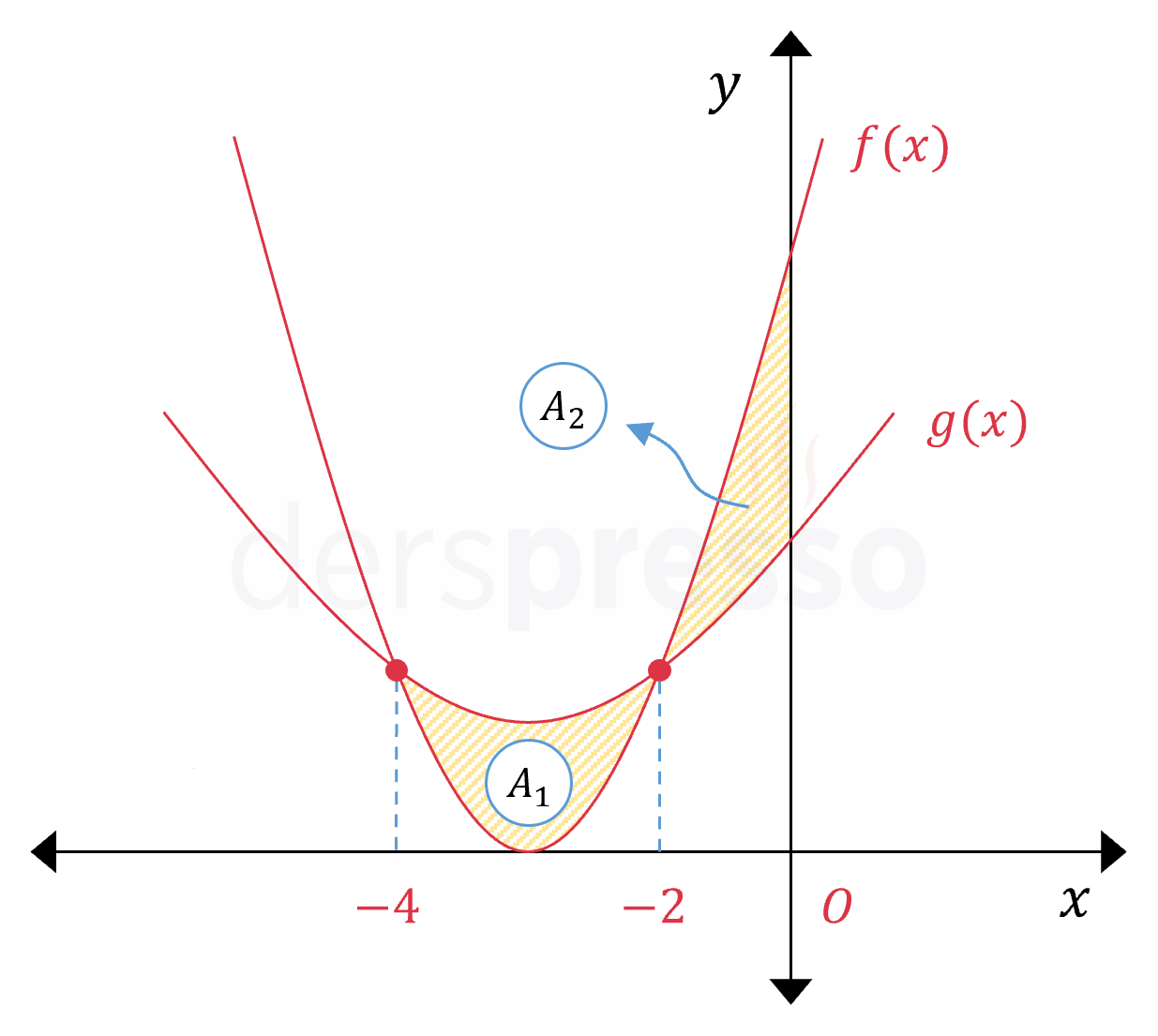
Taralı bölgenin alanı \( [-4, 0] \) aralığında \( f \) ve \( g \) fonksiyonlarının arasında kalan iki bölgenin alanları toplamına eşittir.
\( A = A_1 + A_2 \)
\( [-4, -2] \) ve \( [-2, 0] \) aralıklarında üstte kalan fonksiyon farklı olduğu için belirli integrali iki aralık için ayrı ayrı almalıyız.
Önce \( A_1 \) alanını bulalım. Bu aralıkta \( g \) fonksiyonu \( f \) fonksiyonunun üzerindedir.
\( A_1 = \displaystyle\int_{-4}^{-2}(g(x) - f(x))\ dx \)
\( = \displaystyle\int_{-4}^{-2}(\dfrac{x^2}{2} + 3x + 6 - (2(x + 3)^2))\ dx \)
\( = \displaystyle\int_{-4}^{-2}(\dfrac{x^2}{2} + 3x + 6 - (2x^2 + 12x + 18))\ dx \)
\( = \displaystyle\int_{-4}^{-2}(-\dfrac{3x^2}{2} - 9x - 12)\ dx \)
İfadenin integralini alalım.
\( = (-\dfrac{x^3}{2} - \dfrac{9x^2}{2} - 12x)|_{-4}^{-2} \)
\( = (-\dfrac{(-2)^3}{2} - \dfrac{9(-2)^2}{2} - 12(-2)) - (-\dfrac{(-4)^3}{2} - \dfrac{9(-4)^2}{2} - 12(-4)) \)
\( = (4 - 18 + 24) - (32 - 72 + 48) \)
\( = 2 \)
Şimdi \( A_2 \) alanını bulalım. Bu aralıkta \( f \) fonksiyonu \( g \) fonksiyonunun üzerindedir.
\( A_2 = \displaystyle\int_{-2}^{0}(f(x) - g(x))\ dx \)
\( = \displaystyle\int_{-2}^0(2(x + 3)^2 - (\dfrac{x^2}{2} + 3x + 6))\ dx \)
\( = \displaystyle\int_{-2}^0(2x^2 + 12x + 18 - (\dfrac{x^2}{2} + 3x + 6))\ dx \)
\( = \displaystyle\int_{-2}^0(\dfrac{3x^2}{2} + 9x + 12)\ dx \)
İfadenin integralini alalım.
\( = (\dfrac{x^3}{2} + \dfrac{9x^2}{2} + 12x)|_{-2}^0 \)
\( = (\dfrac{0^3}{2} + \dfrac{9(0)^2}{2} + 12(0)) - (\dfrac{(-2)^3}{2} + \dfrac{9(-2)^2}{2} + 12(-2)) \)
\( = 0 - (-4 + 18 - 24) \)
\( = 10 \)
Taralı bölgenin alanı bulduğumuz iki alanın toplamına eşittir.
\( A = A_1 + A_2 \)
\( = 2 + 10 = 12 \) olarak bulunur.
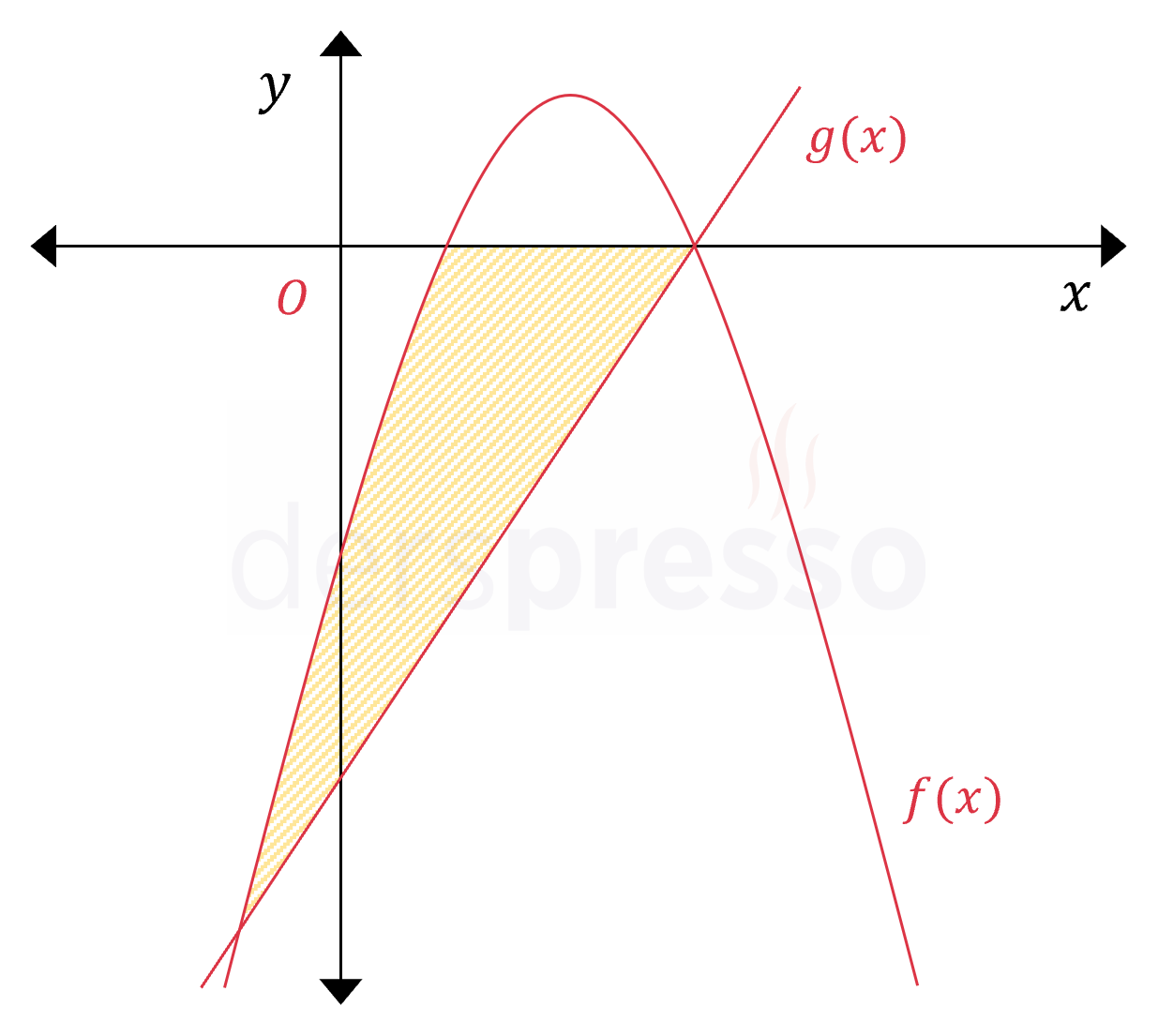
Yukarıda \( f(x) = -x^2 + 5x - 4 \) parabolü ile \( g(x) = 2x - 8 \) doğrusunun grafikleri verilmiştir. Buna göre taralı bölgenin alanı kaç birimkaredir?
Çözümü Göster\( f \) ve \( g \) fonksiyonlarının kesişim noktalarını bulmak için iki denklemi ortak çözelim.
\( f(x) = g(x) \)
\( -x^2 + 5x - 4 = 2x - 8 \)
\( x^2 - 3x - 4 = 0 \)
\( (x + 1)(x - 4) = 0 \)
Buna göre iki fonksiyon \( x = -1 \) ve \( x = 4 \) apsisli noktalarda kesişir.
\( f \) fonksiyonunun \( x \) eksenini kestiği noktaları bulalım.
\( f(x) = -x^2 + 5x - 4 = 0 \)
\( -(x - 1)(x - 4) = 0 \)
Buna göre \( f \) fonksiyonu \( x \) eksenini \( x = 1 \) ve \( x = 4 \) apsisli noktalarda keser.
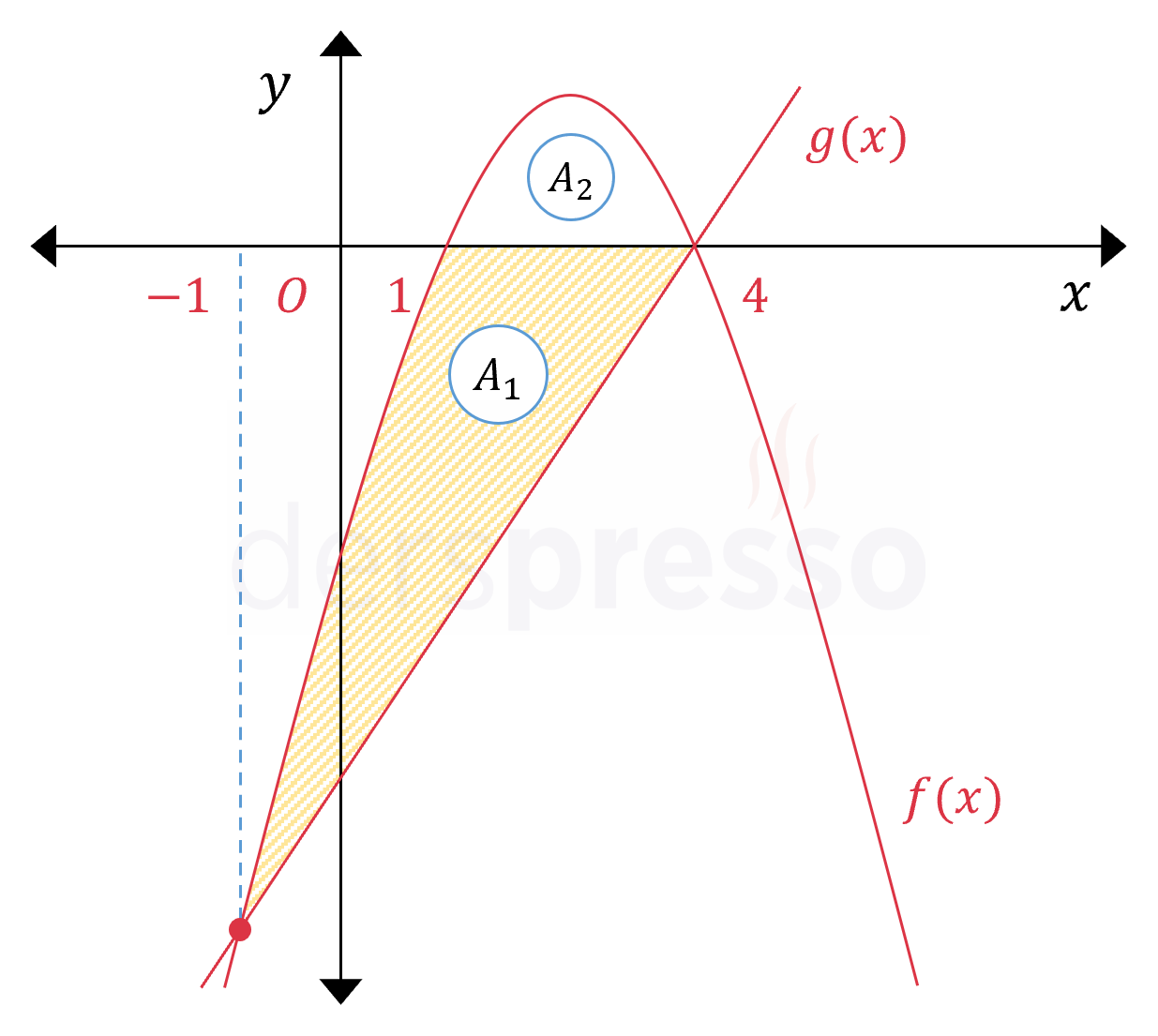
Yukarıdaki grafikteki iki bölgeyi belirli integral cinsinden ifade edelim.
\( A_2 \) alanı \( [1, 4] \) aralığında \( f \) fonksiyonu ile \( x \) ekseni arasında kalan bölgenin alanına eşittir.
\( A_1 + A_2 \) alanı \( [-1, 4] \) aralığında \( f \) ve \( g \) fonksiyonlarının arasında kalan bölgenin alanına eşittir.
Soruda istenen alan bu iki bölgenin alanları farkına eşittir.
\( A_1 = (A_1 + A_2) - A_2 \)
Önce \( A_1 + A_2 \) alanını bulalım.
Bu alanı bu aralıkta üstte kalan \( f \) fonksiyonun \( g \) fonksiyonundan farkının belirli integralini alarak bulabiliriz.
\( A_1 + A_2 = \displaystyle\int_{-1}^4(f(x) - g(x))\ dx \)
\( = \displaystyle\int_{-1}^4(-x^2 + 5x - 4 - (2x - 8))\ dx \)
\( = \displaystyle\int_{-1}^4(-x^2 + 3x + 4)\ dx \)
İfadenin integralini alalım.
\( = (\dfrac{-x^3}{3} + \dfrac{3x^2}{2} + 4x)|_{-1}^4 \)
\( = (\dfrac{-4^3}{3} + \dfrac{3(4)^2}{2} + 4(4)) - (\dfrac{-(-1)^3}{3} + \dfrac{3(-1)^2}{2} + 4(-1)) \)
\( = (\dfrac{-64}{3} + 24 + 16) - (\dfrac{1}{3} + \dfrac{3}{2} - 4) \)
\( = \dfrac{125}{6} \)
Şimdi \( A_2 \) alanını bulalım.
\( A_2 = \displaystyle\int_1^4{f(x)}\ dx \)
\( = \displaystyle\int_1^4(-x^2 + 5x - 4)\ dx \)
İfadenin integralini alalım.
\( = (-\dfrac{x^3}{3} + \dfrac{5x^2}{2} - 4x)|_1^4 \)
\( = (-\dfrac{4^3}{3} + \dfrac{5(4)^2}{2} - 4(4)) - (-\dfrac{1^3}{3} + \dfrac{5(1)^2}{2} - 4(1)) \)
\( = (-\dfrac{64}{3} + 40 - 16) - (-\dfrac{1}{3} + \dfrac{5}{2} - 4) \)
\( = \dfrac{9}{2} \)
Taralı bölge bulduğumuz birinci alanın ikinci alandan farkına eşittir.
\( A_1 = (A_1 + A_2) - A_2 \)
\( = \dfrac{125}{6} - \dfrac{9}{2} \)
\( = \dfrac{49}{3} \) olarak bulunur.
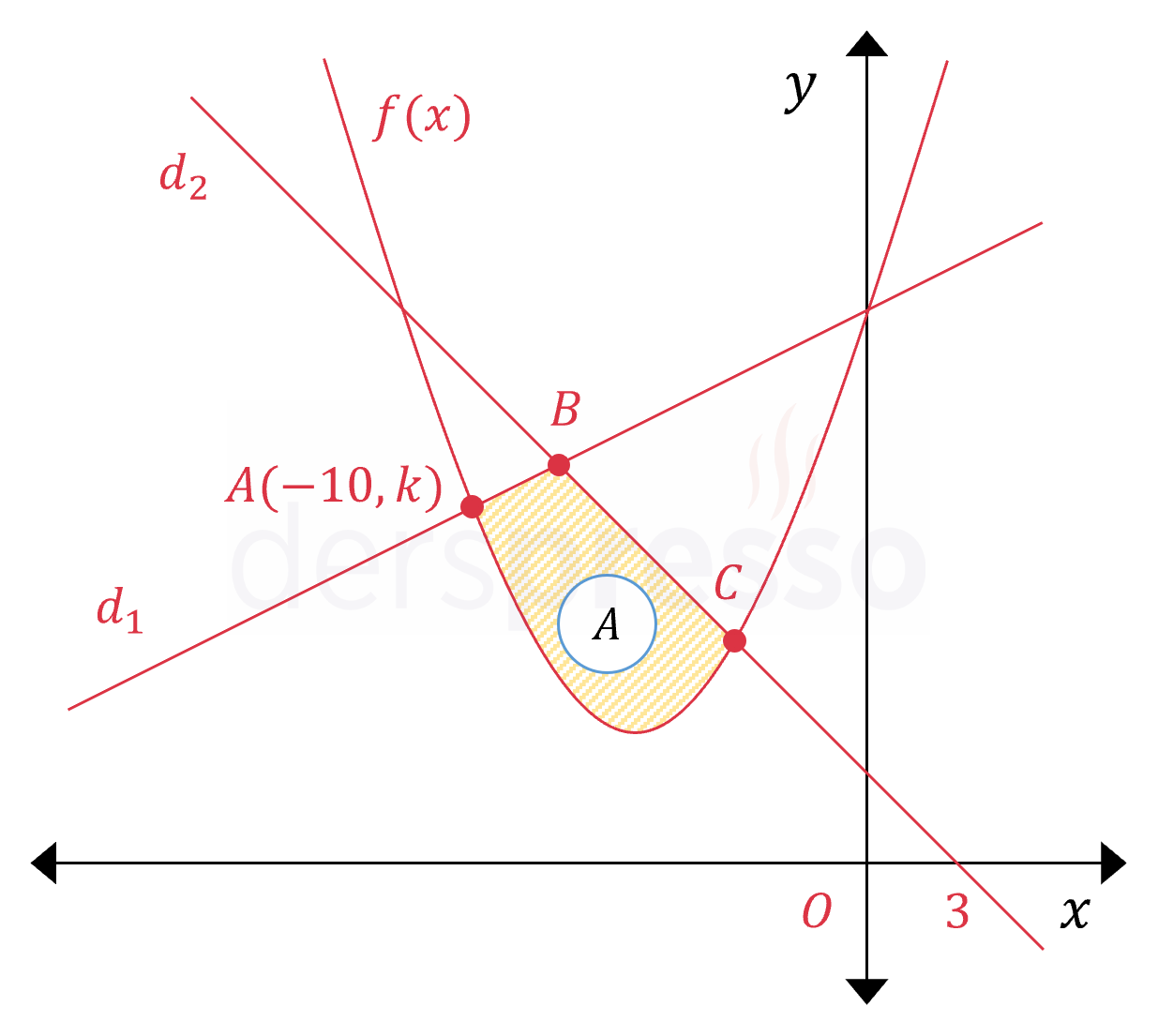
Yukarıda \( d_1 \) ve \( d_2 \) doğruları ile \( f(x) = \dfrac{x^2}{4} + 3x + 15 \) parabolünün grafiği verilmiştir.
\( d_1 \) doğrusu parabolün \( A \) noktasındaki normali olduğuna ve \( d_2 \) doğrusu parabolü \( C(-4, 7) \) noktasında kestiğine göre, taralı bölgenin alanı kaç birimkaredir?
Çözümü GösterÖnce \( d_1 \) ve \( d_2 \) doğrularının denklemlerini bularak kesişimleri olan \( B \) noktasının koordinatlarını bulalım.
Bir fonksiyonun bir noktadaki teğet doğrusuna o noktada dik olan doğruya fonksiyonun o noktadaki normali denir.
\( x = -10 \) apsisli noktadaki teğetin eğimini bulmak için \( f(x) \) fonksiyonunun türevini alalım.
\( f'(x) = \dfrac{x}{2} + 3 \)
\( f'(-10) = \dfrac{-10}{2} + 3 = -2 \)
Bir noktadaki normal ve teğet doğrular birbirine dik olduğu için eğimleri çarpımı -1 olur.
\( m_{d_1} \cdot -2 = -1 \)
\( m_{d_1} = \dfrac{1}{2} \)
\( A \) noktasının ordinat değerini bulalım.
\( f(-10) = \dfrac{(-10)^2}{4} + 3(-10) + 15 = 10 \)
\( A(-10, 10) \)
Normal doğrusunun denklemini bulmak için bir noktası ve eğimi bilinen doğru denklemini kullanalım.
\( y - y_1 = m(x - x_1) \)
\( y - 10 = \dfrac{1}{2}(x - (-10)) \)
\( d_1: y = \dfrac{1}{2}x + 15 \)
\( d_2 \) doğrusunun eğimini \( C(-4, 7) \) noktasının ve \( x \) eksenini kestiği \( (3, 0) \) noktasının koordinatlarını kullanarak bulalım.
\( m_{d_2} = \dfrac{7 - 0}{-4 - 3} = -1 \)
\( d_2 \) doğrusunun denklemini bulmak için bir noktası ve eğimi bilinen doğru denklemini kullanalım.
\( y - y_1 = m(x - x_1) \)
\( y - 7 = -1(x - (-4)) \)
\( d_2: y = -x + 3 \)
\( B \) noktasının koordinatlarını bulmak için iki doğru denklemini ortak çözelim.
\( \dfrac{1}{2}x + 15 = -x + 3 \)
\( \dfrac{3}{2}x = -12 \)
\( x = -8, \quad y = 11 \)
\( B(-8, 11) \)
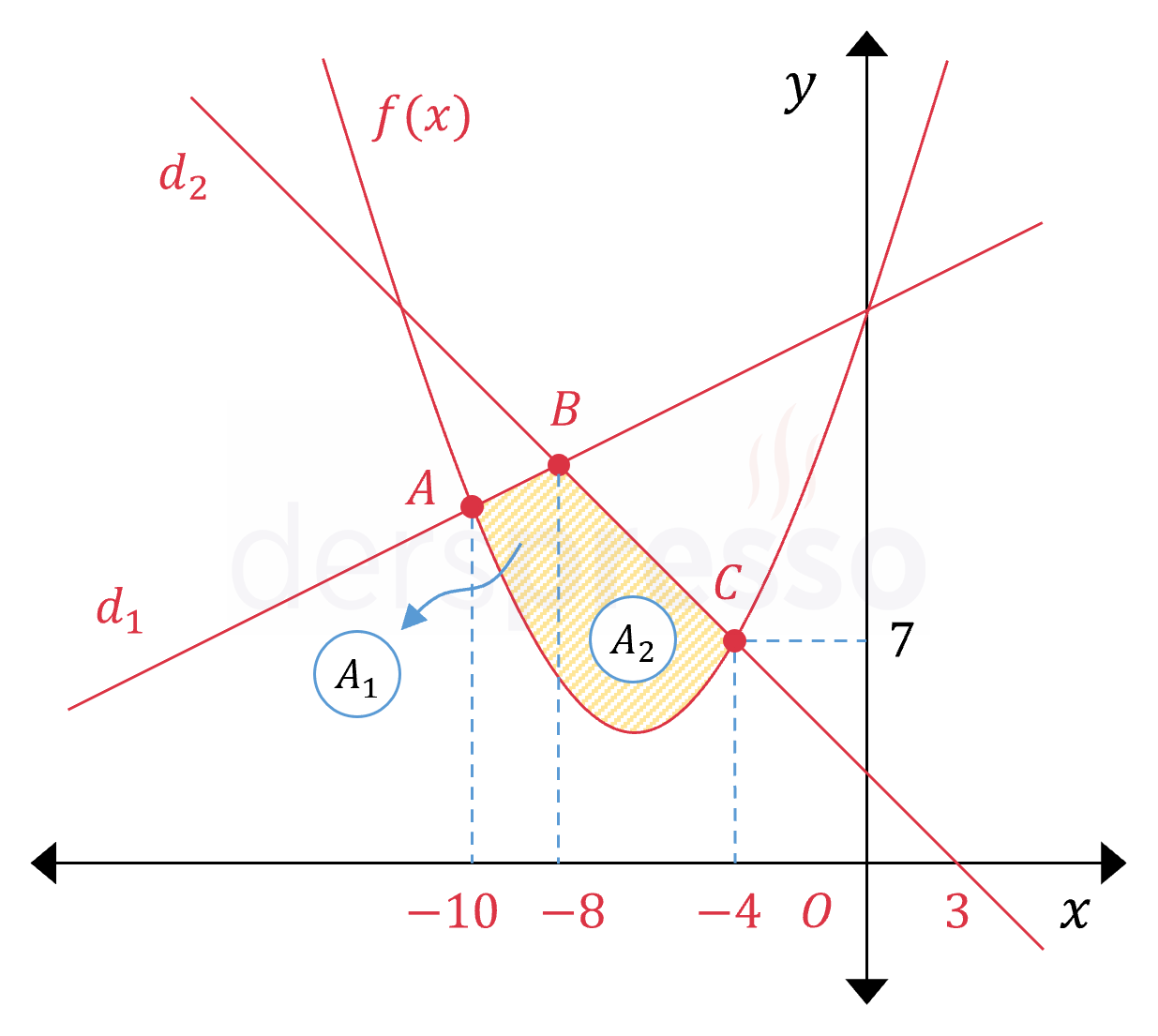
Taralı bölgenin alanı \( [-10, -4] \) aralığında \( f \) fonksiyonu ile iki doğru arasında kalan alana eşittir.
\( [-10, -8] \) ve \( [-8, -4] \) aralıklarında bu alan \( f \) fonksiyonu ile farklı bir doğru arasında kalan alana karşılık geldiği için alanı iki aralığa ayıralım ve belirli integralini ayrı ayrı alalım.
\( A = A_1 + A_2 \)
Önce \( [-10, -8] \) aralığında \( f \) fonksiyonu ile \( d_1 \) doğrusu arasında kalan bölgenin alanını bulalım. Bu aralıkta \( d_1 \) doğrusu \( f \) fonksiyonunun üzerindedir.
\( A_1 = \displaystyle\int_{-10}^{-8}(\dfrac{1}{2}x + 15 - f(x))\ dx \)
\( = \displaystyle\int_{-10}^{-8}(\dfrac{x}{2} + 15 - (\dfrac{x^2}{4} + 3x + 15))\ dx \)
\( = \displaystyle\int_{-10}^{-8}(-\dfrac{x^2}{4} - \dfrac{5x}{2} )\ dx \)
İfadenin integralini alalım.
\( = (-\dfrac{x^3}{12} - \dfrac{5x^2}{4})|_{-10}^{-8} \)
\( = (-\dfrac{(-8)^3}{12} - \dfrac{5(-8)^2}{4}) - (-\dfrac{(-10)^3}{12} - \dfrac{5(-10)^2}{4}) \)
\( = (\dfrac{128}{3} - 80) - (\dfrac{250}{3} - 125) \)
\( = \dfrac{13}{3} \)
Şimdi \( [-8, -4] \) aralığında \( f \) fonksiyonu ile \( d_2 \) doğrusu arasında kalan bölgenin alanını bulalım. Bu aralıkta \( d_2 \) doğrusu \( f \) fonksiyonunun üzerindedir.
\( A_2 = \displaystyle\int_{-8}^{-4}(-x + 3 - f(x))\ dx \)
\( = \displaystyle\int_{-8}^{-4}(-x + 3 - (\dfrac{x^2}{4} + 3x + 15))\ dx \)
\( = \displaystyle\int_{-8}^{-4}(-\dfrac{x^2}{4} - 4x - 12)\ dx \)
İfadenin integralini alalım.
\( = (-\dfrac{x^3}{12} - 2x^2 - 12x)_{-8}^{-4} \)
\( = (-\dfrac{(-4)^3}{12} - 2(-4)^2 - 12(-4)) - (-\dfrac{(-8)^3}{12} - 2(-8)^2 - 12(-8)) \)
\( = (\dfrac{16}{3} - 32 + 48) - (\dfrac{128}{3} - 128 + 96) \)
\( = \dfrac{32}{3} \)
Taralı bölgenin alanı bulduğumuz iki alanın toplamına eşittir.
\( A = A_1 + A_2 \)
\( = \dfrac{13}{3} + \dfrac{32}{3} = 15 \) olarak bulunur.