Eğri ile x-Ekseni Arasında Kalan Alan
Belirli integralin en önemli uygulaması bir fonksiyonun grafiği ile \( x \) ekseni arasında kalan alanın hesaplanmasıdır. Bu hesaplamalarda belirli integrali pozitif ve negatif değer alabilen, alanı ise sadece pozitif değer alabilen bir büyüklük olarak anlamamız önem taşımaktadır.
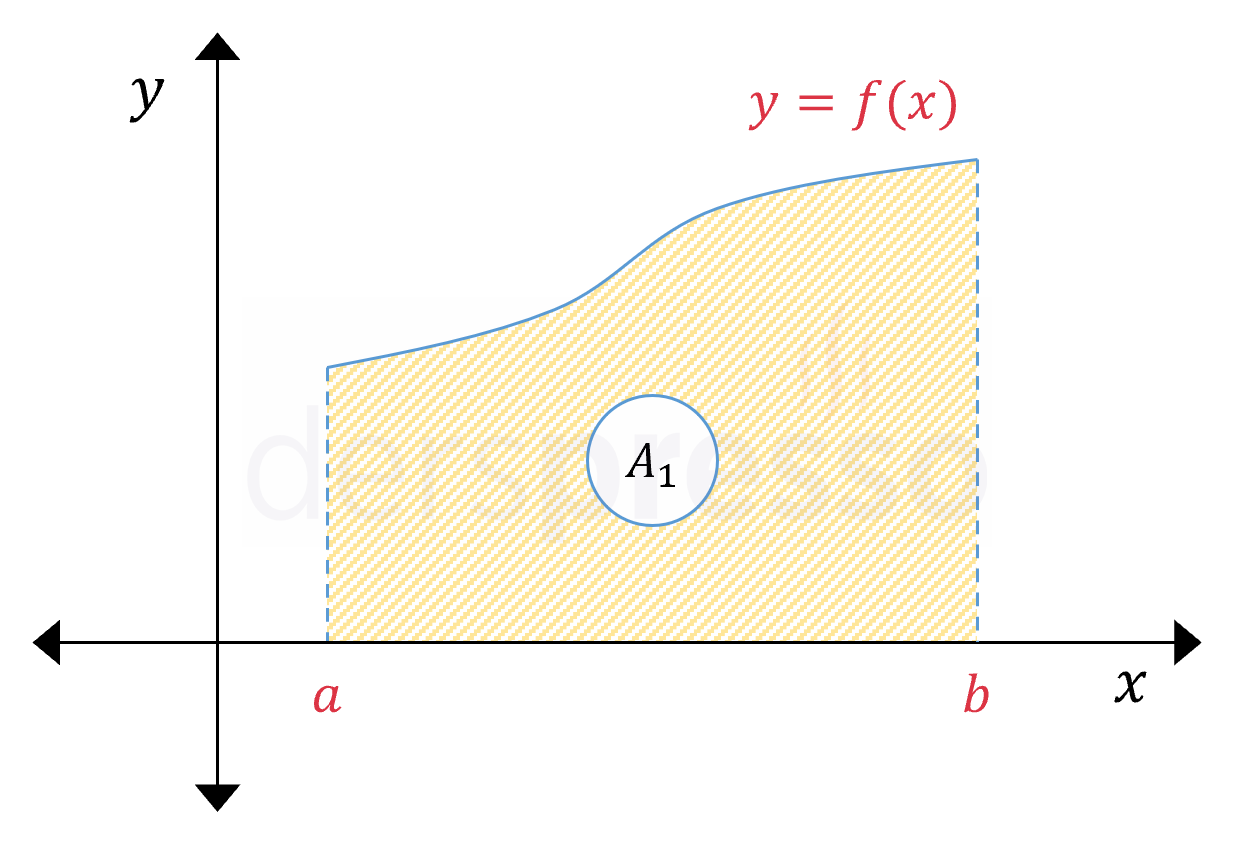
Bir fonksiyonun değerinin pozitif olduğu (\( f(x) \gt 0 \)), yani grafiğinin \( x \) ekseninin üstünde kaldığı bir aralıktaki belirli integrali pozitif işaretlidir. Bu aralıkta fonksiyon grafiği ile \( x \) ekseni arasında kalan alan da bu pozitif integral değerine eşittir.
\( A_1 = \displaystyle\int_a^b {f(x)\ dx} \)
\( (+) = (+) \)
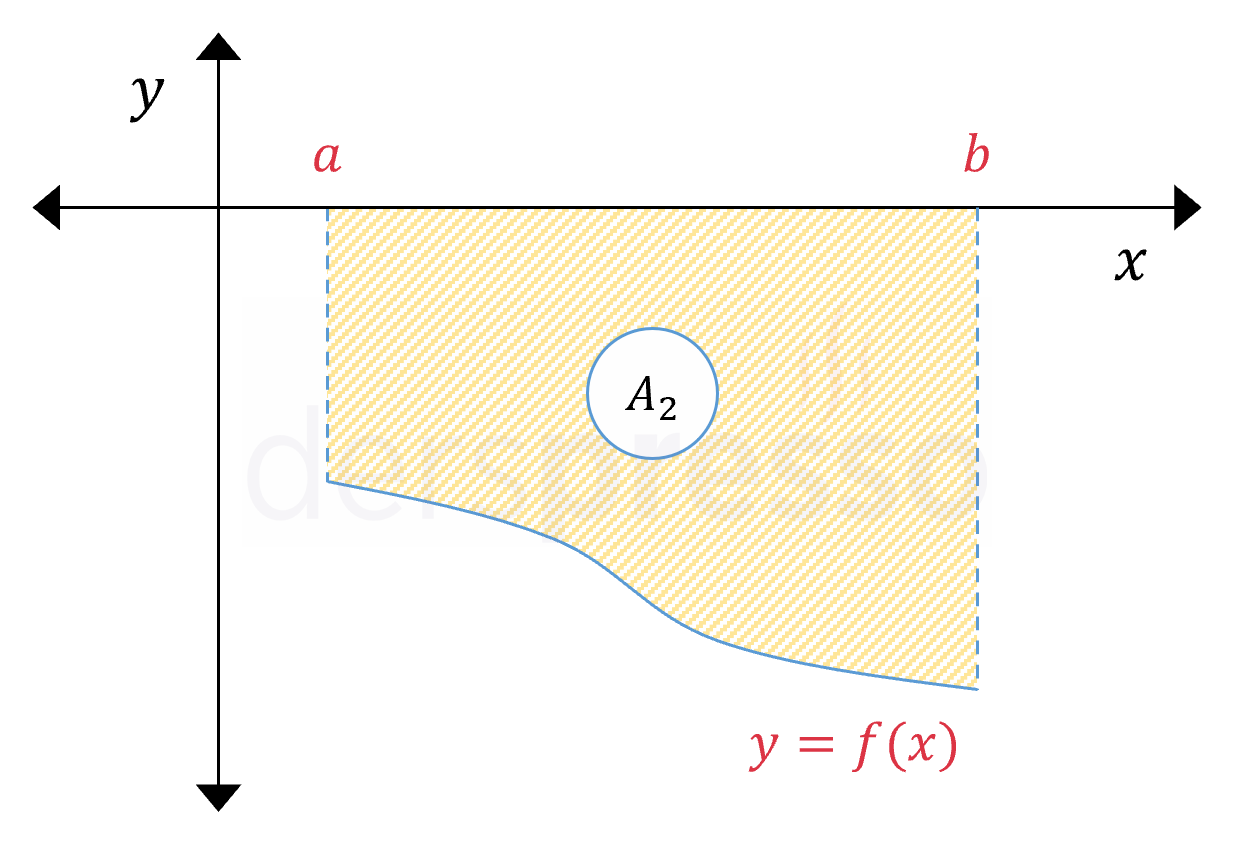
Bir fonksiyonun değerinin negatif olduğu (\( f(x) \lt 0 \)), yani grafiğinin \( x \) ekseninin altında kaldığı bir aralıktaki belirli integrali negatif işaretlidir. Alan pozitif bir büyüklük olduğu için, bu aralıkta fonksiyon grafiği ile \( x \) ekseni arasında kalan alan bu negatif integral değerinin ters işaretlisine eşittir.
\( A_2 = -\displaystyle\int_a^b {f(x)\ dx} \)
\( (+) = -(-) \)
Buna göre, bir fonksiyonun aşağıdaki gibi hem pozitif hem negatif değerler aldığı bir aralıkta grafiğinin \( x \) ekseni ile arasında kalan toplam alanı, fonksiyonun \( x \) ekseninin üstünde kaldığı aralıklardaki belirli integralinden altında kaldığı aralıklardaki belirli integralini çıkararak bulabiliriz.
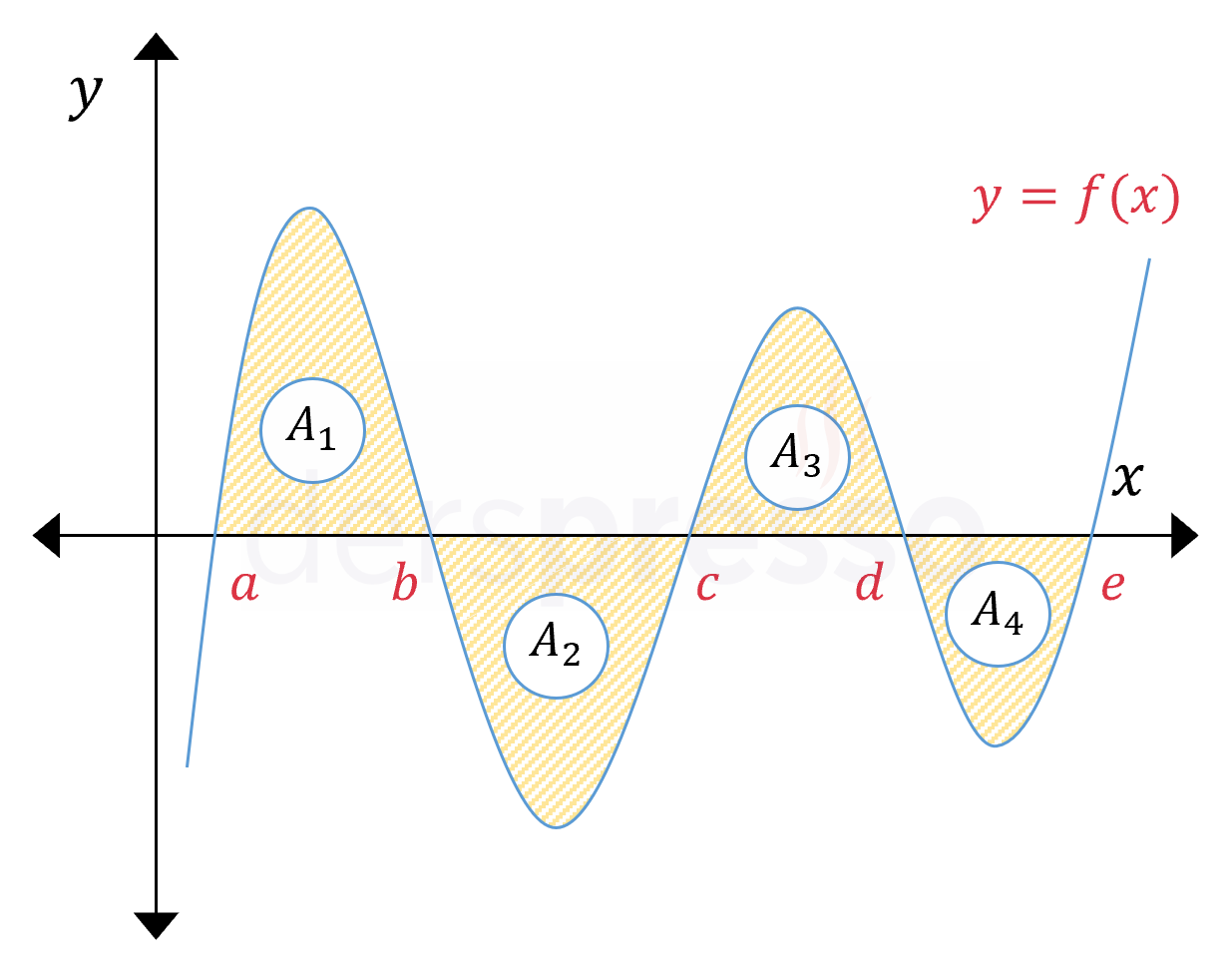
\( A = A_1 + A_2 + A_3 + A_4 \) olmak üzere,
\( A = \displaystyle\int_a^b {f(x)\ dx} \textcolor{red}{- \displaystyle\int_b^c {f(x)\ dx}} + \displaystyle\int_c^d {f(x)\ dx} \textcolor{red}{- \displaystyle\int_d^e {f(x)\ dx}} \)
Bir aralıktaki toplam alanı bulmak için bir integrali yukarıdaki gibi alt integrallere bölerken kullanmamız gereken sınır noktaları, fonksiyonun \( x \) eksenini keserek işaret değiştirdiği noktalardır. Bu noktalar \( f(x) = 0 \) denkleminin tek katlı kökleridir. Çift katlı köklerde ise fonksiyon \( x \) eksenini işaret değiştirmeden keser.
Benzer şekilde, bir fonksiyonun bir aralıktaki belirli integrali, bu aralıkta \( x \) ekseninin üstünde kalan alanlarla altında kalan alanların farkına eşittir.
\( \displaystyle\int_a^e {f(x)\ dx} = (A_1 + A_3) - (A_2 + A_4) \)
Bir fonksiyonun mutlak değeri \( x \) ekseninin altında kalan noktaların \( x \) eksenine göre yansımasını aldığı için, bir fonksiyonun mutlak değerinin belirli integrali grafiğin bu aralıkta \( x \) ekseni ile arasında kalan toplam alana eşittir.
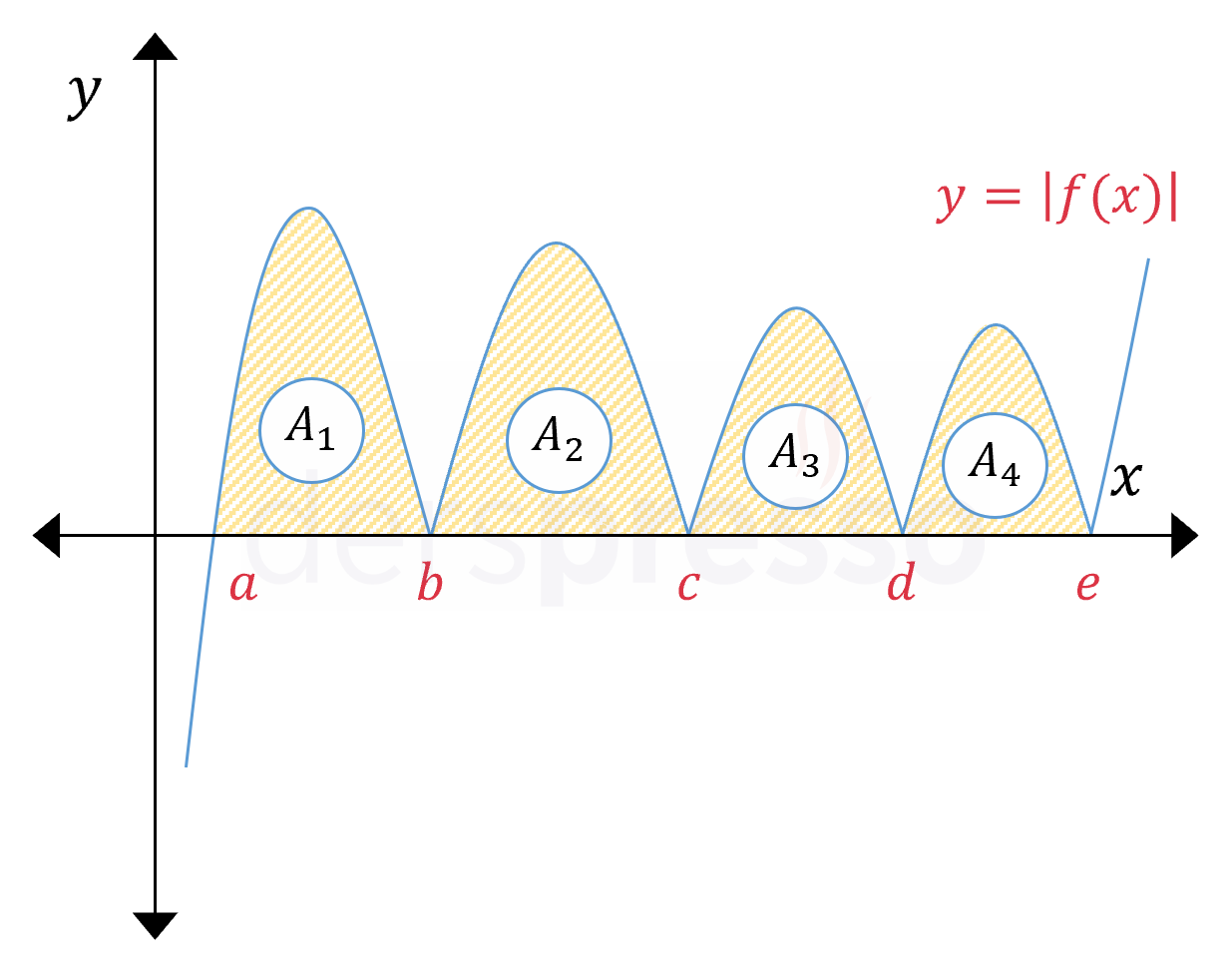
\( A = A_1 + A_2 + A_3 + A_4 \) olmak üzere,
\( A = \displaystyle\int_a^e {\abs{f(x)}\ dx} \)
Bir fonksiyonun belirli integrali ile \( x \) ekseni ile arasında kalan alan ilişkisini bir örnek üzerinden inceleyelim.

\( f(x) = 6x^2 - 54x + 108 \)
Yukarıda denklemi ve grafiği verilen fonksiyonun grafiğindeki taralı bölgenin alanını bulalım.
Taralı alan \( [1, 8] \) aralığında fonksiyon grafiği ile \( x \) ekseni arasında kalan alana karşılık gelmektedir.
Taralı alan fonksiyonun \( x \) ekseninin üstünde ve altında kaldığı bölgelerden oluştuğu için aralığı fonksiyonun \( x \) eksenini kestiği noktalara göre alt aralıklara bölmemiz ve her aralık için ayrı integral hesaplamamız gerekir.
Fonksiyon \( [1, 3] \) aralığında \( x \) ekseninin üstünde kaldığı için bu aralıktaki integral değeri pozitiftir ve \( A_1 \) bu integral değerine eşittir.
\( A_1 = \displaystyle\int_1^3 (6x^2 - 54x + 108)\ dx \)
\( = (2x^3 - 27x^2 + 108x)|_1^3 \)
\( = (2(3)^3 - 27(3)^2 + 108(3)) - (2(1)^3 - 27(1)^2 + 108(1)) \)
\( = 135 - 83 = 52 \)
Fonksiyon \( [3, 6] \) aralığında \( x \) ekseninin altında kaldığı için bu aralıktaki integral değeri negatiftir ve \( A_2 \) bu integral değerinin ters işaretlisine eşittir.
\( A_2 = -\displaystyle\int_3^6 (6x^2 - 54x + 108)\ dx \)
\( = -(2x^3 - 27x^2 + 108x)|_3^6 \)
\( = -[(2(6)^3 - 27(6)^2 + 108(6)) - (2(3)^3 - 27(3)^2 + 108(3))] \)
\( = -[108 - 135] = 27 \)
Fonksiyon \( [6, 8] \) aralığında \( x \) ekseninin üstünde kaldığı için bu aralıktaki integral değeri pozitiftir ve \( A_3 \) bu integral değerine eşittir.
\( A_3 = \displaystyle\int_6^8 {(6x^2 - 54x + 108)\ dx} \)
\( = (2x^3 - 27x^2 + 108x)|_6^8 \)
\( = (2(8)^3 - 27(8)^2 + 108(8)) - (2(6)^3 - 27(6)^2 + 108(6)) \)
\( = 160 - 108 = 52 \)
Taralı bölgenin alanı bu üç bölgenin alanları toplamına eşittir.
\( A = A_1 + A_2 + A_3 \)
\( = 52 + 27 + 52 = 131 \)
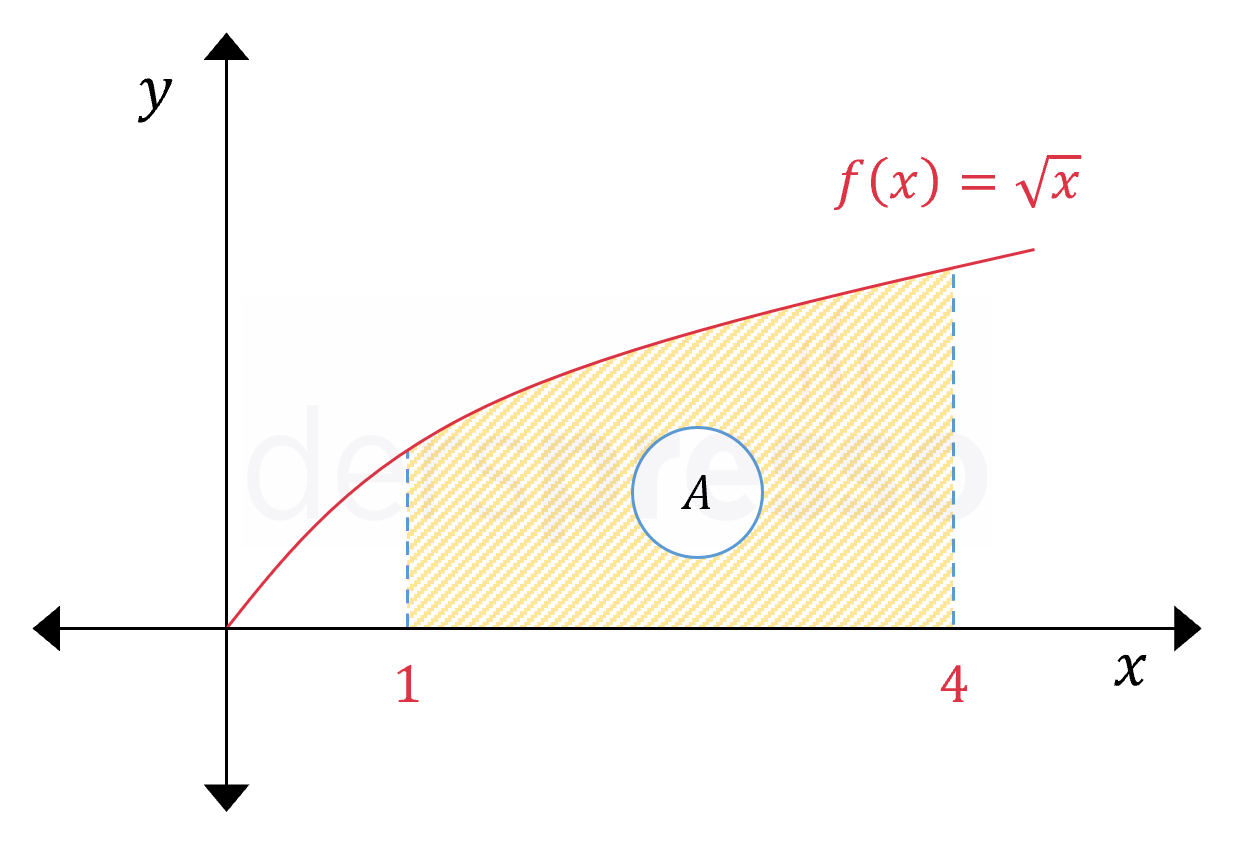
\( f(x) = \sqrt{x} \) olmak üzere, yukarıdaki şekildeki taralı bölgenin alanı nedir?
Çözümü GösterTaralı alan \( [1, 4] \) aralığında fonksiyon grafiği ile \( x \) ekseni arasında kalan alana karşılık gelmektedir.
\( f \) fonksiyonu bu aralıkta \( x \) ekseninin üstünde kaldığı için belirli integrali pozitif işaretlidir. Bu aralıkta fonksiyon grafiği ile \( x \) ekseni arasında kalan alan da bu pozitif integral değerine eşittir.
\( A = \displaystyle\int_1^4 {\sqrt{x}\ dx} \)
\( = \displaystyle\int_1^4 {x^{\frac{1}{2}}\ dx} \)
İfadenin integralini alalım.
\( = (\dfrac{2}{3}x^{\frac{3}{2}})|_1^4 \)
\( = \dfrac{2}{3}4^{\frac{3}{2}} - \dfrac{2}{3}1^{\frac{3}{2}} \)
\( = \dfrac{16}{3} - \dfrac{2}{3} = \dfrac{14}{3} \) bulunur.
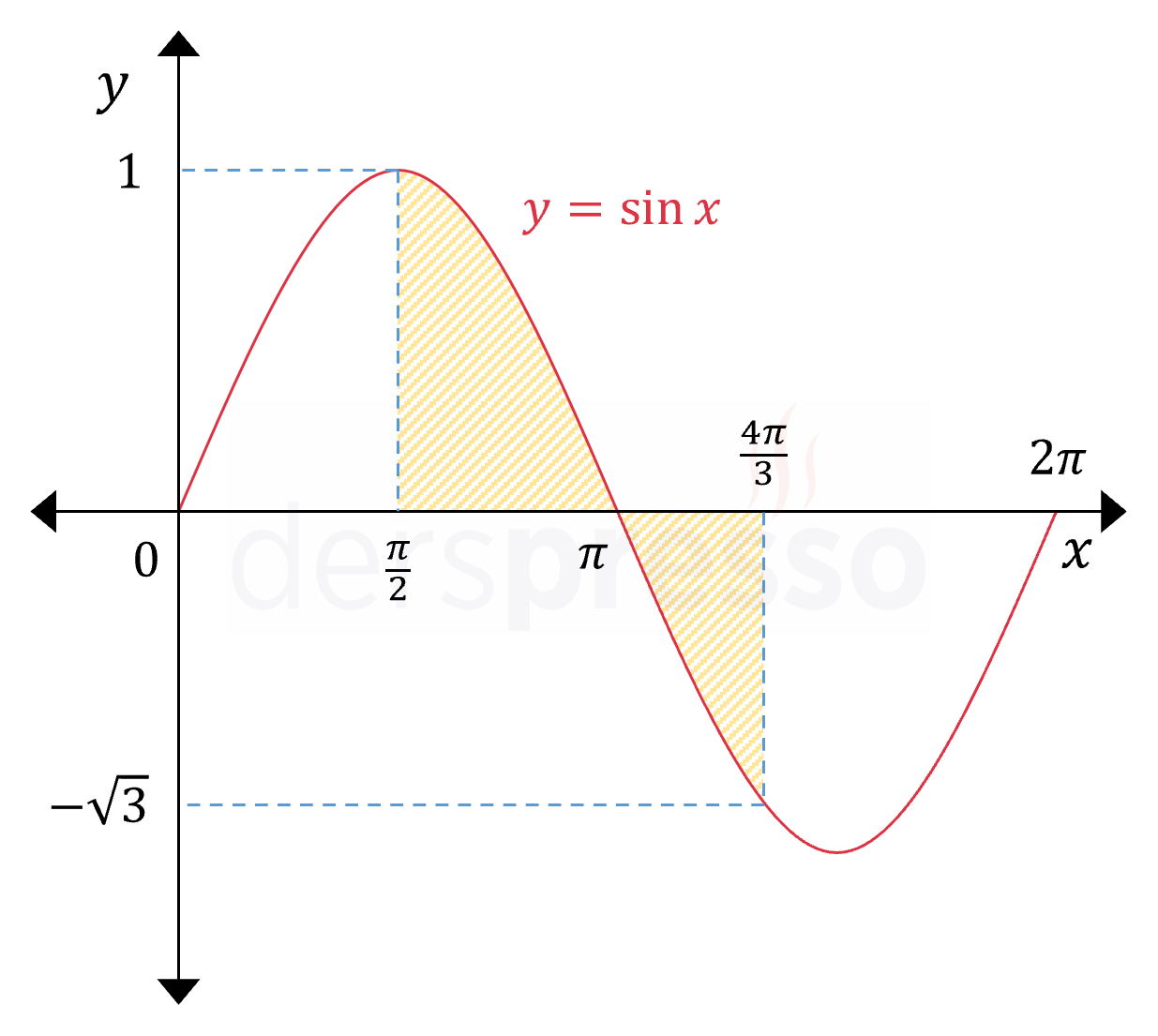
\( y = \sin{x} \) olmak üzere, yukarıdaki şekildeki taralı bölgenin alanı nedir?
Çözümü GösterTaralı alan \( [\frac{\pi}{2}, \frac{4\pi}{3}] \) aralığında fonksiyon grafiği ile \( x \) ekseni arasında kalan alana karşılık gelmektedir.
Taralı alan fonksiyonun \( x \) ekseninin üstünde ve altında kaldığı bölgelerden oluştuğu için, bu alanı fonksiyonun \( x \) ekseninin üstünde kaldığı aralıklardaki belirli integralinden altında kaldığı aralıklardaki belirli integralini çıkarak bulabiliriz.
\( A = \displaystyle\int_{\frac{\pi}{2}}^{\pi} \sin{x}\ dx - \displaystyle\int_{\pi}^{\frac{4\pi}{3}} \sin{x}\ dx \)
İfadenin integralini alalım.
\( = (-\cos{x})|_{\frac{\pi}{2}}^{\pi} - (-\cos{x})|_{\pi}^{\frac{4\pi}{3}} \)
\( = (-\cos{\pi} - (-\cos{\frac{\pi}{2}})) - (-\cos{\frac{4\pi}{3}} - (-\cos{\pi})) \)
\( = (1 + 0) - (\dfrac{1}{2} - 1) \)
\( = \dfrac{3}{2} \) bulunur.
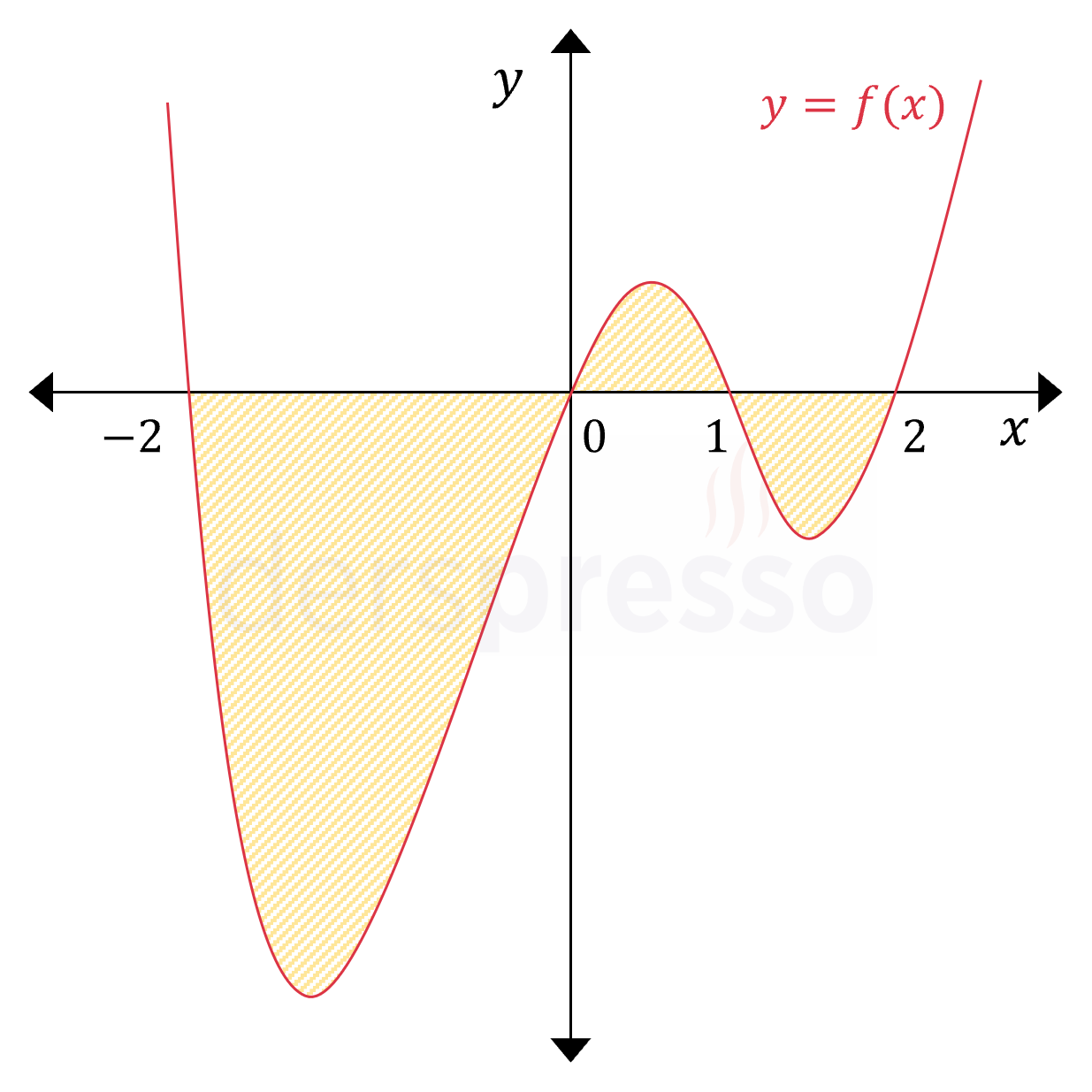
\( f(x) = (x + 2)x(x - 1)(x - 2) \) olmak üzere, yukarıdaki şekildeki taralı bölgenin alanı nedir?
Çözümü GösterFonksiyon tanımındaki çarpanları genişletelim.
\( f(x) = (x^2 - 4)(x^2 - x) \)
\( = x^4 - x^3 - 4x^2 + 4x \)
Taralı alan \( [-2, 2] \) aralığında fonksiyon grafiği ile \( x \) ekseni arasında kalan alana karşılık gelmektedir.
Taralı alan fonksiyonun \( x \) ekseninin üstünde ve altında kaldığı bölgelerden oluştuğu için aralığı fonksiyonun \( x \) eksenini kestiği noktalara göre alt aralıklara bölmemiz ve her aralık için ayrı integral hesaplamamız gerekir.
\( [-2, 0] \), \( [0, 1] \) ve \( [1, 2] \) aralıkları için hesaplamak istediğimiz alan değerlerine sırasıyla \( A_1 \), \( A_2 \) ve \( A_3 \) diyelim.
\( A_1 \) aralığı:
Fonksiyon bu aralıkta \( x \) ekseninin altında kaldığı için bu aralıktaki integral değeri negatiftir ve alan bu integral değerinin ters işaretlisine eşittir.
\( A_1 = -\displaystyle\int_{-2}^0 (x^4 - x^3 - 4x^2 + 4x)\ dx \)
\( = -(\frac{x^5}{5} - \frac{x^4}{4} - \frac{4x^3}{3} + 2x^2)|_{-2}^0 \)
\( = -[(\frac{0^5}{5} - \frac{0^4}{4} - \frac{4(0)^3}{3} + 2(0)^2) - (\frac{(-2)^5}{5} - \frac{(-2)^4}{4} - \frac{4(-2)^3}{3} + 2(-2)^2)] \)
\( = -[0 - (-\frac{32}{5} - 4 + \frac{32}{3} + 8)] \)
\( = 8\frac{4}{15} \)
\( A_2 \) aralığı:
Fonksiyon bu aralıkta \( x \) ekseninin üstünde kaldığı için bu aralıktaki integral değeri pozitiftir ve alan bu integral değerine eşittir.
\( A_2 = \displaystyle\int_0^1 (x^4 - x^3 - 4x^2 + 4x)\ dx \)
\( = (\frac{x^5}{5} - \frac{x^4}{4} - \frac{4x^3}{3} + 2x^2)|_0^1 \)
\( = [(\frac{(1)^5}{5} - \frac{(1)^4}{4} - \frac{4(1)^3}{3} + 2(1)^2) - (\frac{0^5}{5} - \frac{0^4}{4} - \frac{4(0)^3}{3} + 2(0)^2)] \)
\( = [(\frac{1}{5} - \frac{1}{4} - \frac{4}{3} + 2) - (0)] \)
\( = \frac{37}{60} \)
\( A_3 \) aralığı:
Fonksiyon bu aralıkta \( x \) ekseninin altında kaldığı için bu aralıktaki integral değeri negatiftir ve alan bu integral değerinin ters işaretlisine eşittir.
\( A_3 = -\displaystyle\int_1^2 (x^4 - x^3 - 4x^2 + 4x)\ dx \)
\( = -(\frac{x^5}{5} - \frac{x^4}{4} - \frac{4x^3}{3} + 2x^2)|_1^2 \)
\( = -[(\frac{2^5}{5} - \frac{2^4}{4} - \frac{4(2)^3}{3} + 2(2)^2) - (\frac{1^5}{5} - \frac{(1)^4}{4} - \frac{4(1)^3}{3} + 2(1)^2)] \)
\( = -[(\frac{32}{5} - 4 - \frac{32}{3} + 8) - (\frac{1}{5} - \frac{1}{4} - \frac{4}{3} + 2)] \)
\( = \frac{53}{60} \)
Sorudaki taralı bölgenin alanı bu üç alanın toplamına eşittir.
\( A = A_1 + A_2 + A_3 \)
\( = 8\frac{4}{15} + \frac{37}{60} + \frac{53}{60} \)
\( = 9\frac{23}{30} \) bulunur.
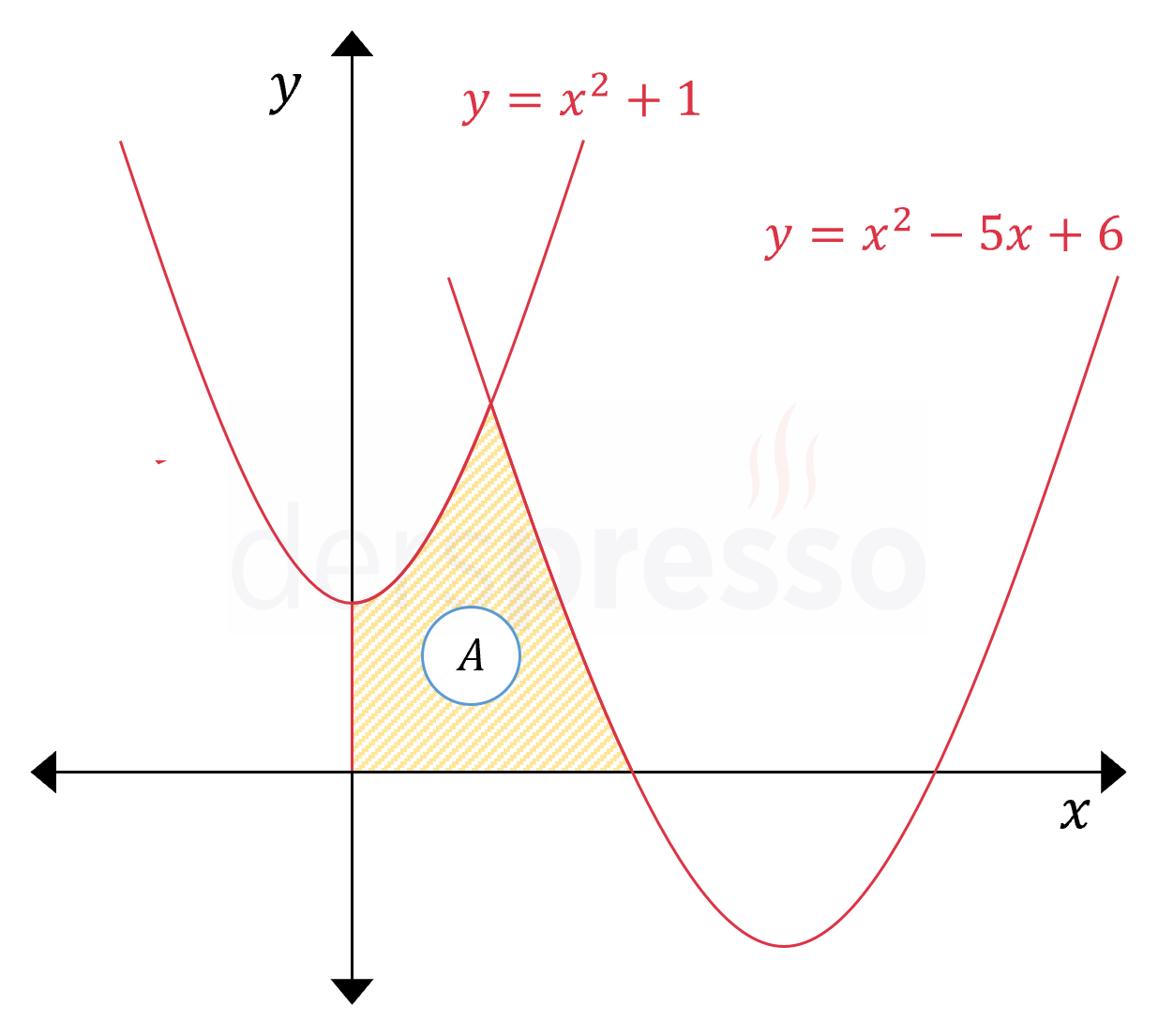
Yukarıdaki şekildeki iki eğri ve eksenler arasında kalan taralı bölgenin alanı nedir?
Çözümü GösterTaralı alan iki eğrinin iki farklı aralıkta \( x \) ekseni ile aralarında kalan alanların toplamına eşittir.
Bu iki alanı ayıran geçiş noktası iki eğrinin kesişim noktasıdır. İki denklemi ortak çözerek bu noktanın apsis değerini bulalım.
\( x^2 + 1 = x^2 - 5x + 6 \)
\( 5x = 5 \)
\( x = 1 \)
Buna göre taralı alanı aşağıdaki şekildeki gibi ikiye bölebiliriz.
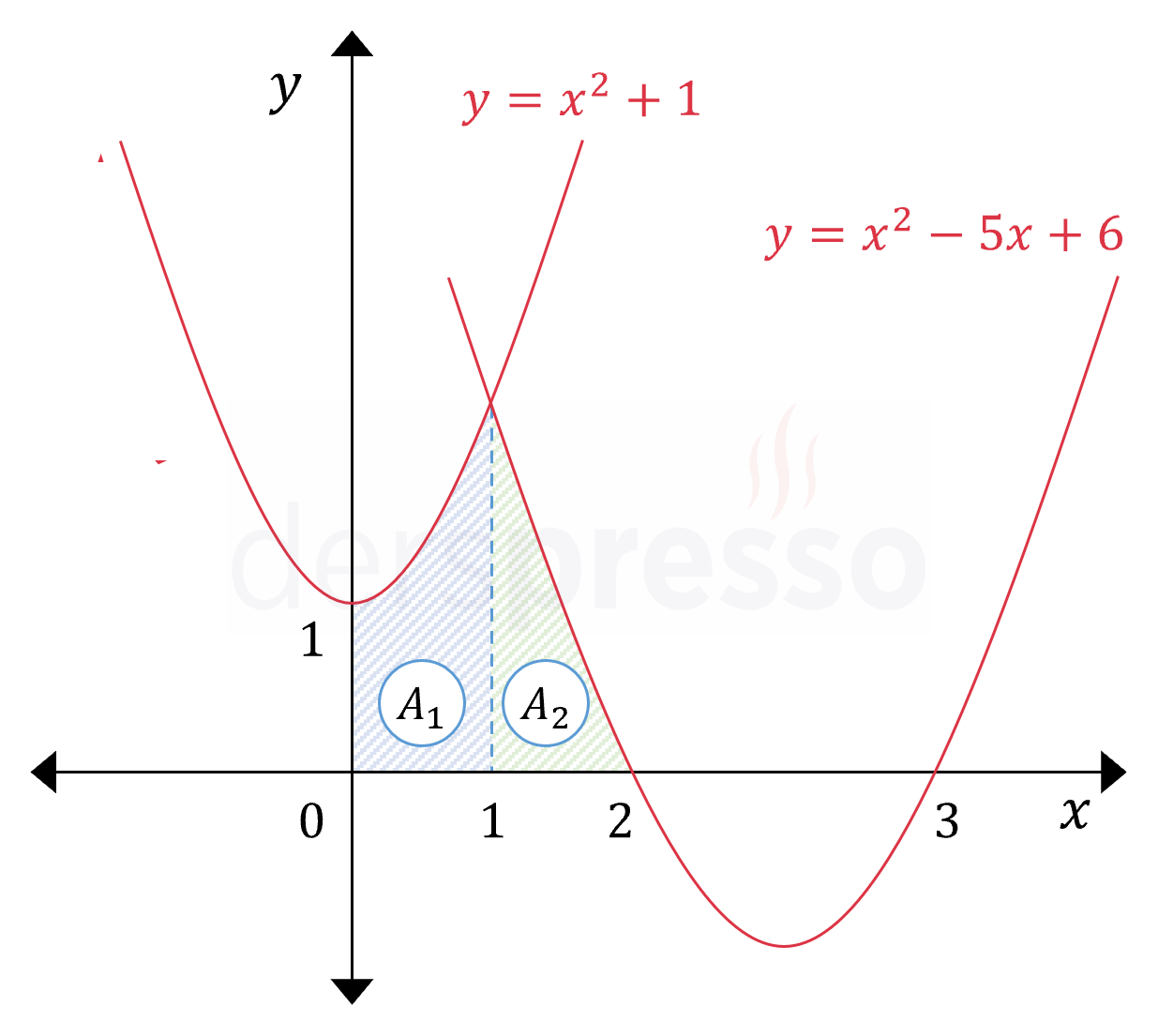
Bu alanlardan \( A_1 \) soldaki eğrinin \( [0, 1] \) aralığında, \( A_2 \) de sağdaki eğrinin \( [1, 2] \) aralığında \( x \) ekseni ile aralarında kalan alanlara karşılık gelmektedir.
Bu iki alanı sırayla hesaplayalım.
\( A_1 = \displaystyle\int_0^1 (x^2 + 1)\ dx \)
\( = (\dfrac{x^3}{3} + x)|_0^1 \)
\( = (\dfrac{1^3}{3} + 1) - (\dfrac{0^3}{3} + 0) \)
\( = \dfrac{4}{3} \)
\( A_2 = \displaystyle\int_1^2 (x^2 - 5x + 6)\ dx \)
\( = (\dfrac{x^3}{3} - \dfrac{5x^2}{2} + 6x)|_1^2 \)
\( = (\dfrac{2^3}{3} - \dfrac{5(2)^2}{2} + 6(2)) - (\dfrac{1^3}{3} - \dfrac{5(1)^2}{2} + 6(1)) \)
\( = \dfrac{5}{6} \)
Taralı bölgenin alanı bu iki alanın toplamına eşittir.
\( A_1 + A_2 = \dfrac{4}{3} + \dfrac{5}{6} \)
\( = \dfrac{13}{6} \) bulunur.
\( f(x) = x^6 - kx^2 \)
\( g(x) = k - x^4 \) fonksiyonları veriliyor.
Buna göre hangi \( k \) değeri için fonksiyonların \( x \) ekseniyle aralarında kalan alanlar birbirine eşit olur?
Çözümü GösterBir fonksiyonun belirli bir aralıktaki belirli integralinin mutlak değeri fonksiyonun grafiğinin \( x \) ekseni ile arasında kalan alanı verir.
\( f(x) \) fonksiyonu ile \( x \) ekseni arasında kalan alanı bulmak için fonksiyonun köklerini (\( x \) eksenini kestiği noktaları) bulalım.
\( x^6 - kx^2 = 0 \)
\( x^2(x^4 - k) = 0 \)
\( x^2(x^2 - \sqrt{k})(x^2 + \sqrt{k}) = 0 \)
\( x^2(x - \sqrt[4]{k})(x + \sqrt[4]{k})(x^2 + \sqrt{k}) = 0 \)
Denklemin kökleri her bir çarpanı sıfır yapan \( x \) değerlerinden oluşur.
\( x \in \{-\sqrt[4]{k}, 0, \sqrt[4]{k}\} \)
Fonksiyon çift fonksiyon olduğu için \( x = 0 \) noktasının solunda ve sağında grafik \( x \) eksenine göre aynı tarafta kalır, dolayısıyla istediğimiz alanı bulmak için integrali \( [-\sqrt[4]{k}, \sqrt[4]{k}] \) aralığında alabiliriz.
\( \displaystyle\int_{-\sqrt[4]{k}}^{\sqrt[4]{k}} (x^6 - kx^2)\ dx \)
İfadenin integralini alalım.
\( = (\dfrac{x^7}{7} - \dfrac{kx^3}{3})|_{-\sqrt[4]{k}}^{\sqrt[4]{k}} \)
\( = (\dfrac{k^{\frac{7}{4}}}{7} - \dfrac{k \cdot k^\frac{3}{4}}{3}) - (\dfrac{-k^{\frac{7}{4}}}{7} - \dfrac{k \cdot (-k^\frac{3}{4})}{3}) \)
\( = \dfrac{2 \cdot k^{\frac{7}{4}}}{7} - \dfrac{2 \cdot k^\frac{7}{4}}{3} \)
\( = -\dfrac{8 \cdot k^{\frac{7}{4}}}{21} \)
Aynı işlemi \( g(x) \) fonksiyonuna uygulayalım.
\( k - x^4 = 0 \)
\( x^4 = k \)
Denklemin kökleri her bir çarpanı sıfır yapan \( x \) değerlerinden oluşur.
\( x \in \{-\sqrt[4]{k}, \sqrt[4]{k}\} \)
\( \displaystyle\int_{-\sqrt[4]{k}}^{\sqrt[4]{k}} (k - x^4)\ dx \)
İfadenin integralini alalım.
\( = (kx - \dfrac{x^5}{5})|_{-\sqrt[4]{k}}^{\sqrt[4]{k}} \)
\( = (k \cdot k^{\frac{1}{4}} - \dfrac{k^{\frac{5}{4}}}{5}) - (k \cdot (-k)^{\frac{1}{4}} - \dfrac{(-k)^{\frac{5}{4}}}{5}) \)
\( = 2k^{\frac{5}{4}} - \dfrac{2k^{\frac{5}{4}}}{5} \)
\( = \dfrac{8k^{\frac{5}{4}}}{5} \)
Bu iki alanın mutlak değeri birbirine eşittir.
\( \abs{\dfrac{-8 \cdot k^{\frac{7}{4}}}{21}} = \abs{\dfrac{8k^{\frac{5}{4}}}{5}} \)
\( \abs{k^{\frac{1}{2}}} = \dfrac{21}{5} \)
\( k = \dfrac{441}{25} \) olarak bulunur.
\( \displaystyle\int_0^{50\pi} \abs{\cos{x}}\ dx \) integralinin değeri kaçtır?
Çözümü GösterKosinüs fonksiyonu \( [-1, 1] \) aralığında değer alan ve periyodu \( 2\pi \) olan periyodik bir fonksiyondur.
\( \abs{\cos{x}} \) fonksiyonunun grafiği \( \cos{x} \) fonksiyonunun \( x \) ekseni altında kalan kısımlarının \( x \) eksenine göre simetriğinin alınmasıyla oluşur.
\( \cos{x} \) ve \( \abs{\cos{x}} \) grafiklerinin birer periyodu aşağıda verilmiştir.
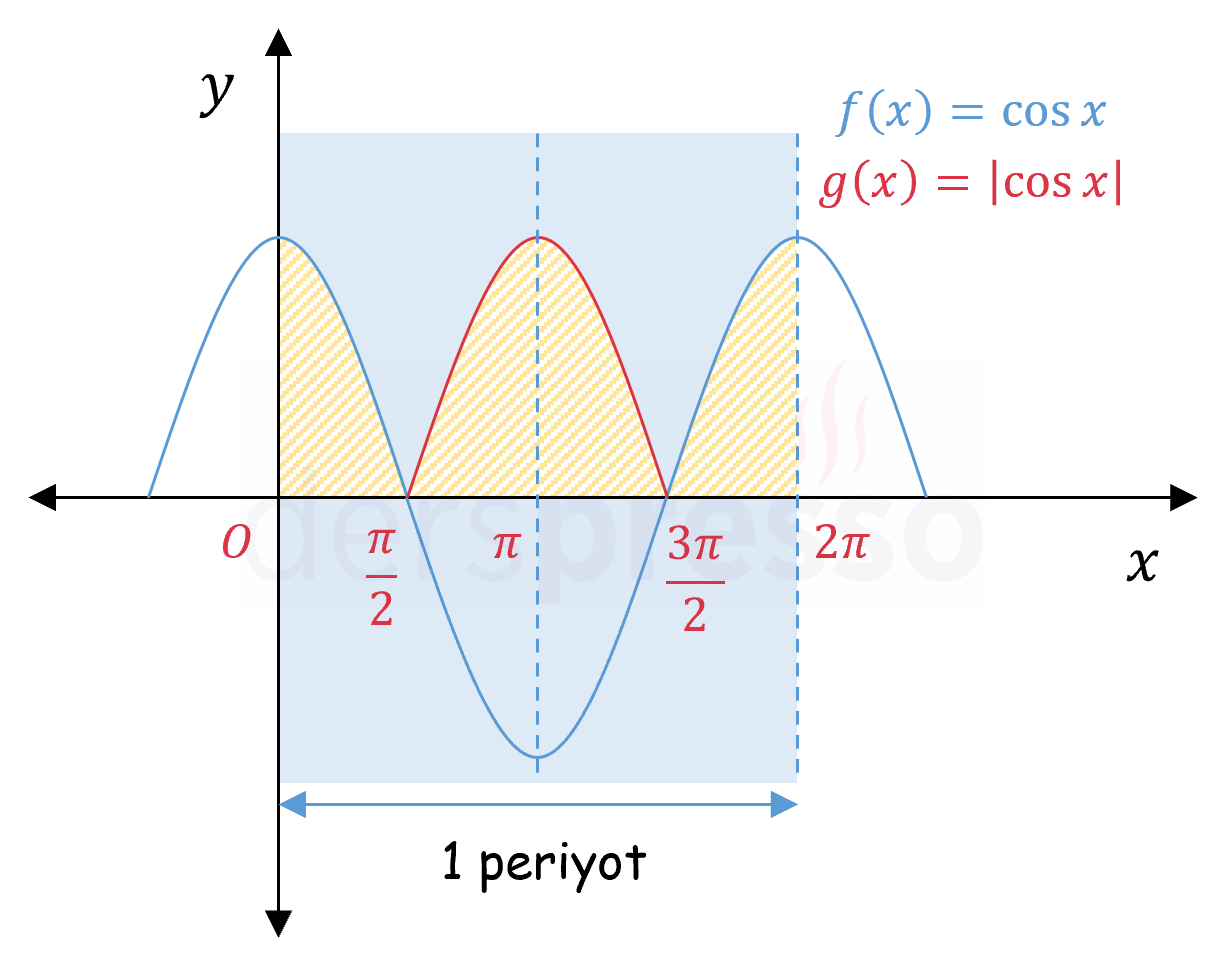
Buna göre \( \abs{\cos{x}} \) fonksiyonunun \( [0, \frac{\pi}{2}] \), \( [\frac{\pi}{2}, \pi] \), \( [\pi, \frac{3\pi}{2}] \) ve \( [\frac{3\pi}{2}, 2\pi] \) aralıklarındaki belirli integralleri birbirine eşit olur.
Dolayısıyla \( \abs{\cos{x}} \) fonksiyonunun \( [0, 50\pi] \) aralığındaki integrali, \( \cos{x} \) fonksiyonunun \( [0, \frac{\pi}{2}] \) aralığındaki integralinin \( 4 \cdot 25 = 100 \) katına eşit olur.
\( \displaystyle\int_0^{50\pi} \abs{\cos{x}}\ dx = 100\displaystyle\int_0^{\frac{\pi}{2}} \cos{x}\ dx \)
İfadenin integralini alalım.
\( = 100(\sin{x})|_0^\frac{\pi}{2} \)
\( = 100(\sin\frac{\pi}{2} - \sin{0}) \)
\( = 100 \) bulunur.
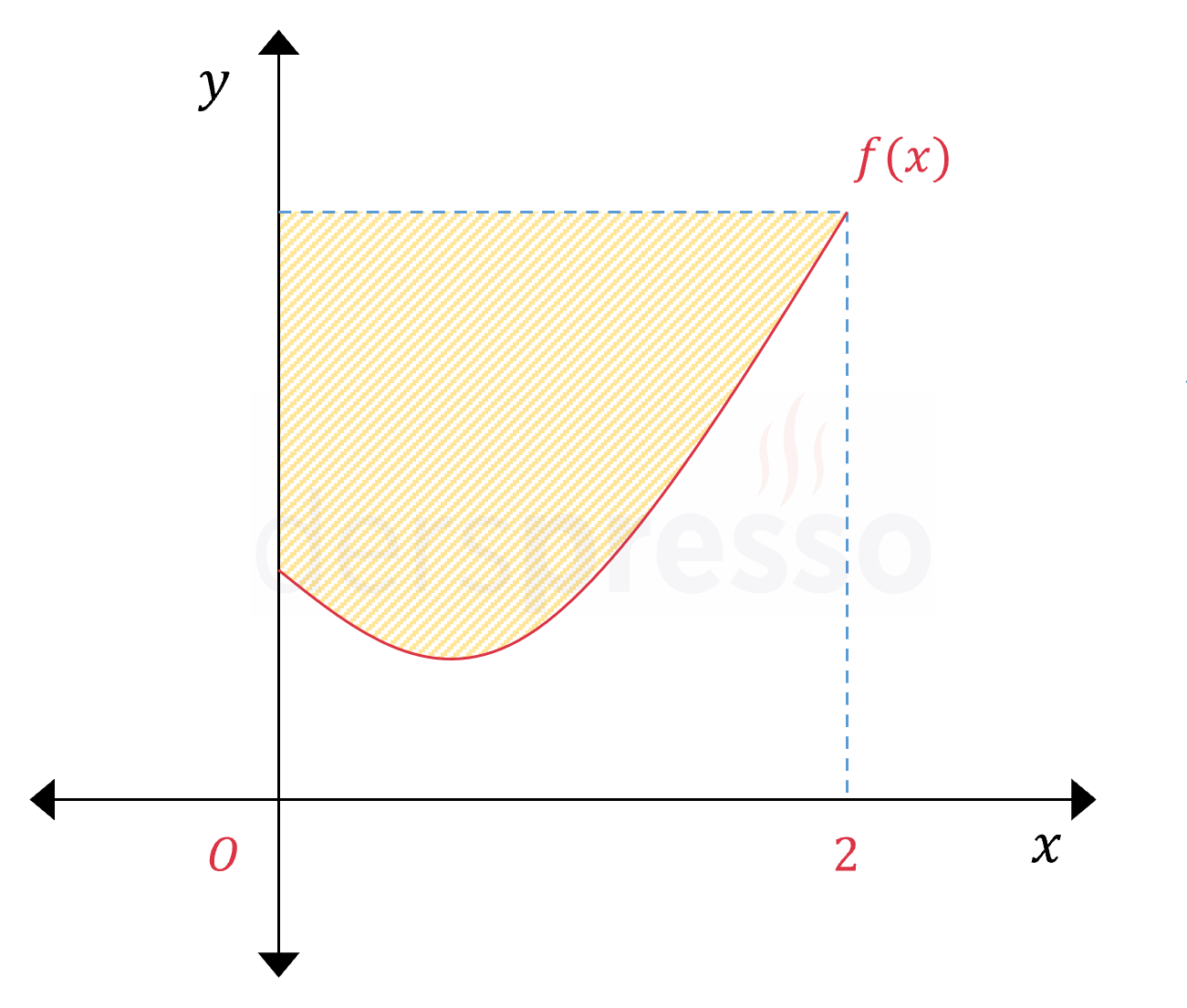
Yukarıda \( f(x) = 2x^4 - 5x + 13 \) eğrisinin grafiği verilmiştir. Buna göre taralı bölgenin alanı kaç birimkaredir?
Çözümü GösterTaralı alana \( A_1 \), \( f(x) \) fonksiyonunun \( [0, 2] \) aralığında \( x \) ekseni ile arasında kalan alana \( A_2 \), bu iki alanın toplamının oluşturduğu dikdörtgen şeklindeki alana \( A \) diyelim.
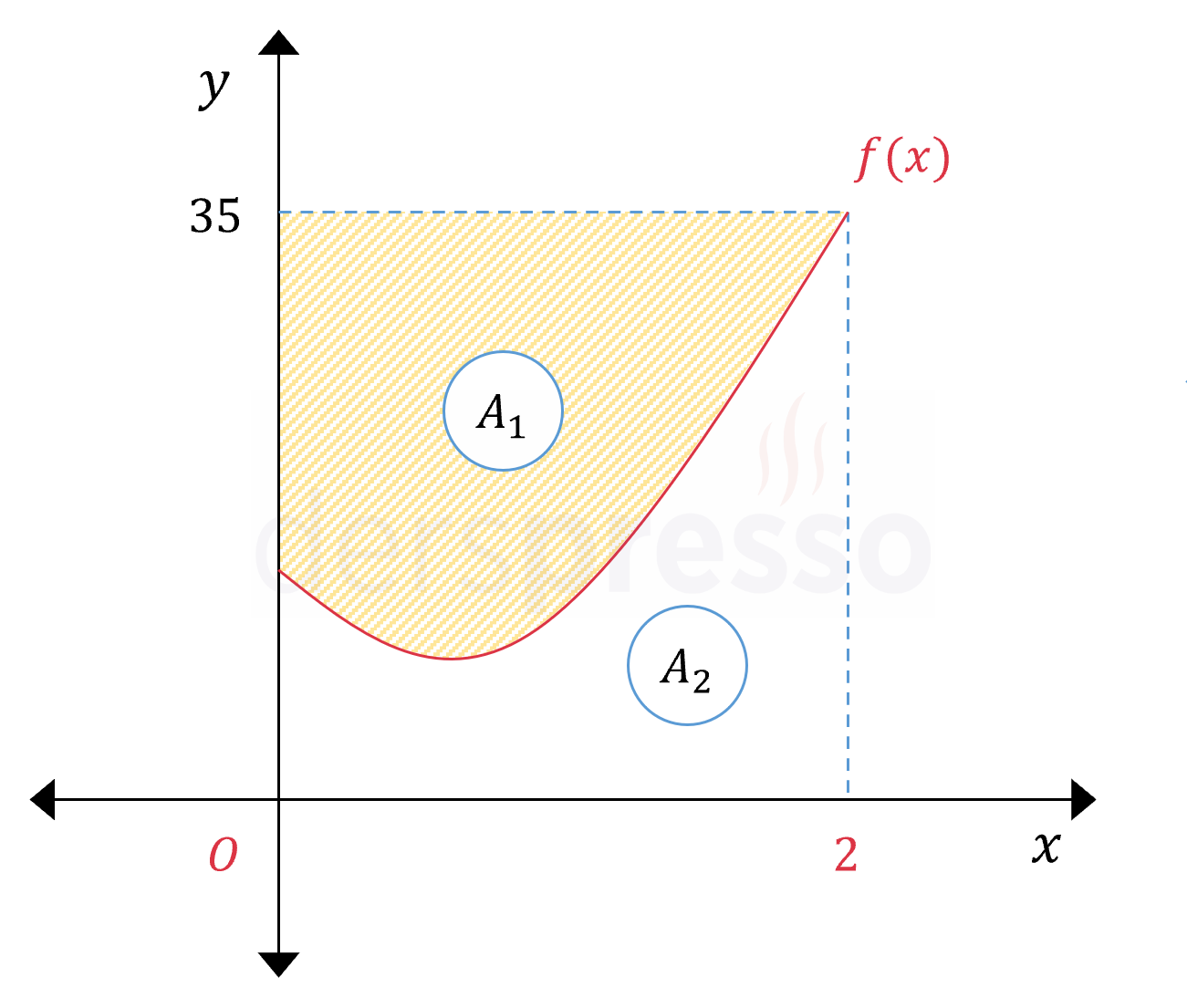
\( A = A_1 + A_2 \)
\( A_1 = A - A_2 \)
Fonksiyonun \( x = 2 \) noktasındaki değerini bulalım.
\( f(2) = 2(2)^4 - 5(2) + 13 = 35 \)
Dikdörtgenin alanını bulalım.
\( A = 2 \cdot 35 = 70 \)
Eğrinin \( [0, 2] \) aralığında \( x \) ekseni ile arasında kalan alan fonksiyonun bu aralıktaki belirli integraline eşittir.
\( A_2 = \displaystyle\int_0^2(2x^4 - 5x + 13)\ dx \)
İfadenin integralini alalım.
\( = (\dfrac{2x^5}{5} - \dfrac{5x^2}{2} + 13x)|_0^2 \)
\( = (\dfrac{2(2)^5}{5} - \dfrac{5(2)^2}{2} + 13(2)) - (\dfrac{2(0)^5}{5} - \dfrac{5(0)^2}{2} + 13(0)) \)
\( = (\dfrac{64}{5} - 10 + 26) - (0) \)
\( = \dfrac{144}{5} \)
Taralı alanı bulalım.
\( A_1 = 70 - \dfrac{144}{5} = \dfrac{206}{5} \) olarak bulunur.
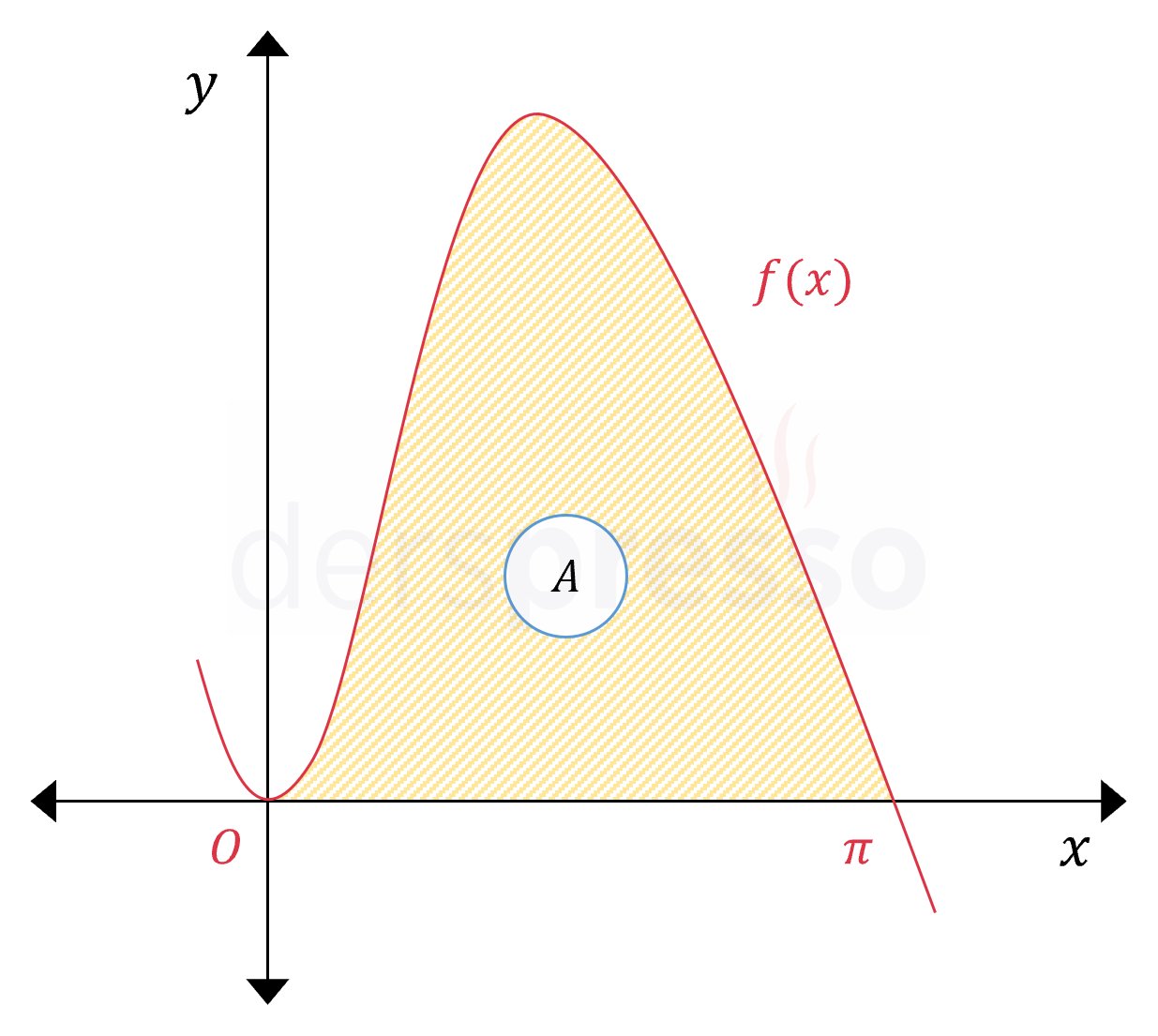
Yukarıda \( y = 4x\sin{x} \) eğrisinin grafiği verilmiştir. Buna göre taralı bölgenin alanı kaç birimkaredir?
Çözümü GösterTaralı bölgenin alanı eğrinin \( [0, \pi] \) aralığındaki belirli integraline eşittir.
\( A = \displaystyle\int_0^{\pi}(4x\sin{x})\ dx \)
İfadenin integralini almak için kısmi integral alma yöntemini kullanalım.
\( u \) ve \( dv \) ifadelerini aşağıdaki gibi belirleyelim.
\( u = 4x \)
\( dv = \sin{x}\ dx \)
Buna göre \( du \) ve \( v \) aşağıdaki gibi olur.
\( du = 4\ dx \)
\( v = -\cos{x} \)
Değişkenleri kısmi integral formülünde yerine koyalım.
\( \displaystyle\int_a^b{u\ dv} = (u\ v)|_a^b - \displaystyle\int_a^b{v\ du} \)
\( \displaystyle\int_0^{\pi}{4x\sin{x}\ dx} = (-4x\cos{x})|_0^{\pi} - \displaystyle\int_0^{\pi}{-4\cos{x}\ dx} \)
\( = (-4x\cos{x})|_0^{\pi} + (4\sin{x})|_0^{\pi} \)
\( = [(-4\pi\cos{\pi}) - (-4 \cdot 0 \cdot \cos{0})] + [(4\sin{\pi}) - (4\sin{0})] \)
\( = (4\pi - 0) + (0 - 0) \)
\( = 4\pi \) olarak bulunur.
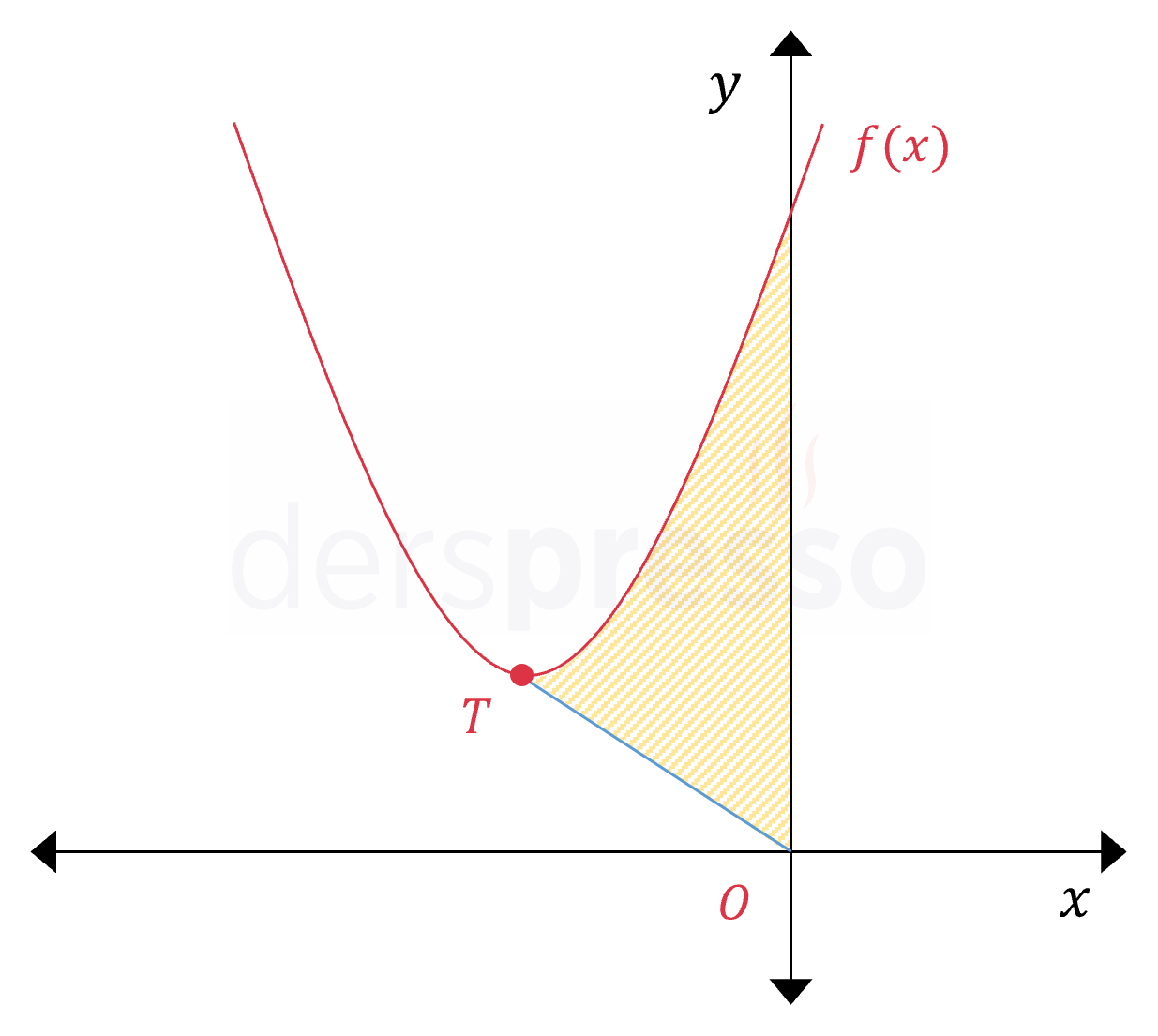
Yukarıda \( f(x) = x^2 + 10x + 26 \) parabolünün grafiği verilmiştir. \( T \) parabolün tepe noktası olduğuna göre, taralı bölgenin alanı kaç birimkaredir?
Çözümü Göster\( T(r, k) \) noktasının koordinatlarını bulalım.
\( r = -\dfrac{b}{2a} = -\dfrac{10}{2} = -5 \)
\( k = f(r) = (-5)^2 + 10(-5) + 26 = 1 \)
Taralı bölgenin alanı, \( [-5, 0] \) aralığında parabolle \( x \) ekseni arasında kalan alan (\( A_1 + A_2 \)) ile köşeleri \( T(-5, 1) \), \( (-5, 0) \) ve \( (0, 0) \) noktaları olan üçgenin alanının (\( A_2 \)) farkına eşittir.
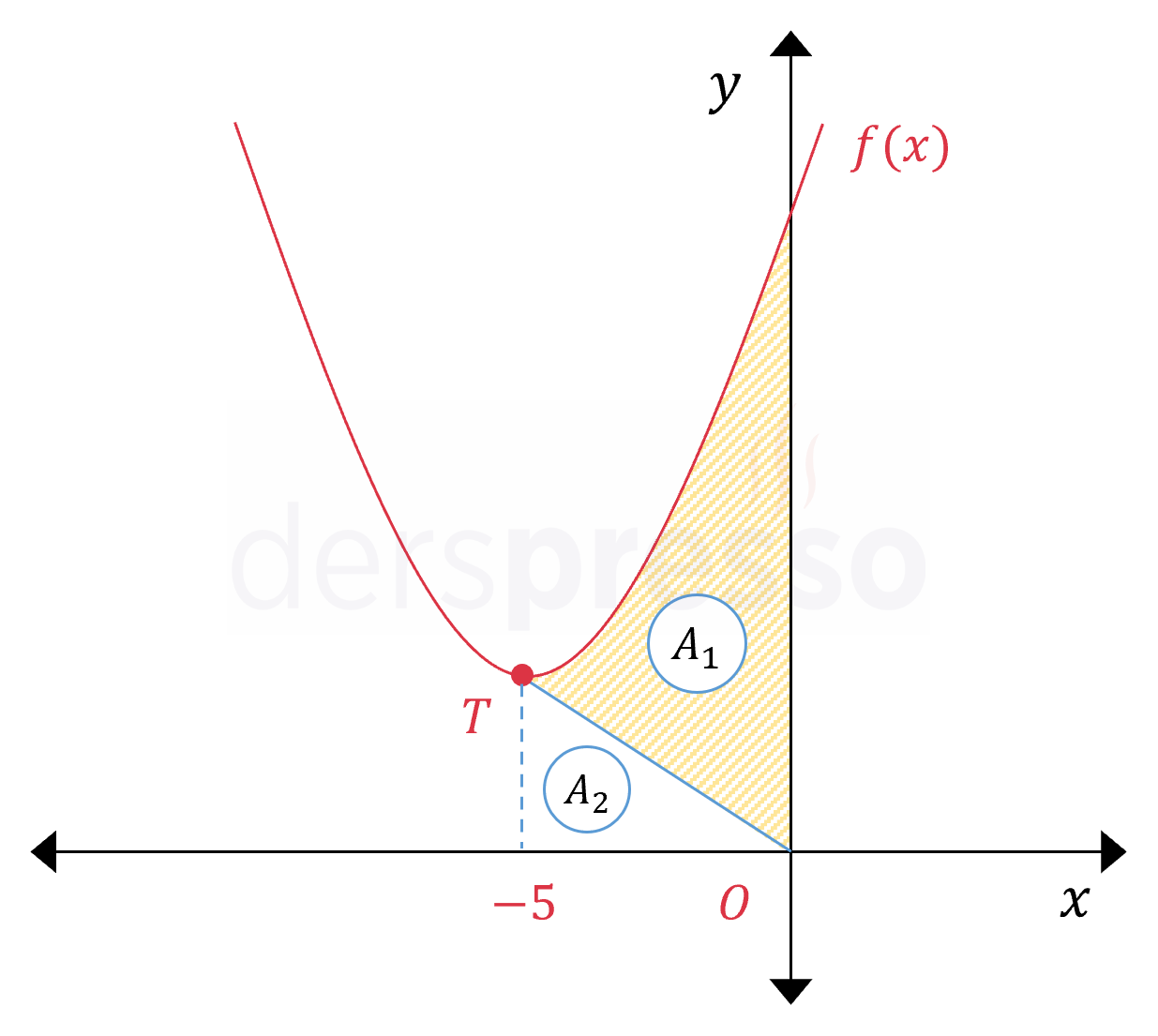
Önce \( [-5, 0] \) aralığında parabol ile \( x \) ekseni arasında kalan alanı bulalım.
\( A_1 + A_2 = \displaystyle\int_{-5}^0(x^2 + 10x + 26)\ dx \)
İfadenin integralini alalım.
\( = (\dfrac{x^3}{3} + 5x^2 + 26x)|_{-5}^0 \)
\( = (\dfrac{0^3}{3} + 5(0)^2 + 26(0)) - (\dfrac{(-5)^3}{3} + 5(-5)^2 + 26(-5)) \)
\( = 0 - (-\dfrac{125}{3} + 125 - 130) \)
\( = \dfrac{140}{3} \)
Üçgenin alanını bulalım.
\( A_2 = \dfrac{5 \cdot 1}{2} = \dfrac{5}{2} \)
Taralı bölge bulduğumuz birinci alanın ikinci alandan farkına eşittir.
\( A_1 = (A_1 + A_2) - A_2 \)
\( = \dfrac{140}{3} - \dfrac{5}{2} \)
\( = \dfrac{265}{6} \) olarak bulunur.

Yukarıda \( f(x) = -x^2 + 3x + 4 \) parabolü ile \( g(x) = 2x - 2 \) doğrusunun grafiği verilmiştir. Buna göre taralı bölgenin alanı kaç birimkaredir?
Çözümü Göster\( f \) ve \( g \) fonksiyonlarının kesişim noktalarını bulmak için iki denklemi ortak çözelim.
\( f(x) = g(x) \)
\( -x^2 + 3x + 4 = 2x - 2 \)
\( x^2 - x - 6 = 0 \)
\( (x + 2)(x - 3) = 0 \)
Buna göre iki fonksiyon \( x = -2 \) ve \( x = 3 \) apsisli noktalarda kesişir.
\( f \) fonksiyonunun \( x \) eksenini kestiği noktaları bulalım.
\( f(x) = -x^2 + 3x + 4 = 0 \)
\( -(x + 1)(x - 4) = 0 \)
Buna göre \( f \) fonksiyonu \( x \) eksenini \( x = -1 \) ve \( x = 4 \) apsisli noktalarda keser.
\( g \) doğrusunun \( x \) eksenini kestiği noktayı bulalım.
\( g(x) = 2x - 2 = 0 \)
\( x = 1 \)
Buna göre \( g \) doğrusu \( x \) eksenini \( x = 1 \) apsisli noktada keser.
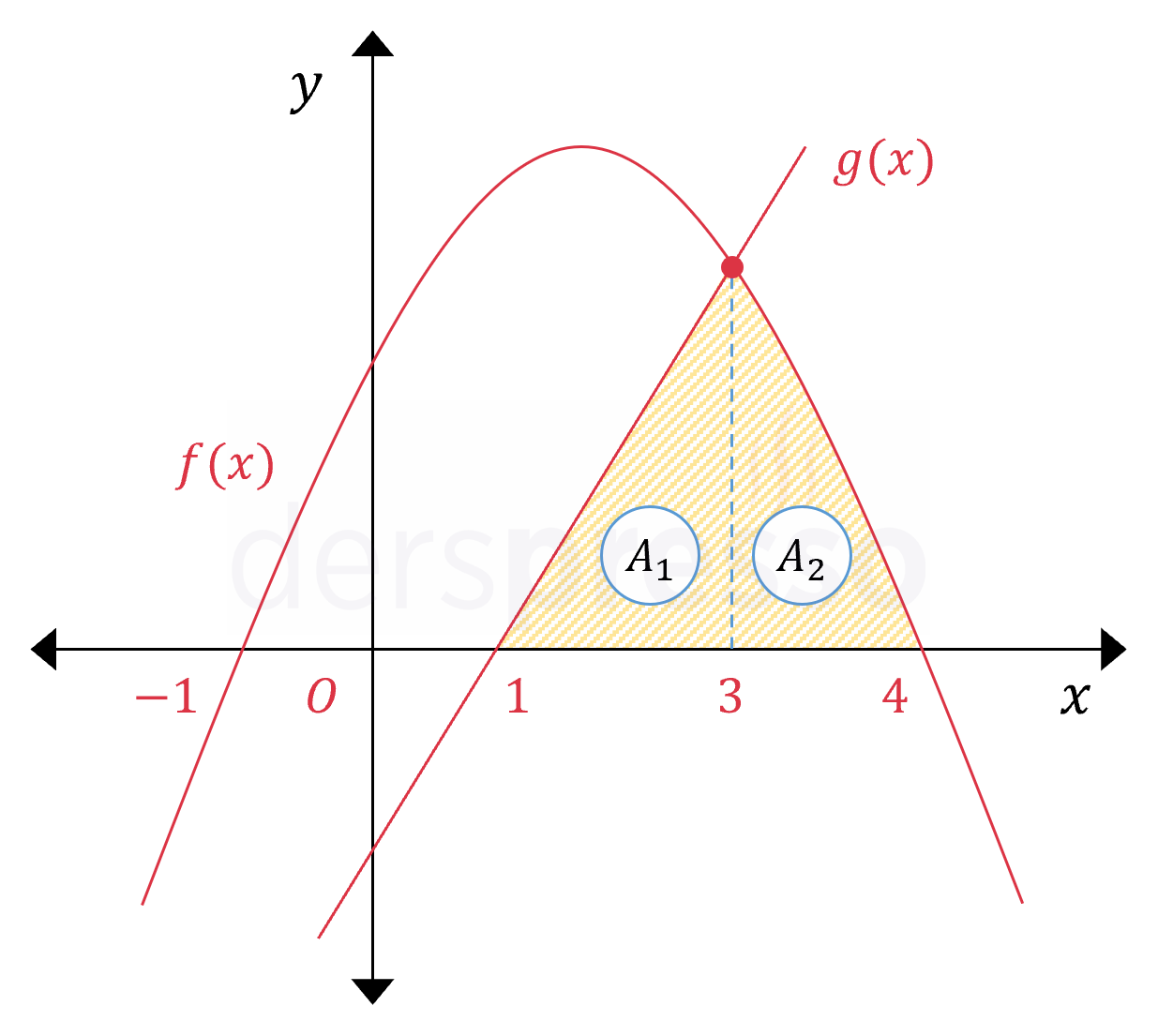
Taralı bölgenin alanı \( [1, 4] \) aralığında \( f \) ve \( g \) fonksiyonlarının \( x \) ekseni ile aralarında kalan alanların toplamına eşittir.
\( A = A_1 + A_2 \)
\( [1, 3] \) ve \( [3, 4] \) aralıklarında taralı alan farklı fonksiyonun \( x \) ekseni ile arasında kalan alana karşılık geldiği için belirli integrali iki aralık için ayrı ayrı almalıyız.
Önce \( [1, 3] \) aralığında \( g \) fonksiyonu ile \( x \) ekseni arasında kalan alanı bulalım.
\( A_1 = \displaystyle\int_1^3(2x - 2)\ dx \)
İfadenin integralini alalım.
\( = (x^2 - 2x)|_1^3 \)
\( = (3^2 - 2(3)) - (1^2 - 2(1)) \)
\( = 4 \)
Şimdi \( [3, 4] \) aralığında \( f \) fonksiyonu ile \( x \) ekseni arasında kalan alanı bulalım.
\( A_2 = \displaystyle\int_3^4(-x^2 + 3x + 4)\ dx \)
İfadenin integralini alalım.
\( = (-\dfrac{x^3}{3} + \dfrac{3x^2}{2} + 4x)|_3^4 \)
\( = (-\dfrac{4^3}{3} + \dfrac{3(4)^2}{2} + 4(4)) - (-\dfrac{3^3}{3} + \dfrac{3(3)^2}{2} + 4(3)) \)
\( = (-\dfrac{64}{3} + 24 + 16) - (-9 + \dfrac{27}{2} + 12) \)
\( = \dfrac{13}{6} \)
Taralı bölgenin alanı bulduğumuz iki alanın toplamına eşittir.
\( A = A_1 + A_2 \)
\( = 4 + \dfrac{13}{6} = \dfrac{37}{6} \) olarak bulunur.
\( a, b, c, d, e \in \mathbb{R} \),
\( a \lt b \lt c \lt d \lt e \) olmak üzere,
\( f(x) = -(x - a)(x - b)(x - c)^2(x - d)(x - e) \) polinom fonksiyonu veriliyor.
Fonksiyonun \( x \) ekseni ile arasında kalan alanlar \( [a, b] \), \( [b, c] \), \( [c, d] \) ve \( [d, e] \) aralıkları için sırasıyla 23, 35, 14 ve 51 birimdir.
Buna göre \(\displaystyle\int_a^e f(x)\ dx \) integralinin sonucu nedir?
Çözümü GösterFonksiyonun biri çift katlı olmak üzere 5 reel kökü vardır, dolayısıyla fonksiyon 6. derecedendir.
Fonksiyonun başkatsayısı negatif olduğu için \( x \) pozitif ve negatif sonsuza giderken \( y \) negatif sonsuza gider.
\( c \) noktasındaki çift katlı kökte grafik \( x \) eksenini işaret değiştirmeden keser, diğer tek katlı köklerde işaret değiştirerek keser.
Buna göre fonksiyonun grafiği aşağıdaki gibi olur. Grafiğin farklı aralıklarda \( x \) ekseni ile arasında kalan alanlar grafikte işaretlenmiştir.
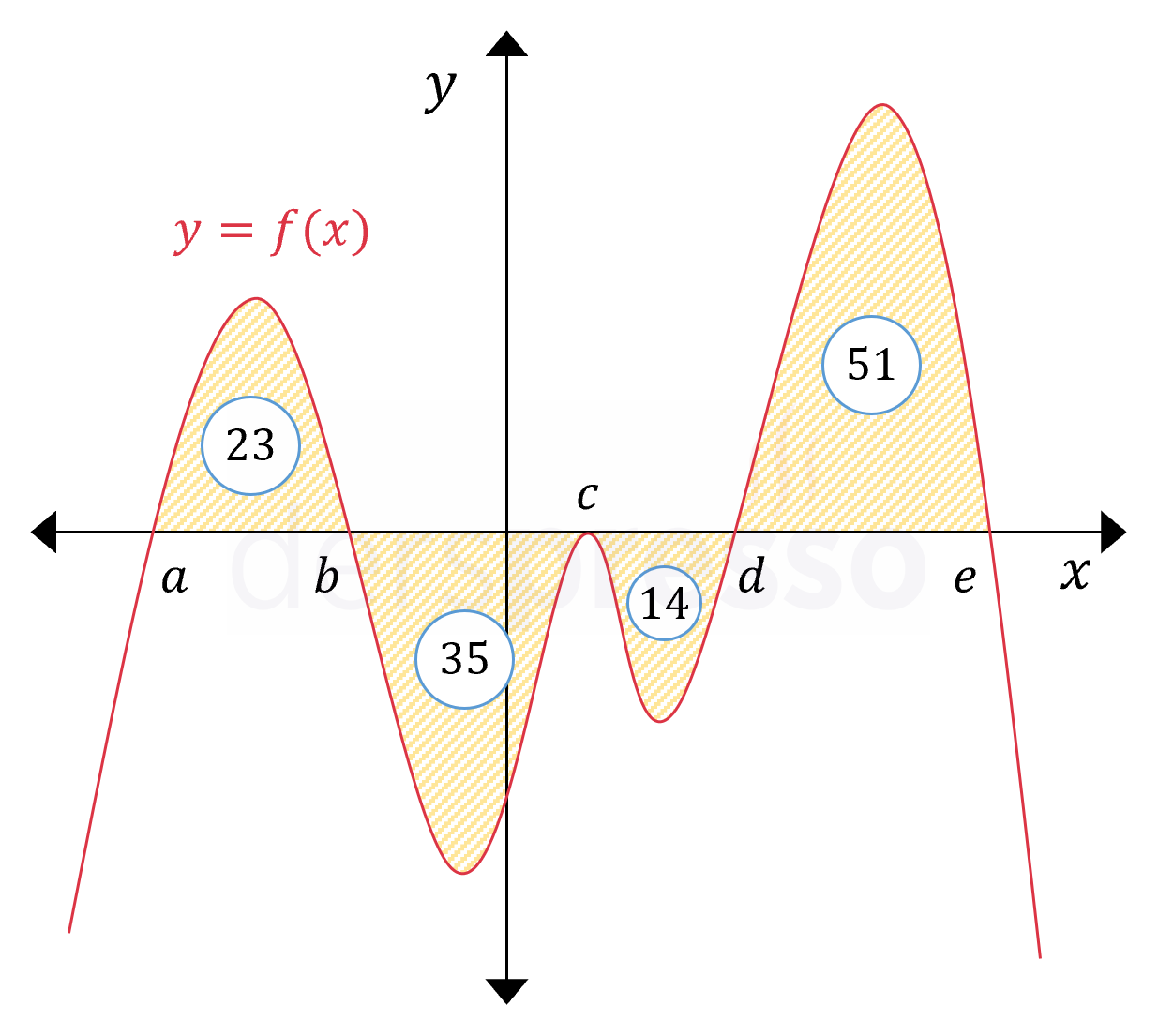
Fonksiyonun \( [a, e] \) aralığındaki belirli integrali, bu aralıkta \( x \) ekseninin üstünde kalan alanlarla altında kalan alanların farkına eşittir.
\( \displaystyle\int_a^e f(x)\ dx = 23 - 35 - 14 + 51 = 25 \) birim bulunur.

Yukarıda \( f(x) = \dfrac{x^2}{2} - 3x \) fonksiyonunun grafiği verilmiştir.
\( d_1 \) ve \( d_2 \) doğruları bu fonksiyona köklerinde teğet olduğuna göre, taralı bölgenin alanı kaç birimkaredir?
Çözümü Göster\( f \) fonksiyonunun köklerini bulalım.
\( f(x) = x(\dfrac{x}{2} - 3) = 0 \)
Buna göre \( f \) fonksiyonu \( x \) eksenini \( x = 0 \) ve \( x = 6 \) apsisli noktalarda keser.
\( d_1 \) ve \( d_2 \) doğrularının denklemlerini bularak kesişimleri olan \( B \) noktasının koordinatlarını bulalım.
\( x = 0 \) ve \( x = 6 \) apsisli noktalardaki teğetlerin eğimini bulmak için \( f(x) \) fonksiyonunun türevini alalım.
\( f'(x) = x - 3 \)
\( f'(0) = 0 - 3 = -3 \)
\( f'(6) = 6 - 3 = 3 \)
Buna göre \( f \) fonksiyonunun \( x = 0 \) noktasındaki eğimi -3, \( x = 6 \) noktasındaki eğimi 3'tür.
Teğet doğruların denklemini bulmak için bir noktası ve eğimi bilinen doğru denklemini kullanalım.
\( y - y_1 = m(x - x_1) \)
\( d_1 \) doğrusu için:
\( y - 0 = -3(x - 0) \)
\( d_1: y = -3x \)
\( d_2 \) doğrusu için:
\( y - 0 = 3(x - 6) \)
\( d_2: y = 3x - 18 \)
\( B \) noktasının koordinatlarını bulmak için \( d_1 \) ve \( d_2 \) denklemlerini ortak çözelim.
\( -3x = 3x - 18 \)
\( 6x = 18 \)
\( x = 3, \quad y = -9 \)
\( B(3, -9) \)
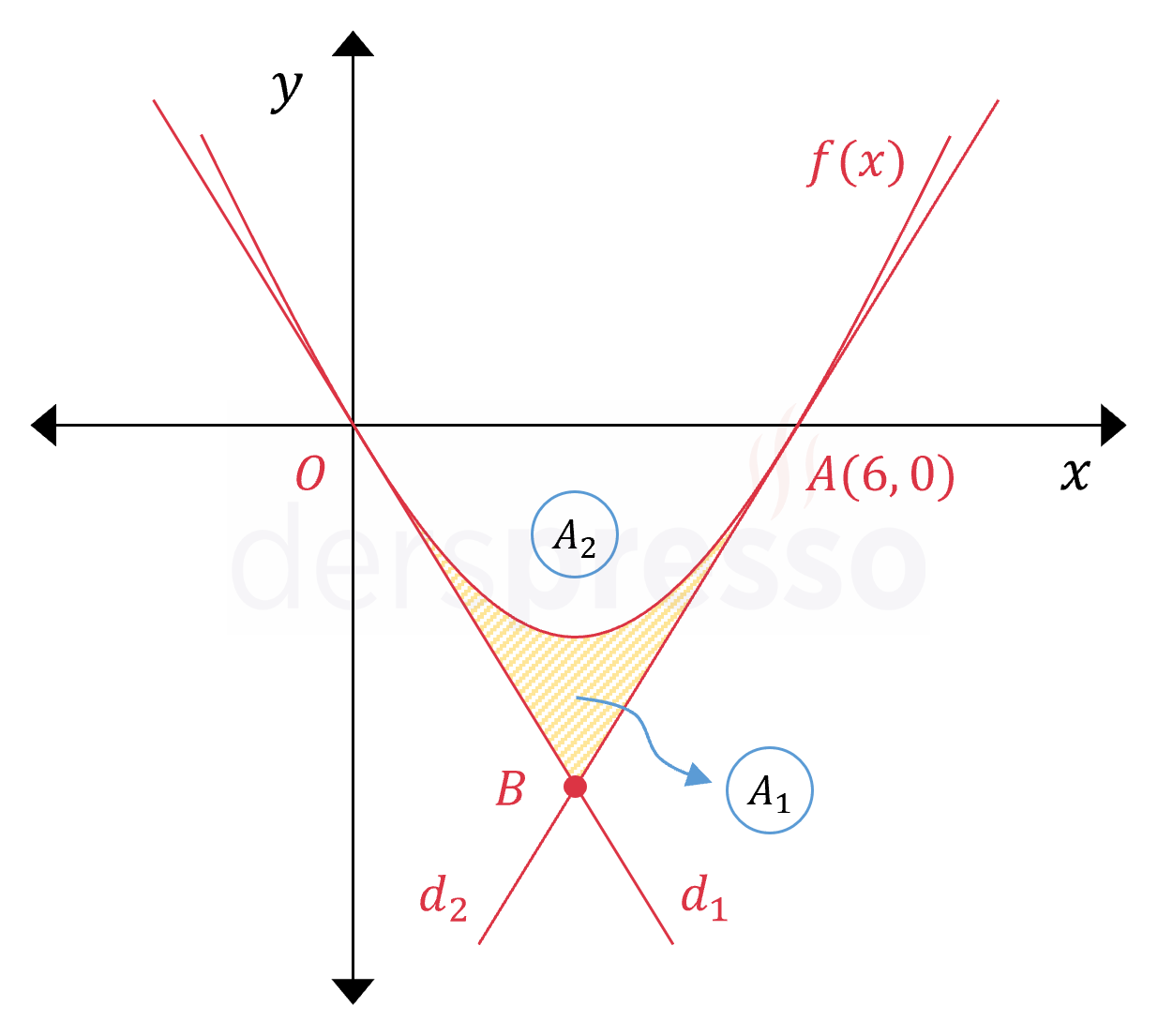
Taralı bölgeninin alanını bulmak için \( OAB \) üçgeninin alanından \( f(x) \) fonksiyonunun \( [0, 6] \) aralığında \( x \) ekseni ile arasında kalan alanı çıkaralım.
\( A_1 = A(OAB) - A_2 \)
\( OAB \) üçgeninin alanını bulalım.
\( A(OAB) = \dfrac{6 \cdot 9}{2} = 27 \)
\( A_2 \) alanı \( f(x) \) fonksiyonunun \( [0, 6] \) aralığındaki belirli integralinin mutlak değerine eşittir.
\( \displaystyle\int_0^6(\dfrac{x^2}{2} - 3x)\ dx \)
İfadenin integralini alalım.
\( = (\dfrac{x^3}{6} - \dfrac{3x^2}{2})|_0^6 \)
\( = (\dfrac{6^3}{6} - \dfrac{3(6)^2}{2}) - (\dfrac{0^3}{6} - \dfrac{3(0)^2}{2}) \)
\( = (36 - 54) - 0 \)
\( = -18 \)
Alan pozitif bir büyüklük olduğu için \( f(x) \) fonksiyonunun \( [0, 6] \) aralığında \( x \) ekseni ile arasında kalan alan fonksiyonun bu aralıktaki belirli integralinin mutlak değerine eşittir.
\( A_2 = \abs{-18} = 18 \)
Taralı bölgenin alanını bulalım.
\( A_1 = A(OAB) - A_2 \)
\( = 27 - 18 = 9 \) olarak bulunur.
\( f(x) = x^4 + 6x^3 + 9x^2 \) eğrisi ile \( x \) ekseni arasında kalan kapalı bölgenin alanı kaç birimkaredir?
Çözümü GösterVerilen fonksiyon 4. dereceden polinom fonksiyonudur.
Fonksiyon tanımını çarpanlarına ayıralım.
\( f(x) = x^2(x^2 + 6x + 9) \)
\( = x^2(x + 3)^2 \)
Buna göre fonksiyonun \( x = -3 \) ve \( x = 0 \) noktalarında olmak üzere iki tane çift katlı kökü vardır.
Çift dereceli ve pozitif başkatsayılı polinomların grafiklerinde \( x \) negatif ve pozitif sonsuza giderken \( y \) pozitif sonsuza gider.
Bir polinom fonksiyonunun grafiği tek katlı köklerde \( x \) eksenini keser ve eksenin öteki tarafına geçer, çift katlı köklerde ise \( x \) eksenini teğet keser ve eksenin öteki tarafına geçmeden geri döner.
Bu bilgiler doğrultusunda fonksiyonun grafiği aşağıdaki gibi olur.
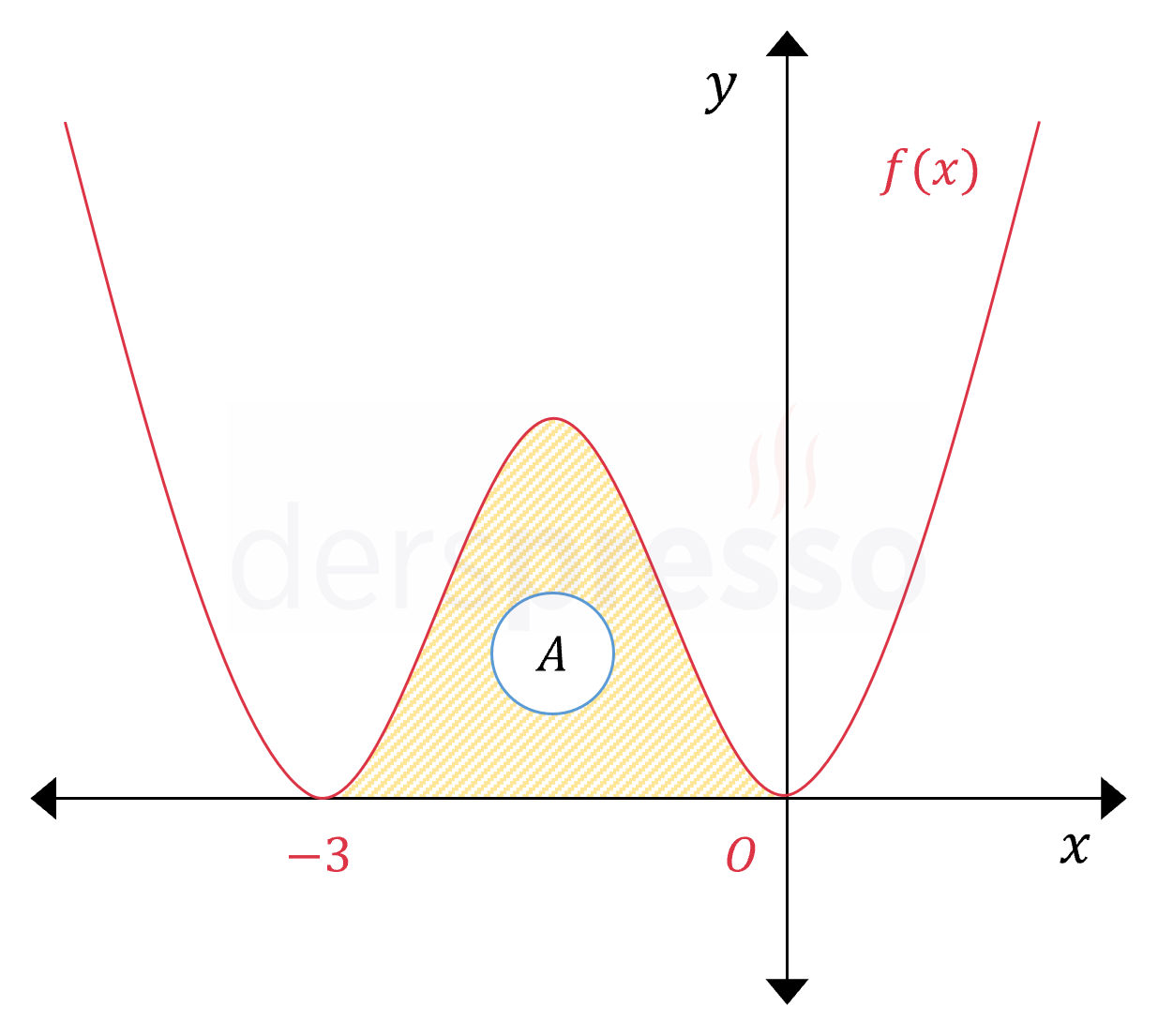
Buna göre istenen alan şekildeki taralı bölgeye karşılık gelir ve fonksiyonun \( [-3, 0] \) aralığındaki belirli integraline eşittir.
\( A = \displaystyle\int_{-3}^0(x^4 + 6x^3 + 9x^2)\ dx \)
İfadenin integralini alalım.
\( = (\dfrac{x^5}{5} + \dfrac{6x^4}{4} + 3x^3)|_{-3}^0 \)
\( = (\dfrac{0^5}{5} + \dfrac{6(0)^4}{4} + 3(0)^3) - (\dfrac{(-3)^5}{5} + \dfrac{6(-3)^4}{4} + 3(-3)^3) \)
\( = 0 - (-\dfrac{243}{5} + \dfrac{243}{2} - 81) \)
\( = \dfrac{81}{10} \) olarak bulunur.
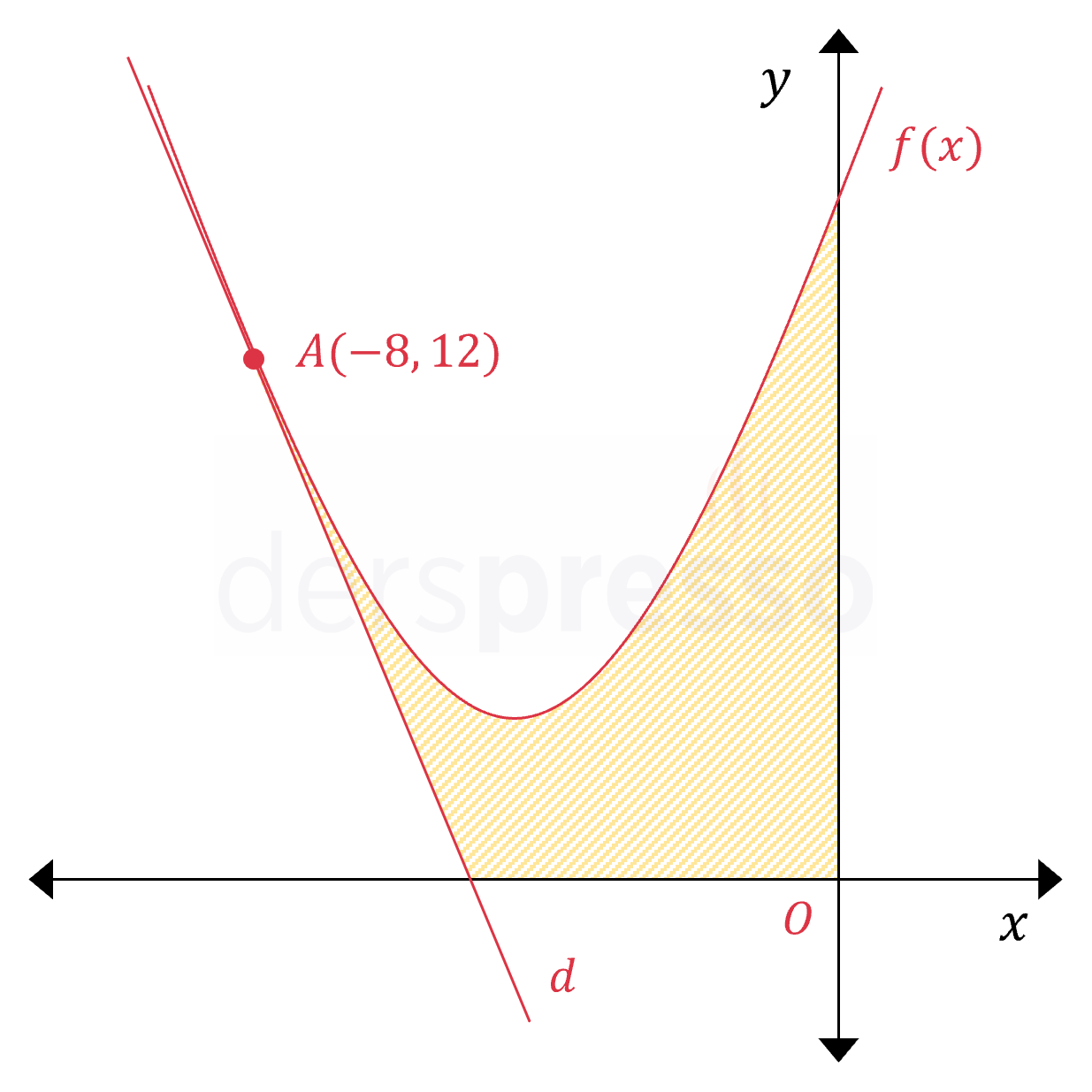
Yukarıda \( f(x) = x^2 + 10x + 28 \) fonksiyonu ile \( d \) doğrusu verilmiştir. Parabol ile doğru \( A(-8, 12) \) noktasında birbirine teğet olduğuna göre, taralı bölgenin alanı kaç birimkaredir?
Çözümü GösterBir fonksiyona bir noktada teğet olan doğrunun eğimi fonksiyonun o noktadaki birinci türev değerine eşittir.
Buna göre \( f(x) \) fonksiyonunun \( x = -8 \) noktasındaki türevinden yararlanarak \( d \) doğrusunun denklemini yazalım.
\( f'(x) = 2x + 10 \)
\( f'(-8) = 2(-8) + 10 = -6 \)
Bir noktası ve eğimi bilinen doğrunun denklemini yazalım.
\( y - y_1 = m(x - x_1) \)
\( y - 12 = -6(x - (-8)) \)
\( y = -6x - 36 \)
\( d \) doğrusunun \( x \) eksenini kestiği noktayı bulmak için doğru denkleminde \( y = 0 \) yazalım.
\( 0 = -6x - 36 \)
\( x = -6 \)
Bu durumda \( d \) doğrusu \( x \) eksenini \( (-6, 0) \) noktasında keser.
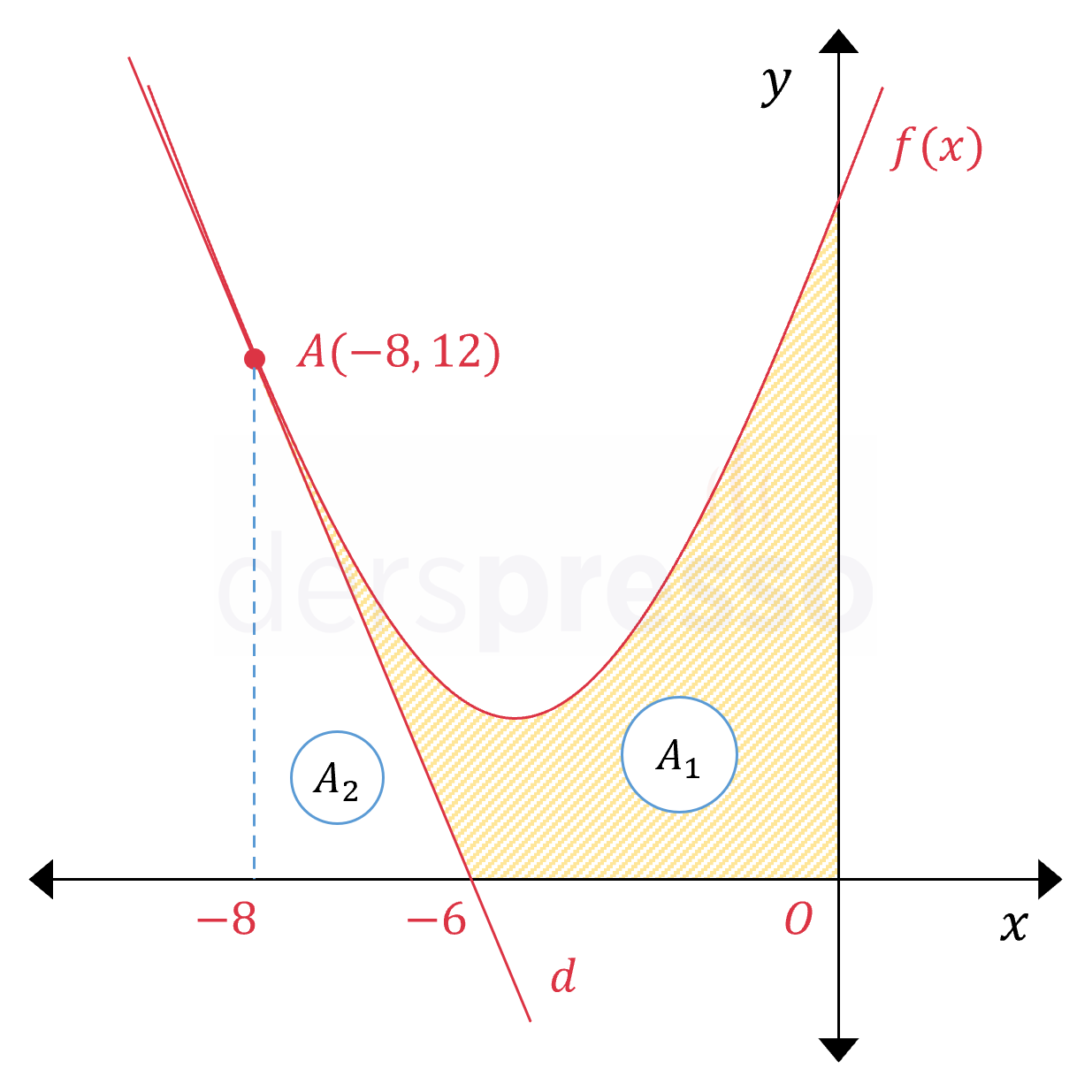
Taralı bölgenin alanını bulmak için \( f(x) \) fonksiyonunun \( [-8, 0] \) aralığındaki belirli integralinden \( A_2 \) ile işaretli üçgenin alanını çıkaralım.
Üçgenin alanını bulalım.
\( A_2 = \dfrac{2 \cdot 12}{2} = 12 \)
Taralı bölgenin alanını bulalım.
\( A_1 = \displaystyle\int_{-8}^0 (x^2 + 10x + 28)\ dx - A_2 \)
İfadenin integralini alalım.
\( = (\dfrac{x^3}{3} + 5x^2 + 28x)|_{-8}^0 - 12 \)
\( = (\dfrac{0^3}{3} + 5(0)^2 + 28(0)) - (\dfrac{(-8)^3}{3} + 5(-8)^2 + 28(-8)) - 12 \)
\( = 0 - (\dfrac{-512}{3} + 320 - 224) - 12 \)
\( = \dfrac{224}{3} - 12 \)
\( = \dfrac{188}{3} \) bulunur.
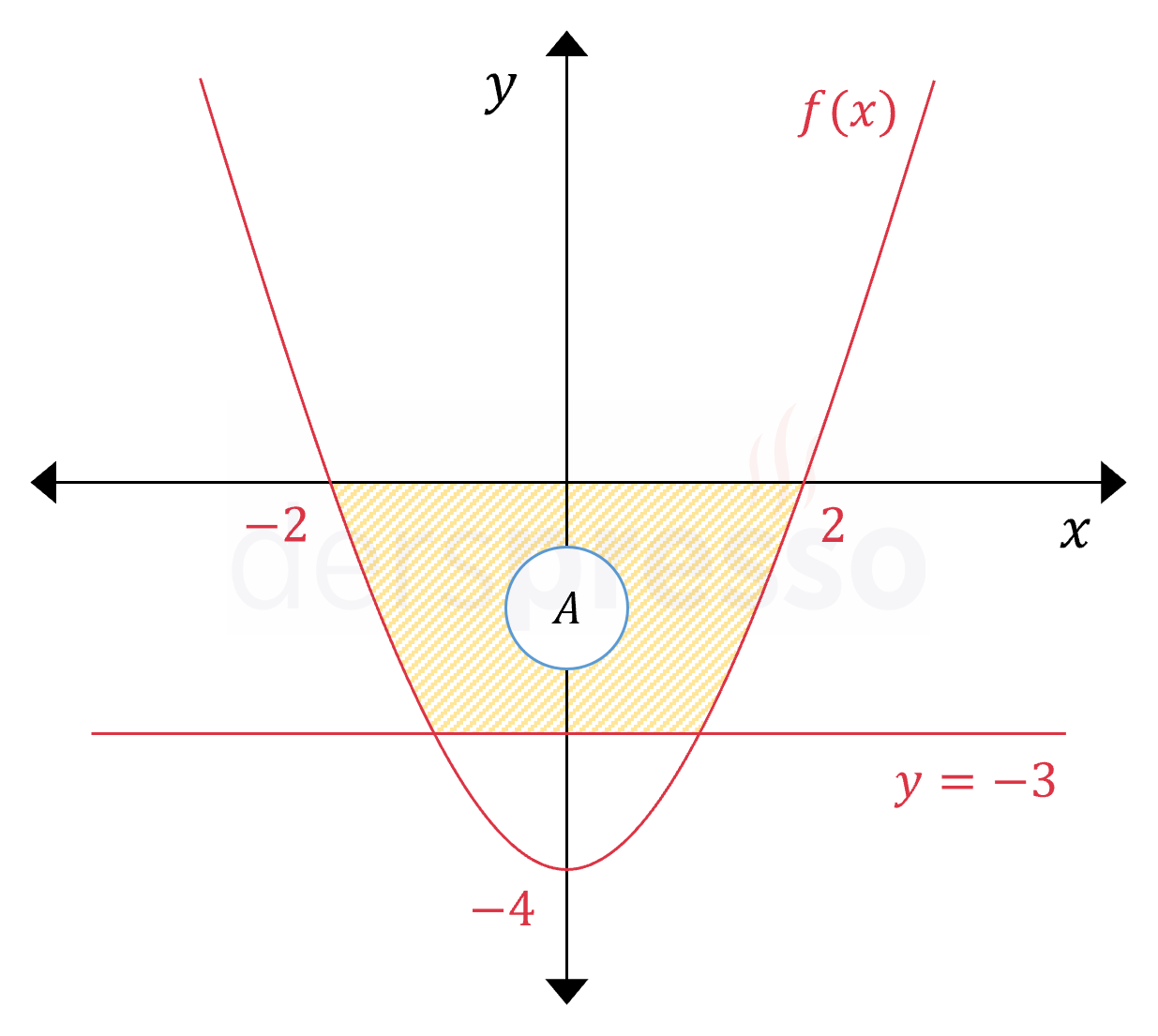
Yukarıda \( f(x) \) parabolünün eksenleri kestiği noktalar ile \( y = -3 \) doğrusunun grafiği verilmiştir. Buna göre taralı bölgenin alanı kaç birimkaredir?
Çözümü GösterParabolün denklemini bulmak için kökleri ve ek bir noktası bilinen parabol denklem formülünü kullanalım.
\( f(x) = a(x - x_1)(x - x_2) \)
\( f(x) = a(x + 2)(x - 2) \)
\( a \) değerini bulmak için \( (0, -4) \) noktasının koordinatlarını denklemde yerine koyalım.
\( f(0) = a(0 + 2)(0 - 2) = -4 \)
\( a = 1 \)
\( f \) fonksiyonunun denklemi aşağıdaki gibi bulunur.
\( f(x) = (x + 2)(x - 2) = x^2 - 4 \)
Parabol ile \( y = -3 \) doğrusunun kesişim noktalarını bulmak için iki denklemi ortak çözelim.
\( x^2 - 4 = -3 \)
\( x^2 = 1 \)
\( x = \pm 1 \)
Buna göre parabol ve doğru \( x = -1 \) ve \( x = 1 \) apsisli noktalarda kesişir.
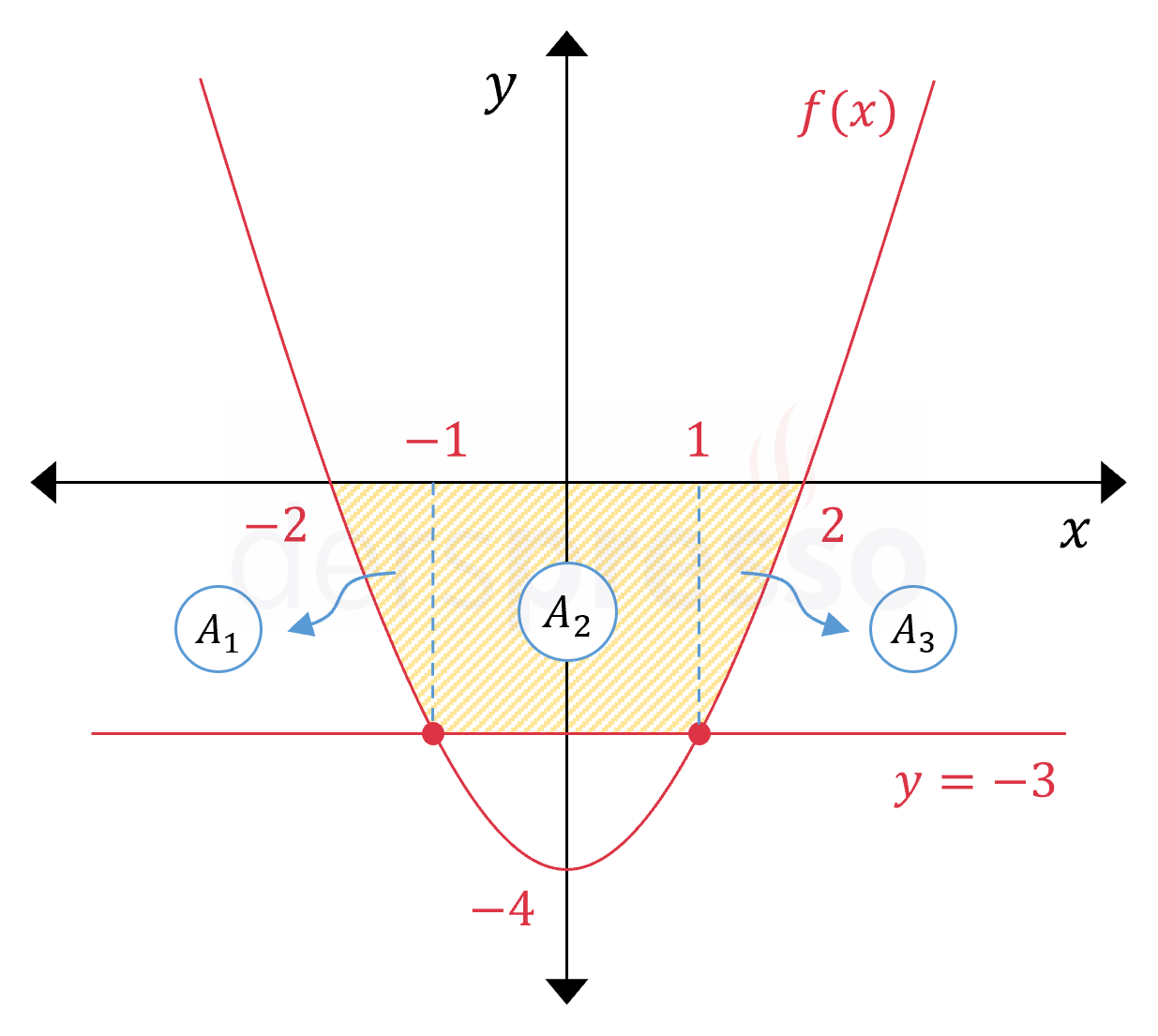
Taralı bölgenin alanını bulmak için \( f(x) \) fonksiyonunun \( [-2, -1] \) ve \( [1, 2] \) aralıklarında \( x \) ekseni ile arasında kalan alan ile köşeleri \( (-1, 0) \), \( (-1, -3) \), \( (1, -3) \) ve \( (1, 0) \) olan dikdörtgenin alanını toplayalım.
\( A = A_1 + A_2 + A_3 \)
Dikdörtgenin alanını bulalım.
\( A_2 = 2 \cdot 3 = 6 \)
\( f(x) \) fonksiyonunun \( [-2, -1] \) ve \( [1, 2] \) aralıklarında \( x \) ekseni ile arasında kalan alan fonksiyonun bu aralıklardaki belirli integralinin mutlak değerine eşittir.
\( \displaystyle\int_{-2}^{-1}(x^2 - 4)\ dx \)
İfadenin integralini alalım.
\( = (\dfrac{x^3}{3} - 4x)|_{-2}^{-1} \)
\( = (\dfrac{(-1)^3}{3} - 4(-1)) - (\dfrac{(-2)^3}{3} - 4(-2)) \)
\( = \dfrac{7}{3} - 4 = -\dfrac{5}{3} \)
Alan pozitif bir büyüklük olduğu için \( f(x) \) fonksiyonunun \( [-2, -1] \) aralığında \( x \) ekseni ile arasında kalan alan fonksiyonun bu aralıktaki belirli integralinin mutlak değerine eşittir.
\( A_1 = \abs{-\dfrac{5}{3}} = \dfrac{5}{3} \)
\( f(x) \) çift fonksiyon olduğu için \( [-2, -1] \) ve \( [1, 2] \) aralıklarındaki belirli integral değerleri birbirine eşittir.
\( A_3 = A_1 = \dfrac{5}{3} \)
Taralı bölge bulduğumuz üç alanın toplamına eşittir.
\( A = A_1 + A_2 + A_3 \)
\( A = \dfrac{5}{3} + 6 + \dfrac{5}{3} \)
\( = \dfrac{28}{3} \) olarak bulunur.
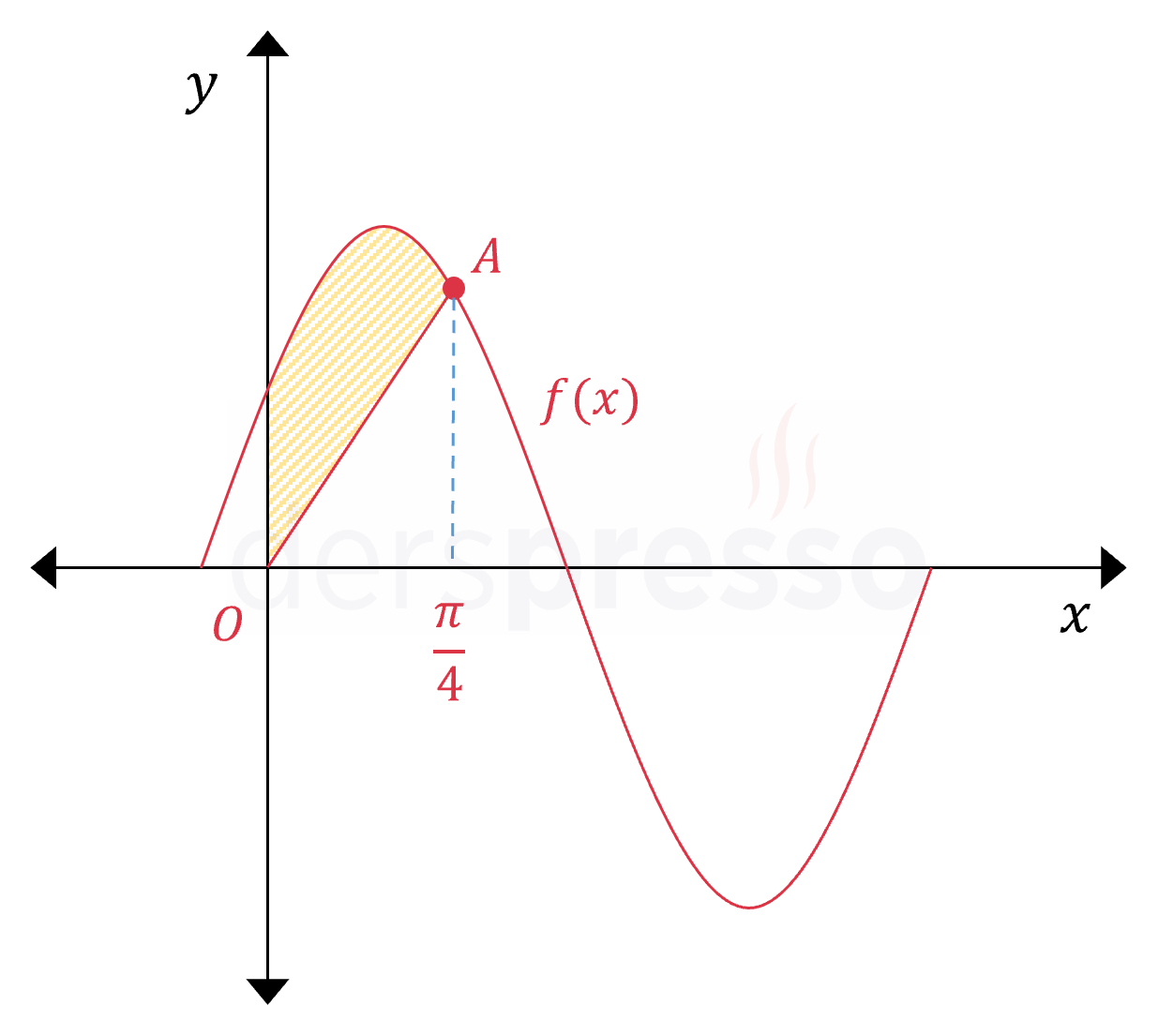
Yukarıda \( f(x) = \sin(3x) + 1 \) fonksiyonunun grafiği verilmiştir. \( A \) noktasının apsisi \( \frac{\pi}{4} \) olduğuna göre, taralı bölgenin alanı kaç birimkaredir?
Çözümü Göster\( A \) noktasının ordinatını bulalım.
\( A \) noktası \( f \) eğrisi üzerinde olduğu için koordinatları denklemi sağlar.
\( f(\dfrac{\pi}{4}) = \sin(3 \cdot \dfrac{\pi}{4}) + 1 \)
\( = \dfrac{\sqrt{2}}{2} + 1 \)
\( A(\dfrac{\pi}{4}, \dfrac{\sqrt{2}}{2} + 1) \)
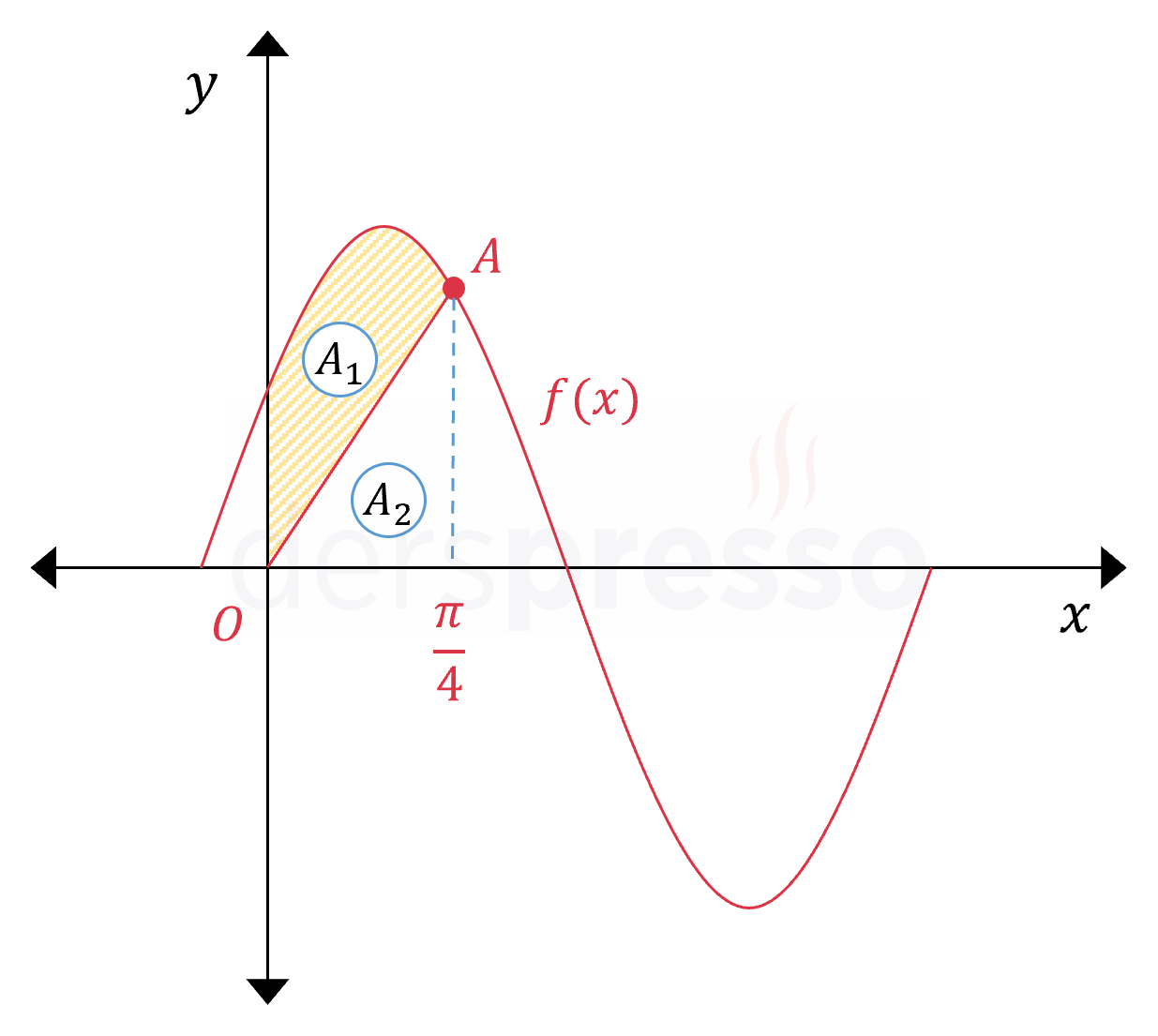
Taralı bölgenin alanını bulmak için \( f(x) \) fonksiyonunun \( [0, \frac{\pi}{4}] \) aralığındaki belirli integralinden köşeleri \( (\frac{\pi}{4}, 0) \), \( A \) ve orijin olan üçgenin alanını çıkaralım.
Üçgenin alanını bulalım.
\( A_2 = \dfrac{1}{2} \cdot \dfrac{\pi}{4} \cdot (\dfrac{\sqrt{2}}{2} + 1) = \dfrac{\sqrt{2}\pi + 2\pi}{16} \)
Taralı bölgenin alanını bulalım.
\( A_1 = \displaystyle\int_0^{\frac{\pi}{4}}(\sin(3x) + 1)\ dx - \dfrac{\sqrt{2}\pi + 2\pi}{16} \)
İfadenin integralini alalım.
\( = (\dfrac{-\cos(3x)}{3} + x)|_0^{\frac{\pi}{4}} - \dfrac{\sqrt{2}\pi + 2\pi}{16} \)
\( = [(\dfrac{-\cos(\frac{3\pi}{4})}{3} + \dfrac{\pi}{4}) - (\dfrac{-\cos{0}}{3}) + 0] - \dfrac{\sqrt{2}\pi + 2\pi}{16} \)
\( = [(\dfrac{\frac{\sqrt{2}}{2}}{3} + \dfrac{\pi}{4}) - (\dfrac{-1}{3}) + 0)] - \dfrac{\sqrt{2}\pi + 2\pi}{16} \)
\( = \dfrac{\sqrt{2}}{6} + \dfrac{\pi}{4} + \dfrac{1}{3} - \dfrac{\sqrt{2}\pi + 2\pi}{16} \)
\( = \dfrac{8\sqrt{2} + 6\pi - 3\sqrt{2}\pi + 16}{48} \) olarak bulunur.
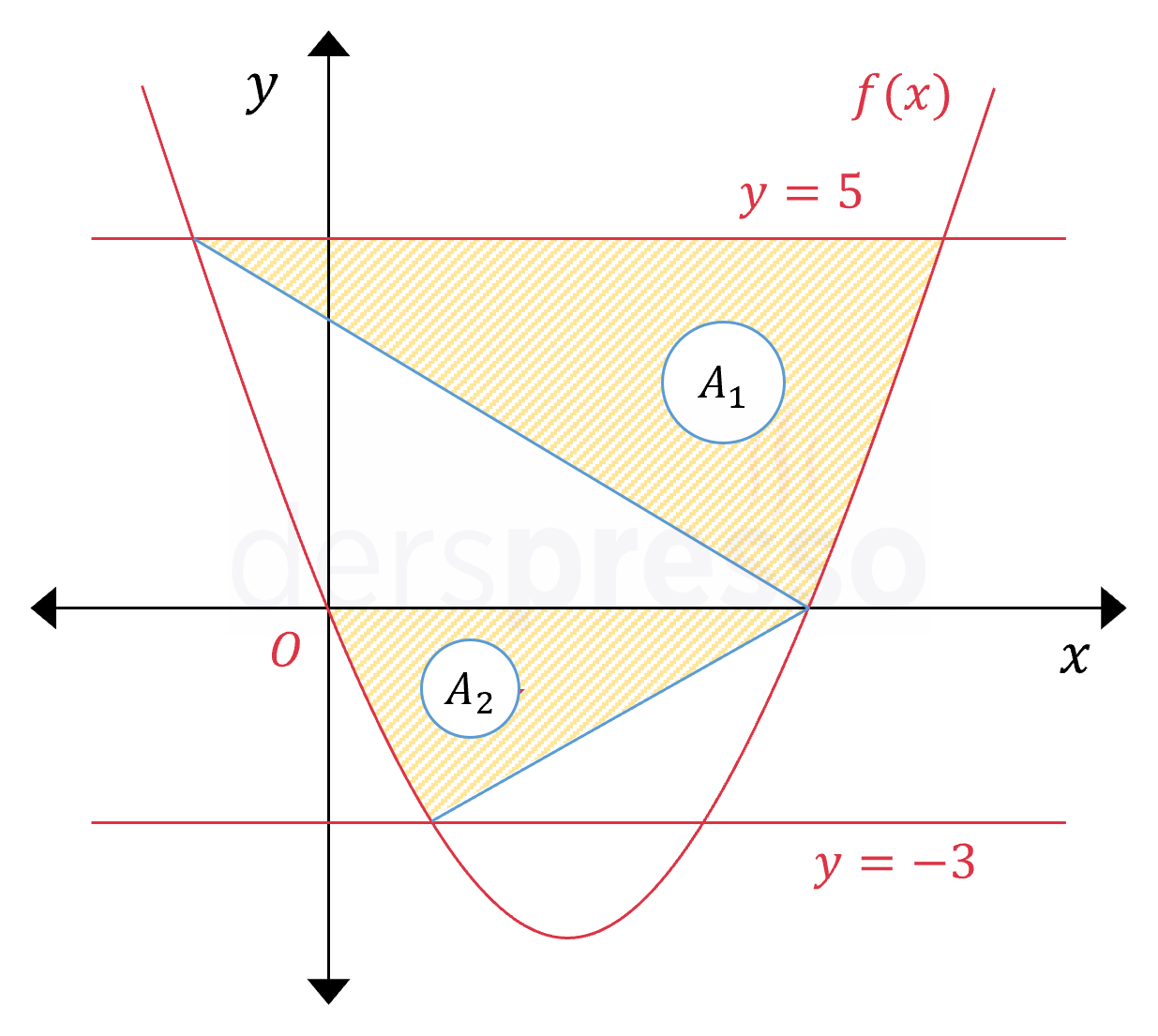
Yukarıda \( f(x) = x^2 - 4x \) parabolü ile \( y = 5 \) ve \( y = -3 \) doğrularının grafikleri verilmiştir.
Buna göre \( A_1 - A_2 \) kaç birimkaredir?
Çözümü GösterParabolün \( x \) eksenini kestiği noktaların koordinatlarını bulalım.
\( f(x) = x(x - 4) = 0 \)
Parabol \( x \) eksenini \( x = 0 \) ve \( x = 4 \) apsisli noktalarda keser.
Parabol ile doğruların kesişim noktalarını bulalım.
Parabol ile \( y = 5 \) doğrusunun kesişim noktalarını bulmak için iki denklemi ortak çözelim.
\( x^2 - 4x = 5 \)
\( x^2 - 4x - 5 = 0 \)
\( (x + 1)(x - 5) = 0 \)
Parabol ve \( y = 5 \) doğrusu \( x = -1 \) ve \( x = 5 \) apsisli noktalarda kesişir.
Parabol ile \( y = -3 \) doğrusunun kesişim noktalarını bulmak için iki denklemi ortak çözelim.
\( x^2 - 4x = -3 \)
\( x^2 - 4x + 3 = 0 \)
\( (x - 1)(x - 3) = 0 \)
Parabol ve \( y = -3 \) doğrusu \( x = 1 \) ve \( x = 3 \) apsisli noktalarda kesişir.
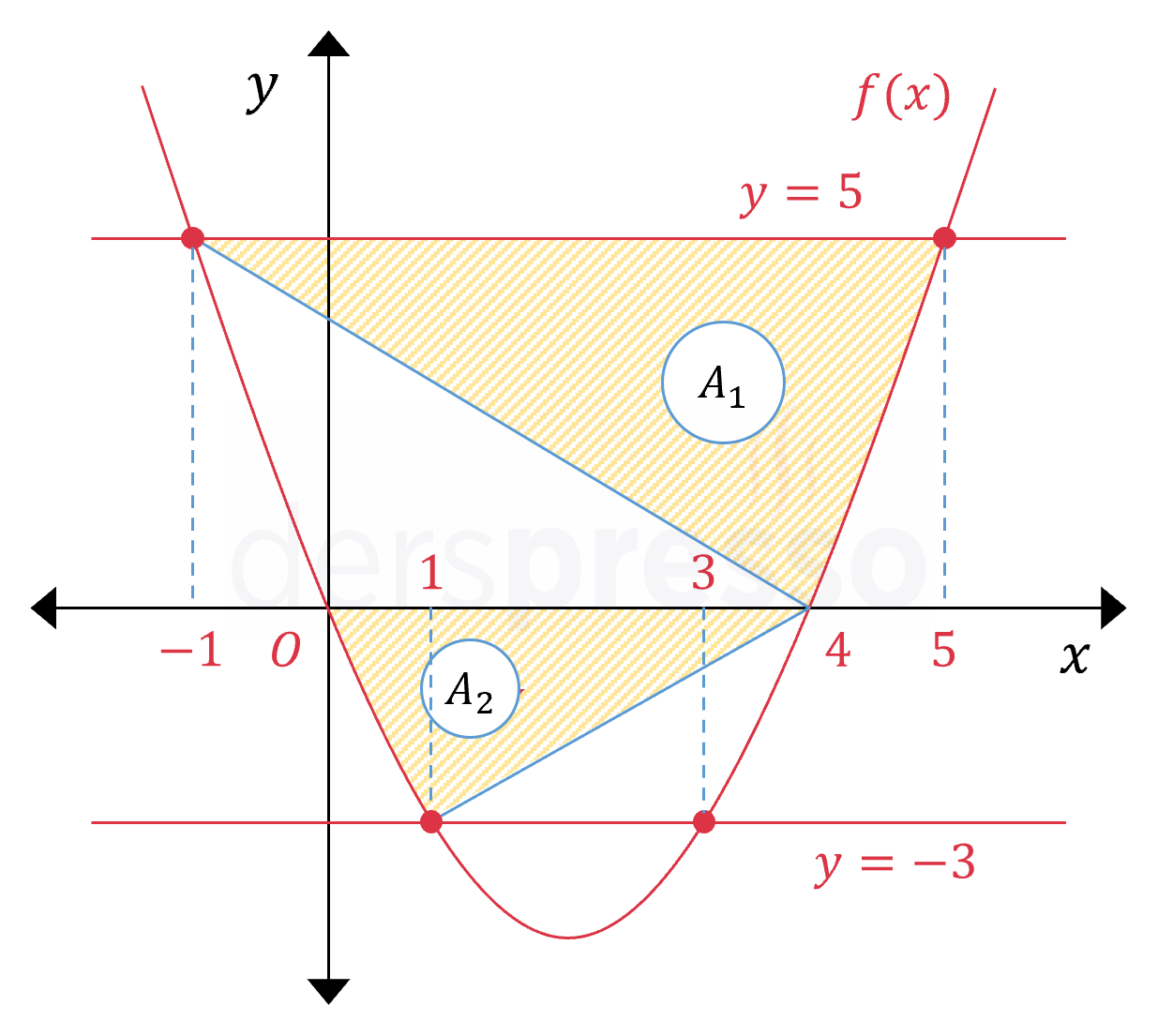
\( A_1 \) alanını bulmak için köşeleri \( (-1, 5) \), \( (5, 5) \), \( (5, 0) \) ve \( (4, 0) \) olan yamuğun alanından \( f(x) \) fonksiyonunun \( [4, 5] \) aralığında \( x \) ekseni ile arasında kalan alanı çıkaralım.
Yamuğun alanını bulalım.
\( \dfrac{6 + 1}{2} \cdot 5 = \dfrac{35}{2} \)
\( f(x) \) fonksiyonunun \( [4, 5] \) aralığında \( x \) ekseni ile arasında kalan alanı bulalım.
\( \displaystyle\int_4^5(x^2 - 4x)\ dx \)
İfadenin integralini alalım.
\( = (\dfrac{x^3}{3} - 2x^2)|_4^5 \)
\( = (\dfrac{5^3}{3} - 2(5)^2) - (\dfrac{4^3}{3} - 2(4)^2) \)
\( = (\dfrac{125}{3} - 50) - (\dfrac{64}{3} - 32) \)
\( = \dfrac{7}{3} \)
Bulduğumuz iki alanın farkını bulalım.
\( A_1 = \dfrac{35}{2} - \dfrac{7}{3} = \dfrac{91}{6} \)
\( A_2 \) alanını bulmak için \( f(x) \) fonksiyonunun \( [0, 1] \) aralığında \( x \) ekseni ile arasında kalan alan ile köşeleri \( (1, 0) \), \( (1, -3) \) ve \( (4, 0) \) noktaları olan üçgenin alanı ile toplayalım.
Üçgenin alanını bulalım.
\( \dfrac{1}{2} \cdot 3 \cdot 3 = \dfrac{9}{2} \)
\( f(x) \) fonksiyonunun \( [0, 1] \) aralığında \( x \) ekseni ile arasında kalan alanı bulalım.
\( \displaystyle\int_0^1(x^2 - 4x)\ dx \)
İfadenin integralini alalım.
\( = (\dfrac{x^3}{3} - 2x^2)|_0^1 \)
\( = (\dfrac{1^3}{3} - 2(1)^2) - (\dfrac{0^3}{3} - 2(0)^2) \)
\( = -\dfrac{5}{3} \)
Alan pozitif bir büyüklük olduğu için \( f(x) \) fonksiyonunun \( [0, 1] \) aralığında \( x \) ekseni ile arasında kalan alan fonksiyonun bu aralıktaki belirli integralinin mutlak değerine eşittir.
\( A_2 = \dfrac{9}{2} + \abs{-\dfrac{5}{3}} = \dfrac{37}{6} \)
\( A_1 - A_2 = \dfrac{91}{6} - \dfrac{37}{6} = 9 \) birimkare bulunur.
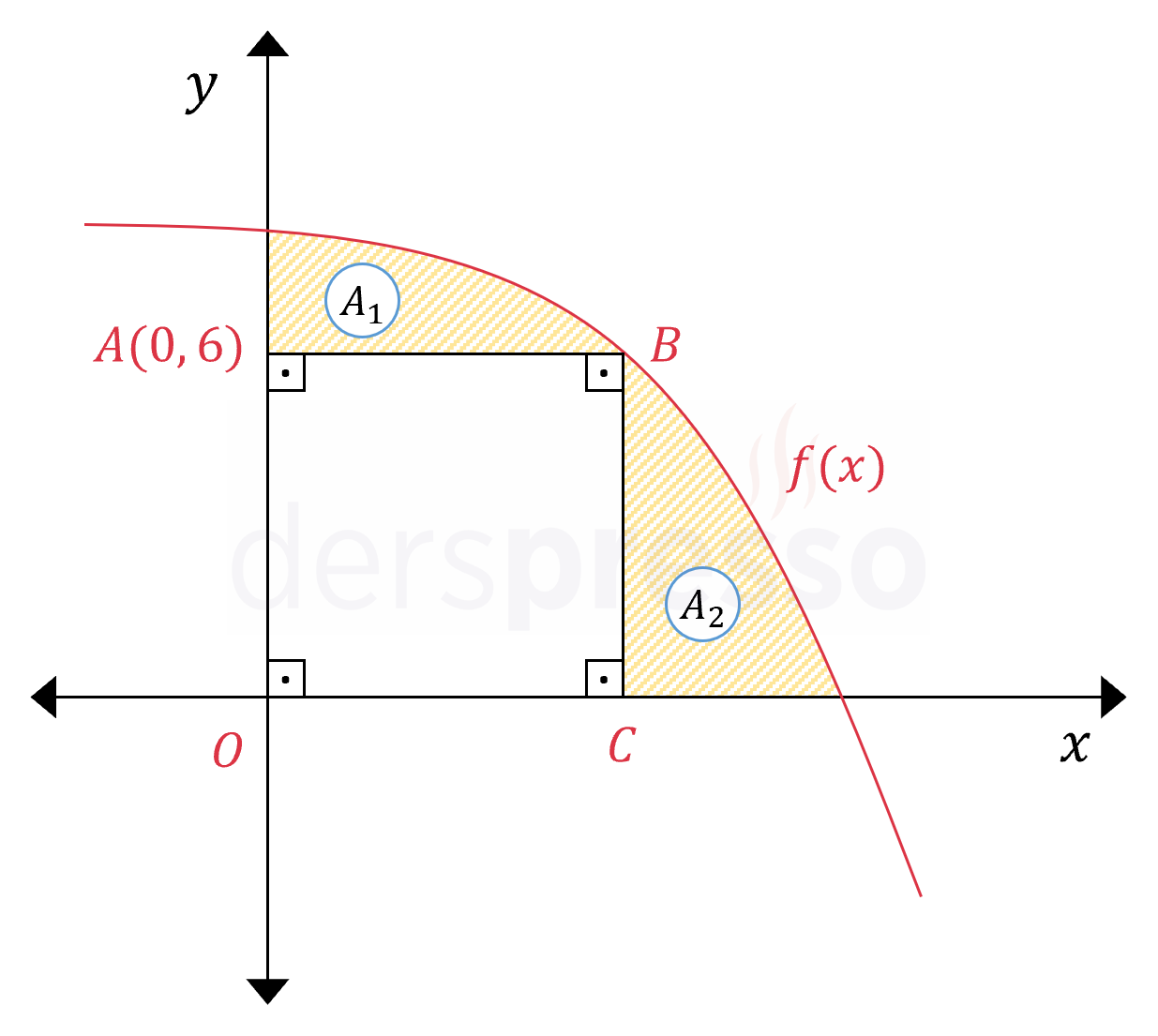
Yukarıda \( f(x) = 9 - e^{\frac{x}{3}} \) eğrisinin grafiği verilmiştir. \( B \) noktası \( y = 6 \) doğrusunun üzerinde olduğuna göre, \( \frac{A_2}{A_1} \) oranı kaçtır?
Çözümü Göster\( B \) noktasının koordinatlarını bulalım.
\( B \) noktası \( f \) eğrisi üzerinde olduğu için eğri denklemini sağlar.
\( f(x) = 9 - e^{\frac{x}{3}} = 6 \)
\( e^{\frac{x}{3}} = 3 \)
Her iki tarafın \( e \) tabanında logaritmasını alalım.
\( \dfrac{x}{3} = \ln{3} \)
\( x = 3\ln{3} \)
\( B(3\ln{3}, 6) \)
\( f \) fonksiyonunun \( [0, 3\ln{3}] \) aralığındaki belirli integrali \( A_1 \) alanı ile \( ABCO \) dikdörtgeninin alanının toplamına eşittir.
\( \displaystyle\int_0^{3\ln{3}}(9 - e^{\frac{x}{3}})\ dx = A_1 + A(ABCO) \)
Eşitliğin sol tarafının integralini alalım.
\( (9x - 3e^{\frac{x}{3}})|_0^{3\ln{3}} \)
\( = (9(3\ln{3}) - 3e^{\frac{3\ln{3}}{3}}) - (9(0) - 3e^{\frac{0}{3}}) \)
\( = 27\ln{3} - 9 - 0 + 3 \)
\( = 27\ln{3} - 6 \)
Dikdörtgenin alanını bulalım.
\( A(ABCO) = 6 \cdot 3\ln{3} = 18\ln{3} \)
Bulduğumuz değerleri yukarıdaki eşitlikte yerine koyalım.
\( 27\ln{3} - 6 = A_1 + 18\ln{3} \)
\( A_1 = 9\ln{3} - 6 \)
\( A_2 \) değerini bulmak için eğrinin \( x \) eksenini kestiği noktanın apsisini bulalım.
\( f(x) = 9 - e^{\frac{x}{3}} = 0 \)
\( e^{\frac{x}{3}} = 9 \)
Her iki tarafın \( e \) tabanında logaritmasını alalım.
\( \dfrac{x}{3} = \ln{9} = 2\ln{3} \)
\( x = 6\ln{3} \)
\( A_2 \) alanı eğrinin \( [3\ln{3}, 6\ln{3}] \) aralığındaki belirli integraline eşittir.
\( A_2 = \displaystyle\int_{3\ln{3}}^{6\ln{3}}(9 - e^{\frac{x}{3}})\ dx \)
İfadenin integralini alalım.
\( = (9x - 3e^{\frac{x}{3}})|_{3\ln{3}}^{6\ln{3}} \)
\( = (9(6\ln{3}) - 3e^{\frac{6\ln{3}}{3}}) - (9(3\ln{3}) - 3e^{\frac{3\ln{3}}{3}}) \)
\( = 54\ln{3} - 27 - 27\ln{3} + 9 \)
\( = 27\ln{3} - 18 \)
\( \dfrac{A_2}{A_1} \) oranını bulalım.
\( \dfrac{A_2}{A_1} = \dfrac{27\ln{3} - 18}{9\ln{3} - 6} = 3 \) olarak bulunur.
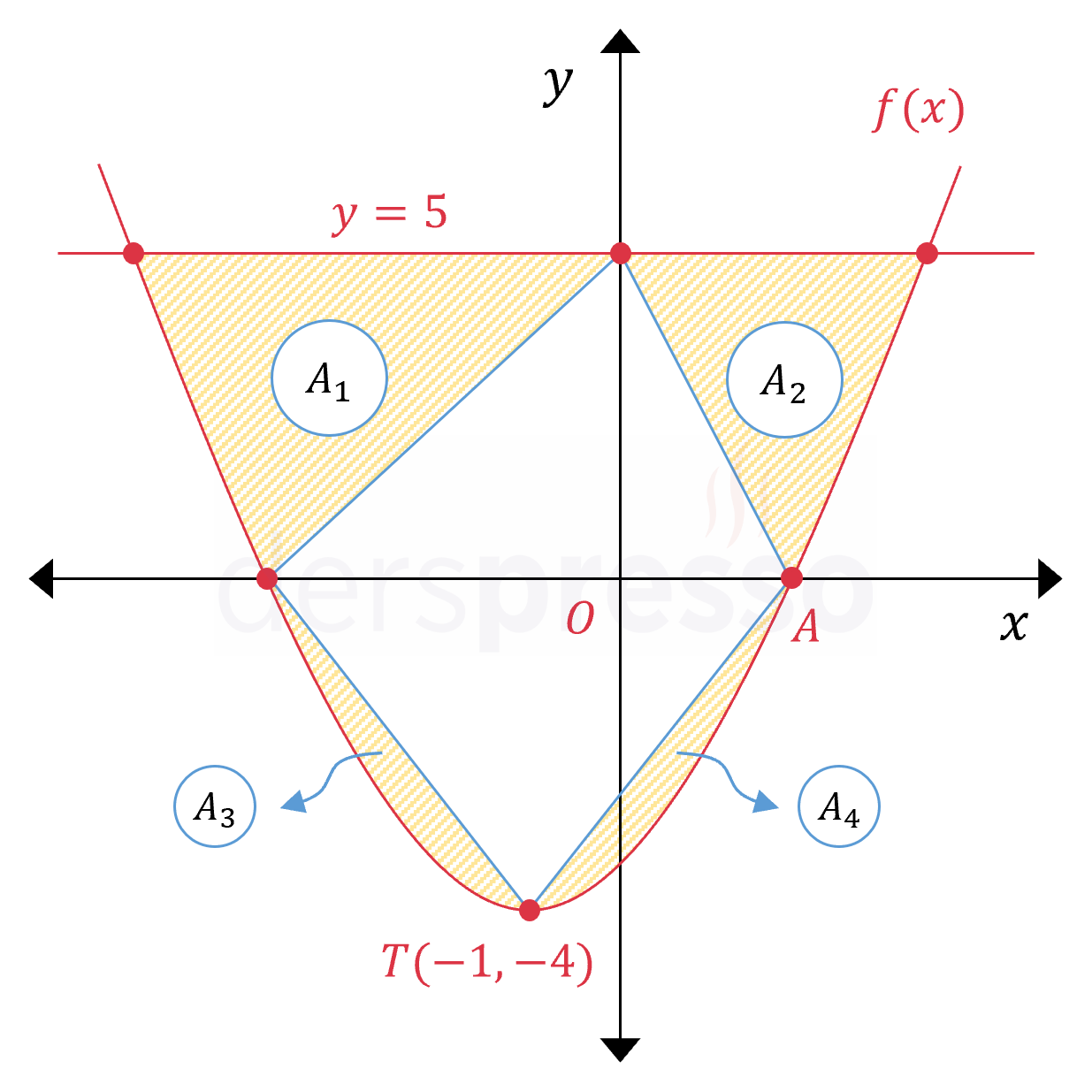
Yukarıda \( f(x) \) parabolü ve \( y = 5 \) doğrusunun grafiği verilmiştir. \( T(-1, -4) \) parabolün tepe noktası ve \( A(1, 0) \) parabolün \( x \) eksenini kestiği noktalardan biri olduğuna göre, \( A_1 + A_2 + A_3 + A_4 \) kaç birimkaredir?
Çözümü GösterTepe noktası \( T(r, k) \) olan parabolün denklemini yazalım.
\( f(x) = a(x - r)^2 + k \)
\( f(x) = a(x + 1)^2 - 4 \)
\( A \) noktası parabol üzerinde olduğu için denklemi sağlar.
\( f(1) = a(1 + 1)^2 - 4 = 0 \)
\( a = 1 \)
\( f(x) = (x + 1)^2 - 4 \)
Fonksiyonun \( x \) eksenini kestiği diğer noktanın apsisini bulmak için \( f(x) = 0 \) denklemini çözelim.
\( f(x) = (x + 1)^2 - 2^2 = 0 \)
\( (x + 1 - 2)(x + 1 + 2) = 0 \)
\( (x - 1)(x + 3) = 0 \)
Parabol \( x \) eksenini \( x = -3 \) ve \( x = 1 \) apsisli noktalarda keser.
\( A_3 + A_4 \) alanını bulmak için parabolün \( [-3, 1] \) aralığında \( x \) ekseniyle arasında kalan alandan \( BAT \) üçgeninin alanını çıkaralım.
Üçgenin alanını bulalım.
\( A(BAT) = \dfrac{4 \cdot 4}{2} = 8 \)
Parabolün \( [-3, 1] \) aralığında \( x \) ekseniyle arasında kalan alanı bulalım.
\( \displaystyle\int_{-3}^1{((x + 1)^2 - 4)\ dx} \)
İfadenin integralini alalım.
\( = (\dfrac{(x + 1)^3}{3} - 4x)|_{-3}^1 \)
\( = (\dfrac{(1 + 1)^3}{3} - 4(1)) - (\dfrac{(-3 + 1)^3}{3} - 4(-3)) \)
\( = (\dfrac{8}{3} - 4) - (\dfrac{-8}{3} + 12) \)
\( = -\dfrac{32}{3} \)
Alan pozitif bir büyüklük olduğu için \( f(x) \) fonksiyonunun \( [-3, 1] \) aralığında \( x \) ekseni ile arasında kalan alan fonksiyonun bu aralıktaki belirli integralinin mutlak değerine eşittir.
\( A_3 + A_4 = \abs{-\dfrac{32}{3}} - A(BAT) \)
\( = \abs{-\dfrac{32}{3}} - 8 = \dfrac{8}{3} \)
\( A_1 + A_2 \) alanını bulmak için parabolün \( y = 5 \) doğrusuyla kesişim noktalarını bulalım.
\( (x + 1)^2 - 4 = 5 \)
\( (x + 1)^2 - 3^2 = 0 \)
\( (x + 1 - 3)(x + 1 + 3) = 0 \)
\( (x - 2)(x + 4) = 0 \)
Parabol \( y = 5 \) doğrusunu \( x = -4 \) ve \( x = 2 \) apsisli noktalarda keser.
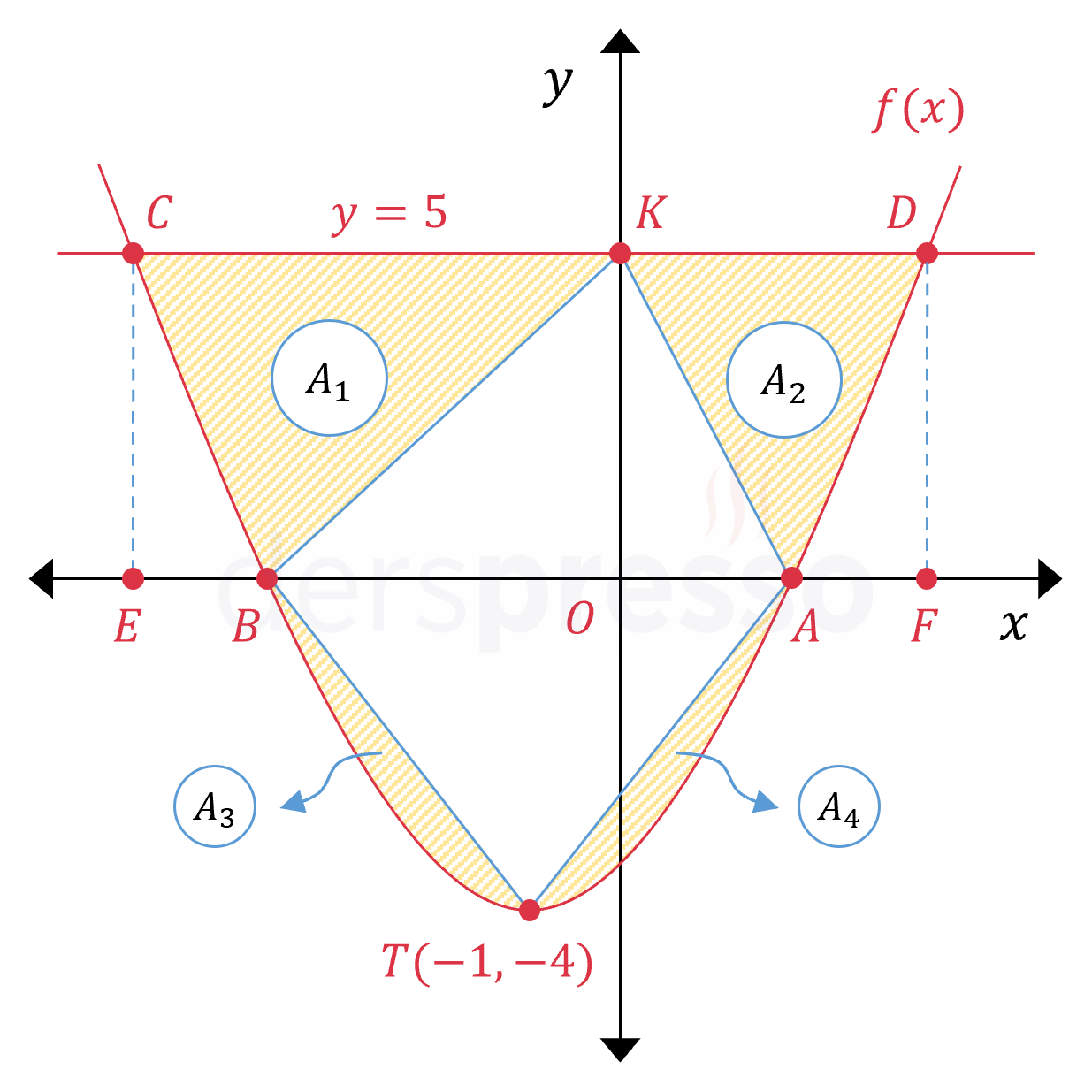
\( A_1 + A_2 \) alanını bulmak için \( CDFE \) dikdörtgeninin alanından parabolün \( [-4, -3] \) ve \( [1, 2] \) aralıklarında \( x \) ekseni ile arasında kalan alanı ve \( BAK \) üçgeninin alanını çıkaralım.
Dikdörtgenin alanını bulalım.
\( A(CDFE) = 5 \cdot 6 = 30 \)
Üçgenin alanını bulalım.
\( A(BAK) = \dfrac{4 \cdot 5}{2} = 10 \)
Parabolün \( [-4, -3] \) ve \( [1, 2] \) aralıklarında \( x \) ekseniyle arasında kalan alanı bulalım.
\( \displaystyle\int_{-4}^{-3}((x + 1)^2 - 4)\ dx + \displaystyle\int_1^2((x + 1)^2 - 4)\ dx \)
İfadenin integralini alalım.
\( = (\dfrac{(x + 1)^3}{3} - 4x)|_{-4}^{-3} + (\dfrac{(x + 1)^3}{3} - 4x)|_1^2 \)
\( = [(\dfrac{(-3 + 1)^3}{3} - 4(-3)) - (\dfrac{(-4 + 1)^3}{3} - 4(-4))] + [(\dfrac{(2 + 1)^3}{3} - 4(2)) - (\dfrac{(1 + 1)^3}{3} - 4(1))] \)
\( = [(\dfrac{-8}{3} + 12) - (-9 + 16)] + [(9 - 8) - (\dfrac{8}{3} - 4)] \)
\( = \dfrac{14}{3} \)
\( A_1 + A_2 = A(CDFE) - \dfrac{14}{3} - A(BAK) \)
\( = 30 - \dfrac{14}{3} - 10 = \dfrac{46}{3} \)
\( A_1 + A_2 + A_3 + A_4 = \dfrac{46}{3} + \dfrac{8}{3} \)
\( = 18 \) birimkare olarak bulunur.
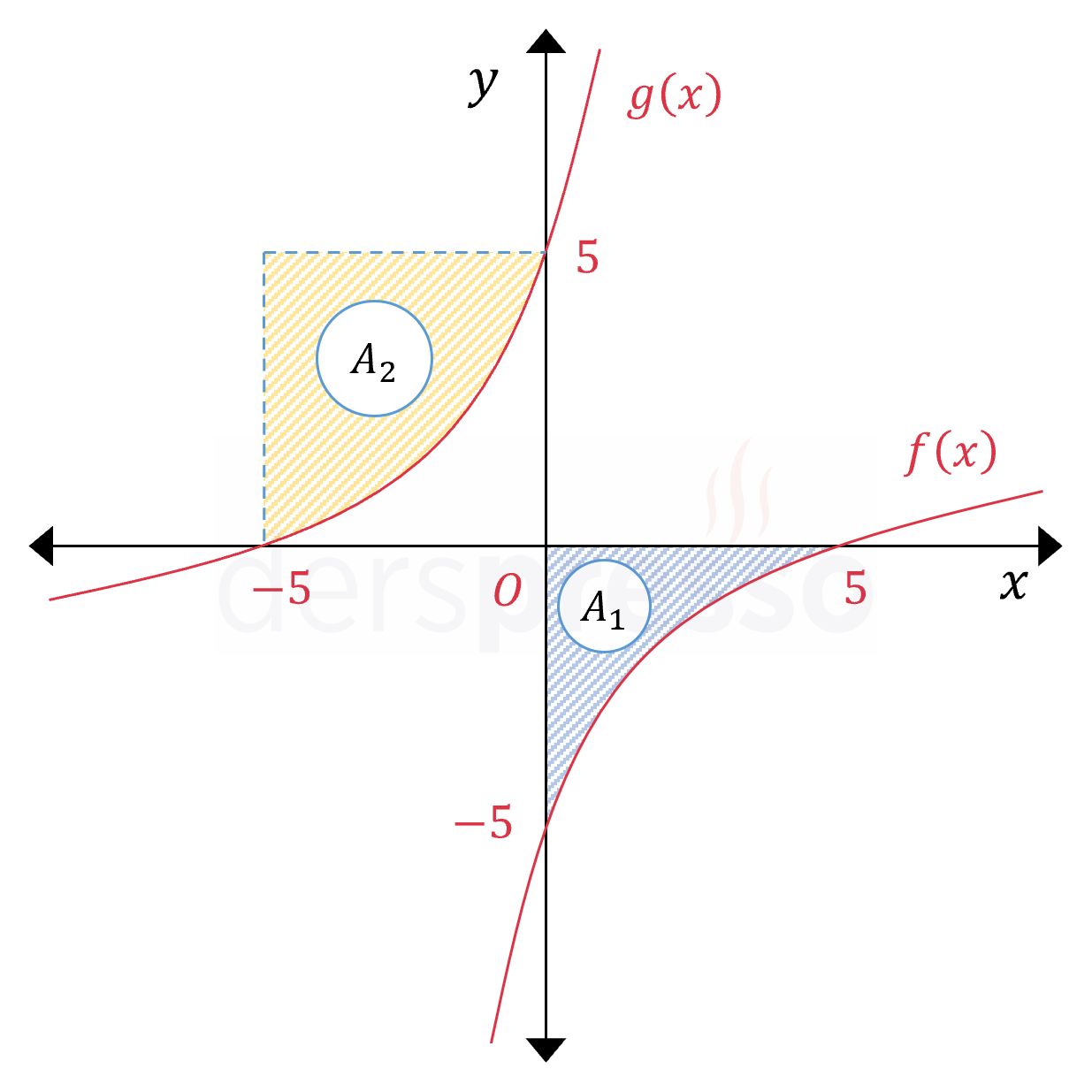
Yukarıda \( f(x) = \dfrac{x - 5}{x + 1} \) ve \( g(x) = \dfrac{-x - 5}{x - 1} \) fonksiyonlarının grafiklerinin bir kısmı verilmiştir.
Buna göre \( A_1 + A_2 \) toplamı kaç birimkaredir?
Çözümü Göster1. yöntem:
\( A_1 \) alanını bulmak için \( f(x) \) fonksiyonunun \( [0, 5] \) aralığındaki belirli integralini bulalım.
\( \displaystyle\int_0^5{\dfrac{x - 5}{x + 1}}\ dx \)
İfadenin integralini almak için basit kesirlere ayırma yöntemini kullanalım.
\( = \displaystyle\int_0^5(1 - \dfrac{6}{x + 1})\ dx \)
İfadenin integralini alalım.
\( = (x - 6\ln{\abs{x + 1}})|_0^5 \)
\( = (5 - 6\ln{\abs{5 + 1}}) - (0 - 6\ln{\abs{0 + 1}}) \)
\( = 5 - 6\ln{6} \)
Alan pozitif bir büyüklük olduğu için \( A_1 \) bu aralıktaki belirli integralin mutlak değerine eşit olur.
\( A_1 = \abs{5 - 6\ln{6}} = 6\ln{6} - 5 \)
\( A_2 \) alanını bulmak için köşeleri orijin, \( (0, 5) \), \( (-5, 5) \) ve \( (-5, 0) \) noktaları olan karenin alanından \( g(x) \) fonksiyonunun \( [-5, 0] \) aralığındaki belirli integralini çıkaralım.
Karenin alanı \( = 5 \cdot 5 = 25 \)
\( g(x) \) fonksiyonunun \( [-5, 0] \) aralığındaki belirli integralini bulalım.
\( \displaystyle\int_{-5}^0{\dfrac{-x - 5}{x - 1}}\ dx \)
İfadenin integralini almak için basit kesirlere ayırma yöntemini kullanalım.
\( = \displaystyle\int_{-5}^0(-1 - \dfrac{6}{x - 1})\ dx \)
İfadenin integralini alalım.
\( = (-x - 6\ln{\abs{x - 1}})|_{-5}^0 \)
\( = (-0 - 6\ln{\abs{0 - 1}}) - (-(-5) - 6\ln{\abs{(-5) - 1}}) \)
\( = 6\ln{6} - 5 \)
\( A_2 = 25 - (6\ln{6} - 5) = 30 - 6\ln{6} \)
\( A_1 + A_2 = (6\ln{6} - 5) + (30 - 6\ln{6}) = 25 \) bulunur.
2. yöntem:
\( \frac{ax + b}{cx + d} \) formundaki bir fonksiyonun tersi \( \frac{-dx + b}{cx - a} \) fonksiyonudur.
\( f \) ve \( g \) fonksiyonlarını incelediğimizde birbirinin tersi fonksiyonlar olduğunu görürüz.
\( f^{-1}(x) = \dfrac{-x - 5}{x - 1} = g(x) \)
Bir fonksiyonun kendisinin ve tersinin grafikleri \( y = x \) doğrusuna göre simetriktir.
Buna göre \( f(x) \) fonksiyonunun tersinin \( [-5, 0] \) aralığında \( x \) ekseni ile arasında kalan alan, \( g(x) \) fonksiyonunun aynı aralıkta \( x \) ekseni ile arasında kalan alanı kareye tamamlayan alandır.
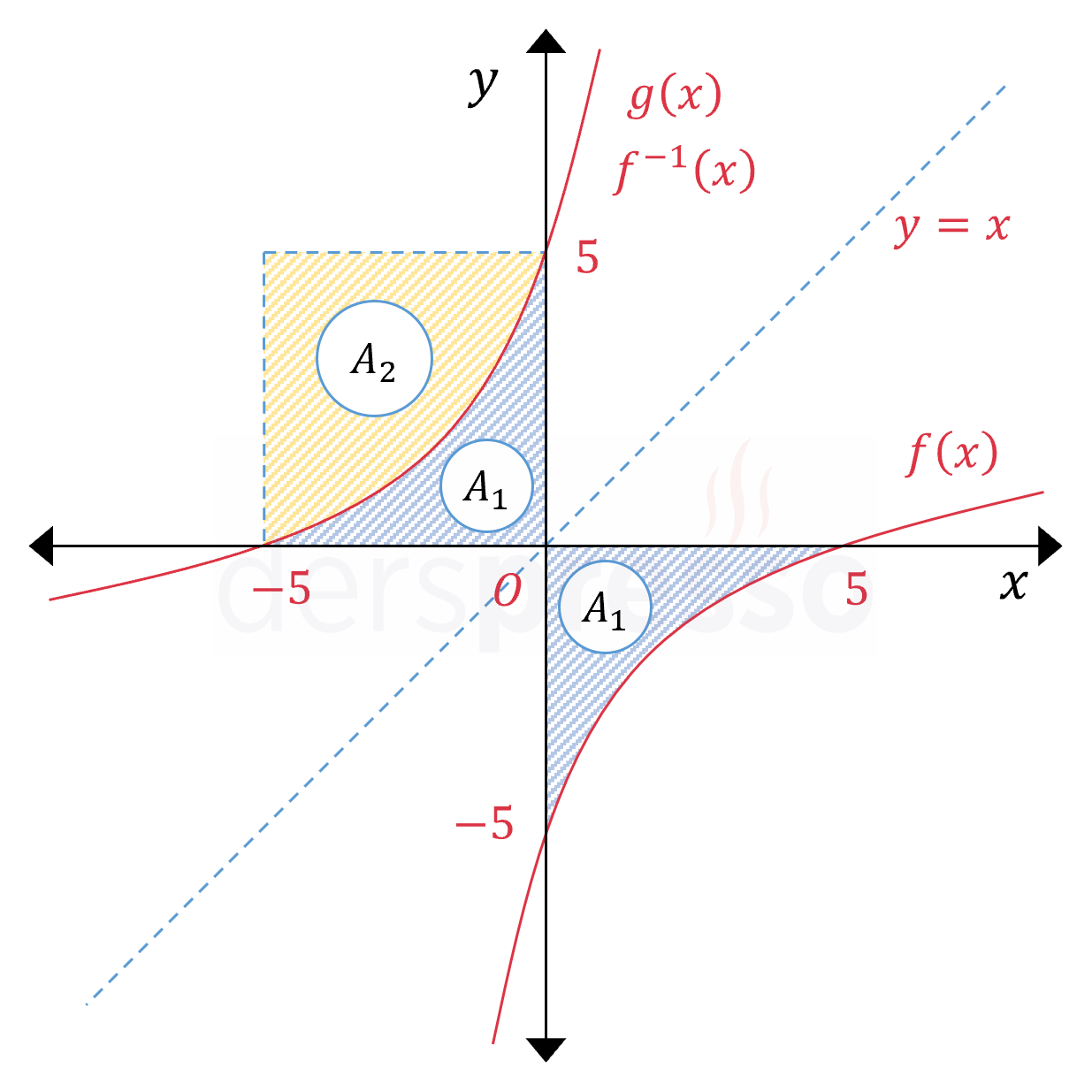
\( A_1 + A_2 = 5 \cdot 5 = 25 \) bulunur.
Analitik düzlemde \( A(0, 0), B(5, 0), C(5, 100), D(0, 100) \) noktalarını köşe kabul eden dikdörtgenin içinden rastgele seçilen bir noktanın koordinatları \( (a, b) \) ise \( b \gt 3a^2 \) olma olasılığı kaçtır?
Çözümü GösterSoruda \( ABCD \) dikdörtgeninin içinden seçilen bir noktanın \( y = 3x^2 \) eğrisinin üzerinde kalan bölgede bulunma olasılığı sorulmaktadır.
Nokta rastgele seçileceği için koordinatlarının verilen koşulu sağlama olasılığı bu bölgenin alanının (\( A_1 \)) dikdörtgenin alanına (\( A_1 + A_2 \)) oranına eşittir.
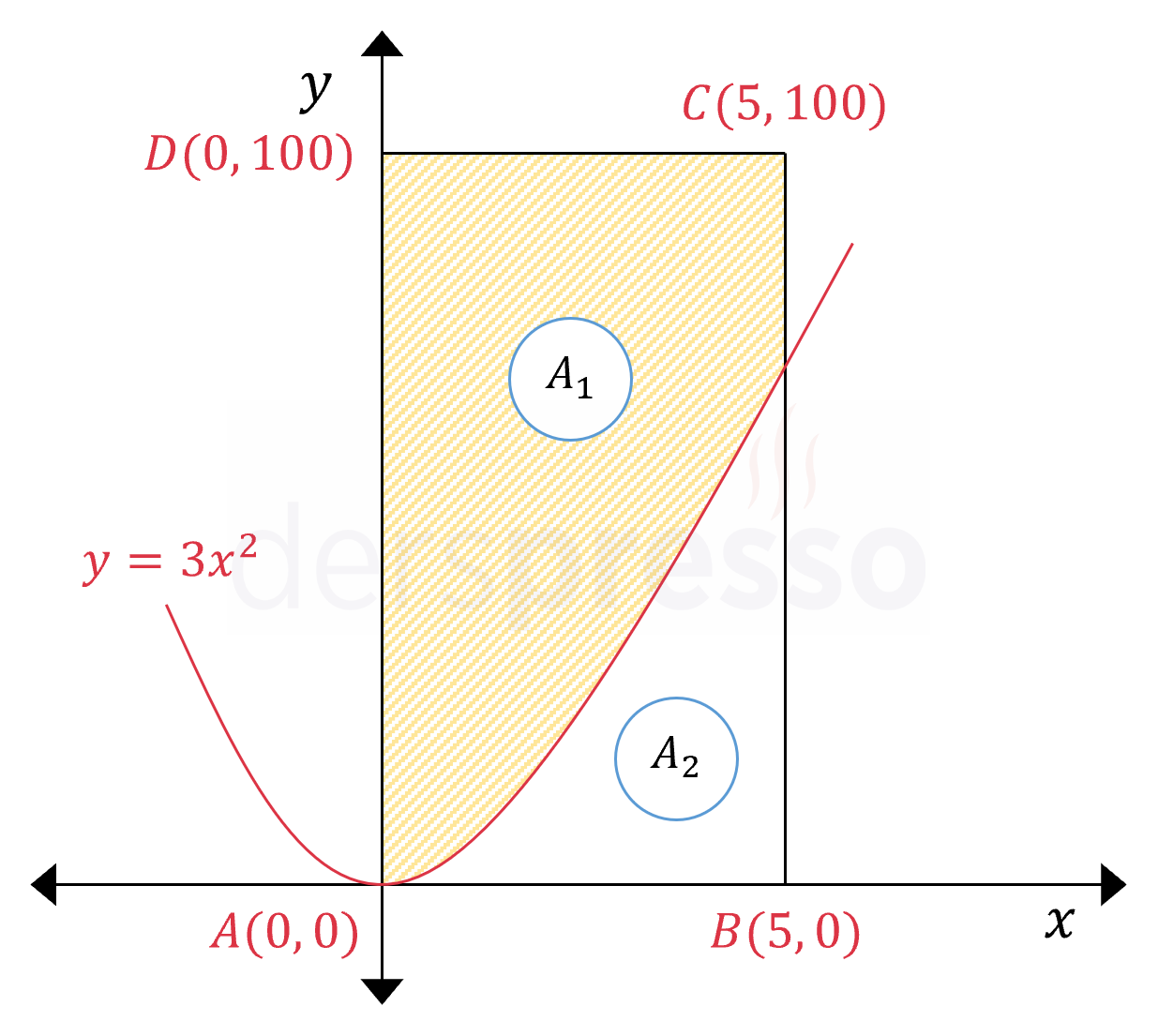
\( [0, 5] \) aralığında \( y = 3x^2 \) eğrisi ile \( x \) ekseni arasında kalan alanı bulalım.
\( A_2 = \displaystyle\int_0^5 3x^2\ dx = x^3|_0^5 \)
\( = 5^3 - 0^3 = 125 \)
Dikdörtgenin alanını bulalım.
\( A_1 + A_2 = 5 \cdot 100 = 500 \)
Eğrinin üstünde kalan alanı bulalım.
\( A_1 = 500 - 125 = 375 \)
Eğrinin üstünde kalan alanın dikdörtgenin alanına oranı:
\( = \dfrac{375}{500} = \dfrac{3}{4} \) bulunur.