Belirli İntegral
Önceki bölümde bir \( [a, b] \) aralığını böldüğümüz alt aralık sayısını (\( n \)) artırarak, yani \( \Delta x_i \) aralıklarını daraltarak hesapladığımız Riemann toplamının (\( S_n \)) eğrinin altında kalan gerçek alan değerine (\( A \)) yaklaşmasını sağlayabileceğimizi gösterdik. Buna göre \( n \) sonsuza yaklaştıkça, yani aralıkların genişliği sıfıra yaklaştıkça hesapladığımız Riemann toplamının gerçek alan değerine eşit olacağını söyleyebiliriz.
Buna göre, Riemann toplamı formülünün \( n \) sonsuza giderkenki limitini aldığımızda elde edeceğimiz değer bize fonksiyonun grafiği ile \( x \) ekseni arasında kalan alanın gerçek değerini verir.
\( f: [a, b] \to \mathbb{R} \)
\( A = \lim_{n \to \infty} \displaystyle\sum_{i = 1}^{n}{f(x_i^*) \cdot \Delta x_i} \)
\( \Delta x_i \): \( i \). aralığın genişliği
\( x_i^* \): \( i \). aralıkta dikdörtgenin yüksekliğini belirlemek için seçilen \( x \) değeri
\( f(x_i^*) \): \( i \). aralıktaki dikdörtgenin yüksekliği
Yukarıda tanımını verdiğimiz limit tanımlı ise bu limit değerine \( f \) fonksiyonunun \( [a, b] \) aralığındaki Riemann integrali ya da belirli integrali denir ve aşağıdaki şekilde gösterilir.
\( \displaystyle\int_a^b {f(x)\ dx} = \lim_{n \to \infty} \displaystyle\sum_{i = 1}^{n}{f(x_i^*) \cdot \Delta x_i} \)
Bu limit tanımlıysa fonksiyon bu aralıkta integrali alınabilir bir fonksiyondur.
Bu gösterimde \( \int \) ile ifade edilen integral işareti, kendisinden sonra gelen ifade ya da fonksiyonun integralinin alınacağını gösterir. Bu sembol integralin dayandığı Riemann toplamında kullandığımız toplama sembolü sebebiyle İngilizce'deki "sum" (toplam) kelimesinin ilk harfinden esinlenmiş bir semboldür.
\( dx \) ifadesi integral alma işleminin \( x \) değişkenine göre yapılacağını gösterir. Yapılan bu işleme de integral alma işlemi denir.
Yukarıdaki integral ifadesindeki \( \int \) sembolünün \( \sum \) sembolü ile ve \( dx \) ifadesinin \( \Delta x \) ifadesi ile benzerliğini dikkate alarak, integral işlemini \( [a, b] \) aralığını sonsuz sayıda aralığa böldüğümüzde oluşan ve her birinin genişliği sonsuz küçüklükte \( dx \) ve yüksekliği \( f(x) \) olan dikdörtgenlerin alanlarını toplama işlemi olarak düşünebiliriz.
İntegral işaretinin altında ve üstündeki \( a \) ve \( b \) sayıları integral işleminin sınırlarını, yani integralin alındığı değişkenin değer aralığını gösterir. İşaretin altındaki sayıya alt sınır, üstündeki sayıya üst sınır denir. Bu değerler aynı zamanda eğrinin altında kalan alanın hesaplanacağı aralığı temsil eder.
Bir integral işleminde fonksiyonun bağlı olduğu ve integralin alındığı değişken için herhangi bir harf seçilebilir. Buna göre aşağıdaki belirli integraller birbirine eşittir.
\( \displaystyle\int_a^b {f(x)\ dx} \) \( = \displaystyle\int_a^b {f(t)\ dt} \) \( = \displaystyle\int_a^b {f(u)\ du} \)
İntegrali hesaplanan fonksiyon \( [a, b] \) aralığında sürekli olduğu sürece, yukarıdaki limit değeri Riemann toplamında seçilen aralık genişlikleri ve \( x^* \) değerini belirlemek için kullanılan yöntemden (sol, sağ, orta nokta, alt ya da üst Riemann toplamı) bağımsız olur.
Önceki bölümde gördüğümüz üzere, belirli integral geometrik olarak integrali alınan fonksiyonun bu aralıkta \( x \) ekseni ile arasında kalan alana karşılık gelir.
Şimdi integralin limit tanımını kullanarak bir örnek yapalım.
\( f(x) = x^2 \) fonksiyonunun \( [0, 2] \) aralığındaki integral değerini, integralin limit tanımını ve sağ Riemann toplamı yöntemini kullanarak hesaplayalım.
Önce Riemann toplam formülünü yazalım.
\( S_n = \sum_{i = 1}^{n}{f(x_i^*) \cdot \Delta x_i} \)
\( [0, 2] \) aralığını \( n \) eşit aralığa bölelim. Aralıklar eşit genişlikte olduğu için \( \Delta x \) değerini sabit olarak alabiliriz.
\( \Delta x = \dfrac{2 - 0}{n} = \dfrac{2}{n} \)
Sağ Riemann toplamı yönteminde \( i \). aralıkta dikdörtgenin yüksekliği için kullanacağımız \( x_i^* \) değeri aralığın üst sınırının apsis değeri olur.
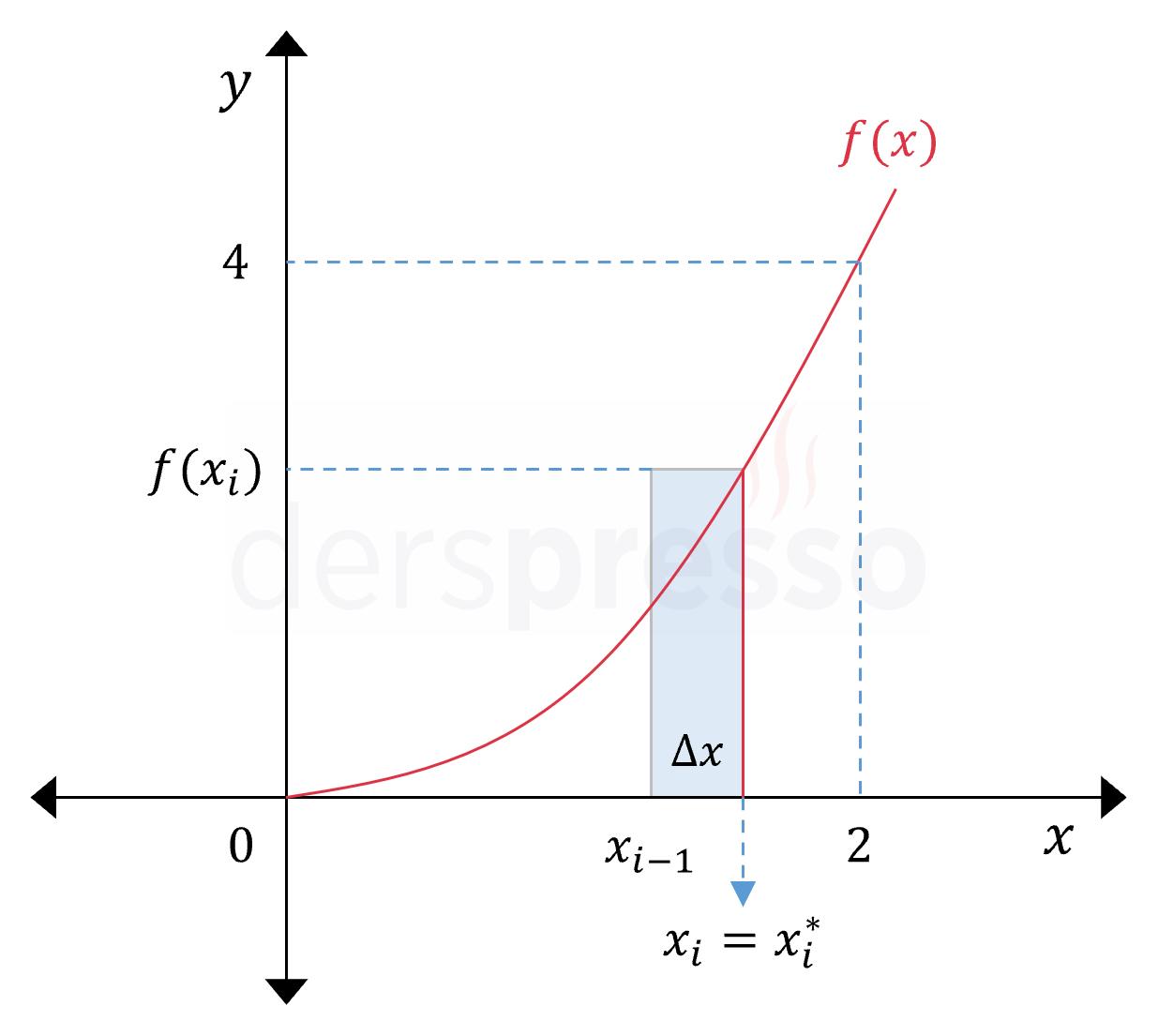
Buna göre \( i. \) aralığın üst sınırı \( x = 0 \) noktasından \( \Delta x \cdot i \) uzaklıkta olur.
\( x_i^* = 0 + \Delta x \cdot i = \dfrac{2i}{n} \)
\( f(x_i^*) = (\dfrac{2i}{n})^2 \)
Bu değerleri Riemann toplam formülünde yerine koyalım.
\( S_n = \displaystyle\sum_{i = 1}^{n}{(\dfrac{2i}{n})^2 \cdot \dfrac{2}{n}} \)
\( = \displaystyle\sum_{i = 1}^{n}{\dfrac{8i^2}{n^3}} \)
\( n \) bu ifadede sabit bir sayı olduğu için toplamın dışına alabiliriz.
\( = \dfrac{8}{n^3} \cdot \displaystyle\sum_{i = 1}^{n}{i^2} \)
Diziler konusunda gördüğümüz toplam formüllerini kullanalım.
\( \displaystyle\sum_{i = 1}^{n}{i^2} = \dfrac{n \cdot (n + 1) \cdot (2n + 1)}{6} \)
\( = \dfrac{8}{n^3} \cdot \dfrac{n \cdot (n + 1) \cdot (2n + 1)}{6} \)
\( = \dfrac{8}{n^3} \cdot \dfrac{2n^3 + 3n^2 + n}{6} \)
\( = \dfrac{8n^3 + 12n^2 + 4n}{3n^3} \)
Hesaplamak istediğimiz belirli integral değeri bu Riemann toplamının \( n \) sonsuza giderkenki limitine eşittir.
\( A = \lim_{n \to \infty} S_n \)
\( = \lim_{n \to \infty} \dfrac{8n^3 + 12n^2 + 4n}{3n^3} \)
Her bir terimin limiti tanımlı olduğu için, limit toplam kuralı ile ifadeyi limitlerin toplamı şeklinde yazabiliriz.
\( = \lim_{n \to \infty} \dfrac{8n^3}{3n^3} + \lim_{n \to \infty} \dfrac{12n^2}{3n^3} \) \( + \lim_{n \to \infty} \dfrac{4n}{3n^3} \)
\( = \lim_{n \to \infty} \dfrac{8}{3} + \lim_{n \to \infty} \dfrac{4}{n} \) \( + \lim_{n \to \infty} \dfrac{4}{3n^2} \)
\( n \) sonsuza giderken 2. ve 3. terimlerin limiti sıfırdır.
\( = \dfrac{8}{3} + 0 + 0 = \dfrac{8}{3} \)
Buna göre \( f(x) = x^2 \) fonksiyonunun \( [0, 2] \) aralığındaki belirli integral değerini, yani fonksiyonun bu aralıkta \( x \) ekseni ile arasında kalan alanı \( \frac{8}{3} \) olarak buluruz.
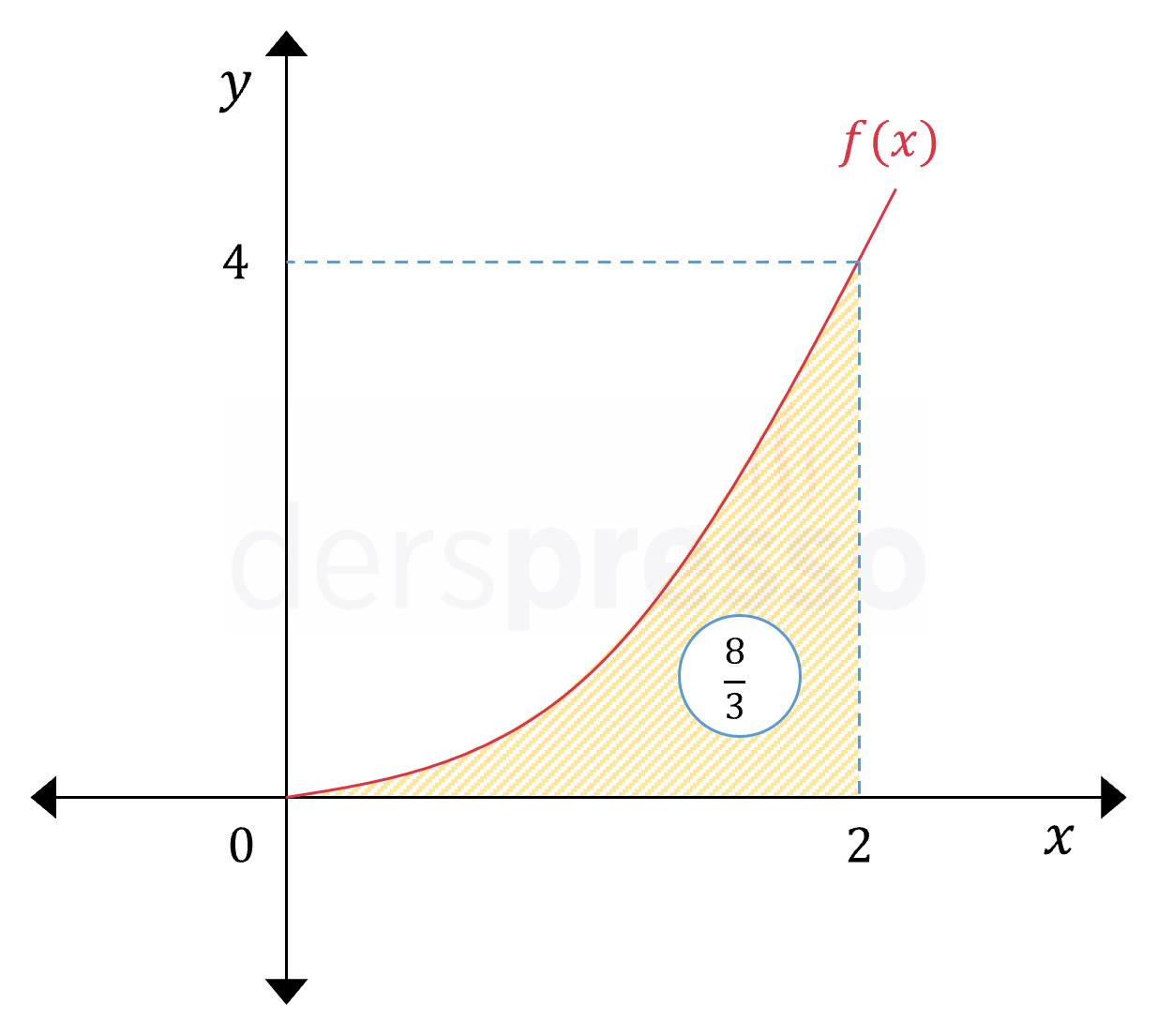
Aynı örneği sol Riemann toplamı yöntemi ile hesaplayarak aynı sonucu bulup bulmayacağımızı kontrol edelim.
\( f(x) = x^2 \) fonksiyonunun \( [0, 2] \) aralığındaki integral değerini, integralin limit tanımını ve sol Riemann toplamı yöntemini kullanarak hesaplayalım.
Sol Riemann toplamı yönteminde \( i. \) aralıkta dikdörtgenin yüksekliği için kullanacağımız \( x_i^* \) değeri aralığın alt sınırının apsis değeri olur.
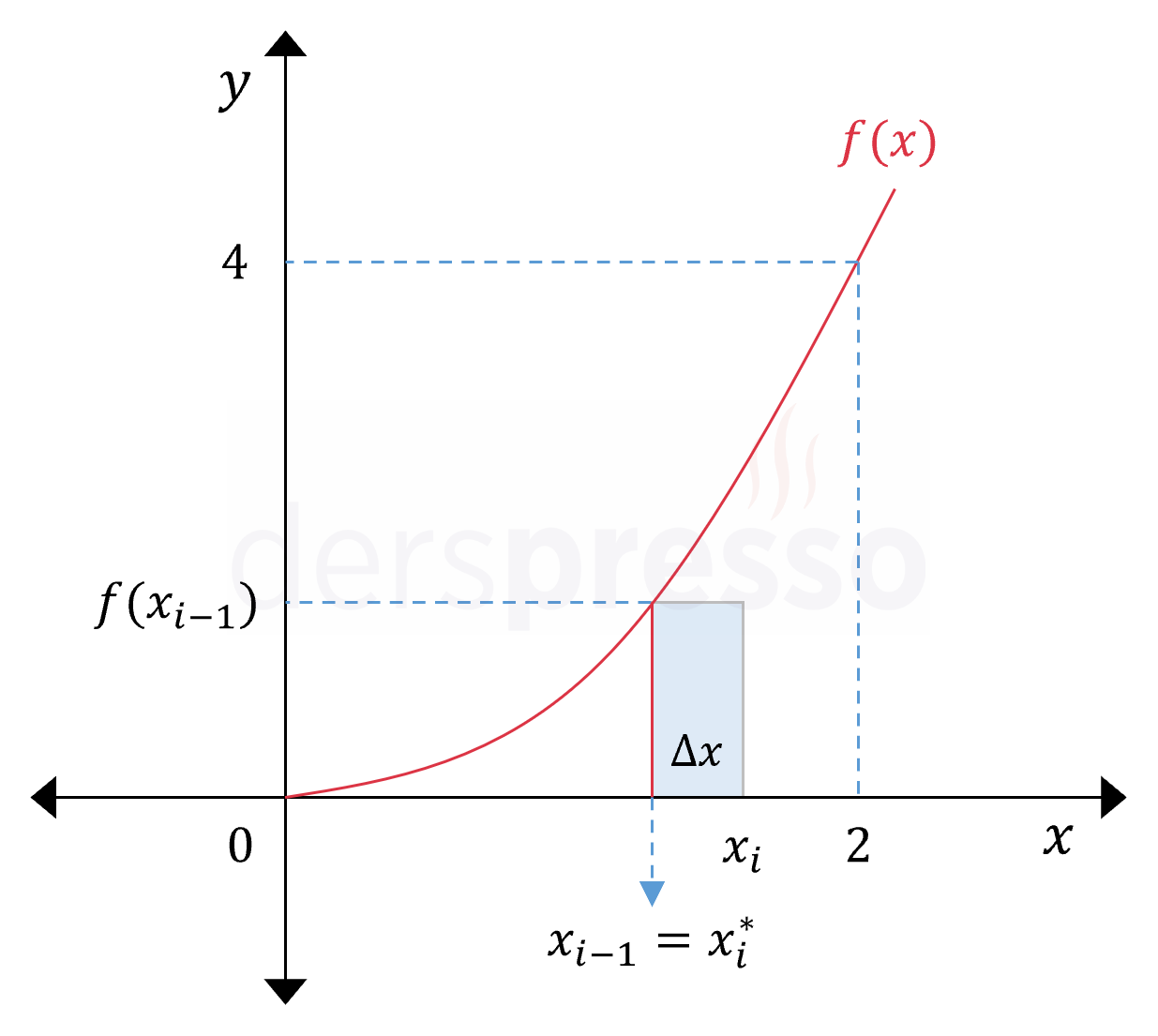
Buna göre \( i. \) aralığın üst sınırı \( x = 0 \) noktasından \( \Delta x \cdot (i - 1) \) uzaklıkta olur.
\( x_i^* = 0 + \Delta x \cdot (i - 1) = \dfrac{2(i - 1)}{n} \)
\( f(x_i^*) = (\dfrac{2(i - 1)}{n})^2 \)
Bu değerleri Riemann toplam formülünde yerine koyalım.
\( S_n = \displaystyle\sum_{i = 1}^{n}{(\dfrac{2(i - 1)}{n})^2 \cdot \dfrac{2}{n}} \)
\( = \displaystyle\sum_{i = 1}^{n}{\dfrac{8(i - 1)^2}{n^3}} \)
\( n \) bu ifadede sabit bir sayı olduğu için toplamın dışına alabiliriz.
\( = \dfrac{8}{n^3} \cdot \displaystyle\sum_{i = 1}^{n}{(i - 1)^2} \)
Diziler konusunda gördüğümüz toplam formüllerini kullanalım.
\( = \dfrac{8}{n^3} \cdot \dfrac{(n - 1) \cdot n \cdot (2(n - 1) + 1)}{6} \)
\( = \dfrac{8}{n^3} \cdot \dfrac{2n^3 - 3n^2 + n}{6} \)
\( = \dfrac{8n^3 - 12n^2 + 4n}{3n^3} \)
Hesaplamak istediğimiz belirli integral değeri bu Riemann toplamının \( n \) sonsuza giderkenki limitine eşittir.
\( A = \lim_{n \to \infty} S_n \)
\( = \lim_{n \to \infty} \dfrac{8n^3 - 12n^2 + 4n}{3n^3} \)
Her bir terimin limiti tanımlı olduğu için, limit toplam kuralı ile ifadeyi limitlerin toplamı şeklinde yazabiliriz.
\( = \lim_{n \to \infty} \dfrac{8n^3}{3n^3} - \lim_{n \to \infty} \dfrac{12n^2}{3n^3} \) \( + \lim_{n \to \infty} \dfrac{4n}{3n^3} \)
\( = \lim_{n \to \infty} \dfrac{8}{3} - \lim_{n \to \infty} \dfrac{4}{n} \) \( + \lim_{n \to \infty} \dfrac{4}{3n^2} \)
\( n \) sonsuza giderken 2. ve 3. terimlerin limiti sıfırdır.
\( = \dfrac{8}{3} - 0 + 0 = \dfrac{8}{3} \)
Sol Riemann toplamı yöntemi ile de aynı sonucu elde etmiş olduk.
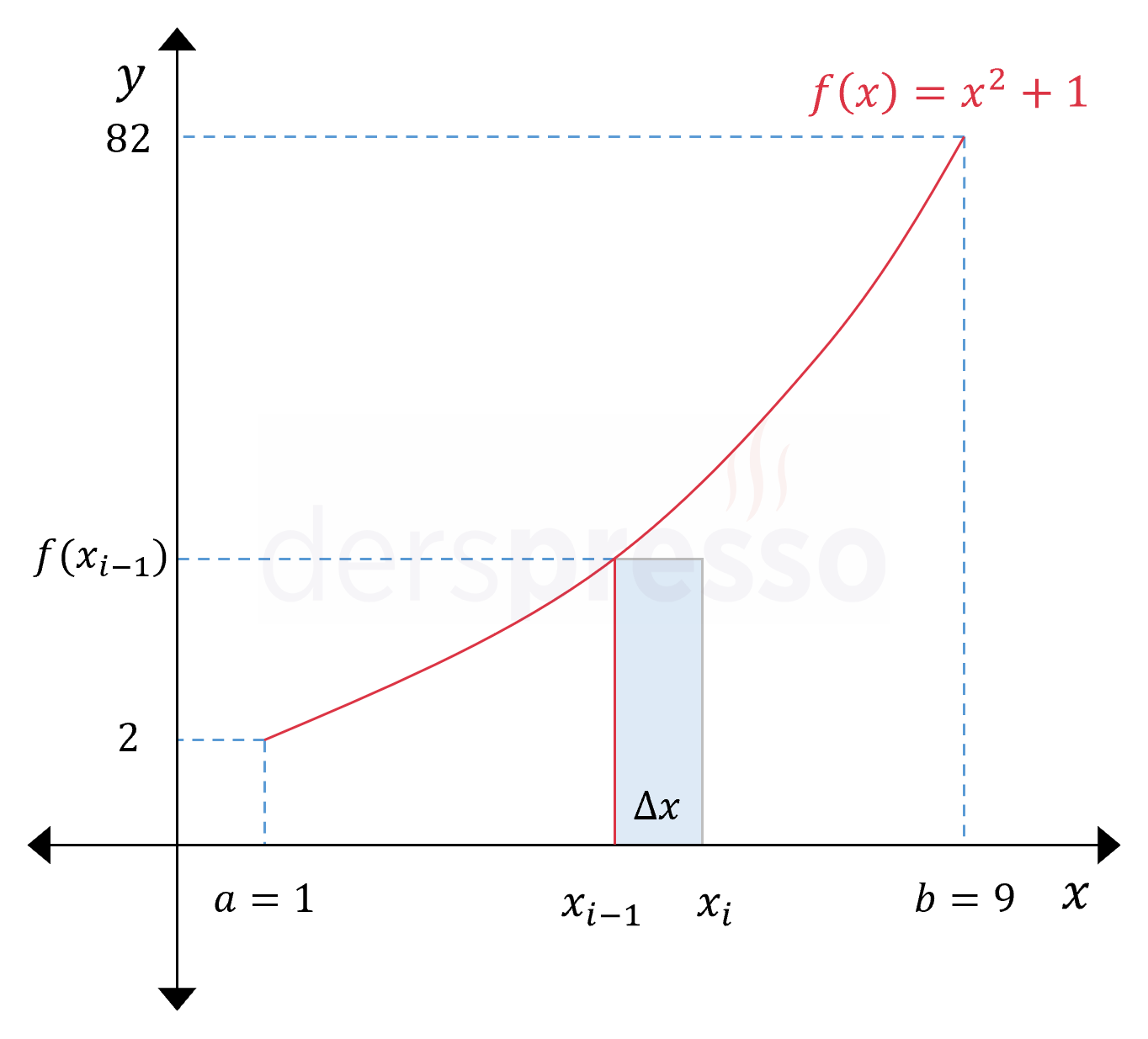
\( f(x) = x^2 + 1 \) fonksiyonunun \( [1, 9] \) aralığındaki integral değerini, integralin limit tanımını ve sağ Riemann toplamı yöntemini kullanarak hesaplayın.
Çözümü GösterÖnce Riemann toplam formülünü yazalım.
\( S_n = \displaystyle\sum_{i = 1}^{n}{f(x_i^*) \cdot \Delta x_i} \)
\( [1, 9] \) aralığını \( n \) eşit aralığa bölelim. Aralıklar eşit genişlikte olduğu için \( \Delta x \) değerini sabit olarak alabiliriz.
\( \Delta x = \dfrac{9 - 1}{n} = \dfrac{8}{n} \)
Sağ Riemann toplamı yönteminde \( i \). aralıkta dikdörtgenin yüksekliği için kullanacağımız \( x_i^* \) değeri aralığın üst sınırının apsis değeri olur.
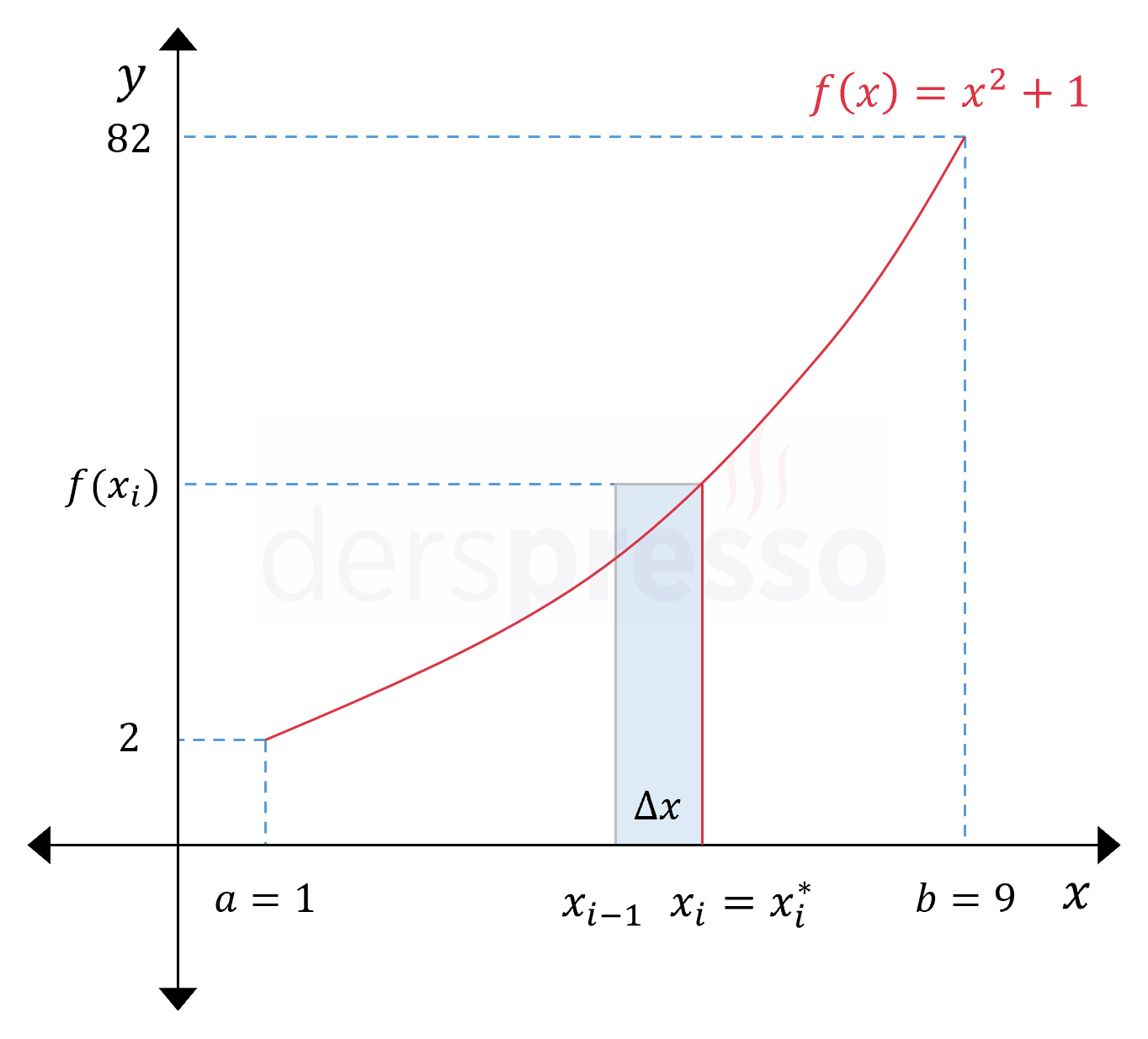
Buna göre \( i. \) aralığın üst sınırı \( x = 1 \) noktasından \( \Delta x \cdot i \) uzaklıkta olur.
\( x_i^* = 1 + \Delta x \cdot i = 1 + \dfrac{8i}{n} \)
\( f(x_i^*) = (1 + \dfrac{8i}{n})^2 + 1 \)
\( = 1^2 + 2\dfrac{8i}{n} + (\dfrac{8i}{n})^2 + 1 \)
\( = \dfrac{64i^2}{n^2} + \dfrac{16i}{n} + 2 \)
Bu değerleri Riemann toplam formülünde yerine koyalım.
\( S_n = \displaystyle\sum_{i = 1}^{n}{(\dfrac{64i^2}{n^2} + \dfrac{16i}{n} + 2) \cdot \dfrac{8}{n}} \)
\( = \displaystyle\sum_{i = 1}^{n}(\dfrac{512i^2}{n^3} + \dfrac{128i}{n^2} + \dfrac{16}{n}) \)
Toplam işlemini terimlere dağıtabiliriz. Ayrıca \( n \) bu ifadede sabit bir sayı olduğu için toplamın dışına alabiliriz.
\( = \dfrac{512}{n^3}\displaystyle\sum_{i = 1}^{n}{i^2} + \dfrac{128}{n^2}\displaystyle\sum_{i = 1}^{n}{i} + \dfrac{16}{n}\displaystyle\sum_{i = 1}^{n}{1} \)
Diziler konusunda gördüğümüz toplam formüllerini kullanalım.
\( \displaystyle\sum_{i = 1}^{n}{i} = \dfrac{n(n + 1)}{2} \)
\( \displaystyle\sum_{i = 1}^{n}{i^2} = \dfrac{n(n + 1)(2n + 1)}{6} \)
\( = \dfrac{512}{n^3} \cdot \dfrac{n(n + 1)(2n + 1)}{6} \) \( + \dfrac{128}{n^2} \cdot \dfrac{n(n + 1)}{2} \) \( + \dfrac{16}{n} \cdot n \)
İfadeyi tek bir paydada birleştirelim.
\( = \dfrac{1024n^3 + 1536n^2 + 512n}{6n^3} \) \( + \dfrac{384n^3 + 384n^2}{6n^3} \) \( + \dfrac{96n^3}{6n^3} \)
\( = \dfrac{1504n^3 + 1920n^2 + 512n}{6n^3} \)
Hesaplamak istediğimiz belirli integral değeri bu Riemann toplamının \( n \) sonsuza giderkenki limitine eşittir.
\( A = \lim_{n \to \infty} {S_n} \)
\( = \lim_{n \to \infty} \dfrac{1504n^3 + 1920n^2 + 512n}{6n^3} \)
Her bir terimin limiti tanımlı olduğu için, limit toplam kuralı ile ifadeyi limitlerin toplamı şeklinde yazabiliriz.
\( = \lim_{n \to \infty} \dfrac{1504n^3}{6n^3} \) \( + \lim_{n \to \infty} \dfrac{1920n^2}{6n^3} \) \( + \lim_{n \to \infty} \dfrac{512n}{6n^3} \)
\( = \lim_{n \to \infty} \dfrac{752}{3} \) \( + \lim_{n \to \infty} \dfrac{320}{n} \) \( + \lim_{n \to \infty} \dfrac{256}{3n^2} \)
\( n \) sonsuza giderken 2. ve 3. terimlerin limiti sıfırdır.
\( = \dfrac{752}{3} + 0 + 0 = \dfrac{752}{3} \)
Buna göre \( f(x) = x^2 + 1 \) fonksiyonunun \( [1, 9] \) aralığındaki belirli integral değerini, yani fonksiyonun bu aralıkta \( x \) ekseni ile arasında kalan alanı \( \dfrac{752}{3} = 250,666... \) olarak buluruz.
Bu değerin aynı zamanda önceki bölümde Riemann toplamı yöntemiyle bulduğumuz tahmini alan değerlerinin yaklaştığı değer olduğunu hatırlatalım.
\( f(x) = x^2 + 1 \) fonksiyonunun \( [1, 9] \) aralığındaki integral değerini, integralin limit tanımını ve sol Riemann toplamı yöntemini kullanarak hesaplayın.
Çözümü GösterÖnce Riemann toplam formülünü yazalım.
\( S_n = \displaystyle\sum_{i = 1}^{n}{f(x_i^*) \cdot \Delta x_i} \)
\( [1, 9] \) aralığını \( n \) eşit aralığa bölelim. Aralıklar eşit genişlikte olduğu için \( \Delta x \) değerini sabit olarak alabiliriz.
\( \Delta x = \dfrac{9 - 1}{n} = \dfrac{8}{n} \)
Sol Riemann toplamı yönteminde \( i \). aralıkta dikdörtgenin yüksekliği için kullanacağımız \( x_i^* \) değeri aralığın alt sınırının apsis değeri olur.
Buna göre \( i. \) aralığın üst sınırı \( x = 1 \) noktasından \( \Delta x \cdot (i - 1) \) uzaklıkta olur.
\( x_i^* = 1 + \Delta x \cdot i = 1 + \dfrac{8(i - 1)}{n} \)
\( f(x_i^*) = (1 + \dfrac{8(i - 1)}{n})^2 + 1 \)
\( = 1^2 + 2\dfrac{8(i - 1)}{n} + (\dfrac{8(i - 1)}{n})^2 + 1 \)
\( = \dfrac{64(i - 1)^2}{n^2} + \dfrac{16(i - 1)}{n} + 2 \)
Bu değerleri Riemann toplam formülünde yerine koyalım.
\( S_n = \displaystyle\sum_{i = 1}^{n}{(\dfrac{64(i - 1)^2}{n^2} + \dfrac{16(i - 1)}{n} + 2) \cdot \dfrac{8}{n}} \)
\( = \displaystyle\sum_{i = 1}^{n}(\dfrac{512(i - 1)^2}{n^3} + \dfrac{128(i - 1)}{n^2} + \dfrac{16}{n}) \)
Toplam işlemini terimlere dağıtabiliriz. Ayrıca \( n \) bu ifadede sabit bir sayı olduğu için toplamın dışına alabiliriz.
\( = \dfrac{512}{n^3}\displaystyle\sum_{i = 1}^{n}{(i - 1)^2} + \dfrac{128}{n^2}\displaystyle\sum_{i = 1}^{n}{(i - 1)} \) \( + \dfrac{16}{n}\displaystyle\sum_{i = 1}^{n}{1} \)
Diziler konusunda gördüğümüz toplam formüllerini kullanalım.
\( \displaystyle\sum_{i = 1}^{n}{i} = \dfrac{n(n + 1)}{2} \)
\( \displaystyle\sum_{i = 1}^{n}{i^2} = \dfrac{n(n + 1)(2n + 1)}{6} \)
\( = \dfrac{512}{n^3} \cdot \dfrac{(n - 1)((n - 1) + 1)(2(n - 1) + 1)}{6} \) \( + \dfrac{128}{n^2} \cdot \dfrac{(n - 1)((n - 1) + 1)}{2} \) \( + \dfrac{16}{n} \cdot n \)
İfadeyi tek bir paydada birleştirelim.
\( = \dfrac{1024n^3 - 1536n^2 + 512n}{6n^3} \) \( + \dfrac{384n^3 - 384n^2}{6n^3} \) \( + \dfrac{96n^3}{6n^3} \)
\( = \dfrac{1504n^3 - 1920n^2 + 512n}{6n^3} \)
Hesaplamak istediğimiz belirli integral değeri bu Riemann toplamının \( n \) sonsuza giderkenki limitine eşittir.
\( A = \lim_{n \to \infty} {S_n} \)
\( = \lim_{n \to \infty} \dfrac{1504n^3 - 1920n^2 + 512n}{6n^3} \)
Her bir terimin limiti tanımlı olduğu için, limit toplam kuralı ile ifadeyi limitlerin toplamı şeklinde yazabiliriz.
\( = \lim_{n \to \infty} \dfrac{1504n^3}{6n^3} \) \( - \lim_{n \to \infty} \dfrac{1920n^2}{6n^3} \) \( + \lim_{n \to \infty} \dfrac{512n}{6n^3} \)
\( = \lim_{n \to \infty} \dfrac{752}{3} \) \( - \lim_{n \to \infty} \dfrac{320}{n} \) \( + \lim_{n \to \infty} \dfrac{256}{3n^2} \)
\( n \) sonsuza giderken 2. ve 3. terimlerin limiti sıfırdır.
\( = \dfrac{752}{3} - 0 + 0 = \dfrac{752}{3} \)
Buna göre \( f(x) = x^2 + 1 \) fonksiyonunun \( [1, 9] \) aralığındaki belirli integral değerini, yani fonksiyonun bu aralıkta \( x \) ekseni ile arasında kalan alanı \( \dfrac{752}{3} = 250,666... \) olarak buluruz.
Bu değerin aynı zamanda önceki bölümde Riemann toplamı yöntemiyle bulduğumuz tahmini alan değerlerinin yaklaştığı değer olduğunu hatırlatalım.
Fonksiyonların İntegralinin Alınabilirliği
Bir fonksiyonun integralinin alınabilirliği genellikle türevlenebilirliğinden daha esnek bir koşuldur. Örneğin sürekli bir fonksiyon tüm tanım aralığında türevlenebilir olmak zorunda değildir (örnek: mutlak değer fonksiyonu), ama tüm sürekli fonksiyonların integrali tanımlıdır.
Aşağıdaki iki tip fonksiyonun \( [a, b] \) aralığında integrali alınabilirdir, bir diğer ifadeyle yukarıda tanımladığımız limit değeri seçilen aralık genişliğinden ve \( x^* \) değerini belirlemek için kullanılan yöntemden bağımsız olarak aynı sonucu verir.
- Bu aralıkta sürekli olan fonksiyonlar
- Bu aralıkta sonlu sayıda sıçrama süreksizliği olan parçalı fonksiyonlar