Alan Problemi
Türevi bir fonksiyonun belirli bir noktasındaki anlık değişim oranını (eğimini) hesaplama problemi olarak tanımlamıştık. İntegrali de kısaca sonsuz sayıda sonsuz küçüklükteki "parçayı" toplama problemi olarak tanımlayabiliriz. Bu bölümde integrale, önemli uygulamalarından biri olan fonksiyon grafiği ile \( x \) ekseni arasında kalan bölgenin alanını hesaplama problemi üzerinden giriş yapacağız.
Aşağıdaki gibi bir \( f(x) \) doğrusu ile \( x \) ekseni arasında kalan mavi alanı (\( A \)), bu alanı oluşturan dikdörtgen ve üçgenin alan formüllerini kullanarak hesaplayabiliriz.
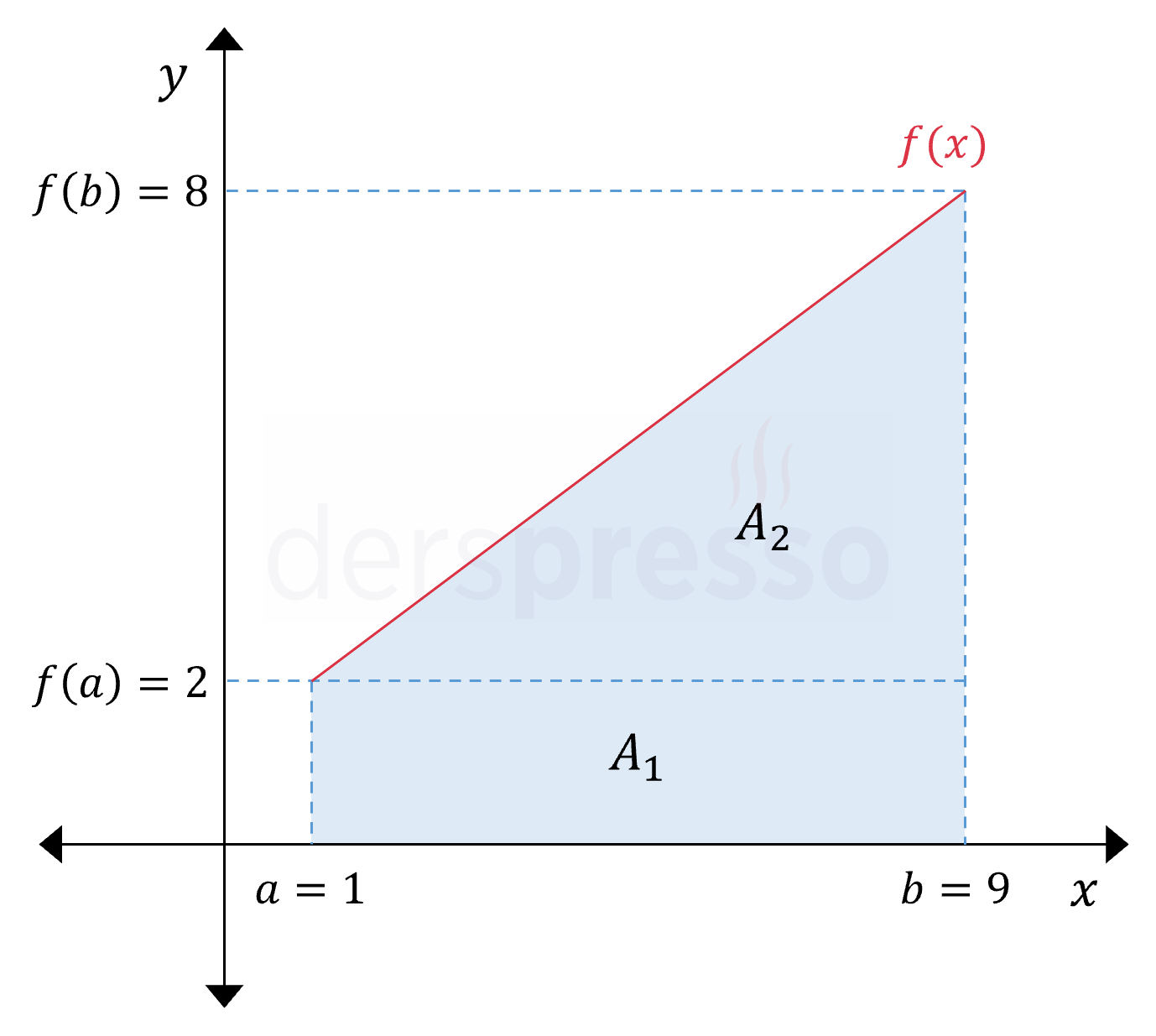
\( A_1 = (9 - 1) \cdot 2 = 16 \)
\( A_2 = \dfrac{(9 - 1) \cdot (8 - 2)}{2} = 24 \)
\( A = A_1 + A_2 = 40 \)
Tüm aralıklarda doğrusal olan aşağıdaki gibi bir parçalı fonksiyon için de bu \( A \) alanını yine geometrik alan formüllerini kullanarak hesaplayabiliriz.
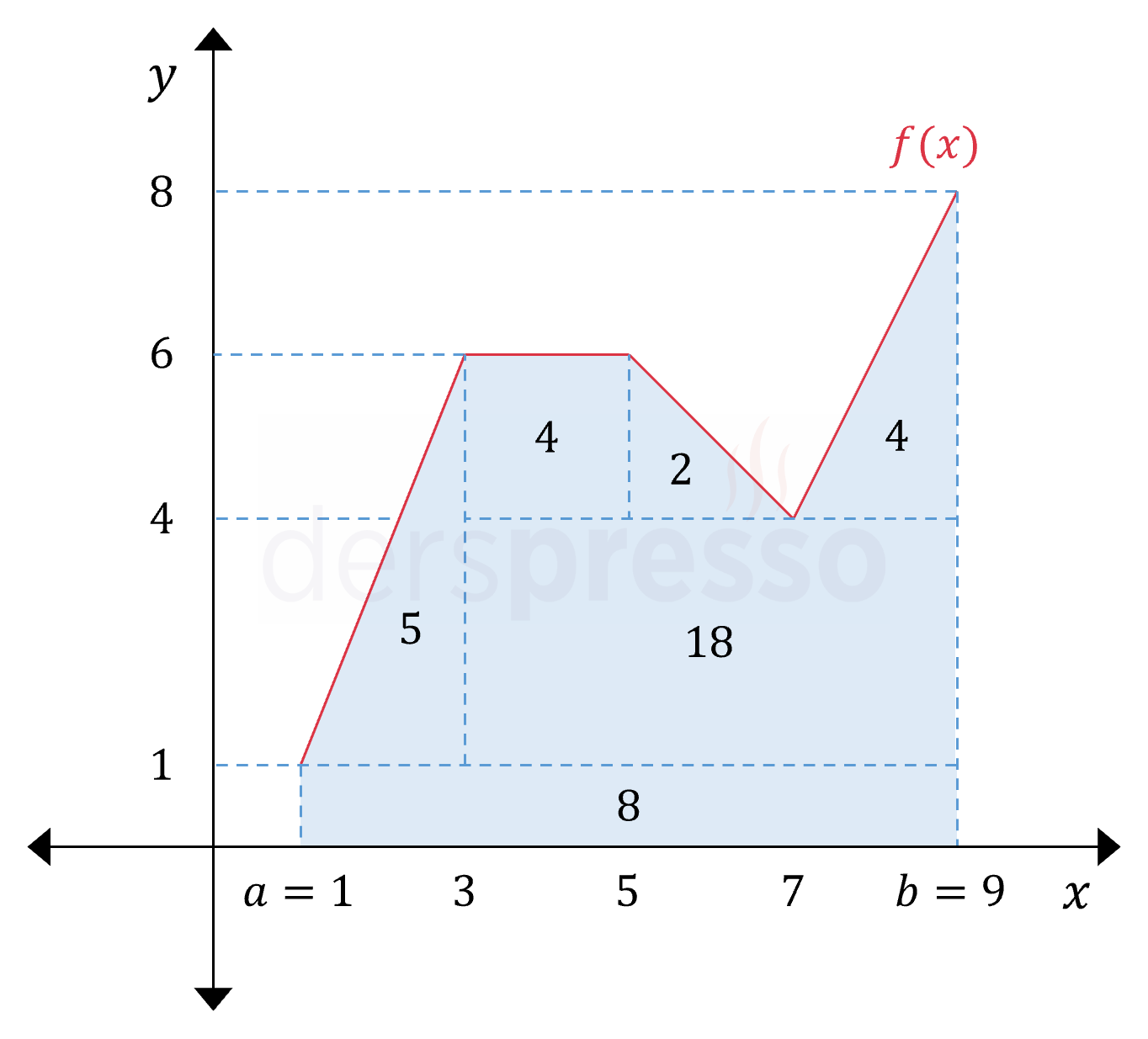
\( A = 8 + 5 + 18 + 4 + 2 + 4 = 41 \)
Elimizdeki grafik aşağıdaki \( f(x) = x^2 + 1 \) fonksiyonu gibi bir eğri ise bu \( A \) alanının tam değerini benzer bir yaklaşımla, yani geometrik alan formüllerini kullanarak hesaplayamayacağımızı görebiliriz.
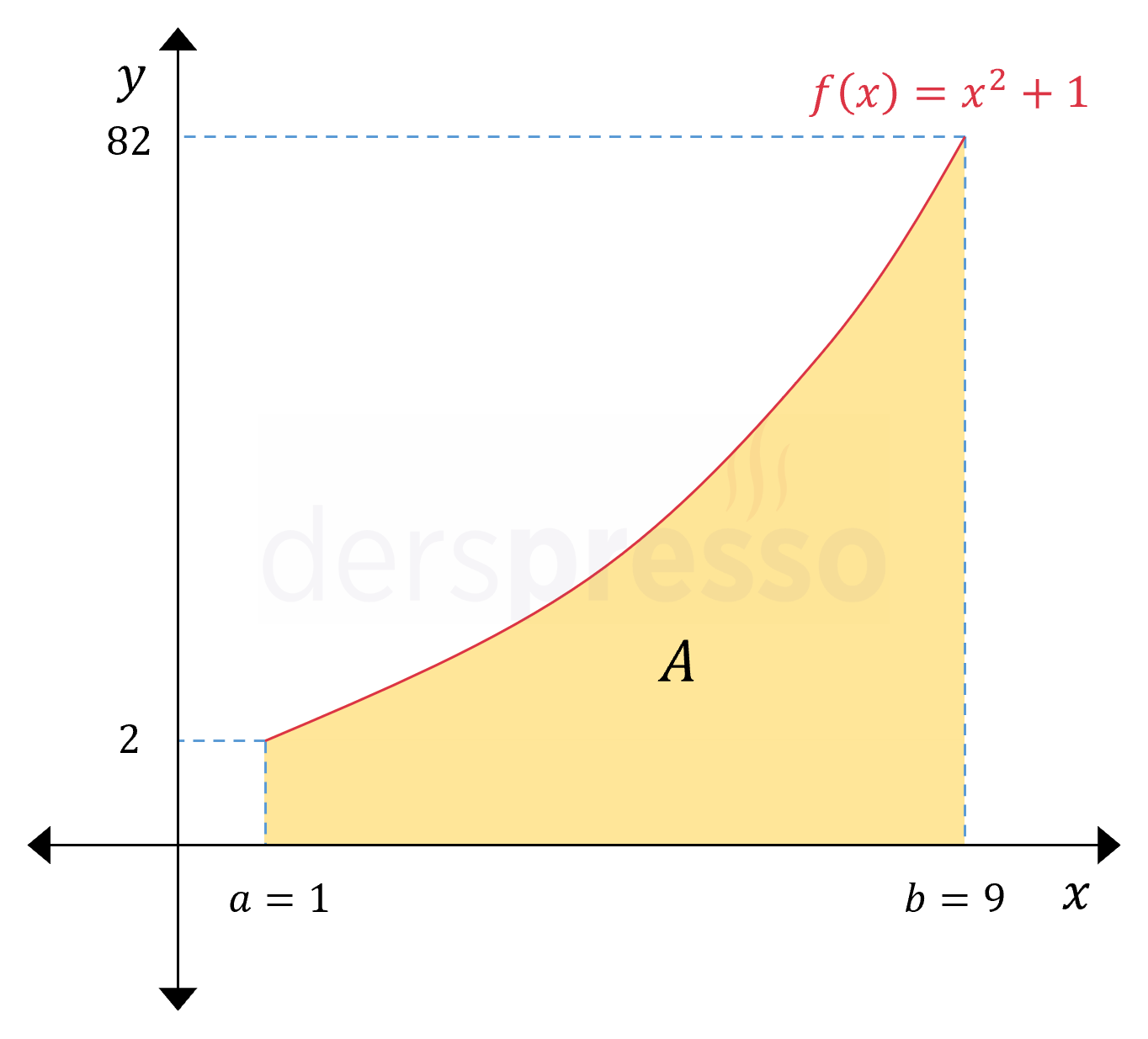
Bu alanın gerçek değerini vermeyecek olsa da yaklaşık değerini hesaplamak için izleyebileceğimiz bir yöntem, verilen aralığı alt aralıklara bölmek, her aralık için \( x \) ekseninden fonksiyon grafiğine dikdörtgenler çizmek ve bu dikdörtgenlerin alanlarının toplamını almak olabilir.
Bunun için \( f \) fonksiyonunun \( [1, 9] \) aralığını 4 eşit aralığa bölelim, her aralık için \( x \) ekseninden o aralıktaki en küçük fonksiyon değerine dikdörtgenler çizelim ve bu dikdörtgenlerin alanlarını bulalım. Her aralıktaki en küçük fonksiyon değerini kullanarak hesaplayacağımız bu alan değerine kısaca alt toplam diyeceğiz.
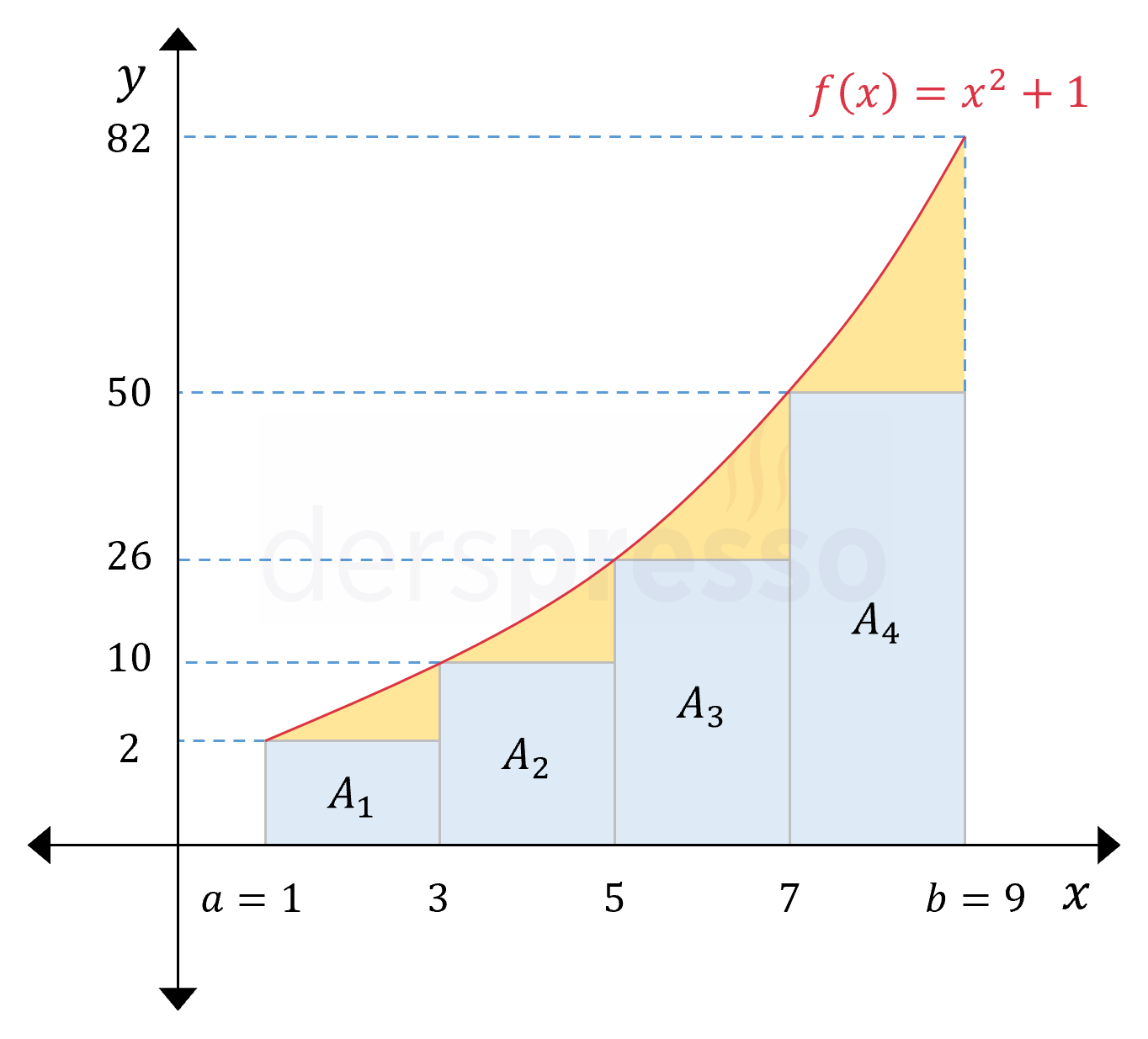
\( \Delta x \) her bir aralığın genişliği olmak üzere,
\( \Delta x = \dfrac{9 - 1}{4} = 2 \)
\( A_1 = f(1) \cdot \Delta x = 2 \cdot 2 = 4 \)
\( A_2 = f(3) \cdot \Delta x = 10 \cdot 2 = 20 \)
\( A_3 = f(5) \cdot \Delta x = 26 \cdot 2 = 52 \)
\( A_4 = f(7) \cdot \Delta x = 50 \cdot 2 = 100 \)
\( S_{4k} \) aralığı 4 alt aralığa bölerek ve her aralıktaki en küçük fonksiyon değerini kullanarak hesapladığımız yaklaşık alan değeri olmak üzere,
\( S_{4k} \approx A \)
\( S_{4k} = A_1 + A_2 + A_3 + A_4 \)
\( = 4 + 20 + 52 + 100 = 176 \)
Bu grafikte mavi bölgeler doğru hesapladığımız, turuncu bölgeler ise kullandığımız yöntem gereği eksik hesapladığımız alanlara karşılık gelmektedir. Çizdiğimiz dikdörtgenlerin yüksekliği olarak her aralıktaki en küçük fonksiyon değerini aldığımız için, gerçek alan değerinin hesapladığımız yaklaşık alan değerinden büyük (ya da ona eşit) olduğundan emin olabiliriz.
\( A \ge 176 \)
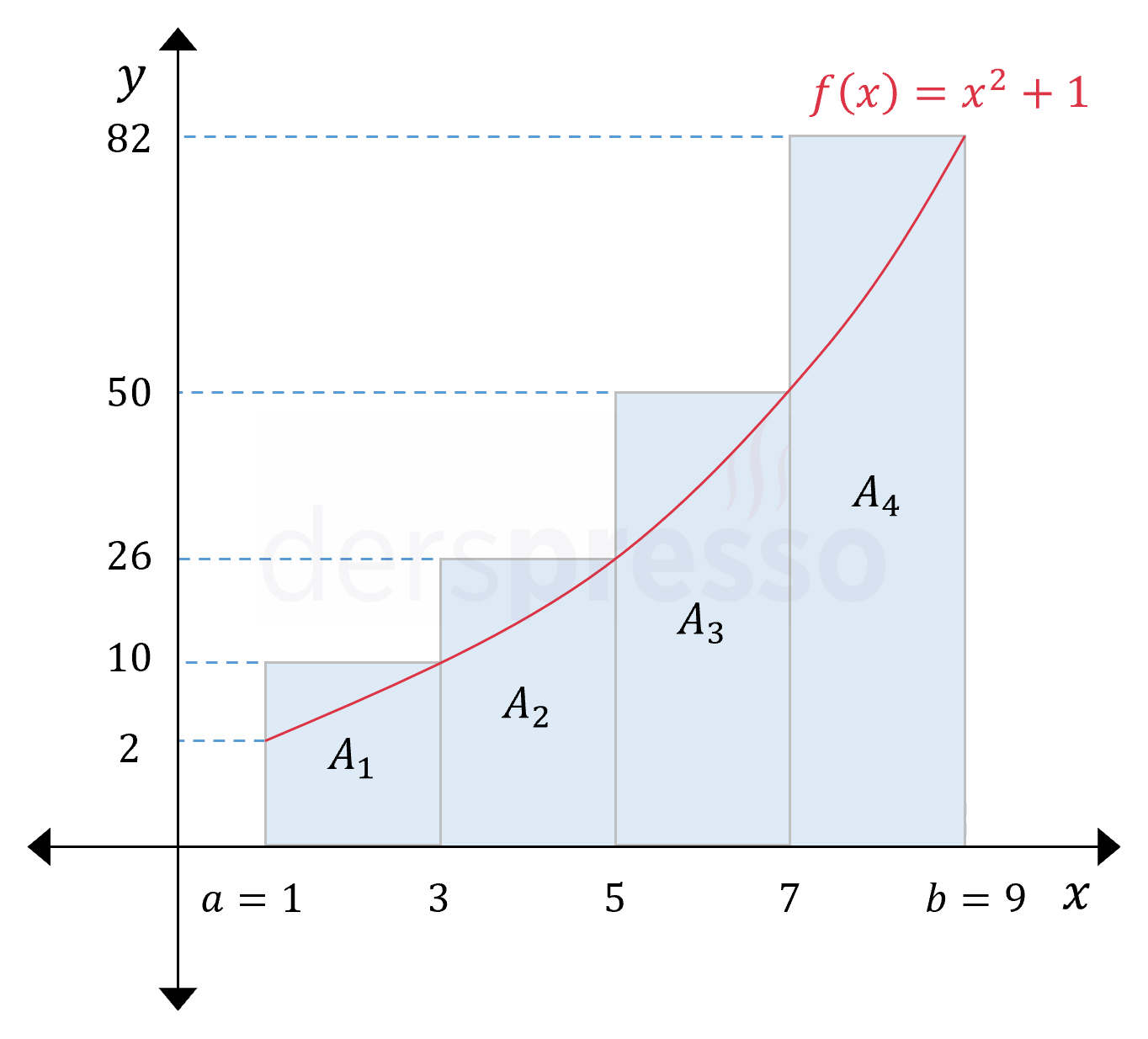
Alternatif bir yöntem olarak bu aralığı yine 4 eşit aralığa bölelim, ancak bu sefer her aralık için \( x \) ekseninden o aralıktaki en büyük fonksiyon değerine dikdörtgenler çizelim ve bu dikdörtgenlerin alanlarını bulalım. Her aralıktaki en büyük fonksiyon değerini kullanarak hesaplayacağımız bu alan değerine kısaca üst toplam diyeceğiz.
\( \Delta x = \dfrac{9 - 1}{4} = 2 \)
\( A_1 = f(3) \cdot \Delta x = 10 \cdot 2 = 20 \)
\( A_2 = f(5) \cdot \Delta x = 26 \cdot 2 = 52 \)
\( A_3 = f(7) \cdot \Delta x = 50 \cdot 2 = 100 \)
\( A_4 = f(9) \cdot \Delta x = 82 \cdot 2 = 164 \)
\( S_{4b} \) aralığı 4 alt aralığa bölerek ve her aralıktaki en büyük fonksiyon değerini kullanarak hesapladığımız yaklaşık alan değeri olmak üzere,
\( S_{4b} \approx A \)
\( S_{4b} = A_1 + A_2 + A_3 + A_4 \)
\( = 20 + 52 + 100 + 164 = 336 \)
Bu grafikte eğrinin altında kalan bölgeler doğru hesapladığımız, üstünde kalan bölgeler ise kullandığımız yöntem gereği fazla hesapladığımız alanlara karşılık gelmektedir. Çizdiğimiz dikdörtgenlerin yüksekliği olarak her aralıktaki en büyük fonksiyon değerini aldığımız için, gerçek alan değerinin hesapladığımız yaklaşık alan değerinden küçük (ya da ona eşit) olduğundan emin olabiliriz.
\( 176 \le A \le 336 \)
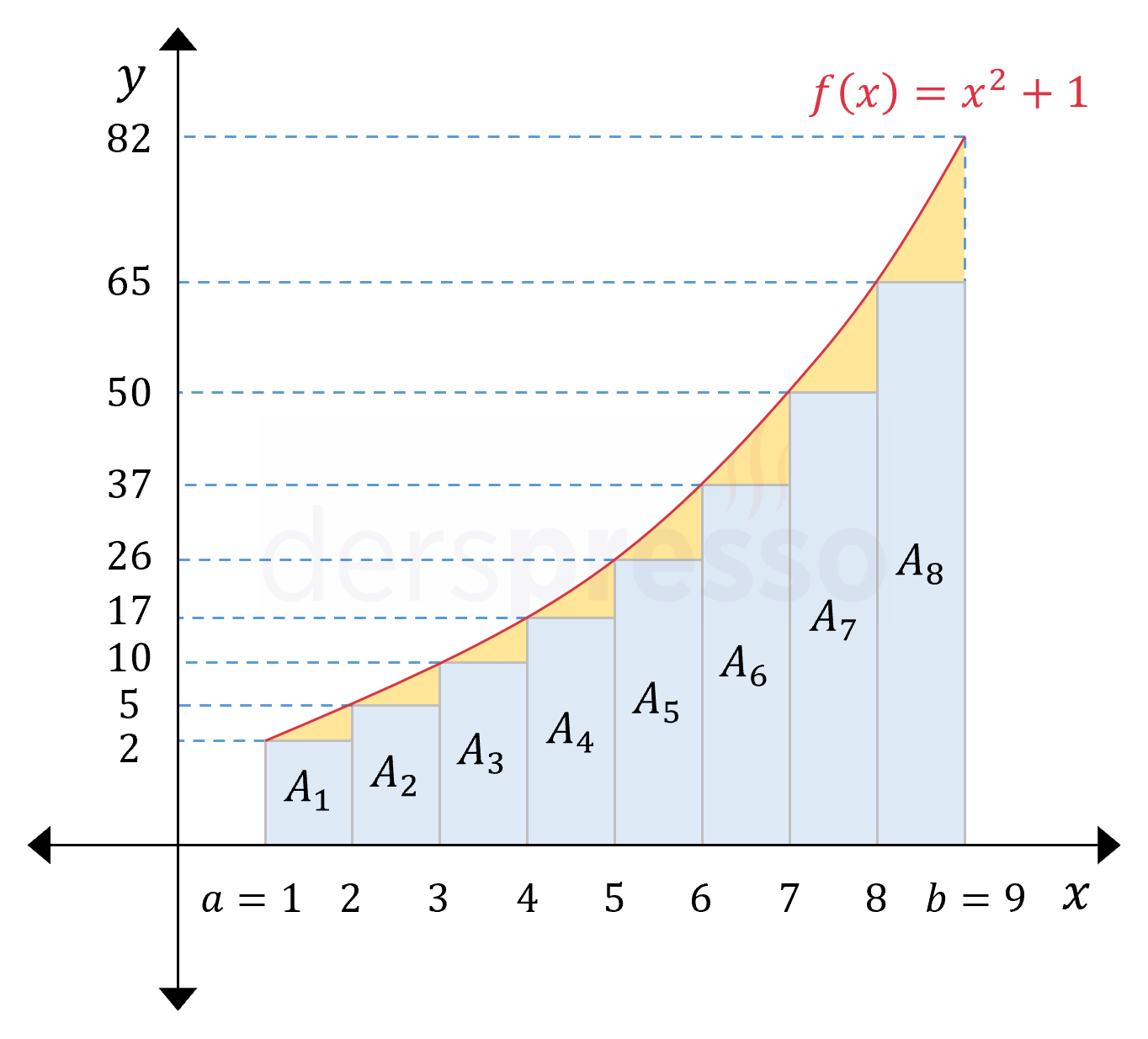
Görebileceğimiz gibi, geniş bir aralık olsa da gerçek değerini bulmak istediğimiz \( A \) alanı için bir değer aralığı elde etmiş olduk. Bu aralığı daraltma hedefiyle, verilen aralığı 4 yerine 8 eşit aralığa bölerek aynı yöntemi tekrarlayalım.
\( \Delta x = \dfrac{9 - 1}{8} = 1 \)
\( A_1 = f(1) \cdot \Delta x = 2 \cdot 1 = 2 \)
\( A_2 = f(2) \cdot \Delta x = 5 \cdot 1 = 5 \)
\( A_3 = f(3) \cdot \Delta x = 10 \cdot 1 = 10 \)
\( A_4 = f(4) \cdot \Delta x = 17 \cdot 1 = 17 \)
\( A_5 = f(5) \cdot \Delta x = 26 \cdot 1 = 26 \)
\( A_6 = f(6) \cdot \Delta x = 37 \cdot 1 = 37 \)
\( A_7 = f(7) \cdot \Delta x = 50 \cdot 1 = 50 \)
\( A_8 = f(8) \cdot \Delta x = 65 \cdot 1 = 65 \)
\( S_{8k} \) aralığı 8 alt aralığa bölerek ve her aralıktaki en küçük fonksiyon değerini kullanarak hesapladığımız yaklaşık alan değeri olmak üzere,
\( S_{8k} \approx A \)
\( S_{8k} = A_1 + A_2 + \ldots + A_8 \)
\( = 2 + 5 + \ldots + 65 = 212 \)
Aralık sayısını arttırdığımızda eksik hesapladığımız turuncu alanların küçüldüğünü hem görsel hem de sayısal olarak görebiliriz. Nitekim \( A \) değerinin alt sınırı olarak daha önce bulduğumuz 176 değeri yerine 212 değerini elde etmiş olduk.
\( A \ge 212 \)
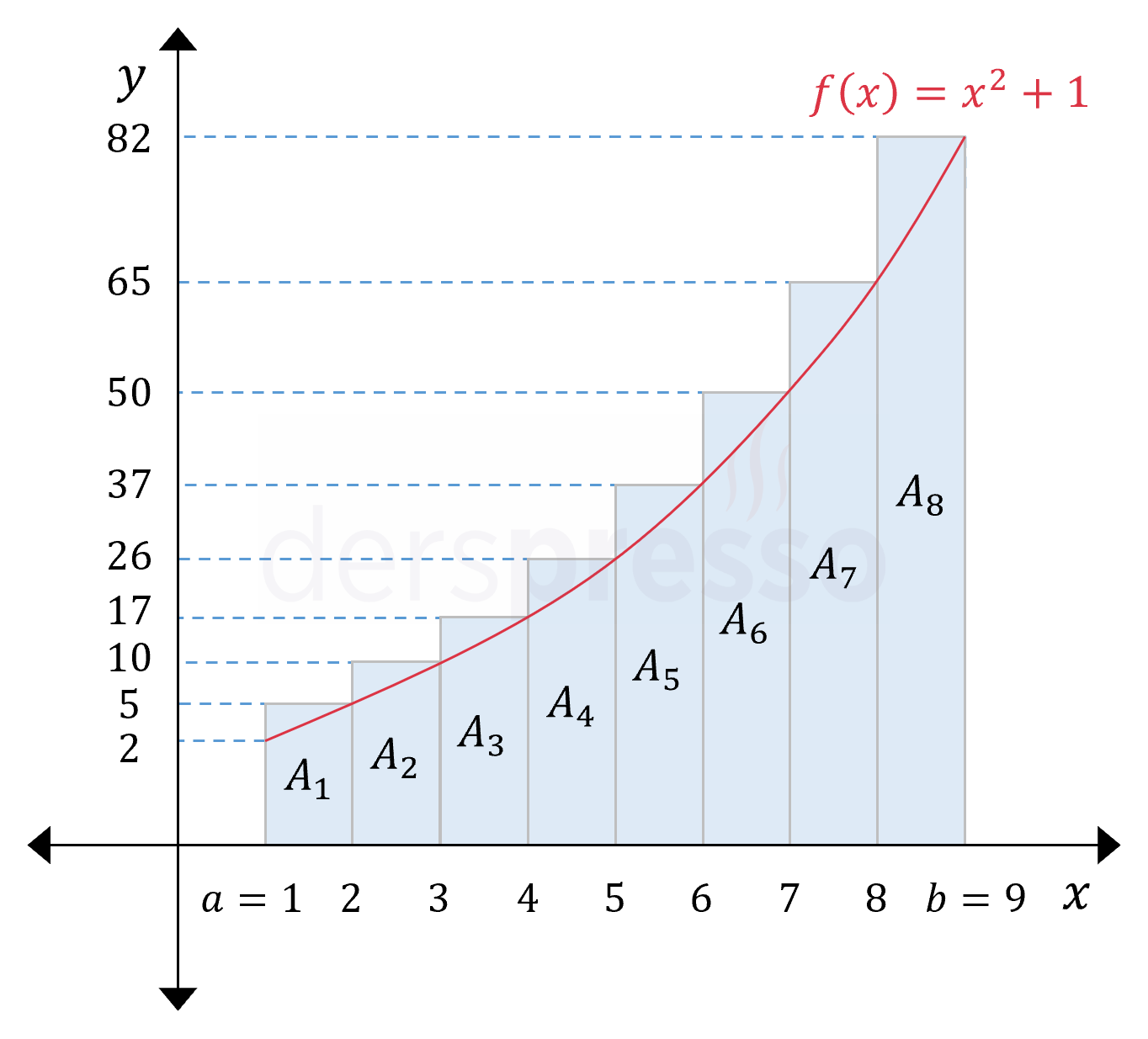
Şimdi de bu aralığı yine 8 eşit aralığa bölerek, ancak bu sefer her aralık için \( x \) ekseninden o aralıktaki en büyük fonksiyon değerine dikdörtgenler çizerek aynı yöntemi tekrarlayalım.
\( \Delta x = \dfrac{9 - 1}{8} = 1 \)
\( A_1 = f(2) \cdot \Delta x = 5 \cdot 1 = 5 \)
\( A_2 = f(3) \cdot \Delta x = 10 \cdot 1 = 10 \)
\( A_3 = f(4) \cdot \Delta x = 17 \cdot 1 = 17 \)
\( A_4 = f(5) \cdot \Delta x = 26 \cdot 1 = 26 \)
\( A_5 = f(6) \cdot \Delta x = 37 \cdot 1 = 37 \)
\( A_6 = f(7) \cdot \Delta x = 50 \cdot 1 = 50 \)
\( A_7 = f(8) \cdot \Delta x = 65 \cdot 1 = 65 \)
\( A_8 = f(9) \cdot \Delta x = 82 \cdot 1 = 82 \)
\( S_{8b} \) aralığı 8 alt aralığa bölerek ve her aralıktaki en büyük fonksiyon değerini kullanarak hesapladığımız yaklaşık alan değeri olmak üzere,
\( S_{8b} \approx A \)
\( S_{8b} = A_1 + A_2 + \ldots + A_8 \)
\( = 5 + 10 + \ldots + 82 = 292 \)
Benzer şekilde aralık sayısını arttırdığımızda fazla hesapladığımız eğrinin üstünde kalan alanların küçüldüğünü görüyoruz. Nitekim \( A \) değerinin üst sınırı olarak daha önce bulduğumuz 336 değeri yerine 292 değerini elde etmiş olduk.
\( 212 \le A \le 292 \)
Buna göre \( [a, b] \) aralığını böldüğümüz alt aralık sayısı arttıkça bu eksik/fazla bulduğumuz alanların küçüleceği ve gerçek alan değerine gitgide yaklaşan değerler elde edeceğimiz sonucuna varabiliriz. Yukarıdaki yöntemi daha büyük aralık sayıları ile tekrarladığımızda elde edeceğimiz alt ve üst toplam değerleri aşağıdaki tabloda verilmiştir.
| Aralık Sayısı | Alt Toplam | Üst Toplam |
|---|---|---|
| \( 4 \) | \( 176 \) | \( 336 \) |
| \( 8 \) | \( 212 \) | \( 292 \) |
| \( 20 \) | \( 234,88 \) | \( 266,88 \) |
| \( 50 \) | \( 244,3008 \) | \( 257,1008 \) |
| \( 100 \) | \( 247,4752 \) | \( 253,8752 \) |
| \( 1000 \) | \( 250,346752 \) | \( 250,986752 \) |
| \( 10000 \) | \( 250,63466752 \) | \( 250,69866752 \) |
Görebileceğimiz gibi, aralık sayısı arttıkça alt ve üst toplamlar arasındaki fark kapanmakta ve her iki toplam gerçek alan değeri olduğunu düşündüğümüz değere yaklaşmaktadır. Nitekim bu örnek için gerçek alan değerinin \( A = 250,666... \) olduğunu ön bir bilgi olarak verebiliriz.
Riemann Toplamı
Yukarıdaki örneklerde \( [a, b] \) aralığını böldüğümüz alt aralıkları eşit kabul etmiş olsak da bu aralıklar farklı genişliklerde olabilir. Buna göre yukarıda kullandığımız yöntemi aşağıdaki şekilde genelleştirebiliriz.

\( f: [a, b] \to \mathbb{R} \) olmak üzere,
\( [a, b] \) aralığını aşağıdaki koşul sağlanacak şekilde eşit ya da farklı genişliklerde \( n \) alt aralığa bölelim.
\( a = x_0 \lt x_1 \lt x_2 \lt \ldots \lt b = x_n \)
Bu durumda \( i \). aralığın genişliği aşağıdaki şekilde olur.
\( \Delta x_i = x_i - x_{i-1} \)
Buna göre \( f \) fonksiyonunun grafiği ile \( x \) ekseni arasında kalan alanı tahmin etmek için hesapladığımız aşağıdaki ifadeye \( f \) fonksiyonunun \( [a, b] \) aralığındaki Riemann toplamı denir.
\( S_n = f(x_1^*) \cdot \Delta x_1 + f(x_2^*) \cdot \Delta x_2 + \ldots + f(x_n^*) \cdot \Delta x_n \)
Bu toplamı toplam sembolü ile yazabiliriz.
\( S_n = \displaystyle\sum_{i = 1}^n {f(x_i^*) \cdot \Delta x_i} \)
\( x_i^* \): \( i \). aralıkta dikdörtgenin yüksekliğini belirlemek için seçilen \( x \) değeri
\( f(x_i^*) \): \( i \). aralıktaki dikdörtgenin yüksekliği
Yukarıdaki formülde kullandığımız toplam sembolü (\( \sum \)) hakkında detaylı bilgi için toplam sembolü bölümünü inceleyebilirsiniz.
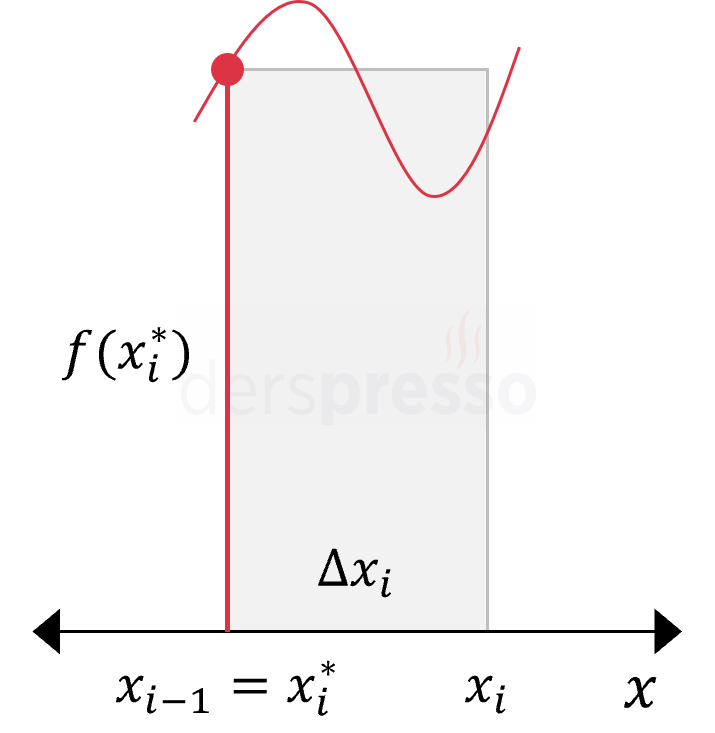
Bir Riemann toplamında çizilen dikdörtgenlerin yüksekliklerini belirlemek için \( x_i^* \) değerini farklı şekillerde seçebiliriz. Aşağıdaki tabloda kullanabileceğimiz 5 farklı yöntem verilmiştir.
| Grafik | Açıklama |
|---|---|
|
Sol Riemann Toplamı Sol Riemann toplamında dikdörtgenin yüksekliği aralığın sol uç noktasındaki fonksiyon değeri olur. \( x_i^* = x_{i-1} \) \( \text{Alan} = f(x_i^*) \cdot \Delta x_i \) |
|
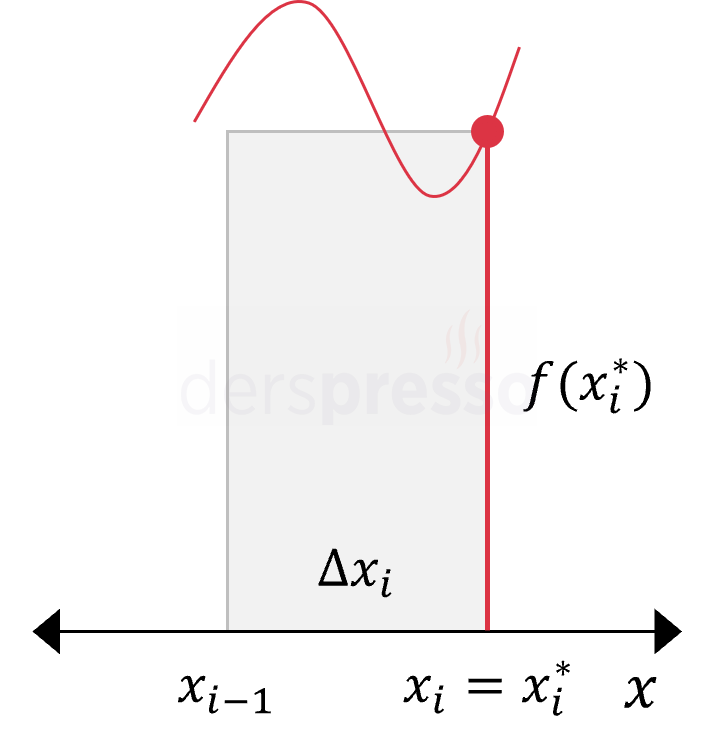
Sağ Riemann Toplamı Sağ Riemann toplamında dikdörtgenin yüksekliği aralığın sağ uç noktasındaki fonksiyon değeri olur. \( x_i^* = x_i \) \( \text{Alan} = f(x_i^*) \cdot \Delta x_i \) |
|
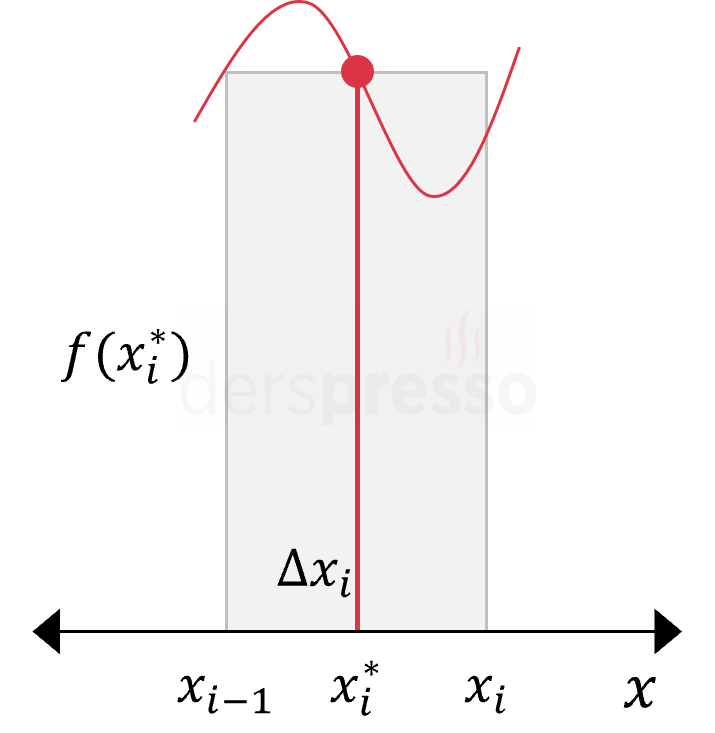
Orta Nokta Riemann Toplamı Orta nokta Riemann toplamında dikdörtgenin yüksekliği aralığın orta noktasındaki fonksiyon değeri olur. \( x_i^* = \dfrac{x_{i-1} + x_i}{2} \) \( \text{Alan} = f(x_i^*) \cdot \Delta x_i \) Bu yöntem artan ya da azalan aralıklarda ortalama fonksiyon değerine daha yakın \( f(x_i^*) \) değerleri kullandığı için, diğer yöntemlere göre gerçek değere daha yakın sonuç verir. |
|
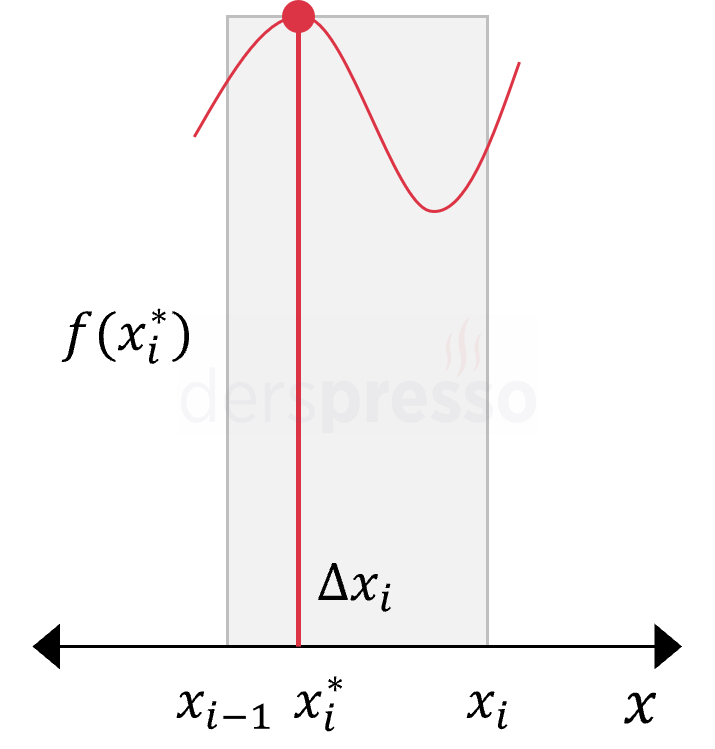
Üst Riemann Toplamı Üst Riemann toplamında dikdörtgenin yüksekliği her aralıktaki en büyük fonksiyon değeri olur. \( x_i^* \): fonksiyonun \( [x_{i-1}, x_i] \) aralığında en büyük değerini aldığı apsis değeri \( \text{Alan} = f(x_i^*) \cdot \Delta x_i \) Bu yöntem her aralıktaki en büyük \( f(x_i^*) \) değerini kullandığı için, her zaman gerçek değerden daha büyük (ya da ona eşit) sonuç verir. Üst Riemann toplamı artan aralıklarda sağ Riemann toplamına, azalan aralıklarda sol Riemann toplamına eşit olur. |
|
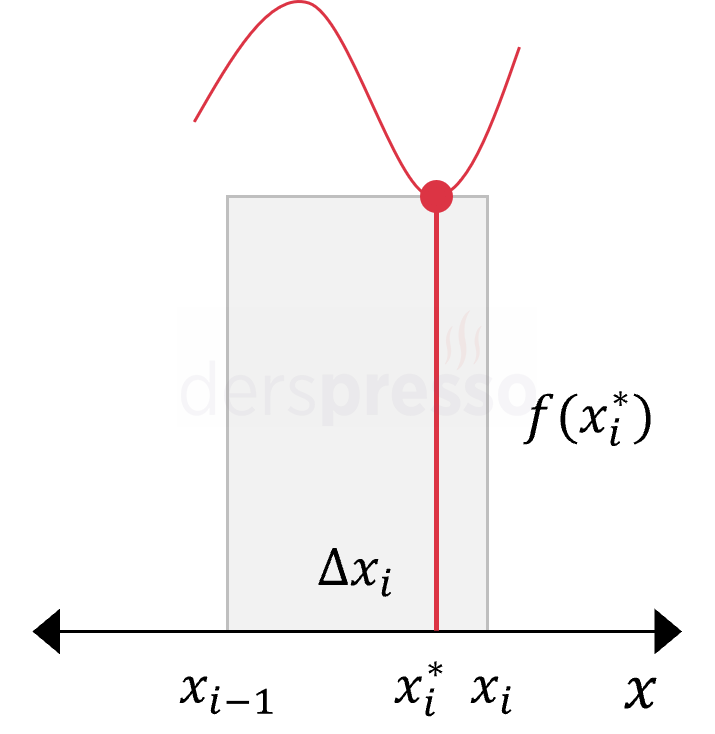
Alt Riemann Toplamı Alt Riemann toplamında dikdörtgenin yüksekliği her aralıktaki en küçük fonksiyon değeri olur. \( x_i^* \): fonksiyonun \( [x_{i-1}, x_i] \) aralığında en küçük değerini aldığı apsis değeri \( \text{Alan} = f(x_i^*) \cdot \Delta x_i \) Bu yöntem her aralıktaki en küçük \( f(x_i^*) \) değerini kullandığı için, her zaman gerçek değerden daha küçük (ya da ona eşit) sonuç verir. Alt Riemann toplamı artan aralıklarda sol Riemann toplamına, azalan aralıklarda sağ Riemann toplamına eşit olur. |
Riemann toplamı yöntemi bir eğrinin altında kalan alanın hesaplanması dışında ileriki bölümlerde göreceğimiz üzere, yay uzunluğu, yüzey alanı ve hacim hesaplamalarında da kullanabileceğimiz bir yöntemdir.
Her ne kadar bir Riemann toplamını farklı aralık genişlikleri ve \( x_i^* \) değerleri ile hesaplayabiliyor olsak da, aralığı böldüğümüz alt aralık sayısı çok büyük değerler aldıkça tüm yöntemlerde elde edilen yaklaşık değerler aynı gerçek değere yaklaşır. Bir diğer deyişle, aralık sayısı büyüdükçe aralık genişliklerini ve \( x_i^* \) değerlerini nasıl seçtiğimizin sonuca etkisi azalır.
Yukarıdaki tabloya orta nokta Riemann toplamını da eklediğimizde, aralık sayısı arttıkça tüm yöntemlerin aynı gerçek alan değerine yaklaştığını görebiliriz.
| Aralık Sayısı | Alt Toplam | Orta Nokta Toplam | Üst Toplam |
|---|---|---|---|
| \( 4 \) | \( 176 \) | \( 248 \) | \( 336 \) |
| \( 8 \) | \( 212 \) | \( 250 \) | \( 292 \) |
| \( 20 \) | \( 234,88 \) | \( 250,56 \) | \( 266,88 \) |
| \( 50 \) | \( 244,3008 \) | \( 250,6496 \) | \( 257,1008 \) |
| \( 100 \) | \( 247,4752 \) | \( 250,6624 \) | \( 253,8752 \) |
| \( 1000 \) | \( 250,346752 \) | \( 250,666624 \) | \( 250,986752 \) |
| \( 10000 \) | \( 250,63466752 \) | \( 250,66666624 \) | \( 250,69866752 \) |
Önümüzdeki bölümde Riemann toplamına dayanan ve eğrilerin altında kalan alanı kolaylıkla hesaplamamızı sağlayan integral işleminden bahsedeceğiz. İntegral işlemi pek çok matematiksel ve bilimsel hesaplamada büyük kolaylık sağlasa da, integralinin alınması kolay olmayan fonksiyonlar için Riemann toplamı yöntemi her zaman kullanabileceğimiz bir yöntemdir.
Net Alan
Riemann toplamı formülünü aşağıdaki gibi negatif değer alabilen bir fonksiyona uyguladığımızı düşünelim. Bunun için \( [2, 14] \) aralığını genişlikleri eşit 6 aralığa bölelim ve orta nokta yöntemini kullanalım.
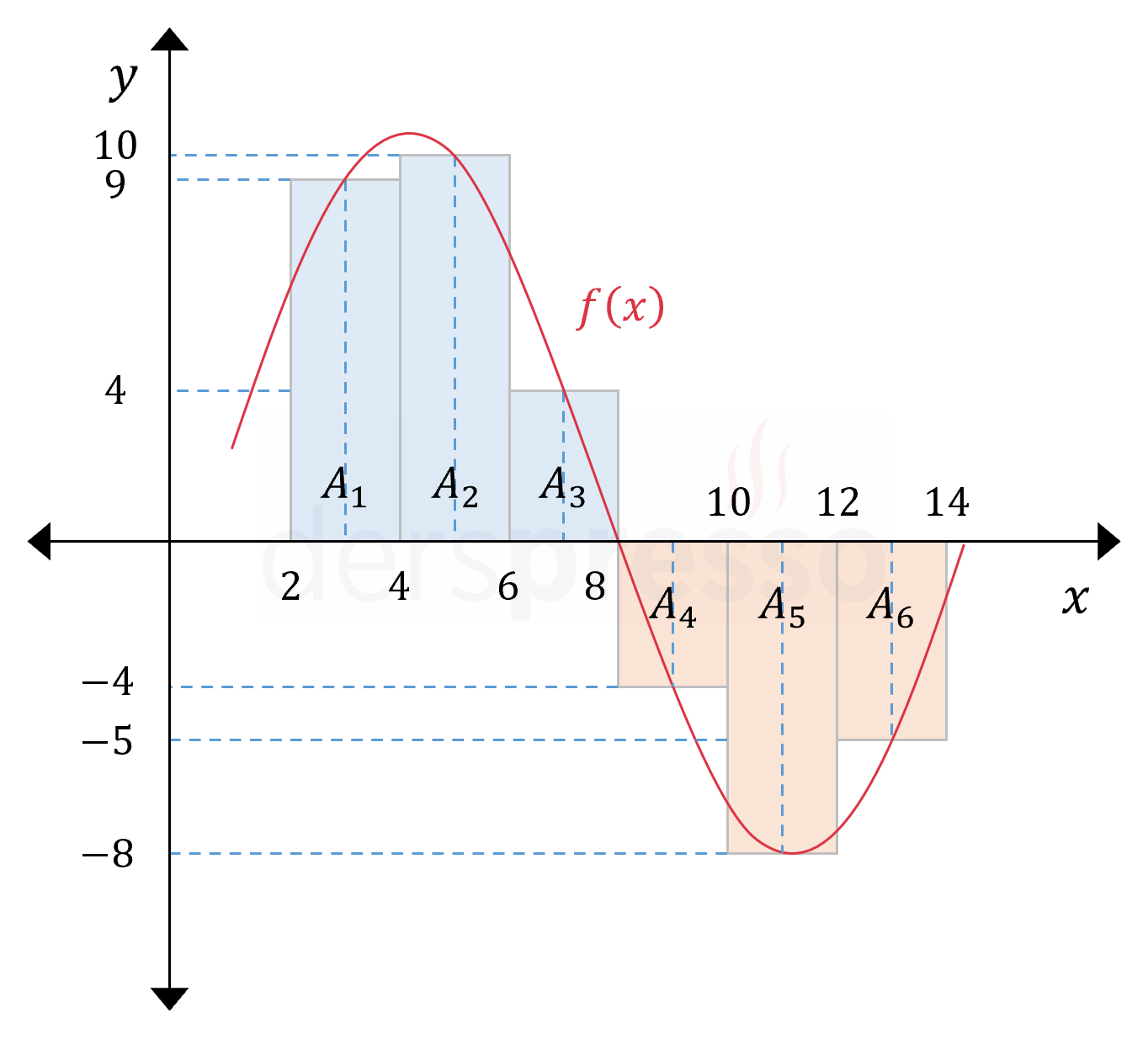
Bu aralıktaki Riemann toplamını aşağıdaki gibi buluruz.
\( S_6 = \displaystyle\sum_{i = 1}^6 {f(x_i^*) \cdot \Delta x_i} \)
\( = 9 \cdot 2 + 10 \cdot 2 + 4 \cdot 2 + \textcolor{red}{(-4)} \cdot 2 + \textcolor{red}{(-8)} \cdot 2 + \textcolor{red}{(-5)} \cdot 2 \)
\( = 12 \)
Buna göre eğrinin \( x \) ekseninin üstünde kaldığı ve fonksiyonun pozitif değer aldığı aralıklarda alan pozitif olurken eğrinin \( x \) ekseninin altında kaldığı ve fonksiyonun negatif değer aldığı aralıklarda alan negatif olmaktadır.
Geometride gördüğümüz alan mutlak bir değer iken burada bir eğrinin altında kalan alan karşımıza negatif olabilen bir değer olarak çıkmaktadır. Buna göre geometrik alandan farklı olarak, Riemann toplamı bir eğrinin altında kalan net alanı hesaplamaktadır. Net alanı \( x \) ekseninin üstünde kalan alanlar ile altında kalan alanların negatiflerinin toplamı olarak tanımlayabiliriz.
\( A_1, \ldots, A_6 \) dikdörtgenlerin geometrik (mutlak) alanları olmak üzere,
\( A_1 = 18, A_2 = 20, A_3 = 8 \)
\( A_4 = 8, A_5 = 16, A_6 = 10 \)
\( S_6 = A_1 + A_2 + A_3 + (-A_4) + (-A_5) + (-A_6) \)
\( f(x) = x^2 + 1 \) fonksiyonunun \( [2, 14] \) aralığını 6 eşit aralığa bölerek orta nokta Riemann toplamını hesaplayın.
Çözümü GösterVerilen fonksiyonun \( [2, 14] \) aralığını 6 eşit aralığa bölelim.
\( \Delta x \) her aralığın genişliği olmak üzere,
\( \Delta x = \dfrac{14 - 2}{6} = 2 \)
Oluşan aralıkların uç noktalarının apsis değerleri aşağıdaki gibi olur.
\( x_i \in \{2, 4, 6, 8, 10, 12, 14\} \)
Dikdörtgenlerin yüksekliklerini hesaplamak için kullanacağımız aralıkların orta noktalarının apsis değerleri aşağıdaki gibi olur.
\( x_i^* \in \{3, 5, 7, 9, 11, 13\} \)
Bu \( x_i^* \) değerleri için fonksiyon değerlerini bulalım.
\( f(3) = 3^2 + 1 = 10 \)
\( f(5) = 5^2 + 1 = 26 \)
\( f(7) = 7^2 + 1 = 50 \)
\( f(9) = 9^2 + 1 = 82 \)
\( f(11) = 11^2 + 1 = 122 \)
\( f(13) = 13^2 + 1 = 170 \)
Her aralığın orta noktası için fonksiyon değerini yükseklik kabul eden dikdörtgenler çizelim.
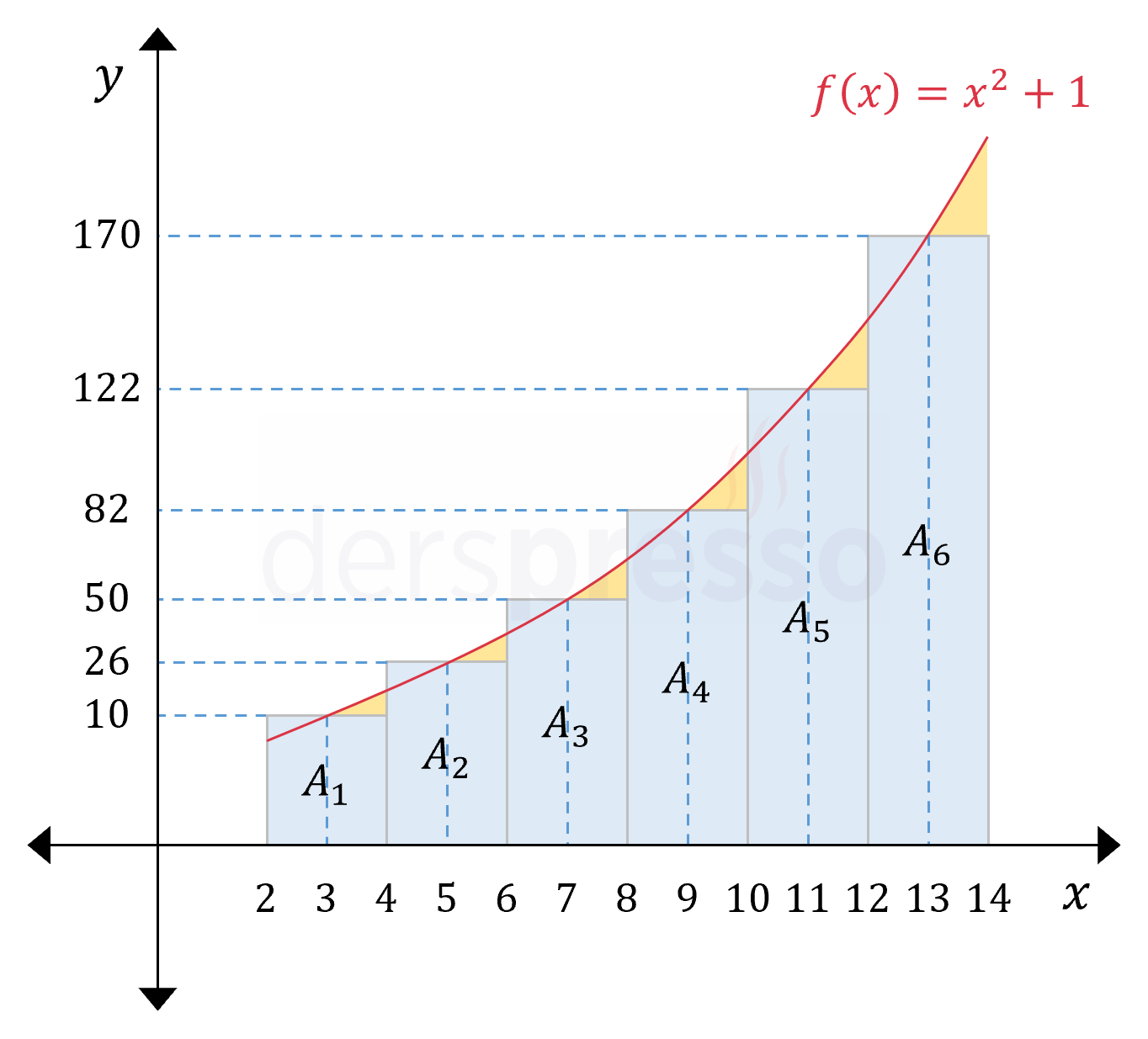
Orta nokta yöntemi ile hesaplayacağımız Riemann toplamı bu dikdörtgenlerin alanlarının toplamına eşittir.
Dikdörtgenlerin alanlarını hesaplayalım.
\( A_1 = f(3) \cdot \Delta x = 10 \cdot 2 = 20 \)
\( A_2 = f(5) \cdot \Delta x = 26 \cdot 2 = 52 \)
\( A_3 = f(7) \cdot \Delta x = 50 \cdot 2 = 100 \)
\( A_4 = f(9) \cdot \Delta x = 82 \cdot 2 = 164 \)
\( A_5 = f(11) \cdot \Delta x = 122 \cdot 2 = 244 \)
\( A_6 = f(13) \cdot \Delta x = 170 \cdot 2 = 340 \)
\( S_6 \) yaklaşık alan değerini verecek olan orta nokta Riemann toplamı olmak üzere,
\( S_6 = A_1 + A_2 + A_3 + A_4 + A_5 + A_6 \)
\( = 20 + 52 + 100 + 164 + 244 + 340 \)
\( = 920 \)
\( f(x) = x^3 - 4x^2 - 11x + 30 \) fonksiyonunun \( [-2, 4] \) aralığını 6 eşit aralığa bölerek sol Riemann toplamını hesaplayın.
Çözümü GösterVerilen fonksiyonun \( [-2, 4] \) aralığını 6 eşit aralığa bölelim.
\( \Delta x \) her aralığın genişliği olmak üzere,
\( \Delta x = \dfrac{4 - (-2)}{6} = 1 \)
Oluşan aralıkların uç noktalarının apsis değerleri aşağıdaki gibi olur.
\( x_i \in \{-2, -1, 0, 1, 2, 3, 4\} \)
Dikdörtgenlerin yüksekliklerini hesaplamak için kullanacağımız aralıkların sol uç noktalarının apsis değerleri aşağıdaki gibi olur.
\( x_i^* \in \{-2, -1, 0, 1, 2, 3\} \)
Bu \( x_i^* \) değerleri için fonksiyon değerlerini bulalım.
\( f(-2) = (-2)^3 - 4(-2)^2 - 11(-2) + 30 = 28 \)
\( f(-1) = (-1)^3 - 4(-1)^2 - 11(-1) + 30 = 36 \)
\( f(0) = 0^3 - 4(0)^2 - 11(0) + 30 = 30 \)
\( f(1) = 1^3 - 4(1)^2 - 11(1) + 30 = 16 \)
\( f(2) = 2^3 - 4(2)^2 - 11(2) + 30 = 0 \)
\( f(3) = 3^3 - 4(3)^2 - 11(3) + 30 = -12 \)
Her aralığın sol uç noktası için fonksiyon değerini yükseklik kabul eden dikdörtgenler çizelim.
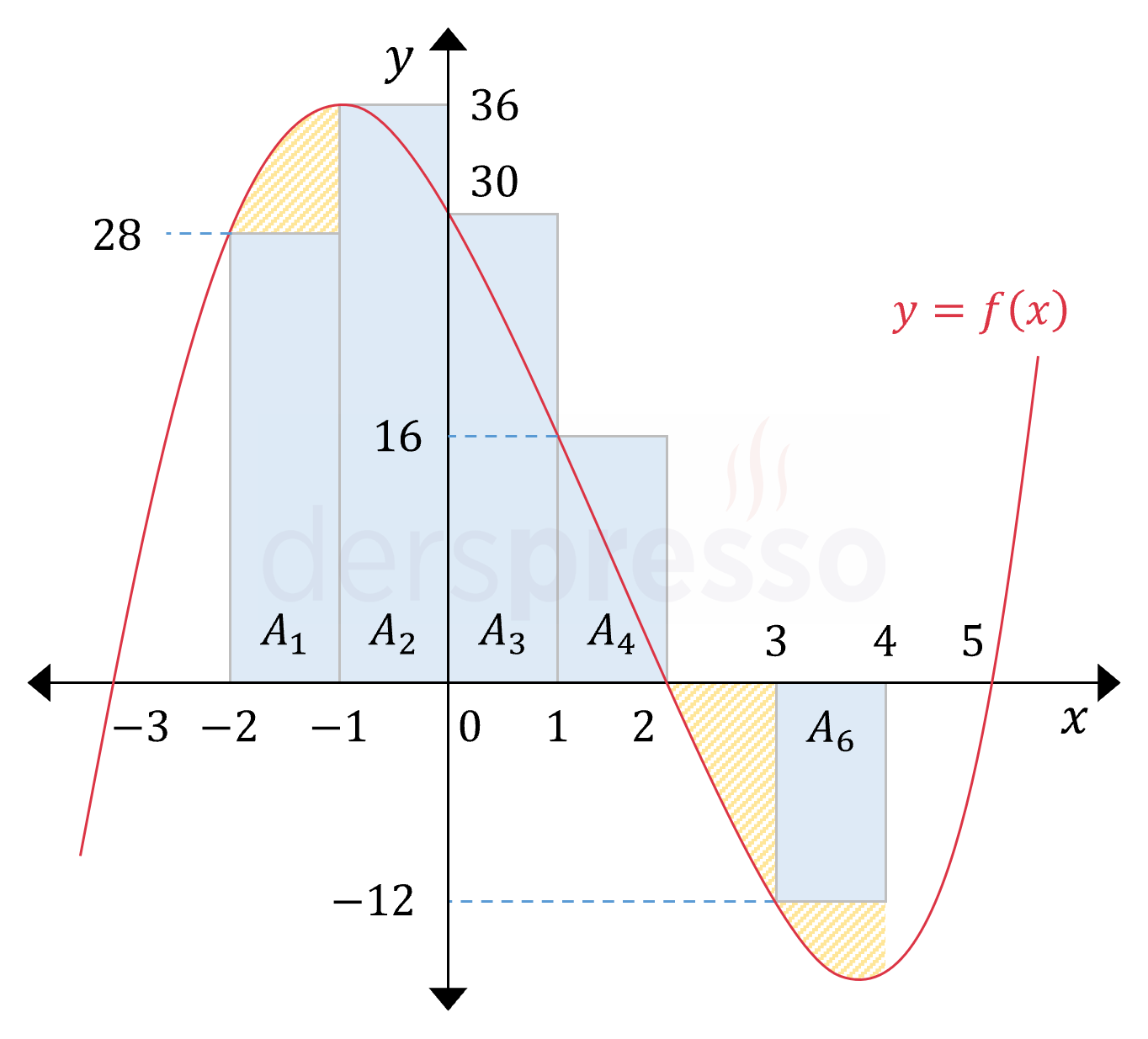
Hesaplayacağımız sol Riemann toplamı bu dikdörtgenlerin alanlarının toplamına eşittir.
Dikdörtgenlerin alanlarını hesaplayalım.
5. aralıkta sol uç noktada fonksiyon değeri sıfır olduğu için bu aralıkta dikdörtgenin alanı sıfır olur.
\( A_1 = f(-2) \cdot \Delta x = 28 \cdot 1 = 28 \)
\( A_2 = f(-1) \cdot \Delta x = 36 \cdot 1 = 36 \)
\( A_3 = f(0) \cdot \Delta x = 30 \cdot 1 = 30 \)
\( A_4 = f(1) \cdot \Delta x = 16 \cdot 1 = 16 \)
\( A_5 = f(2) \cdot \Delta x = 0 \cdot 1 = 0 \)
\( A_6 = f(3) \cdot \Delta x = -12 \cdot 1 = -12 \)
Görebileceğimiz gibi fonksiyon değerinin negatif olduğu ve dikdörtgenin \( x \) ekseninin altında kaldığı aralıklarda Riemann toplamının terimi de negatif olur.
\( S_6 \) yaklaşık alan değerini verecek olan sol Riemann toplamı olmak üzere,
\( S_6 = A_1 + A_2 + A_3 + A_4 + A_5 + A_6 \)
\( = 28 + 36 + 30 + 16 + 0 + (-12) \)
\( = 98 \)
\( f(x) = x^3 - 4x^2 - 11x + 30 \) fonksiyonunun \( [-2, 4] \) aralığını 6 eşit aralığa bölerek sağ Riemann toplamını hesaplayın.
Çözümü GösterVerilen fonksiyonun \( [-2, 4] \) aralığını 6 eşit aralığa bölelim.
\( \Delta x \) her aralığın genişliği olmak üzere,
\( \Delta x = \dfrac{4 - (-2)}{6} = 1 \)
Oluşan aralıkların uç noktalarının apsis değerleri aşağıdaki gibi olur.
\( x_i \in \{-2, -1, 0, 1, 2, 3, 4\} \)
Dikdörtgenlerin yüksekliklerini hesaplamak için kullanacağımız aralıkların sağ uç noktalarının apsis değerleri aşağıdaki gibi olur.
\( x_i^* \in \{-1, 0, 1, 2, 3, 4\} \)
Bu \( x_i^* \) değerleri için fonksiyon değerlerini bulalım.
\( f(-1) = (-1)^3 - 4(-1)^2 - 11(-1) + 30 = 36 \)
\( f(0) = 0^3 - 4(0)^2 - 11(0) + 30 = 30 \)
\( f(1) = 1^3 - 4(1)^2 - 11(1) + 30 = 16 \)
\( f(2) = 2^3 - 4(2)^2 - 11(2) + 30 = 0 \)
\( f(3) = 3^3 - 4(3)^2 - 11(3) + 30 = -12 \)
\( f(4) = 4^3 - 4(4)^2 - 11(4) + 30 = -14 \)
Her aralığın sağ uç noktası için fonksiyon değerini yükseklik kabul eden dikdörtgenler çizelim.
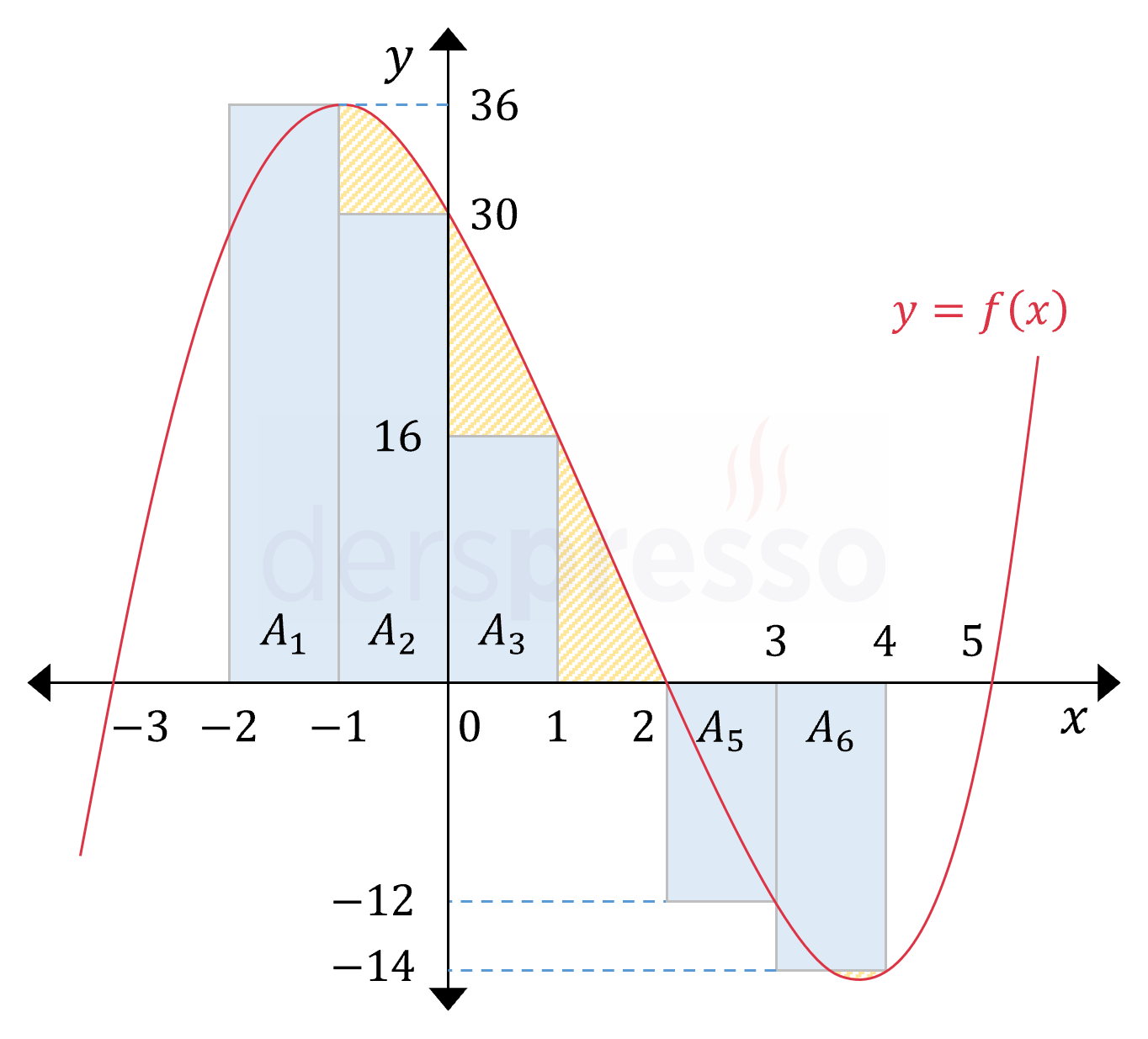
Hesaplayacağımız sağ Riemann toplamı bu dikdörtgenlerin alanlarının toplamına eşittir.
Dikdörtgenlerin alanlarını hesaplayalım.
4. aralıkta sağ uç noktada fonksiyon değeri sıfır olduğu için bu aralıkta dikdörtgenin alanı sıfır olur.
\( A_1 = f(-1) \cdot \Delta x = 36 \cdot 1 = 36 \)
\( A_2 = f(0) \cdot \Delta x = 30 \cdot 1 = 30 \)
\( A_3 = f(1) \cdot \Delta x = 16 \cdot 1 = 16 \)
\( A_4 = f(2) \cdot \Delta x = 0 \cdot 1 = 0 \)
\( A_5 = f(3) \cdot \Delta x = -12 \cdot 1 = -12 \)
\( A_6 = f(4) \cdot \Delta x = -14 \cdot 1 = -14 \)
Görebileceğimiz gibi fonksiyon değerinin negatif olduğu ve dikdörtgenin \( x \) ekseninin altında kaldığı aralıklarda Riemann toplamının terimi de negatif olur.
\( S_6 \) yaklaşık alan değerini verecek olan sağ Riemann toplamı olmak üzere,
\( S_6 = A_1 + A_2 + A_3 + A_4 + A_5 + A_6 \)
\( = 36 + 30 + 16 + 0 + (-12) + (-14) \)
\( = 56 \)
\( f(x) = x^3 - 4x^2 - 11x + 30 \) fonksiyonunun \( [-2, 4] \) aralığını 6 eşit aralığa bölerek orta nokta Riemann toplamını hesaplayın.
Çözümü GösterVerilen fonksiyonun \( [-2, 4] \) aralığını 6 eşit aralığa bölelim.
\( \Delta x \) her aralığın genişliği olmak üzere,
\( \Delta x = \dfrac{4 - (-2)}{6} = 1 \)
Oluşan aralıkların uç noktalarının apsis değerleri aşağıdaki gibi olur.
\( x_i \in \{-2, -1, 0, 1, 2, 3, 4\} \)
Dikdörtgenlerin yüksekliklerini hesaplamak için kullanacağımız aralıkların orta noktalarının apsis değerleri aşağıdaki gibi olur.
\( x_i^* \in \{-\frac{3}{2}, -\frac{1}{2}, \frac{1}{2}, \frac{3}{2}, \frac{5}{2}, \frac{7}{2}\} \)
Bu \( x_i^* \) değerleri için fonksiyon değerlerini bulalım.
\( f(-\frac{3}{2}) = (-\frac{3}{2})^3 - 4(-\frac{3}{2})^2 - 11(-\frac{3}{2}) + 30 = 34\frac{1}{8} \)
\( f(-\frac{1}{2}) = (-\frac{1}{2})^3 - 4(-\frac{1}{2})^2 - 11(-\frac{1}{2}) + 30 = 34\frac{3}{8} \)
\( f(\frac{1}{2}) = (\frac{1}{2})^3 - 4(\frac{1}{2})^2 - 11(\frac{1}{2}) + 30 = 23\frac{5}{8} \)
\( f(\frac{3}{2}) = (\frac{3}{2})^3 - 4(\frac{3}{2})^2 - 11(\frac{3}{2}) + 30 = 7\frac{7}{8} \)
\( f(\frac{5}{2}) = (\frac{5}{2})^3 - 4(\frac{5}{2})^2 - 11(\frac{5}{2}) + 30 = -6\frac{7}{8} \)
\( f(\frac{7}{2}) = (\frac{7}{2})^3 - 4(\frac{7}{2})^2 - 11(\frac{7}{2}) + 30 = -14\frac{5}{8} \)
Her aralığın orta noktası için fonksiyon değerini yükseklik kabul eden dikdörtgenler çizelim.
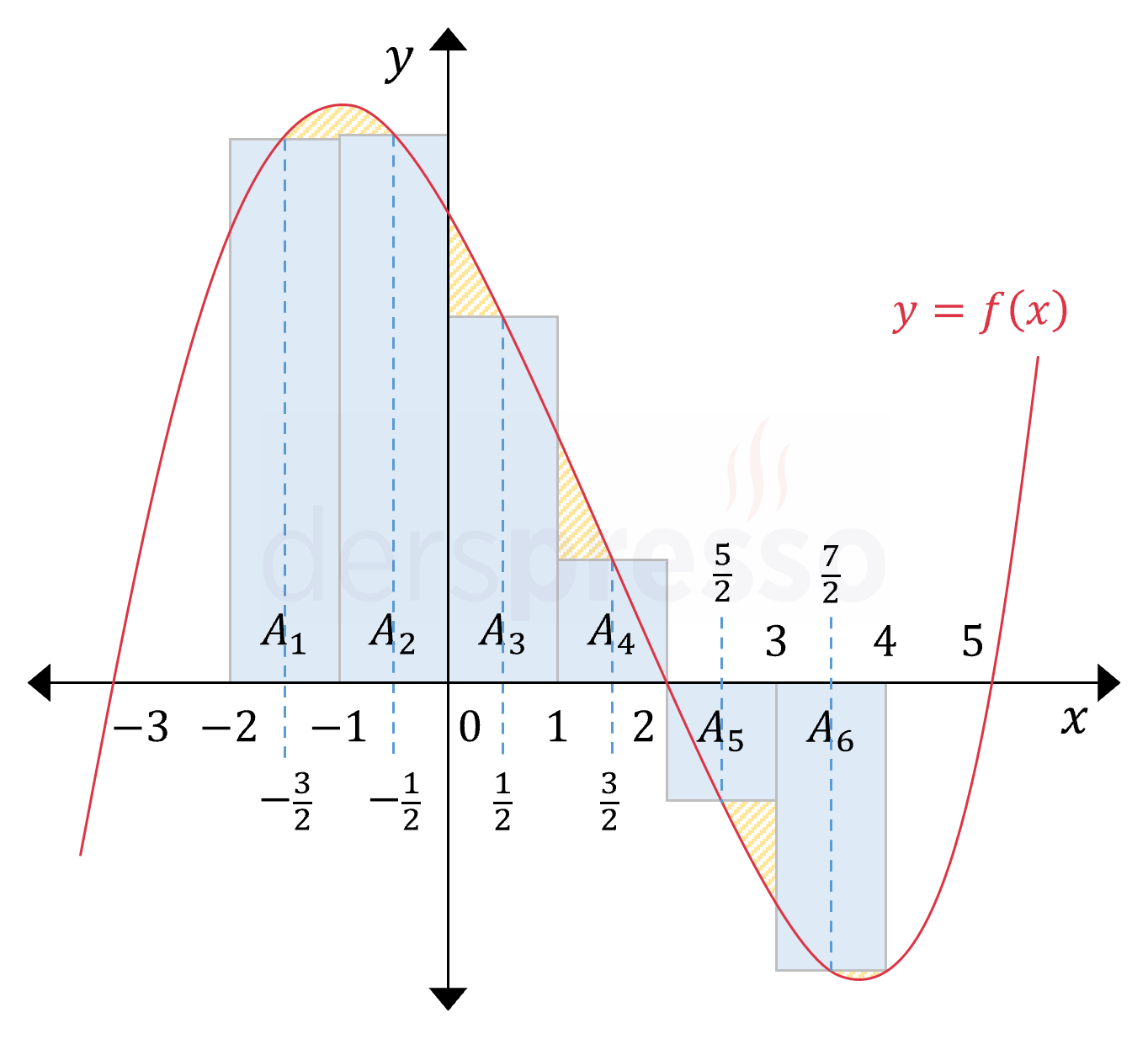
Hesaplayacağımız orta nokta Riemann toplamı bu dikdörtgenlerin alanlarının toplamına eşittir.
Dikdörtgenlerin alanlarını hesaplayalım.
\( A_1 = f(-\frac{3}{2}) \cdot \Delta x = 34\frac{1}{8} \cdot 1 = 34\frac{1}{8} \)
\( A_2 = f(-\frac{1}{2}) \cdot \Delta x = 34\frac{3}{8} \cdot 1 = 34\frac{3}{8} \)
\( A_3 = f(\frac{1}{2}) \cdot \Delta x = 23\frac{5}{8} \cdot 1 = 23\frac{5}{8} \)
\( A_4 = f(\frac{3}{2}) \cdot \Delta x = 7\frac{7}{8} \cdot 1 = 7\frac{7}{8} \)
\( A_5 = f(\frac{5}{2}) \cdot \Delta x = -6\frac{7}{8} \cdot 1 = -6\frac{7}{8} \)
\( A_6 = f(\frac{7}{2}) \cdot \Delta x = -14\frac{5}{8} \cdot 1 = -14\frac{5}{8} \)
Görebileceğimiz gibi fonksiyon değerinin negatif olduğu ve dikdörtgenin \( x \) ekseninin altında kaldığı aralıklarda Riemann toplamının terimi de negatif olur.
\( S_6 \) yaklaşık alan değerini verecek olan orta nokta Riemann toplamı olmak üzere,
\( S_6 = A_1 + A_2 + A_3 + A_4 + A_5 + A_6 \)
\( = 34\frac{1}{8} + 34\frac{3}{8} + 23\frac{5}{8} + 7\frac{7}{8} + (-6\frac{7}{8}) + (-14\frac{5}{8}) \)
\( = 78\frac{1}{2} \)
\( f(x) = 2\sin{x} \) fonksiyonunun \( [0, 2\pi] \) aralığını 6 eşit aralığa bölerek üst Riemann toplamını hesaplayın.
Çözümü GösterVerilen fonksiyonun \( [0, 2\pi] \) aralığını 6 eşit aralığa bölelim.
\( \Delta x \) her aralığın genişliği olmak üzere,
\( \Delta x = \dfrac{2\pi - 0}{6} = \dfrac{\pi}{3} \)
Oluşan aralıkların uç noktalarının apsis değerleri aşağıdaki gibi olur.
\( x_i \in \{0, \frac{\pi}{3}, \frac{2\pi}{3}, \pi, \frac{4\pi}{3}, \frac{5\pi}{3}, 2\pi\} \)
Dikdörtgenlerin yüksekliklerini hesaplamak için kullanacağımız, her aralıkta fonksiyonun en büyük değerini aldığı apsis değerleri aşağıdaki gibi olur.
\( x_i^* \in \{\frac{\pi}{3}, \frac{\pi}{2}, \frac{2\pi}{3}, \pi, \frac{4\pi}{3}, 2\pi\} \)
Dikkat edilirse \( [\frac{\pi}{3}, \frac{2\pi}{3}] \) aralığında fonksiyon en büyük değerini aralığın uç noktalarında değil, orta noktasında almaktadır.
Bu \( x_i^* \) değerleri için fonksiyon değerlerini bulalım.
\( f(\frac{\pi}{3}) = 2\sin{\frac{\pi}{3}} = \sqrt{3} \)
\( f(\frac{\pi}{2}) = 2\sin{\frac{\pi}{2}} = 2 \)
\( f(\frac{2\pi}{3}) = 2\sin{\frac{2\pi}{3}} = \sqrt{3} \)
\( f(\pi) = 2\sin{\pi} = 0 \)
\( f(\frac{4\pi}{3}) = 2\sin{\frac{4\pi}{3}} = -\sqrt{3} \)
\( f(2\pi) = 2\sin{2\pi} = 0 \)
Her aralığın en büyük fonksiyon değerini yükseklik kabul eden dikdörtgenler çizelim.
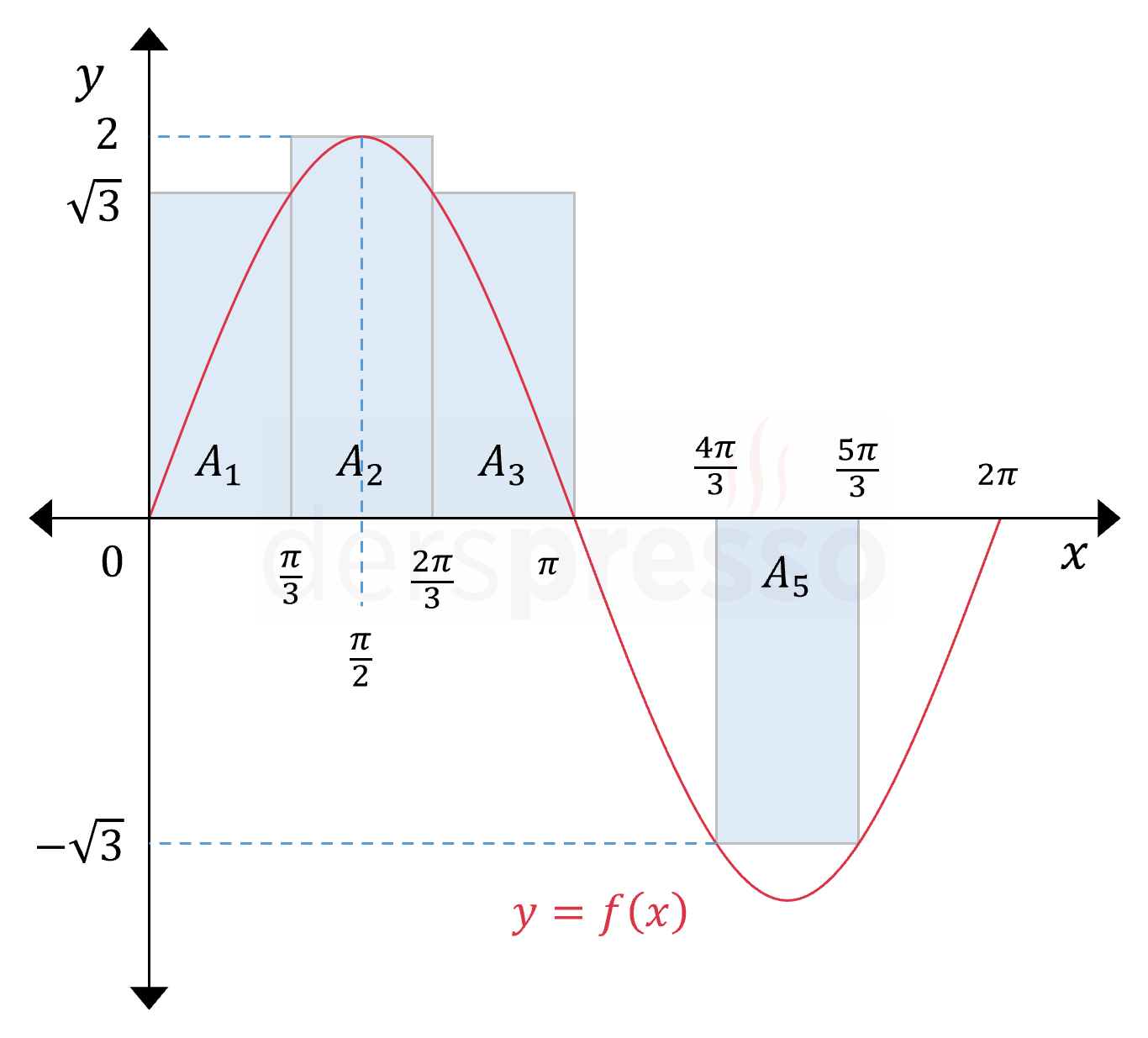
Hesaplayacağımız üst Riemann toplamı bu dikdörtgenlerin alanlarının toplamına eşittir.
Dikdörtgenlerin alanlarını hesaplayalım.
\( A_1 = f(\frac{\pi}{3}) \cdot \Delta x = \sqrt{3} \cdot \frac{\pi}{3} = \frac{\sqrt{3}\pi}{3} \)
\( A_2 = f(\frac{\pi}{2}) \cdot \Delta x = 2 \cdot \frac{\pi}{3} = \frac{2\pi}{3} \)
\( A_3 = f(\frac{2\pi}{3}) \cdot \Delta x = \sqrt{3} \cdot \frac{\pi}{3} = \frac{\sqrt{3}\pi}{3} \)
\( A_4 = f(\pi) \cdot \Delta x = 0 \cdot \frac{\pi}{3} = 0 \)
\( A_5 = f(\frac{4\pi}{3}) \cdot \Delta x = -\sqrt{3} \cdot \frac{\pi}{3} = -\frac{\sqrt{3}\pi}{3} \)
\( A_6 = f(2\pi) \cdot \Delta x = 0 \cdot \frac{\pi}{3} = 0 \)
Görebileceğimiz gibi fonksiyon değerinin negatif olduğu ve dikdörtgenin \( x \) ekseninin altında kaldığı aralıklarda Riemann toplamının terimi de negatif olur.
\( S_6 \) yaklaşık alan değerini verecek olan üst Riemann toplamı olmak üzere,
\( S_6 = A_1 + A_2 + A_3 + A_4 + A_5 + A_6 \)
\( = \frac{\sqrt{3}\pi}{3} + \frac{2\pi}{3} + \frac{\sqrt{3}\pi}{3} + 0 + (-\frac{\sqrt{3}\pi}{3}) + 0 \)
\( = \dfrac{(\sqrt{3} + 2)\pi}{3} \)
\( f(x) = 2\sin{x} \) fonksiyonunun \( [0, 2\pi] \) aralığını 6 eşit aralığa bölerek alt Riemann toplamını hesaplayın.
Çözümü GösterVerilen fonksiyonun \( [0, 2\pi] \) aralığını 6 eşit aralığa bölelim.
\( \Delta x \) her aralığın genişliği olmak üzere,
\( \Delta x = \dfrac{2\pi - 0}{6} = \dfrac{\pi}{3} \)
Oluşan aralıkların uç noktalarının apsis değerleri aşağıdaki gibi olur.
\( x_i \in \{0, \frac{\pi}{3}, \frac{2\pi}{3}, \pi, \frac{4\pi}{3}, \frac{5\pi}{3}, 2\pi\} \)
Dikdörtgenlerin yüksekliklerini hesaplamak için kullanacağımız, her aralıkta fonksiyonun en küçük değerini aldığı apsis değerleri aşağıdaki gibi olur.
\( x_i^* \in \{0, \frac{\pi}{3}, \pi, \frac{4\pi}{3}, \frac{3\pi}{2}, \frac{5\pi}{3}\} \)
Dikkat edilirse \( [\frac{4\pi}{3}, \frac{5\pi}{3}] \) aralığında fonksiyon en küçük değerini aralığın uç noktalarında değil, orta noktasında almaktadır.
Bu \( x_i^* \) değerleri için fonksiyon değerlerini bulalım.
\( f(0) = 2\sin{0} = 0 \)
\( f(\frac{\pi}{3}) = 2\sin{\frac{\pi}{3}} = \sqrt{3} \)
\( f(\pi) = 2\sin{\pi} = 0 \)
\( f(\frac{4\pi}{3}) = 2\sin{\frac{4\pi}{3}} = -\sqrt{3} \)
\( f(\frac{3\pi}{2}) = 2\sin{\frac{3\pi}{2}} = -2 \)
\( f(\frac{5\pi}{3}) = 2\sin{\frac{5\pi}{3}} = -\sqrt{3} \)
Her aralığın en küçük fonksiyon değerini yükseklik kabul eden dikdörtgenler çizelim.
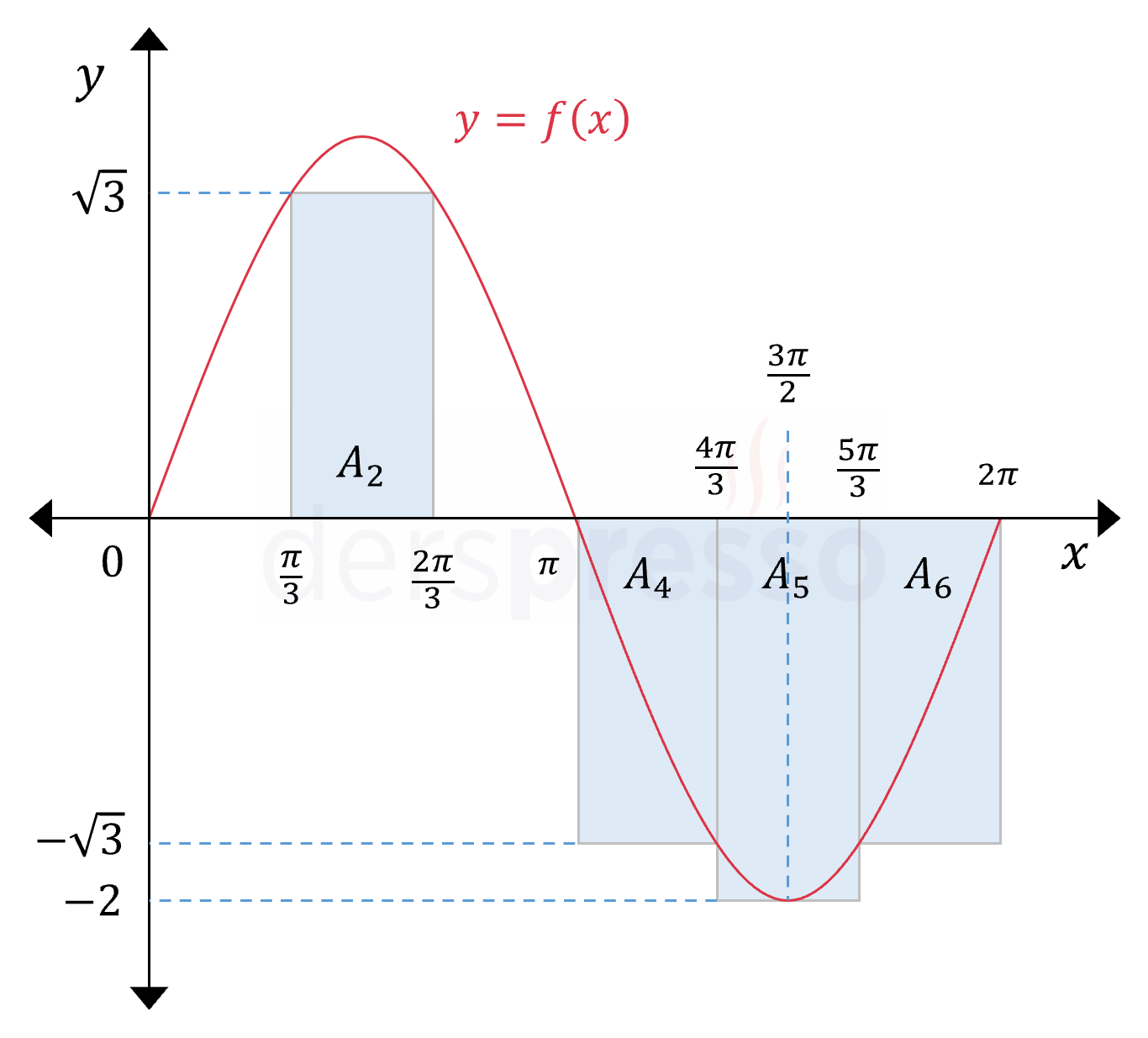
Hesaplayacağımız alt Riemann toplamı bu dikdörtgenlerin alanlarının toplamına eşittir.
Dikdörtgenlerin alanlarını hesaplayalım.
\( A_1 = f(0) \cdot \Delta x = 0 \cdot \frac{\pi}{3} = 0 \)
\( A_2 = f(\frac{\pi}{3}) \cdot \Delta x = \sqrt{3} \cdot \frac{\pi}{3} = \frac{\sqrt{3}\pi}{3} \)
\( A_3 = f(\pi) \cdot \Delta x = 0 \cdot \frac{\pi}{3} = 0 \)
\( A_4 = f(\frac{4\pi}{3}) \cdot \Delta x = -\sqrt{3} \cdot \frac{\pi}{3} = -\frac{\sqrt{3}\pi}{3} \)
\( A_5 = f(\frac{3\pi}{2}) \cdot \Delta x = -2 \cdot \frac{\pi}{3} = -\frac{2\pi}{3} \)
\( A_6 = f(\frac{5\pi}{3}) \cdot \Delta x = -\sqrt{3} \cdot \frac{\pi}{3} = -\frac{\sqrt{3}\pi}{3} \)
Görebileceğimiz gibi fonksiyon değerinin negatif olduğu ve dikdörtgenin \( x \) ekseninin altında kaldığı aralıklarda Riemann toplamının terimi de negatif olur.
\( S_6 \) yaklaşık alan değerini verecek olan alt Riemann toplamı olmak üzere,
\( S_6 = A_1 + A_2 + A_3 + A_4 + A_5 + A_6 \)
\( = 0 + \frac{\sqrt{3}\pi}{3} + 0 + (-\frac{\sqrt{3}\pi}{3}) + (-\frac{2\pi}{3}) + (-\frac{\sqrt{3}\pi}{3}) \)
\( = -\dfrac{(\sqrt{3} + 2)\pi}{3} \)
\( f(x) = x^2 \) fonksiyonunun \( [0, 4] \) aralığının \( n \) eşit aralığa bölündüğü durum için sağ Riemann toplamını veren bir formül yazın ve \( n = 20 \), \( n = 50 \) ve \( n = 100 \) için sağ Riemann toplamını hesaplayın.
Çözümü GösterÖnce Riemann toplam formülünü yazalım.
\( S_n = \sum_{i = 1}^{n}{f(x_i^*) \cdot \Delta x_i} \)
\( [0, 4] \) aralığını \( n \) eşit aralığa bölelim. Aralıklar eşit genişlikte olduğu için \( \Delta x \) değerini sabit olarak alabiliriz.
\( \Delta x = \dfrac{4 - 0}{n} = \dfrac{4}{n} \)
Sağ Riemann toplamı yönteminde \( i \). aralıkta dikdörtgenin yüksekliği için kullanacağımız \( x_i^* \) değeri aralığın üst sınırının apsis değeri olur.
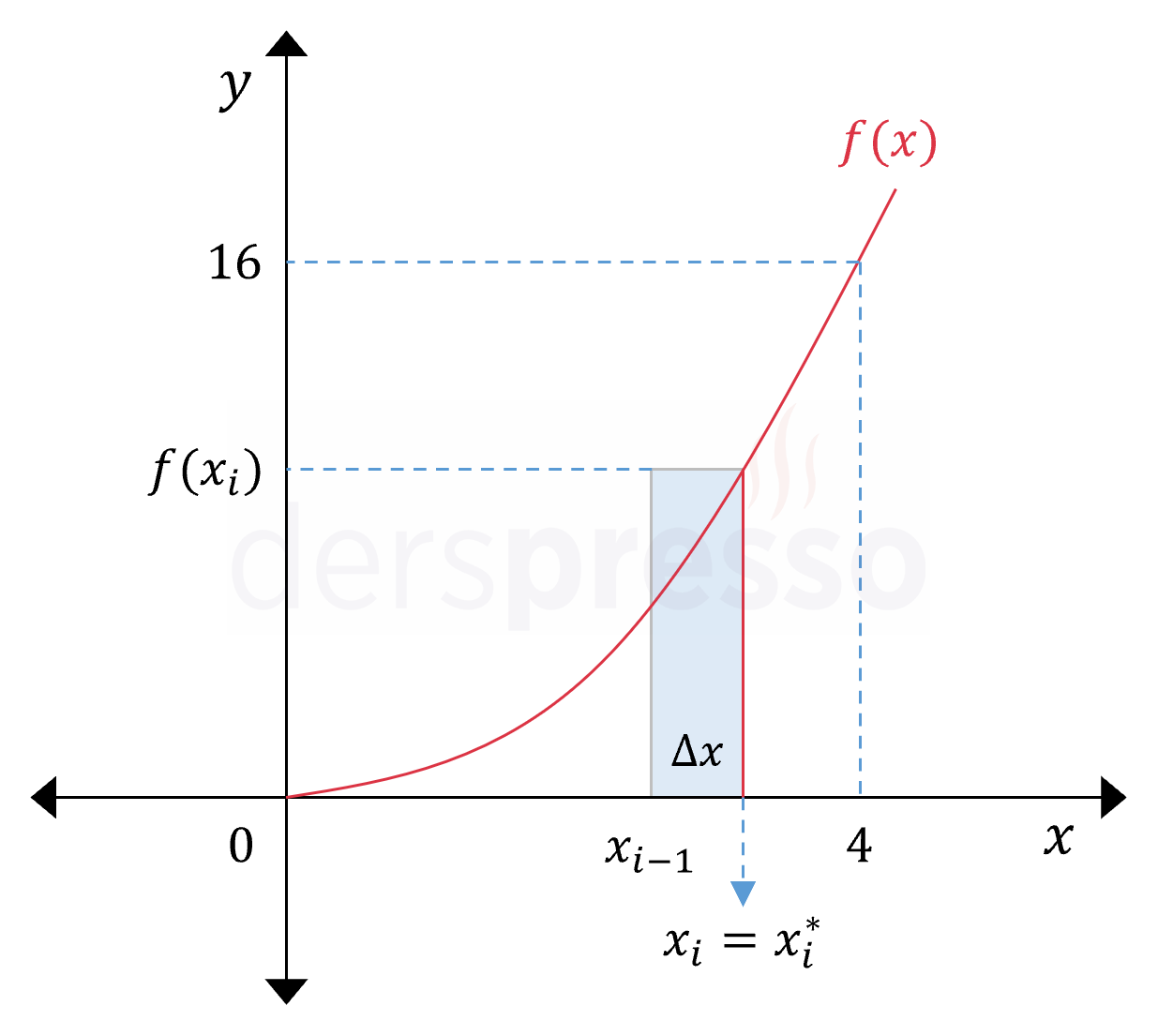
Buna göre \( i. \) aralığın üst sınırı \( x = 0 \) noktasından \( \Delta x \cdot i \) uzaklıkta olur.
\( x_i^* = 0 + \Delta x \cdot i = \dfrac{4i}{n} \)
\( f(x_i^*) = (\dfrac{4i}{n})^2 \)
Bu değerleri Riemann toplam formülünde yerine koyalım.
\( S_n = \displaystyle\sum_{i = 1}^{n}{(\dfrac{4i}{n})^2 \cdot \dfrac{4}{n}} \)
\( = \displaystyle\sum_{i = 1}^{n}{\dfrac{64i^2}{n^3}} \)
\( n \) bu ifadede sabit bir sayı olduğu için toplamın dışına alabiliriz.
\( = \dfrac{64}{n^3} \cdot \displaystyle\sum_{i = 1}^{n}{i^2} \)
Diziler konusunda gördüğümüz toplam formüllerini kullanalım.
\( \displaystyle\sum_{i = 1}^{n}{i^2} = \dfrac{n \cdot (n + 1) \cdot (2n + 1)}{6} \)
\( = \dfrac{64}{n^3} \cdot \dfrac{n \cdot (n + 1) \cdot (2n + 1)}{6} \)
\( = \dfrac{64}{n^3} \cdot \dfrac{2n^3 + 3n^2 + n}{6} \)
\( = \dfrac{64n^3 + 96n^2 + 32n}{3n^3} \)
Buna göre \( f \) fonksiyonunun \( [0, 4] \) aralığının \( n \) eşit aralığa bölündüğü durum için sağ Riemann toplamını veren formül aşağıdaki gibi olur.
\( S_n = \dfrac{64}{3} + \dfrac{32}{n} + \dfrac{32}{3n^2} \)
Aralığı 20 eşit aralığa böldüğümüz durumda hesaplanacak sağ Riemann toplamını bulmak için formülde \( n = 20 \) koyalım.
\( S_{20} = \dfrac{64}{3} + \dfrac{32}{20} + \dfrac{32}{3(20)^2} \)
\( = 22,96 \)
Aralığı 50 eşit aralığa böldüğümüz durumda hesaplanacak sağ Riemann toplamını bulmak için formülde \( n = 50 \) koyalım.
\( S_{50} = \dfrac{64}{3} + \dfrac{32}{50} + \dfrac{32}{3(50)^2} \)
\( = 21,9776 \)
Aralığı 100 eşit aralığa böldüğümüz durumda hesaplanacak sağ Riemann toplamını bulmak için formülde \( n = 100 \) koyalım.
\( S_{100} = \dfrac{64}{3} + \dfrac{32}{100} + \dfrac{32}{3(100)^2} \)
\( = 21,6544 \)
\( f(x) = x^2 \) fonksiyonunun \( [0, 4] \) aralığının \( n \) eşit aralığa bölündüğü durum için sol Riemann toplamını veren bir formül yazın ve \( n = 200 \), \( n = 500 \) ve \( n = 1000 \) için sol Riemann toplamını hesaplayın.
Çözümü GösterÖnce Riemann toplam formülünü yazalım.
\( S_n = \sum_{i = 1}^{n}{f(x_i^*) \cdot \Delta x_i} \)
\( [0, 4] \) aralığını \( n \) eşit aralığa bölelim. Aralıklar eşit genişlikte olduğu için \( \Delta x \) değerini sabit olarak alabiliriz.
\( \Delta x = \dfrac{4 - 0}{n} = \dfrac{4}{n} \)
Sol Riemann toplamı yönteminde \( i \). aralıkta dikdörtgenin yüksekliği için kullanacağımız \( x_i^* \) değeri aralığın alt sınırının apsis değeri olur.
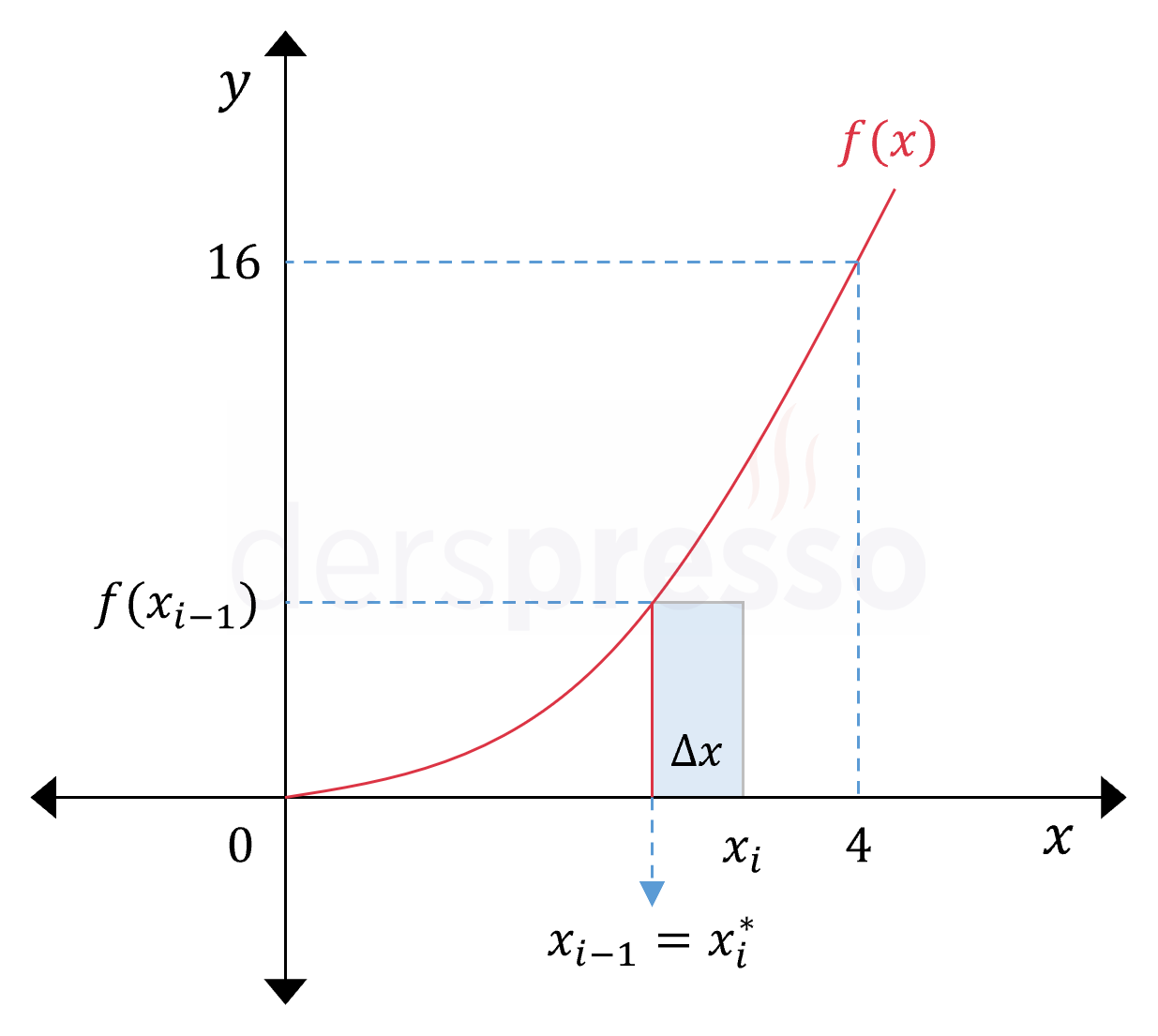
Buna göre \( i. \) aralığın üst sınırı \( x = 0 \) noktasından \( \Delta x \cdot (i - 1) \) uzaklıkta olur.
\( x_i^* = 0 + \Delta x \cdot (i - 1) = \dfrac{4(i - 1)}{n} \)
\( f(x_i^*) = (\dfrac{4(i - 1)}{n})^2 \)
Bu değerleri Riemann toplam formülünde yerine koyalım.
\( S_n = \displaystyle\sum_{i = 1}^{n}{(\dfrac{4(i - 1)}{n})^2 \cdot \dfrac{4}{n}} \)
\( = \displaystyle\sum_{i = 1}^{n}{\dfrac{64(i - 1)^2}{n^3}} \)
\( n \) bu ifadede sabit bir sayı olduğu için toplamın dışına alabiliriz.
\( = \dfrac{64}{n^3} \cdot \displaystyle\sum_{i = 1}^{n}{(i - 1)^2} \)
Diziler konusunda gördüğümüz toplam formüllerini kullanalım.
\( = \dfrac{64}{n^3} \cdot \dfrac{(n - 1) \cdot n \cdot (2(n - 1) + 1)}{6} \)
\( = \dfrac{64}{n^3} \cdot \dfrac{2n^3 - 3n^2 + n}{6} \)
\( = \dfrac{64n^3 - 96n^2 + 32n}{3n^3} \)
Buna göre \( f \) fonksiyonunun \( [0, 4] \) aralığının \( n \) eşit aralığa bölündüğü durum için sol Riemann toplamını veren formül aşağıdaki gibi olur.
\( S_n = \dfrac{64}{3} - \dfrac{32}{n} + \dfrac{32}{3n^2} \)
Aralığı 200 eşit aralığa böldüğümüz durumda hesaplanacak sol Riemann toplamını bulmak için formülde \( n = 200 \) koyalım.
\( S_{200} = \dfrac{64}{3} - \dfrac{32}{200} + \dfrac{32}{3(200)^2} \)
\( = 21,1736 \)
Aralığı 500 eşit aralığa böldüğümüz durumda hesaplanacak sol Riemann toplamını bulmak için formülde \( n = 500 \) koyalım.
\( S_{500} = \dfrac{64}{3} - \dfrac{32}{500} + \dfrac{32}{3(500)^2} \)
\( = 21,269376 \)
Aralığı 1000 eşit aralığa böldüğümüz durumda hesaplanacak sol Riemann toplamını bulmak için formülde \( n = 1000 \) koyalım.
\( S_{1000} = \dfrac{64}{3} - \dfrac{32}{1000} + \dfrac{32}{3(1000)^2} \)
\( = 21,301344 \)