Mutlak Değerli İfadelerin İntegrali
Konu tekrarı için: Mutlak Değerli İfadelerin Parçalı Yazılışı
Mutlak değerli ifadelerin tek adımda integralini alabileceğimiz bir integral kuralı yoktur, bunun sebebi mutlak değerli ifadelerin aslında farklı aralıklarda farklı tanımlara sahip birer parçalı fonksiyon olmalarıdır.
Bir mutlak değer fonksiyonunun integralini alırken önce tüm mutlak değerli ifadelerin içini sıfır yapan \( x \) değerleri bulunur. Bu değerler fonksiyonun kritik noktalarıdır. Daha sonra fonksiyon bir parçalı fonksiyon şeklinde yazılır ya da bir işaret tablosu yardımıyla fonksiyonun farklı aralıklardaki tanımları belirlenir. Her iki yöntemde de amacımız her aralıkta fonksiyon tanımını mutlak değersiz bir şekilde ifade etmektir.
- Eğer fonksiyonun bir kritik noktasını içeren bir aralıkta integrali alınıyorsa integral işlemi her biri kritik noktaların ayırdığı tek bir aralığa karşılık gelecek şekilde birden fazla integral işleminin toplamı şeklinde yazılır.
- Eğer integral işleminin sınır değerleri fonksiyonun tek bir aralığına karşılık geliyorsa bu tanım kullanılarak integral alınır.
Mutlak değerli bir ifadenin belirli integralini nasıl hesaplayabileceğimizi bir örnek üzerinden gösterelim.
\( \displaystyle\int_0^5 \abs{2x - 6}\ dx \) integralinin sonucu kaçtır?
\( 2x - 6 = 0 \Longrightarrow x = 3 \)
Buna göre fonksiyonun kritik noktası \( x = 3 \) noktasıdır.
Bu kritik noktanın oluşturduğu farklı aralıklarda mutlak değer içindeki ifadenin işareti ve fonksiyon tanımı aşağıdaki gibi olur.
Bu kritik nokta integral sınır değerleri arasında kaldığı için integral işlemini her biri fonksiyonun tek bir tanımına karşılık gelecek şekilde birden fazla integral işleminin toplamı şeklinde yazalım.
\( \displaystyle\int_0^5 \abs{2x - 6}\ dx = \displaystyle\int_0^3 (-2x + 6)\ dx + \displaystyle\int_3^5 (2x - 6)\ dx \)
İfadenin integralini alalım.
\( = (-x^2 + 6x)|_0^3 + (x^2 - 6x)|_3^5 \)
Sınır değerlerini yerine koyarak belirli integral değerini bulalım.
\( = [(-3^2 + 6(3)) \) \( - (-0^2 + 6(0))] \) \( + [(5^2 - 6(5)) \) \( - (3^2 - 6(3))] \)
\( = (9 - 0) + (-5 - (-9)) \)
\( = 13 \) bulunur.
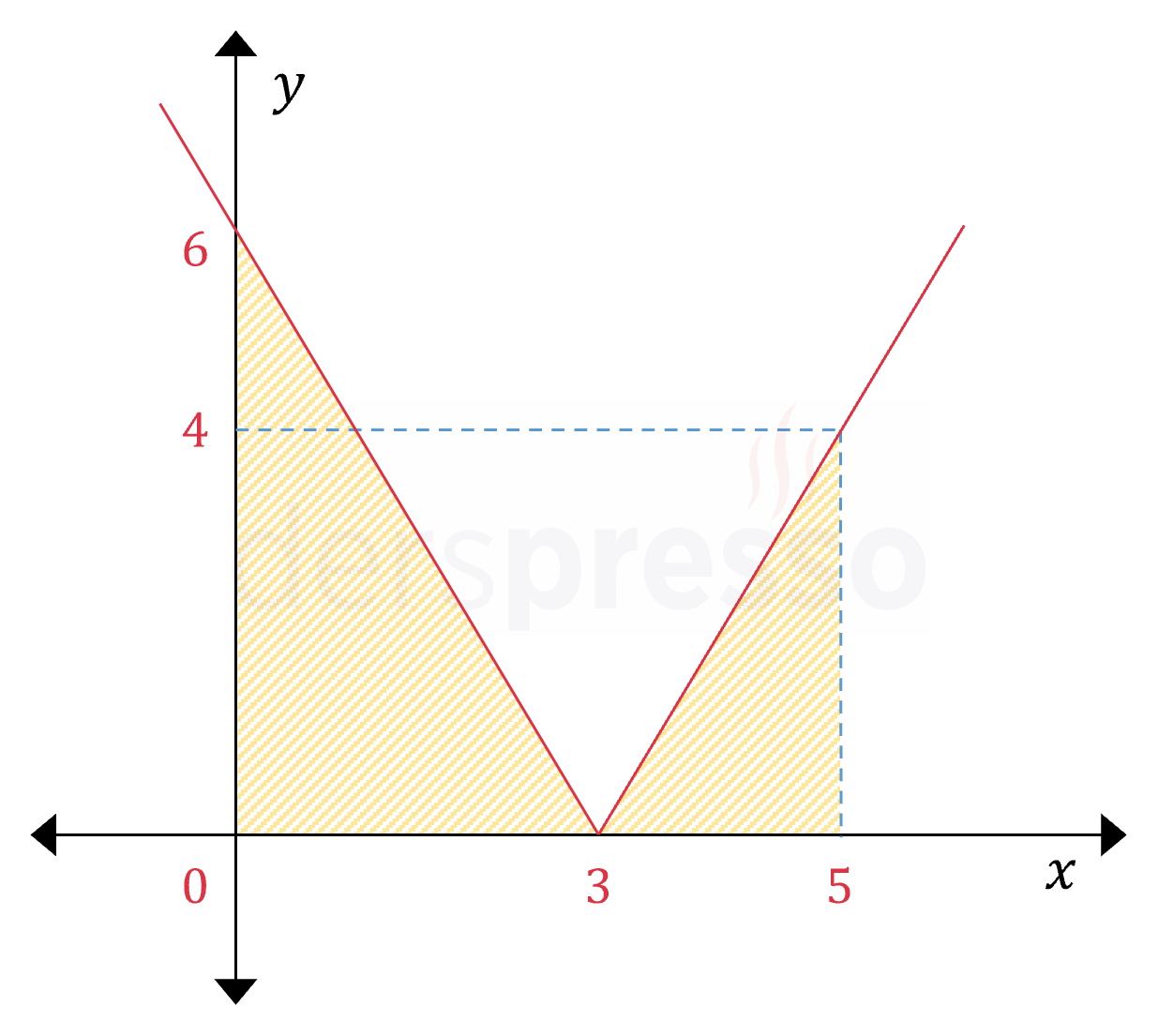
Mutlak değerli fonksiyonun grafiği ve her aralıkta belirli integralin karşılık geldiği alanlar aşağıdaki şekilde gösterilmiştir.
Bir mutlak değerli ifadenin birden fazla kritik noktası olabilir.
\( \displaystyle\int_{-2}^2 \abs{x^2 - 2x - 3}\ dx \) integralinin sonucu kaçtır?
\( x^2 - 2x - 3 = 0 \Longrightarrow x \in \{-1, 3\} \)
Buna göre fonksiyonun kritik noktaları \( x = -1 \) ve \( x = 3 \) noktalarıdır.
Bu kritik noktaların oluşturduğu farklı aralıklarda mutlak değer içindeki ifadenin işareti ve fonksiyon tanımı aşağıdaki gibi olur.
Bu kritik noktalardan \( x = -1 \) integral sınır değerleri arasında kaldığı için integral işlemini her biri fonksiyonun tek bir tanımına karşılık gelecek şekilde birden fazla integral işleminin toplamı şeklinde yazalım.
\( \displaystyle\int_{-2}^2 \abs{x^2 - 2x - 3}\ dx = \displaystyle\int_{-2}^{-1} (x^2 - 2x - 3)\ dx + \displaystyle\int_{-1}^2 (-x^2 + 2x + 3)\ dx \)
İfadenin integralini alalım.
\( = (\dfrac{x^3}{3} - x^2 - 3x)|_{-2}^{-1} + (-\dfrac{x^3}{3} + x^2 + 3x)|_{-1}^2 \)
Sınır değerlerini yerine koyarak belirli integral değerini bulalım.
\( = [(\dfrac{(-1)^3}{3} - (-1)^2 - 3(-1)) \) \( - (\dfrac{(-2)^3}{3} - (-2)^2 - 3(-2))] \) \( + [(-\dfrac{2^3}{3} + 2^2 + 3(2)) \) \( - (-\dfrac{(-1)^3}{3} + (-1)^2 + 3(-1))] \)
\( = (\dfrac{5}{3} - (-\dfrac{2}{3})) + (\dfrac{22}{3} - (-\dfrac{5}{3})) \)
\( = \dfrac{34}{3} \) bulunur.
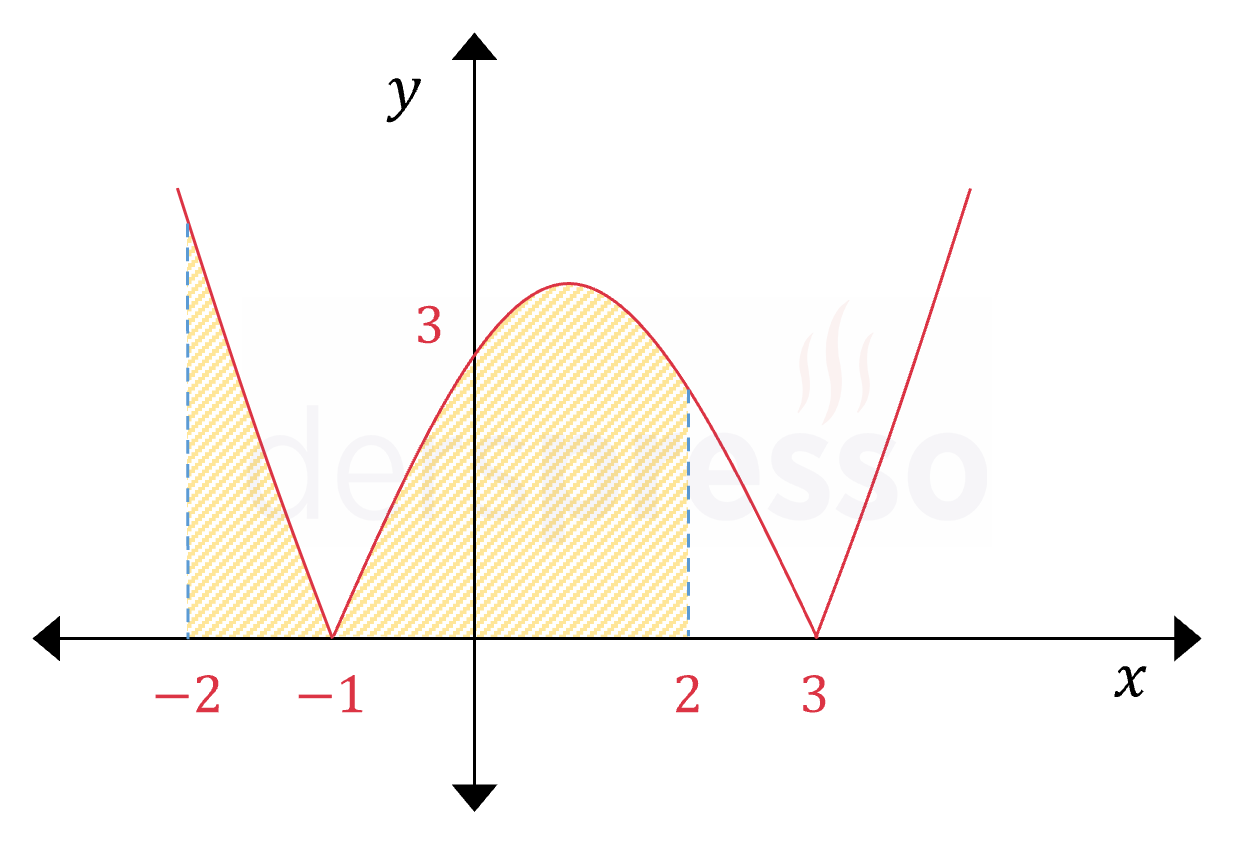
Mutlak değerli fonksiyonun grafiği ve her aralıkta belirli integralin karşılık geldiği alanlar aşağıdaki şekilde gösterilmiştir.
Birden fazla mutlak değerden oluşan bir ifadenin belirli integralini de benzer bir yöntemle hesaplayabiliriz.
\( \displaystyle\int_{-2}^3 (\abs{x + 1} + \abs{6 - 3x} - 7)\ dx \) integralinin sonucu kaçtır?
\( x + 1 = 0 \Longrightarrow x = -1 \)
\( 6 - 3x = 0 \Longrightarrow x = 2 \)
Buna göre fonksiyonun kritik noktaları \( x = -1 \) ve \( x = 2 \) noktalarıdır.
Bu kritik noktaların oluşturduğu farklı aralıklarda mutlak değer içindeki ifadenin işareti ve fonksiyon tanımı aşağıdaki gibi olur.
Bu kritik noktaların ikisi de integral sınır değerleri arasında kaldığı için integral işlemini her biri fonksiyonun tek bir tanımına karşılık gelecek şekilde birden fazla integral işleminin toplamı şeklinde yazalım.
\( \displaystyle\int_{-2}^3 (\abs{x + 1} + \abs{6 - 3x} - 7)\ dx \) \( = \displaystyle\int_{-2}^{-1} (-4x - 2)\ dx \) \( + \displaystyle\int_{-1}^2 (-2x)\ dx \) \( + \displaystyle\int_2^3 (4x - 12)\ dx \)
İfadenin integralini alalım.
\( = (-2x^2 - 2x)|_{-2}^{-1} + (-x^2)|_{-1}^2 + (2x^2 - 12x)|_2^3 \)
Sınır değerlerini yerine koyarak belirli integral değerini bulalım.
\( = [(-2(-1)^2 - 2(-1)) - (-2(-2)^2 - 2(-2))] \) \( + [(-2^2) - (-(-1)^2)] \) \( + [(2(3)^2 - 12(3)) - (2(2)^2 - 12(2))] \)
\( = (0 - (-4)) + (-4 - (-1)) + (-18 - (-16))\)
\( = 4 - 3 - 2 = -1 \) bulunur.
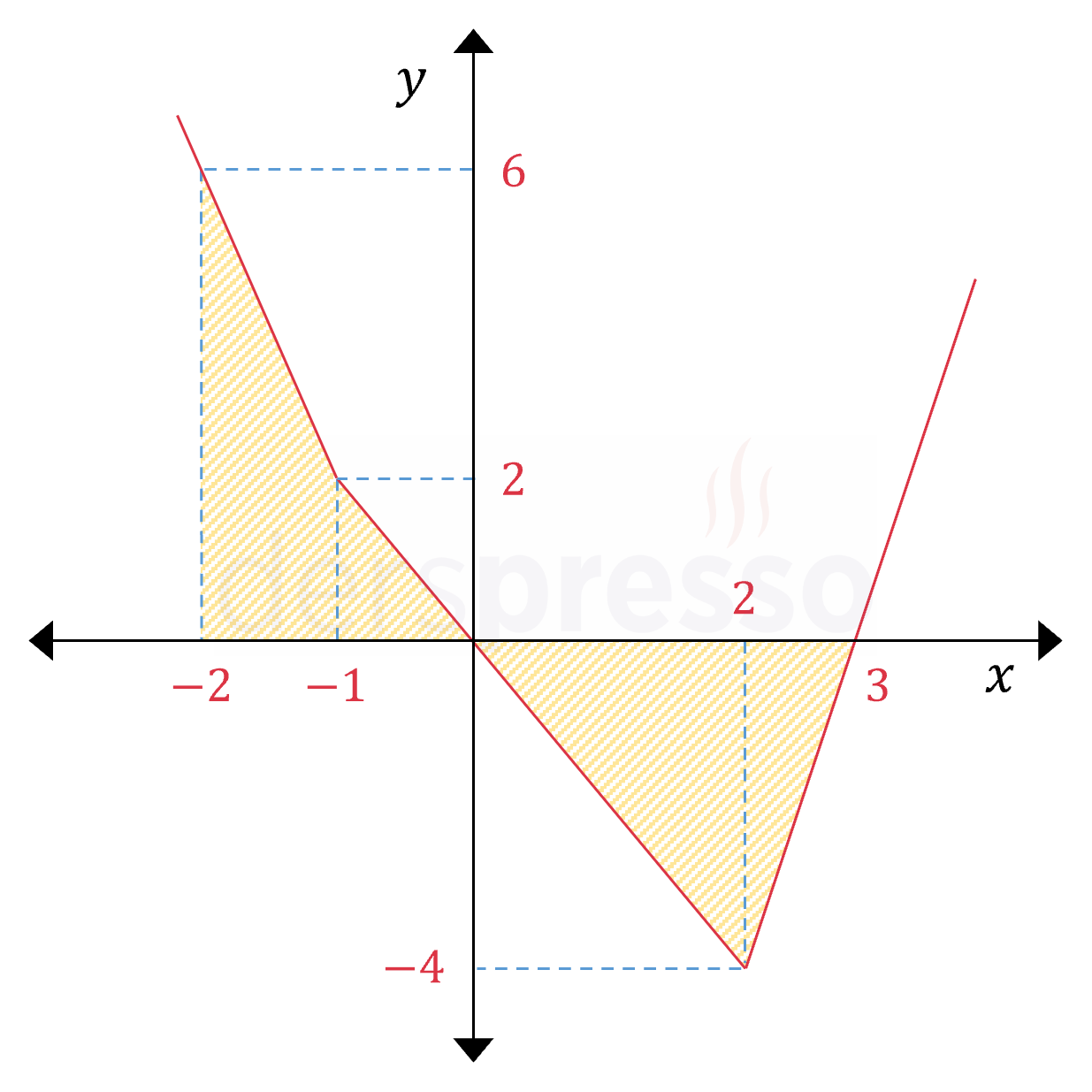
Mutlak değerli fonksiyonun grafiği ve her aralıkta belirli integralin karşılık geldiği alanlar aşağıdaki şekilde gösterilmiştir.
\( \displaystyle\int_{-2}^4 x\abs{x^2 - 9}\ dx \) integralinin sonucu kaçtır?
Çözümü GösterBir mutlak değer ifadesinin içini sıfır yapan değerler o ifadenin kritik noktalarıdır.
Mutlak değer ifadesinin kritik noktasını bulalım.
\( \abs{x^2 - 9} = 0 \Longrightarrow x \in \{-3, 3\} \)
Buna göre integrali alınan mutlak değer ifadesinin kritik noktaları \( x = -3 \) ve \( x = 3 \) noktalarıdır.
İntegral ifadesini bu kritik noktalara göre üç aralığa bölelim ve her aralıktaki \( x \) değerine göre ifadeleri mutlak değerden çıkaralım.
\( -2 \le x \lt 3 \) için:
Bu aralıkta mutlak değer içindeki ifade negatif olur, dolayısıyla mutlak değerden negatif işaretli çıkar.
\( \displaystyle\int_{-2}^3 (9x - x^3)\ dx \)
\( = (\dfrac{9x^2}{2} - \dfrac{x^4}{4})|_{-2}^3 \)
\( = (\dfrac{9(3)^2}{2} - \dfrac{3^4}{4}) - (\dfrac{9(-2)^2}{2} - \dfrac{(-2)^4}{4}) \)
\( = (\dfrac{81}{2} - \dfrac{81}{4}) - (18 - 4) \)
\( = \dfrac{81}{4} - 14 = \dfrac{25}{4} \)
\( 3 \le x \lt 4 \) için:
Bu aralıkta mutlak değer içindeki ifade pozitiftir olur, dolayısıyla mutlak değerden olduğu gibi çıkar.
\( \displaystyle\int_3^4 (x^3 - 9x)\ dx \)
\( = (\dfrac{x^4}{4} - \dfrac{9x^2}{2})|_3^4 \)
\( = (\dfrac{4^4}{4} - \dfrac{9(4)^2}{2}) - (\dfrac{3^4}{4} - \dfrac{9(3)^2}{2}) \)
\( = (64 - 72) - (\dfrac{81}{4} - \dfrac{81}{2}) \)
\( = -8 + \dfrac{81}{4} = \dfrac{49}{4} \)
İstenen integral değeri bu iki aralıktaki integral değerlerinin toplamına eşittir.
\( \dfrac{25}{4} + \dfrac{49}{4} = \dfrac{37}{2} \) bulunur.
\( \displaystyle\int_{-5}^5 x\abs{x - 2}\ dx \) integralinin sonucu kaçtır?
Çözümü GösterBir mutlak değer ifadesinin içini sıfır yapan değerler o ifadenin kritik noktalarıdır.
Mutlak değer ifadesinin kritik noktasını bulalım.
\( x - 2 = 0 \Longrightarrow x = 2 \)
İntegral ifadesini bu kritik noktaya göre iki aralığa bölelim ve her aralıktaki \( x \) değerine göre ifadeleri mutlak değerden çıkaralım.
\( \displaystyle\int_{-5}^5 x\abs{x - 2}\ dx = \displaystyle\int_{-5}^2 x(2 - x)\ dx \) \( + \displaystyle\int_2^5 x(x - 2)\ dx \)
\( = \displaystyle\int_{-5}^2 (2x - x^2)\ dx + \displaystyle\int_2^5 (x^2 - 2x)\ dx \)
İfadelerin integralini alalım.
\( = (x^2 - \dfrac{x^3}{3})|_{-5}^2 + (\dfrac{x^3}{3} - x^2)|_2^5 \)
\( = [(2^2 - \dfrac{2^3}{3}) - ((-5)^2 - \dfrac{(-5)^3}{3})] \) \( + [(\dfrac{5^3}{3} - 5^2) - (\dfrac{2^3}{3} - 2^2)] \)
\( = [(4 - \dfrac{8}{3}) - (25 + \dfrac{125}{3})] \) \( + [(\dfrac{125}{3} - 25) - (\dfrac{8}{3} - 4)] \)
\( = -\dfrac{196}{3} + 18 = -\dfrac{142}{3} \) bulunur.
\( \displaystyle\int_{-2}^3 \abs{e^x - e}\ dx \) integralinin sonucu nedir?
Çözümü GösterBir mutlak değer ifadesinin içini sıfır yapan değerler o ifadenin kritik noktalarıdır.
Mutlak değer ifadesinin kritik noktasını bulalım.
\( e^x - e = 0 \Longrightarrow x = 1 \)
Kritik noktanın solunda ve sağında mutlak değer içindeki ifadenin işareti farklı olacağı için integrali birden fazla integral işleminin toplamı şeklinde yazalım.
\( -2 \le x \lt 1 \) aralığında \( e^x - e \) ifadesi mutlak değerden negatif işaretli çıkar.
\( 1 \lt x \le 3 \) aralığında \( e^x - e \) ifadesi mutlak değerden olduğu gibi çıkar.
\( \displaystyle\int_{-2}^3 \abs{e^x - e}\ dx \)
\( = \displaystyle\int_{-2}^1 (e - e^x)\ dx + \displaystyle\int_1^3 (e^x - e)\ dx \)
İfadelerin integralini alalım.
\( = (ex - e^x)|_{-2}^1 + (e^x - ex)|_1^3 \)
\( = [(1e - e^1) - (-2e - e^{-2})] + [(e^3 - 3e) - (e^1 - 1e)] \)
\( = 0 - (-2e - \dfrac{1}{e^2}) + (e^3 - 3e) - 0 \)
\( = e^3 - e + \dfrac{1}{e^2} \) bulunur.
\( \displaystyle\int_{-2}^4 \abs{3x} \cdot (2x - 3)\ dx \) integralinin sonucu nedir?
Çözümü GösterMutlak değer içindeki \( 3x \) ifadesini sıfır yapan \( x \) değerini bulalım.
\( 3x = 0 \Longrightarrow x = 0 \)
Bu kritik nokta integral sınır değerleri arasında kaldığı için integral işlemini her biri fonksiyonun tek bir tanımına karşılık gelecek şekilde birden fazla integral işleminin toplamı şeklinde yazalım.
\( x \lt 0 \) aralığında \( 3x \) ifadesinin değeri negatif olur ve mutlak değerden negatif işaretli çıkar. \( x \ge 0 \) aralığında \( 3x \) ifadesinin değeri sıfır ya da pozitif olur ve mutlak değerden olduğu gibi çıkar.
\( \displaystyle\int_{-2}^4 \abs{3x} \cdot (2x - 3)\ dx = \displaystyle\int_{-2}^0 -3x \cdot (2x - 3)\ dx + \displaystyle\int_0^4 3x \cdot (2x - 3)\ dx \)
\( = \displaystyle\int_{-2}^0 (-6x^2 + 9x)\ dx + \displaystyle\int_0^4 (6x^2 - 9x)\ dx \)
İfadelerin integralini alalım.
\( = (-2x^3 + \dfrac{9x^2}{2})|_{-2}^0 + (2x^3 - \dfrac{9x^2}{2})|_0^4 \)
\( = (-2(0)^3 + \dfrac{9(0)^2}{2}) - (-2(-2)^3 + \dfrac{9(-2)^2}{2}) \) \( + (2(4)^3 - \dfrac{9(4)^2}{2}) - (2(0)^3 - \dfrac{9(0)^2}{2}) \)
\( = 0 - (16 + 18) + (128 - 72) - 0 \)
\( = 22 \) bulunur.
\( \displaystyle\int_0^4 \abs{\abs{2 - x} - x}\ dx \) integralinin sonucu kaçtır?
Çözümü GösterBir mutlak değer ifadesinin içini sıfır yapan değerler o ifadenin kritik noktalarıdır.
İçteki mutlak değer ifadesinin kritik noktasını bulalım.
\( \abs{2 - x} = 0 \Longrightarrow x = 2 \)
Durum 1: \( x \lt 2 \)
Bu durumda içteki mutlak değer içindeki ifade pozitif olur ve mutlak değerden olduğu gibi çıkar.
\( 2 - x - x = 0 \Longrightarrow x = 1 \)
Durum 2: \( x \ge 2 \)
Bu durumda içteki mutlak değer içindeki ifade negatif olur ve mutlak değerden ters işaretli çıkar.
\( x - 2 - x = 0 \Longrightarrow \) Bu aralıkta kritik nokta yoktur.
Buna göre integrali alınan mutlak değer ifadesinin kritik noktaları \( x = 1 \) ve \( x = 2 \) noktalarıdır.
İntegral ifadesini bu kritik noktalara göre üç aralığa bölelim ve her aralıktaki \( x \) değerine göre ifadeleri mutlak değerden çıkaralım.
\( 0 \le x \lt 1 \) için:
\( \displaystyle\int_0^1 \abs{2 - x - x}\ dx = \displaystyle\int_0^1 (2 - 2x)\ dx \)
\( = (2x - x^2)|_0^1 \)
\( = (2(1) - 1^2) - (2(0) - 0^2) = 1 \)
\( 1 \le x \lt 2 \) için:
\( \displaystyle\int_1^2 \abs{2 - x - x}\ dx = \displaystyle\int_0^1 (2x - x)\ dx \)
\( = (x^2 - 2x)|_1^2 \)
\( = (2^2 - 2(2)) - (1^2 - 2(1)) = 1 \)
\( 2 \le x \lt 4 \) için:
\( \displaystyle\int_2^4 \abs{x - 2 - x}\ dx = \displaystyle\int_2^4 2\ dx \)
\( = (2x)|_2^4 \)
\( = 2(4) - 2(2) = 4 \)
Sorulan integral değeri bu üç aralıktaki integral değerlerinin toplamına eşittir.
\( 1 + 1 + 4 = 6 \) bulunur.
\( \displaystyle\int_0^{\frac{\pi}{2}} \abs{\sin{x} - \cos{x}}\ dx \) integralinin sonucu kaçtır?
Çözümü GösterSinüs grafiği \( (0, \frac{\pi}{4}) \) aralığında kosinüs grafiğinin altında, \( (\frac{\pi}{4}, \frac{\pi}{2}) \) aralığında üstünde kalır.
Mutlak değerden kurtulmak için ifadeyi daha büyük olan fonksiyondan daha küçük olan fonksiyonu çıkaracak şekilde bu iki aralık için ayrı ayrı yazalım.
\( \displaystyle\int_0^{\frac{\pi}{2}} \abs{\sin{x} - \cos{x}}\ dx \) \( = \displaystyle\int_0^{\frac{\pi}{4}} (\cos{x} - \sin{x})\ dx \) \( + \displaystyle\int_{\frac{\pi}{4}}^{\frac{\pi}{2}} (\sin{x} - \cos{x})\ dx \)
İfadenin integralini alalım.
\( = (\sin{x} + \cos{x})|_0^{\frac{\pi}{4}} \) \( + (-\cos{x} - \sin{x})|_{\frac{\pi}{4}}^{\frac{\pi}{2}} \)
\( = [(\sin{\frac{\pi}{4}} + \cos{\frac{\pi}{4}}) \) \( - (\sin{0} + \cos{0})] \) \( + [(-\cos{\frac{\pi}{2}} \) \( - \sin{\frac{\pi}{2}}) \) \( - (-\cos{\frac{\pi}{4}} - \sin{\frac{\pi}{4}})] \)
\( = [(\frac{\sqrt{2}}{2} \) \( + \frac{\sqrt{2}}{2}) \) \( - (0 + 1)] + [(-0 - 1) \) \( - (-\frac{\sqrt{2}}{2} \) \( - \frac{\sqrt{2}}{2})] \)
\( = 2\sqrt{2} - 2 \) bulunur.