Mutlak Değer Fonksiyonunun Parçalı Yazılışı
Mutlak değer fonksiyonları mutlak değer içindeki ifadelerin pozitif ya da negatif olma durumuna göre farklı davranış gösterdikleri için birer parçalı fonksiyon şeklinde yazılabilirler.
Mutlak değer içinin \( ax + b \) şeklinde doğrusal bir ifade olduğu durumda, mutlak değer fonksiyonu aşağıdaki adımlar takip edilerek parçalı fonksiyon şeklinde yazılabilir.
- Önce mutlak değer içini sıfır yapan \( x \) değeri bulunur. Bu değere mutlak değerli ifadenin kritik noktası denir. Bu kritik nokta fonksiyonu her birinin tanımı farklı olan iki parçaya ayırır.
- \( x \) bu kritik değere eşit olduğunda mutlak değer içindeki ifade sıfır olur, dolayısıyla ifade mutlak değer dışına olduğu gibi çıkar.
- \( x \)'in katsayısı pozitif ise \( x \) bu kritik değerden büyük olduğunda, \( x \)'in katsayısı negatif ise de küçük olduğunda mutlak değer içindeki ifade pozitif olur, dolayısıyla ifade mutlak değer dışına olduğu gibi çıkar.
- \( x \)'in katsayısı pozitif ise \( x \) bu kritik değerden küçük olduğunda, \( x \)'in katsayısı negatif ise de büyük olduğunda mutlak değer içindeki ifade negatif olur, dolayısıyla ifade mutlak değer dışına negatif işaretli çıkar. Bu negatif işareti mutlak değer içindeki ifadenin negatif değerini pozitife çevirmektedir.
\( f(x) = \abs{2x - 6} \) ifadesini parçalı fonksiyon şeklinde yazalım.
Mutlak değerli bir ifadenin kritik noktası mutlak değer içini sıfır yapan \( x \) değeridir.
\( 2x - 6 = 0 \Longrightarrow x = 3 \) kritik noktadır.
Mutlak değer içindeki ifadede \( x \)'in katsayısı pozitif olduğu için, ifade kritik noktanın sağında pozitif, solunda negatif değer alır, kritik noktada ise sıfır olur.
Buna göre fonksiyonun parçalı fonksiyon tanımı aşağıdaki gibi olur.
\( f(x) = \begin{cases} 2x - 6 & x \ge 3 \\ 6 - 2x & x \lt 3 \end{cases} \)
Farklı \( x \) değerleri için fonksiyonun negatif değerleri pozitife çevirdiğini kontrol edelim.
\( f(5) = 2(5) - 6 = 4 \)
\( f(3) = 2(3) - 6 = 0 \)
\( f(1) = 6 - 2(1) = 4 \)
\( f(x) = \abs{8 - 4x} \) ifadesini parçalı fonksiyon şeklinde yazalım.
Mutlak değerli bir ifadenin kritik noktası mutlak değer içini sıfır yapan \( x \) değeridir.
\( 8 - 4x = 0 \Longrightarrow x = 2 \) kritik noktadır.
Mutlak değer içindeki ifadede \( x \)'in katsayısı negatif olduğu için, ifade kritik noktanın sağında negatif, solunda pozitif değer alır, kritik noktada ise sıfır olur.
Buna göre fonksiyonun bir kritik nokta ve iki aralıktan oluşan parçalı fonksiyon tanımı aşağıdaki gibi olur.
\( f(x) = \begin{cases} 4x - 8 & x \ge 2 \\ 8 - 4x & x \lt 2 \end{cases} \)
Farklı \( x \) değerleri için fonksiyonun negatif değerleri pozitife çevirdiğini kontrol edelim.
\( f(4) = 4(4) - 8 = 8 \)
\( f(2) = 4(2) - 8 = 0 \)
\( f(0) = 8 - 4(0) = 8 \)
Birden Fazla Mutlak Değerli İfadeler
Birden fazla mutlak değerli ifade içeren fonksiyonlarda her mutlak değerli ifadenin farklı kritik noktaları olabilir ve her kritik nokta parçalı fonksiyonda tanımları farklı yeni aralıkların oluşmasına sebep olur.
\( f(x) = \abs{x + 2} + \abs{3x - 9} \) ifadesini parçalı fonksiyon şeklinde yazalım.
Mutlak değerli bir ifadenin kritik noktası mutlak değer içini sıfır yapan \( x \) değeridir.
\( \abs{x + 2} \) ifadesi için:
\( x + 2 = 0 \Longrightarrow x = -2 \) kritik noktadır.
\( \abs{3x - 9} \) ifadesi için:
\( 3x - 9 = 0 \Longrightarrow x = 3 \) kritik noktadır.
Mutlak değer içindeki iki ifadede de \( x \)'in katsayısı pozitif olduğu için, ifadeler kritik noktanın sağında pozitif, solunda negatif değer alır, kritik noktada ise sıfır olur.
Buna göre fonksiyonun iki kritik nokta ve üç aralıktan oluşan parçalı fonksiyon tanımı aşağıdaki gibi olur.
\( f(x) = \begin{cases} 4x - 7 & x \ge 3 \\ -2x + 11 & -2 \le x \lt 3 \\ -4x + 7 & x \lt -2 \end{cases} \)
\( f(x) = 2\abs{4 - x} - \abs{2x + 2} \) ifadesini parçalı fonksiyon şeklinde yazalım.
Mutlak değerli bir ifadenin kritik noktası mutlak değer içini sıfır yapan \( x \) değeridir.
\( \abs{4 - x} \) ifadesi için:
\( 4 - x = 0 \Longrightarrow x = 4 \) kritik noktadır.
Bu ifadede \( x \)'in katsayısı negatif olduğu için, ifade kritik noktanın sağında negatif, solunda pozitif değer alır, kritik noktada ise sıfır olur.
\( \abs{2x + 2} \) ifadesi için:
\( 2x + 2 = 0 \Longrightarrow x = -1 \) kritik noktadır.
Bu ifadede \( x \)'in katsayısı pozitif olduğu için, ifade kritik noktanın sağında pozitif, solunda negatif değer alır, kritik noktada ise sıfır olur.
Buna göre fonksiyonun iki kritik nokta ve üç aralıktan oluşan parçalı fonksiyon tanımı aşağıdaki gibi olur.
\( f(x) = \begin{cases} -10 & x \ge 4 \\ -4x + 6 & -1 \le x \lt 4 \\ 10 & x \lt -1 \end{cases} \)
İkinci Dereceden İfadelerin Mutlak Değeri
İkinci dereceden ifadeler \( x \) eksenini iki kez kesebildikleri ve sıfır değerini iki kez alabildikleri için mutlak değer içinde yer aldıklarında iki kritik noktaya sahip olabilirler. Bu tip ifadelerin kritik noktalarını ve bu noktalar arasındaki işaretlerini bulabilmek için parabollerde kök ve grafik bilgisine ihtiyaç duyulur.
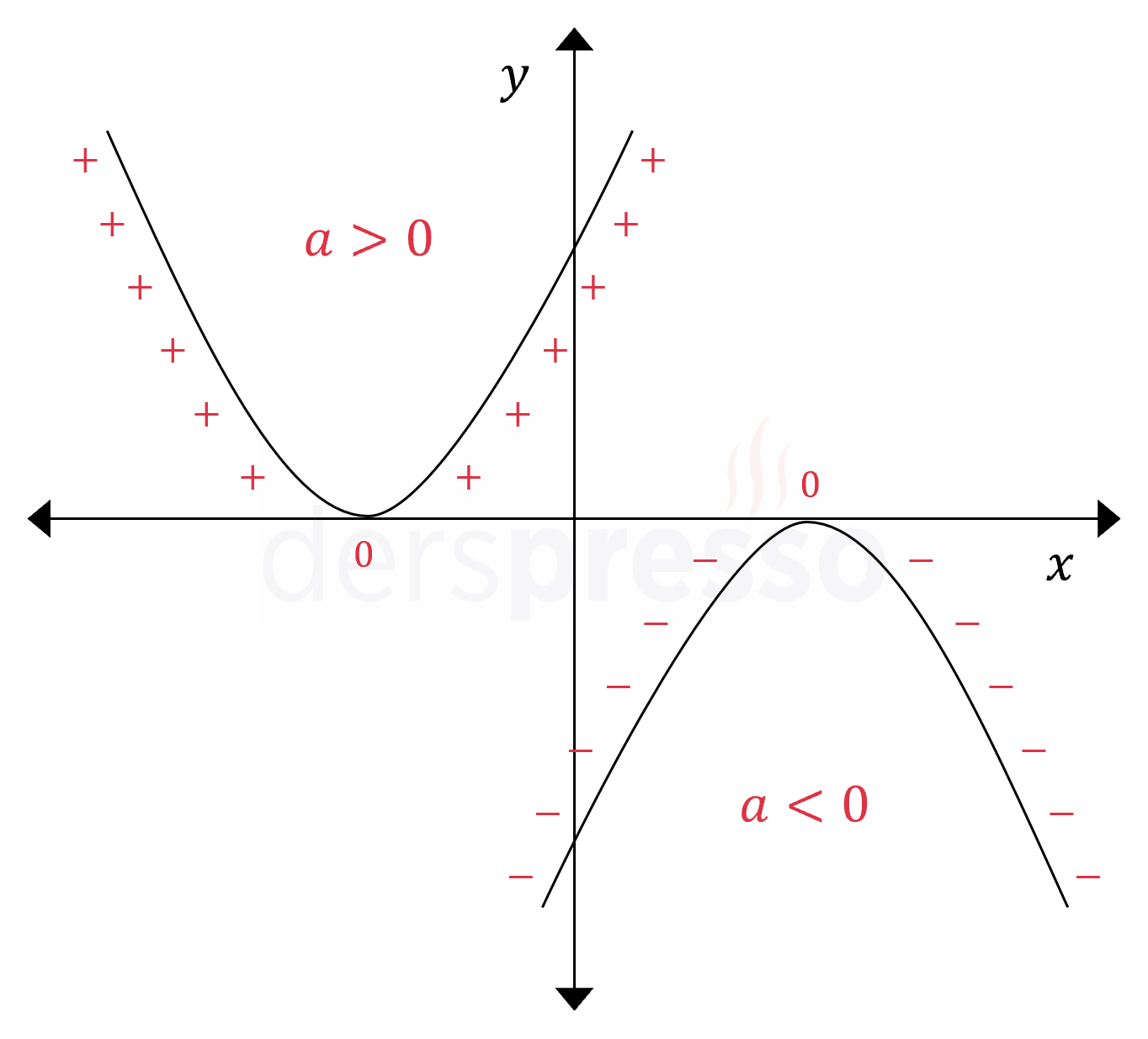
Bir parabolün deltası sıfırdan büyükse parabol \( x \) eksenini iki noktada keser ve mutlak değerli ifadenin iki kritik noktası olur. Başkatsayı pozitif ise parabolün kolları yukarı yönlü olduğu için parabol bu iki nokta arasında negatif değer alır (ifade mutlak değerden ters işaretli çıkar), dışında da pozitif değer alır (ifade mutlak değerden olduğu gibi çıkar). Başkatsayı negatif ise parabolün kolları aşağı yönlü olduğu için parabol bu iki nokta arasında pozitif değer alır (ifade mutlak değerden olduğu gibi çıkar), dışında da negatif değer alır (ifade mutlak değerden ters işaretli çıkar).
Parabolün deltası sıfır ise parabol \( x \) eksenini teğet keser. Başkatsayı pozitif ise parabol \( x \) ekseninin üstünde kaldığı için hiçbir noktada negatif değer almaz (ifade mutlak değerden olduğu gibi çıkar). Başkatsayı negatif ise parabol \( x \) ekseninin altında kaldığı için hiçbir noktada pozitif değer almaz (ifade mutlak değerden ters işaretli çıkar).
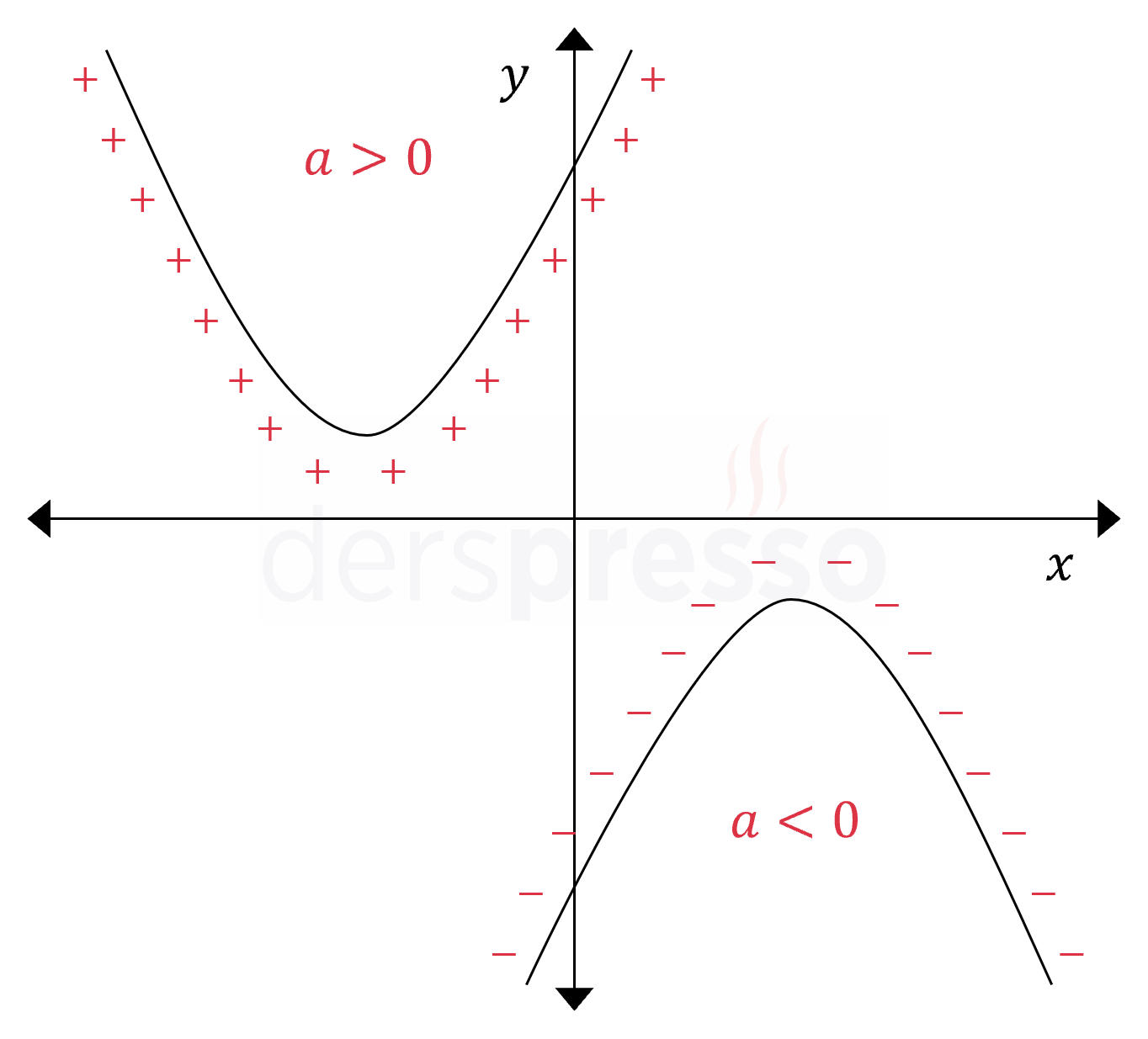
Parabolün deltası sıfırdan küçükse parabol \( x \) eksenini kesmez. Başkatsayı pozitif ise parabol \( x \) ekseninin üstünde kaldığı için tüm noktalarda pozitif değer alır (ifade mutlak değerden olduğu gibi çıkar). Başkatsayı negatif ise parabol \( x \) ekseninin altında kaldığı için tüm noktalarda negatif değer alır (ifade mutlak değerden ters işaretli çıkar).
\( f(x) = \abs{x^2 - x - 6} \) ifadesini parçalı fonksiyon şeklinde yazalım.
İkinci dereceden ifadeyi çarpanlarına ayıralım.
\( f(x) = \abs{(x + 2)(x - 3)} \)
Mutlak değerli bir ifadenin kritik noktaları mutlak değer içini sıfır yapan \( x \) değerleridir.
\( (x + 2)(x - 3) = 0 \Longrightarrow x = -2 \) ve \( x = 3 \) kritik noktalardır.
İkinci dereceden ifadenin iki kökü olduğu ve başkatsayısı pozitif olduğu için, ifade bu iki kritik nokta arasında negatif, dışında da pozitif değer alır.
Buna göre fonksiyonun iki kritik nokta ve üç aralıktan oluşan parçalı fonksiyon tanımı aşağıdaki gibi olur.
\( f(x) = \begin{cases} x^2 - x - 6 & x \ge 3 \\ -(x^2 - x - 6) & -2 \le x \lt 3 \\ x^2 - x - 6 & x \lt -2 \end{cases} \)
\( f(x) = \abs{x} + \abs{x + 2} \) mutlak değer fonksiyonunu parçalı fonksiyon biçiminde yazınız.
Çözümü GösterMutlak değerli ifadeleri sıfır yapan \( x \) değerleri fonksiyonun kritik noktalarıdır.
\( x = 0 \)
\( x + 2 = 0 \Longrightarrow x = -2 \)
Bu kritik noktalar arasında oluşan \( (-\infty, -2) \), \( [-2, 0) \) ve \( [0, \infty) \) aralıklarındaki fonksiyon tanımlarını bulalım.
\( x \lt -2 \) aralığında iki mutlak değerli ifadenin de içi dışarıya negatif işaretli çıkar.
\( f(x) = -x - (x + 2) = -2x - 2 \)
\( -2 \le x \lt 0 \) aralığında birinci mutlak değerli ifadenin içi dışarıya negatif işaretli, ikinci ifadenin içi olduğu gibi çıkar.
\( f(x) = -x + (x + 2) = 2 \)
\( x \ge 0 \) aralığında iki mutlak değerli ifadenin de içi dışarıya olduğu gibi çıkar.
\( f(x) = x + (x + 2) = 2x + 2 \)
Buna göre fonksiyonun parçalı fonksiyon şeklinde yazılışı aşağıdaki gibi olur.
\( f(x) = \begin{cases} -2x - 2 & x \lt -2 \\ 2 & -2 \le x \lt 0 \\ 2x + 2 & x \ge 0 \end{cases} \)