Polinom Fonksiyonu Grafikleri
Derece ve Başkatsayının Grafiğe Etkisi
Polinomlar farklı derecelerde ve katsayılarda olabilse de grafiklerinin davranışı bazı temel prensiplere dayanmaktadır. Polinom grafiklerini polinomun derecesinin tek ya da çift olmasına ve başkatsayının (\( a \)) sıfırdan büyük ya da küçük olmasına göre dört başlık altında inceleyebiliriz.
Çift Dereceli Polinomlar
Çift dereceli polinomların grafiklerinde \( x \) negatif ve pozitif sonsuza giderken \( y \) aynı yöne gider. Bu yön \( a \gt 0 \) için pozitif sonsuz, \( a \lt 0 \) için negatif sonsuzdur.
Çift dereceli polinomların grafiklerinin bu iki durumdaki davranışı aşağıdaki gibidir. Paraboller ikinci dereceden polinom fonksiyonları oldukları için bu davranışın parabol grafikleri için de geçerli olduğunu görebiliriz.
| Polinom Tipi | Grafik |
|---|---|
|
Çift dereceli polinom \( a \gt 0 \) |

|
|
Çift dereceli polinom \( a \lt 0 \) |

|
Tek Dereceli Polinomlar
Tek dereceli polinomların grafiklerinde \( x \) negatif ve pozitif sonsuza giderken \( y \) farklı yönlere gider. Bu yön \( a \gt 0 \) için \( x \) negatif sonsuza giderken negatif sonsuz, \( x \) pozitif sonsuza giderken pozitif sonsuzdur. \( a \lt 0 \) için yönler bunun tersidir.
Tek dereceli polinomların grafiklerinin bu iki durumdaki davranışı aşağıdaki gibidir.
| Polinom Tipi | Grafik |
|---|---|
|
Tek dereceli polinom \( a \gt 0 \) |
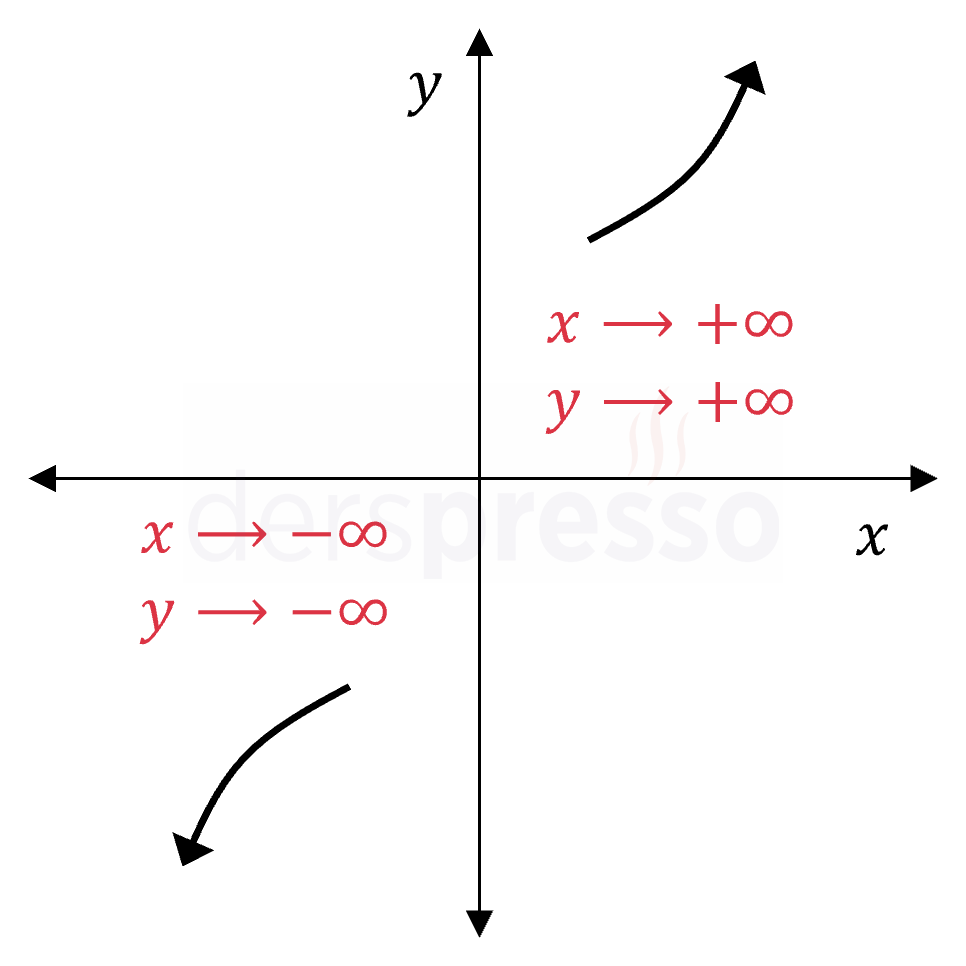
|
|
Tek dereceli polinom \( a \lt 0 \) |

|
2. Dereceden Polinomların (Parabol) Grafiği
Aşağıdaki 2. dereceden polinomların kökleri ile ilgili farklı durumlar verilmiştir. Verilen tüm grafikler \( a \gt 0 \) için olup, \( a \lt 0 \) olduğu durumlarda bu grafiklerin \( x \) eksenine göre yansımaları oluşacaktır.
\( f: \mathbb{R} \rightarrow \mathbb{R} \)
\( f(x) = ax^2 + bx + c \)
Tüm Köklerin Reel Olduğu Durumlar
2. dereceden bir polinomun tüm kökleri reel ise polinomun kökleri, katları ve grafikleri aşağıdaki şekillerde olabilir.
| Kökler ve Denklem | Grafik |
|---|---|
|
Tek katlı iki reel kök \( f(x) = a(x - x_1)(x - x_2) \) |

|
|
İki katlı bir reel kök \( f(x) = a(x - x_1)^2 \) |

|
Reel Olmayan Köklerin Olduğu Durumlar
2. dereceden bir polinomunun reel olmayan kökleri varsa, polinomun kökleri, katları ve grafikleri aşağıdaki şekilde olabilir. Bir denklemin reel olmayan kökleri varsa bu kökler hep ikişerli ve birbirinin eşleniği olur.
| Kökler ve Denklem | Grafik |
|---|---|
|
İki reel olmayan kök \( f(x) = ax^2 + bx + c \) |

|
2. dereceden polinomların grafikleri ile ilgili bazı önemli noktalar aşağıdaki gibidir.
- \( a \gt 0 \) ise grafik artı sonsuzdan gelip artı sonsuza gider.
- \( a \lt 0 \) ise grafik eksi sonsuzdan gelip eksi sonsuza gider.
- \( y \) eksenini her zaman ve sadece bir noktada keser.
- \( x \) eksenini en az sıfır, en fazla iki noktada keser.
- Bir yerel ekstremum noktası vardır.
- Tepe noktası etrafında simetriktir.
- Yatay doğru testini geçemediği için birebir değildir.
- \( \mathbb{R} \rightarrow \mathbb{R} \) için içinedir.
3. Dereceden Polinomların Grafiği
Aşağıdaki 3. dereceden polinomların kökleri ile ilgili farklı durumlar verilmiştir. Verilen tüm grafikler \( a \gt 0 \) için olup, \( a \lt 0 \) olduğu durumlarda bu grafiklerin \( x \) eksenine göre yansımaları oluşacaktır.
\( f: \mathbb{R} \rightarrow \mathbb{R} \)
\( f(x) = ax^3 + bx^2 + cx + d \)
Tüm Köklerin Reel Olduğu Durumlar
3. dereceden bir polinomun tüm kökleri reel ise polinomun kökleri, katları ve grafikleri aşağıdaki şekillerde olabilir.
| Kökler ve Denklem | Grafik |
|---|---|
|
Tek katlı üç reel kök \( f(x) = a(x - x_1)(x - x_2)(x - x_3) \) |
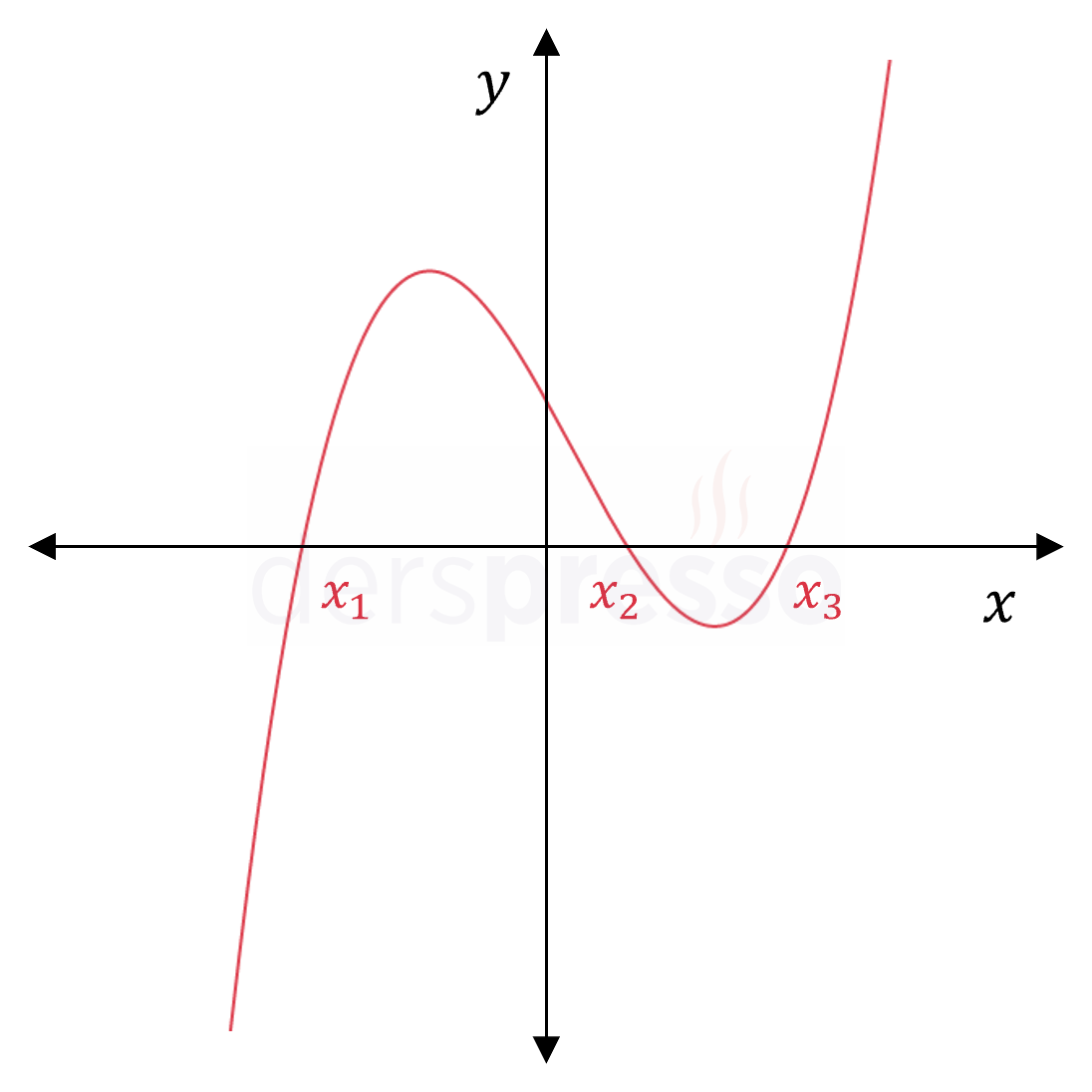
|
|
İki katlı bir reel kök + tek katlı bir reel kök \( f(x) = a(x - x_1)^2(x - x_2) \) |
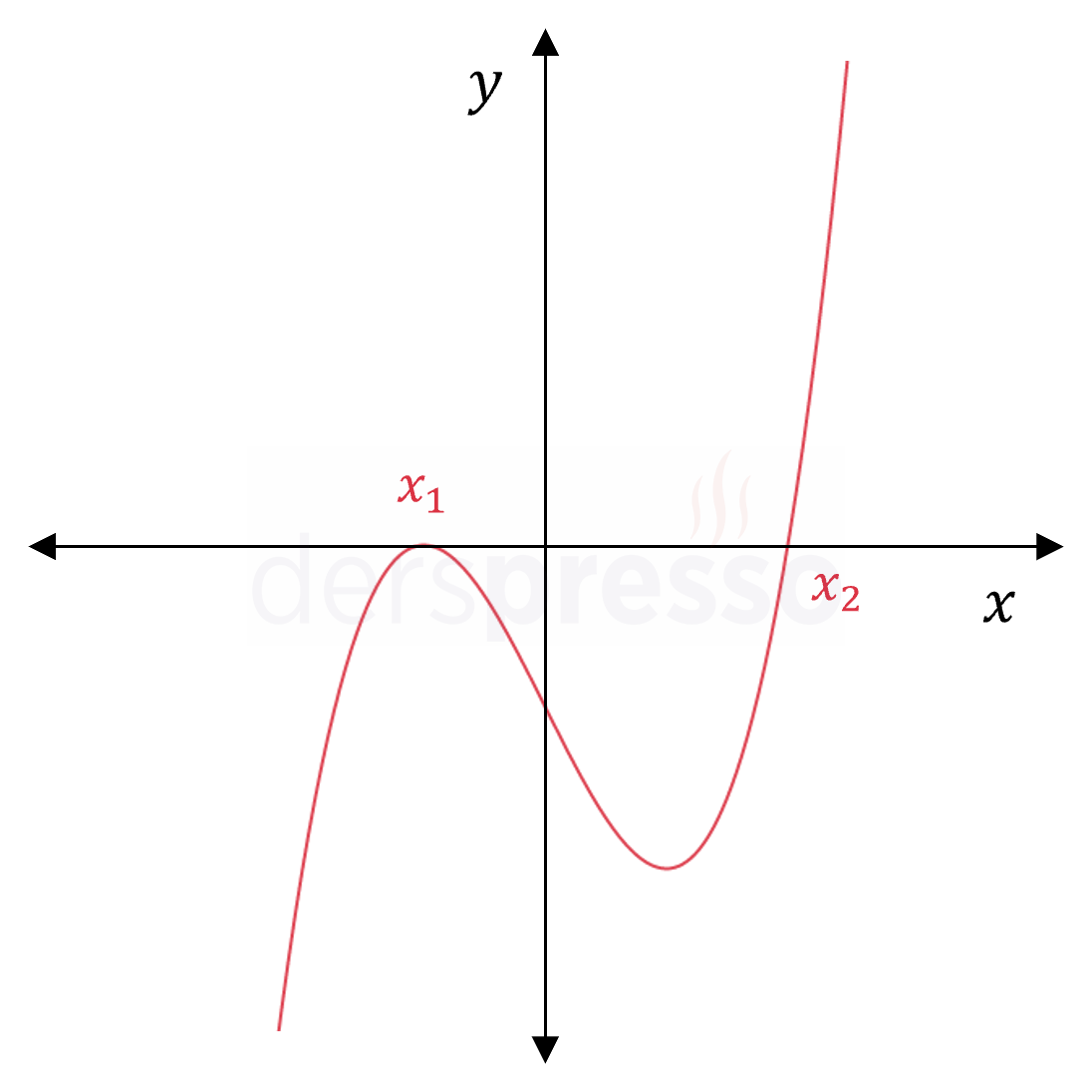
|
|
Üç katlı bir reel kök \( f(x) = a(x - x_1)^3 \) |

|
Reel Olmayan Köklerin Olduğu Durumlar
3. dereceden bir polinomunun reel olmayan kökleri varsa, polinomun kökleri, katları ve grafikleri aşağıdaki şekilde olabilir. Tek dereceli polinomlar \( x \) eksenini kesmek zorunda olduğu için, bu polinomların en azından bir reel kökü vardır. Bir denklemin reel olmayan kökleri varsa, bu kökler hep ikişerli ve birbirinin eşleniği olur.
| Kökler ve Denklem | Grafik |
|---|---|
|
Tek katlı bir reel kök + iki reel olmayan kök \( f(x) = a(x - x_1)(x^2 + bx + c) \) |
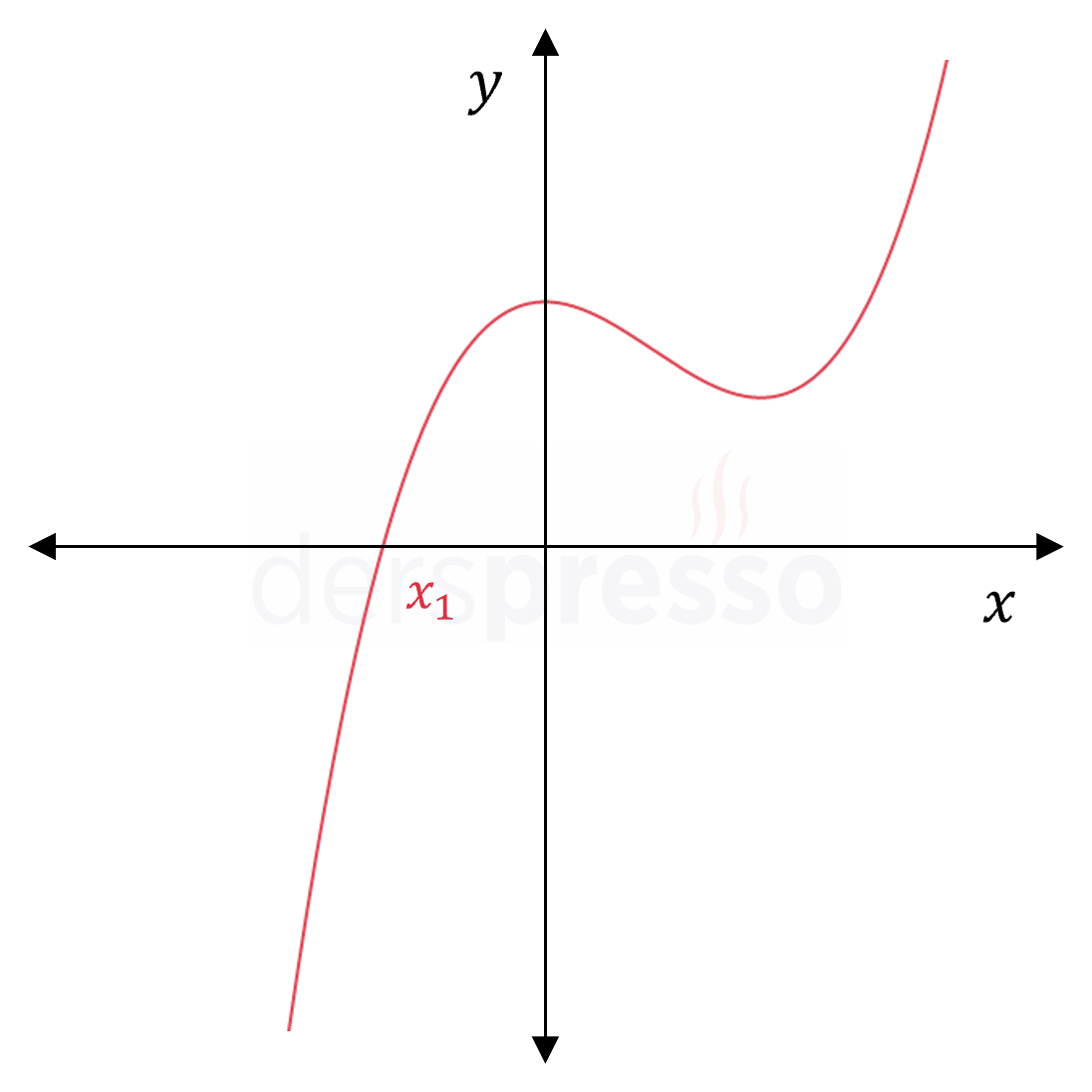
|
3. dereceden polinomların grafikleri ile ilgili bazı önemli noktalar aşağıdaki gibidir.
- \( a \gt 0 \) ise grafik eksi sonsuzdan gelip artı sonsuza gider.
- \( a \lt 0 \) ise grafik artı sonsuzdan gelip eksi sonsuza gider.
- \( y \) eksenini her zaman ve sadece bir noktada keser.
- \( x \) eksenini en az bir, en fazla üç noktada keser, dolayısıyla her zaman en az bir reel kökü vardır.
- En az sıfır, en fazla iki yerel ekstremum noktası vardır.
- Tek bir büküm noktası vardır ve o nokta etrafında simetriktir.
- Birebir olabilir ya da olmayabilir.
- \( \mathbb{R} \rightarrow \mathbb{R} \) için örtendir.
4. Dereceden Polinomların Grafiği
Aşağıdaki 4. dereceden polinomların kökleri ile ilgili farklı durumlar verilmiştir. Verilen tüm grafikler \( a \gt 0 \) için olup, \( a \lt 0 \) olduğu durumlarda bu grafiklerin \( x \) eksenine göre yansımaları oluşacaktır.
\( f: \mathbb{R} \rightarrow \mathbb{R} \)
\( f(x) = ax^4 + bx^3 + cx^2 + dx + e \)
Tüm Köklerin Reel Olduğu Durumlar
4. dereceden bir polinomun tüm kökleri reel ise polinomun kökleri, katları ve grafikleri aşağıdaki şekillerde olabilir.
| Kökler ve Denklem | Grafik |
|---|---|
|
Tek katlı dört reel kök \( f(x) = a(x - x_1)(x - x_2)(x - x_3)(x - x_4) \) |
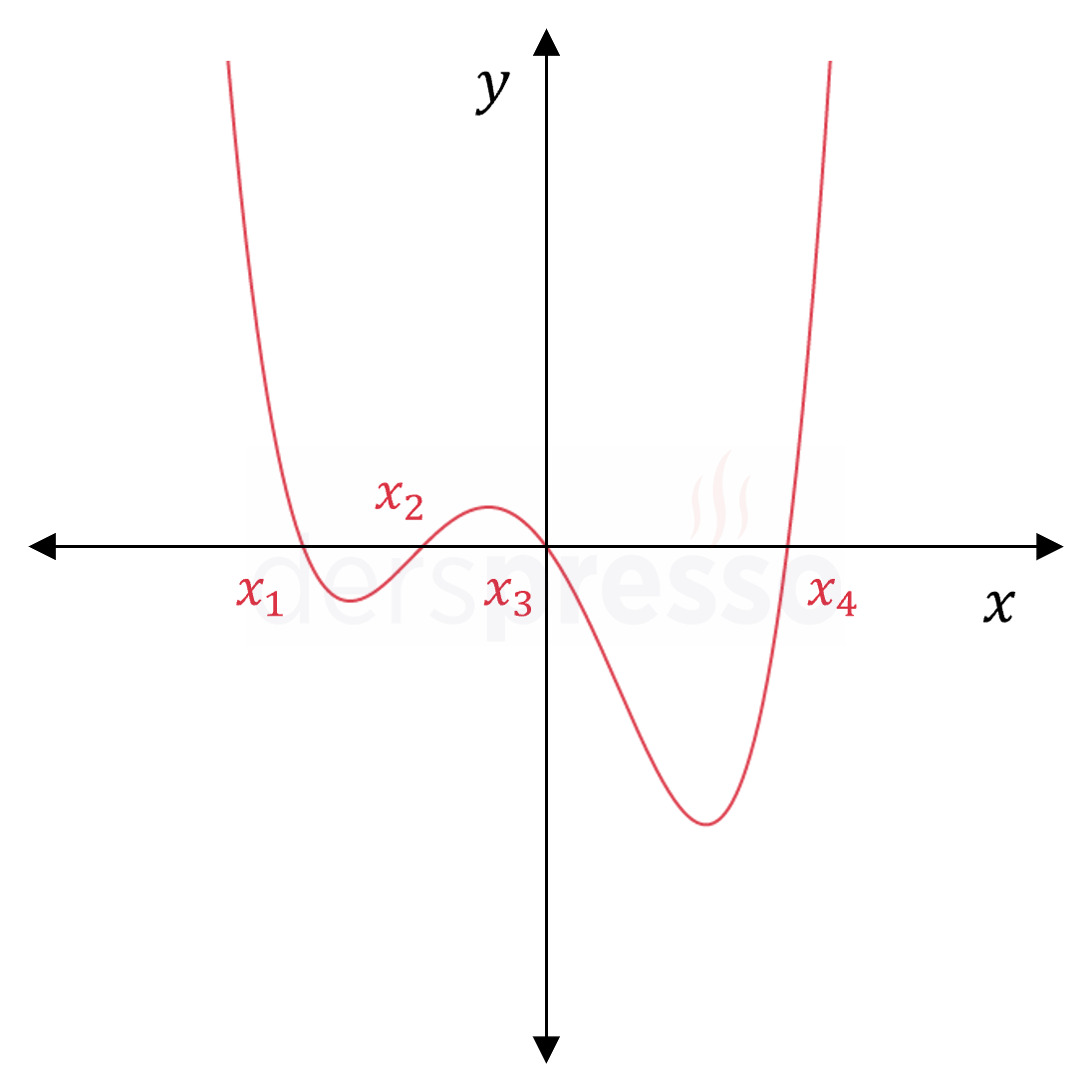
|
|
İki katlı bir reel kök + tek katlı iki reel kök \( f(x) = a(x - x_1)^2(x - x_2)(x - x_3) \) |
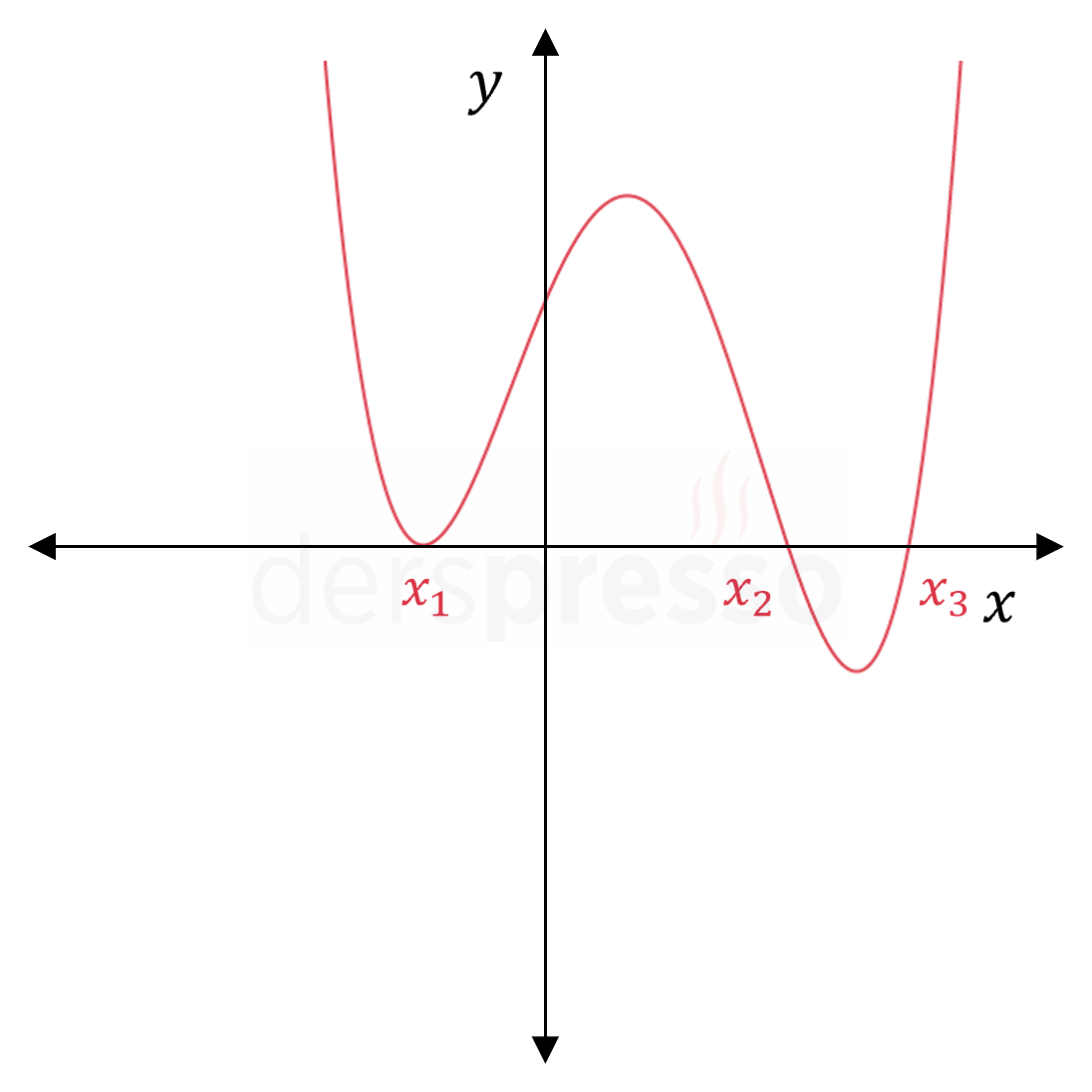
|
|
İki katlı iki reel kök \( f(x) = a(x - x_1)^2(x - x_2)^2 \) |
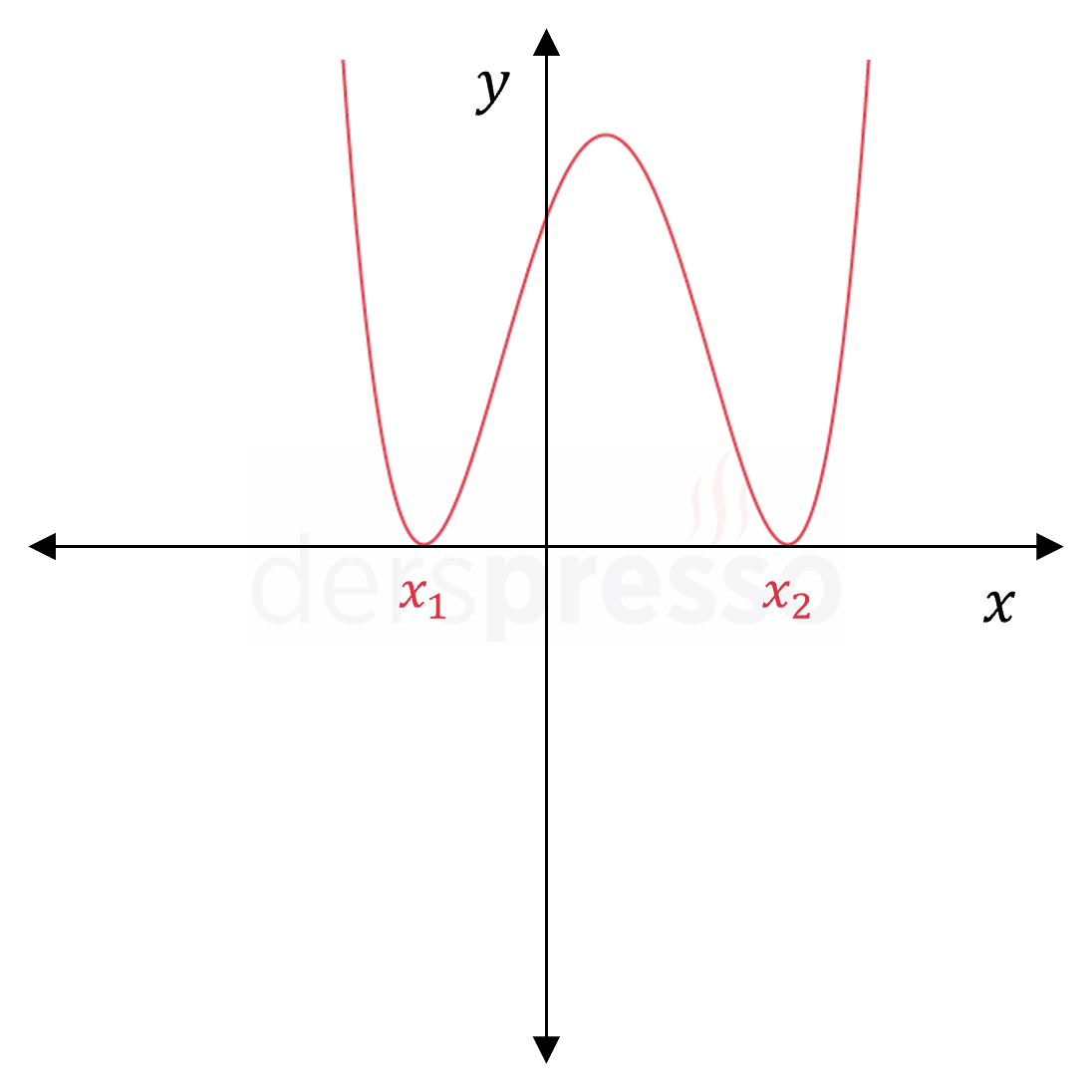
|
|
Üç katlı bir reel kök + tek katlı bir kök \( f(x) = a(x - x_1)^3(x - x_2) \) |
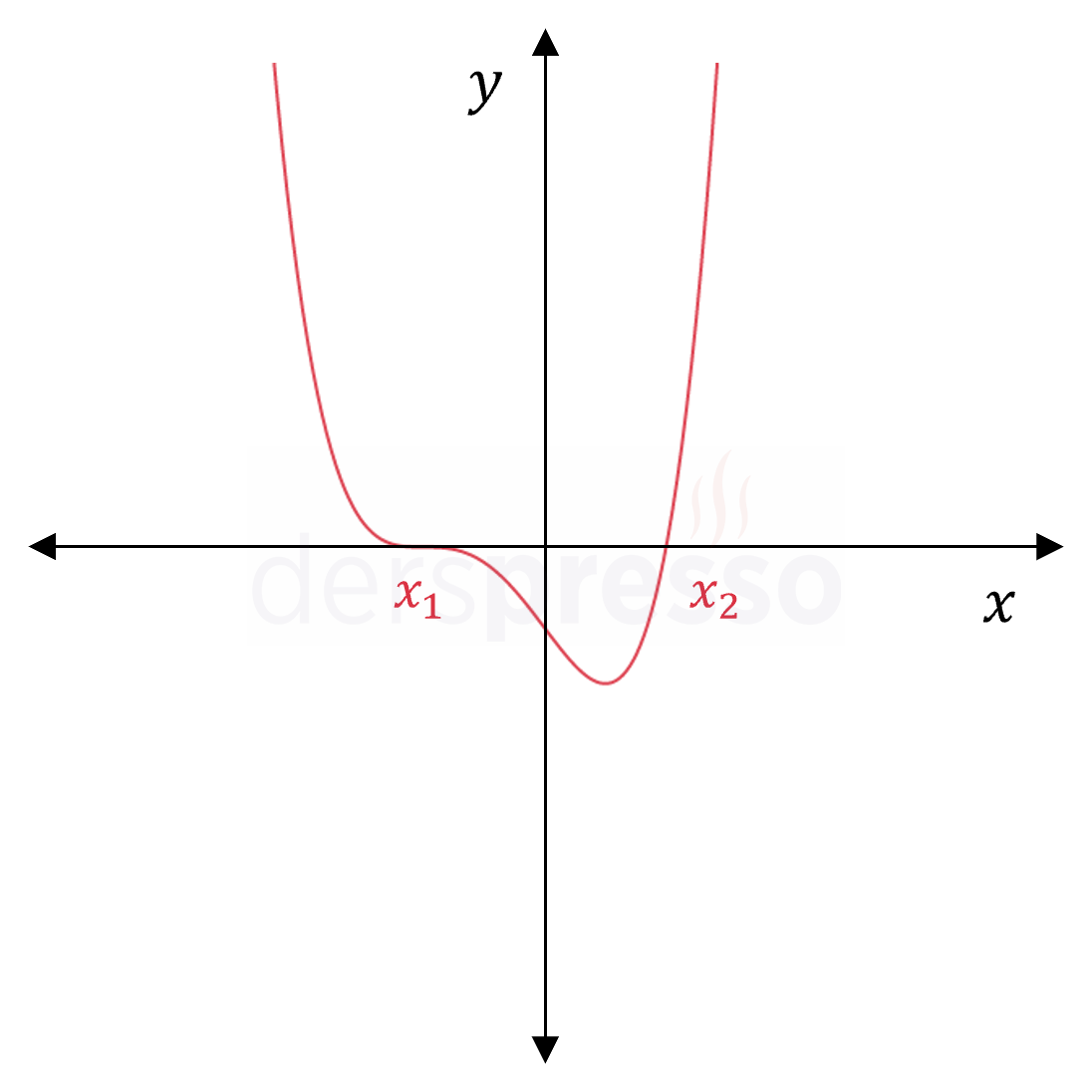
|
|
Dört katlı bir reel kök \( f(x) = a(x - x_1)^4 \) |

|
Reel Olmayan Köklerin Olduğu Durumlar
4. dereceden bir polinomunun reel olmayan kökleri varsa, polinomun kökleri, katları ve grafikleri aşağıdaki şekilde olabilir. Çift dereceli polinomlar \( x \) eksenini kesmek zorunda olmadığı için, reel bir kökü olmak zorunda değildir (son satırdaki dört reel olmayan köklü durum). Bir denklemin reel olmayan kökleri varsa, bu kökler hep ikişerli ve birbirinin eşleniği olur.
| Kökler ve Denklem | Grafik |
|---|---|
|
Tek katlı iki reel kök + iki reel olmayan kök \( f(x) = a(x - x_1)(x - x_2)(x^2 + bx + c) \) |

|
|
İki katlı bir reel kök + iki reel olmayan kök \( f(x) = a(x - x_1)^2(x^2 + bx + c) \) |

|
|
Dört reel olmayan kök \( f(x) = ax^4 + bx^3 + cx^2 + dx + e \) |

|
4. dereceden polinomların grafikleri ile ilgili bazı önemli noktalar aşağıdaki gibidir.
- \( a \gt 0 \) ise polinom grafiği artı sonsuzdan gelip artı sonsuza gider.
- \( a \lt 0 \) ise grafik eksi sonsuzdan gelip eksi sonsuza gider.
- \( y \) eksenini her zaman ve sadece bir noktada keser.
- \( x \) eksenini en az sıfır, en fazla dört noktada keser.
- En az bir, en fazla üç yerel ekstremum noktası vardır.
- Yatay doğru testini geçemediği için birebir değildir.
- \( \mathbb{R} \rightarrow \mathbb{R} \) için içinedir.
\( a, b, c, d, e \in \mathbb{R} \) olmak üzere,
\( p(x) = ax^5 + bx^3 + c \) ve \( q(x) = ax^5 + dx + e \) polinomları veriliyor.
Bu polinomların grafiklerinin birbiriyle kesiştiği en fazla kaç nokta olabilir?
Çözümü GösterGrafiklerin kesiştiği noktalarda \( p(x) = q(x) \) eşitliği sağlanır.
İki denklemin ortak çözümünü bulalım.
\( ax^5 + bx^3 + c = ax^5 + dx + e \)
\( bx^3 - dx + c - e = 0 \)
Bu üçüncü dereceden polinomun kökleri iki polinomun grafiklerinin kesişim noktalarının apsis değerlerini verir.
Üçüncü dereceden bir polinomun en fazla üç farklı reel kökü olabilir.
Buna göre polinomların grafikleri en fazla üç noktada kesişebilir.