Polinom Fonksiyonları
Polinom tanımını sağlayan fonksiyonlara polinom fonksiyonu denir. Aşağıda tanımı verilen polinomlar bir değişkenin sadece pozitif tam sayı kuvvetlerini içerebilir.
\( n \in \mathbb{N}, \quad a_0, a_1, \ldots, a_n \in \mathbb{R} \) olmak üzere,
\( f(x) = a_nx^n + a_{n-1}x^{n-1} + a_{n-2}x^{n-2} + \ldots + a_2x^2 + a_1x + a_0 \)
Bu tanıma göre ikinci dereceden, doğrusal, sabit fonksiyonlar ve kuvvet fonksiyonları da birer polinom fonksiyonudur. Polinom fonksiyonunun en yüksek dereceli terimi fonksiyonun derecesini belirler.
| Polinom Fonksiyon Denklemi | Derece | Polinom Fonksiyon Tipi |
|---|---|---|
| \( f(x) = -x^5 + 2x^3 - 3x^2 + 8 \) | \( 5 \) | \( 5 \). dereceden polinom fonksiyonu |
| \( g(x) = x^2 + 3x - 1 \) | \( 2 \) | İkinci dereceden fonksiyon (parabol) |
| \( h(x) = 2x - 5 \) | \( 1 \) | Doğrusal fonksiyon |
| \( k(x) = 4 \) | \( 0 \) | Sabit fonksiyon |
Değer Tablosu ve Grafiği
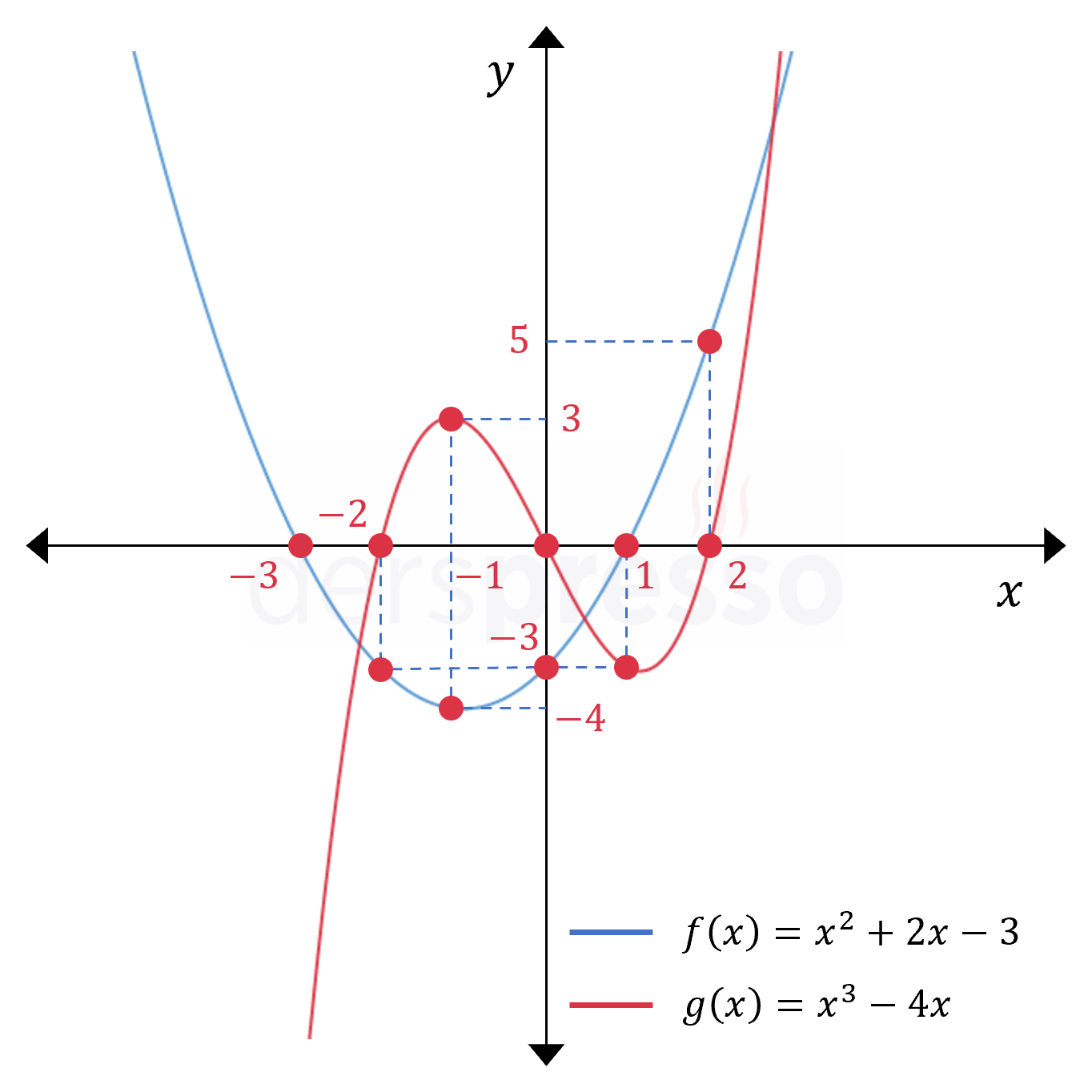
İkinci dereceden \( f(x) = x^2 + 2x - 3 \) ve üçüncü dereceden \( g(x) = x^3 - 4x \) fonksiyonlarının bazı değerleri için değer tablosu aşağıdaki gibidir.
| \( x \) | \( f(x) = x^2 + 2x - 3 \) | \( g(x) = x^3 - 4x \) |
|---|---|---|
| \( -3 \) | \( f(-3) = (-3)^2 + 2(-3) - 3 = 0 \) | \( g(-3) = (-3)^3 - 4(-3) = -15 \) |
| \( -2 \) | \( f(-2) = (-2)^2 + 2(-2) - 3 = -3 \) | \( g(-2) = (-2)^3 - 4(-2) = 0\) |
| \( -1 \) | \( f(-1) = (-1)^2 + 2(-1) - 3 = -4 \) | \( g(-1) = (-1)^3 - 4(-1) = 3 \) |
| \( 0 \) | \( f(0) = 0^2 + 2\cdot0 - 3 = -3 \) | \( g(0) = 0^3 - 4\cdot0 = 0 \) |
| \( 1 \) | \( f(1) = 1^2 + 2\cdot1 - 3 = 0 \) | \( g(1) = 1^3 - 4\cdot1 = -3 \) |
| \( 2 \) | \( f(2) = 2^2 + 2\cdot2 - 3 = 5 \) | \( g(2) = 2^3 - 4\cdot2 = 0 \) |
| \( 3 \) | \( f(3) = 3^2 + 2\cdot3 - 3 = 12 \) | \( g(3) = 3^3 - 4\cdot3 = 15 \) |
Her iki fonksiyon için bulunan bu noktalar koordinat düzleminde işaretlendiğinde aşağıdaki grafikler elde edilir.
Polinom Fonksiyonu Dönüşümleri
Fonksiyonların dönüşümü konusunda gördüğümüz tüm dönüşümler polinom fonksiyonlarına uygulanarak fonksiyonun denkleminde, grafiğinin konumunda ve şeklinde değişiklikler meydana getirilebilir.
İkinci dereceden \( P(x + 1) \) polinomunun birbirinden farklı iki kökü \( 2 \) ve \( a \)'dır.
\( P^n(2 - x) = 0 \) denkleminin farklı kökleri toplamı 7 olduğuna göre, \( a \) kaçtır?
Çözümü Göster\( P(x + 1) \) polinomunu bir fonksiyon olarak düşünerek soruyu grafik dönüşümleri üzerinden çözelim.
\( P(x + 1) \) fonksiyonunun kökleri \( 2 \) ve \( a \) ise fonksiyon \( x \) eksenini bu noktalarda keser.
\( P(x + 1) \) fonksiyonu \( P(x) \) fonksiyonunun grafiğinin 1 birim sola ötelenmesi ile elde edildiği için \( P(x) \) fonksiyonu \( x \) eksenini \( 3 \) ve \( a + 1 \) noktalarında keser.
\( P^n(2 - x) = P^n(-(x - 2)) \)
\( P(-(x - 2)) \) fonksiyonunu elde etmek için \( P(x) \) fonksiyonunun grafiğinin önce \( y \) eksenine göre yansıması alınır, sonra 2 birim sağa ötelenir.
Grafiğin \( y \) eksenine göre yansıması alınınca \( x \) eksenini kestiği noktalar \( -3 \) ve \( -a - 1 \) olur.
Grafik 2 birim sağa ötelenince \( x \) eksenini kestiği noktalar \( -3 + 2 = -1 \) ve \( -a - 1 + 2 = -a + 1 \) olur.
Fonksiyonun \( n \). kuvvetinin alınmasının \( P(x) = 0 \) olduğu noktalardaki fonksiyon değerini değiştirmediği için fonksiyonun \( x \) eksenini kestiği noktalar değişmez.
Buna göre \( P^n(2 - x) \) fonksiyonunun \( x \) eksenini kestiği noktalar \( -1 \) ve \( -a + 1 \) olur.
\( -1 + (-a + 1) = 7 \)
\( a = -7 \) bulunur.