Rasyonel Fonksiyonlar
İki polinomun oranı şeklinde yazılabilen fonksiyonlara rasyonel fonksiyon denir.
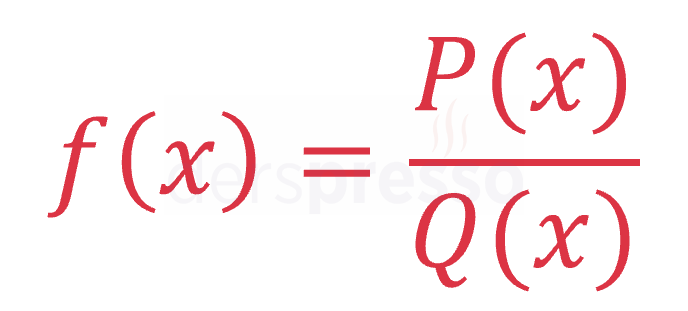
RASYONEL FONKSİYON:
\( P(x), Q(x) \) birer polinom ve \( Q(x) \ne 0 \) olmak üzere,
\( f: A \to B \)
\( f(x) = \dfrac{P(x)}{Q(x)} \)
ÖRNEK:
\( f(x) = \dfrac{1}{x} \)
\( g(x) = \dfrac{x + 3}{x^2 - 4} \)
\( h(x) = \dfrac{x^3 - 2x^2 - 6}{x + 1} \)
Değer Tablosu ve Grafiği
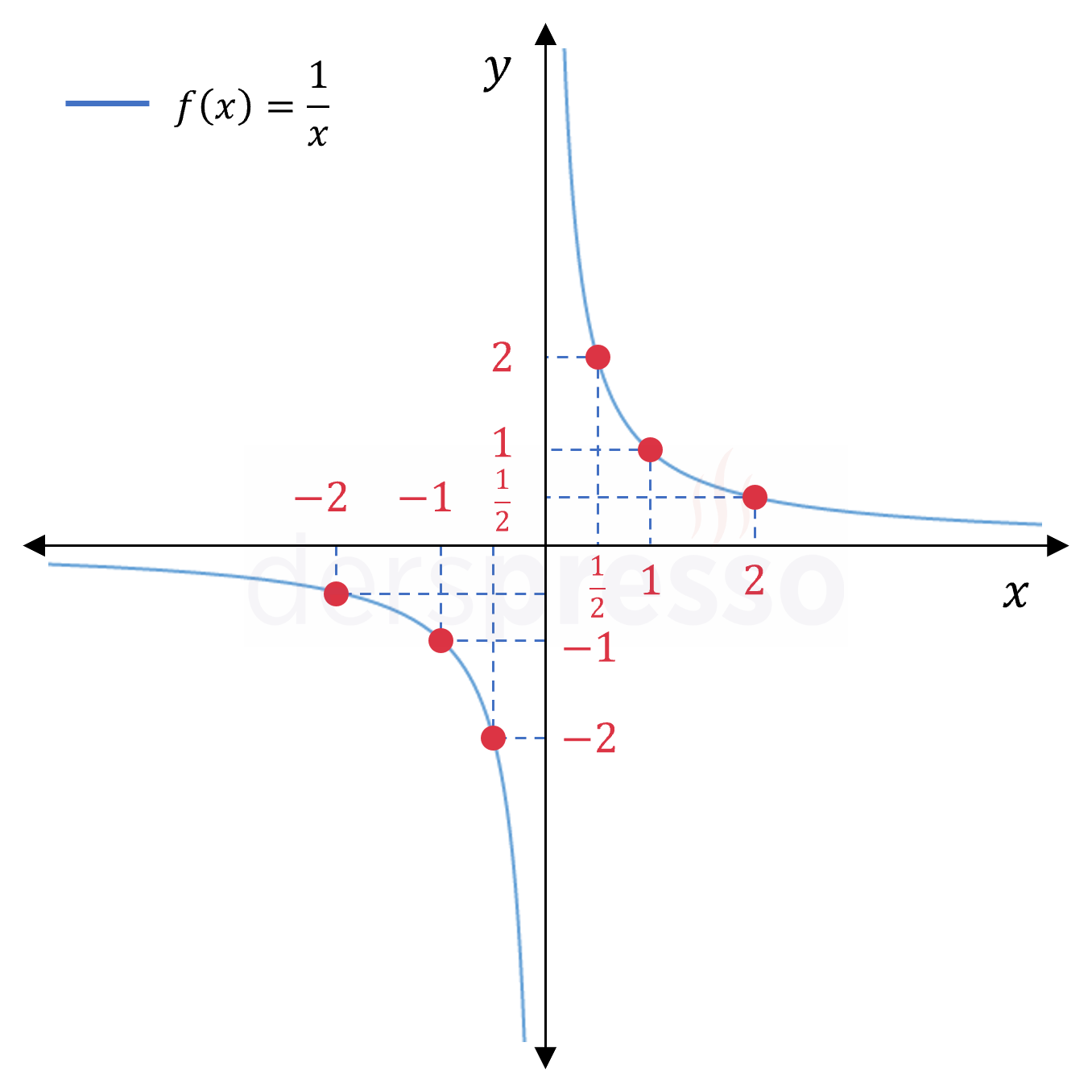
Rasyonel fonksiyonlar çok farklı grafiklere sahip olabilseler de, örnek olarak \( f(x) = \frac{1}{x} \) fonksiyonunun bazı değerleri için değer tablosu aşağıdaki gibidir:
| \( x \) | \( f(x) = \dfrac{1}{x} \) |
|---|---|
| \( -2 \) | \( f(-2) = -\dfrac{1}{2} \) |
| \( -1 \) | \( f(-1) = -\dfrac{1}{1} = -1\) |
| \( -\dfrac{1}{2} \) | \( f(-\dfrac{1}{2}) = \dfrac{1}{-\dfrac{1}{2}} = -2 \) |
| \( 0 \) | \( f(0) = \dfrac{1}{0} \Longrightarrow \) Tanımsız |
| \( \dfrac{1}{2} \) | \( f(\dfrac{1}{2}) = \dfrac{1}{\dfrac{1}{2}} = 2 \) |
| \( 1 \) | \( f(1) = \dfrac{1}{1} = 1 \) |
| \( 2 \) | \( f(2) = \dfrac{1}{2} \) |
Bulunan bu noktalar analitik düzlemde işaretlendiğinde aşağıdaki grafik elde edilir.
Rasyonel Fonksiyon Dönüşümleri
Fonksiyonların dönüşümü konusunda gördüğümüz tüm dönüşümler rasyonel fonksiyonlara uygulanarak fonksiyonun denkleminde, grafiğinin konumunda ve şeklinde değişiklikler meydana getirilebilir.
« Önceki
Polinom Fonksiyonu Tanım ve Görüntü Kümesi
Sonraki »
Rasyonel Fonksiyonları Tanımsız ve Sıfır Yapan Değerler