Mutlak Değer Fonksiyonları
Bir değişkenin mutlak değer işareti içinde bulunduğu fonksiyonlara mutlak fonksiyonu denir.
Mutlak değer fonksiyonları en sade haliyle aşağıdaki şekildedir.

\( f: \mathbb{R} \to \mathbb{R} \)
\( f(x) = \abs{x} \)
Mutlak değer konusunda gördüğümüz gibi, mutlak değer işlemi içinde bulunan ifadenin değerinin işaretini pozitife çevirir. Mutlak değer fonksiyonları mutlak değer içindeki ifadelerin pozitif ya da negatif olma durumuna göre farklı davranış gösterdikleri için birer parçalı fonksiyon şeklinde yazılabilirler.
\( f(x) = \abs{x} = \begin{cases} x & x \ge 0 \\ -x & x \lt 0 \end{cases} \)
Mutlak Değer Fonksiyonu Değer Tablosu ve Grafiği
\( f(x) = \abs{x} \) ve \( g(x) = \abs{x + 1} - 2 \) fonksiyonlarının bazı değerleri için değer tablosu aşağıdaki gibidir.
| \( x \) | \( f(x) = \abs{x} \) | \( g(x) = \abs{x + 1} - 2 \) |
|---|---|---|
| \( -3 \) | \( f(-3) = \abs{-3} = 3 \) | \( g(-3) = \abs{-3 + 1} - 2 = 0 \) |
| \( -2 \) | \( f(-2) = \abs{-2} = 2 \) | \( g(-2) = \abs{-2 + 1} - 2 = -1 \) |
| \( -1 \) | \( f(-1) = \abs{-1} = 1 \) | \( g(-1) = \abs{-1 + 1} - 2 = -2 \) |
| \( 0 \) | \( f(0) = \abs{0} = 0 \) | \( g(0) = \abs{0 + 1} - 2 = -1 \) |
| \( 1 \) | \( f(1) = \abs{1} = 1 \) | \( g(1) = \abs{1 + 1} - 2 = 0 \) |
| \( 2 \) | \( f(2) = \abs{2} = 2 \) | \( g(2) = \abs{2 + 1} - 2 = 1 \) |
| \( 3 \) | \( f(3) = \abs{3} = 3 \) | \( g(3) = \abs{3 + 1} - 2 = 2 \) |
Her iki fonksiyon için bulunan bu noktalar koordinat düzleminde işaretlendiğinde aşağıdaki grafikler elde edilir. Mutlak değer fonksiyonlarının grafikleri çoğu zaman aşağıdaki şekilde olduğu gibi "V" şeklindedir.
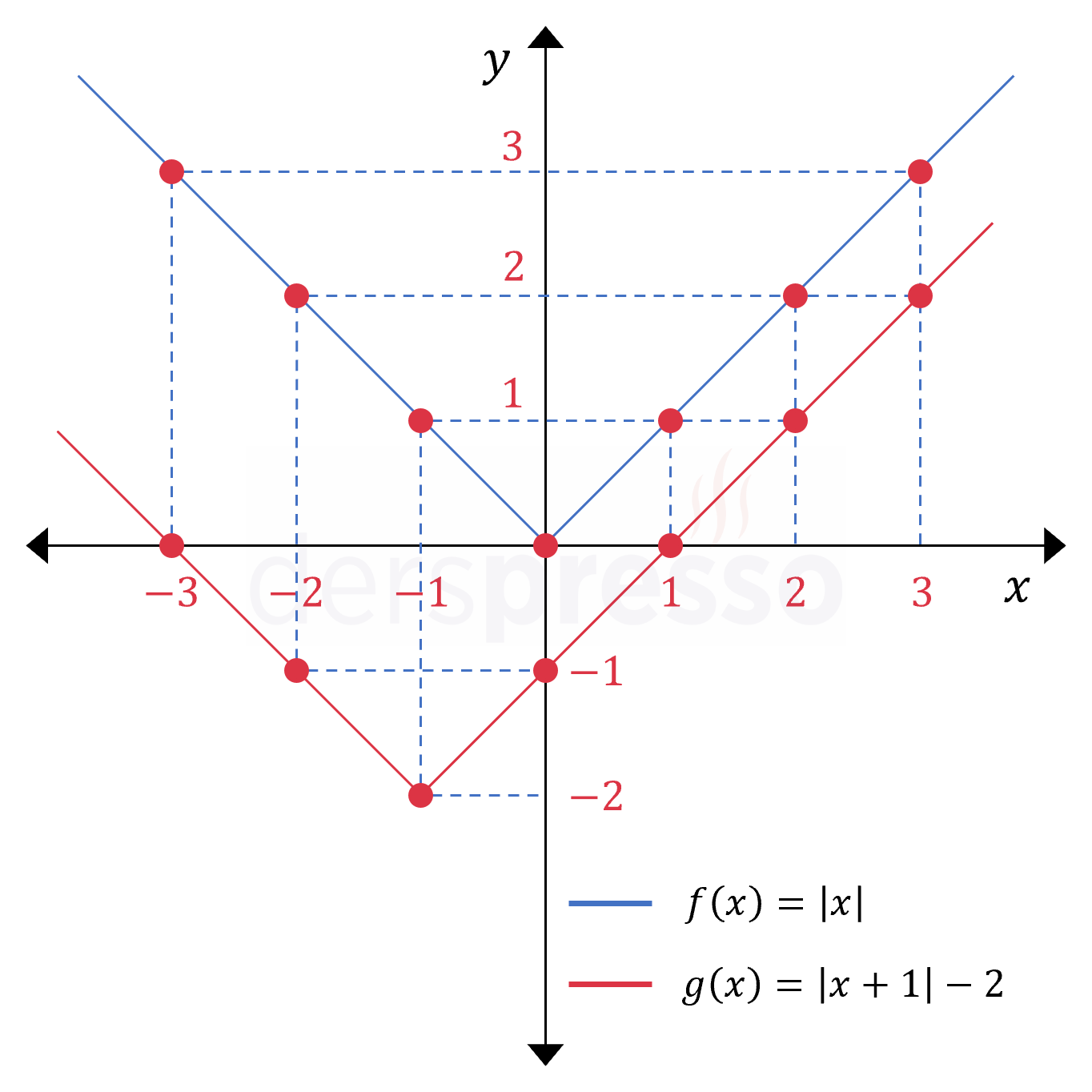
Mutlak Değer Fonksiyon Dönüşümleri
Fonksiyonların dönüşümü konusunda gördüğümüz tüm dönüşümler mutlak değeri fonksiyonlarına uygulanarak fonksiyonun denkleminde, grafiğinin konumunda ve şeklinde değişiklikler meydana getirilebilir.
Bu dönüşümlere aşağıdaki gibi birkaç örnek verilebilir.
\( f(x) = \abs{2x - 3} \)
\( g(x) = \abs{x^2 - 2x - 3} \)
\( h(x) = -2\abs{3x - 1} + 5 \)
\( f: \mathbb{R} \to \mathbb{R} \) olmak üzere,
\( f(x) = \abs{8 + x} - \abs{15 - 5x} + \abs{3x - 24} + \abs{9 - x} \)
Buna göre, \( f \) hangi aralıkta sabit fonksiyondur?
Çözümü Göster\( f(x) = \abs{8 + x} - \abs{15 - 5x} + \abs{3x - 24} + \abs{9 - x} \)
Mutlak değer ifadelerinin içlerini düzenleyelim.
\( = \abs{x + 8} - \abs{5x - 15} + \abs{3x - 24} + \abs{x - 9} \)
Mutlak değer ifadelerini sıfır yapan noktalar fonksiyonun kritik noktalarıdır.
Verilen fonksiyonun kritik noktaları \( x \in \{-8, 3, 8, 9\} \) noktalarıdır.
Bu dört kritik noktanın oluşturduğu beş aralığı ayrı ayrı inceleyelim ve her aralıkta mutlak değer içindeki ifadeleri o aralıktaki işaretlerine göre mutlak değerden çıkaralım.
Durum 1: \( x \lt -8 \)
\( f(x) = -(x + 8) + (5x - 15) - (3x - 24) - (x - 9) \)
\( = -x - 8 + 5x - 15 - 3x + 24 - x + 9 \)
\( = 10 \)
Fonksiyon bu aralıkta sabittir.
Durum 2: \( -8 \le x \lt 3 \)
\( f(x) = (x + 8) + (5x - 15) - (3x - 24) - (x - 9) \)
\( = x + 8 + 5x - 15 - 3x + 24 - x + 9 \)
\( = 2x + 26 \)
Fonksiyon bu aralıkta sabit değildir.
Durum 3: \( 3 \le x \lt 8 \)
\( f(x) = (x + 8) - (5x - 15) - (3x - 24) - (x - 9) \)
\( = x + 8 - 5x + 15 - 3x + 24 - x + 9 \)
\( = -8x + 56 \)
Fonksiyon bu aralıkta sabit değildir.
Durum 4: \( 8 \le x \lt 9 \)
\( f(x) = (x + 8) - (5x - 15) + (3x - 24) - (x - 9) \)
\( = x + 8 - 5x + 15 + 3x - 24 - x + 9 \)
\( = -2x + 8 \)
Fonksiyon bu aralıkta sabit değildir.
Durum 5: \( 9 \le x \)
\( f(x) = (x + 8) - (5x - 15) + (3x - 24) + (x - 9) \)
\( = x + 8 - 5x + 15 + 3x - 24 + x - 9 \)
\( = -10 \)
Fonksiyon bu aralıkta sabittir.
Buna göre \( f \) fonksiyonu \( (-\infty, -8) \cup (9, \infty) \) aralıklarında sabit fonksiyondur.
\( k \in \mathbb{R} \) olmak üzere,
\( \abs{5x - 3} = 3k - 24 \) denkleminin çözüm kümesi tek elemanlıdır.
\( \abs{\abs{k^2 - 6k + m} - 8} = 17 \) olduğuna göre, \( m \)'nin alabileceği değerler toplamı kaçtır?
Çözümü Göster\( \abs{ax + b} \) biçimindeki bir ifadenin grafiği \( f(x) = \abs{x} \) grafiğinin \( x \) ekseni boyunca ötelenmiş halidir.
\( \abs{ax + b} = k \) şeklindeki bir denklemin çözüm kümesini \( y = \abs{ax + b} \) grafiği ile \( y = k \) doğrusunun kesişim kümesi olarak düşünebiliriz. Buna göre \( k \gt 0 \) olursa iki grafik iki noktada, \( k = 0 \) olursa iki grafik tek noktada kesişir. \( k \lt 0 \) olursa iki grafik kesişmez.
Buna göre verilen denklemin çözüm kümesinin tek elemanlı olması için mutlak değer ifadesi sıfıra eşit olmalıdır.
\( 3k - 24 = 0 \Longrightarrow k = 8 \)
Bu değeri ikinci eşitlikte yerine koyalım.
\( \abs{\abs{8^2 - 6(8) + m} - 8} = 17 \)
\( \abs{\abs{16 + m} - 8} = 17 \)
Bu denklemin iki çözümü vardır.
Durum 1:
\( \abs{16 + m} - 8 = 17 \)
\( \abs{16 + m} = 25 \)
Bu denklemin iki çözümü vardır.
Durum 1.1:
\( 16 + m = 25 \)
\( m = 9 \)
Durum 1.2:
\( 16 + m = -25 \)
\( m = -41 \)
Durum 2:
\( \abs{16 + m} - 8 = -17 \)
\( \abs{16 + m} = -9 \)
Mutlak değerli bir ifadenin sonucu negatif olamayacağı için bu durum için geçerli bir çözüm yoktur.
Çözüm kümesi: \( m \in \{ -41, 9 \} \)
Buna göre \( m \)'nin alabileceği değerler toplamı \( -41 + 9 = -32 \) olarak bulunur.