Mutlak Değer Fonksiyonu Grafikleri
Mutlak değer içindeki bir fonksiyonun grafiği biliniyorsa grafik önce mutlak değer yokmuş gibi çizilir. Daha sonra \( x \) ekseninin altında kalan kısımların \( x \) eksenine göre yansıması alınır. Fonksiyonun sıfır ya da pozitif olduğu noktalarda bir değişiklik olmaz.
Eğer fonksiyonun grafiği bilinmiyorsa fonksiyon önceki bölümde gördüğümüz şekilde bir parçalı fonksiyona dönüştürülür ve parçalı fonksiyonun her tanımının grafiği tanımlı olduğu aralıkta ayrı ayrı çizilir.
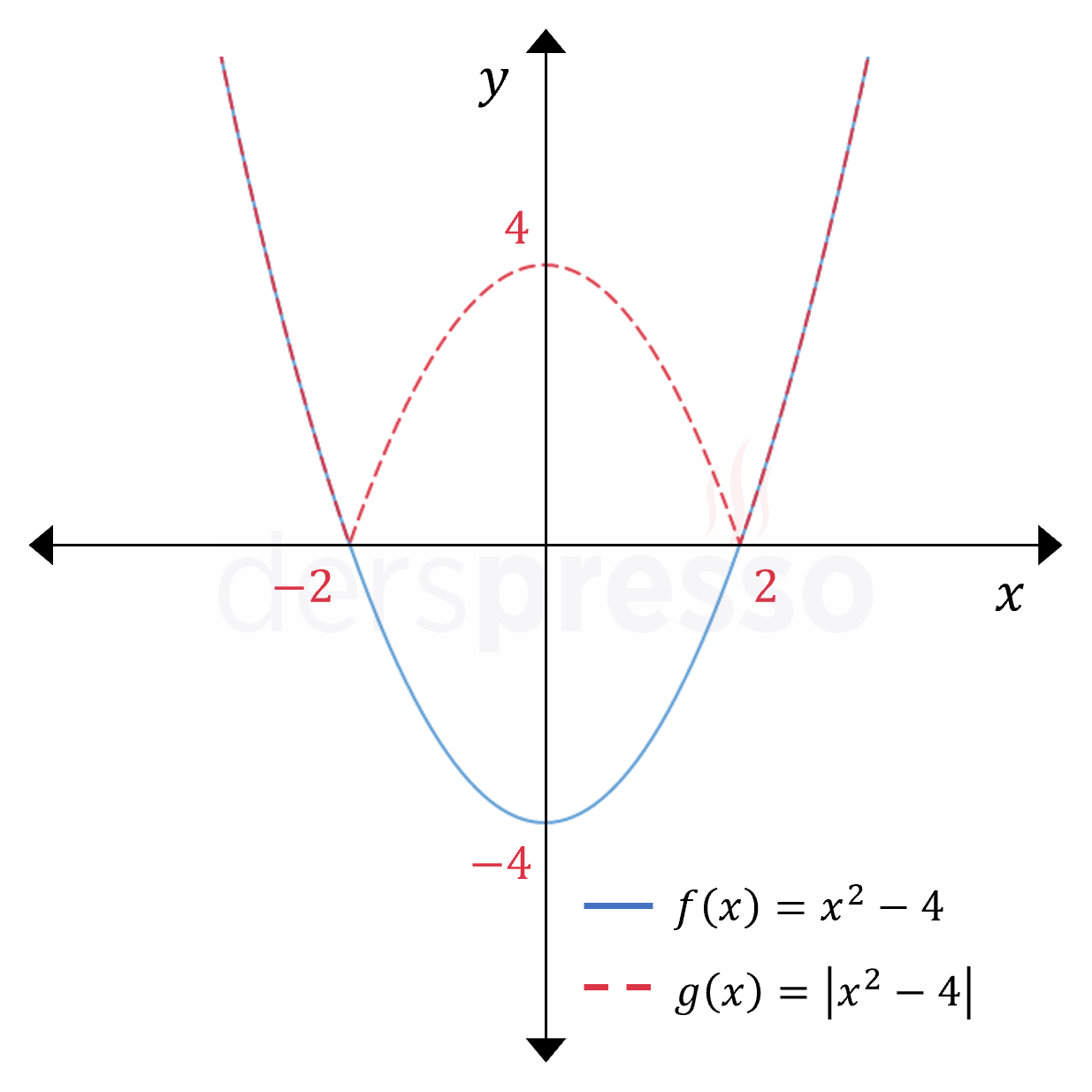
Aşağıdaki \( f(x) = x \) ve \( g(x) = \abs{x} \) grafiklerinde görülebileceği gibi, \( f \) fonksiyonunun negatif değerlerinde mutlak değer grafiği \( f \)'in \( x \) eksenine göre yansımasıdır, diğer noktalarda ise iki fonksiyonun grafikleri aynıdır.

\( g \) fonksiyonunun grafiğinin mutlak değerin parçalı fonksiyon yazılışı ile uyumlu olduğu görülebilir. Buna göre mutlak değer grafiği \( x \)'in sıfır ve pozitif değerlerinde 1. açıortay doğrusu, negatif değerlerinde de 2. açıortay doğrusudur.
\( g(x) = \abs{x} = \begin{cases} x & x \ge 0 \\ -x & x \lt 0 \end{cases} \)
\( g \) fonksiyonunun grafiğinin mutlak değerin uzaklık tanımı ile de uyumlu olduğu görülebilir. Buna göre fonksiyonun \( x = 2 \) ve \( x = -2 \) noktalarındaki değeri, bu iki noktanın sayı doğrusu üzerinde orijine uzaklığı olan 2'dir.
Aşağıdaki parabol fonksiyonunun mutlak değer grafiğinde de benzer şekilde parabolün fonksiyon değeri negatif olan noktalarının \( x \) eksenine göre yansıması oluşmaktadır.
Mutlak Değer Fonksiyonlarının Dönüşümleri
Fonksiyonlar konusunda gördüğümüz dönüşümler mutlak değer fonksiyonlarına uygulanarak aşağıdaki formdaki geniş bir fonksiyon ailesinin grafikleri çizilebilir.
\( f(x) = -a \cdot \abs{-b(x + c)} + k \)
\( a \): Dikey daralma/genişleme ve yansıma
\( k \): Dikey öteleme
\( b \): Yatay daralma/genişleme ve yansıma
\( c \): Yatay öteleme
Bu dönüşümleri mutlak değer fonksiyonlarına uygulayabilmek için öncelikle fonksiyonların dönüşümü ve mutlak değer dönüşümleri bölümleri incelenmelidir.
\( f(x) = \abs{x - 1} - 3 \) fonksiyonunun grafiğini çizelim.
Bu fonksiyonun grafiğini \( \abs{x} \) grafiğini baz alarak ve standart fonksiyon dönüşümlerini uygulayarak çizelim.
\( f(x) = \abs{x - 1} - 3 \) grafiğini 3 adımda elde edebiliriz. Bu adımlar aşağıda grafik üzerinde de gösterilmiştir.
- \( \abs{x} \): Standart mutlak değer grafiği mavi sürekli çizgi ile gösterilmiştir.
- \( \abs{x - 1} \): Fonksiyonun girdisinden 1 birim çıkarırsak grafik sağa doğru 1 birim ötelenir. Bu grafik yeşil kesikli çizgi ile gösterilmiştir.
- \( \abs{x - 1} - 3 \): Fonksiyonun çıktısından 3 birim çıkarırsak grafik aşağı doğru 3 birim ötelenir. Bu grafik kırmızı sürekli çizgi ile gösterilmiştir.
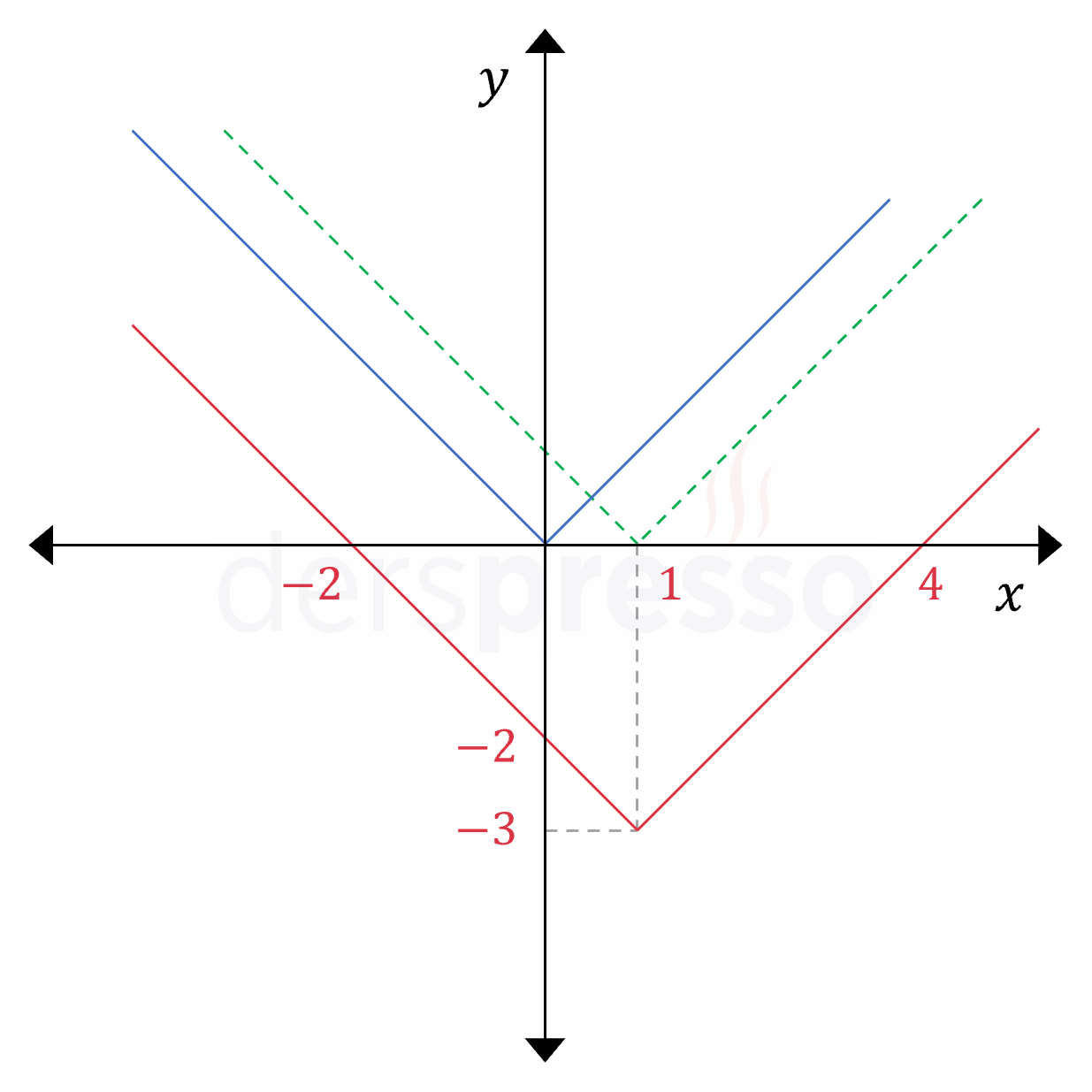
Elde ettiğimiz bu grafik \( f \) fonksiyonunun aşağıdaki parçalı fonksiyon şeklinde yazılışının grafiği ile aynıdır (mutlak değer fonksiyonunun parçalı yazılışı konu anlatımı).
\( f(x) = \begin{cases} -x - 2 & x \lt 1 \\ x - 4 & x \ge 1 \end{cases} \)
\( f(x) = -\abs{2x} + 4 \) fonksiyonunun grafiğini çizelim.
Bu fonksiyonun grafiğini \( \abs{x} \) grafiğini baz alarak ve standart fonksiyon dönüşümlerini uygulayarak çizelim.
\( f(x) = -\abs{2x} + 4 \) fonksiyon grafiğini 4 adımda elde edebiliriz. Bu adımlar aşağıda grafik üzerinde de gösterilmiştir.
- \( \abs{x} \): Standart mutlak değer grafiği mavi sürekli çizgi ile gösterilmiştir.
- \( \abs{2x} \): Fonksiyonun girdisini 2 ile çarparsak grafiğin tüm noktaları \( y \) eksenine bu katsayı oranında yakınlaşır. Bu grafik yeşil kesikli çizgi ile gösterilmiştir.
- \( -\abs{2x} \): Fonksiyonun çıktısının negatifini alırsak grafiğin \( x \) eksenine göre yansıması oluşur. Bu grafik mavi kesikli çizgi ile gösterilmiştir.
- \( -\abs{2x} + 4 \): Fonksiyonun çıktısına 4 birim eklersek grafik yukarı doğru 4 birim ötelenir. Bu grafik kırmızı sürekli çizgi ile gösterilmiştir.
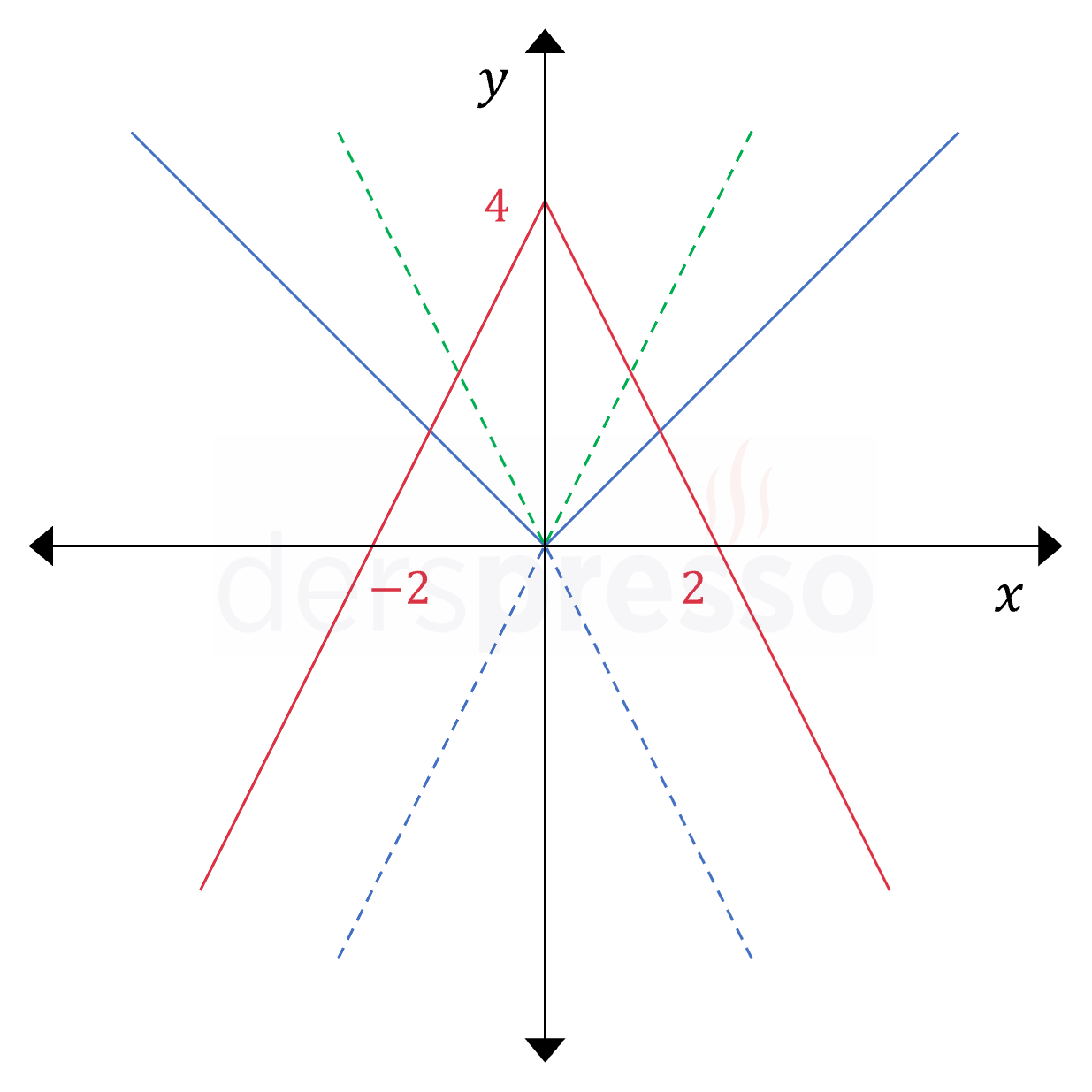
Elde ettiğimiz bu grafik \( f \) fonksiyonunun aşağıdaki parçalı fonksiyon şeklinde yazılışının grafiği ile aynıdır (mutlak değer fonksiyonunun parçalı yazılışı konu anlatımı).
\( f(x) = \begin{cases} 2x + 4 & x \lt 0 \\ -2x + 4 & x \ge 0 \end{cases} \)
İç İçe Mutlak Değerli İfadeler
Birden fazla mutlak değerli ifadenin iç içe yer aldığı fonksiyonların grafiği de aynı dönüşüm adımları uygulanarak çizilebilir.
\( f(x) = \abs{\abs{2x + 2} - 4} \) fonksiyonunun grafiğini çizelim.
Bu fonksiyonun grafiğini \( \abs{x} \) grafiğini baz alarak ve standart fonksiyon dönüşümlerini uygulayarak çizebiliriz.
İçteki mutlak değer ifadesini düzenleyelim.
\( f(x) = \abs{\abs{2x + 2} - 4} = \abs{\abs{2(x + 1)} - 4} \)
\( f(x) = \abs{\abs{2(x + 1)} - 4} \) fonksiyon grafiğini 5 adımda elde edebiliriz. Bu adımlar aşağıda grafik üzerinde de gösterilmiştir.
- \( \abs{x} \): Standart mutlak değer grafiği mavi sürekli çizgi ile gösterilmiştir.
- \( \abs{2x} \): Fonksiyonun girdisini 2 ile çarparsak grafiğin tüm noktaları \( y \) eksenine bu katsayı oranında yakınlaşır. Bu grafik yeşil kesikli çizgi ile gösterilmiştir.
- \( \abs{2(x + 1)} \): Fonksiyonun girdisine 1 birim eklersek grafik sola doğru 1 birim ötelenir. Bu grafik kırmızı kesikli çizgi ile gösterilmiştir.
- \( \abs{2(x + 1)} - 4 \): Fonksiyonun çıktısından 4 birim çıkarırsak grafik aşağı doğru 4 birim ötelenir. Bu grafik mavi kesikli çizgi ile gösterilmiştir.
- \( \abs{\abs{2(x + 1)} - 4} \): Fonksiyonun mutlak değerini alırsak grafiğin negatif değerli (\( x \) ekseninin altında kalan) kısımlarının \( x \) eksenine göre yansıması oluşur. Bu grafik kırmızı sürekli çizgi ile gösterilmiştir.
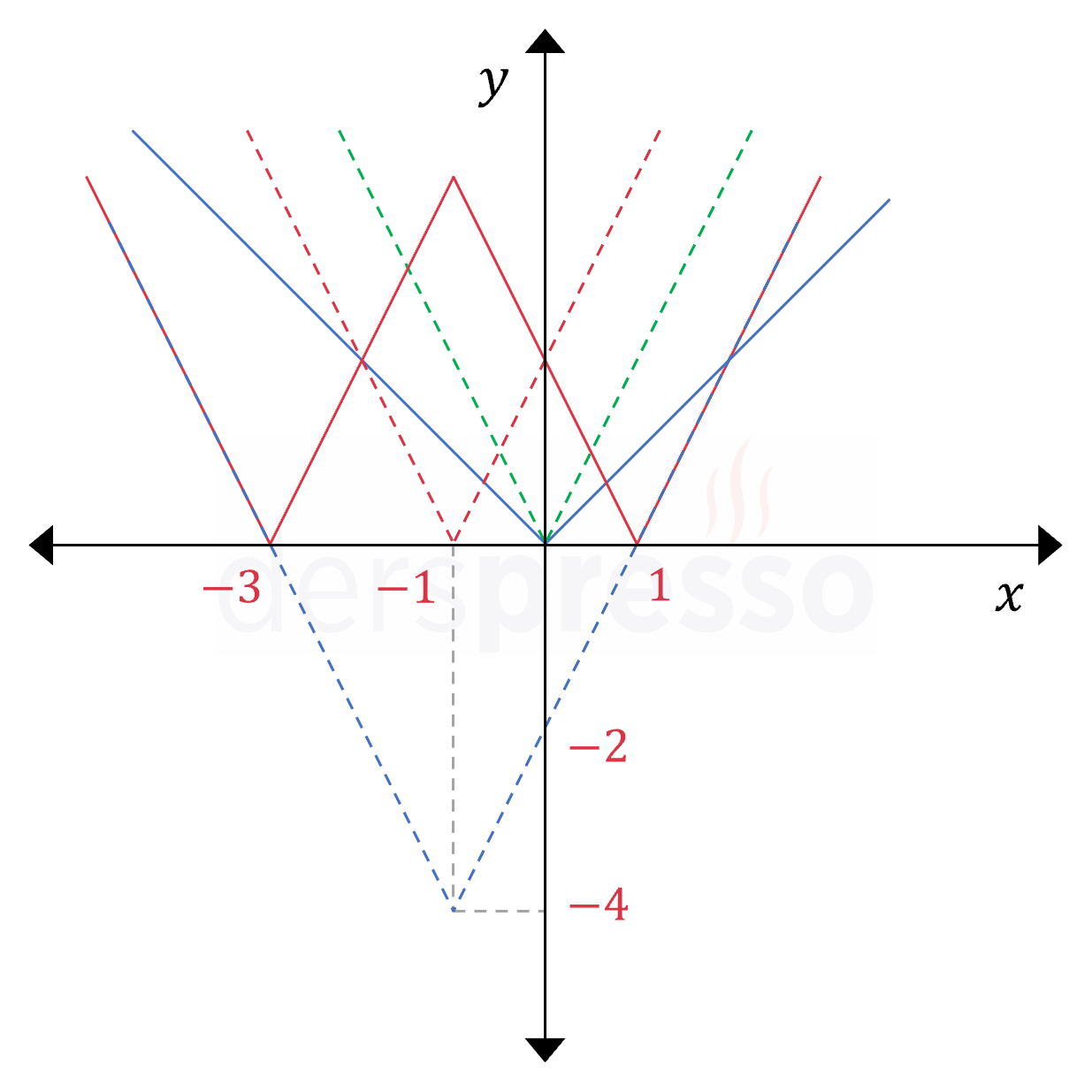
Elde ettiğimiz bu grafik \( f \) fonksiyonunun aşağıdaki parçalı fonksiyon şeklinde yazılışının grafiği ile aynıdır.
\( f(x) = \begin{cases} -2x - 6 & x \le -3 \\ 2x + 6 & -3 \lt x \le -1 \\ -2x + 2 & -1 \lt x \le 1 \\ 2x - 2 & x \gt 1 \end{cases} \)
Mutlak Değerli İfadeler Arasında İşlemler
Birden fazla mutlak değerli ifade arasında işlem içeren fonksiyonların grafiği, fonksiyonlar önce parçalı fonksiyona çevrilerek daha sonra her parçanın grafiği ilgili aralıklarda çizilerek elde edilebilir.
\( f(x) = \abs{x + 1} + \abs{x - 3} \) fonksiyonunun grafiğini çizelim.
Fonksiyonun kritik noktaları mutlak değerli ifadeleri sıfır yapan \( x = -1 \) ve \( x = 3 \) noktalarıdır.
Mutlak değer fonksiyonunu parçalı fonksiyon şeklinde yazalım.
\( f(x) = \begin{cases} -2x + 2 & x \lt -1 \\ 4 & -1 \le x \lt 3 \\ 2x - 2 & x \ge 3 \end{cases} \)
Bu parçalı fonksiyonunun her aralıktaki grafiğini çizdiğimizde aşağıdaki grafiği elde ederiz.

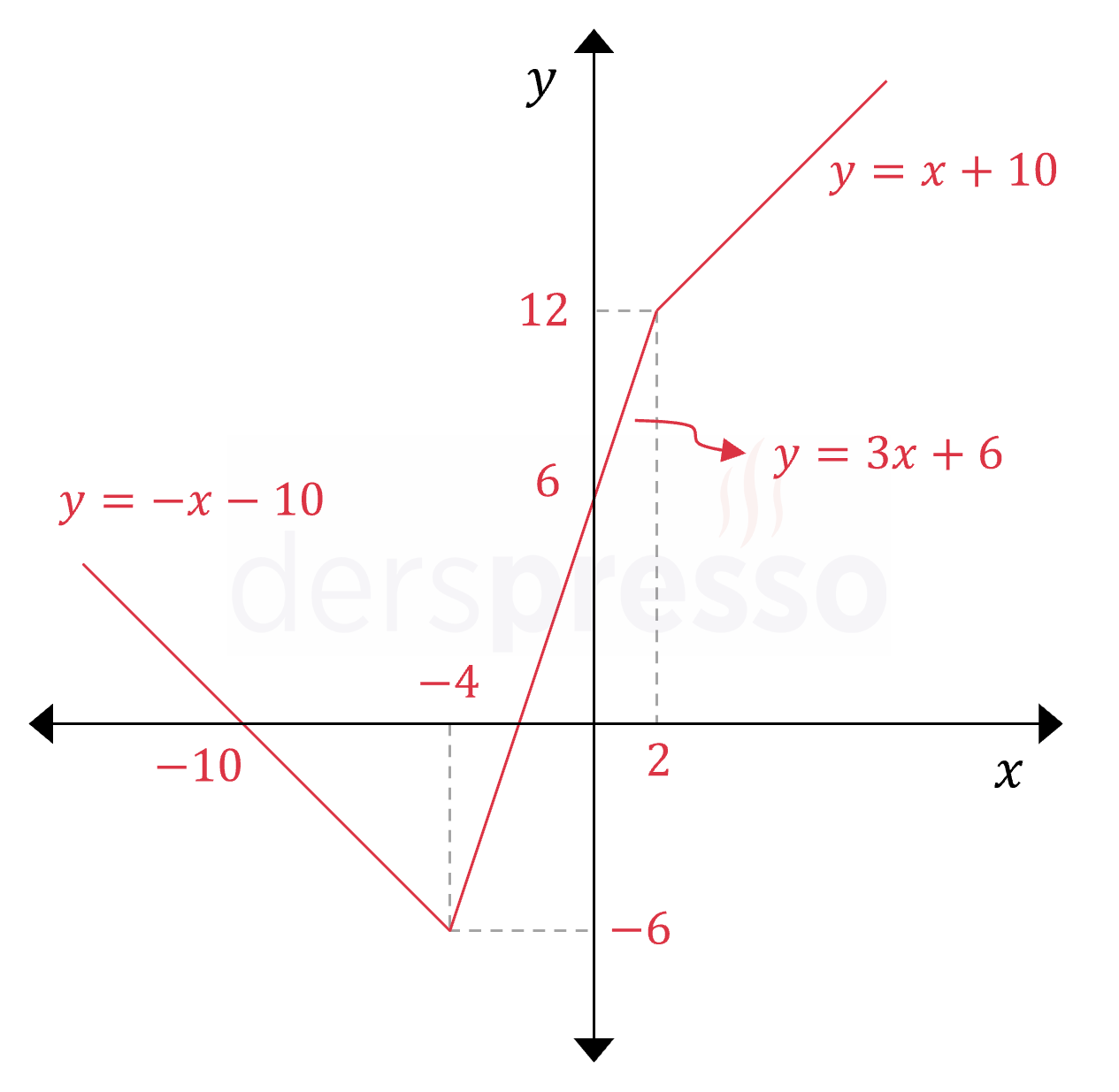
\( f(x) = 2\abs{x + 4} - \abs{x - 2} \) fonksiyonunun grafiğini çizelim.
Fonksiyonun kritik noktaları mutlak değerli ifadeleri sıfır yapan \( x = -4 \) ve \( x = 2 \) noktalarıdır.
Mutlak değer fonksiyonunu parçalı fonksiyon şeklinde yazalım.
\( f(x) = \begin{cases} -x - 10 & x \lt -4 \\ 3x + 6 & -4 \le x \lt 2 \\ x + 10 & x \ge 2 \end{cases} \)
Bu parçalı fonksiyonunun her aralıktaki grafiğini çizdiğimizde aşağıdaki grafiği elde ederiz.
\( y \)'nin Mutlak Değer İçinde Olduğu İfadeler
\( x \) ve \( y \) değişkenleri arasındaki bağıntılarda \( y \) değişkeni de mutlak değer içinde yer alabilir. Bu tip bağıntıların grafikleri dikey doğru testini geçemeyeceği için (her \(x \) değeri birden fazla \( y \) değeri ile eşlenebileceği için) birer fonksiyon olmazlar.
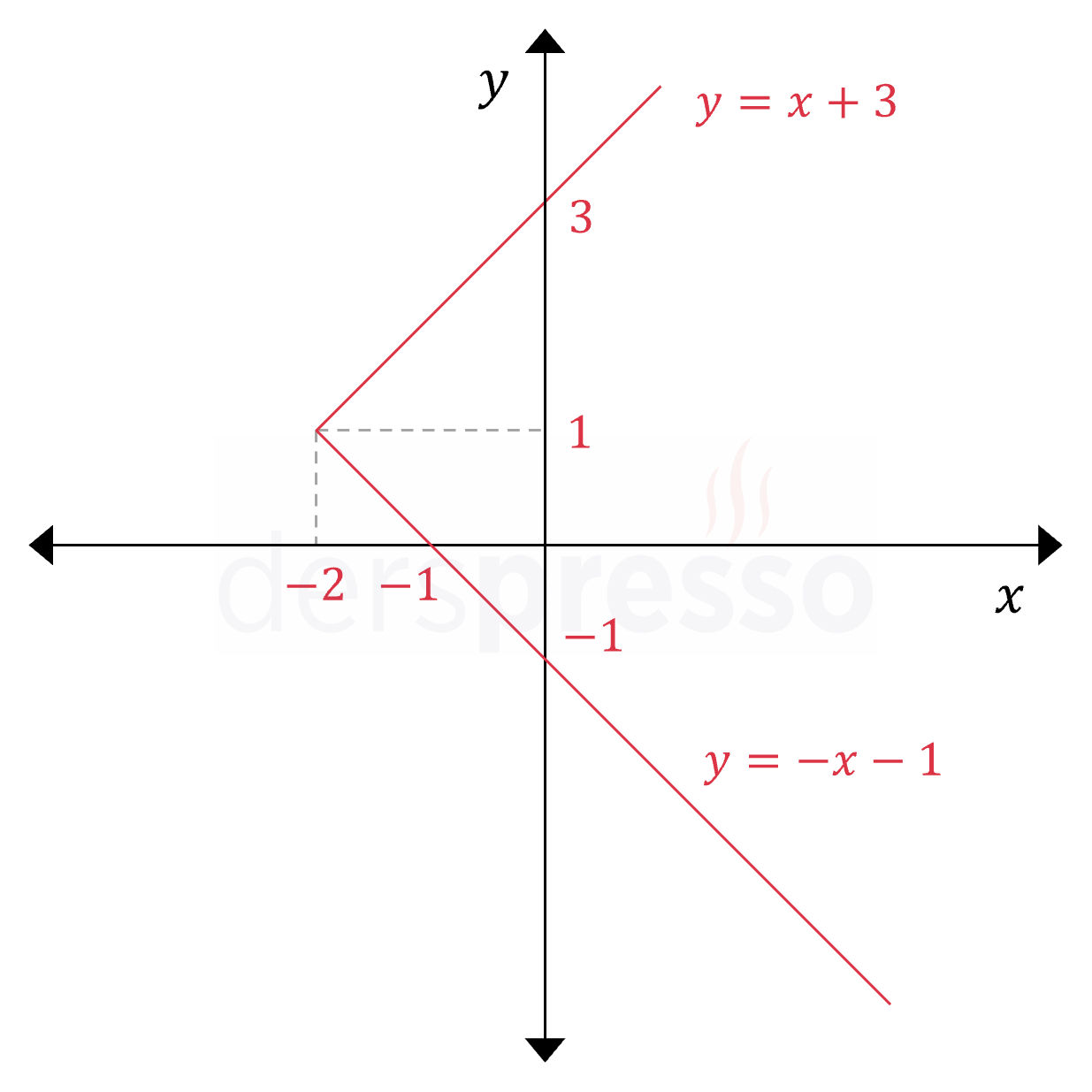
\( \abs{y - 1} = x + 2 \) bağıntısının grafiğini çizelim.
\( y \) değişkeni mutlak değer içinde olduğu için \( y \) için kritik noktaları bulalım.
\( y - 1 = 0 \Longrightarrow y = 1 \) kritik noktadır.
Mutlak değer içindeki ifadede \( y \)'nin katsayısı pozitif olduğu için, ifade kritik noktanın sağında pozitif, solunda negatif değer alır, kritik noktada ise sıfır olur.
\( y \ge 1 \) için:
\( y - 1 = x + 2 \)
\( y = x + 3 \)
\( y \lt 1 \) için:
\( -(y - 1) = x + 2 \)
\( y = -x - 1 \)
Buna göre bağıntının bir kritik nokta ve iki aralıktan oluşan parçalı tanımı aşağıdaki gibi olur.
\( y = \begin{cases} x + 3 & y \ge 1 \\ -x - 1 & y \lt 1 \end{cases} \)
Bu parçalı bağıntının her aralıktaki grafiğini çizdiğimizde aşağıdaki grafiği elde ederiz.
Aşağıdaki örnekte görülebileceği gibi, bir bağıntıda \( x \) ve \( y \) değişkenlerinin ikisi de mutlak değer içinde yer alabilir.
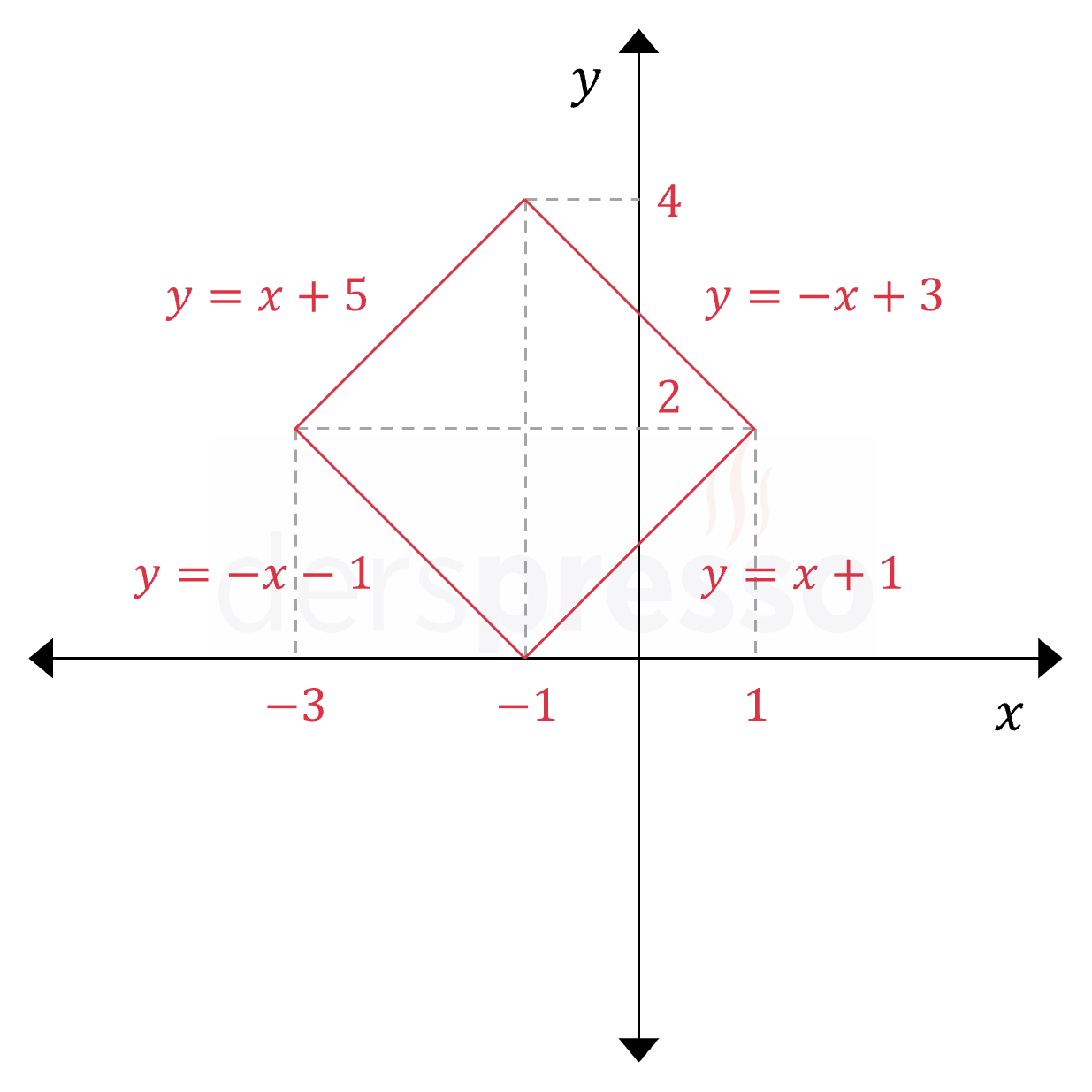
\( \abs{y - 2} = -\abs{x + 1} + 2 \) bağıntısının grafiğini çizelim.
Hem \( y \) hem de \( x \) değişkeni mutlak değer içinde olduğu için iki değişken için kritik noktaları bulalım.
\( y - 2 = 0 \Longrightarrow y = 2 \) kritik noktadır.
\( x + 1 = 0 \Longrightarrow x = -1 \) kritik noktadır.
Mutlak değer içindeki iki ifadede de değişkenlerin katsayıları pozitif olduğu için, ifadeler kritik noktanın sağında pozitif, solunda negatif değer alır, kritik noktada ise sıfır olur.
\( y \ge 2, \quad x \ge -1 \) için:
\( y - 2 = -(x + 1) + 2 \)
\( y = -x + 3 \)
\( y \ge 2, \quad x \lt -1 \) için:
\( y - 2 = (x + 1) + 2 \)
\( y = x + 5 \)
\( y \lt 2, \quad x \ge -1 \) için:
\( -(y - 2) = -(x + 1) + 2 \)
\( y = x + 1 \)
\( y \lt 2, \quad x \lt -1 \) için:
\( -(y - 2) = (x + 1) + 2 \)
\( y = -x - 1 \)
Buna göre bağıntının iki kritik nokta ve dört aralıktan oluşan parçalı tanımı aşağıdaki gibi olur.
\( y = \begin{cases} -x + 3 & y \ge 2, x \ge -1 \\ x + 5 & y \ge 2, x \lt -1 \\ x + 1 & y \lt 2, x \ge -1 \\ -x - 1 & y \lt 2, x \lt -1 \end{cases} \)
Bu parçalı bağıntının her aralıktaki grafiğini çizdiğimizde aşağıdaki grafiği elde ederiz.
\( m \in \mathbb{R^+} \) olmak üzere,
\( \abs{\abs{2x - 6} - m} = 2 \)
denkleminin 4 farklı kökü olması için \( m \)'nin alabileceği en küçük tam sayı değeri kaçtır?
Çözümü GösterSoruyu grafik yardımıyla çözelim.
\( y = \abs{2x - 6} \) mutlak değer fonksiyonunun grafiği aşağıdaki gibi olur.

Bu fonksiyonu \( m \) birim aşağı ötelediğimizde elde edeceğimiz \( y = \abs{2x - 6} - m \) fonksiyonunun grafiği aşağıdaki gibi olur.
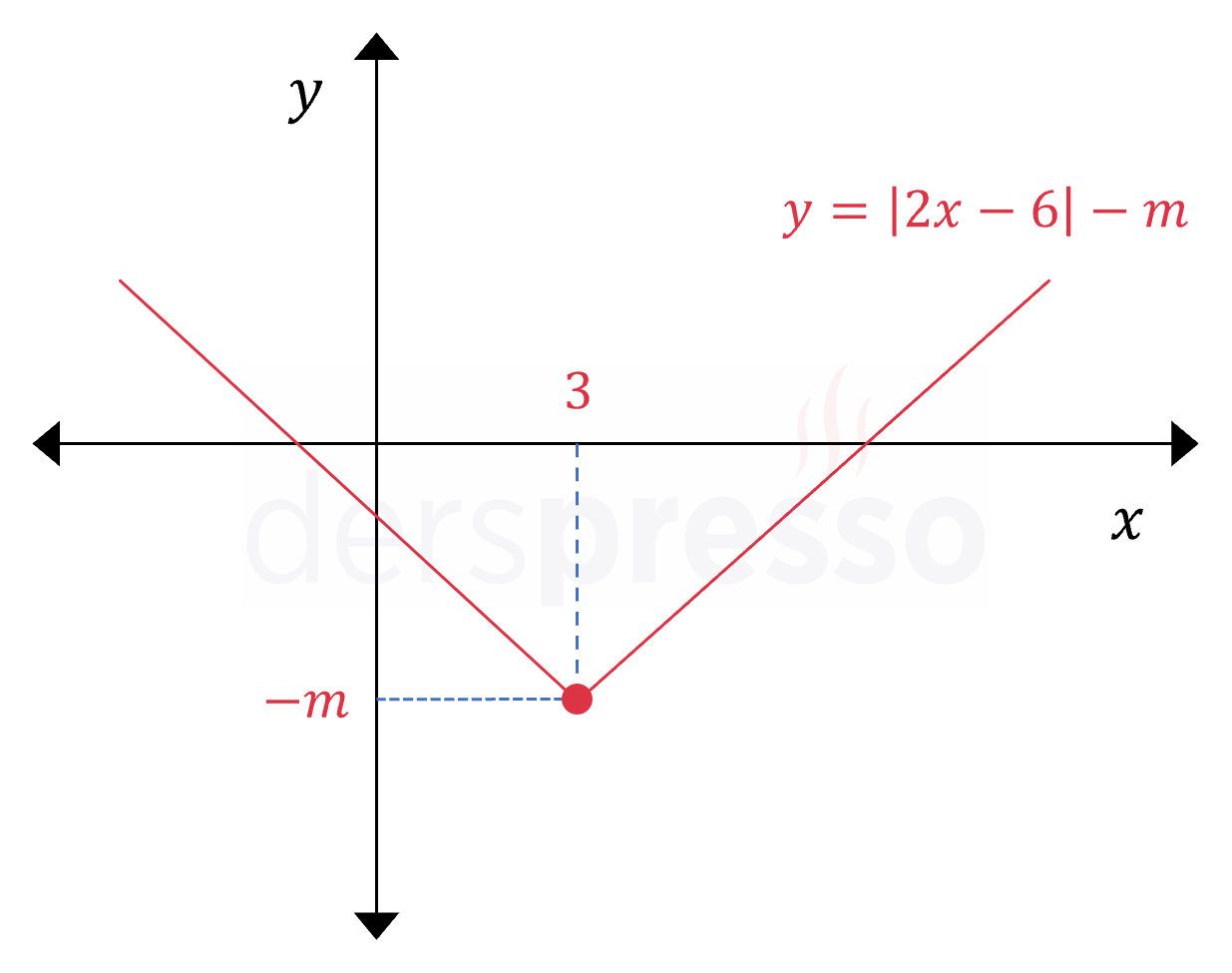
Bu fonksiyonun mutlak değerini aldığımızda elde edeceğimiz \( y = \abs{\abs{2x - 6} - m} \) fonksiyonunun grafiği aşağıdaki gibi olur.
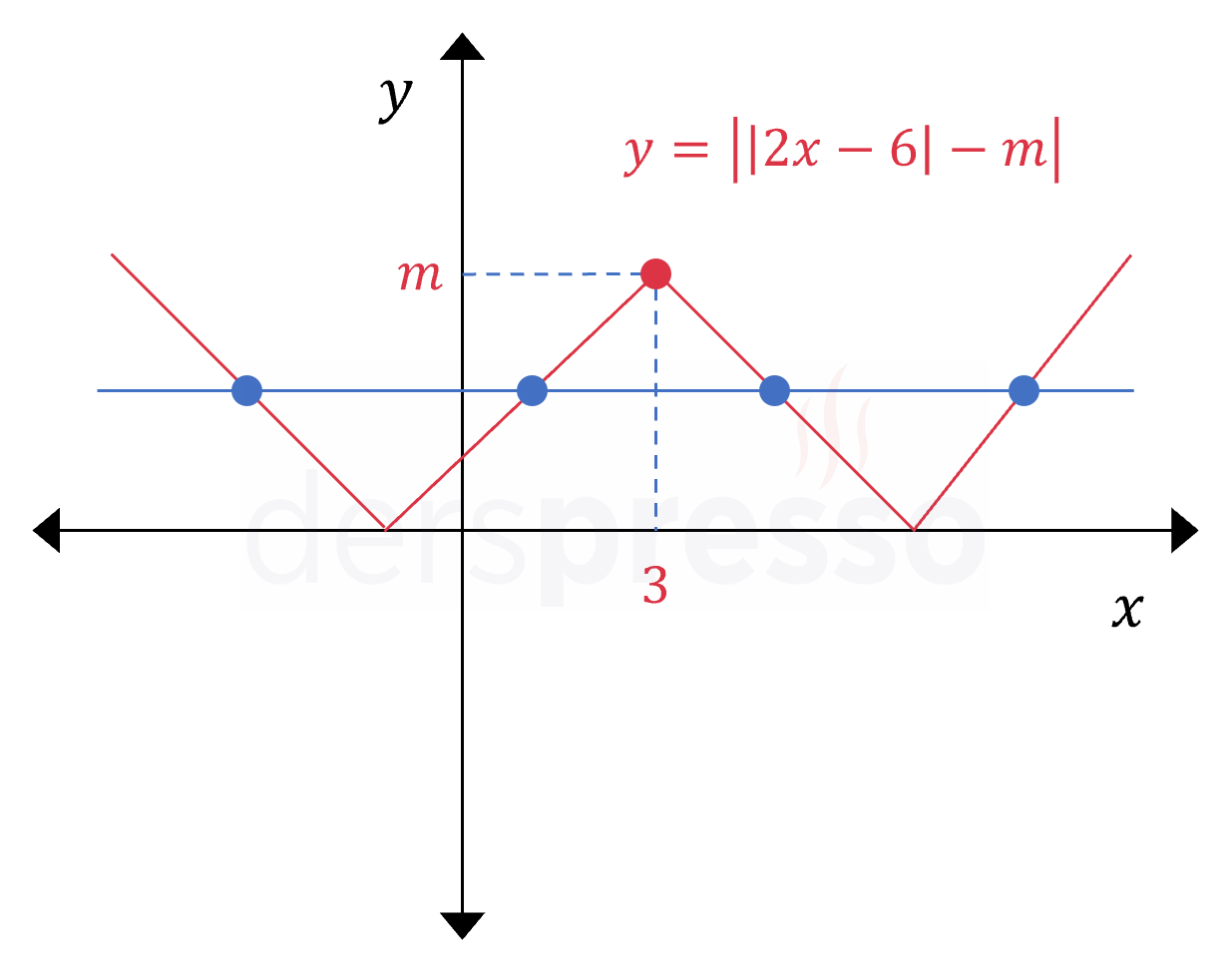
Son elde ettiğimiz grafiğin \( y = 2 \) doğrusu ile 4 noktada kesişmesi için 2 sayısı \( (0, m) \) açık aralığında olmalıdır.
\( 0 \lt 2 \lt m \)
Buna göre \( m \)'nin en küçük tam sayı değeri 3 olmalıdır.
\( \abs{x^2 - 4} = m \) denkleminin çözüm kümesinin aşağıdaki koşulları sağlaması için \( m \) değerleri ya da değer aralıkları ne olmalıdır?
(a) 4 elemanlı
(b) 3 elemanlı
(c) 2 elemanlı
(d) 1 elemanlı
(e) boş küme
Çözümü GösterVerilen eşitliğin çözüm kümesini aşağıdaki iki fonksiyonun grafiklerinin kesişim noktalarının kümesi olarak düşünebiliriz.
\( f(x) = \abs{x^2 - 4} \)
\( g(x) = m \)
\( f \) fonksiyonunun ve farklı \( m \) değerleri için \( g \) fonksiyonunun grafikleri ve her bir durum için kesişim noktaları aşağıdaki şekilde verilmiştir.
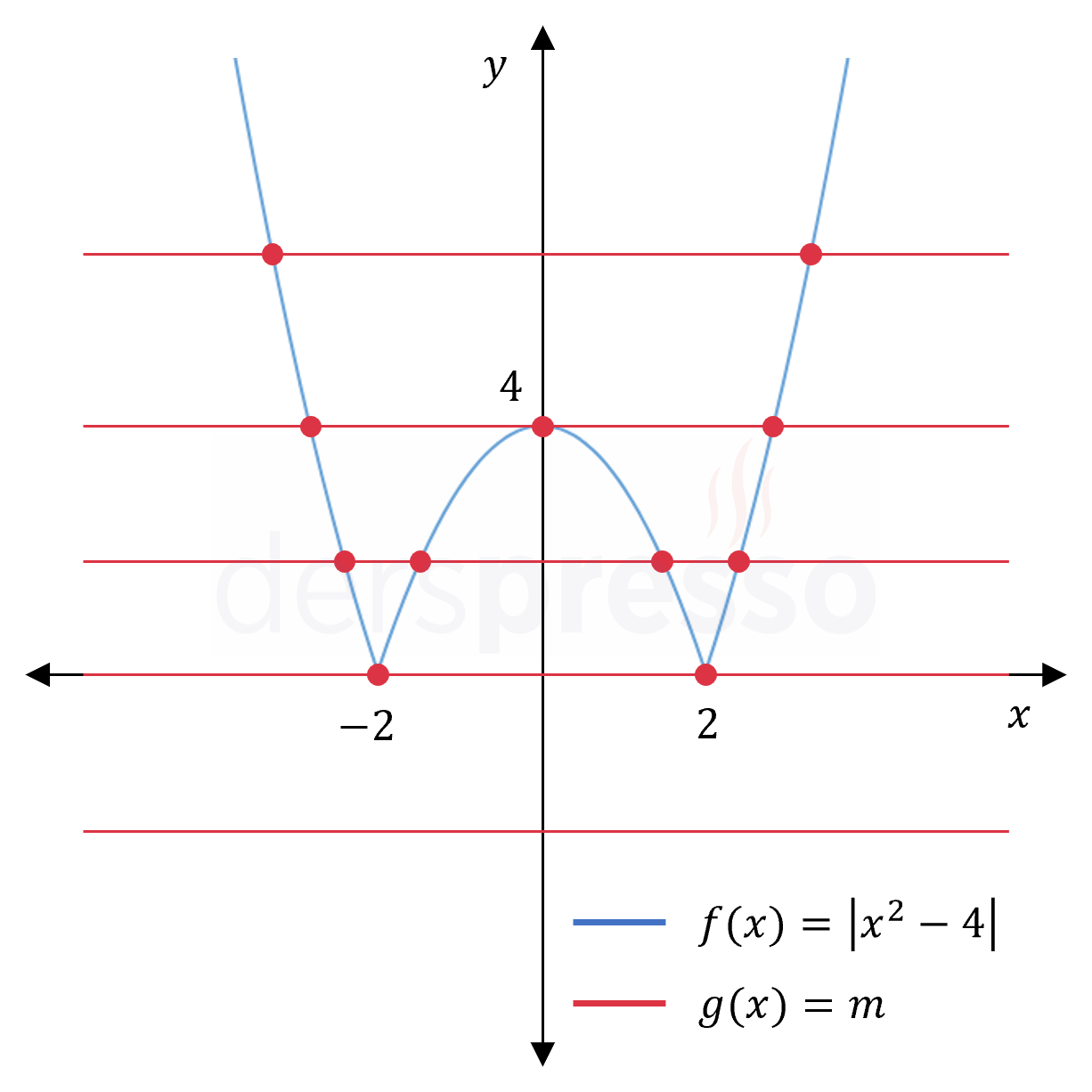
Buna göre denklemin çözüm kümesindeki eleman sayısı \( m \) değerlerine göre aşağıdaki şekilde değişir.
4 elemanlı çözüm kümesi:
\( 0 \lt m \lt 4 \)
3 elemanlı çözüm kümesi:
\( m = 4 \)
2 elemanlı çözüm kümesi:
\( m = 0 \) ya da \( m \gt 4 \)
1 elemanlı çözüm kümesi:
Çözüm kümesi hiçbir durumda 1 elemanlı olamaz.
0 elemanlı çözüm kümesi:
\( m \lt 0 \)