Fonksiyonların Dönüşümü
Bir fonksiyonun tanımında yapılan belirli değişiklikler sonucunda fonksiyon grafiğinde meydana gelen konum ve şekil değişikliklerine dönüşüm denir.
Hatırlatma olarak, bir fonksiyonda \( x \) değerleri fonksiyonun tanım kümesini ve girdi değerlerini, \( f(x) \) değerleri de fonksiyonun görüntü kümesini ve çıktı değerlerini temsil eder.
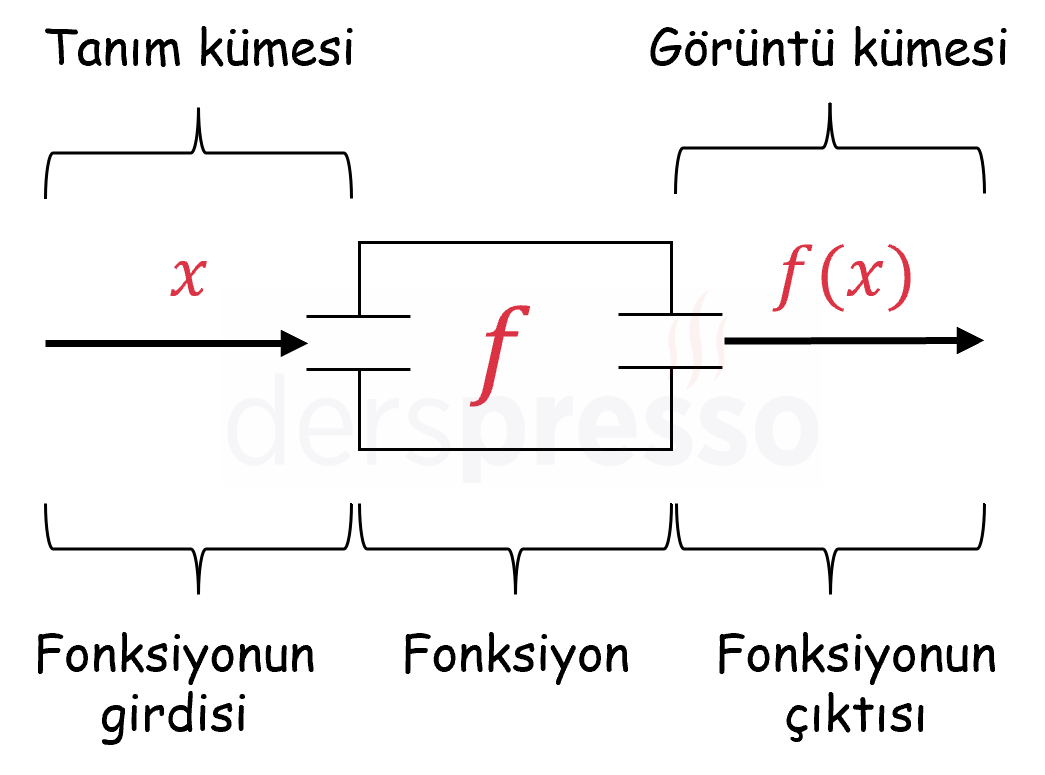
Dönüşüm Tipleri
Dönüşümleri üç başlık altında inceleyebiliriz.
Dikey Dönüşümler
Dikey (çıktıdaki) dönüşümler \( f(x) \) ifadesinin bütününe uygulanan ve fonksiyonun çıktısı olan \( y = f(x) \) değerinde değişikliğe yol açan dönüşümlerdir. Bu dönüşümler fonksiyon grafiğinde \( y \) ekseni boyunca (dikey yönde) konum ve şekil değişimlerine yol açar.
Bir fonksiyona aşağıdaki şekildeki işlemleri kullanarak öteleme, daralma/genişleme, yansıma ve mutlak değer olmak üzere dört dikey dönüşüm uygulayabiliriz. Bu dönüşümlerin her birini önümüzdeki bölümlerde inceleyeceğiz.

\( f(x) = x^2 \) olmak üzere,
\( g(x) = -3f(x) + 2 = -3x^2 + 2 \)
Yatay Dönüşümler
Yatay (girdideki) dönüşümler \( f(x) \) ifadesinde parantezin içine uygulanan ve fonksiyonun girdisi olan \( x \) değerinde değişikliğe yol açan dönüşümlerdir. Bu dönüşümler fonksiyon grafiğinde \( x \) ekseni boyunca (yatay yönde) konum ve şekil değişimlerine yol açar.
Bir fonksiyona aşağıdaki şekildeki işlemleri kullanarak öteleme, daralma/genişleme, yansıma ve mutlak değer olmak üzere dört yatay dönüşüm uygulayabiliriz. Bu dönüşümlerin her birini önümüzdeki bölümlerde inceleyeceğiz.

\( f(x) = x^2 \) olmak üzere,
\( g(x) = f(-2(x + 1)) = (-2(x + 1))^2 \)
Aşağıdaki örnekte dikey ve yatay dönüşümlerin fonksiyon değerlerine olan etkisini görebiliriz.
| \( x \) | \( f(x) = x^2 \) | \( g(x) = f(x) + 2 \) | \( h(x) = f(x + 2) \) |
|---|---|---|---|
| \( 0 \) | \( 0 \) | \( 2 \) | \( 4 \) |
| \( 1 \) | \( 1 \) | \( 3 \) | \( 9 \) |
| \( 2 \) | \( 4 \) | \( 6 \) | \( 16 \) |
| \( 3 \) | \( 9 \) | \( 11 \) | \( 25 \) |
| \( 4 \) | \( 16 \) | \( 18 \) | \( 36 \) |
| \( 5 \) | \( 25 \) | \( 27 \) | \( 49 \) |
| \( 6 \) | \( 36 \) | \( 38 \) | \( 64 \) |
Bu tablodan yapabileceğimiz iki çıkarım aşağıdaki gibidir.
- Dikey (çıktıdaki) bir dönüşüm sonucunda fonksiyon aynı \( x \) değeri için yeni bir \( y \) değeri üretmektedir, bu da fonksiyon grafiğinde \( y \) ekseni boyunca (dikey) bir değişime yol açmaktadır.
- Yatay (girdideki) bir dönüşüm sonucunda (renkli kodlamalarda görülebileceği gibi) fonksiyon aynı \( y \) değerini farklı bir \( x \) değeriyle üretmektedir, bu da fonksiyon grafiğinde \( x \) ekseni boyunca (yatay) bir değişime yol açmaktadır.
Döndürme
Bu dönüşümler fonksiyon grafiğini orijin etrafında belirli açılarda döndüren dönüşümlerdir.
Dikey ve Yatay Dönüşüm Tipleri
Dikey ve yatay dönüşümleri fonksiyon grafiğinin şekil ve konumunda oluşturdukları değişim açısından dört başlık altında inceleyebiliriz.
| Dönüşüm Tipi | Dikey Dönüşüm | Yatay Dönüşüm |
|---|---|---|
| Ötemele | \( f(x) + k \) | \( f(x + c) \) |
| Daralma/Genişleme | \( a \cdot f(x) \) | \( f(bx) \) |
| Yansıma (Simetri) | \( -f(x) \) | \( f(-x) \) |
| Mutlak Değer | \( \abs{f(x)} \) | \( f(\abs{x}) \) |
Bir fonksiyona uygulanabilecek dikey ve yatay dönüşümler (mutlak değer dönüşümü dışında) aşağıdaki şekilde özetlenmiştir. Görülebileceği gibi, dikey dönüşümler parantezin dışına, yani fonksiyonun çıktısına, yatay dönüşümler de parantezin içine, yani fonksiyonun girdisine uygulanmaktadır.
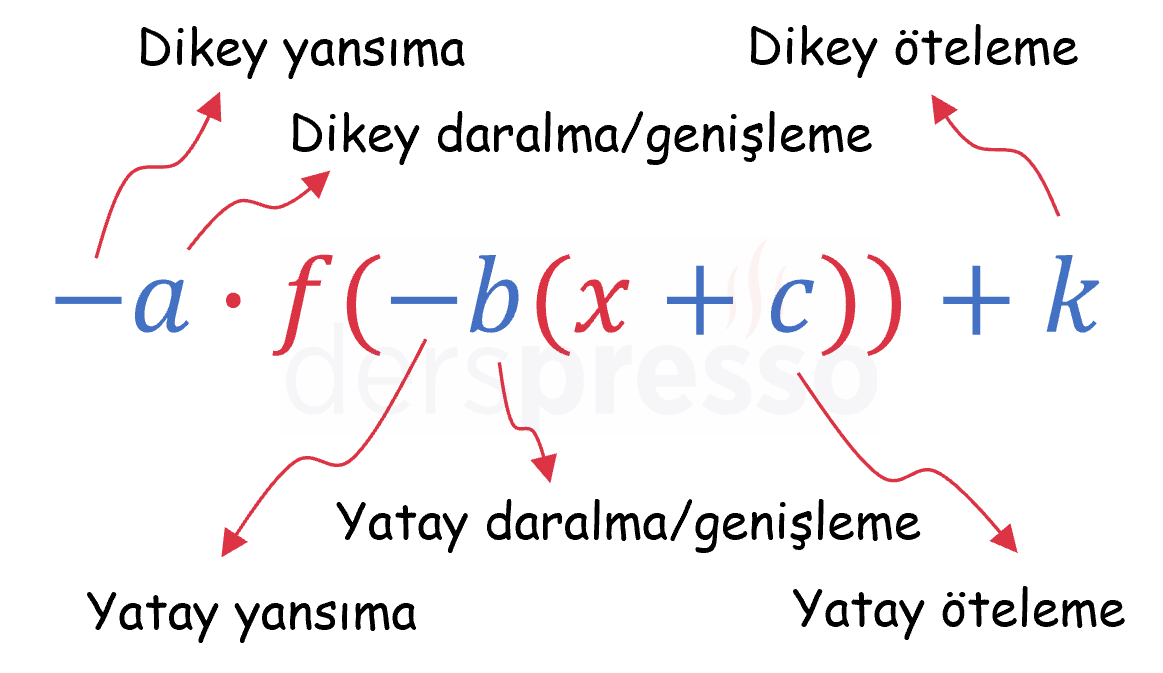
Örnek olarak, farklı \( f(x) \) fonksiyonlarına \( g(x) = -3f(2(x + 1)) - 4 \) dönüşümü uygulandığında oluşan yeni fonksiyonlar aşağıdaki tabloda verilmiştir.
| Fonksiyon | Dönüşüm |
|---|---|
| \( f(x) = x \) | \( g(x) = -3(2(x + 1)) - 4 \) |
| \( f(x) = x^2 \) | \( g(x) = -3(2(x + 1))^2 - 4 \) |
| \( f(x) = \sqrt{x} \) | \( g(x) = -3\sqrt{2(x + 1)} - 4 \) |
| \( f(x) = \sin{x} \) | \( g(x) = -3\sin(2(x + 1)) - 4 \) |
| \( f(x) = 2^x \) | \( g(x) = -3 \cdot 2^{2(x + 1)} - 4 \) |
| \( f(x) = \log{x} \) | \( g(x) = -3\log(2(x + 1)) - 4 \) |
| \( f(x) = \abs{x} \) | \( g(x) = -3\abs{2(x + 1)} - 4 \) |
\( f(x) = 2 - e^{3x + 4} \) fonksiyonu önce 3 birim sağa öteleniyor, daha sonra sonra \( x \) eksenine göre simetriği alınıp 5 birim yukarı öteleniyor.
Bu dönüşümler sonucunda elde edilen \( g(x) \) fonksiyonunun denklemi nedir?
Çözümü Göster\( f(x) \) fonksiyonu 3 birim sağa ötelendiğinde \( f(x - 3) \) fonksiyonu elde edilir.
\( f(x - 3) = 2 - e^{3(x - 3) + 4} \)
\( = 2 - e^{3x - 5} \)
\( f(x) \) fonksiyonunun \( x \) eksenine göre simetriği alındığında \( -f(x) \) fonksiyonu elde edilir.
\( -f(x - 3) = -(2 - e^{3x - 5}) \)
\( = e^{3x - 5} - 2 \)
\( f(x) \) fonksiyonu 5 birim yukarı ötelendiğinde \( f(x) + 5 \) fonksiyonu elde edilir.
\( -f(x - 3) + 5 = e^{3x - 5} - 2 + 5 \)
\( = e^{3x - 5} + 3 \)
Buna göre belirtilen dönüşümler uygulandığında aşağıdaki fonksiyon elde edilir.
\( g(x) = -f(x - 3) + 5 \)
\( = e^{3x - 5} + 3 \)
\( f(x) = 5^{x^2} \) fonksiyonu veriliyor.
\( g(x) = 5^{x^2 - 6x + 7} - 4 \) fonksiyonunu \( f \) fonksiyonu cinsinden yazınız.
Çözümü Göster\( x^2 - 6x + 7 \) ifadesini \( x^2 \) ifadesinin bir dönüşümü olarak ifade edelim.
\( x^2 - 6x + 7 = x^2 - 6x + 9 - 2 \)
\( = (x - 3)^2 - 2 \)
\( f \) fonksiyonuna \( x \longmapsto x - 3 \) dönüşümü uygulayalım.
\( f(x - 3) = 5^{(x - 3)^2} \)
Elde ettiğimiz fonksiyonu 25'e bölelim.
\( \dfrac{f(x - 3)}{25} = \dfrac{5^{(x - 3)^2}}{25} = 5^{(x - 3)^2 - 2} \)
Elde ettiğimiz fonksiyondan 4 çıkaralım.
\( \dfrac{f(x - 3)}{25} - 4 = 5^{(x - 3)^2 - 2} - 4 \)
Elde ettiğimiz ifade \( g(x) \)'e eşittir.
\( g(x) = \dfrac{f(x - 3)}{25} - 4 \) bulunur.
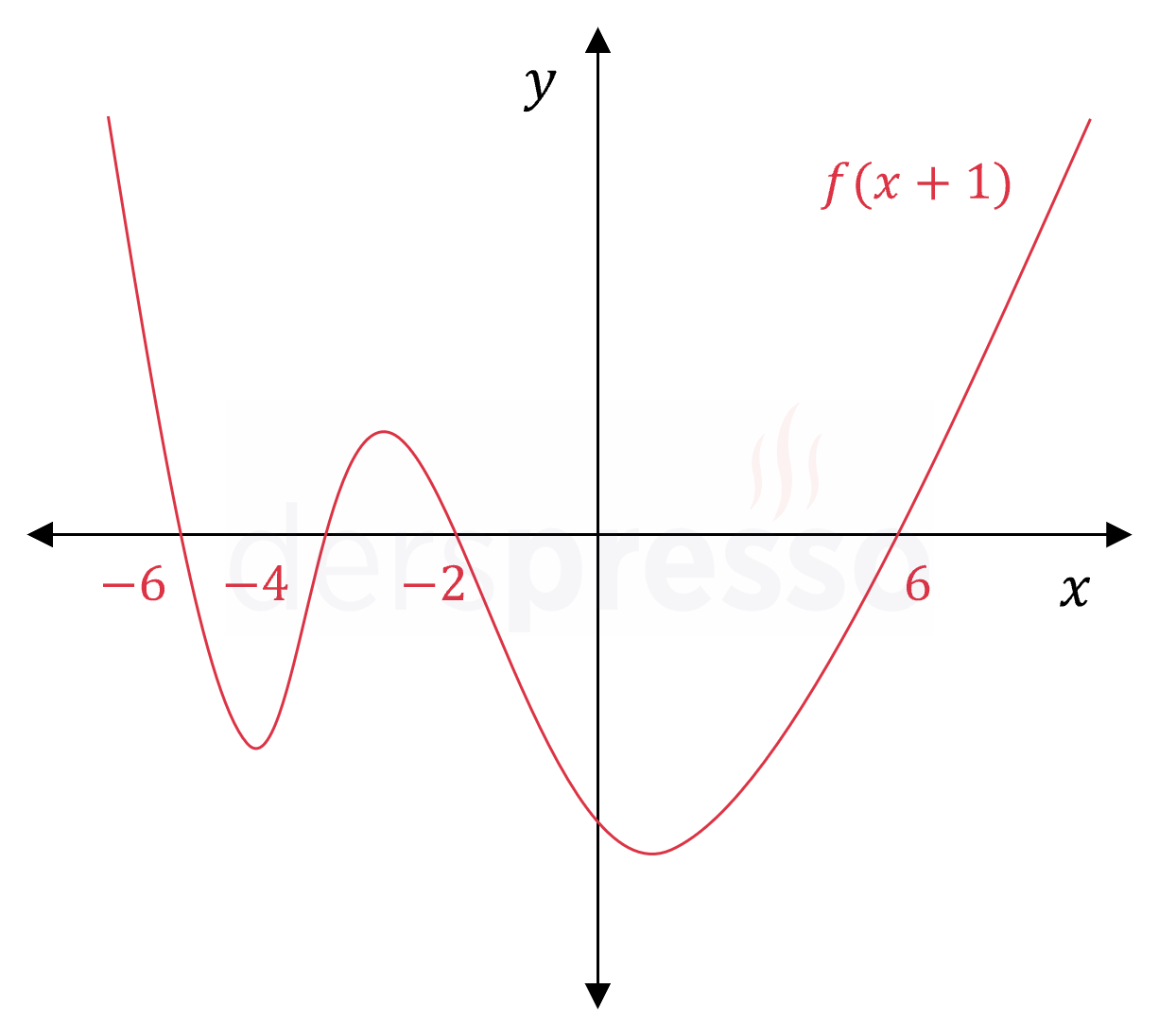
Verilen grafik \( y = f(x + 1) \) fonksiyonuna ait olduğuna göre, \( f(2x + 7) \) fonksiyonunun kökler toplamı kaçtır?
Çözümü GösterGrafiği verilen \( f(x + 1) \) fonksiyonu \( x \) eksenini \( \{ -6, -4, -2, 6 \} \) noktalarında keser.
\( y = f(x + 1) \) fonksiyonuna iki dönüşüm uygulayarak \( f(2x + 7) \) fonksiyonunu elde edebiliriz.
1. dönüşüm: Yatay daralma
\( x \longmapsto 2x \)
\( f(x + 1) \longmapsto f(2x + 1) \)
Bu dönüşüm sonucunda fonksiyonun grafiği üzerindeki tüm noktaların \( y \) eksenine uzaklığı \( \times \frac{1}{2} \) olur ve grafiğin \( x \) eksenini kestiği noktalar \( \{ -3, -2, -1, 3 \} \) olur.
2. dönüşüm: 3 birim sola öteleme
\( x \longmapsto x + 3 \)
\( f(2x + 1) \longmapsto f(2(x + 3) + 1) = f(2x + 7) \)
Bu dönüşüm sonucunda fonksiyonun \( x \) eksenini kestiği noktalar 3 birim sola ötelenir ve grafiğin \( x \) eksenini kestiği noktalar \( \{ -6, -5, -4, 0 \} \) olur.
Buna göre \( f(2x + 7) \) fonksiyonunun kökler toplamı \( (-6) + (-5) + (-4) + 0 = -15 \) olur.
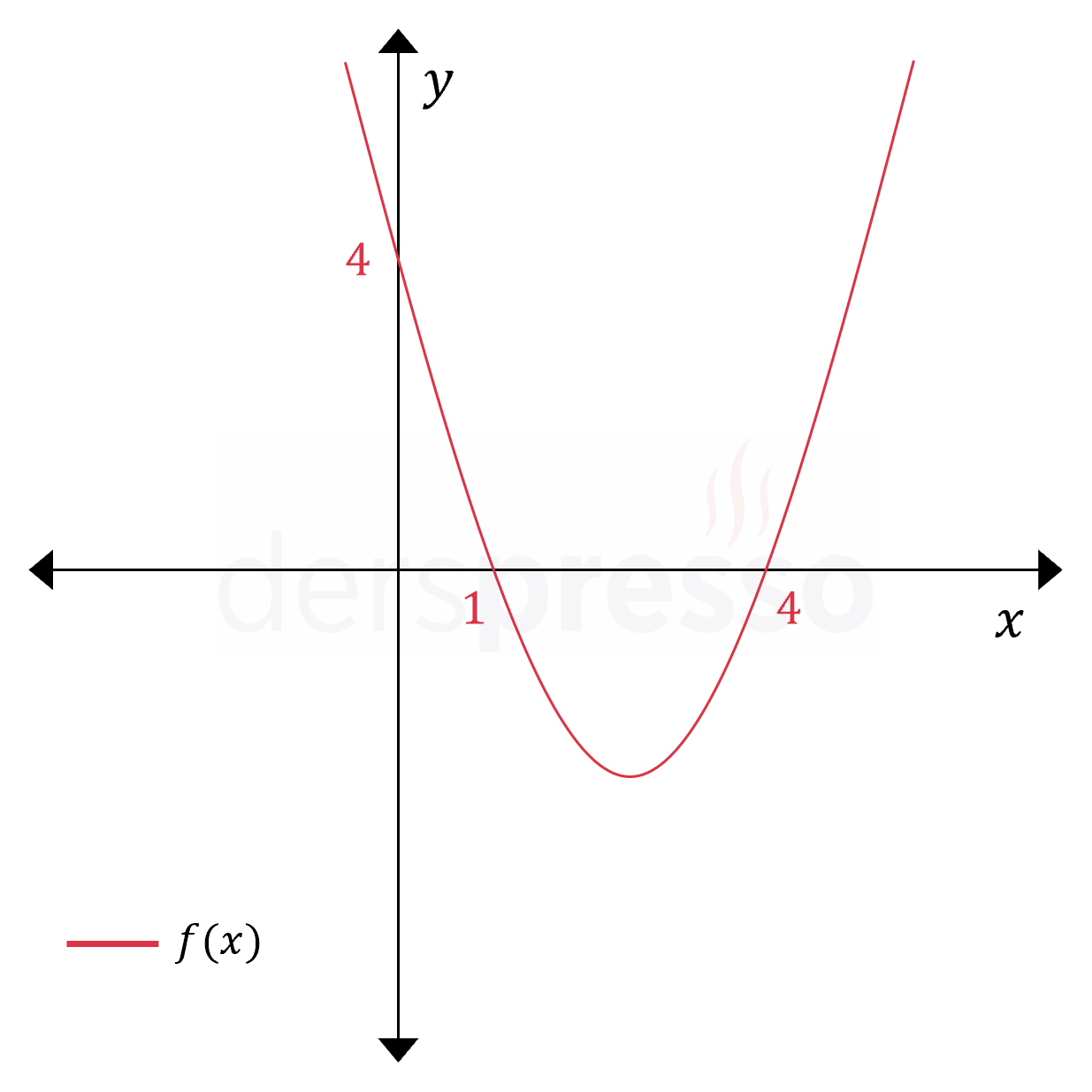
Yukarıda \( f(x) = (x - 1)(x - 4) \) fonksiyonunun grafiği verilmiştir.
Buna göre aşağıdaki fonksiyonlardan hangisinin eksenleri kestiği üç noktadan en az ikisi \( f(x) \) ile ortak değildir?
(a) \( -2f(x) \)
(b) \( f(\frac{1}{4}x) \)
(c) \( \abs{f(4x)} \)
(d) \( -2f(x + 3) \)
(e) \( -f(2x + 2) \)
Çözümü Göster(a) seçeneği:
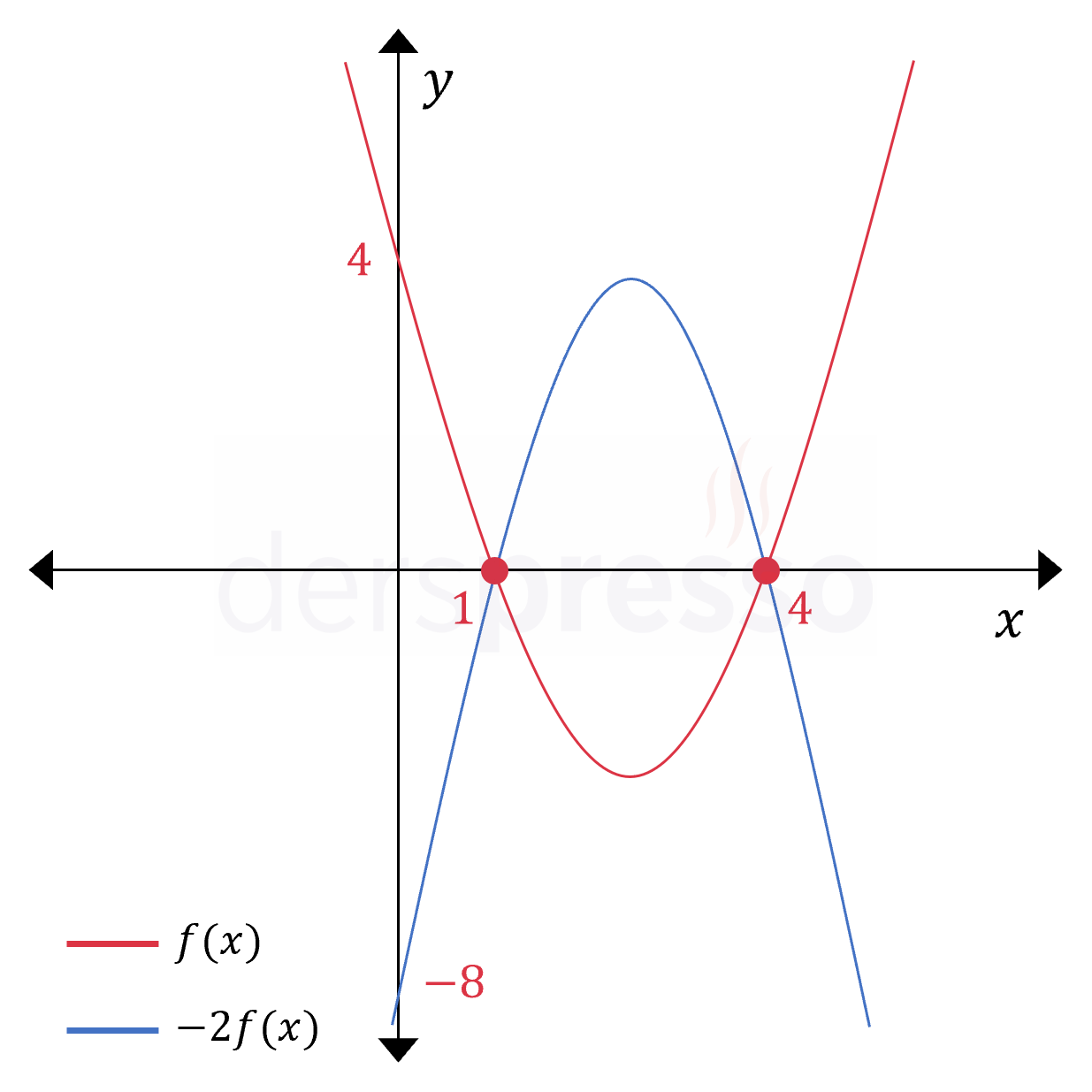
\( -2f(x) \)
\( f \) fonksiyonunun çıktısı 2 ile çarpıldığında grafiğin \( x \) eksenini kestiği noktalar değişmez ve \( x \in \{1, 4\} \) olarak kalır, \( y \) eksenini kestiği noktanın \( x \) eksenine uzaklığı \( \times 2 \) olur (\( y = 8 \)).
Elde edilen fonksiyonun çıktısı -1 ile çarpıldığında grafiğin \( x \) eksenini kestiği noktalar değişmez ve \( x \in \{1, 4\} \) olarak kalır, \( y \) eksenini kestiği nokta \( y = -8 \) olur.
Buna göre oluşan fonksiyonun grafiği aşağıdaki gibi olur. Grafiğin eksenleri kestiği noktalardan ikisi \( f(x) \) ile aynı olur.
(b) seçeneği:
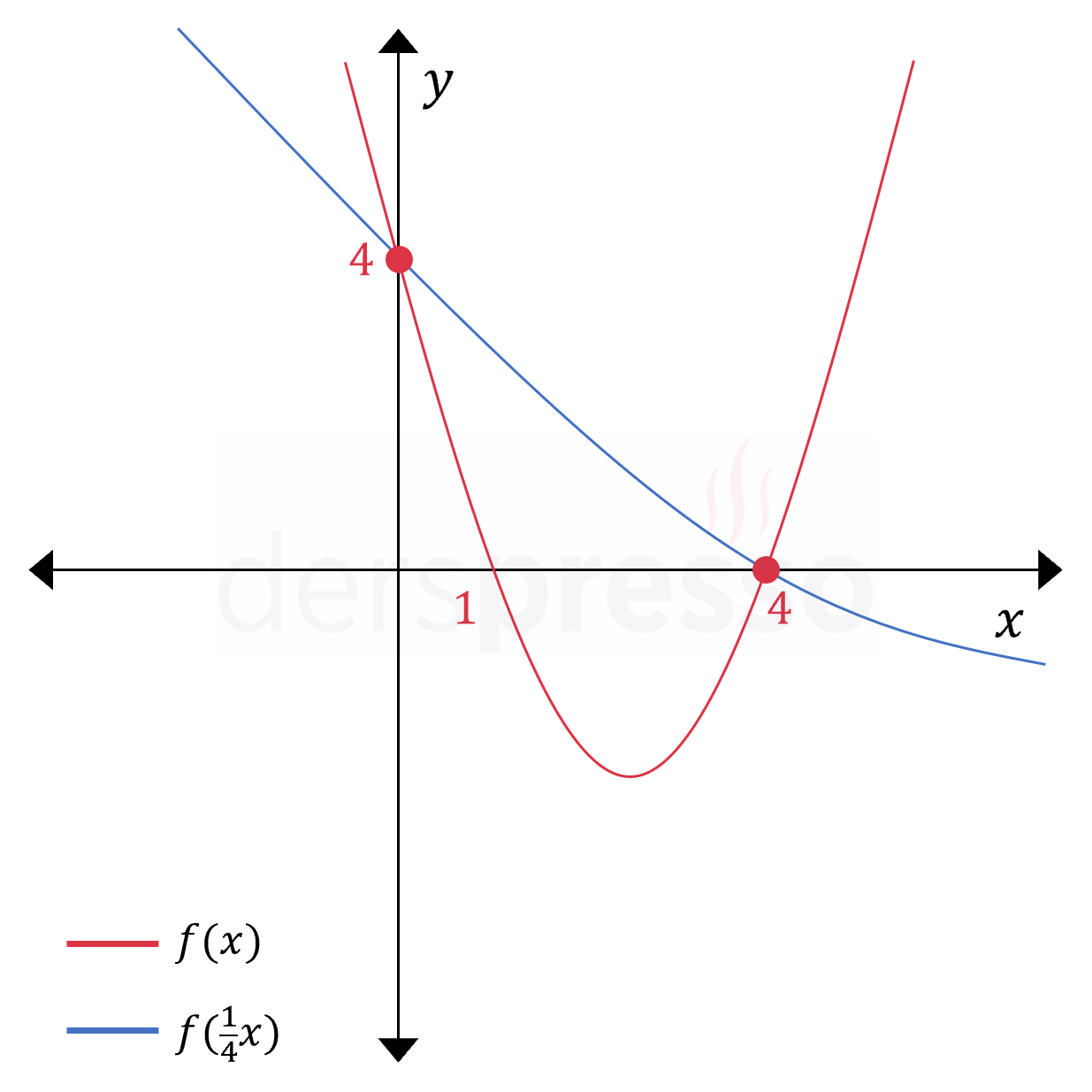
\( f(\frac{1}{4}x) \)
\( f \) fonksiyonunun girdisi 4'e bölününce grafiğin \( x \) eksenini kestiği noktaların \( y \) eksenine uzaklığı \( \times 4 \) olur (\( x \in \{4, 16\} \)), \( y \) eksenini kestiği nokta değişmez ve \( y = 4 \) olarak kalır.
Buna göre oluşan fonksiyonun grafiği aşağıdaki gibi olur. Grafiğin eksenleri kestiği noktalardan ikisi \( f(x) \) ile aynı olur.
(c) seçeneği:
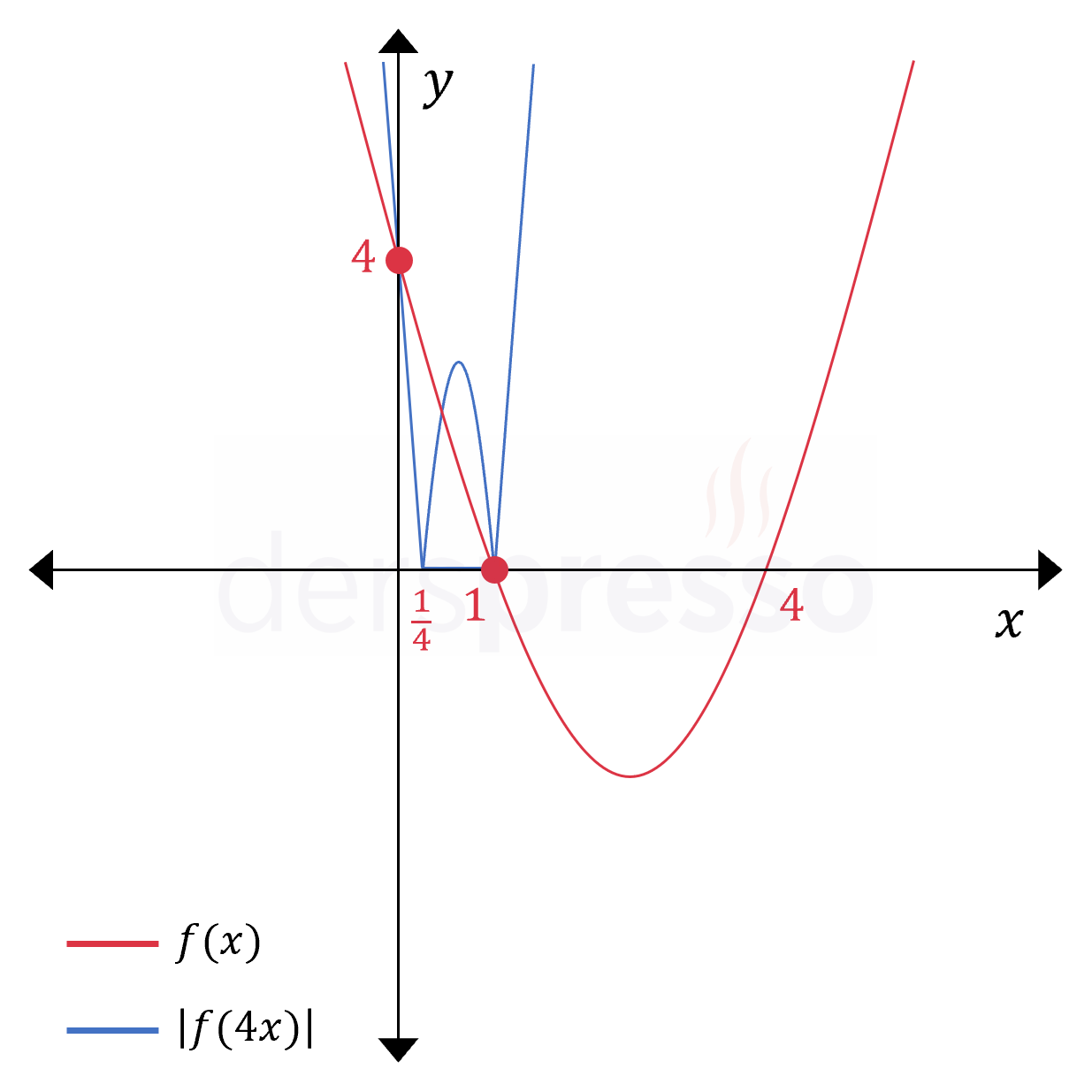
\( \abs{f(4x)} \)
\( f \) fonksiyonunun girdisi 4 ile çarpıldığında grafiğin \( x \) eksenini kestiği noktaların \( y \) eksenine uzaklığı \( \times \frac{1}{4} \) olur (\( x \in \{\frac{1}{4}, 1\} \)), \( y \) eksenini kestiği nokta değişmez ve \( y = 4 \) olarak kalır.
Elde edilen fonksiyonun çıktısının mutlak değeri alındığında grafiğin \( x \) eksenini kestiği noktalar değişmez, \( y \) eksenini kestiği nokta da pozitif tarafta olduğu için değişmez ve \( y = 4 \) olarak kalır.
Buna göre oluşan fonksiyonun grafiği aşağıdaki gibi olur. Grafiğin eksenleri kestiği noktalardan ikisi \( f(x) \) ile aynı olur.
(d) seçeneği:
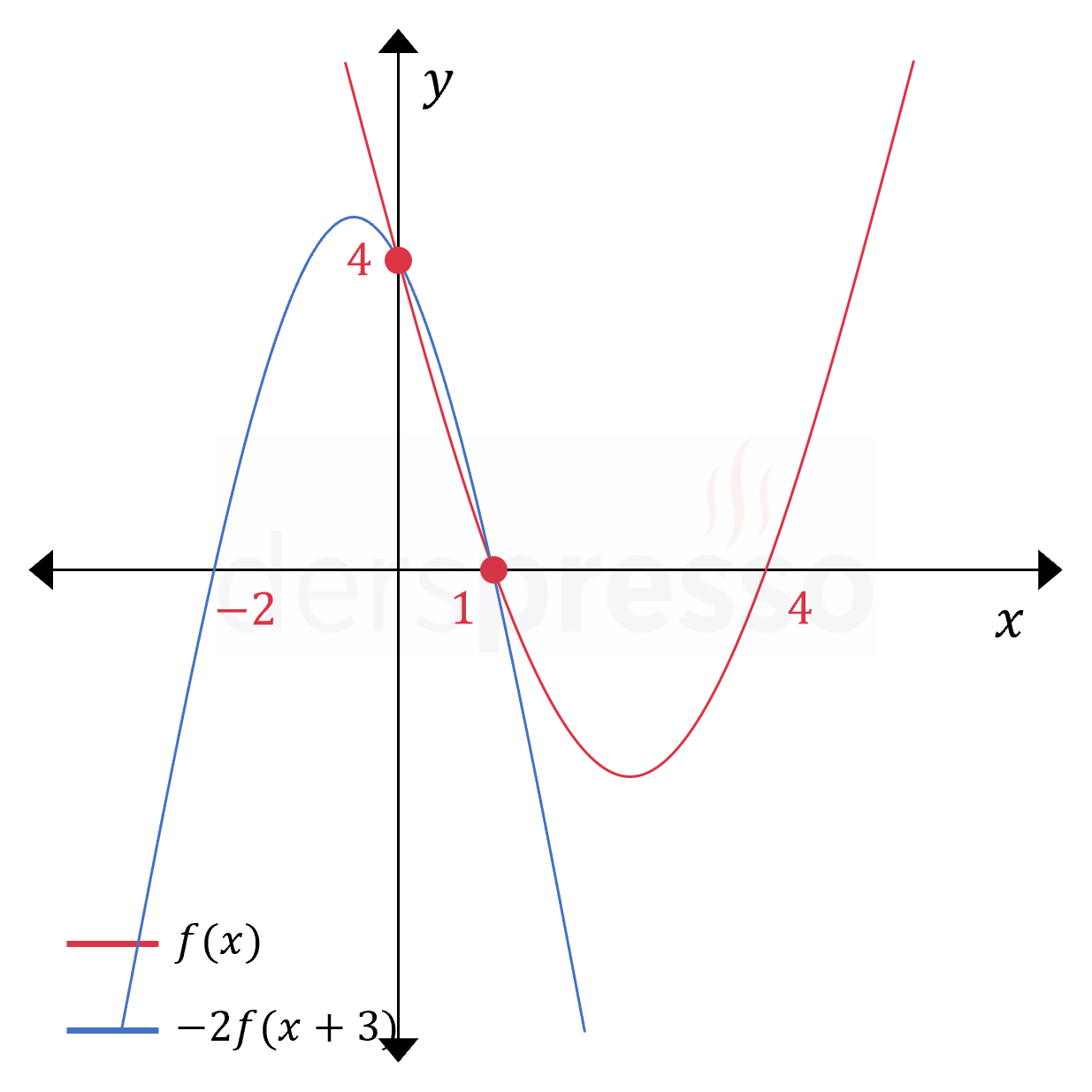
\( -2f(x + 3) \)
\( f \) fonksiyonunun girdisine 3 eklendiğinde grafiğin \( x \) eksenini kestiği noktalar 3 birim sola ötelenir ve \( x \in \{-2, 1\} \) olur.
Elde edilen fonksiyonun çıktısı -2 ile çarpıldığında grafiğin \( x \) eksenini kestiği noktalar değişmez.
Elde edilen fonksiyonun \( y \) eksenini kestiği noktayı bulmak için \( x = 0 \) koyalım.
\( -2f(0 + 3) = -2f(3) \)
\( = -2(3 - 1)(3 - 4) = 4 \)
Elde edilen fonksiyon \( y \) eksenini \( y = 4 \) noktasında keser.
Buna göre oluşan fonksiyonun grafiği aşağıdaki gibi olur. Grafiğin eksenleri kestiği noktalardan ikisi \( f(x) \) ile aynı olur.
(e) seçeneği:
\( -f(2x + 2) \)
\( -f(2x + 2) = -f(2(x + 1)) \)
\( f \) fonksiyonunun girdisi 2 ile çarpıldığında grafiğin \( x \) eksenini kestiği noktaların \( y \) eksenine uzaklığı \( \times \frac{1}{2} \) olur (\( x \in \{\frac{1}{2}, 2\} \)), \( y \) eksenini kestiği nokta değişmez ve \( y = 4 \) olarak kalır.
Elde edilen fonksiyonun girdisine 1 eklendiğinde grafiğin \( x \) eksenini kestiği noktalar 1 birim sola ötelenir ve \( x \in \{-\frac{1}{2}, 1\} \) olur.
Elde edilen fonksiyonun çıktısı -1 ile çarpıldığında grafiğin \( x \) eksenini kestiği noktalar değişmez.
Elde edilen fonksiyonun \( y \) eksenini kestiği noktayı bulmak için \( x = 0 \) koyalım.
\( -f(2(0 + 1)) = -f(2) \)
\( = -(2 - 1)(2 - 4) = 2 \)
Elde edilen fonksiyon \( y \) eksenini \( y = 2 \) noktasında keser.
Buna göre oluşan fonksiyonun grafiği aşağıdaki gibi olur. Grafiğin eksenleri kestiği noktalardan sadece biri \( f(x) \) ile aynı olur.
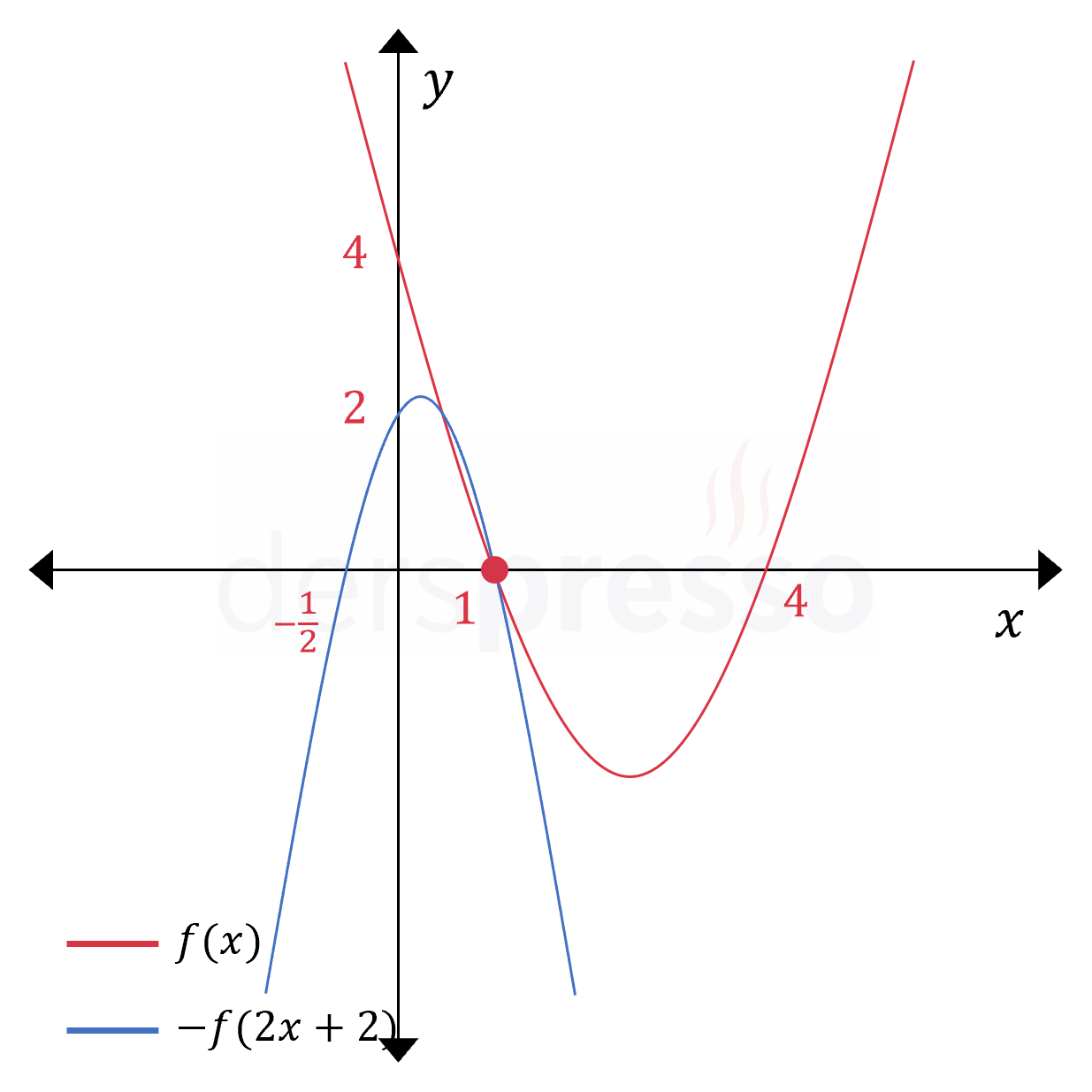
Buna göre doğru cevap (e) seçeneğidir.