Döndürme
Fonksiyon grafiğini orijin etrafında saat yönünün tersi yönde aşağıda belirtilen açılarda döndürmek için \( x \) ve \( y \) değişkenlerine aşağıdaki dönüşümler uygulanır.
90° Döndürme
Fonksiyon grafiğini orijin etrafında saat yönünün tersi yönde 90° döndürmek için fonksiyondaki her \( x \) yerine \( y \), \( y \) yerine de \( -x \) konur.
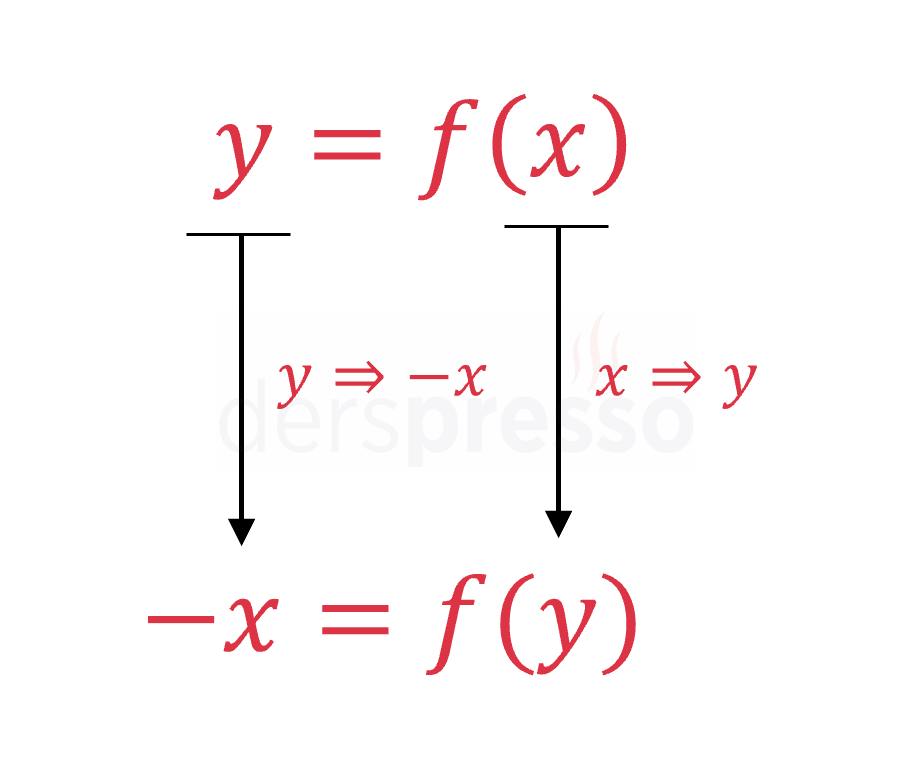
\( y = f(x) = x^2 \Longrightarrow -x = f(y) = y^2 \)

180° Döndürme
Fonksiyon grafiğini orijin etrafında saat yönünün tersi yönde 180° döndürmek için fonksiyondaki her \( x \) yerine \( -x \), \( y \) yerine de \( -y \) konur.
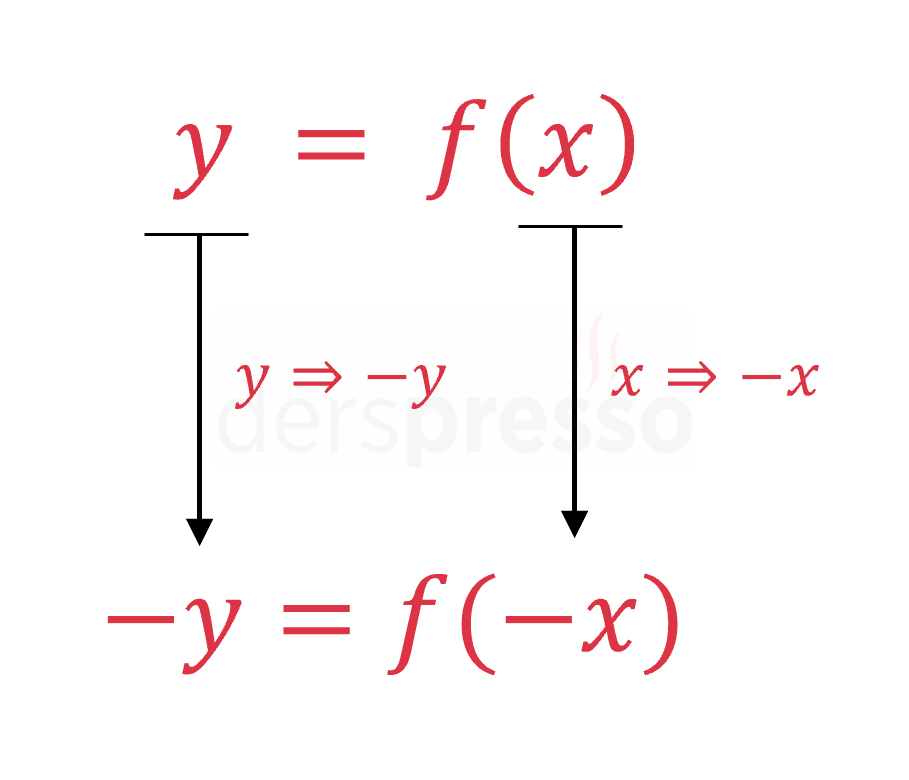
\( y = f(x) = x^2 \Longrightarrow -y = f(-x) = (-x)^2 \)

270° Döndürme
Fonksiyon grafiğini orijin etrafında saat yönünün tersi yönde 270° döndürmek için fonksiyondaki her \( x \) yerine \( -y \), \( y \) yerine de \( x \) konur.
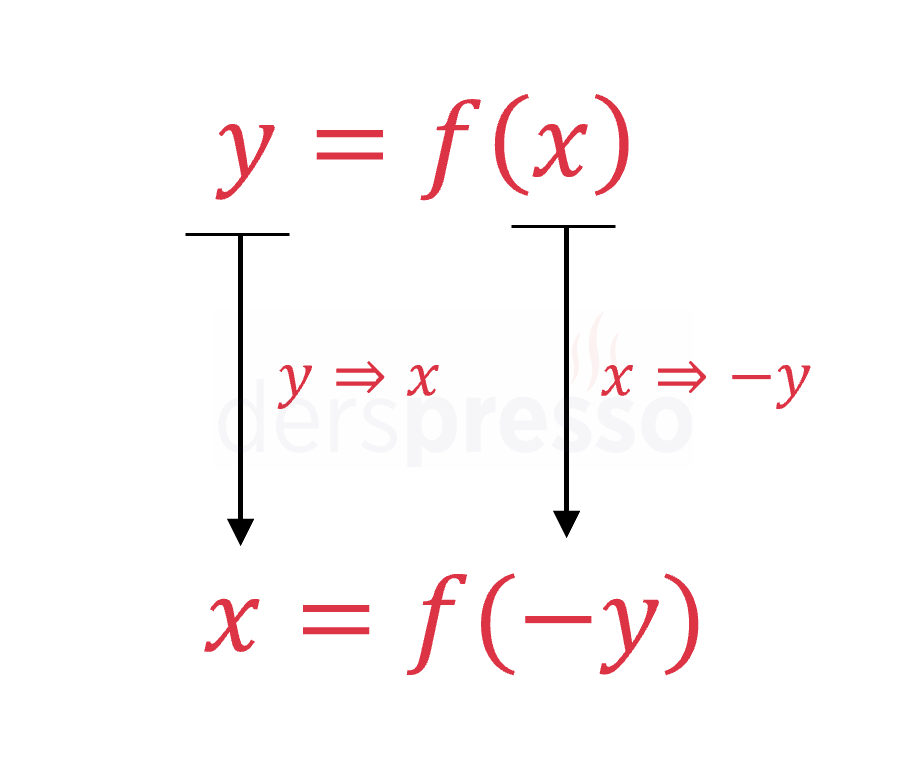
\( y = f(x) = x^2 \Longrightarrow x = f(-y) = (-y)^2 \)
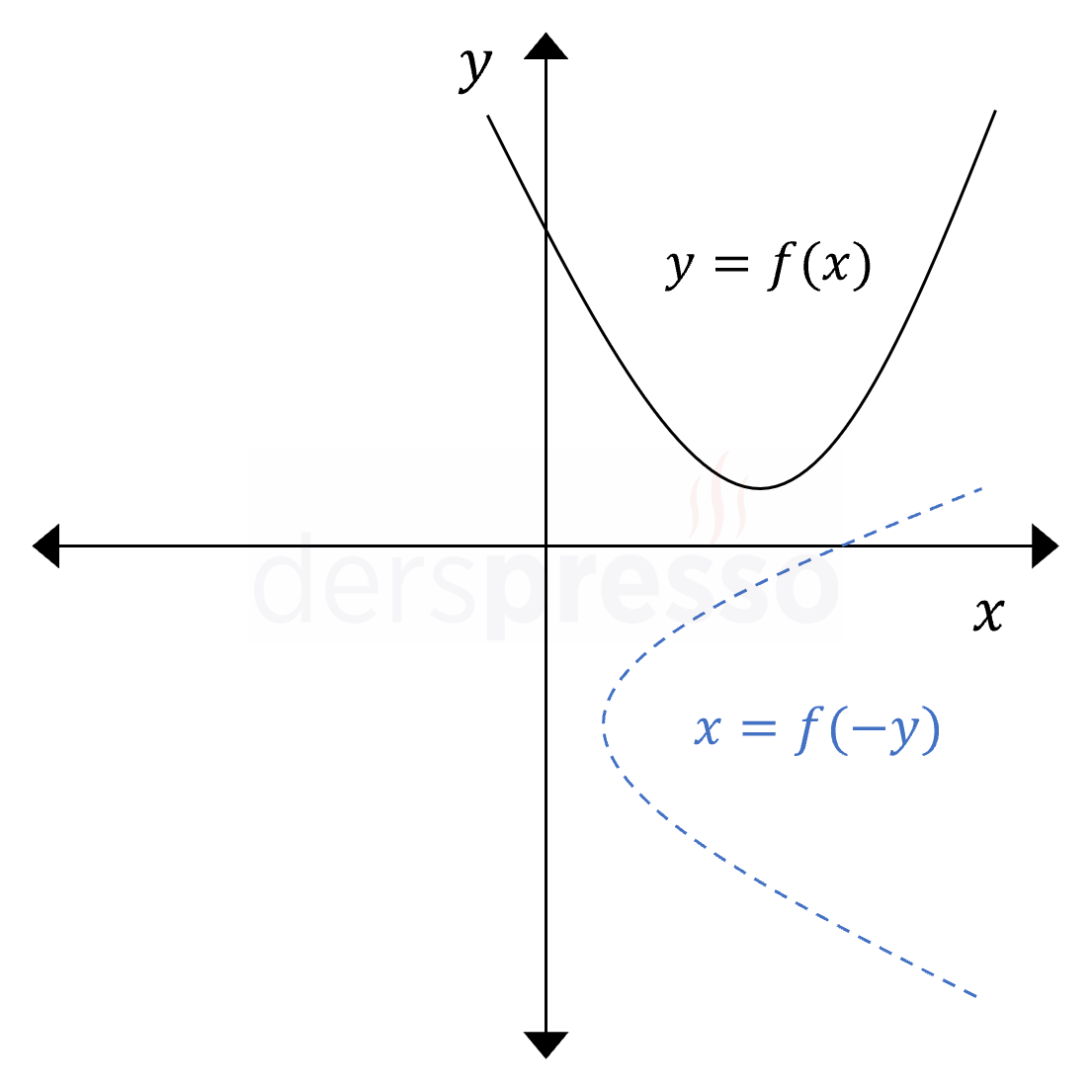
Grafik ya da herhangi bir geometrik şekil sonuçta aynı noktaya geleceği için, saat yönünün tersi yönde 270° ve saat yönünde 90° döndürme işlemleri özdeştir.
\( A(1, 3) \) noktasının orijin etrafında pozitif yönde 810° döndürülmesiyle \( A' \) noktası elde ediliyor. Bu iki nokta arasındaki uzaklık kaç birimdir?
Çözümü GösterBir nokta orijin etrafında pozitif ya da negatif yönde 360° döndürüldüğünde aynı noktaya dönülür.
Bu yüzden noktanın orijin etrafında pozitif yönde 810° döndürülmesi ile 90° döndürülmesi aynı noktaya karşılık gelir.
\( 810° = 2 \cdot 360° + 90° \)
Bir \( (x, y) \) noktasının orijin etrafında pozitif yönde \( 90° \) döndürülmesi ile \( (y, -x) \) noktası elde edilir.
Buna göre \( A(1, 3) \) noktasına bu döndürme dönüşümü uygulanırsa \( A'(3, -1) \) noktası elde edilir.
İki nokta arası uzaklık formülünü kullanalım.
\( d = \sqrt{(3 - 1)^2 + (-1 - 3)^2} \)
\( = \sqrt{20} = 2\sqrt{5} \) bulunur.
Koordinat düzlemindeki \( A(-1, 3) \) noktasının 2 birim sola 1 birim yukarı ötelenmesiyle \( A' \) noktası elde ediliyor.
\( A' \) noktasının orijin etrafında negatif yönde \( 90° \) döndürülmesi ile de \( A'' \) noktası elde ediliyor.
Buna göre \( AA'A'' \) üçgeninin alanı kaç birimkaredir?
Çözümü Göster\( A(-1, 3) \) noktasının 2 birim sola 1 birim yukarı ötelenmesi ile \( A'(-3, 4) \) noktası elde edilir.
Bir \( (x, y) \) noktasının orijin etrafında negatif yönde \( 90° \) döndürülmesi ile \( (y, -x) \) noktası elde edilir.
Buna göre \( A'(-3, 4) \) noktasına bu döndürme dönüşümü uygulandığında \( A''(4, 3) \) noktası elde edilir.
Bu üç nokta koordinat düzleminde aşağıdaki \( AA'A'' \) üçgenini oluşturur.
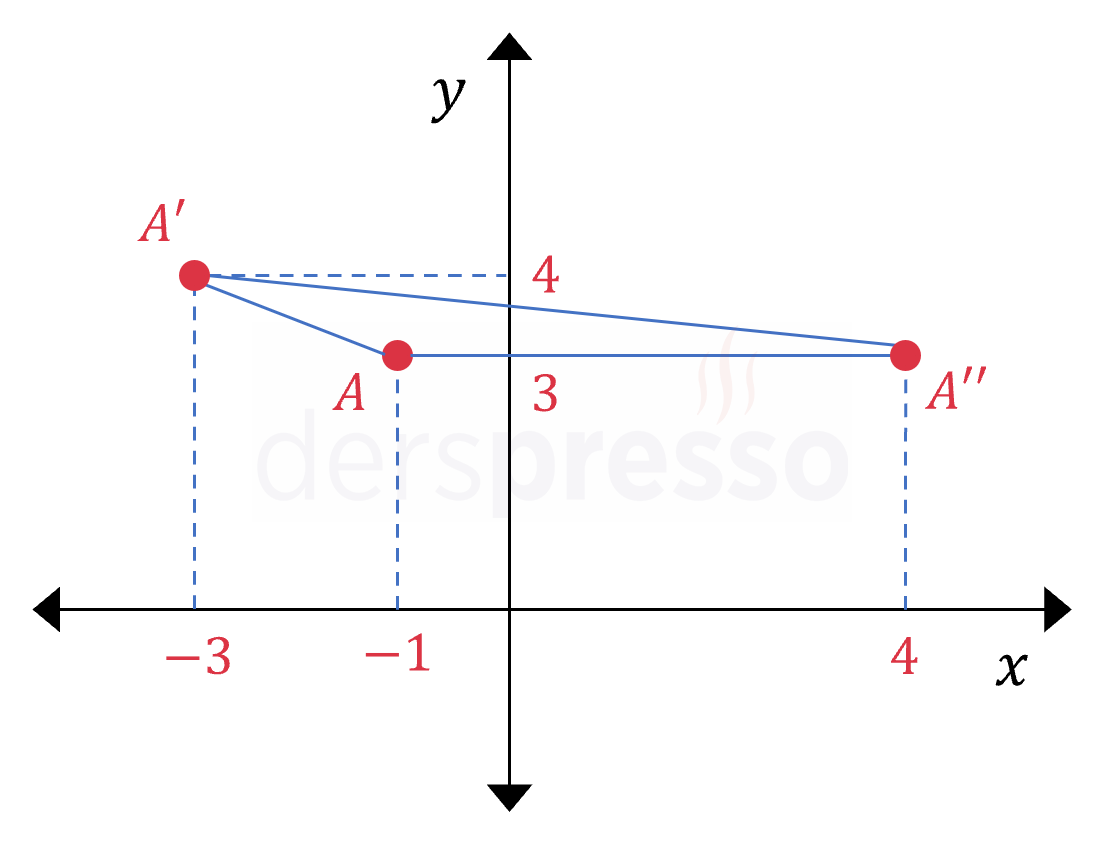
Bu üçgenin \( A \) ve \( A'' \) köşelerinin ordinat değerleri aynı olduğu için bu kenarı taban kabul edelim. Bu durumda üçgenin yüksekliği \( A \) ve \( A' \) köşelerinin ordinat değerlerinin farkı olur.
Alan \( = \dfrac{\text{taban} \cdot \text{yükseklik}}{2} \)
\( = \dfrac{(4 - (-1)) \cdot (4 - 3)}{2} = \dfrac{5}{2} \) bulunur.
\( A(2\sqrt{2}, 4\sqrt{2}) \) noktasının \( y = x \) doğrusuna göre simetriği alınarak \( A' \) noktası, yine \( A \) noktasının orijin etrafında pozitif yönde \( 270° \) döndürülmesiyle de \( A'' \) noktası elde ediliyor.
Buna göre \( OA'A'' \) üçgeninin alanı kaç birimkaredir?
Çözümü GösterBir noktanın \( y = x \) doğrusuna göre simetriği alınırken \( x \) ve \( y \) değerleri aralarında yer değiştirir.
Buna göre \( A(2\sqrt{2}, 4\sqrt{2}) \) noktasının \( y = x \) doğrusuna göre simetriği alındığında \( A'(4\sqrt{2}, 2\sqrt{2}) \) noktası elde edilir.
\( (x, y) \) noktası orijin etrafında pozitif yönde \( 270° \) döndürülürse \( (y, -x) \) noktası elde edilir.
Buna göre \( A(2\sqrt{2}, 4\sqrt{2}) \) noktasına bu dönüşüm uygulandığında \( A''(4\sqrt{2}, -2\sqrt{2}) \) noktası elde edilir.
Bu noktalar aşağıdaki şekilde gösterilmiştir.
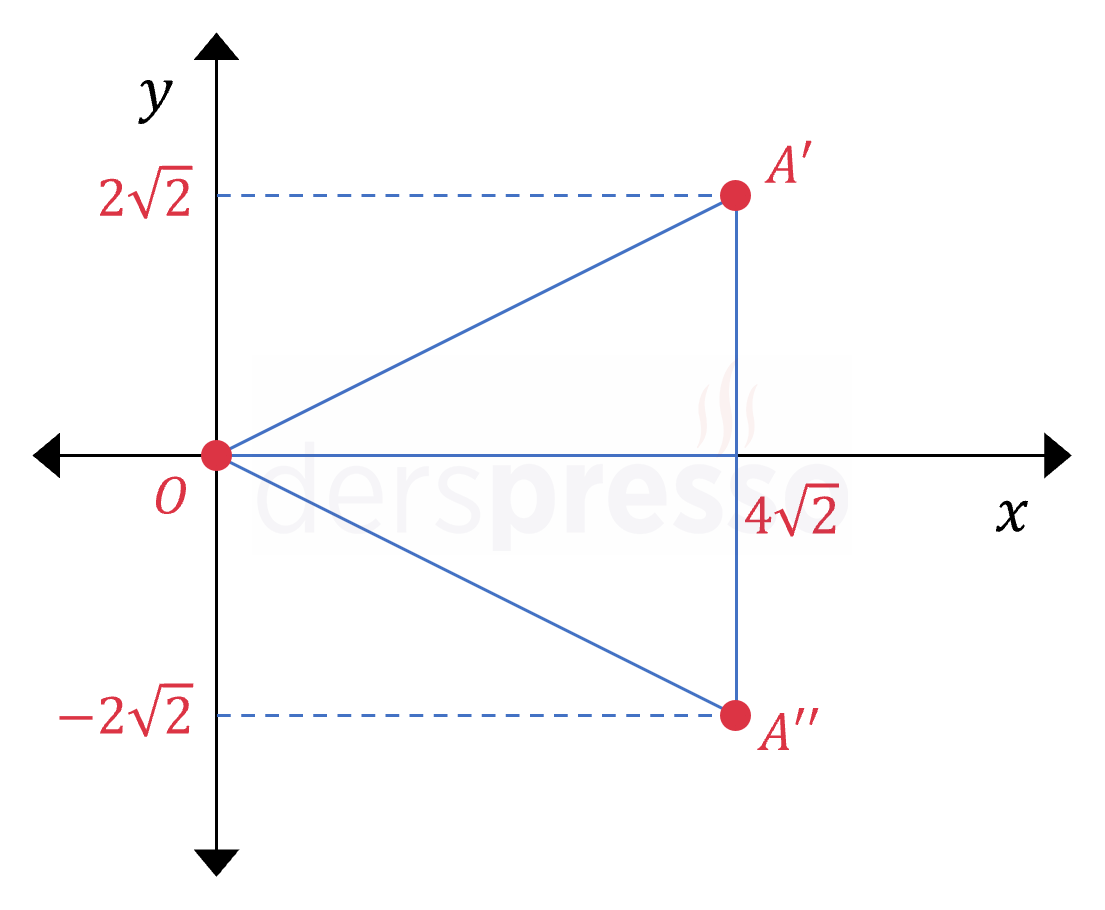
Oluşan üçgenin alanını hesaplayalım.
Alan \( = \dfrac{\text{taban} \cdot \text{yükseklik}}{2} \)
\( = \dfrac{4\sqrt{2} \cdot 4\sqrt{2}}{2} = 16 \) bulunur.