Sürekli ve Süreksiz Fonksiyonlar

Süreklilik konusu her ne kadar ileride ayrı bir başlık olarak incelenecek olsa da, bu bölümde kısa bir giriş yapıyor olacağız.

Bir fonksiyonun grafiği apsisi \( x = a \) olan noktadan geçerken kalem kaldırılmadan çizilebiliyorsa fonksiyon bu noktada süreklidir, eğer çizilemiyorsa fonksiyon bu noktada süreksizdir. Bu tanım her ne kadar sürekliliğin doğru matematiksel tanımı olmasa da şu aşamada yeterlidir.

Bir fonksiyon belirli bir \( (a, b) \) aralığındaki tüm noktalarda sürekli ise fonksiyon bu aralıkta süreklidir.

Kavramı pekiştirmek adına aşağıda sürekli ve süreksiz fonksiyon grafiklerine birkaç örnek vereceğiz.

Sürekli Noktalar

Aşağıda \( x = a \) noktasında sürekli iki fonksiyon örneği verilmiştir.

Grafik	Açıklama
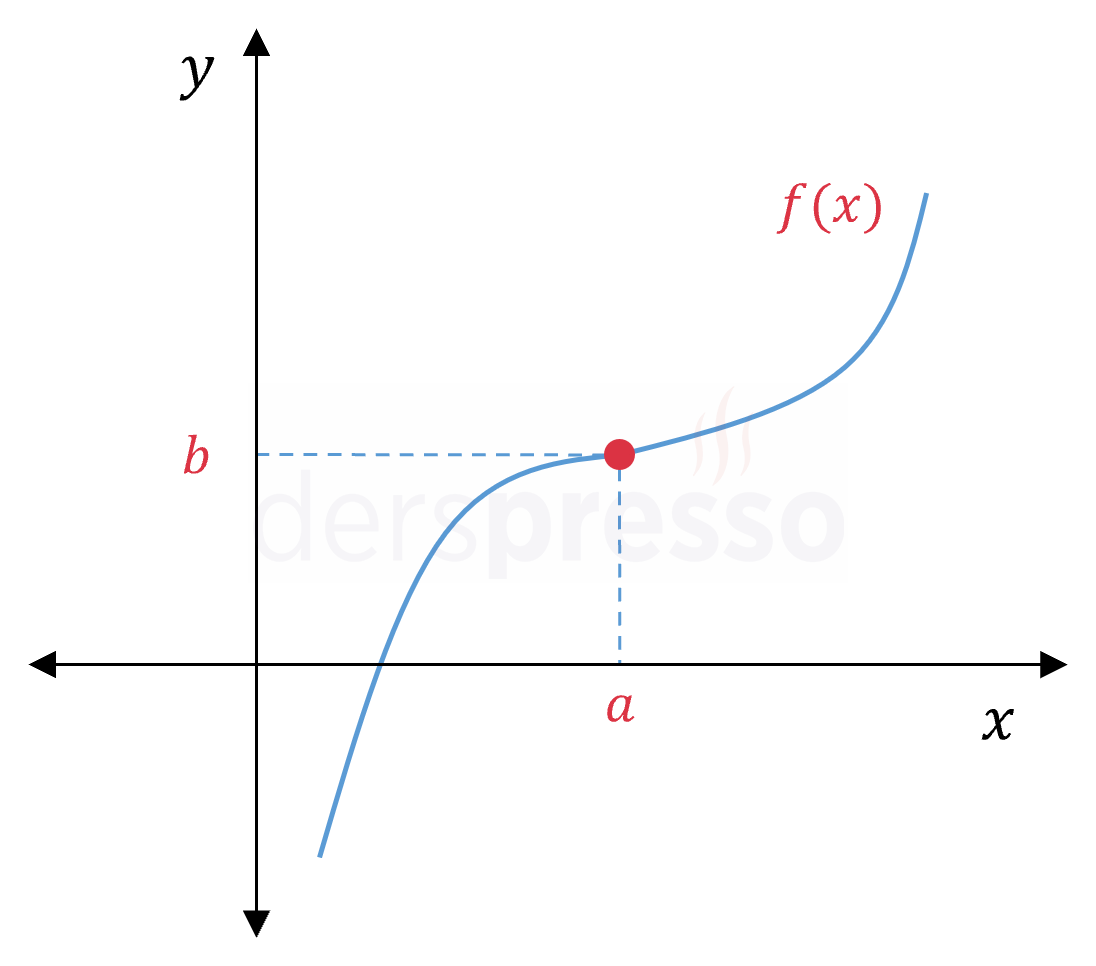
	Grafikte \( x = a \) noktasında hiçbir tanımsızlık ya da sıçrama olmadığı ve grafik bu noktada "kalem" testini geçtiği için fonksiyon bu noktada süreklidir.
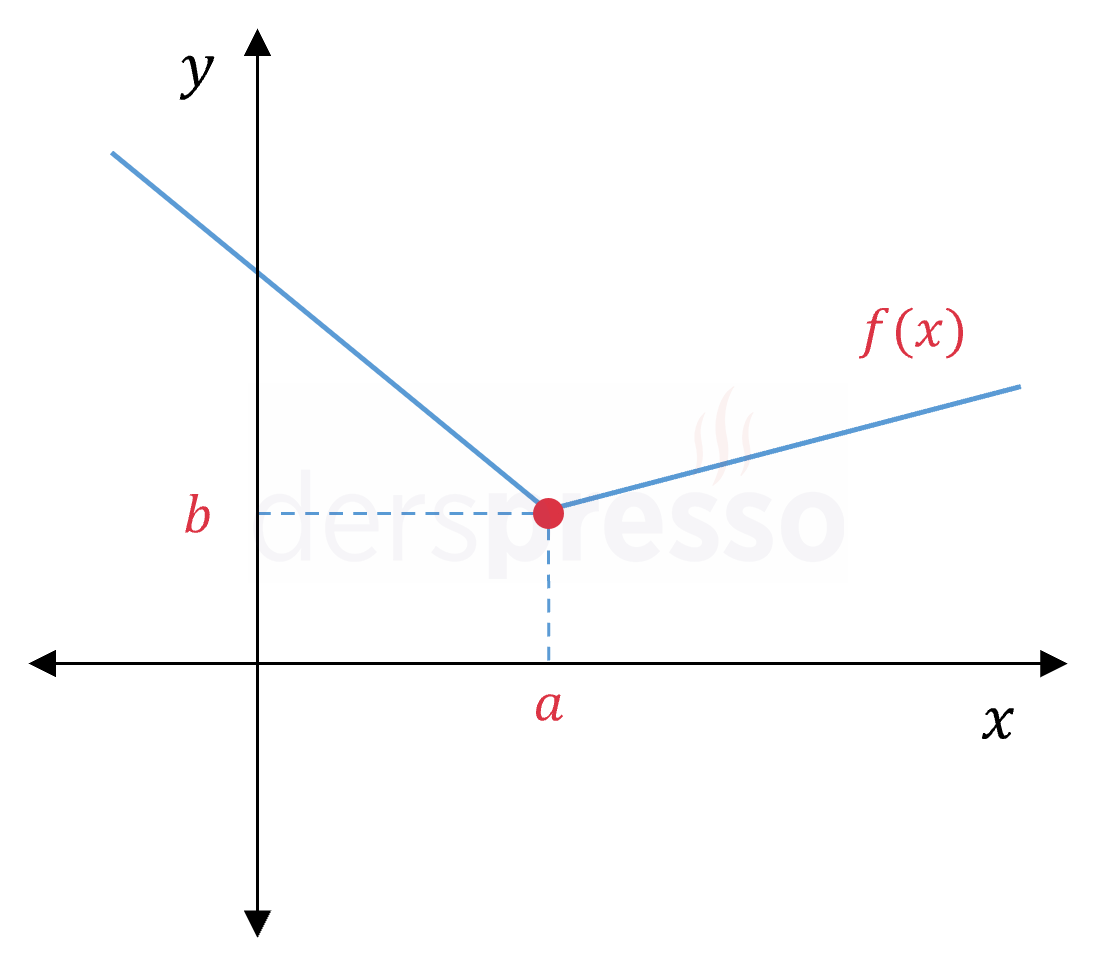
	Fonksiyon parçalı bir fonksiyon olsa da, grafikte \( x = a \) noktasında hiçbir tanımsızlık ya da sıçrama olmadığı ve grafik "kalem" testini geçtiği için fonksiyon bu noktada süreklidir.

Süreksiz Noktalar

Aşağıda farklı tipteki süreksizliklere birer örnek verilmiştir.

Grafik	Açıklama
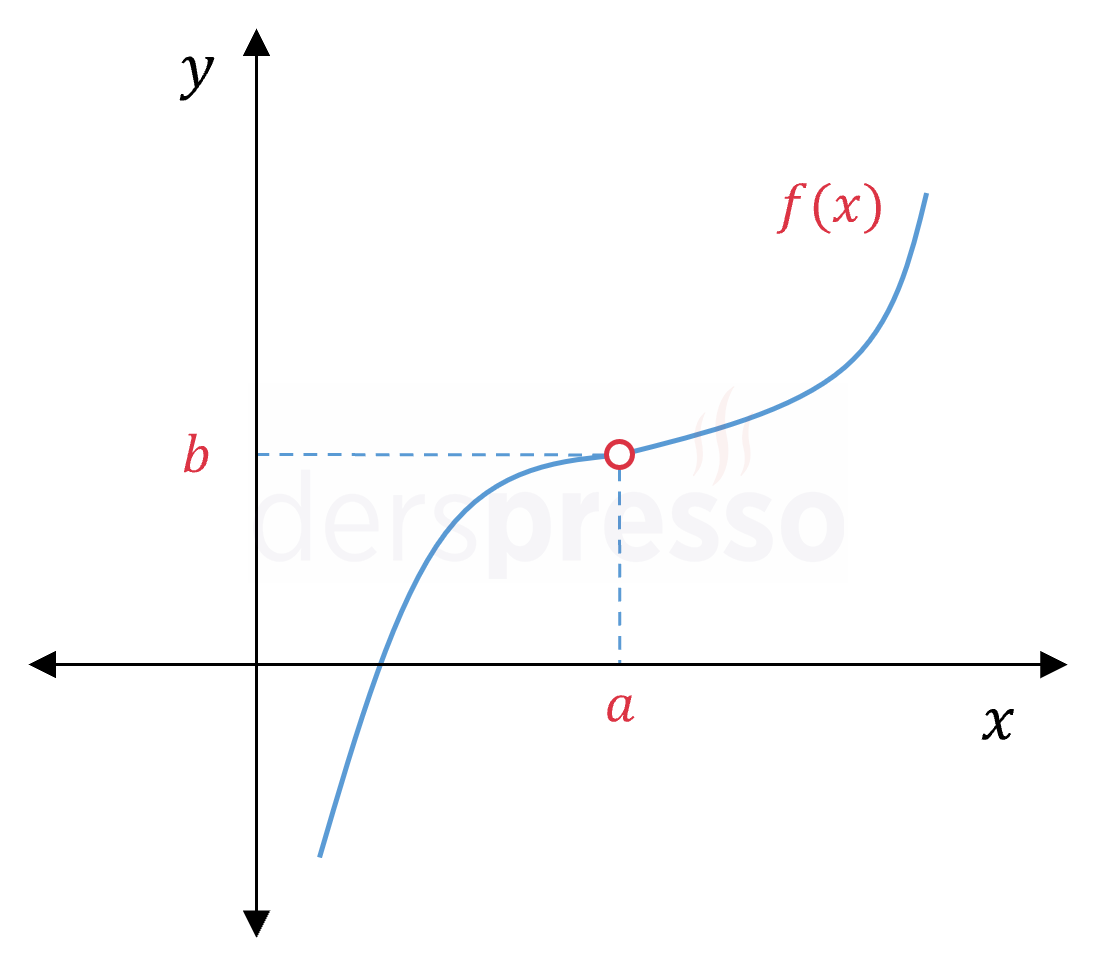
	Grafikte \( x = a \) noktasında tanımsız olduğu için grafik "kalem" testini geçemez, dolayısıyla fonksiyon bu noktada süreksizdir.
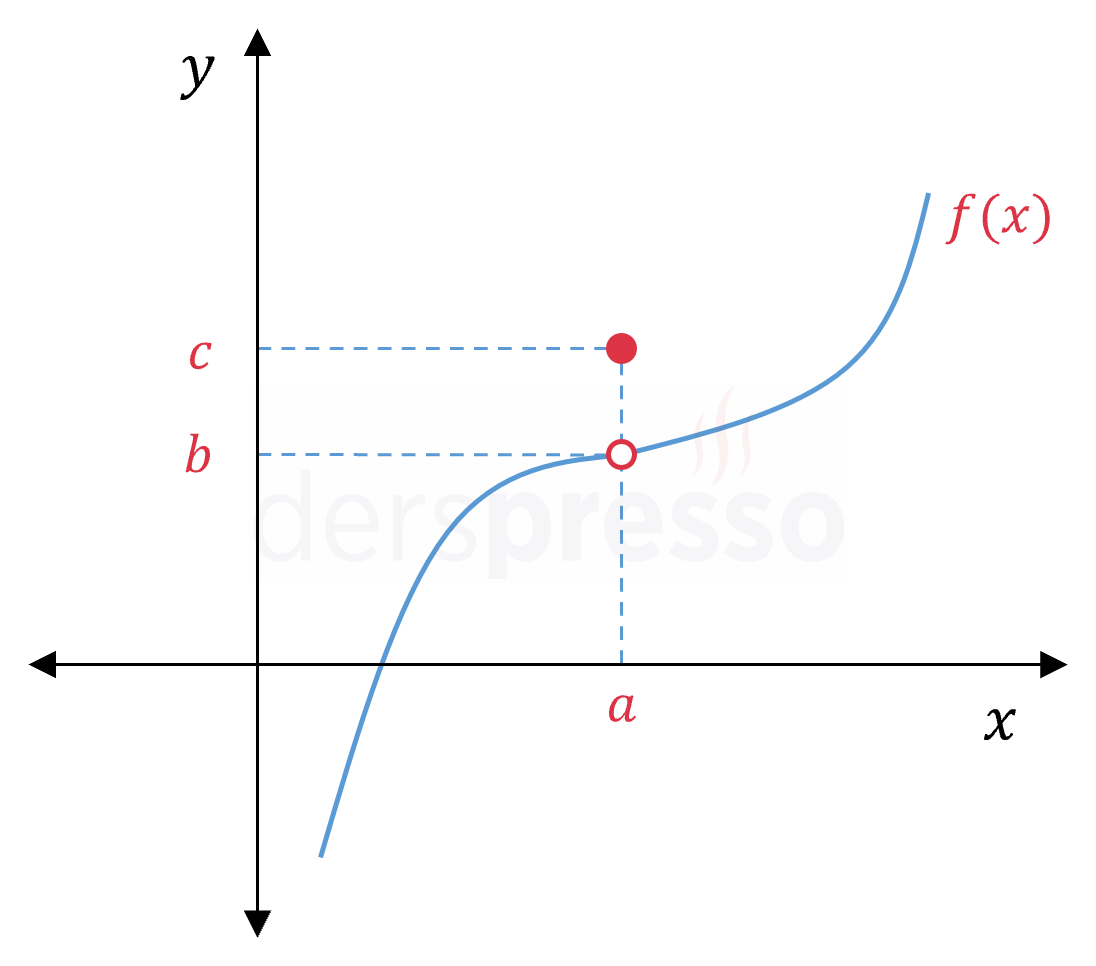
	Fonksiyon her ne kadar \( a \) noktasında tanımlı olsa da grafikte bu noktada boşluk olduğu için grafik "kalem" testini geçemez, dolayısıyla fonksiyon bu noktada süreksizdir.
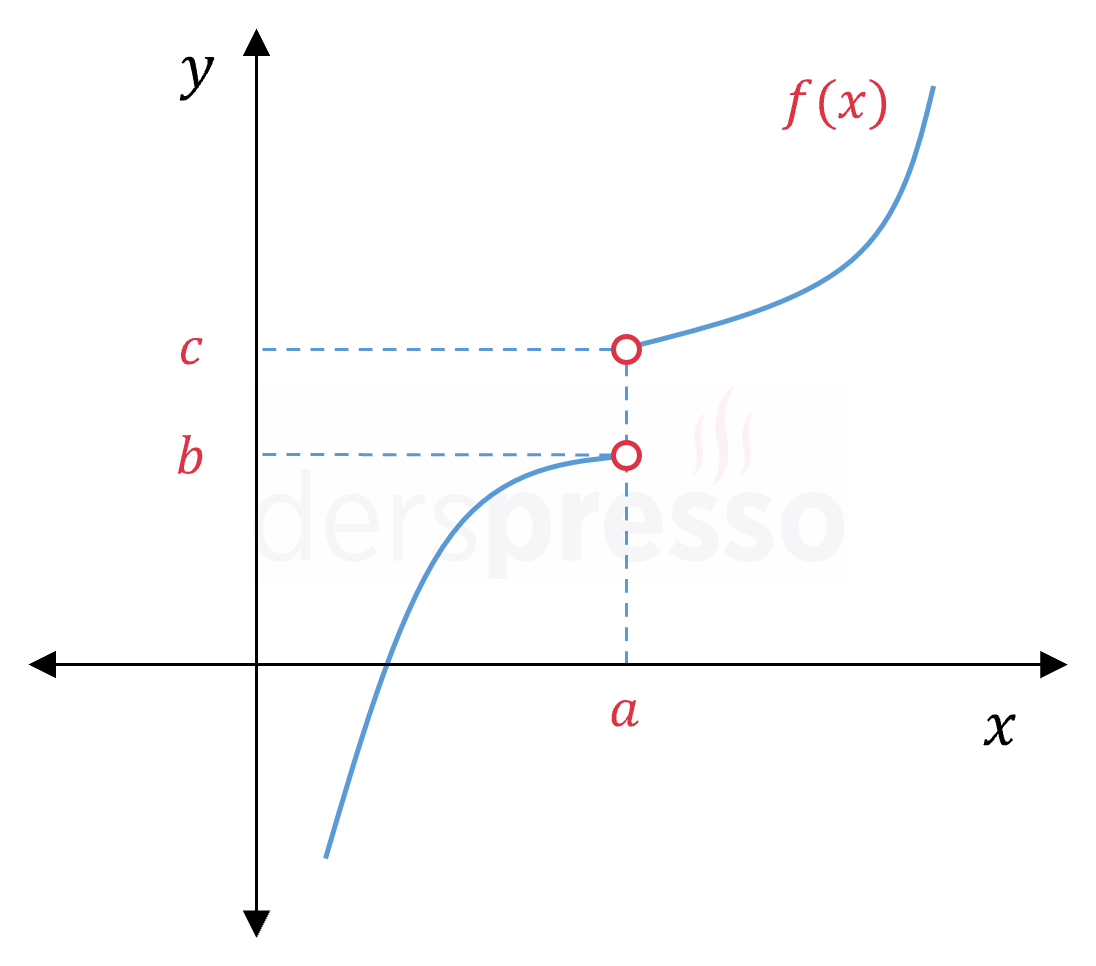
	Grafikte \( x = a \) noktasında sıçrama olduğu için grafik "kalem" testini geçemez, dolayısıyla fonksiyon bu noktada süreksizdir.
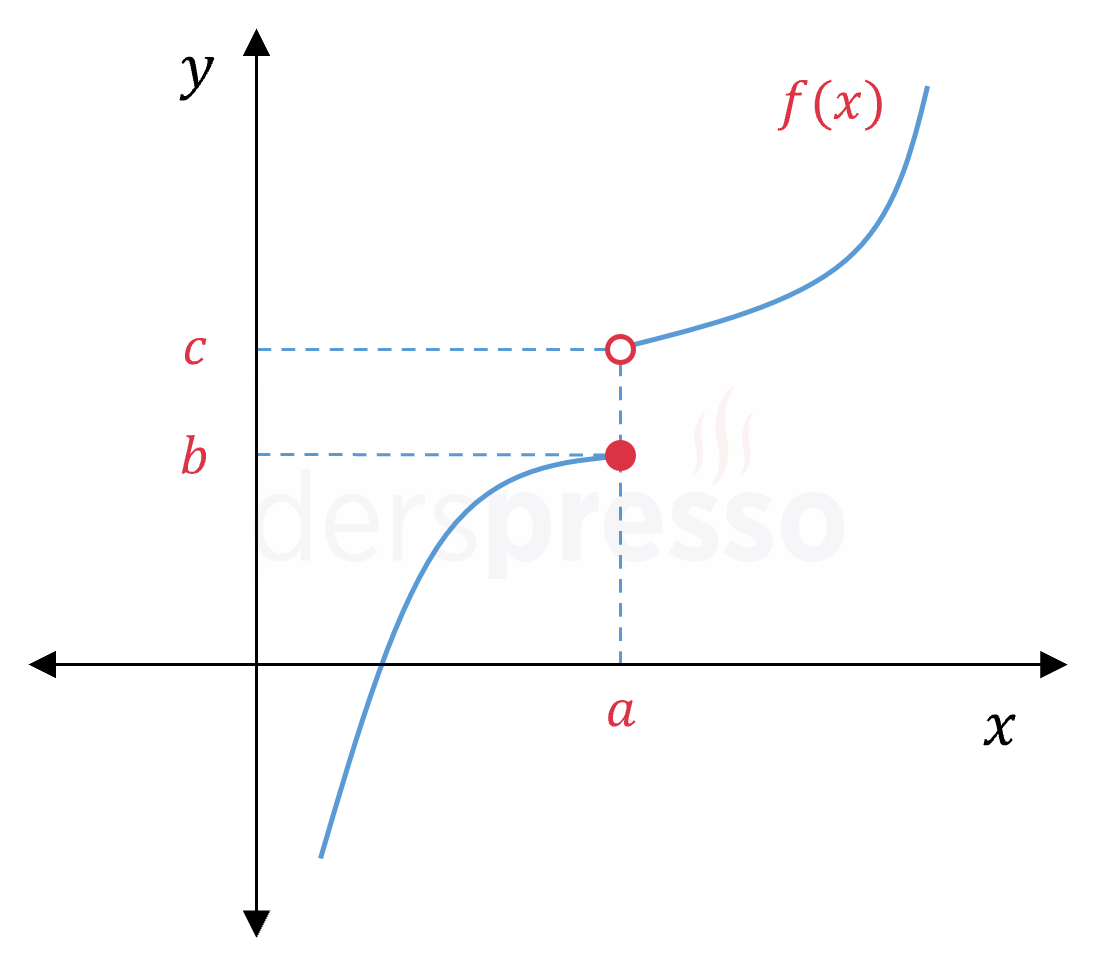
	Fonksiyon her ne kadar \( x = a \) noktasında tanımlı olsa da grafikte bu noktada sıçrama olduğu için grafik "kalem" testini geçemez, dolayısıyla fonksiyon bu noktada süreksizdir.
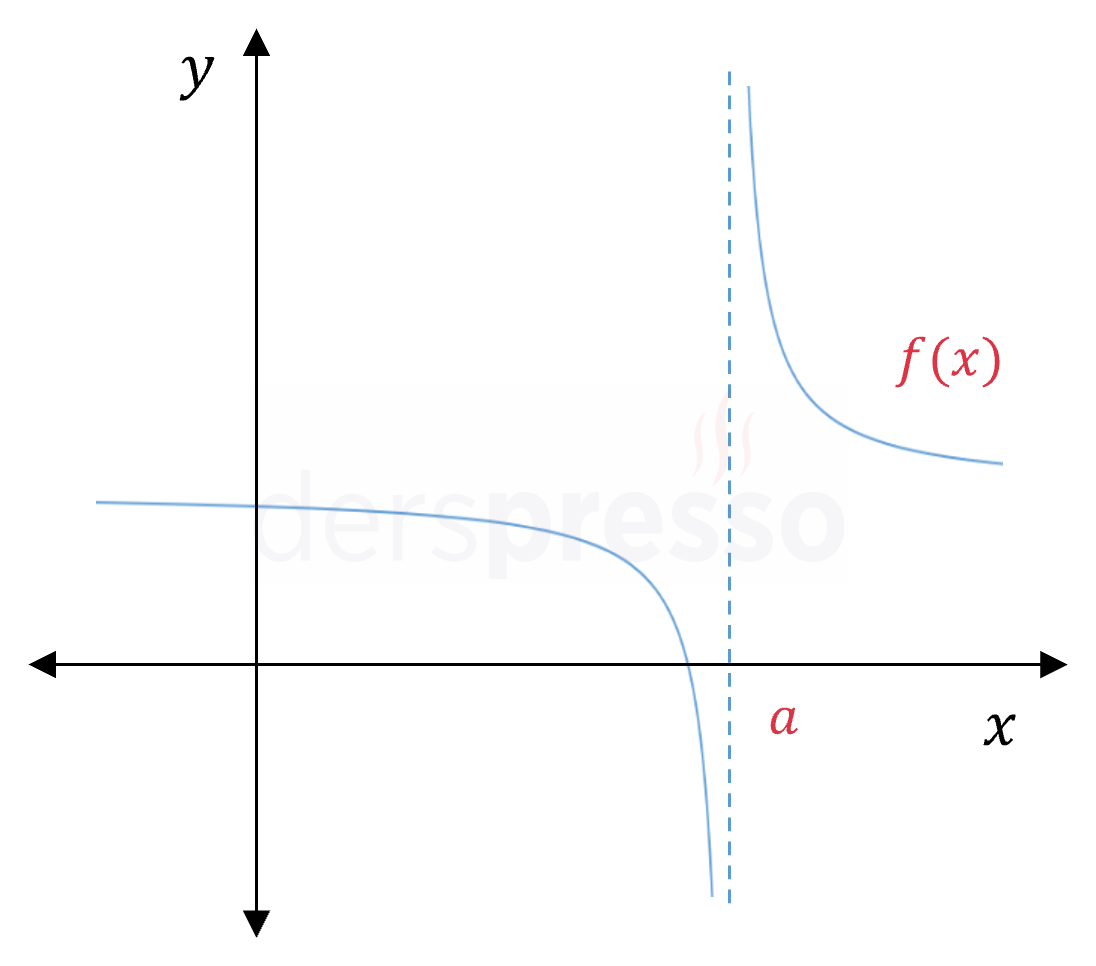
	Grafiğin \( x = a \) noktasında bir dikey asimptotu olduğu için grafik "kalem" testini geçemez, dolayısıyla fonksiyon bu noktada süreksizdir.

Fonksiyonların Sürekliliği

Fonksiyonlar konusunda incelediğimiz aşağıdaki fonksiyonların tümü tanımlı oldukları nokta ve aralıklarda süreklidir. Bu fonksiyonların grafiklerinde görülebilecek süreksizlikler (örneğin tanjant grafiğinde \( x = \frac{\pi}{2} \) noktasında oluşan dikey asimptot) fonksiyonun tanım aralığının dışında kaldığı için fonksiyonun sürekliliği bozmaz.

Bu fonksiyonlar ve tanımlı oldukları aralıklar aşağıdaki gibidir.

Fonksiyon	Denklem	Tanım Kümesi
Sabit fonksiyon	\( f(x) = c \)	\( \mathbb{R} \)
Doğrusal fonksiyon	\( f(x) = mx + c \)	\( \mathbb{R} \)
Kuvvet fonksiyonu	\( f(x) = x^n \)	\( \mathbb{R} \)
Köklü fonksiyon (çift dereceli)	\( f(x) = \sqrt[2n]{x} \)	\( [0, \infty) \)
Köklü fonksiyon (tek dereceli)	\( f(x) = \sqrt[2n + 1]{x} \)	\( \mathbb{R} \)
Mutlak değer fonksiyonu	\( f(x) = \abs{x} \)	\( \mathbb{R} \)
Polinom fonksiyonu	\( f(x) = a_nx^n + a_{n-1}x^{n-1} + \ldots + a_1x + a_0 \)	\( \mathbb{R} \)
Rasyonel fonksiyon	\( f(x) = \dfrac{P(x)}{Q(x)} \)	Paydayı sıfır yapan reel kökler dışında \( \mathbb{R} \)
Sinüs fonksiyonu	\( f(x) = \sin{x} \)	\( \mathbb{R} \)
Kosinüs fonksiyonu	\( f(x) = \cos{x} \)	\( \mathbb{R} \)
Tanjant fonksiyonu	\( f(x) = \tan{x} \)	\( \mathbb{R} - \{ \frac{\pi}{2} + k\pi, k \in \mathbb{Z} \} \)
Kotanjant fonksiyonu	\( f(x) = \cot{x} \)	\( \mathbb{R} - \{ k\pi, k \in \mathbb{Z} \} \)
Sekant fonksiyonu	\( f(x) = \sec{x} \)	\( \mathbb{R} - \{ \frac{\pi}{2} + k\pi, k \in \mathbb{Z} \} \)
Kosekant fonksiyonu	\( f(x) = \csc{x} \)	\( \mathbb{R} - \{ k\pi, k \in \mathbb{Z} \} \)
Üstel fonksiyon	\( f(x) = a^x \)	\( \mathbb{R} \)
Logaritma fonksiyonu	\( f(x) = \log_a{x} \)	\( (0, \infty) \)

SORU 1 :

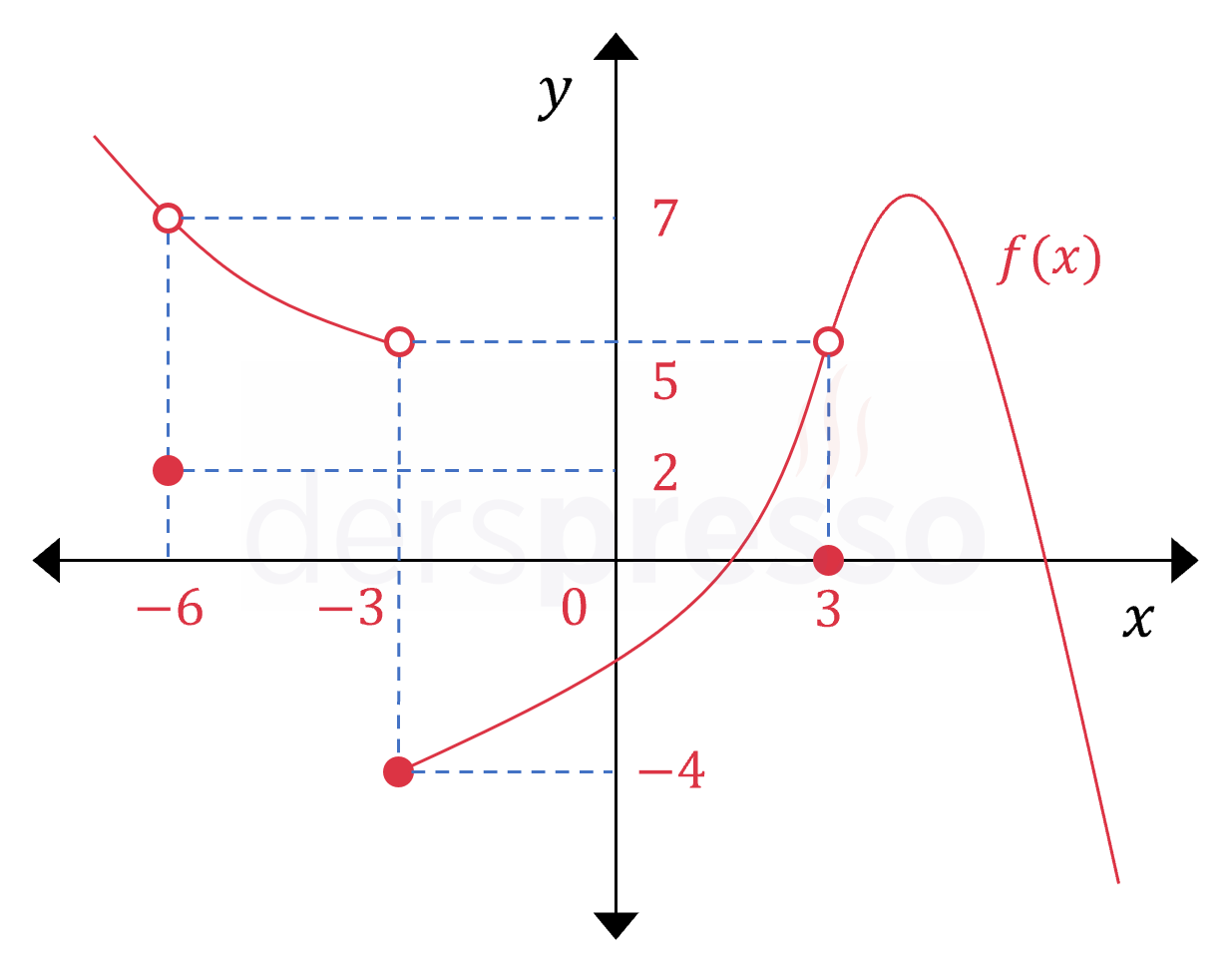
Yukarıdaki grafiğe göre \( f \) fonksiyonu verilen aralıkta kaç noktada süreksizdir?

Çözümü Göster

Sürekliliğin pratik tanımına göre, bir fonksiyonun grafiğini belirli bir noktadan geçerken kalemi kaldırmadan çizebiliyorsak fonksiyon bu noktada süreklidir, aksi takdirde fonksiyon bu noktada süreksizdir.

Bu tanıma göre fonksiyon \( x = -6 \), \( x = -3 \) ve \( x = 3 \) noktaları olmak üzere 3 noktada süreksizdir.

Chatbot'a canlı soru sorun Soru sorun (e-mail) Soruda hata bildirin