Mutlak Değer
Mutlak değer dönüşümleri, fonksiyonun çıktısının, girdisinin ya da her ikisinin mutlak değer içine alınması ile oluşur.
Fonksiyonun Çıktısının Mutlak Değeri
\( f(x) \longmapsto \abs{f(x)} \)
Fonksiyonun çıktısının mutlak değeri alındığında \( x \) ekseninin altında kalan (negatif \( y \) değerli) noktaların \( x \) eksenine göre yansıması oluşur. Bunun sebebi, fonksiyonun bu değişiklik sonucunda bir \( x \) değeri için ürettiği negatif \( y \) değerlerinin pozitife dönmesidir.
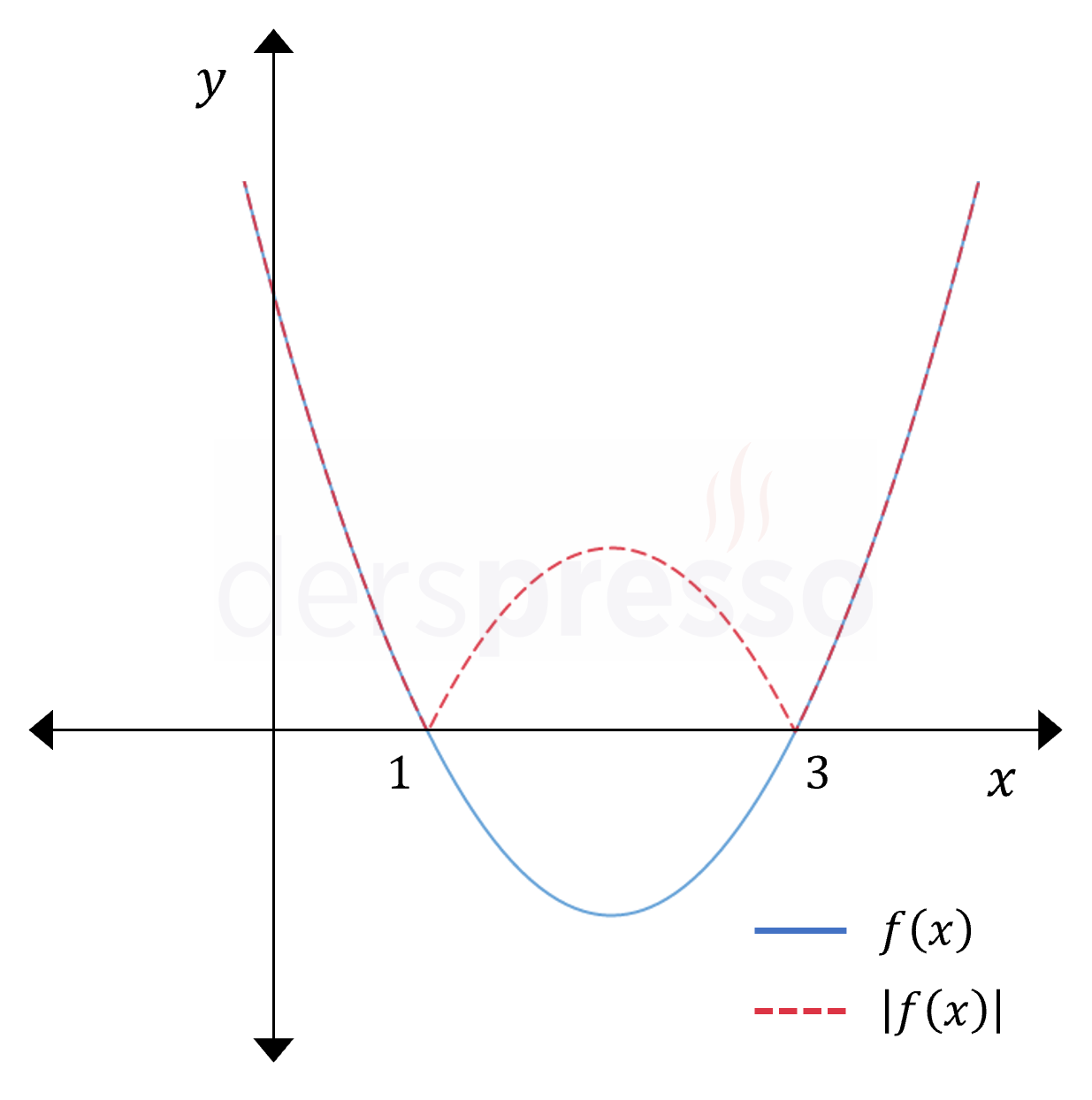
Fonksiyonun Girdisinin Mutlak Değeri
\( f(x) \longmapsto f(\abs{x}) \)
Fonksiyonun girdisinin mutlak değeri alındığında \( y \) ekseninin solunda kalan noktalar silinir ve \( y \) ekseninin sağında kalan noktaların \( y \) eksenine göre yansıması oluşur. Bunun sebebi, fonksiyonun bu değişiklik sonucunda negatif bir \( x \) değeri için ürettiği \( y \) değerinin aynı \( x \) değerinin pozitif işaretlisi için ürettiği \( y \) değerine eşit olmasıdır.
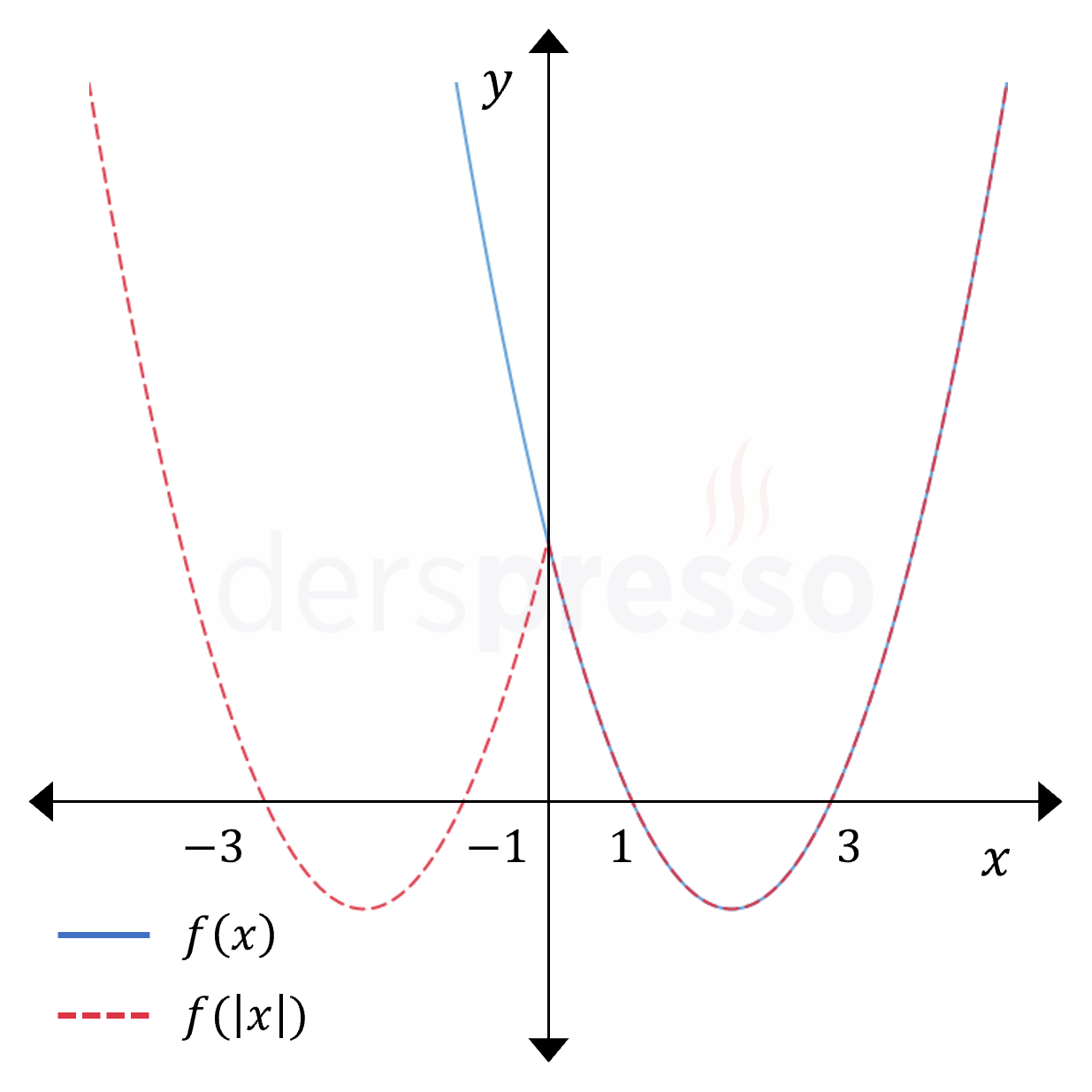
Fonksiyonun Çıktısının ve Girdisinin Mutlak Değeri
\( f(x) \longmapsto \abs{f(\abs{x})} \)
Fonksiyonun çıktısının ve girdisinin birlikte mutlak değeri alındığında hem \( x \) ekseninin altında kalan noktaların \( x \) eksenine göre yansıması oluşur, hem de \( y \) ekseninin solunda kalan noktalar silinir ve \( y \) ekseninin sağında kalan noktaların \( y \) eksenine göre yansıması oluşur. Bunun sebebi, yukarıda bahsettiğimiz iki etkinin birlikte oluşmasıdır.
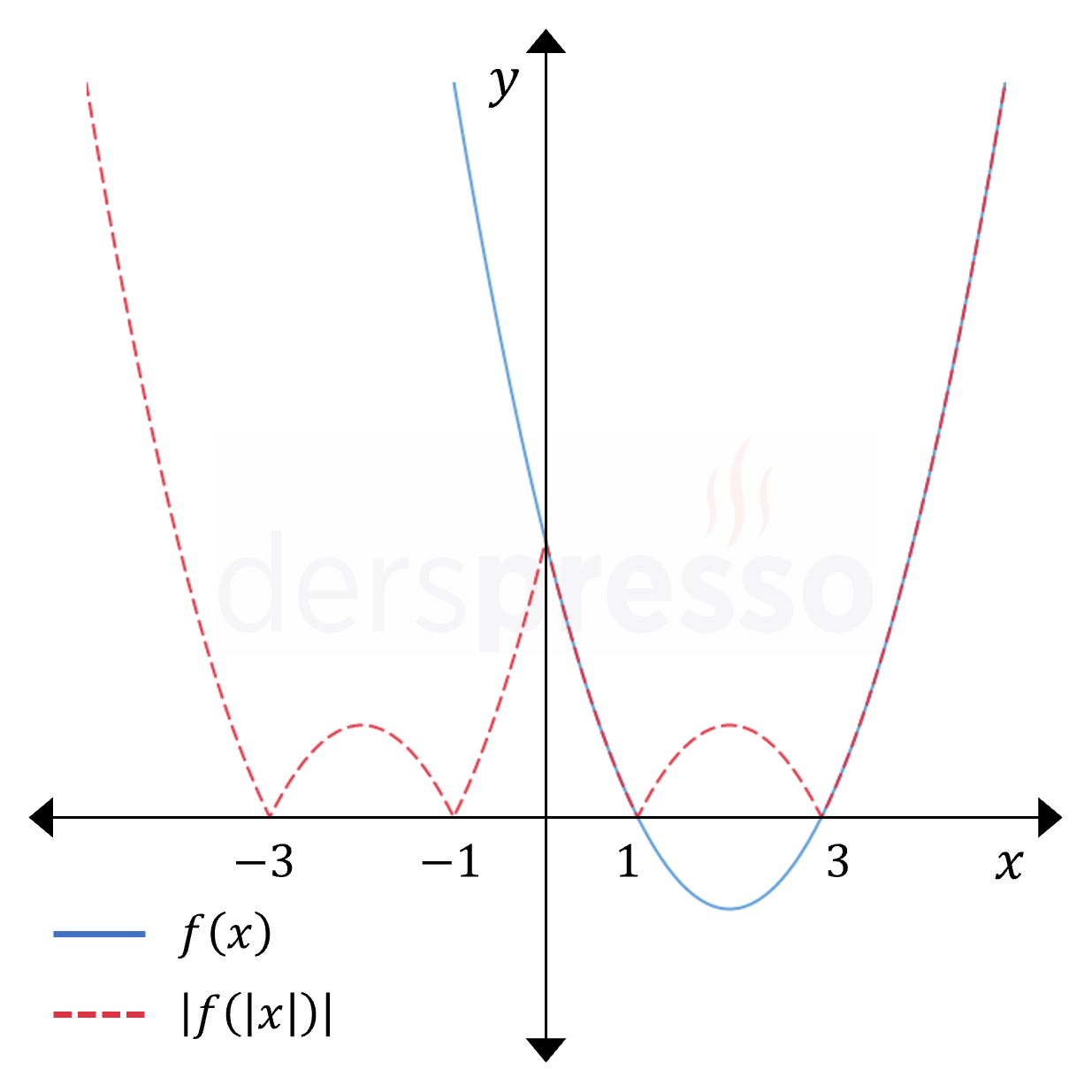
Aşağıda verilen fonksiyonların 2. sütunda çıktılarına, 3. sütunda da girdilerine mutlak değer dönüşümü uygulanmıştır.
| Fonksiyon | Dikey Dönüşüm | Yatay Dönüşüm |
|---|---|---|
| \( f(x) = x + 1 \) | \( \abs{f(x)} = \abs{x + 1} \) | \( f(\abs{x}) = \abs{x} + 1 \) |
| \( f(x) = x^2 \) | \( \abs{f(x)} = \abs{x^2} \) | \( f(\abs{x}) = \abs{x}^2 \) |
| \( f(x) = \sqrt[3]{x} \) | \( \abs{f(x)} = \abs{\sqrt[3]{x}} \) | \( f(\abs{x}) = \sqrt[3]{\abs{x}} \) |
| \( f(x) = \sin{x} \) | \( \abs{f(x)} = \abs{\sin{x}} \) | \( f(\abs{x}) = \sin{\abs{x}} \) |
| \( f(x) = 2^x \) | \( \abs{f(x)} = \abs{2^x} \) | \( f(\abs{x}) = 2^{\abs{x}} \) |
| \( f(x) = \log{x} \) | \( \abs{f(x)} = \abs{\log{x}} \) | \( f(\abs{x}) = \log{\abs{x}} \) |

Yukarıda \( y = f(x - 6) \) grafiği verilmiştir.
Buna göre \( y = \abs{f(x + 3)} \) grafiği \( y \) eksenini hangi noktada keser?
Çözümü Göster\( y = f(x - 6) \) fonksiyonunun denklemini yazalım.
\( \dfrac{x}{3} + \dfrac{y}{8} = 1 \)
\( y = -\dfrac{8}{3}x + 8 \)
\( f(x + 3) \) fonksiyonu \( f(x - 6) \) fonksiyonunun 9 birim sola ötelenmesi ile ve \( x \) yerine \( x + 9 \) yazarak elde edilir.
\( y = -\dfrac{8}{3}(x + 9) + 8 \)
\( y = -\dfrac{8}{3}x - 16 \)
Bu fonksiyonun \( y \) eksenini kestiği noktayı bulmak için \( x = 0 \) yazalım.
\( y = -\dfrac{8}{3}(0) - 16 = -16 \)
\( \abs{f(x + 3)} \) fonksiyonunun grafiği, \( f(x + 3) \) grafiğinde \( x \) ekseninin altında kalan noktaların \( x \) eksenine göre yansıması alınarak elde edilir.
Buna göre \( y = \abs{f(x + 3)} \) fonksiyonu \( y \) eksenini \( (0, 16) \) noktasında keser.
\( f(x) = \log{\abs{x}} + 3 \) fonksiyonunun grafiği \( y = x \) doğrusu ile kaç noktada kesişir?
Çözümü GösterÖnce \( \log{x} \) fonksiyonuna iki dönüşüm uygulayarak sorudaki fonksiyonu elde edelim.
Fonksiyonun girdisinin mutlak değeri alındığında \( y \) ekseninin solunda kalan noktalar (varsa) silinir ve \( y \) ekseninin sağında kalan noktaların \( y \) eksenine göre yansıması oluşur.
\( f(x) \longmapsto f(\abs{x}) \)
\( f(\abs{x}) = \log{\abs{x}} \)
Bir fonksiyonun çıktısına 3 birim eklendiğinde grafiği 3 birim yukarı ötelenir.
\( f(\abs{x}) \longmapsto f(\abs{x}) + 3 \)
\( f(\abs{x}) + 3 = \log{\abs{x}} + 3 \)
Aşağıda bu iki dönüşüm sonucunda oluşan fonksiyonun ve \( y = x \) doğrusunun grafikleri verilmiştir.
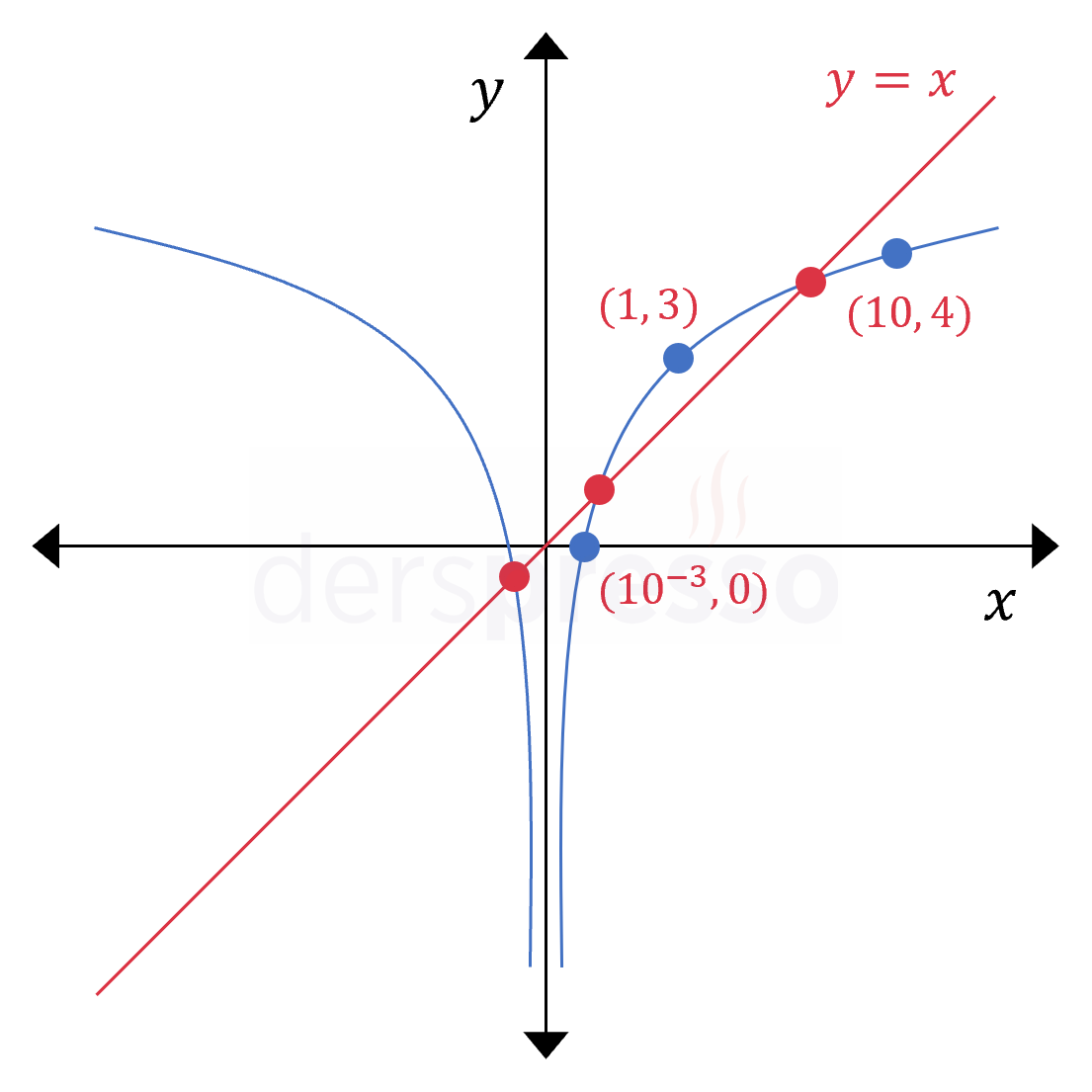
\( y = x \) doğrusunun fonksiyonun \( y \) ekseninin solunda kalan kısmını tek noktada kestiğinden emin olabiliriz, \( y \) ekseninin sağında kalan kısmını kesip kesmediğinden ya da kesiyorsa kaç noktada kestiğinden emin olmak için ya bir programla grafiğini çizmeliyiz ya da iki denklemi ortak çözmeliyiz.
Alternatif olarak \( y = x \) doğrusunun fonksiyonun \( y \) ekseninin sağında kalan kısmını 2 noktada kestiğini daha pratik bir yöntemle bulabiliriz.
Verilen logaritma fonksiyonunda \( y = 0 \) verip \( x \) değerini ve \( x = 1 \) ve \( x = 10 \) verip \( y \) değerlerini hesapladığımızda fonksiyonun aşağıdaki noktalardan geçtiğini buluruz.
\( (10^{-3}, 0), (1, 3), (10, 4) \)
Bu noktalardan 1. ve 3.sünün ordinat değerleri apsis değerlerinden küçük olduğu için \( y = x \) doğrusunun altında kalır, 2. noktanın ise ordinat değeri daha büyük olduğu için \( y = x \) doğrusunun üstünde kalır.
Buna göre fonksiyon grafiğinin doğrunun altındayken doğruyu kesip üstüne geçtiği, sonra tekrar kesip altına indiği sonucuna varabiliriz.
Buna göre verilen fonksiyon ve doğru 3 noktada kesişirler.