0/0 Belirsizliği
\( \frac{0}{0} \) belirsizliği ayrı ayrı limitleri 0 olan iki ifadenin bölümünün limiti alındığında oluşur.
\( \lim\limits_{x \to a} \dfrac{f(x)}{g(x)} \) limitinde,
\( \lim\limits_{x \to a} {f(x)} = 0 \) ve \( \lim\limits_{x \to a} {g(x)} = 0 \) değerleri elde ediliyorsa,
bu limit için \( \frac{0}{0} \) belirsizliği vardır.
\( \lim\limits_{x \to 2} \dfrac{x^2 - 4}{x - 2} \) limitinde,
\( \lim\limits_{x \to 2} (x^2 - 4) = 0 \) ve \( \lim\limits_{x \to 2} (x - 2) = 0 \) olduğu için, \( \frac{0}{0} \) belirsizliği vardır.
\( \lim\limits_{x \to 0} \dfrac{\sin{x}}{x} \) limitinde,
\( \lim\limits_{x \to 0} {\sin{x}} = 0 \) ve \( \lim\limits_{x \to 0} {x} = 0 \) olduğu için, \( \frac{0}{0} \) belirsizliği vardır.
Tüm belirsizliklerde olduğu gibi, bir fonksiyonun limitini hesaplarken \( \frac{0}{0} \) belirsizliği elde etmemiz fonksiyonun bu noktada limitinin tanımsız ya da sıfır olduğu anlamına gelmez. Fonksiyonun bu noktada limiti tanımlı olabilir ve bu limit değerini bulmak için kullanabileceğimiz bazı yöntemler aşağıdaki gibidir.
Çarpanlara Ayırma ve Sadeleştirme
Konu tekrarı için: Özdeşlikler ve Çarpanlara Ayırma
\( \frac{0}{0} \) belirsizliği olan bir ifadede pay ve paydanın ortak bir çarpanı varsa ve limiti alınan değer bu çarpanı sıfır yapıyorsa pay ve payda çarpanlarına ayrılarak ve bu ortak çarpan sadeleştirilerek belirsizlik giderilebilir. Belirsizlik ortadan kalktıktan sonra ifadenin sadeleşmiş haliyle limit değeri tekrar hesaplanır.
\( \lim\limits_{x \to 2} \dfrac{x^3 - 4x^2 + 6x - 4}{x - 2} \) limitinin değerini bulalım.
\( \lim\limits_{x \to 2} (x^3 - 4x^2 + 6x - 4) = 2^3 - 4(2)^2 + 6(2) - 4 = 0 \)
\( \lim\limits_{x \to 2} (x - 2) = 2 - 2 = 0 \)
Buna göre verilen limit ifadesinde \( \frac{0}{0} \) belirsizliği vardır.
Bu belirsizlik bize fonksiyonun \( x = 2 \) noktasında tanımsız olduğunu gösterir, ama bu noktada limitin olmadığı sonucuna varamayız.
2 değeri pay ve paydadaki ifadelerin ikisini de sıfır yaptığı için iki polinom ifadesinin de bir kökü olmalıdır. Paydaki üçüncü dereceden ifadeyi çarpanlarına ayırmak için elimizde kolay bir yöntem olmadığı için polinom bölmesi ile bu ifadeyi \( x - 2 \)'ye bölerek diğer çarpanını bulalım.
\( x^3 - 4x^2 + 6x - 4 = (x - 2)(x^2 - 2x + 2) \)
Pay ve paydadaki ifadeleri bu şekilde çarpanlarına ayırıp ortak çarpanları sadeleştirelim.
\( \lim\limits_{x \to 2} \dfrac{x^3 - 4x^2 + 6x - 4}{x - 2} = \lim\limits_{x \to 2} \dfrac{(x - 2)(x^2 - 2x + 2)}{x - 2} \)
\( = \lim\limits_{x \to 2} (x^2 - 2x + 2) \)
Elde edilen ifade bir polinom fonksiyonu olduğu için limit değeri fonksiyonun bu noktadaki değerine eşittir.
\( = 2^2 - 2(2) + 2 = 2 \)
Yukarıdaki örnekte pay ve paydadaki ortak çarpanları sadeleştirdiğimizde \( \frac{0}{0} \) belirsizliğinin ortadan kalktığını ve ifadenin sadeleşmiş halinde \( x \) değerini yerine koyarak limit değerini elde edebileceğimizi gördük. Peki ortak çarpanları sadeleştirdiğimizde elde ettiğimiz yeni fonksiyonun bu noktadaki limitinin orijinal fonksiyonun aynı noktadaki limitine eşit olduğundan nasıl emin olabiliriz? Aşağıda bu soruyu cevaplamaya çalışacağız.
Sorudaki orijinal fonksiyonun (birinci grafik) ve sadeleşmiş halinin (ikinci grafik) grafikleri aşağıda verilmiştir.
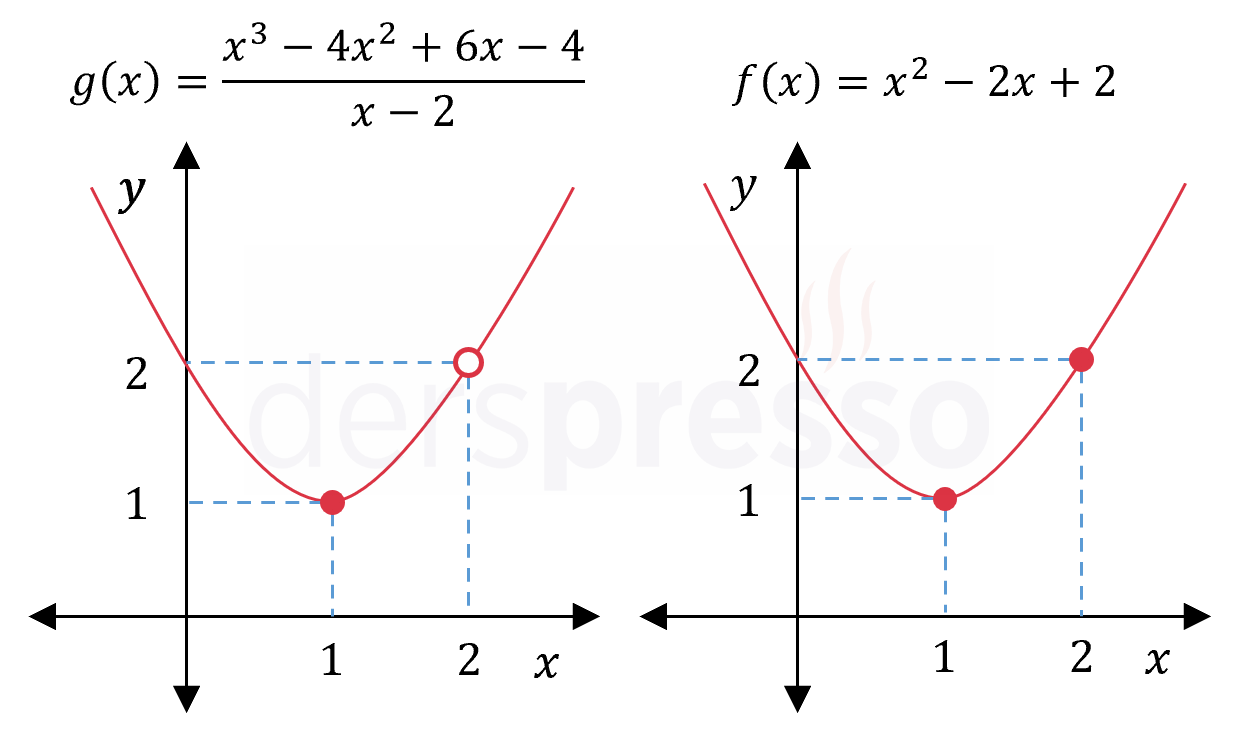
Bu iki grafikle ilgili şu yorumları yapabiliriz.
- Bir rasyonel fonksiyon ve o fonksiyonun pay ve paydasındaki ortak bir çarpanın sadeleşmiş hali bir nokta dışında aynı fonksiyonlardır ve grafikleri özdeştir.
- Farkı yaratan bu nokta pay ve paydada sadeleşen çarpanı sıfır yapan ve belirsizliğe yol açan \( x \) değerinin karşılık geldiği noktadır.
- Bu nokta orijinal fonksiyonun grafiğinde tanımsız, sadeleşmiş fonksiyonun grafiğinde ise tanımlıdır.
- Limit bir noktadaki fonksiyon değeri ile değil, o nokta civarındaki davranışla ilgilendiği için, iki fonksiyon arasındaki bu ayrımın limit hesaplamasına bir etkisi yoktur, dolayısıyla her ne kadar bu çarpanın sadeleşmesi yeni bir fonksiyon üretse de, bu noktadaki limit değeri açısından iki fonksiyon özdeştir.
Bir rasyonel fonksiyonda \( x \to a \) iken \( \frac{0}{0} \) belirsizliği elde ediliyorsa çarpan teoremine göre \( x - a \) payın ve paydanın birer çarpanıdır, dolayısıyla iki polinom da bu ortak çarpana ayrılarak ifade sadeleştirilebilir.
\( \lim\limits_{x \to -3} \dfrac{x^2 + 5x + 6}{x + 3} \) limitinin sonucunu bulunuz.
Çözümü Göster\( \lim\limits_{x \to -3} (x^2 + 5x + 6) = (-3)^2 + 5(-3) + 6 = 0 \)
\( \lim\limits_{x \to -3} (x + 3) = -3 + 3 = 0 \)
Buna göre verilen limit ifadesinde \( \frac{0}{0} \) belirsizliği vardır.
Belirsizliği gidermek için çarpanlara ayırma ve sadeleştirme yöntemini kullanalım.
\( \lim\limits_{x \to -3} \dfrac{x^2 + 5x + 6}{x + 3} = \lim\limits_{x \to -3} \dfrac{(x + 2)(x + 3)}{x + 3} \)
\( = \lim\limits_{x \to -3} (x + 2) \)
Polinom fonksiyonlarının bir noktadaki limiti o noktadaki fonksiyon değerine eşittir.
\( = -3 + 2 = -1 \) bulunur.
\( \lim\limits_{x \to 1} \dfrac{x^{40} - 1}{x^{20} - 1} \) limitinin sonucunu bulunuz.
Çözümü Göster\( \lim\limits_{x \to 1} (x^{40} - 1) = 1^{40} - 1 = 0 \)
\( \lim\limits_{x \to 1} (x^{20} - 1) = 1^{20} - 1 = 0 \)
Buna göre verilen limit ifadesinde \( \frac{0}{0} \) belirsizliği vardır.
Belirsizliği gidermek için çarpanlara ayırma ve sadeleştirme yöntemini kullanalım.
\( \lim\limits_{x \to 1} \dfrac{x^{40} - 1}{x^{20} - 1} = \lim\limits_{x \to 1} \dfrac{(x^{20} - 1)(x^{20} + 1)}{x^{20} - 1} \)
\( = \lim\limits_{x \to 1} (x^{20} + 1) \)
Polinom fonksiyonlarının bir noktadaki limiti o noktadaki fonksiyon değerine eşittir.
\( = 1^{20} + 1 = 2 \) bulunur.
\( \lim\limits_{x \to -3} \dfrac{2x^2 + 5x - 3}{x^2 + 5x + 6} \) limitinin sonucunu bulunuz.
Çözümü Göster\( \lim\limits_{x \to -3} (2x^2 + 5x - 3) = 2(-3)^2 + 5(-3) - 3 = 0 \)
\( \lim\limits_{x \to -3} (x^2 + 5x + 6) = (-3)^2 + 5(-3) + 6 = 0 \)
Buna göre verilen limit ifadesinde \( \frac{0}{0} \) belirsizliği vardır.
\( x = -3 \) pay ve paydadaki ifadelerin ikisini de sıfır yaptığı için iki ifade de \( x + 3 \) çarpanına ayrılabilir.
\( \lim\limits_{x \to -3} \dfrac{2x^2 + 5x - 3}{x^2 + 5x + 6} = \lim\limits_{x \to -3} \dfrac{(2x - 1)(x + 3)}{(x + 2)(x + 3)} \)
\( = \lim\limits_{x \to -3} \dfrac{2x - 1}{x + 2} \)
Limiti alınan nokta paydayı sıfır yapmamak koşuluyla, rasyonel fonksiyonların bir noktadaki limiti o noktadaki fonksiyon değerine eşittir.
\( = \dfrac{2(-3) - 1}{-3 + 2} \)
\( = \dfrac{-7}{-1} = 7 \) bulunur.
\( \lim\limits_{x \to 8} {\dfrac{\frac{1}{x} - \frac{1}{8}}{x - 8}} \) limitinin sonucunu bulunuz.
Çözümü Göster\( \lim\limits_{x \to 8} {(\dfrac{1}{x} - \dfrac{1}{8})} = 0 \)
\( \lim\limits_{x \to 8} {(x - 8)} = 0 \)
Buna göre verilen limit ifadesinde \( \frac{0}{0} \) belirsizliği vardır.
Bu belirsizliği gidermek için payı düzenleyelim.
\( = \lim\limits_{x \to 8} {\dfrac{\frac{8 - x}{8x}}{{x - 8}}} \)
\( = \lim\limits_{x \to 8} {\dfrac{-(x - 8)}{8x(x - 8)}} \)
\( = \lim\limits_{x \to 8} {\dfrac{-1}{8x}} \)
Limiti alınan nokta paydayı sıfır yapmamak koşuluyla, rasyonel fonksiyonların bir noktadaki limiti o noktadaki fonksiyon değerine eşittir.
\( = \dfrac{-1}{8 \cdot 8} = -\dfrac{1}{64} \) bulunur.
Aşağıdaki limitlerin sonucunu bulunuz.
(a) \( \lim\limits_{x \to 2} \dfrac{x^2 - 4}{(x - 2)^2} \)
(b) \( \lim\limits_{x \to 2} \dfrac{(x - 2)^2}{x^2 - 4} \)
(c) \( \lim\limits_{x \to 2} \dfrac{x^2 - 4}{x - 2} \)
Çözümü Göster(a) seçeneği:
\( \lim\limits_{x \to 2} (x^2 - 4) = (2^2 - 4) = 0 \)
\( \lim\limits_{x \to 2} (x - 2)^2 = (2 - 2)^2 = 0 \)
Buna göre verilen limit ifadesinde \( \frac{0}{0} \) belirsizliği vardır.
Belirsizliği gidermek için çarpanlara ayırma ve sadeleştirme yöntemini kullanalım.
\( \lim\limits_{x \to 2} \dfrac{x^2 - 4}{(x - 2)^2} = \lim\limits_{x \to 2} \dfrac{(x - 2)(x + 2)}{(x - 2)^2} \)
\( = \lim\limits_{x \to 2} \dfrac{x + 2}{x - 2} \)
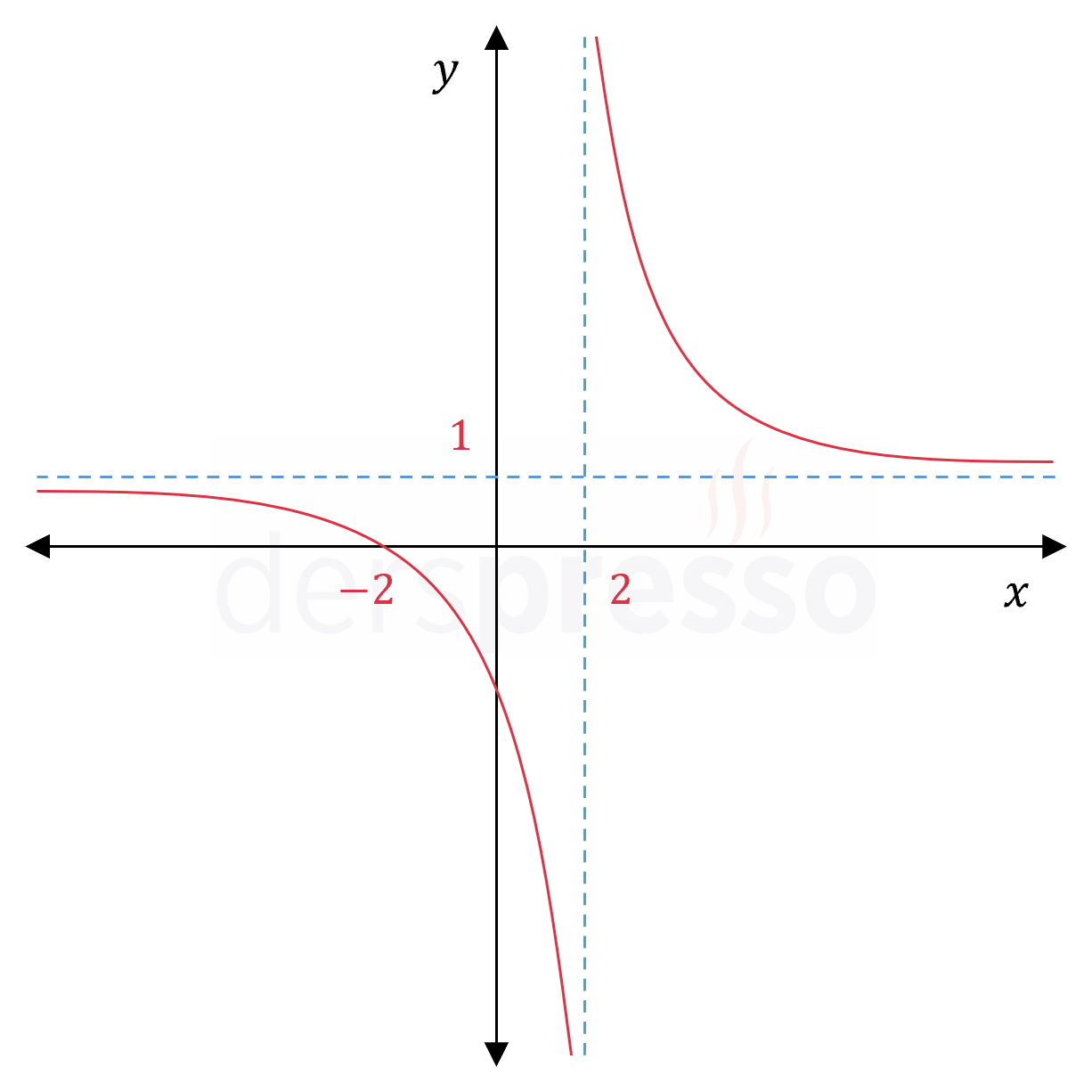
\( x = 2 \) değeri paydayı sıfır yaptığı, ancak payı sıfır yapmadığı için bu noktada bir dikey asimptot oluşur.
Bu noktadaki soldan ve sağdan limitleri inceleyelim.
\( \lim\limits_{x \to 2^-} \dfrac{x + 2}{x - 2} = -\infty \)
\( \lim\limits_{x \to 2^+} \dfrac{x + 2}{x - 2} = +\infty \)
Soldan ve sağdan limitler birer reel sayı olarak tanımlı olmadığı için fonksiyonun bir noktada limiti tanımlı değildir.
Fonksiyonun grafiği aşağıdaki şekildeki gibidir.
(b) seçeneği:
\( \lim\limits_{x \to 2} (x - 2)^2 = (2 - 2)^2 = 0 \)
\( \lim\limits_{x \to 2} (x^2 - 4) = 2^2 - 4 = 0 \)
Buna göre verilen limit ifadesinde \( \frac{0}{0} \) belirsizliği vardır.
Belirsizliği gidermek için çarpanlara ayırma ve sadeleştirme yöntemini kullanalım.
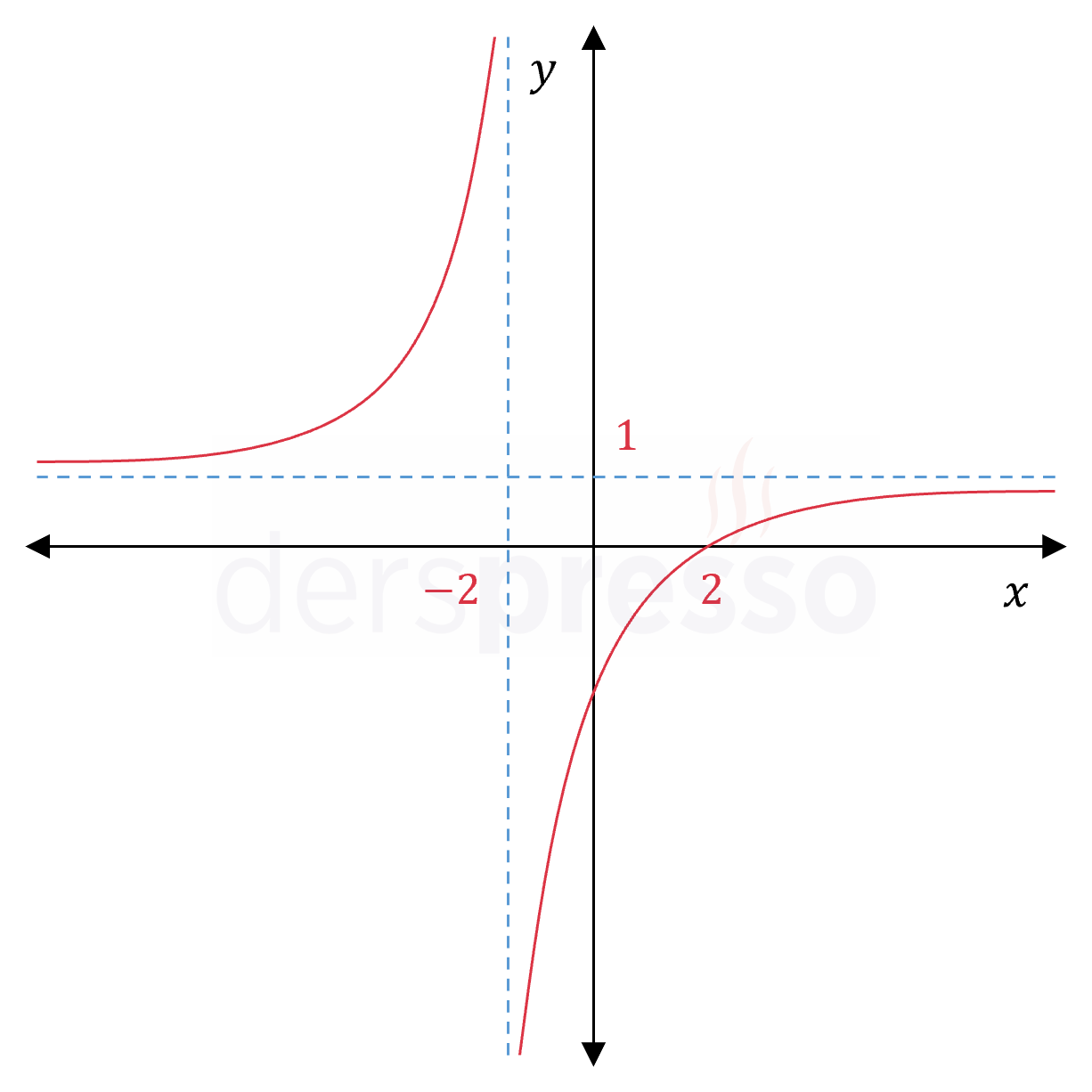
\( \lim\limits_{x \to 2} \dfrac{(x - 2)^2}{x^2 - 4} = \lim\limits_{x \to 2} \dfrac{(x - 2)^2}{(x - 2)(x + 2)} \)
\( = \lim\limits_{x \to 2} \dfrac{x - 2}{x + 2} \)
Limiti alınan nokta paydayı sıfır yapmamak koşuluyla, rasyonel fonksiyonların bir noktadaki limiti o noktadaki fonksiyon değerine eşittir.
\( = \dfrac{2 - 2}{2 + 2} = 0 \)
Fonksiyonun grafiği aşağıdaki şekildeki gibidir.
(c) seçeneği:
\( \lim\limits_{x \to 2} (x^2 - 4) = 2^2 - 4 = 0 \)
\( \lim\limits_{x \to 2} (x - 2) = 2 - 2 = 0 \)
Buna göre verilen limit ifadesinde \( \frac{0}{0} \) belirsizliği vardır.
Belirsizliği gidermek için çarpanlara ayırma ve sadeleştirme yöntemini kullanalım.
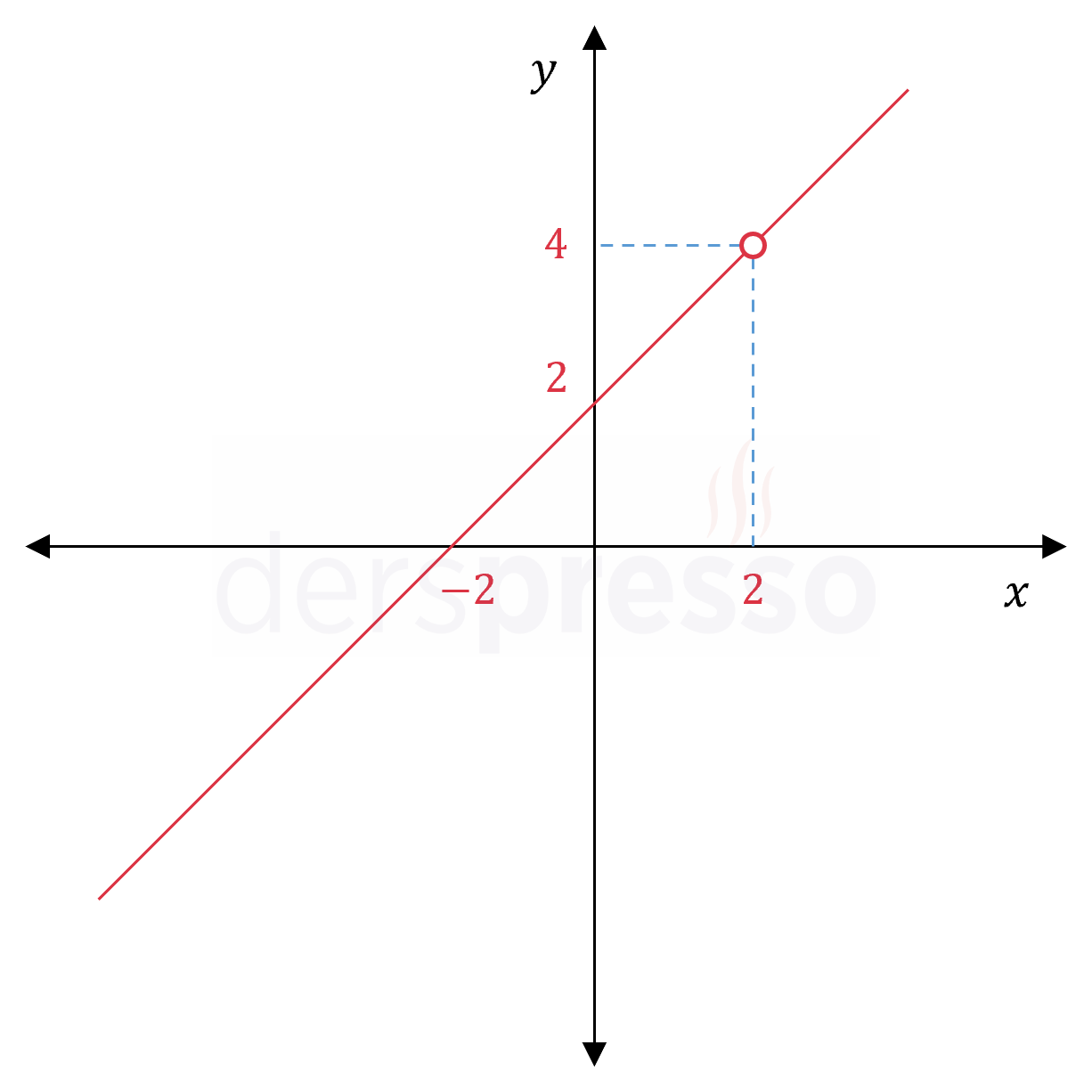
\( \lim\limits_{x \to 2} \dfrac{x^2 - 4}{x - 2} = \lim\limits_{x \to 2} \dfrac{(x - 2)(x + 2)}{x - 2} \)
\( = \lim\limits_{x \to 2} (x + 2) \)
Polinom fonksiyonlarının bir noktadaki limiti o noktadaki fonksiyon değerine eşittir.
\( = 2 + 2 = 4 \)
Fonksiyonun grafiği aşağıdaki şekildeki gibidir.
\( \lim\limits_{x \to 4} \dfrac{x^3 - 6x^2 + 5x + 12}{x - 4} \) limitinin sonucunu bulunuz.
Çözümü Göster\( \lim\limits_{x \to 4} (x^3 - 6x^2 + 5x + 12) = 4^3 - 6(4)^2 + 5(4) + 12 = 0 \)
\( \lim\limits_{x \to 4} (x - 4) = 4 - 4 = 0 \)
Buna göre verilen limit ifadesinde \( \frac{0}{0} \) belirsizliği vardır.
\( x = 4 \) paydaki ifadeyi sıfır yaptığı için \( x - 4 \) çarpanına ayrılabilir. Payı polinom bölmesi ile \( x - 4 \) ifadesine bölerek diğer çarpanı bulabiliriz.
\( \lim\limits_{x \to 4} \dfrac{x^3 - 6x^2 + 5x + 12}{x - 4} = \lim\limits_{x \to 4} \dfrac{(x - 4)(x^2 - 2x - 3)}{x - 4} \)
\( = \lim\limits_{x \to 4} (x^2 - 2x - 3) \)
Polinom fonksiyonlarının bir noktadaki limiti o noktadaki fonksiyon değerine eşittir.
\( = 4^2 - 2(4) - 3 \)
\( = 5 \) bulunur.
\( \lim\limits_{x \to 8} \dfrac{\sqrt[3]{x} - 2}{x - 8} \) limitinin sonucunu bulunuz.
Çözümü Göster\( \lim\limits_{x \to 8} (\sqrt[3]{x} - 2) = \sqrt[3]{8} - 2 = 0 \)
\( \lim\limits_{x \to 8} (x - 8) = 8 - 8 = 0 \)
Buna göre verilen limit ifadesinde \( \frac{0}{0} \) belirsizliği vardır.
Belirsizliği gidermek için çarpanlara ayırma ve sadeleştirme yöntemini kullanalım.
Paydadaki ifadeyi çarpanlarına ayırmak için küp farkı özdeşliğini kullanalım.
\( x - 8 = (\sqrt[3]{x})^3 - 2^3 = (\sqrt[3]{x} - 2)((\sqrt[3]{x})^2 + 2\sqrt[3]{x} + 2^2) \)
\( \lim\limits_{x \to 8} \dfrac{\sqrt[3]{x} - 2}{x - 8} = \lim\limits_{x \to 8} \dfrac{\sqrt[3]{x} - 2}{(\sqrt[3]{x} - 2)((\sqrt[3]{x})^2 + 2\sqrt[3]{x} + 2^2)} \)
\( = \lim\limits_{x \to 8} \dfrac{1}{\sqrt[3]{x^2} + 2\sqrt[3]{x} + 4} \)
Paydadaki ifade tüm reel sayılarda tanımlı ve sürekli olduğu için direkt yerine koyma yöntemiyle limit değerini bulabiliriz.
\( = \dfrac{1}{\sqrt[3]{8^2} + 2\sqrt[3]{8} + 4} \)
\( = \dfrac{1}{4 + 2(2) + 4} \)
\( = \dfrac{1}{12} \) bulunur.
\( a \in \mathbb{R} \) olmak üzere,
\( \lim\limits_{x \to 2} \dfrac{x^3 - 2x^2 + 3x - 6}{x^3 - 2x^2 + 4x - 8} = \dfrac{a}{8} \) olduğuna göre, \( a \) kaçtır?
Çözümü Göster\( \lim\limits_{x \to 2} (x^3 - 2x^2 + 3x - 6) = 2^3 - 2(2)^2 + 3(2) - 6 = 0 \)
\( \lim\limits_{x \to 2} (x^3 - 2x^2 + 4x - 8) = 2^3 - 2(2)^2 + 4(2) - 8 = 0 \)
Buna göre verilen limit ifadesinde \( \frac{0}{0} \) belirsizliği vardır.
\( x = 2 \) pay ve paydadaki ifadeleri sıfır yaptığı için iki ifade de \( x - 2 \) çarpanına ayrılabilir. Payı ve paydayı polinom bölmesi ile \( x - 2 \) ifadesine bölerek diğer çarpanlarını bulabiliriz.
\( \lim\limits_{x \to 2} \dfrac{x^3 - 2x^2 + 3x - 6}{x^3 - 2x^2 + 4x - 8} = \lim\limits_{x \to 2} \dfrac{(x - 2)(x^2 + 3)}{(x - 2)(x^2 + 4)} \)
\( = \lim\limits_{x \to 2} \dfrac{x^2 + 3}{x^2 + 4} \)
Limiti alınan nokta paydayı sıfır yapmamak koşuluyla, rasyonel fonksiyonların bir noktadaki limiti o noktadaki fonksiyon değerine eşittir.
\( = \dfrac{2^2 + 3}{2^2 + 4} = \dfrac{7}{8} = \dfrac{a}{8} \)
\( a = 7 \) olarak bulunur.
\( a, b \in \mathbb{R} \) olmak üzere,
\( \lim\limits_{x \to 3} \dfrac{ax^2 - 18}{x - 3} = b \)
olduğuna göre, \( a + b \) toplamı kaçtır?
Çözümü GösterVerilen limit ifadesinin sonucu bir reel sayı olduğuna göre, bu noktadaki limitin tanımlı olduğunu söyleyebiliriz.
\( \lim\limits_{x \to 3} (x - 3) = 3 - 3 = 0 \)
Paydanın limiti sıfır olduğuna göre, payın limiti de sıfır olmalı ve ifadede giderilebilir bir \( \frac{0}{0} \) belirsizliği olmalıdır, aksi takdirde ifadede \( c \ne 0 \) olacak şekilde \( \frac{c}{0} \) tanımsızlığı oluşacaktır.
Payın limitini sıfıra eşitleyerek \( a \) değerini bulalım.
\( \lim\limits_{x \to 3} (ax^2 - 18) = a(3)^2 - 18 = 0 \)
\( a = 2 \)
\( a \) değerini limit ifadesinde yerine koyalım ve çarpanlara ayırma yöntemiyle ifadeyi sadeleştirelim.
\( \lim\limits_{x \to 3} \dfrac{2x^2 - 18}{x - 3} = \lim\limits_{x \to 3} \dfrac{2(x^2 - 9)}{x - 3} \)
\( = \lim\limits_{x \to 3} \dfrac{2(x - 3)(x + 3)}{x - 3} \)
\( = \lim\limits_{x \to 3} [2(x + 3)} \)
Polinom fonksiyonlarının bir noktadaki limiti o noktadaki fonksiyon değerine eşittir.
\( = 2(3 + 3) = 12 = b \)
\( a + b = 2 + 12 = 14 \) bulunur.
\( \lim\limits_{x \to 1} \dfrac{x^4 + 2x^3 - 9x^2 - 12x + 18}{x^2 + 2x - 3} \) limitinin sonucunu bulunuz.
Çözümü Göster\( \lim\limits_{x \to 1} (x^4 + 2x^3 - 9x^2 - 12x + 18) = 1^4 + 2(1)^3 - 9(1)^2 - 12(1) + 18 = 0 \)
\( \lim\limits_{x \to 1} (x^2 + 2x - 3) = 1^2 + 2(1) - 3 = 0 \)
Buna göre verilen limit ifadesinde \( \frac{0}{0} \) belirsizliği vardır.
Paydadaki ifadeyi çarpanlarına ayıralım.
\( \lim\limits_{x \to 1} \dfrac{x^4 + 2x^3 - 9x^2 - 12x + 18}{x^2 + 2x - 3} = \lim\limits_{x \to 1} \dfrac{x^4 + 2x^3 - 9x^2 - 12x + 18}{(x + 3)(x - 1)} \)
\( x = 1 \) pay ve paydadaki ifadelerin ikisini de sıfır yaptığı için iki ifade de \( x - 1 \) çarpanına ayrılabilir. Payı polinom bölmesi ile \( x - 1 \) ifadesine bölerek diğer çarpanı bulabiliriz.
\( = \lim\limits_{x \to 1} \dfrac{(x^3 + 3x^2 - 6x - 18)(x - 1)}{(x + 3)(x - 1)} \)
\( = \lim\limits_{x \to 1} \dfrac{x^3 + 3x^2 - 6x - 18}{x + 3} \)
Limiti alınan nokta paydayı sıfır yapmamak koşuluyla, rasyonel fonksiyonların bir noktadaki limiti o noktadaki fonksiyon değerine eşittir.
\( = \dfrac{1^3 + 3(1)^2 - 6(1) - 18}{1 + 3} \)
\( = \dfrac{-20}{4} = -5 \) bulunur.
Eşlenik ile Çarpma
Pay ya da payda köklü bir ifade içeriyorsa pay ve payda bu köklü ifadenin eşleniği ile çarpılarak ve oluşan ifadede sadeleştirme yapılarak belirsizliğin giderilmesi denenebilir. Belirsizlik ortadan kalktıktan sonra ifadenin bu sadeleşmiş haliyle limit değeri tekrar hesaplanır.
\( \lim\limits_{x \to 1} \dfrac{\sqrt{x + 3} - 2}{x - 1} \) limitinin değerini bulalım.
\( \lim\limits_{x \to 1} (\sqrt{x + 3} - 2) = \sqrt{1 + 3} - 2 = 0 \)
\( \lim\limits_{x \to 1} (x - 1) = 1 - 1 = 0 \)
Buna göre verilen limit ifadesinde \( \frac{0}{0} \) belirsizliği vardır.
Bu belirsizliği gidermek için payı ve paydayı paydaki köklü ifadenin eşleniği ile çarpalım.
\( \lim\limits_{x \to 1} [ \dfrac{(\sqrt{x + 3} - 2)(\sqrt{x + 3} + 2)}{(x - 1)(\sqrt{x + 3} + 2)} \)
\( = \lim\limits_{x \to 1} \dfrac{(\sqrt{x + 3})^2 - 2^2}{(x - 1)(\sqrt{x + 3} + 2)} \)
\( = \lim\limits_{x \to 1} \dfrac{x - 1}{(x - 1)(\sqrt{x + 3} + 2)} \)
Pay ve paydadaki ortak \( x - 1 \) çarpanını sadeleştirelim.
\( = \lim\limits_{x \to 1} \dfrac{1}{\sqrt{x + 3} + 2} \)
Elde ettiğimiz ifadede \( x = 1 \) koyduğumuzda belirsizliğin ortadan kalktığını görüyoruz, dolayısıyla direkt yerine koyma yöntemiyle limit değerini bulabiliriz.
\( = \dfrac{1}{\sqrt{1 + 3} + 2} = \dfrac{1}{4} \)
\( \lim\limits_{x \to 2} \dfrac{\sqrt{x + 14} - 4}{x^3 - 2x^2} \) limitinin sonucunu bulunuz.
Çözümü Göster\( \lim\limits_{x \to 2} (\sqrt{x + 14} - 4) = \sqrt{2 + 14} - 4 = 0 \)
\( \lim\limits_{x \to 2} (x^3 - 2x^2) = 2^3 - 2(2)^2 = 0 \)
Buna göre verilen limit ifadesinde \( \frac{0}{0} \) belirsizliği vardır.
Bu belirsizliği gidermek için pay ve paydayı payın eşleniği ile çarpalım.
\( \lim\limits_{x \to 2} \dfrac{\sqrt{x + 14} - 4}{x^3 - 2x^2} = \lim\limits_{x \to 2} \dfrac{(\sqrt{x + 14} - 4)(\sqrt{x + 14} + 4)}{(x^3 - 2x^2)(\sqrt{x + 14} + 4)} \)
\( = \lim\limits_{x \to 2} \dfrac{(\sqrt{x + 14})^2 - 4^2}{x^2(x - 2)(\sqrt{x + 14} + 4)} \)
\( = \lim\limits_{x \to 2} \dfrac{x + 14 - 16}{x^2(x - 2)(\sqrt{x + 14} + 4)} \)
\( = \lim\limits_{x \to 2} \dfrac{x - 2}{x^2(x - 2)(\sqrt{x + 14} + 4)} \)
\( = \lim\limits_{x \to 2} \dfrac{1}{x^2(\sqrt{x + 14} + 4)} \)
Paydadaki ifade \( x = 2 \) noktasında sürekli olduğu için doğrudan yerine koyma yöntemi ile limiti bulabiliriz.
\( = \dfrac{1}{2^2(\sqrt{2 + 14} + 4)} \)
\( = \dfrac{1}{32} \) bulunur.
\( \lim\limits_{x \to 5} {\dfrac{\sqrt{x - 3} - \sqrt{2}}{x - 5}} \) limitinin sonucunu bulunuz.
Çözümü Göster\( \lim\limits_{x \to 5} (\sqrt{x - 3} - \sqrt{2}) = 0 \)
\( \lim\limits_{x \to 5} (x - 5) = 0 \)
Buna göre verilen limit ifadesinde \( \frac{0}{0} \) belirsizliği vardır.
Bu belirsizliği gidermek için payı ve paydayı paydaki ifadenin eşleniği ile çarpalım.
\( = \lim\limits_{x \to 5} \dfrac{(\sqrt{x - 3} - \sqrt{2})(\sqrt{x - 3} + \sqrt{2})}{(x - 5)(\sqrt{x - 3} + \sqrt{2})} \)
\( = \lim\limits_{x \to 5} {\dfrac{(\sqrt{x - 3})^2 - (\sqrt{2})^2}{(x - 5)(\sqrt{x - 3} + \sqrt{2})}} \)
\( = \lim\limits_{x \to 5} {\dfrac{x - 3 - 2}{(x - 5)(\sqrt{x - 3} + \sqrt{2})}} \)
\( = \lim\limits_{x \to 5} {\dfrac{x - 5}{(x - 5)(\sqrt{x - 3} + \sqrt{2})}} \)
\( = \lim\limits_{x \to 5} {\dfrac{1}{\sqrt{x - 3} + \sqrt{2}}} \)
Paydadaki ifade \( x = 5 \) noktasında sürekli olduğu için doğrudan yerine koyma yöntemi ile limiti bulabiliriz.
\( = \dfrac{1}{\sqrt{5 - 3} + \sqrt{2}} \)
\( = \dfrac{1}{2\sqrt{2}} \) bulunur.
\( \lim\limits_{x \to 8} \dfrac{\sqrt{\frac{x}{2} + 5} - 3}{x - 8} \) limitinin sonucunu bulunuz.
Çözümü Göster\( \lim\limits_{x \to 8} {(\sqrt{\frac{x}{2} + 5} - 3)} = \sqrt{9} - 3 = 0 \)
\( \lim\limits_{x \to 8} {(x - 8)} = 8 - 8 = 0 \)
Buna göre verilen limit ifadesinde \( \frac{0}{0} \) belirsizliği vardır.
Bu belirsizliği gidermek için payı ve paydayı paydaki köklü ifadenin eşleniği ile çarpalım.
\( \lim\limits_{x \to 8} \dfrac{(\sqrt{\frac{x}{2} + 5} - 3)(\sqrt{\frac{x}{2} + 5} + 3)}{(x - 8)(\sqrt{\frac{x}{2} + 5} + 3)} \)
\( = \lim\limits_{x \to 8}\dfrac{(\sqrt{\frac{x}{2} + 5})^2 - 3^2}{(x - 8)(\sqrt{\frac{x}{2} + 5} + 3)} \)
\( = \lim\limits_{x \to 8}\dfrac{\frac{x}{2} + 5 - 9}{(x - 8)(\sqrt{\frac{x}{2} + 5} + 3)} \)
\( = \lim\limits_{x \to 8}\dfrac{\frac{x}{2} - 4}{2(\frac{x}{2} - 4)(\sqrt{\frac{x}{2} + 5} + 3)} \)
\( = \lim\limits_{x \to 8} \dfrac{1}{2(\sqrt{\frac{x}{2} + 5} + 3)} \)
Paydadaki ifade \( x = 2 \) noktasında sürekli olduğu için doğrudan yerine koyma yöntemi ile limiti bulabiliriz.
\( = \dfrac{1}{2(\sqrt{\frac{8}{2} + 5} + 3)} \)
\( = \dfrac{1}{12} \) bulunur.
\( \lim\limits_{x \to 12} \dfrac{5 - \sqrt{2x + 1}}{x^2 - 7x - 60} \) limitinin sonucunu bulunuz.
Çözümü Göster\( \lim\limits_{x \to 12} (5 - \sqrt{2x + 1}) = 5 - \sqrt{25} = 0 \)
\( \lim\limits_{x \to 12} (x^2 - 7x - 60) = 12^2 - 7(12) - 60 = 0 \)
Buna göre verilen limit ifadesinde \( \frac{0}{0} \) belirsizliği vardır.
Bu belirsizliği gidermek için payı ve paydayı payın eşleniği ile çarpalım.
\( \lim\limits_{x \to 12} \dfrac{(5 - \sqrt{2x + 1})(5 + \sqrt{2x + 1})}{(x^2 - 7x - 60)(5 + \sqrt{2x + 1})} \)
\( =\lim\limits_{x \to 12} \dfrac{5^2 - (\sqrt{2x + 1})^2}{(x^2 - 7x - 60)(5 + \sqrt{2x + 1})} \)
\( = \lim\limits_{x \to 12} \dfrac{25 - (2x + 1)}{(x^2 - 7x - 60)(5 + \sqrt{2x + 1})} \)
\( = \lim\limits_{x \to 12} \dfrac{2(12 - x)}{(x - 12)(x + 5)(5 + \sqrt{2x + 1})} \)
\( = \lim\limits_{x \to 12} \dfrac{-2}{(x + 5)(5 + \sqrt{2x + 1})} \)
Paydadaki ifade \( x = 12 \) noktasında sürekli olduğu için doğrudan yerine koyma yöntemi ile limiti bulabiliriz.
\( = \dfrac{-2}{(12 + 5)(5 + \sqrt{2(12) + 1})} \)
\( = -\dfrac{1}{85} \) bulunur.
\( \lim\limits_{x \to 2} \dfrac{\sqrt{x + 7} - 3}{\sqrt{x - 1} - 1} \) limitinin sonucunu bulunuz.
Çözümü Göster\( \lim\limits_{x \to 2} (\sqrt{x + 7} - 3) = \sqrt{2 + 7} - 3 = 0 \)
\( \lim\limits_{x \to 2} (\sqrt{x - 1} - 1) = \sqrt{2 - 1} - 1 = 0 \)
Buna göre verilen limit ifadesinde \( \frac{0}{0} \) belirsizliği vardır.
Hem pay hem de payda köklü ifade içerdiği için, bu belirsizliği gidermek için payı ve paydayı bu iki köklü ifadenin eşlenikleri ile çarpalım.
\( \lim\limits_{x \to 2} \dfrac{(\sqrt{x + 7} - 3)(\sqrt{x + 7} + 3)(\sqrt{x - 1} + 1)}{(\sqrt{x - 1} - 1)(\sqrt{x + 7} + 3)(\sqrt{x - 1} + 1)} \)
\( = \lim\limits_{x \to 2} \dfrac{((\sqrt{x + 7})^2 - 3^2)(\sqrt{x - 1} + 1)}{((\sqrt{x - 1})^2 - 1^2)(\sqrt{x + 7} + 3)} \)
\( = \lim\limits_{x \to 2} \dfrac{(x + 7 - 9)(\sqrt{x - 1} + 1)}{(x - 1 - 1)(\sqrt{x + 7} + 3)} \)
\( = \lim\limits_{x \to 2} \dfrac{(x - 2)(\sqrt{x - 1} + 1)}{(x - 2)(\sqrt{x + 7} + 3)} \)
\( = \lim\limits_{x \to 2} \dfrac{\sqrt{x - 1} + 1}{\sqrt{x + 7} + 3} \)
Pay ve paydadaki ifadeler \( x = 2 \) noktasında sürekli olduğu için doğrudan yerine koyma yöntemi ile limiti bulabiliriz.
\( = \dfrac{\sqrt{2 - 1} + 1}{\sqrt{2 + 7} + 3} \)
\( = \dfrac{2}{6} = \dfrac{1}{3} \) bulunur.
Özel Trigonometrik Limitler
İspatlarını trigonometrik fonksiyonların limiti bölümünde verdiğimiz trigonometrik ifadelerin limit değerlerini kullanarak da \( \frac{0}{0} \) belirsizliği giderilebilir.
\( \lim\limits_{x \to 0} \dfrac{\sin{x}}{x} = 1 \)
\( \lim\limits_{x \to 0} \dfrac{1 - \cos{x}}{x} = 0 \)
\( \lim\limits_{x \to 0} \dfrac{\tan{x}}{x} = 1 \)
\( \lim\limits_{x \to 0} \dfrac{\sin(2x)}{x\cos{x}} \) limitinin sonucunu bulunuz.
Çözümü Göster\( \lim\limits_{x \to 0} \sin(2x) = \sin{0} = 0 \)
\( \lim\limits_{x \to 0} (x\cos{x}) = 0\cos{0} = 0 \cdot 1 = 0 \)
Buna göre verilen limit ifadesinde \( \frac{0}{0} \) belirsizliği vardır.
Belirsizliği gidermek için trigonometrik özdeşlikleri kullanalım.
Sinüs iki kat açı formülünü kullanalım.
\( \sin(2x) = 2\sin{x}\cos{x} \)
\( \lim\limits_{x \to 0} \dfrac{\sin(2x)}{x\cos{x}} = \lim\limits_{x \to 0} \dfrac{2\sin{x}\cos{x}}{x\cos{x}} \)
\( = \lim\limits_{x \to 0} \dfrac{2\sin{x}}{x} \)
\( = 2\lim\limits_{x \to 0} \dfrac{\sin{x}}{x} \)
İspatıyla birlikte verdiğimiz trigonometrik limit kurallarını kullanalım.
\( \lim\limits_{x \to 0} \dfrac{\sin{x}}{x} = 1 \)
\( = 2 \cdot 1 = 2 \) bulunur.
\( \lim\limits_{x \to 0} \dfrac{1 - \cos(2x)}{x(1 + \cos{x})} \) limitinin değeri kaçtır?
Çözümü Göster\( \lim\limits_{x \to 0} (1 - \cos(2x)) = 1 - \cos{0} = 1 - 1 = 0 \)
\( \lim\limits_{x \to 0} (x(1 + \cos{x})) = 0(1 + \cos{0}) = 0 \cdot 2 = 0 \)
Buna göre verilen limit ifadesinde \( \frac{0}{0} \) belirsizliği vardır.
Belirsizliği gidermek için trigonometrik özdeşlikleri kullanalım.
Kosinüs iki kat açı formülünü kullanalım.
\( \cos(2x) = 2\cos^2{x} - 1 \)
\( \lim\limits_{x \to 0} \dfrac{1 - \cos(2x)}{x(1 + \cos{x})} = \lim\limits_{x \to 0} \dfrac{1 - (2\cos^2{x} - 1)}{x(1 + \cos{x})} \)
\( = \lim\limits_{x \to 0} \dfrac{2 - 2\cos^2{x}}{x(1 + \cos{x})} \)
\( = \lim\limits_{x \to 0} \dfrac{2(1 - \cos^2{x})}{x(1 + \cos{x})} \)
\( = \lim\limits_{x \to 0} \dfrac{2(1 - \cos{x})(1 + \cos{x})}{x(1 + \cos{x})} \)
\( = \lim\limits_{x \to 0} \dfrac{2(1 - \cos{x})}{x} \)
\( = 2\lim\limits_{x \to 0} \dfrac{1 - \cos{x}}{x} \)
İspatıyla birlikte verdiğimiz trigonometrik limit kurallarını kullanalım.
\( \lim\limits_{x \to 0} \dfrac{1 - \cos{x}}{x} = 0 \)
\( = 2 \cdot 0 = 0 \) bulunur.
\( \lim\limits_{x \to 0} \dfrac{1 - \cos(2x)}{\sin{x}\cos{x}} \) limitinin sonucunu bulunuz.
Çözümü Göster\( \lim\limits_{x \to 0} (1 - \cos(2x)) = 1 - \cos{0} = 1 - 1 = 0 \)
\( \lim\limits_{x \to 0} (\sin{x}\cos{x}) = \sin{0}\cos{0} = 0 \cdot 1 = 0 \)
Buna göre verilen limit ifadesinde \( \frac{0}{0} \) belirsizliği vardır.
Belirsizliği gidermek için trigonometrik özdeşlikleri kullanalım.
Kosinüs iki kat açı formülünü kullanalım.
\( \cos(2x) = 1 - 2\sin^2{x} \)
\( \lim\limits_{x \to 0} \dfrac{1 - \cos(2x)}{\sin{x}\cos{x}} = \lim\limits_{x \to 0} \dfrac{1 - (1 - 2\sin^2{x})}{\sin{x}\cos{x}} \)
\( = \lim\limits_{x \to 0} \dfrac{2\sin^2{x}}{\sin{x}\cos{x}} \)
\( = \lim\limits_{x \to 0} \dfrac{2\sin{x}}{\cos{x}} \)
\( = 2\lim\limits_{x \to 0} {\tan{x}} \)
Tanjant fonksiyonu \( x = 0 \) noktasında tanımlı ve sürekli olduğu için bu noktadaki limiti fonksiyon değerine eşittir.
\( = 2\tan{0} = 0 \) bulunur.
\( \lim\limits_{x \to 0} \dfrac{5\sin(9x)}{2\sin(7x)} \) limitinin sonucunu bulunuz.
Çözümü Göster\( \lim\limits_{x \to 0} (5\sin(9x)) = 5\sin{0} = 0 \)
\( \lim\limits_{x \to 0} (2\sin(7x)) = 2\sin{0} = 0 \)
Buna göre verilen limit ifadesinde \( \frac{0}{0} \) belirsizliği vardır.
Payı ve paydayı \( x \) ile çarpalım.
\( \lim\limits_{x \to 0} \dfrac{5\sin(9x) \cdot x}{2\sin(7x) \cdot x} \)
Limit ifadesini düzenleyelim.
\( = \lim\limits_{x \to 0} \left( \dfrac{\sin(9x)}{2x} \cdot \dfrac{5x}{\sin(7x)} \right) \)
Aşağıda göstereceğimiz üzere, iki çarpanın limiti ayrı ayrı birer reel sayı olarak tanımlı olduğu için ifadeyi iki limitin çarpımı şeklinde yazabiliriz.
\( = \lim\limits_{x \to 0} \dfrac{\sin(9x)}{2x} \cdot \lim\limits_{x \to 0} \dfrac{5x}{\sin(7x)} \)
İspatıyla birlikte verdiğimiz trigonometrik limit kurallarını kullanalım.
\( \lim\limits_{x \to 0} \dfrac{\sin(ax)}{bx} = \dfrac{a}{b} \)
\( = \dfrac{9}{2} \cdot \dfrac{5}{7} \)
\( = \dfrac{45}{14} \) bulunur.
\( \lim\limits_{h \to 0} \dfrac{\sin(3h)}{7h^2 + 4h} \) limitinin sonucunu bulunuz.
Çözümü Göster\( \lim\limits_{h \to 0} \sin(3h) = \sin{0} = 0 \)
\( \lim\limits_{h \to 0} (7h^2 + 4h) = 7(0)^2 + 4(0) = 0 \)
Buna göre verilen limit ifadesinde \( \frac{0}{0} \) belirsizliği vardır.
Limit ifadesini düzenleyelim.
\( \lim\limits_{h \to 0} \dfrac{\sin(3h)}{7h^2 + 4h} = \lim\limits_{h \to 0} \dfrac{\sin(3h)}{h(7h + 4)} \)
\( = \lim\limits_{h \to 0} \left( \dfrac{\sin(3h)}{h} \cdot \dfrac{1}{7h + 4} \right) \)
Aşağıda göstereceğimiz üzere, iki çarpanın limiti ayrı ayrı birer reel sayı olarak tanımlı olduğu için ifadeyi iki limitin çarpımı şeklinde yazabiliriz.
\( = \lim\limits_{h \to 0} \dfrac{\sin(3h)}{h} \cdot \lim\limits_{h \to 0} \dfrac{1}{7h + 4} \)
İspatıyla birlikte verdiğimiz trigonometrik limit kurallarını kullanalım.
\( \lim\limits_{x \to 0} \dfrac{\sin(ax)}{bx} = \dfrac{a}{b} \)
\( = \dfrac{3}{1} \cdot \lim\limits_{h \to 0} \dfrac{1}{7h + 4} \)
Limiti alınan nokta paydayı sıfır yapmamak koşuluyla, rasyonel fonksiyonların bir noktadaki limiti o noktadaki fonksiyon değerine eşittir.
\( = 3 \cdot \dfrac{1}{7(0) + 4} = \dfrac{3}{4} \) bulunur.
\( \lim\limits_{x \to 0} \dfrac{1 - \cos{x}}{x^2} \) limitinin sonucunu bulunuz.
Çözümü Göster\( \lim\limits_{x \to 0} (1 - \cos{x}) = 1 - 1 = 0 \)
\( \lim\limits_{x \to 0} x^2 = 0^2 = 0 \)
Buna göre verilen limit ifadesinde \( \frac{0}{0} \) belirsizliği vardır.
Belirsizliği gidermek için payı ve paydayı paydaki ifadenin eşleniği ile çarpalım.
\( \lim\limits_{x \to 0} \dfrac{1 - \cos{x}}{x^2} = \lim\limits_{x \to 0} \dfrac{(1 - \cos{x})(1 + \cos{x})}{x^2(1 + \cos{x})} \)
\( = \lim\limits_{x \to 0} \dfrac{1 - \cos^2{x}}{x^2(1 + \cos{x})} \)
Pisagor özdeşliğini kullanalım.
\( = \lim\limits_{x \to 0} \dfrac{\sin^2{x}}{x^2(1 + \cos{x})} \)
İfadeyi düzenleyelim.
\( = \lim\limits_{x \to 0} \left( \dfrac{\sin{x}}{x} \cdot \dfrac{\sin{x}}{x} \cdot \dfrac{1}{1 + \cos{x}} \right) \)
Aşağıda göstereceğimiz üzere, üç çarpanın limiti ayrı ayrı birer reel sayı olarak tanımlı olduğu için ifadeyi üç limitin çarpımı şeklinde yazabiliriz.
\( = \lim\limits_{x \to 0} \dfrac{\sin{x}}{x} \cdot \lim\limits_{x \to 0} \dfrac{\sin{x}}{x} \cdot \lim\limits_{x \to 0} \dfrac{1}{1 + \cos{x}} \)
İspatıyla birlikte verdiğimiz trigonometrik limit kurallarını kullanalım.
\( \lim\limits_{x \to 0} \dfrac{\sin{x}}{x} = 1 \)
\( = 1 \cdot 1 \cdot \lim\limits_{x \to 0} \dfrac{1}{1 + \cos{x}} \)
Paydadaki ifade \( x = 0 \) noktasında sürekli olduğu için doğrudan yerine koyma yöntemi ile limiti bulabiliriz.
\( = \dfrac{1}{1 + \cos{0}} = \dfrac{1}{1 + 1} = \dfrac{1}{2} \) bulunur.
\( \lim\limits_{x \to 0} \dfrac{4\cos{x} - 4}{5\sin{x}} \) limitinin sonucunu bulunuz.
Çözümü Göster\( \lim\limits_{x \to 0} (4\cos{x} - 4) = 4(1) - 4 = 0 \)
\( \lim\limits_{x \to 0} \sin{x} = 0 \)
Buna göre verilen limit ifadesinde \( \frac{0}{0} \) belirsizliği vardır.
Bu belirsizliği gidermek için limit ifadesinin payını ve paydasını \( x \)'e bölelim.
\( \lim\limits_{x \to 0} \dfrac{4\cos{x} - 4}{5\sin{x}} = \lim\limits_{x \to 0} \dfrac{\frac{4(\cos{x} - 1)}{x}}{\frac{5\sin{x}}{x}} \)
Aşağıda göstereceğimiz üzere, payın ve paydanın limiti ayrı ayrı birer reel sayı olarak tanımlı olduğu için ifadeyi iki limitin bölümü şeklinde yazabiliriz.
\( = \dfrac{\lim\limits_{x \to 0} \frac{4(\cos{x} - 1)}{x}}{\lim\limits_{x \to 0} \frac{5\sin{x}}{x}} \)
\( = \dfrac{4\lim\limits_{x \to 0} \frac{\cos{x} - 1}{x}}{5\lim\limits_{x \to 0} \frac{\sin{x}}{x}} \)
İspatıyla birlikte verdiğimiz trigonometrik limit kurallarını kullanalım.
\( \lim\limits_{x \to 0} \dfrac{\sin{x}}{x} = 1 \)
\( \lim\limits_{x \to 0} \dfrac{1 - \cos{x}}{x} = 0 \)
\( = \dfrac{4 \cdot 0}{5 \cdot 1} = 0 \) bulunur.
\( \lim\limits_{x \to 3} \dfrac{\sin(x - 3)}{x^2 + x - 12} \) limitinin sonucunu bulunuz.
Çözümü Göster\( \lim\limits_{x \to 3} \sin(x - 3) = \sin{0} = 0 \)
\( \lim\limits_{x \to 3} (x^2 + x - 12) = 3^2 + 3 - 12 = 0 \)
Buna göre verilen limit ifadesinde \( \frac{0}{0} \) belirsizliği vardır.
Limit ifadesini düzenleyelim.
\( \lim\limits_{x \to 3} \dfrac{\sin(x - 3)}{x^2 + x - 12} = \lim\limits_{x \to 3} \dfrac{\sin(x - 3)}{(x - 3)(x + 4)} \)
Bu belirsizliği gidermek için sinüs fonksiyonunun içindeki ifadeye değişken değiştirme yöntemi uygulayalım.
\( h = x - 3 \Longrightarrow x = h + 3 \)
\( x \to 3 \) iken \( h \to 0 \) olur.
\( = \lim\limits_{h \to 0} \dfrac{\sin{h}}{h((h + 3) + 4)} = \lim\limits_{h \to 0} \dfrac{\sin{h}}{h(h + 7)} \)
Limit ifadesini düzenleyelim.
\( = \lim\limits_{h \to 0} \left( \dfrac{\sin{h}}{h} \cdot \dfrac{1}{h + 7} \right) \)
Aşağıda göstereceğimiz üzere, iki çarpanın limiti ayrı ayrı birer reel sayı olarak tanımlı olduğu için ifadeyi iki limitin çarpımı şeklinde yazabiliriz.
\( = \lim\limits_{h \to 0} \dfrac{\sin{h}}{h} \cdot \lim\limits_{h \to 0} \dfrac{1}{h + 7} \)
İspatıyla birlikte verdiğimiz trigonometrik limit kurallarını kullanalım.
\( \lim\limits_{x \to 0} \dfrac{\sin{x}}{x} = 1 \)
\( = 1 \cdot \lim\limits_{h \to 0} \dfrac{1}{h + 7} \)
Limiti alınan nokta paydayı sıfır yapmamak koşuluyla, rasyonel fonksiyonların bir noktadaki limiti o noktadaki fonksiyon değerine eşittir.
\( = 1 \cdot \dfrac{1}{0 + 7} = \dfrac{1}{7} \) bulunur.
\( \lim\limits_{x \to 0} \dfrac{x^7\sin(13x)}{\sin^8(2x)} \) limitinin sonucunu bulunuz.
Çözümü Göster\( \lim\limits_{x \to 0} (x^7\sin(13x)) = 0^7 \cdot \sin{0} = 0 \)
\( \lim\limits_{x \to 0} \sin^8(2x) = \sin^8{0} = 0 \)
Buna göre verilen limit ifadesinde \( \frac{0}{0} \) belirsizliği vardır.
Payı ve paydayı \( x \) ile çarpalım.
\( \lim\limits_{x \to 0} \dfrac{x^7\sin(13x) \cdot x}{\sin^8(2x) \cdot x} \)
Limit ifadesini düzenleyelim.
\( = \lim\limits_{x \to 0} \left( \dfrac{\sin(13x)}{x} \cdot \dfrac{x^8}{\sin^8(2x)} \right) \)
Aşağıda göstereceğimiz üzere, iki çarpanın limiti ayrı ayrı birer reel sayı olarak tanımlı olduğu için ifadeyi iki limitin çarpımı şeklinde yazabiliriz.
\( = \lim\limits_{x \to 0} \dfrac{\sin(13x)}{x} \cdot \lim\limits_{x \to 0} \dfrac{x^8}{\sin^8(2x)} \)
\( = \lim\limits_{x \to 0} \dfrac{\sin(13x)}{x} \cdot \lim\limits_{x \to 0} \left( \dfrac{x}{\sin(2x)} \right)^8 \)
İkinci limit ifadesinde, kuvvet fonksiyonu tüm reel sayılarda tanımlı ve sürekli olduğu için bileşke fonksiyon limit kuralı ile limit işlemini parantez içine alabiliriz.
\( = \lim\limits_{x \to 0} \dfrac{\sin(13x)}{x} \cdot \left( \lim\limits_{x \to 0} \dfrac{x}{\sin(2x)} \right)^8 \)
İspatıyla birlikte verdiğimiz trigonometrik limit kurallarını kullanalım.
\( \lim\limits_{x \to 0} \dfrac{\sin(ax)}{bx} = \dfrac{a}{b} \)
\( = 13\left( \dfrac{1}{2} \right)^8 = \dfrac{13}{256} \) bulunur.
\( \lim\limits_{x \to \pi} \dfrac{\sin(x - \pi)}{x^4 - \pi^4} \) limitinin sonucunu bulunuz.
Çözümü Göster\( \lim\limits_{x \to \pi} \sin(x - \pi) = \sin(\pi - \pi) = \sin{0} = 0 \)
\( \lim\limits_{x \to \pi} (x^4 - \pi^4) = \pi^4 - \pi^4 = 0 \)
Buna göre verilen limit ifadesinde \( \frac{0}{0} \) belirsizliği vardır.
Paydadaki ifadeyi çarpanlarına ayıralım.
\( \lim\limits_{x \to \pi} \dfrac{\sin(x - \pi)}{x^4 - \pi^4} = \lim\limits_{x \to \pi} \dfrac{\sin(x - \pi)}{(x^2 - \pi^2)(x^2 + \pi^2)} \)
\( = \lim\limits_{x \to \pi} \dfrac{\sin(x - \pi)}{(x - \pi)(x + \pi)(x^2 + \pi^2)} \)
Sinüs fonksiyonunun içindeki ifadeye değişken değiştirme uygulayalım.
\( h = x - \pi \Longrightarrow x = h + \pi \)
\( x \to \pi \) iken \( h \to 0 \) olur.
\( = \lim\limits_{h \to 0} \dfrac{\sin{h}}{h(h + \pi + \pi)[(h + \pi)^2 + \pi^2]} \)
\( = \lim\limits_{h \to 0} \dfrac{\sin{h}}{h(h + 2\pi)[(h + \pi)^2 + \pi^2]} \)
İfadeyi düzenleyelim.
\( = \lim\limits_{h \to 0} \left( \dfrac{\sin{h}}{h} \cdot \dfrac{1}{(h + 2\pi)[(h + \pi)^2 + \pi^2]} \right) \)
Aşağıda göstereceğimiz üzere, iki çarpanın limiti ayrı ayrı birer reel sayı olarak tanımlı olduğu için ifadeyi iki limitin çarpımı şeklinde yazabiliriz.
\( = \lim\limits_{h \to 0} \dfrac{\sin{h}}{h} \cdot \lim\limits_{h \to 0} \dfrac{1}{(h + 2\pi)[(h + \pi)^2 + \pi^2]} \)
İspatıyla birlikte verdiğimiz trigonometrik limit kurallarını kullanalım.
\( \lim\limits_{h \to 0} \dfrac{\sin{h}}{h} = 1 \)
\( = 1 \cdot \lim\limits_{h \to 0} \dfrac{1}{(h + 2\pi)[(h + \pi)^2 + \pi^2]} \)
Paydadaki ifade \( h = 0 \) noktasında sürekli olduğu için doğrudan yerine koyma yöntemi ile limiti bulabiliriz.
\( = \dfrac{1}{(0 + 2\pi)[(0 + \pi)^2 + \pi^2]} \)
\( = \dfrac{1}{2\pi(2\pi^2)} = \dfrac{1}{4\pi^3} \) bulunur.
\( \lim\limits_{x \to 0} \dfrac{\tan(11x)}{\sin(5x)} \) limitinin sonucunu bulunuz.
Çözümü Göster\( \lim\limits_{x \to 0} \tan(11x) = \tan{0} = 0 \)
\( \lim\limits_{x \to 0} \sin(5x) = \sin{0} = 0 \)
Buna göre verilen limit ifadesinde \( \frac{0}{0} \) belirsizliği vardır.
Bu belirsizliği gidermek için tanjant ifadesini sinüs ve kosinüs cinsinden yazalım.
\( \lim\limits_{x \to 0} \dfrac{\tan(11x)}{\sin(5x)} = \lim\limits_{x \to 0} \dfrac{\frac{\sin(11x)}{\cos(11x)}}{\sin(5x)} \)
\( = \lim\limits_{x \to 0} \dfrac{\sin(11x)}{\cos(11x)\sin(5x)} \)
İfadenin payını ve paydasını \( x \) ile çarpalım.
\( = \lim\limits_{x \to 0} \dfrac{x\sin(11x)}{x\cos(11x)\sin(5x)} \)
İfadeyi düzenleyelim.
\( = \lim\limits_{x \to 0} \left( \dfrac{1}{\cos(11x)} \cdot \dfrac{\sin(11x)}{x} \cdot \dfrac{x}{\sin(5x)} \right) \)
Aşağıda göstereceğimiz üzere, üç çarpanın limiti ayrı ayrı birer reel sayı olarak tanımlı olduğu için ifadeyi üç limitin çarpımı şeklinde yazabiliriz.
\( = \lim\limits_{x \to 0} \dfrac{1}{\cos(11x)} \cdot \lim\limits_{x \to 0} \dfrac{\sin(11x)}{x} \cdot \lim\limits_{x \to 0} \dfrac{x}{\sin(5x)} \)
İspatıyla birlikte verdiğimiz trigonometrik limit kurallarını kullanalım.
\( \lim\limits_{x \to 0} \dfrac{\sin(ax)}{bx} = \dfrac{a}{b} \)
\( = \lim\limits_{x \to 0} \dfrac{1}{\cos(11x)} \cdot \dfrac{11}{1} \cdot \dfrac{1}{5} \)
Paydadaki ifade \( x = 0 \) noktasında sürekli olduğu için doğrudan yerine koyma yöntemi ile limiti bulabiliriz.
\( = \dfrac{1}{\cos{0}} \cdot \dfrac{11}{5} = \dfrac{11}{5} \) bulunur.
\( \lim\limits_{x \to 0} \dfrac{\sin(2x)}{x + \tan{x}} \) limitinin sonucunu bulunuz.
Çözümü Göster\( \lim\limits_{x \to 0} \sin(2x) = \sin{0} = 0 \)
\( \lim\limits_{x \to 0} (x + \tan{x}) = 0 + \tan{0} = 0 \)
Buna göre verilen limit ifadesinde \( \frac{0}{0} \) belirsizliği vardır.
Bu belirsizliği gidermek için payı ve paydayı \( x \)'e bölelim.
\( \lim\limits_{x \to 0} \dfrac{\sin(2x)}{x + \tan{x}} = \lim\limits_{x \to 0} \dfrac{\frac{\sin(2x)}{x}}{\frac{x + \tan{x}}{x}} \)
\( = \lim\limits_{x \to 0} \dfrac{\frac{\sin(2x)}{x}}{1 + \frac{\tan{x}}{x}} \)
Aşağıda göstereceğimiz üzere, payın ve paydanın limiti ayrı ayrı birer reel sayı olarak tanımlı olduğu için ifadeyi iki limitin bölümü şeklinde yazabiliriz.
\( = \dfrac{\lim\limits_{x \to 0} \frac{\sin(2x)}{x}}{\lim\limits_{x \to 0} (1 + \frac{\tan{x}}{x})} \)
\( = \dfrac{\lim\limits_{x \to 0} \frac{\sin(2x)}{x}}{\lim\limits_{x \to 0} 1 + \lim\limits_{x \to 0} \frac{\tan{x}}{x}} \)
İspatıyla birlikte verdiğimiz trigonometrik limit kurallarını kullanalım.
\( \lim\limits_{x \to 0} \dfrac{\sin(ax)}{bx} = \dfrac{a}{b} \)
\( \lim\limits_{x \to 0} \dfrac{\tan{x}}{x} = 1 \)
\( = \dfrac{\frac{2}{1}}{1 + 1} = 1 \) bulunur.
\( \lim\limits_{x \to 0} \dfrac{\tan(5x) - \sin(5x)}{x^3} \) limitinin sonucunu bulunuz.
Çözümü Göster\( \lim\limits_{x \to 0} (\tan(5x) - \sin(5x)) = \tan{0} - \sin{0} = 0 - 0 = 0 \)
\( \lim\limits_{x \to 0} x^3 = 0^3 = 0 \)
Buna göre verilen limit ifadesinde \( \frac{0}{0} \) belirsizliği vardır.
Tanjant ifadesini sinüs ve kosinüs cinsinden yazalım.
\( \lim\limits_{x \to 0} \dfrac{\tan(5x) - \sin(5x)}{x^3} = \lim\limits_{x \to 0} \dfrac{\frac{\sin(5x)}{\cos(5x)} - \sin(5x)}{x^3} \)
\( = \lim\limits_{x \to 0} \dfrac{\frac{\sin(5x) - \sin(5x)\cos(5x)}{\cos(5x)}}{x^3} \)
\( = \lim\limits_{x \to 0} \dfrac{\sin(5x)(1 - \cos(5x))}{x^3 \cos(5x)} \)
Payı ve paydayı \( 1 + \cos(5x) \) ile çarpalım.
\( = \lim\limits_{x \to 0} \dfrac{\sin(5x)(1 - \cos(5x)) (1 + \cos(5x))}{x^3\cos(5x)(1 + \cos(5x))} \)
\( = \lim\limits_{x \to 0} \dfrac{\sin(5x)(1 - \cos^2(5x))}{x^3\cos(5x)(1 + \cos(5x))} \)
Pisagor özdeşliğini kullanalım.
\( = \lim\limits_{x \to 0} \dfrac{\sin(5x)\sin^2(5x)}{x^3\cos(5x)(1 + \cos(5x))} \)
\( = \lim\limits_{x \to 0} \dfrac{\sin^3(5x)}{x^3\cos(5x)(1 + \cos(5x))} \)
Limit ifadesini düzenleyelim.
\( = \lim\limits_{x \to 0} \left( \dfrac{\sin^3(5x)}{x^3} \cdot \dfrac{1}{\cos(5x)(1 + \cos(5x))} \right) \)
Aşağıda göstereceğimiz üzere, iki çarpanın limiti ayrı ayrı birer reel sayı olarak tanımlı olduğu için ifadeyi iki limitin çarpımı şeklinde yazabiliriz.
\( = \lim\limits_{x \to 0} \dfrac{\sin^3(5x)}{x^3} \cdot \lim\limits_{x \to 0} \dfrac{1}{\cos(5x)(1 + \cos(5x))} \)
\( = \lim\limits_{x \to 0} \left( \dfrac{\sin(5x)}{x} \right)^3 \cdot \lim\limits_{x \to 0} \dfrac{1}{\cos(5x)(1 + \cos(5x))} \)
Birinci limit ifadesinde, kuvvet fonksiyonu tüm reel sayılarda tanımlı ve sürekli olduğu için bileşke fonksiyon limit kuralı ile limit işlemini parantez içine alabiliriz.
\( = \left( \lim\limits_{x \to 0} \dfrac{\sin(5x)}{x} \right)^3 \cdot \lim\limits_{x \to 0} \dfrac{1}{\cos(5x)(1 + \cos(5x))} \)
İspatıyla birlikte verdiğimiz trigonometrik limit kurallarını kullanalım.
\( \lim\limits_{x \to 0} \dfrac{\sin(ax)}{bx} = \dfrac{a}{b} \)
\( = 5^3\lim\limits_{x \to 0} \dfrac{1}{\cos(5x)(1 + \cos(5x))} \)
\( = 125\lim\limits_{x \to 0} \dfrac{1}{\cos(5x)(1 + \cos(5x))} \)
Paydadaki ifade \( x = 0 \) noktasında sürekli olduğu için doğrudan yerine koyma yöntemi ile limiti bulabiliriz.
\( = 125 \cdot \dfrac{1}{1 \cdot (1 + 1)} \)
\( = \dfrac{125}{2} \) bulunur.
L'Hospital Kuralı
\( \frac{0}{0} \) ve \( \frac{\infty}{\infty} \) belirsizliklerini gidermek için kullanılabilecek bir yöntem olan L'Hospital kuralını önümüzdeki bölümde inceleyeceğiz.