Sonsuz Limit
Bir \( f \) fonksiyonunda \( x \) değişkeni bir \( a \) değerine soldan ya da sağdan yaklaşırken \( f(x) \) değeri pozitif (ya da negatif) yönde sınırsız büyüyorsa \( f \) fonksiyonunun bu noktadaki tek yönlü limiti pozitif (ya da negatif) sonsuz olur.
\( \lim\limits_{x \to a^-} f(x) = \pm\infty \)
\( \lim\limits_{x \to a^+} f(x) = \pm\infty \)
Aşağıda grafiği verilen \( f \) fonksiyonunun \( x = -3 \) noktasındaki soldan limiti pozitif sonsuz, sağdan limiti negatif sonsuz iken \( x = 4 \) noktasındaki soldan limiti negatif sonsuz, sağdan limiti pozitif sonsuzdur.
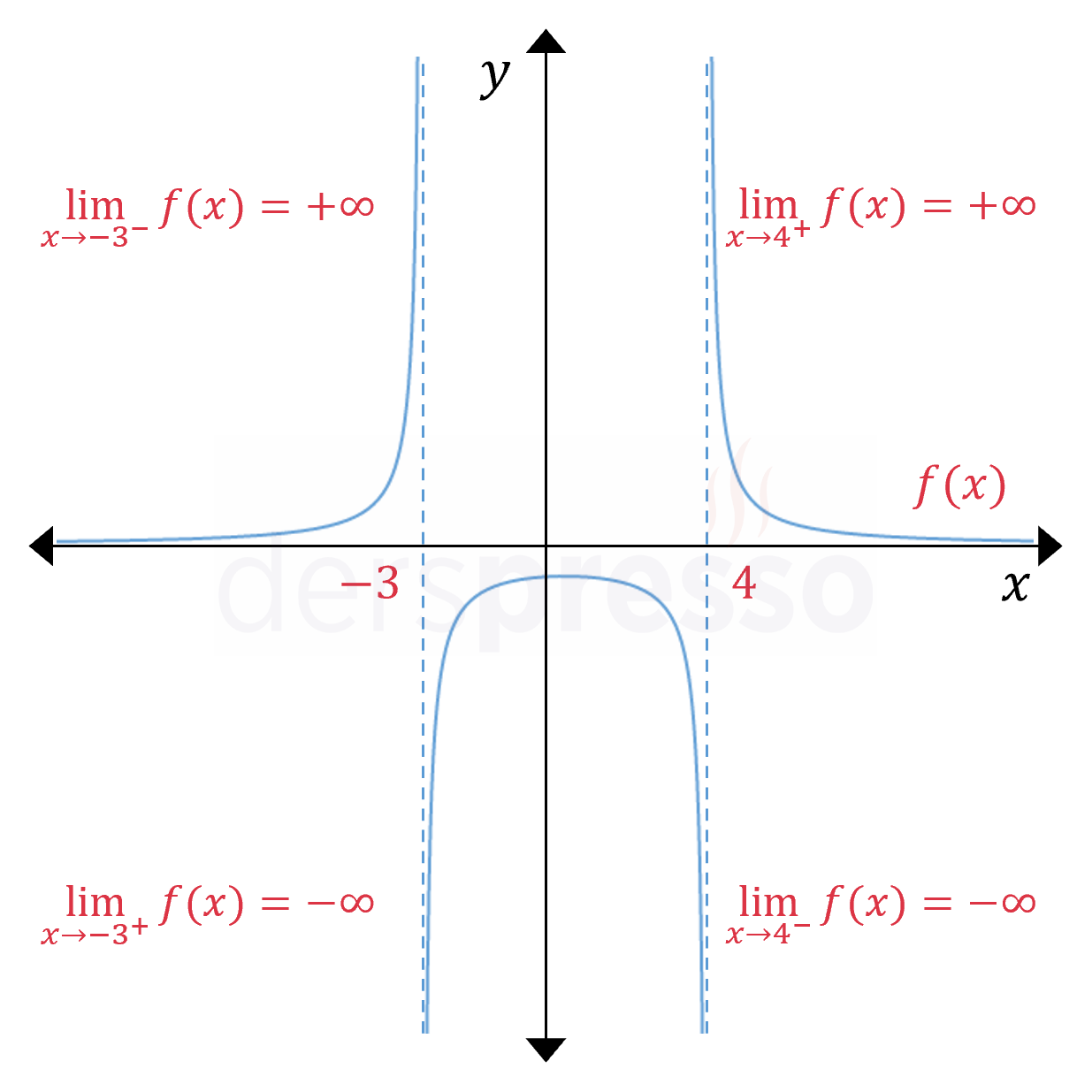
Bir fonksiyonun bir noktadaki soldan ve sağdan limitlerinin ikisi de pozitif (ya da negatif) sonsuz ise bu noktadaki iki taraflı limiti pozitif (ya da negatif) sonsuz olur.
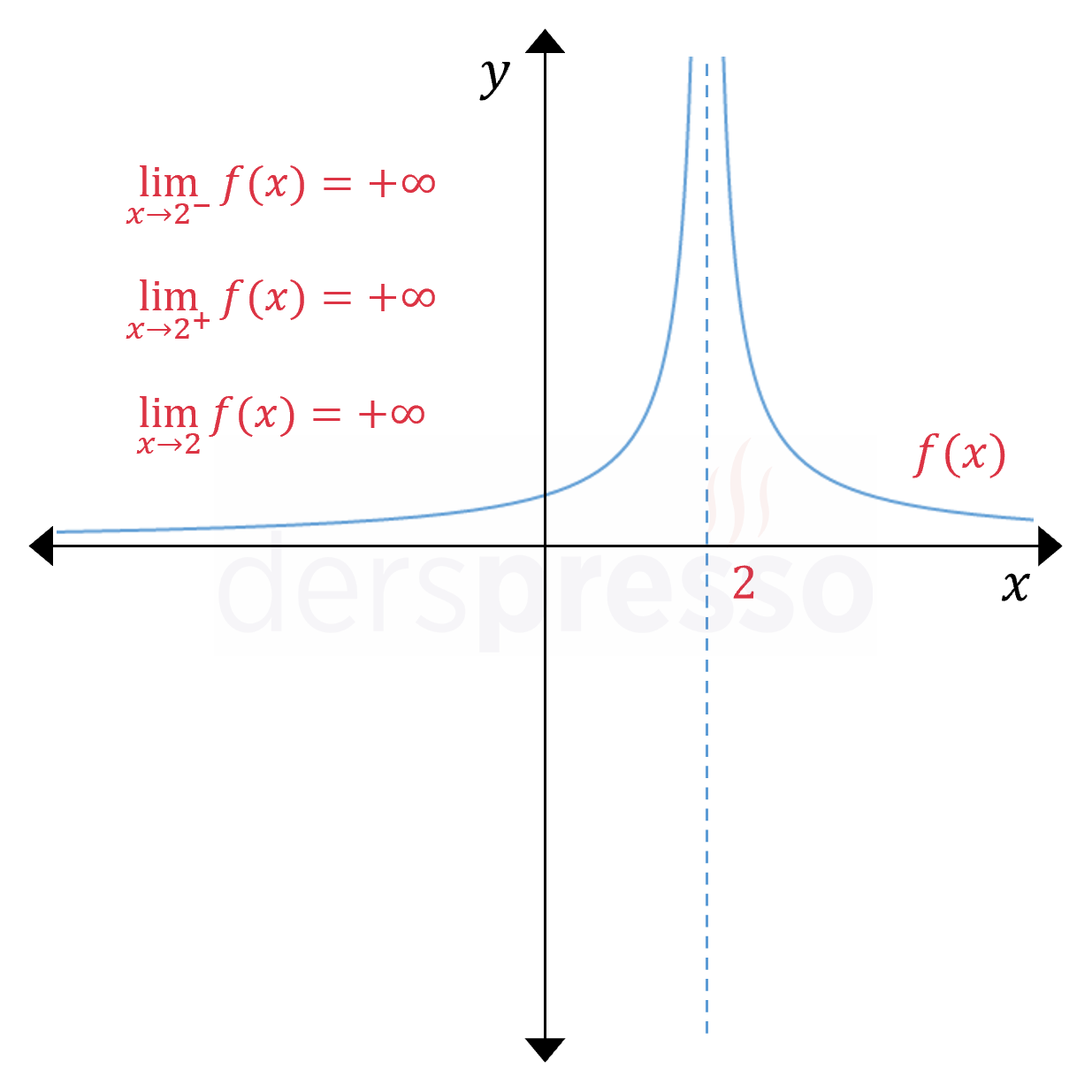
\( \lim\limits_{x \to a^-} f(x) = +\infty \) ve \( \lim\limits_{x \to a^+} f(x) = +\infty \) ise,
\( \lim\limits_{x \to a} f(x) = +\infty \)
\( \lim\limits_{x \to a^-} f(x) = -\infty \) ve \( \lim\limits_{x \to a^+} f(x) = -\infty \) ise,
\( \lim\limits_{x \to a} f(x) = -\infty \)
Yukarıda verilen grafiklerde görülebileceği üzere, bir fonksiyonun bir noktasının her iki tarafındaki tek taraflı limitler aynı ya da farklı yönlerde sonsuza gidebilir.
NOT: Yaptığımız limit tanıma göre, bir noktadaki limit ancak bir reel sayı olarak tanımlı ise o noktada limit tanımlıdır. Bir noktadaki limit için "pozitif ya da negatif sonsuz" ifadesi kullanmamız o noktada limitin tanımlı olduğu anlamına gelmez, sadece tanımsızlığa ek olarak fonksiyonun bu noktadaki davranışı ile ilgili ek bir bilgi verir ve bu noktadaki limiti yine tanımsız olarak kabul etmemiz gerekir.
Dikey Asimptot
Bir fonksiyonun \( x = a \) noktasındaki soldan veya sağdan limiti pozitif ya da negatif sonsuz ise bu noktada bir dikey asimptot oluşur. Bu dikey asimptot denklemi \( x = a \) olan bir doğrudur.
Aşağıdaki grafikte mavi kesikli çizgi ile gösterilen \( x = -2 \) ve \( x = 3 \) doğruları fonksiyonun dikey asimptotlarıdır.
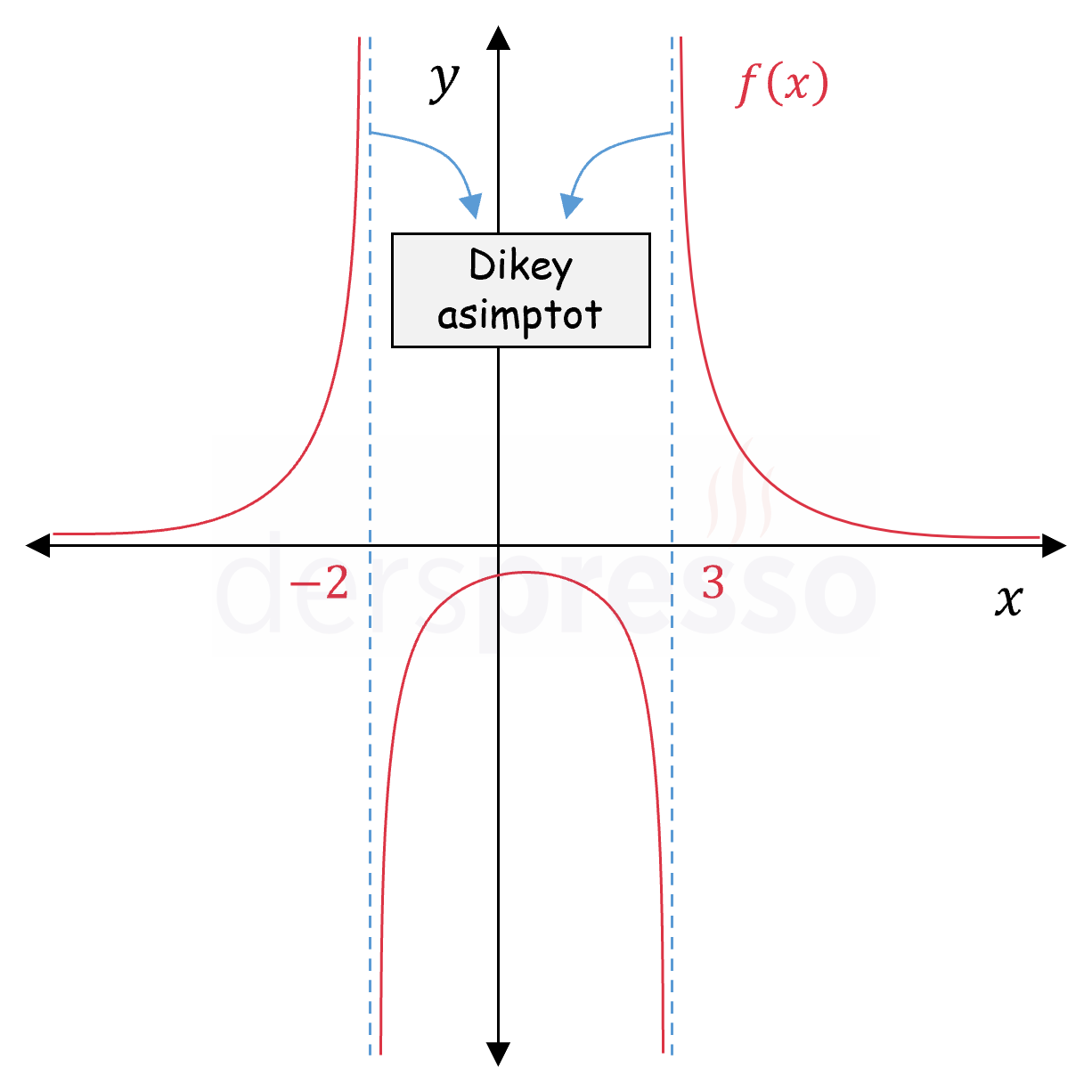
Dikey asimptotlar fonksiyon grafiğinin bir parçası olmayıp fonksiyonun asimptotun oluştuğu nokta civarındaki davranışının daha kolay anlaşılmasını sağlamak için çizilir.
Bir fonksiyonun herhangi bir sayıda dikey asimptotu olabilir ya da hiç olmayabilir.
Bir fonksiyon dikey asimptotun oluştuğu noktada tanımsızdır, dolayısıyla grafiği dikey asimptota yaklaşır, ama hiçbir zaman kesmez. Bununla birlikte, bir fonksiyon parçalı fonksiyon şeklinde tanımlanarak dikey asimptotun oluştuğu noktadaki tanımsızlığı ve süreksizliği giderilebilir.
Fonksiyonların Dikey Asimptotu
Aşağıdaki tipteki fonksiyonlarda belirtilen noktalarda dikey asimptot(lar) oluşur.
Rasyonel İfadeler
Rasyonel ifadelerde paydayı sıfır yapan, ama payı sıfır yapmayan \( x \) değerlerinde birer dikey asimptot oluşur. Buna göre bir rasyonel ifadenin dikey asimptotlarını bulmak için önce paydayı sıfır yapan \( x \) değerleri bulunur, daha sonra bu değerlerden hangilerinin payı sıfır yapmadığı belirlenir.
Rasyonel ifadelerde hem payı hem de paydayı sıfır yapan \( x \) değerlerinde dikey asimptot değil tanımsız nokta oluşur.
\( f(x) = \dfrac{x + 1}{x^2 - 4} \) fonksiyonunun dikey asimptotlarını bulalım.
Paydadaki ifadeyi çarpanlarına ayıralım.
\( f(x) = \dfrac{x + 1}{(x - 2)(x + 2)} \)
Paydayı sıfır yapan değerler \( x \in \{-2, 2\} \) olur.
Bu değerlerden herhangi biri payı sıfır yapmadığı için fonksiyonun \( x = -2 \) ve \( x = 2 \) doğruları olmak üzere iki dikey asimptotu vardır.
Bu iki dikey asimptot aşağıda fonksiyon grafiği üzerinde gösterilmiştir.
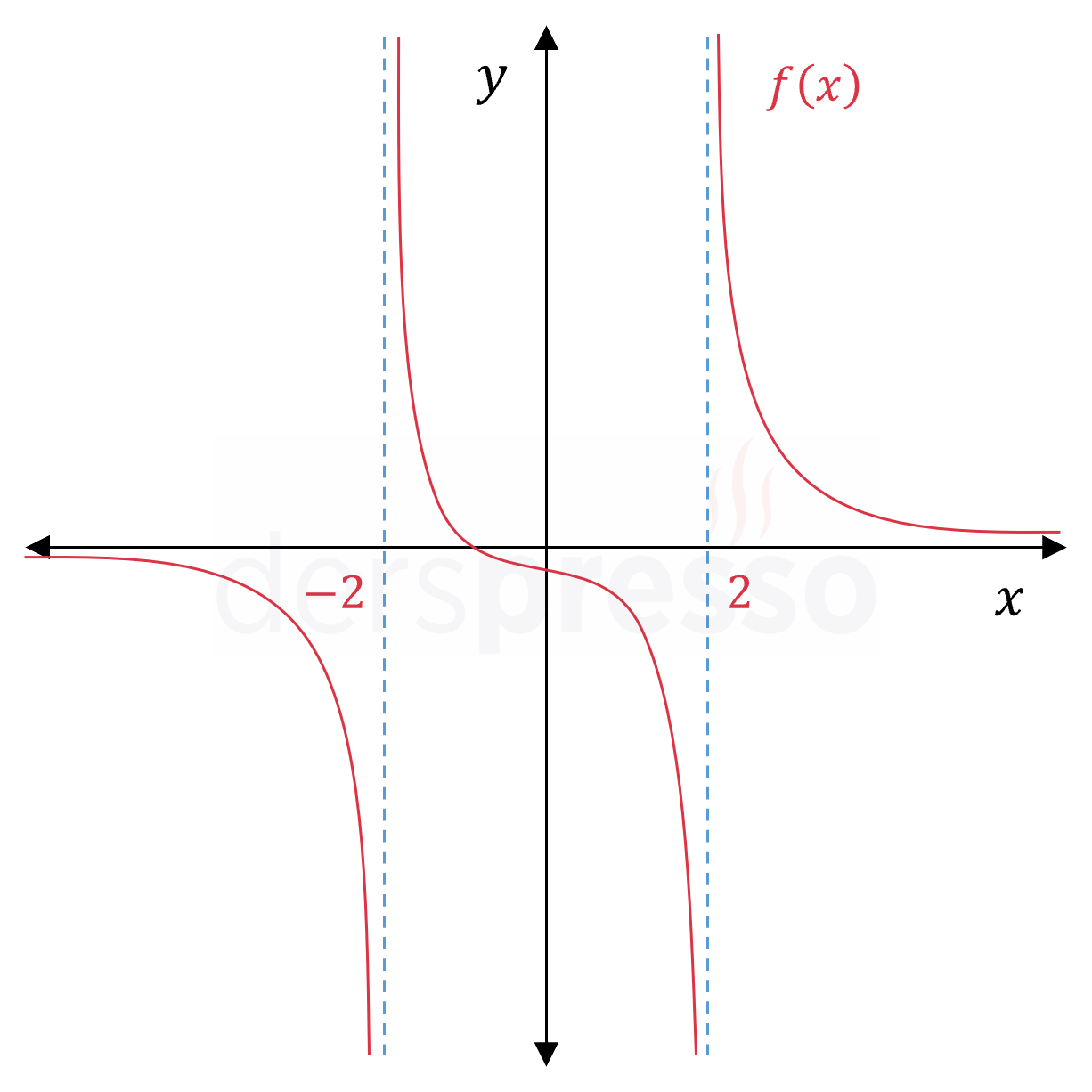
Tanım gereği, dikey asimptot oluşan noktalarda fonksiyonun tek taraflı limitlerinden en az biri sonsuzdur.
\( \lim\limits_{x \to -2^-} f(x) = -\infty \)
\( \lim\limits_{x \to -2^+} f(x) = +\infty \)
\( \lim\limits_{x \to 2^-} f(x) = -\infty \)
\( \lim\limits_{x \to 2^+} f(x) = +\infty \)
\( f(x) = \dfrac{x^2 - x - 2}{x^2 - 2x - 3} \) fonksiyonunun dikey asimptotlarını bulalım.
Pay ve paydadaki ifadeleri çarpanlarına ayıralım.
\( f(x) = \dfrac{(x + 1)(x - 2)}{(x + 1)(x - 3)} \)
Paydayı sıfır yapan değerler \( x \in \{-1, 3\} \) olur.
Bu değerlerden \( x = -1 \) payı da sıfır yaptığı için bu noktada dikey asimptot oluşmaz, dolayısıyla fonksiyonun \( x = 3 \) doğrusu olmak üzere tek dikey asimptotu vardır.
Hem payı hem de paydayı sıfır yapan \( x = -1 \) değerinde dikey asimptot değil, tanımsız nokta oluşur.
Fonksiyonun dikey asimptotu ve \( x = -1 \) değerinde oluşan tanımsız nokta aşağıda fonksiyon grafiği üzerinde gösterilmiştir.
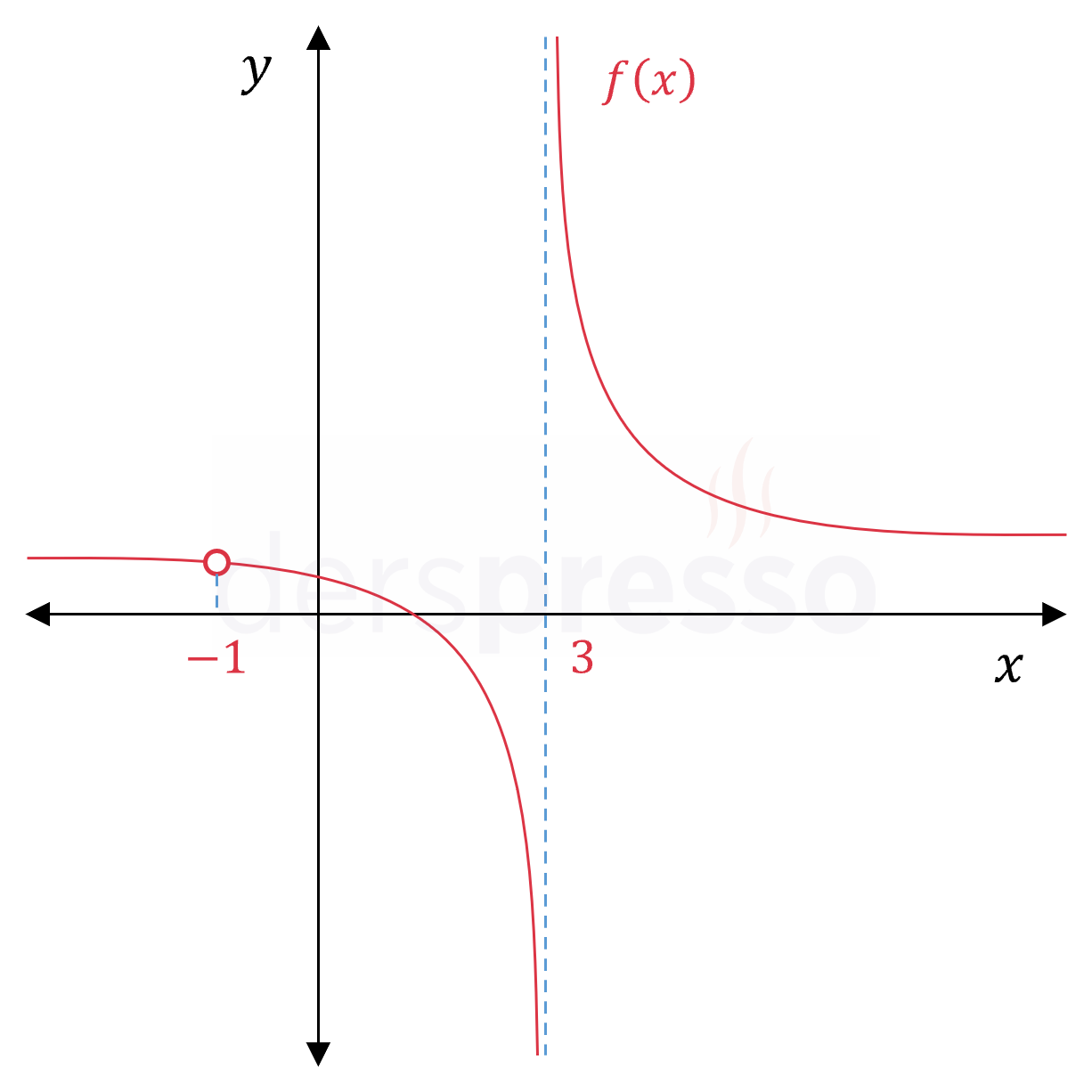
Tanım gereği, dikey asimptot oluşan noktada fonksiyonun tek taraflı limitlerinden en az biri sonsuzdur.
\( \lim\limits_{x \to 3^-} f(x) = -\infty \)
\( \lim\limits_{x \to 3^+} f(x) = +\infty \)
\( n \). dereceden bir polinom fonksiyonunun en fazla \( n \) reel kökü olabileceği için, paydası \( n \). dereceden polinom fonksiyonu olan bir rasyonel fonksiyonun en fazla \( n \) dikey asimptotu olabilir ya da hiç dikey asimptotu olmayabilir.
Trigonometrik Fonksiyonlar
Tanjant, kotanjant, sekant ve kosekant fonksiyonlarını tanımsız yapan \( x \) değerlerinde birer dikey asimptot oluşur.
| Grafik | Fonksiyon ve Asimptotları |
|---|---|
|
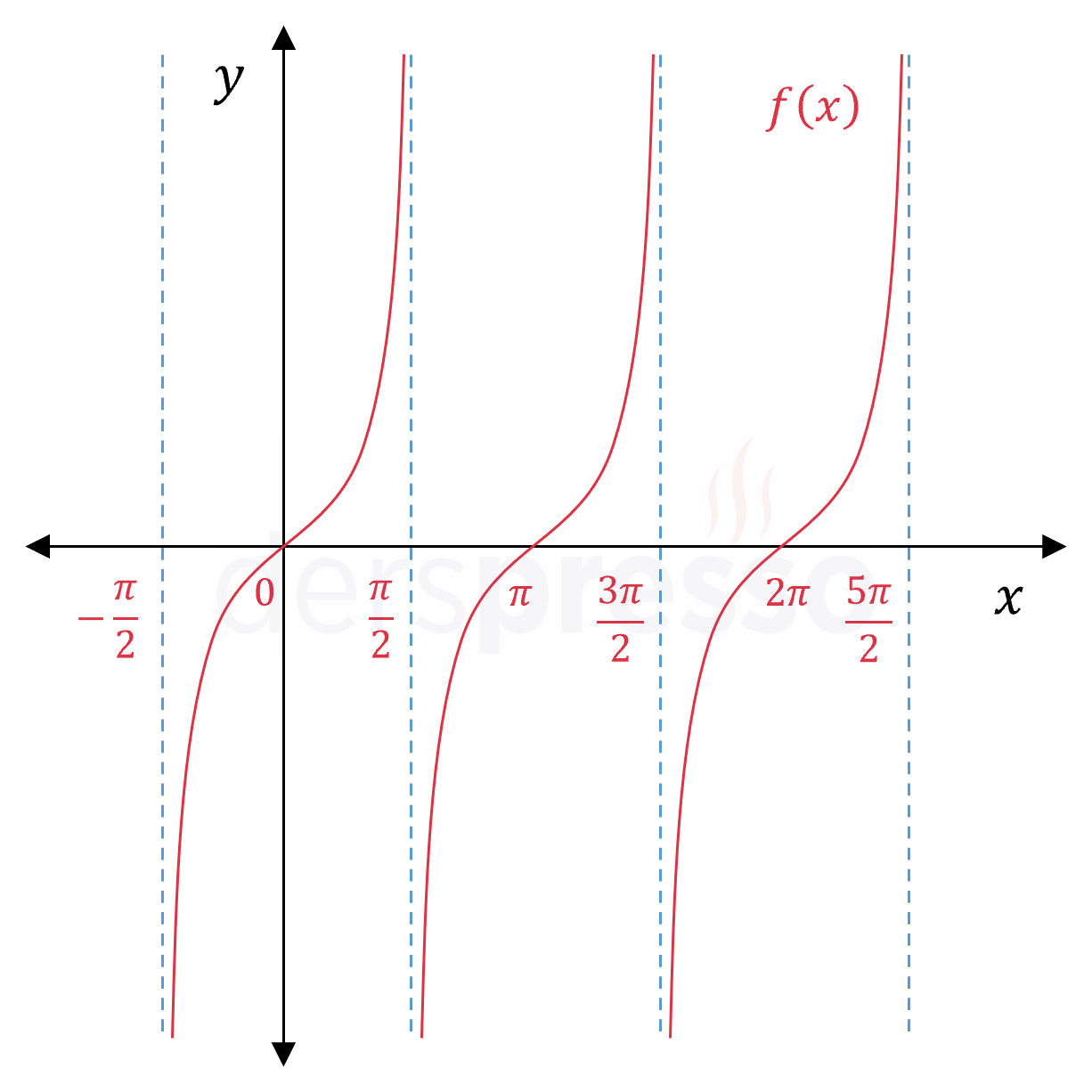
Tanjant fonksiyonu: \( f(x) = \tan{x} \) Fonksiyonun tanımsız olduğu ve dikey asimptot oluşan noktalar: \( x \in \{ \frac{\pi}{2} + k\pi \mid k \in \mathbb{Z} \} \) |
|
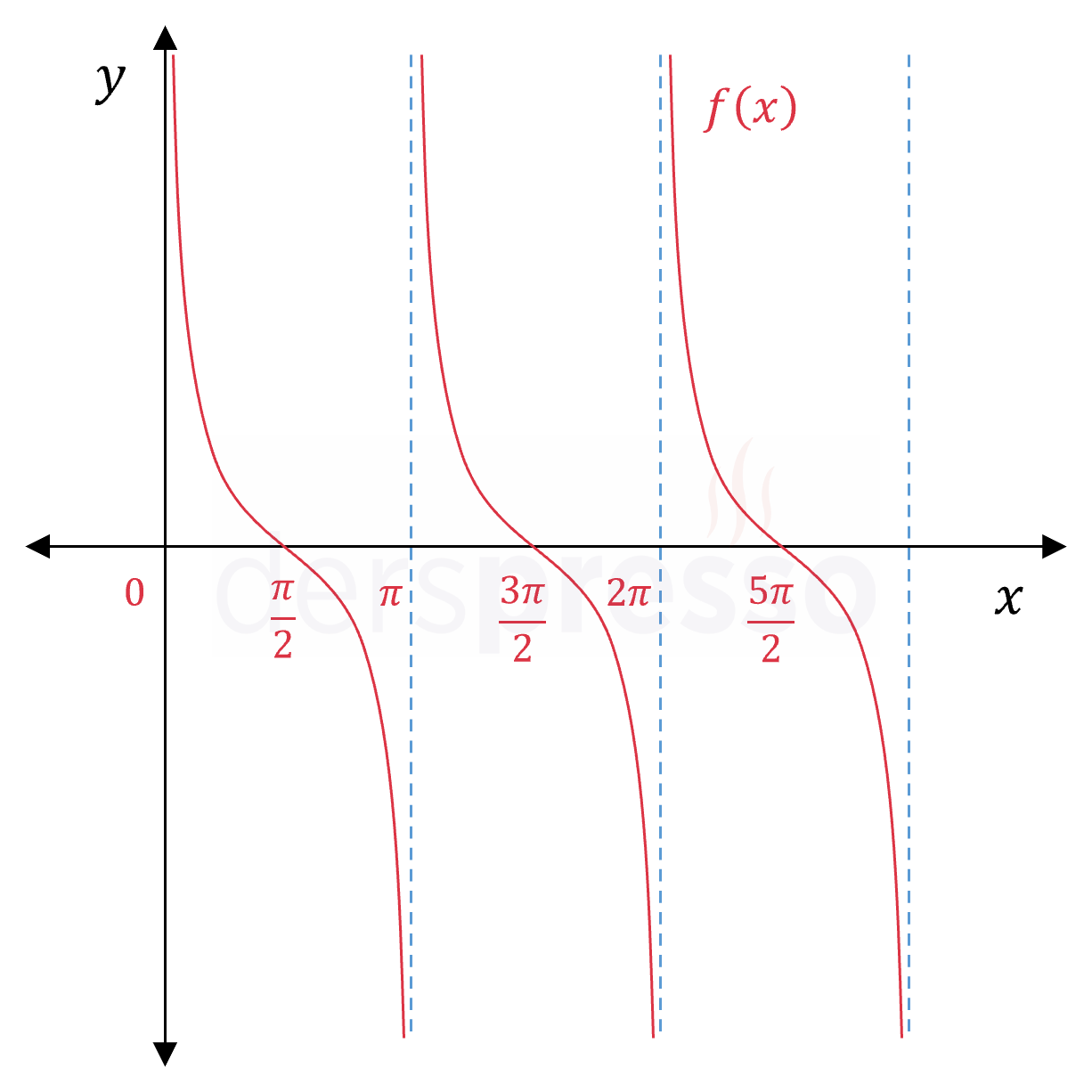
Kotanjant fonksiyonu: \( f(x) = \cot{x} \) Fonksiyonun tanımsız olduğu ve dikey asimptot oluşan noktalar: \( x \in \{ k\pi \mid k \in \mathbb{Z} \} \) |
|
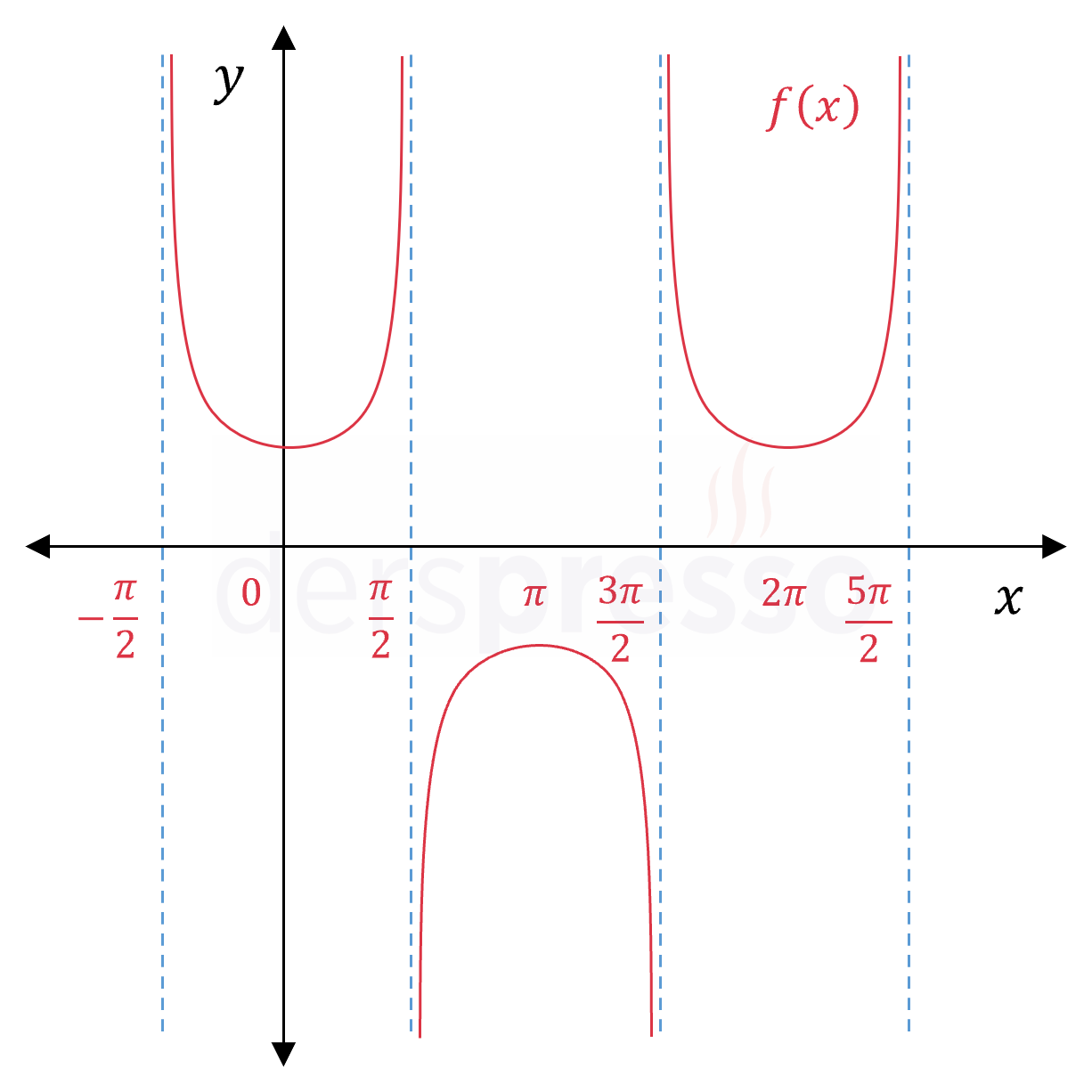
Sekant fonksiyonu: \( f(x) = \sec{x} \) Fonksiyonun tanımsız olduğu ve dikey asimptot oluşan noktalar: \( x \in \{ \frac{\pi}{2} + k\pi \mid k \in \mathbb{Z} \} \) |
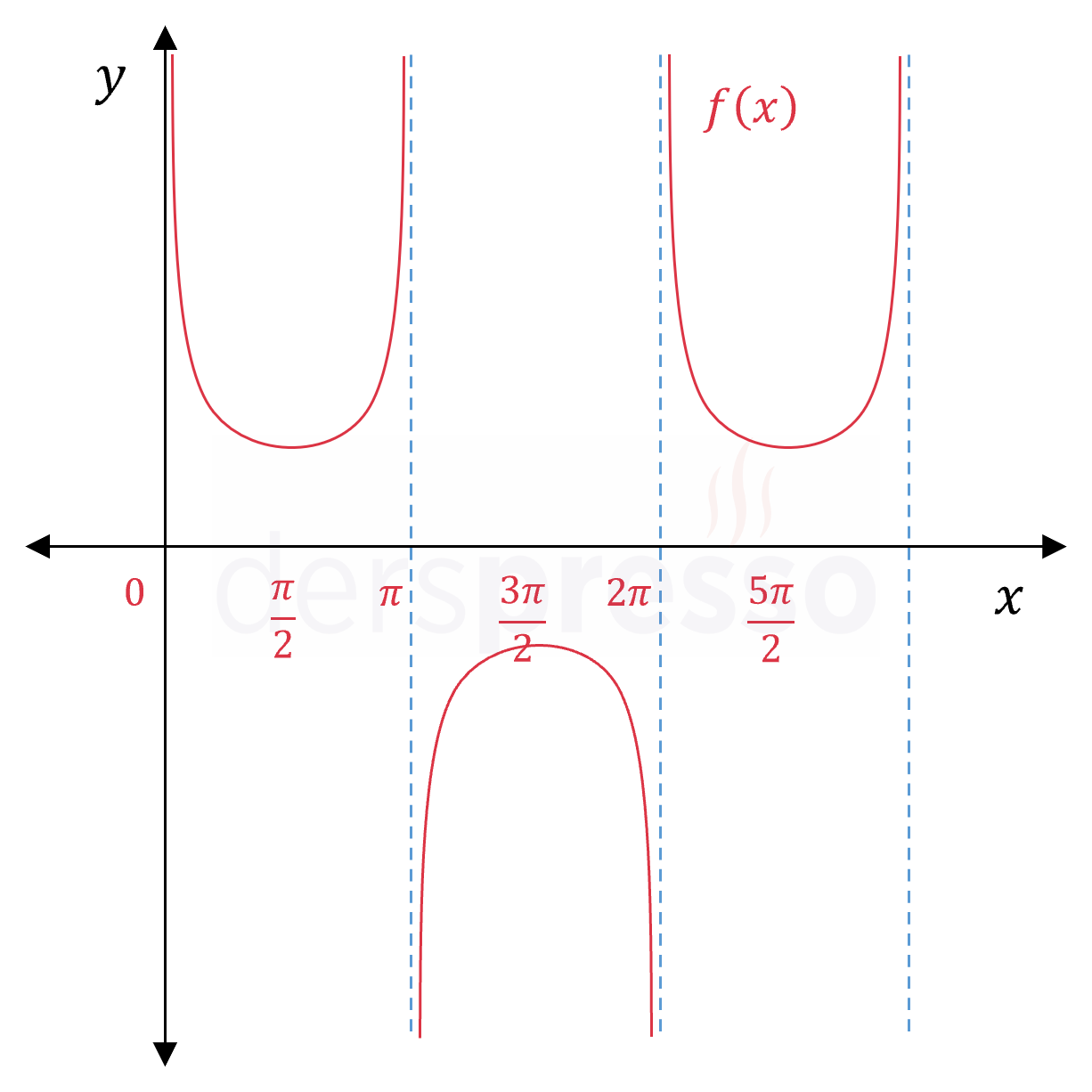
|
Kosekant fonksiyonu: \( f(x) = \csc{x} \) Fonksiyonun tanımsız olduğu ve dikey asimptot oluşan noktalar: \( x \in \{ k\pi \mid k \in \mathbb{Z} \} \) |
Logaritma Fonksiyonu
Logaritma fonksiyonlarında logaritma içini sıfır yapan \( x \) değerlerinde birer dikey asimptot oluşur.
\( f(x) = \log(2x - 5) \) fonksiyonunun dikey asimptotlarını bulalım.
Logaritma için sıfır yapan değer \( x = \frac{5}{2} \) olur.
Buna göre fonksiyonun \( x = \frac{5}{2} \) doğrusu olmak üzere tek dikey asimptotu vardır.
Bu dikey asimptot aşağıda fonksiyon grafiği üzerinde gösterilmiştir.
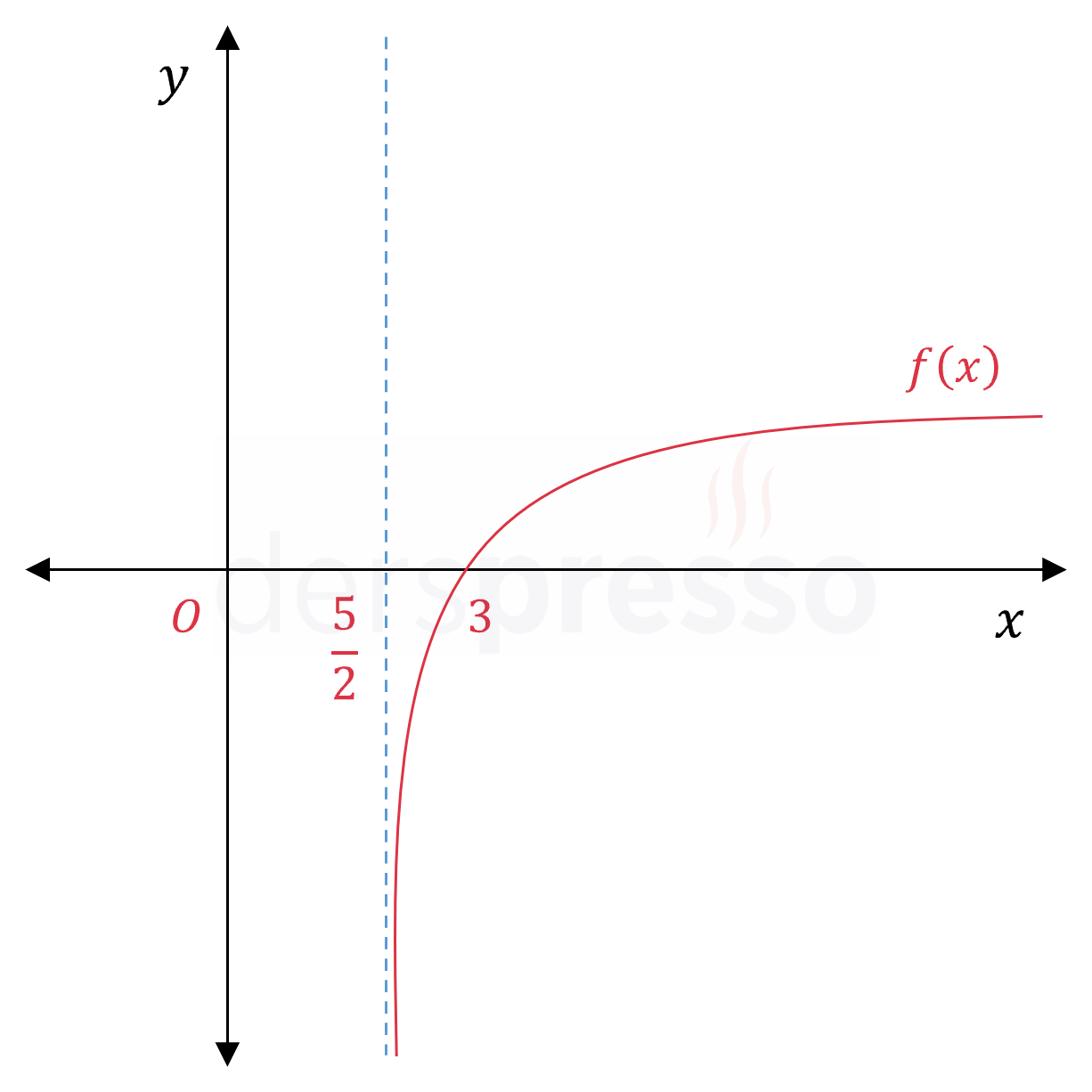
Tanım gereği, dikey asimptot oluşan noktada fonksiyonun tek taraflı limitlerinden en az biri sonsuzdur.
\( \lim\limits_{x \to \frac{5}{2}^+} f(x) = -\infty \)
\( f(x) = \dfrac{5}{x - 1} \) fonksiyonunun \( x = 1 \) noktasındaki tek yönlü limitlerini bulalım.
Verilen noktadaki soldan limiti hesaplayalım.
\( \lim\limits_{x \to 1^-} \dfrac{5}{x - 1} \)
\( x \to 1^- \) iken \( x - 1 \to 0^- \) olur.
\( = \dfrac{5}{0^-} = -\infty \)
Verilen noktadaki sağdan limiti hesaplayalım.
\( \lim\limits_{x \to 1^+} \dfrac{5}{x - 1} \)
\( x \to 1^+ \) iken \( x - 1 \to 0^+ \) olur.
\( = \dfrac{5}{0^+} = +\infty \)
Fonksiyonun bu noktadaki soldan ve sağdan limitleri aşağıdaki grafikte görülebilir.
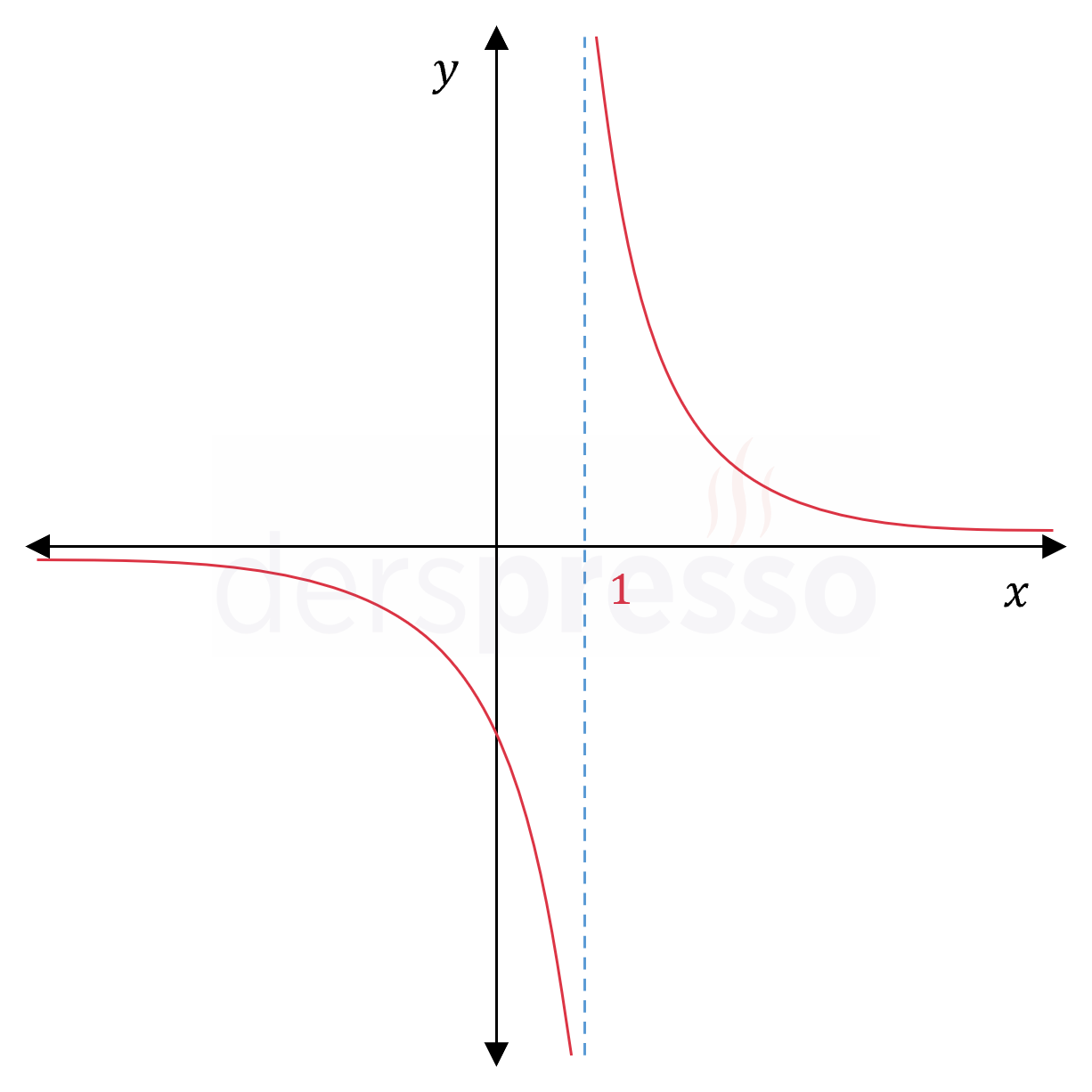
Tek Taraflı Limit Hesaplama
Bir fonksiyonun limitinin sonsuz olduğu, dolayısıyla dikey asimptota sahip olduğu bir noktadaki tek taraflı limitleri bulunurken aşağıdaki noktalara dikkat edilmelidir.
Bir \( a \) noktasındaki sağdan limit için \( x \) değişkeninin \( a \)'dan büyük değerlerden azalarak \( a \) değerine yaklaştığı dikkate alınır.
\( x \to 2^+ \) ise,
\( 2.1 \to 2.01 \to 2.001 \to 2.0001 \to \ldots \)
\( x \to -2^+ \) ise,
\( -1.9 \to -1.99 \to -1.999 \to -1.9999 \to \ldots \)
Bir \( a \) noktasındaki soldan limit için \( x \) değişkeninin \( a \)'dan küçük değerlerden artarak \( a \) değerine yaklaştığı dikkate alınır.
\( x \to 2^- \) ise,
\( 1.9 \to 1.99 \to 1.999 \to 1.9999 \to \ldots \)
\( x \to -2^- \) ise,
\( -2.1 \to -2.01 \to -2.001 \to -2.0001 \to \ldots \)
\( x \) değişkeni \( a \) değerine soldan ya da sağdan yaklaşırken \( x \)'e bağlı farklı ifadelerin farklı limit değerlerine farklı yönlerden yaklaşabileceği göz önünde bulundurulmalıdır.
\( x \to 2^- \) iken;
\( \quad 3x \to 6^- \) olur.
\( \quad 5 - x \to 3^+ \) olur.
\( \quad x^2 \to 4^- \) olur.
\( \quad 9 - x^2 \to 5^+ \) olur.
\( x \to -2^- \) iken;
\( \quad x^2 \to 4^+ \) olur.
\( \quad 9 - x^2 \to 5^- \) olur.
Aynı işlem \( x \)'e bağlı farklı fonksiyonlar için yapılırken bu fonksiyonların tanım kümeleri, grafikleri, dikey asimptotları ve artan/azalan olduğu aralıklar dikkate alınmalıdır.
\( x \to 0^+ \) iken \( \ln{x} \to -\infty \) olur.
\( x \to 0^+ \) iken \( \log_2{x} \to -\infty \) olur.
\( x \to 0^+ \) iken \( \log_{\frac{1}{2}}{x} \to \infty \) olur.
\( x \to 0^+ \) iken \( \frac{1}{x} \to \infty \) olur.
\( x \to 0^- \) iken \( \frac{1}{x} \to -\infty \) olur.
\( x \to \frac{\pi}{2}^- \) iken \( \tan{x} \to \infty \) olur.
\( x \to \frac{\pi}{2}^+ \) iken \( \tan{x} \to -\infty \) olur.
\( x \to 0^- \) iken \( \cot{x} \to -\infty \) olur.
\( x \to 0^+ \) iken \( \cot{x} \to \infty \) olur.
Aşağıdaki fonksiyonların dikey asimptotlarını bulunuz.
(a) \( f(x) = \dfrac{x^2 - 4}{x + 3} \)
(b) \( g(x) = \dfrac{3x^2 + 5x - 1}{x^2 - 1} \)
(c) \( h(x) = \dfrac{x^2 + 6x + 5}{x^2 + x - 12} \)
Çözümü GösterRasyonel ifadelerde paydadaki ifadeyi sıfır yapan, ama paydaki ifadeyi sıfır yapmayan \( x \) değerlerinde birer dikey asimptot oluşur.
(a) seçeneği:
\( f(x) = \dfrac{x^2 - 4}{x + 3} \)
Paydayı sıfır yapan değeri bulalım.
\( x + 3 = 0 \Longrightarrow x = -3 \)
Bu değerin payı sıfır yapıp yapmadığını kontrol edelim.
\( (-3)^2 - 4 = 5 \ne 0 \)
Buna göre \( x = -3 \) doğrusu \( f \) fonksiyonunun dikey asimptotudur.
(b) seçeneği:
\( g(x) = \dfrac{3x^2 + 5x - 1}{x^2 - 1} \)
Paydadaki ifadeyi çarpanlarına ayıralım.
\( = \dfrac{3x^2 + 5x - 1}{(x - 1)(x + 1)} \)
Paydayı sıfır yapan değerleri bulalım.
\( (x - 1)(x + 1) = 0 \)
\( x = 1 \) ve \( x = -1 \)
Bu değerlerin payı sıfır yapıp yapmadığını kontrol edelim.
\( 3(1)^2 + 5(1) - 1 = 7 \ne 0 \)
\( 3(-1)^2 + 5(-1) - 1 = -3 \ne 0 \)
Buna göre \( x = 1 \) ve \( x = -1 \) doğruları \( g \) fonksiyonunun dikey asimptotlarıdır.
(c) seçeneği:
\( h(x) = \dfrac{x^2 + 6x + 5}{x^2 + x - 12} \)
Pay ve paydadaki ifadeleri çarpanlarına ayıralım.
\( = \dfrac{(x + 5)(x + 1)}{(x + 4)(x - 3)} \)
Paydayı sıfır yapan değerleri bulalım.
\( (x + 4)(x - 3) = 0 \)
\( x = -4 \) ve \( x = 3 \)
Bu iki değerin de payı sıfır yapmadığını payın çarpanlarından görebiliriz.
Buna göre \( x = -4 \) ve \( x = 3 \) doğruları \( h \) fonksiyonunun dikey asimptotlarıdır.
Aşağıdaki fonksiyonların dikey asimptotlarını bulunuz.
(a) \( f(x) = \dfrac{5x - 10}{x^2 - 4} \)
(b) \( g(x) = \dfrac{x^2 - 5x + 6}{x^4 - 81} \)
(c) \( h(x) = \dfrac{x^3 + 1}{x^2 - 1} \)
Çözümü GösterRasyonel ifadelerde paydadaki ifadeyi sıfır yapan, ama paydaki ifadeyi sıfır yapmayan \( x \) değerlerinde birer dikey asimptot oluşur.
(a) seçeneği:
\( f(x) = \dfrac{5x - 10}{x^2 - 4} \)
Pay ve paydadaki ifadeleri çarpanlarına ayıralım.
\( = \dfrac{5(x - 2)}{(x - 2)(x + 2)} \)
Paydayı sıfır yapan değerleri bulalım.
\( (x - 2)(x + 2) = 0 \)
\( x = 2 \) ve \( x = -2 \)
Paydayı sıfır yapan değerler \( x \in \{-2, 2\} \)'dir. Bu değerlerden \( x = 2 \) payı da sıfır yaptığı için bu noktada dikey asimptot oluşmaz, dolayısıyla fonksiyonun \( x = -2 \) doğrusu olmak üzere tek bir dikey asimptotu vardır.
(b) seçeneği:
\( g(x) = \dfrac{x^2 - 5x + 6}{x^4 - 81} \)
Pay ve paydadaki ifadeleri çarpanlarına ayıralım.
\( = \dfrac{(x - 3)(x - 2)}{(x^2 - 9)(x^2 + 9)} \)
\( = \dfrac{(x - 3)(x - 2)}{(x - 3)(x + 3)(x^2 + 9)} \)
Paydayı sıfır yapan değerleri bulalım.
\( (x - 3)(x + 3)(x^2 + 9) = 0 \)
\( x = 3 \) ve \( x = -3 \)
Paydayı sıfır yapan değerler \( x \in \{-3, 3\} \)'tür. Bu değerlerden \( x = 3 \) payı da sıfır yaptığı için bu noktada dikey asimptot oluşmaz, dolayısıyla fonksiyonun \( x = -3 \) doğrusu olmak üzere tek bir dikey asimptotu vardır.
(c) seçeneği:
\( h(x) = \dfrac{x^3 + 1}{x^2 - 1} \)
Pay ve paydadaki ifadeleri çarpanlarına ayıralım.
\( = \dfrac{(x + 1)(x^2 - x + 1)}{(x - 1)(x + 1)} \)
Paydayı sıfır yapan değerleri bulalım.
\( (x - 1)(x + 1) = 0 \)
\( x = 1 \) ve \( x = -1 \)
Paydayı sıfır yapan değerler \( x \in \{-1, 1\} \)'dir. Bu değerlerden \( x = -1 \) payı da sıfır yaptığı için bu noktada dikey asimptot oluşmaz, dolayısıyla fonksiyonun \( x = 1 \) doğrusu olmak üzere tek bir dikey asimptotu vardır.
Aşağıdaki tek taraflı limitleri hesaplayınız.
(a) \( \lim\limits_{x \to -7^-} {\dfrac{2x}{x + 7}} \)
(b) \( \lim\limits_{x \to 6^-} {\dfrac{1 - 3x}{x - 6}} \)
(c) \( \lim\limits_{x \to 8^+} {\dfrac{6}{8 - x}} \)
Çözümü Göster(a) seçeneği:
\( \lim\limits_{x \to -7^-} {\dfrac{2x}{x + 7}} \)
\( x \to -7^- \) iken \( x + 7 \to 0^- \) olur.
\( = \dfrac{2(-7)}{0^-} \)
\( = \dfrac{-14}{0^-} = \infty \)
(b) seçeneği:
\( \lim\limits_{x \to 6^-} {\dfrac{1 - 3x}{x - 6}} \)
\( x \to 6^- \) iken \( x - 6 \to 0^- \) olur.
\( = \dfrac{1 - 3(6)}{0^-} \)
\( = \dfrac{-17}{0^-} = \infty \)
(c) seçeneği:
\( \lim\limits_{x \to 8^+} {\dfrac{6}{8 - x}} \)
\( x \to 8^+ \) iken \( 8 - x \to 0^- \) olur.
\( = \dfrac{6}{0^-} = -\infty \)
Aşağıdaki tek taraflı limitleri hesaplayınız.
(a) \( \lim\limits_{x \to 1^+} {\dfrac{x - 2}{x^2 - 1}} \)
(b) \( \lim\limits_{x \to 3^-} {\dfrac{4}{9 - x^2}} \)
(c) \( \lim\limits_{x \to -2^-} {\dfrac{5x + 1}{x^2 - 4}} \)
Çözümü Göster(a) seçeneği:
\( \lim\limits_{x \to 1^+} {\dfrac{x - 2}{x^2 - 1}} \)
\( x \to 1^+ \) iken \( x^2 - 1 \to 0^+ \) olur.
\( = \dfrac{1 - 2}{0^+} \)
\( = \dfrac{-1}{0^+} = -\infty \)
(b) seçeneği:
\( \lim\limits_{x \to 3^-} {\dfrac{4}{9 - x^2}} \)
\( x \to 3^- \) iken \( 9 - x^2 \to 0^+ \) olur.
\( = \dfrac{4}{0^+} = \infty \)
(c) seçeneği:
\( \lim\limits_{x \to -2^-} {\dfrac{5x + 1}{x^2 - 4}} \)
\( x \to -2^- \) iken \( x^2 - 4 \to 0^+ \) olur.
\( = \dfrac{5(-2) + 1}{0^+} \)
\( = \dfrac{-9}{0^+} = -\infty \)
\( f(x) = \dfrac{1}{x^2 - 2x - 15} \) fonksiyonunun \( x = 5 \) noktasındaki tek yönlü limitlerini bulunuz.
Çözümü GösterPaydadaki ifadeyi çarpanlarına ayıralım.
\( f(x) = \dfrac{1}{x^2 - 2x - 15} = \dfrac{1}{(x + 3)(x - 5)} \)
Verilen noktadaki soldan limiti hesaplayalım.
\( \lim\limits_{x \to 5^-} \dfrac{1}{(x + 3)(x - 5)} \)
\( = \dfrac{1}{(5^- + 3)(5^- - 5)} \)
\( = \dfrac{1}{(8^-)(0^-)} \)
\( = \dfrac{1}{0^-} = -\infty \)
Verilen noktadaki sağdan limiti hesaplayalım.
\( \lim\limits_{x \to 5^+} \dfrac{1}{(x + 3)(x - 5)} \)
\( = \dfrac{1}{(5^+ + 3)(5^+ - 5)} \)
\( = \dfrac{1}{(8^+)(0^+)} \)
\( = \dfrac{1}{0^+} = \infty \)
\( f(x) = \dfrac{2x^2}{\ln{x} - 1} \) fonksiyonunun \( x = e \) noktasındaki tek yönlü limitlerini bulunuz.
Çözümü GösterVerilen noktadaki soldan limiti hesaplayalım.
\( \lim\limits_{x \to e^-} \dfrac{2x^2}{\ln{x} - 1} = \dfrac{2e^2}{\ln{e^-} - 1} \)
Doğal logaritma fonksiyonu grafiğini düşünerek aşağıdaki çıkarımı yapabiliriz.
\( x \to e^- \) iken \( \ln{x} \to 1^- \) olur.
\( = \dfrac{2e^2}{1^- - 1} \)
\( = \dfrac{2e^2}{0^-} \)
\( = -\infty \)
Verilen noktadaki sağdan limiti hesaplayalım.
\( \lim\limits_{x \to e^+} \dfrac{2x^2}{\ln{x} - 1} = \dfrac{2e^2}{\ln{e^+} - 1} \)
Doğal logaritma fonksiyonu grafiğini düşünerek aşağıdaki çıkarımı yapabiliriz.
\( x \to e^+ \) iken \( \ln{x} \to 1^+ \) olur.
\( = \dfrac{2e^2}{1^+ - 1} \)
\( = \dfrac{2e^2}{0^+} \)
\( = \infty \)
\( f(x) = \dfrac{3x - 2}{e^x - 1} \) fonksiyonunun \( x = 0 \) noktasındaki tek yönlü limitlerini bulunuz.
Çözümü GösterVerilen noktadaki soldan limiti hesaplayalım.
\( \lim\limits_{x \to 0^-} \dfrac{3x - 2}{e^x - 1} = \dfrac{3(0^-) - 2}{e^{0^-} - 1} \)
\( = \dfrac{-2}{e^{0^-} - 1} \)
Üstel fonksiyon grafiğini düşünerek aşağıdaki çıkarımı yapabiliriz.
\( x \to 0^- \) iken \( e^x \to 1^- \) olur.
\( = \dfrac{-2}{1^- - 1} \)
\( = \dfrac{-2}{0^-} \)
\( = \infty \)
Verilen noktadaki sağdan limiti hesaplayalım.
\( \lim\limits_{x \to 0^+} \dfrac{3x - 2}{e^x - 1} = \dfrac{3(0^+) - 2}{e^{0^+} - 1} \)
\( = \dfrac{-2}{e^{0^+} - 1} \)
Üstel fonksiyon grafiğini düşünerek aşağıdaki çıkarımı yapabiliriz.
\( x \to 0^+ \) iken \( e^x \to 1^+ \) olur.
\( = \dfrac{-2}{1^+ - 1} \)
\( = \dfrac{-2}{0^+} \)
\( = -\infty \)
\( \lim\limits_{x \to -2^+} \dfrac{x}{\sqrt{4 - x^2}} \) limitinin sonucunu bulunuz.
Çözümü Göster\( \lim\limits_{x \to -2^+} \dfrac{x}{\sqrt{4 - x^2}} \)
\( x \to -2^+ \) iken \( x^2 \to 4^- \) olur.
\( = \dfrac{-2}{\sqrt{4 - 4^-}} \)
\( = \dfrac{-2}{\sqrt{0^+}} \)
\( = \dfrac{-2}{0^+} \)
\( = -\infty \)