Sıkıştırma Teoremi
Sıkıştırma teoremi ya da bir diğer adıyla sandviç teoremi, şu ana kadar öğrendiğimiz limit kural ve yöntemlerinin yeterli olmadığı bazı durumlarda bir fonksiyonun limitini bulmamızı sağlar.
Sıkıştırma teoremine göre, bir \( f \) fonksiyonunun \( x = a \) noktasını içeren bir aralıkta, bu noktadaki limit değerlerini birbirine eşit ve \( L \) olarak hesaplayabildiğimiz \( g \) ve \( h \) fonksiyonları arasında kaldığını gösterebiliyorsak, \( f \) fonksiyonunun bu noktadaki limiti de \( L \) olmak zorundadır.
\( I \) reel sayılarda bir aralık ve \( a \in I \) olmak üzere,
Her \( x \in I \) için;
- \( g(x) \le f(x) \le {h(x)} \) ve
- \( \lim\limits_{x \to a} {g(x)} = \lim\limits_{x \to a} {h(x)} = L \)
olduğunu gösterebiliyorsak \( \lim\limits_{x \to a} {f(x)} = L \) olmak zorundadır.
\( x = a \) noktasındaki limit fonksiyonun bu noktadaki değeri ile ilgilenmediği için, sıkıştırma teoreminin bir koşulu olarak belirttiğimiz \( g(x) \le f(x) \le h(x) \) eşitsizliği \( x = a \) noktasında geçerli olmak zorunda değildir, önemli olan \( f(x) \) değerinin bu aralıkta \( x = a \) dışındaki noktalarda iki fonksiyonun arasında kalmasıdır.
Sıkıştırma teoremi grafiksel olarak aşağıdaki gibi gösterilebilir. Bu grafikte \( g \) ve \( h \) fonksiyonları \( f \) fonksiyonunun birer üst ve alt sınırı olmaktadır, dolayısıyla bu iki fonksiyonun bir noktadaki limitinin tanımlı ve eşit olduğunu biliyorsak \( f \) fonksiyonunun da bu noktadaki limitinin bu değere eşit olması gerekmektedir.
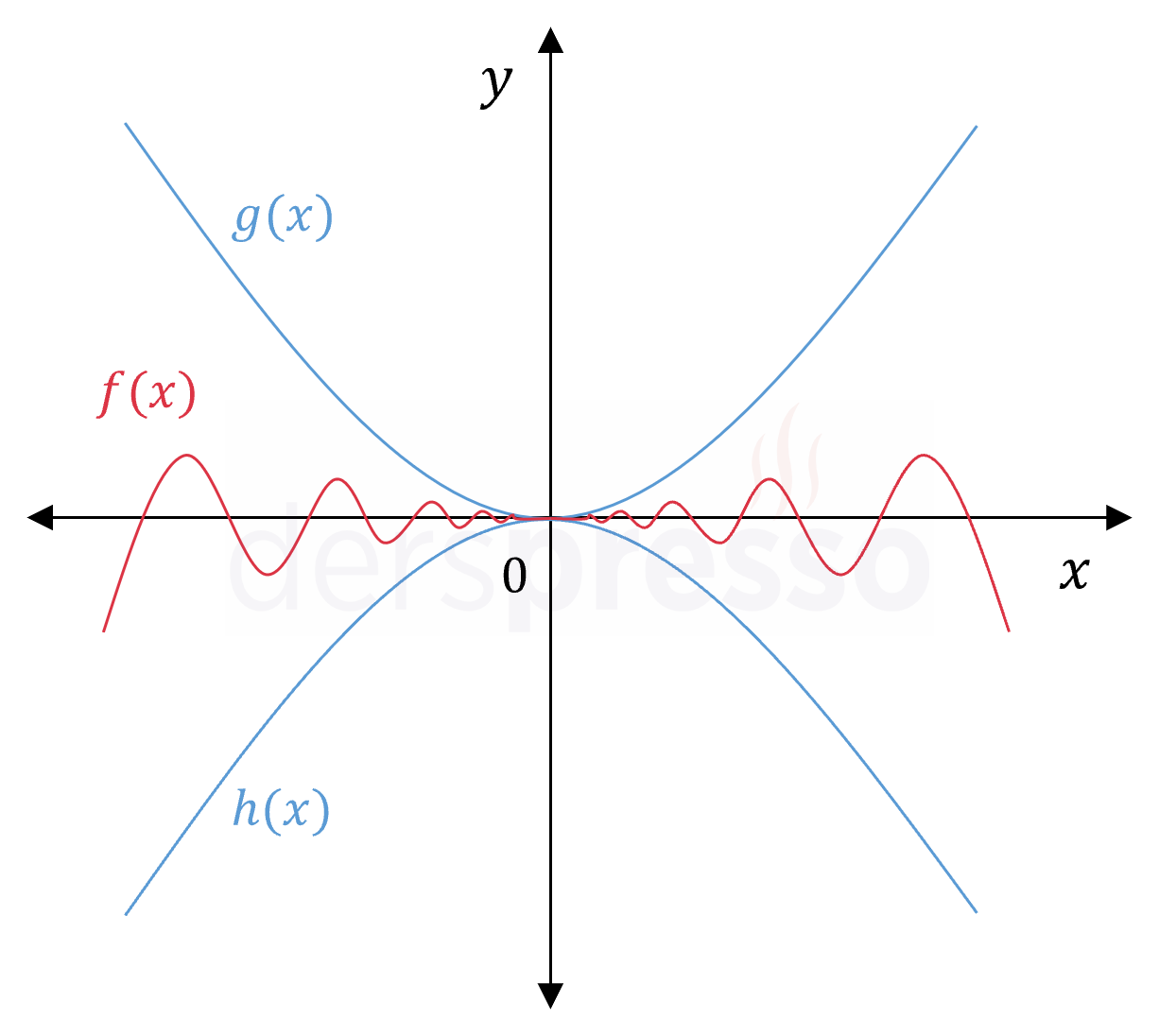
Sıkıştırma teoremi ile limit hesaplamaya bir örnek verelim.
\( \lim\limits_{x \to \infty} \dfrac{\sin{x}}{x} \) ifadesinin limitini bulalım.
Önce sinüs fonksiyonunun değer aralığını yazalım.
\( -1 \le \sin{x} \le 1 \)
Eşitsizliğin üç tarafını da \( x \)'e bölelim. Hesapladığımız limitte \( x \) pozitif sonsuza gittiği için \( x \)'i pozitif bir değer olarak alabiliriz, dolayısıyla eşitsizlik işaretlerinin yönünü değiştirmemize gerek yoktur.
\( \dfrac{-1}{x} \le \dfrac{\sin{x}}{x} \le \dfrac{1}{x} \)
Limitini bulmak istediğimiz ifadenin iki ayrı fonksiyonun arasında kaldığını görüyoruz. Bu iki fonksiyonun \( x \) pozitif sonsuza giderken limit değerlerine baktığımızda, \( \frac{-1}{x} \) ifadesinin negatif taraftan, \( \frac{1}{x} \) ifadesinin pozitif taraftan sıfıra yaklaştığını görebiliriz.
\( \lim\limits_{x \to \infty} \dfrac{-1}{x} = \lim\limits_{x \to \infty} \dfrac{1}{x} = 0 \)
Dolayısıyla bizden istenen fonksiyonun limitinin de bu iki fonksiyonun limit değerlerinin arasında kalacağını, dolayısıyla sıfıra eşit olacağını söyleyebiliriz.
\( \lim\limits_{x \to \infty} \dfrac{\sin{x}}{x} = 0 \)
\( 5 \le f(x) \le x^3 - 5x - 7 \) olduğuna göre,
\( \lim\limits_{x \to 3} f(x) \) limitinin sonucunu bulunuz.
Çözümü Göster\( 5 \le f(x) \le x^3 - 5x - 7 \)
Eşitsizliğin taraflarının \( x \to 3 \) iken limitini alalım.
\( \lim\limits_{x \to 3} 5 \le \lim\limits_{x \to 3} f(x) \le \lim\limits_{x \to 3} (x^3 - 5x - 7) \)
Eşitsizliğin solundaki ve sağındaki limitleri bulalım.
\( \lim\limits_{x \to 3} {5} = 5 \)
\( \lim\limits_{x \to 3} (x^3 - 5x - 7) = 3^3 - 5(3) - 7 = 5 \)
\( 5 \le \lim\limits_{x \to 3} f(x) \le 5 \)
Sıkıştırma teoremine göre, ortadaki ifadenin limiti de bu iki limit değerinin arasında kalır ve 5'e eşit olur.
\( \lim\limits_{x \to 3} f(x) = 5 \)
\( f \) fonksiyonunun grafiğinin tüm reel sayılarda \( g(x) = 2x \) grafiği ile alttan ve \( h(x) = x^2 + 1 \) grafiği ile üstten sınırlı olduğu biliniyor.
Buna göre \( \lim\limits_{x \to 1} f(x) \) limitinin sonucunu bulunuz.
Çözümü GösterDikkat edilirse soruda \( f \) fonksiyonunun tanımı verilmemiş, sadece grafiğinin tüm reel sayılarda \( g(x) \) ve \( h(x) \) grafikleri ile sınırlı olduğu bilgisi verilmiştir.
\( g(x) \le f(x) \le h(x) \)
Eşitsizliğin taraflarının \( x \to 1 \) iken limitini alalım.
\( \lim\limits_{x \to 1} g(x) \le \lim\limits_{x \to 1} f(x) \le \lim\limits_{x \to 1} h(x) \)
\( g(x) \) ve \( h(x) \) fonksiyonlarının \( x = 1 \) noktasındaki limit değerlerini bulalım.
Polinom fonksiyonlarının bir noktadaki limiti o noktadaki fonksiyon değerine eşittir.
\( \lim\limits_{x \to 1} g(x) = g(1) = 2(1) = 2 \)
\( \lim\limits_{x \to 1} h(x) = h(1) = 1^2 + 1 = 2 \)
\( 2 \le \lim\limits_{x \to 1} f(x) \le 2 \)
Sıkıştırma teoremine göre, ortadaki ifadenin limiti de bu iki limit değerinin arasında kalır ve 2'ye eşit olur.
\( \lim\limits_{x \to 1} f(x) = 2 \)
\( \abs{f(x) - 3} \le x^3 \) eşitsizliği veriliyor.
\( \lim\limits_{x \to 0} f(x) \) limitinin sonucunu bulunuz.
Çözümü GösterVerilen eşitsizliği mutlak değerden kurtaralım.
\( -x^3 \le f(x) - 3 \le x^3 \)
\( -x^3 + 3 \le f(x) \le x^3 + 3 \)
Eşitsizliğin taraflarının \( x \to 0 \) iken limitini alalım.
\( \lim\limits_{x \to 0} (-x^3 + 3) \le \lim\limits_{x \to 0} f(x) \le \lim\limits_{x \to 0} (x^3 + 3) \)
Polinom fonksiyonlarının bir noktadaki limiti o noktadaki fonksiyon değerine eşittir.
\( \lim\limits_{x \to 0} (-x^3 + 3) = -0^3 + 3 = 3 \)
\( \lim\limits_{x \to 0} (x^3 + 3) = 0^3 + 3 = 3 \)
\( 3 \le \lim\limits_{x \to 0} f(x) \le 3 \)
Sıkıştırma teoremine göre, ortadaki ifadenin limiti de bu iki limit değerinin arasında kalır ve 3'e eşit olur.
\( \lim\limits_{x \to 0} f(x) = 3 \) bulunur.
\( \lim\limits_{x \to 0} \left( x^6\cos{\dfrac{4}{x^2}} \right) \) limitinin sonucunu bulunuz.
Çözümü GösterKosinüs fonksiyonunun değer aralığını yazalım.
\( -1 \le \cos{\dfrac{4}{x^2}} \le 1 \)
Eşitsizliğin taraflarını \( x^6 \) ile çarpalım.
\( x^6 \) pozitif bir sayı olduğu için eşitsizliğin yönü değişmez.
\( -x^6 \le x^6\cos{\dfrac{4}{x^2}} \le x^6 \)
Eşitsizliğin taraflarının \( x \to 0 \) iken limitini alalım.
\( \lim\limits_{x \to 0} (-x^6) \le \lim\limits_{x \to 0} \left( x^6\cos{\dfrac{4}{x^2}} \right) \le \lim\limits_{x \to 0} x^6 \)
Polinom fonksiyonlarının bir noktadaki limiti o noktadaki fonksiyon değerine eşittir.
\( \lim\limits_{x \to 0} (-x^6) = -0^6 = 0 \)
\( \lim\limits_{x \to 0} {x^6} = 0^6 = 0 \)
\( 0 \le \lim\limits_{x \to 0} \left( x^6\cos{\dfrac{4}{x^2}} \right) \le 0 \)
Sıkıştırma teoremine göre, ortadaki ifadenin limiti de bu iki limit değerinin arasında kalır ve 0'a eşit olur.
\( \lim\limits_{x \to 0} \left( x^6\cos{\dfrac{4}{x^2}} \right) = 0 \)
\( \lim\limits_{x \to \infty} \dfrac{\sin(5x)}{e^\frac{x}{4}} \) limitinin sonucunu bulunuz.
Çözümü GösterSinüs fonksiyonunun değer aralığını yazalım.
\( -1 \le \sin(5x) \le 1 \)
Eşitsizliğin taraflarını \( e^\frac{x}{4} \)'e bölelim.
\( e^\frac{x}{4} \) tüm reel sayılarda pozitif olduğu için eşitsizliğin yönü değişmez.
\( -\dfrac{1}{e^\frac{x}{4}} \le \dfrac{\sin(5x)}{e^\frac{x}{4}} \le \dfrac{1}{e^\frac{x}{4}} \)
Eşitsizliğin taraflarının \( x \to \infty \) iken limitini alalım.
\( \lim\limits_{x \to \infty} -\dfrac{1}{e^\frac{x}{4}} \le \lim\limits_{x \to \infty} \dfrac{\sin(5x)}{e^\frac{x}{4}} \le \lim\limits_{x \to \infty} \dfrac{1}{e^\frac{x}{4}} \)
\( x \to \infty \) iken \( \frac{1}{e^\frac{x}{4}} \to 0 \) olur.
\( 0 \le \lim\limits_{x \to \infty} \dfrac{\sin(5x)}{e^\frac{x}{4}} \le 0 \)
Sıkıştırma teoremine göre, ortadaki ifadenin limiti de bu iki limit değerinin arasında kalır ve 0'a eşit olur.
\( \lim\limits_{x \to \infty} \dfrac{\sin(5x)}{e^\frac{x}{4}} = 0 \) bulunur.
\( \lim\limits_{x \to \infty} \dfrac{5 + e^{-x}\sin{x}}{e^{-x} + 10} \) limitinin sonucunu bulunuz.
Çözümü GösterAşağıda göstereceğimiz üzere, payın ve paydanın limiti ayrı ayrı birer reel sayı olarak tanımlı olduğu için bölme kuralı ile limiti paya ve paydaya dağıtabiliriz.
\( \lim\limits_{x \to \infty} \dfrac{5 + e^{-x}\sin{x}}{e^{-x} + 10} = \dfrac{\lim\limits_{x \to \infty} (5 + e^{-x}\sin{x})}{\lim\limits_{x \to \infty} (e^{-x} + 10)} \)
Paydaki limit ifadesinin değerini sıkıştırma teoremi ile bulalım.
Sinüs fonksiyonunun değer aralığını yazalım.
\( -1 \le \sin{x} \le 1 \)
Eşitsizliğin taraflarını \( e^{-x} \) ile çarpalım.
\( -e^{-x} \le e^{-x}\sin{x} \le e^{-x} \)
Eşitsizliğin taraflarına 5 ekleyelim.
\( 5 - e^{-x} \le 5 + e^{-x}\sin{x} \le 5 + e^{-x} \)
Eşitsizliğin taraflarının \( x \to \infty \) iken limitini alalım.
\( \lim\limits_{x \to \infty} (5 - e^{-x}) \le \lim\limits_{x \to \infty} (5 + e^{-x}\sin{x}) \le \lim\limits_{x \to \infty} (5 + e^{-x}) \)
\( x \to \infty \) iken \( e^{-x} = \frac{1}{e^x} \to 0 \) olur.
\( \lim\limits_{x \to \infty} (5 - e^{-x}) = 5 - 0 = 5 \)
\( \lim\limits_{x \to \infty} (5 + e^{-x}) = 5 + 0 = 5 \)
\( 5 \le \lim\limits_{x \to \infty} (5 + e^{-x}\sin{x}) \le 5 \)
Sıkıştırma teoremine göre, ortadaki ifadenin limiti de bu iki limit değerinin arasında kalır ve 5'e eşit olur.
\( \lim\limits_{x \to \infty} (5 + e^{-x}\sin{x}) = 5 \)
Değerini bulmak istediğimiz limit ifadesini hatırlayalım.
\( \dfrac{\lim\limits_{x \to \infty} (5 + e^{-x}\sin{x})}{\lim\limits_{x \to \infty} (e^{-x} + 10)} \)
Paydadaki limit ifadesinin değerini bulalım.
\( x \to \infty \) iken \( e^{-x} \to 0 \) olur.
\( \lim\limits_{x \to \infty} (e^{-x} + 10) = 10 \)
Tüm ifadenin değerini bulalım.
\( \dfrac{\lim\limits_{x \to \infty} (5 + e^{-x}\sin{x})}{\lim\limits_{x \to \infty} (e^{-x} + 10)} = \dfrac{5}{10} = \dfrac{1}{2} \) bulunur.
\( \lim\limits_{x \to 0} \dfrac{3x^4\sin{\frac{1}{x^3}}}{\sin(2x)} \) limitinin sonucunu bulunuz.
Çözümü GösterLimit ifadesini düzenleyelim.
\( \lim\limits_{x \to 0} \left( \dfrac{3x}{\sin(2x)} \cdot x^3\sin{\dfrac{1}{x^3}} \right) \)
Aşağıda göstereceğimiz üzere, iki çarpanın limiti ayrı ayrı birer reel sayı olarak tanımlı olduğu için ifadeyi iki limitin çarpımı şeklinde yazabiliriz.
\( = \underbrace{\lim\limits_{x \to 0} \dfrac{3x}{\sin(2x)}}_{L_1} \cdot \underbrace{\lim\limits_{x \to 0} (x^3\sin{\dfrac{1}{x^3}})}_{L_2} \)
Birinci çarpan için ispatıyla birlikte verdiğimiz trigonometrik limit kurallarını kullanalım.
\( \lim\limits_{x \to 0} \dfrac{\sin(ax)}{bx} = \dfrac{a}{b} \)
\( L_1 = \lim\limits_{x \to 0} \dfrac{3x}{\sin(2x)} = \dfrac{3}{2} \)
İkinci çarpan için sıkıştırma teoremini kullanalım.
Sinüs fonksiyonunun değer aralığını yazalım.
\( -1 \le \sin{\dfrac{1}{x^3}} \le 1 \)
Eşitsizliğin taraflarını \( x^3 \) ile çarpalım.
\( -x^3 \le x^3\sin{\dfrac{1}{x^3}} \le x^3 \)
Eşitsizliğin taraflarının \( x \) sıfıra giderken limitini alalım.
\( \lim\limits_{x \to 0} (-x^3) \le \lim\limits_{x \to 0} \left( x^3\sin{\dfrac{1}{x^3}} \right) \le \lim\limits_{x \to 0} x^3 \)
Polinom fonksiyonlarının bir noktadaki limiti o noktadaki fonksiyon değerine eşittir.
\( \lim\limits_{x \to 0} (-x^3) = -0^3 = 0 \)
\( \lim\limits_{x \to 0} {x^3} = 0^3 = 0 \)
\( 0 \le \lim\limits_{x \to 0} \left( x^3\sin{\dfrac{1}{x^3}} \right) \le 0 \)
Sıkıştırma teoremine göre, ortadaki ifadenin limiti de bu iki limit değerinin arasında kalır ve 0'a eşit olur.
\( L_2 = \lim\limits_{x \to 0} \left( x^3\sin{\dfrac{1}{x^3}} \right) = 0 \)
\( L_1 \cdot L_2 = \dfrac{3}{2} \cdot 0 = 0 \) bulunur.