Limit Tanımı
Süreklilik, türev, integral, diziler ve seriler gibi matematiksel analiz konularının en temel tanımları bu bölümde inceleyeceğimiz limite dayanır, dolayısıyla limit kavramının iyi anlaşılması tüm bu konuların teorik altyapısı açısından oldukça kritiktir.
Bir fonksiyonun davranışını incelerken çoğu zaman fonksiyonun belirli noktalardaki değeri ile ilgileniriz. Örneğin aşağıdaki gibi tanımlı bir \( f \) fonksiyonunun \( x = 1 \) noktasındaki değerini bulmak için \( x \) değişkenine \( 1 \) değeri vererek \( f(1) \) değerini hesaplarız.
\( f(x) = \dfrac{x^2 - 4}{x - 2} \) olmak üzere,
\( f(1) = \dfrac{1^2 - 4}{1 - 2} = 3 \)
Aynı fonksiyonun \( x = 2 \) noktasındaki değerini bulmak istersek fonksiyonun bu noktada tanımsız olduğunu görürüz.
\( f(2) = \dfrac{2^2 - 4}{2 - 2} = \dfrac{0}{0} \)
Fonksiyonun tanımlı olmadığı bu nokta civarında fonksiyonun davranışını bilmek istediğimizi varsayalım. Bu durumda kullanabileceğimiz bir yöntem, \( x \) değişkenine 2'ye yakın değerler vererek fonksiyon değerini hesaplamak olabilir.
Aşağıdaki tabloda ilk iki sütunda \( x \)'in 2'den küçük ve artarak 2'ye yaklaşan değerleri için, sonraki iki sütunda da 2'den büyük ve azalarak 2'ye yaklaşan değerleri için fonksiyon değerleri verilmiştir.

Tabloyu incelediğimizde \( x \) 2'ye daha küçük değerlerden (grafik olarak soldan) yaklaştıkça fonksiyon değerinin 4'e daha küçük değerlerden yaklaştığını, \( x \) 2'ye daha büyük değerlerden (grafik olarak sağdan) yaklaştıkça da fonksiyon değerinin 4'e daha büyük değerlerden yaklaştığını görürüz. Bu değerlere bakarak, fonksiyon \( x = 2 \) noktasında tanımsız olsa da fonksiyon grafiğinin bu nokta civarında hem soldan hem de sağdan 4 değerine yaklaştığını söyleyebiliriz.
Bir program kullanarak fonksiyonun grafiğini çizdiğimizde aşağıdaki grafiği elde ederiz.
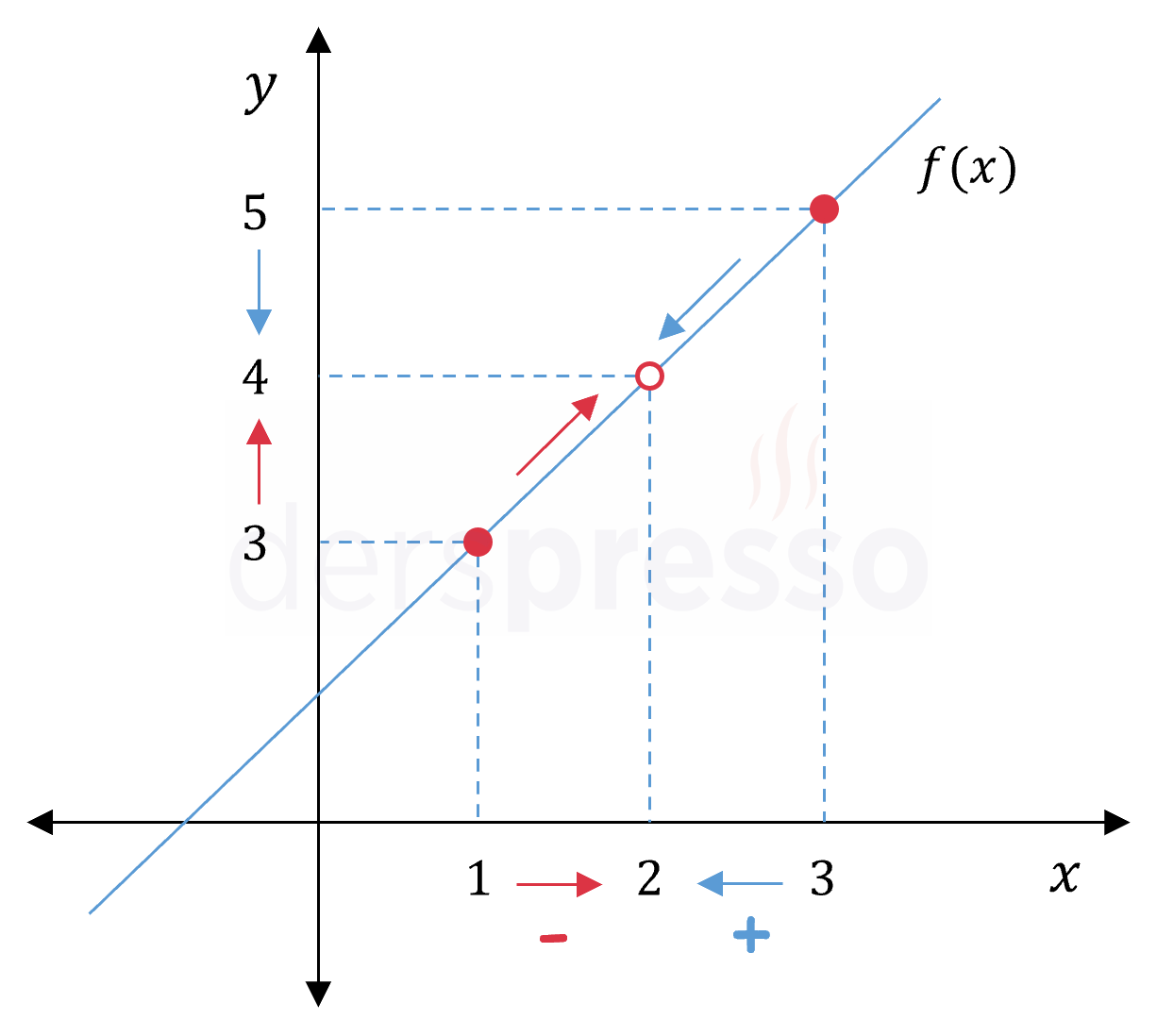
Yukarıdaki tablo için yaptığımız yorumu grafik üzerinden de teyit edebiliriz. Fonksiyon \( x = 2 \) noktasında tanımsızdır, ancak bu noktaya soldan ve sağdan yaklaştıkça fonksiyon değeri 4'e yaklaşmaktadır. Bu şekilde değer tablolaları kullanarak ya da fonksiyonun grafiğini inceleyerek bir fonksiyonun tanımlı ya da tanımsız bir nokta civarındaki davranışı ile ilgili ek bilgiler edinebiliriz.
Limitin Pratik Tanımı
Soldan Limit
Bir \( f \) fonksiyonunda \( x \) değişkenine bir \( a \) değerine \( x \lt a \) olmak koşulu ile sınırsız yaklaşan (ama hiçbir zaman \( x = a \) olmayan) değerler verdiğimizde \( f(x) \) değerleri bir \( L_1 \) değerine sınırsız yaklaşıyorsa ve yakın kalıyorsa, bu \( L_1 \) değerine \( f \) fonksiyonunun \( a \) noktası için soldan limiti denir.
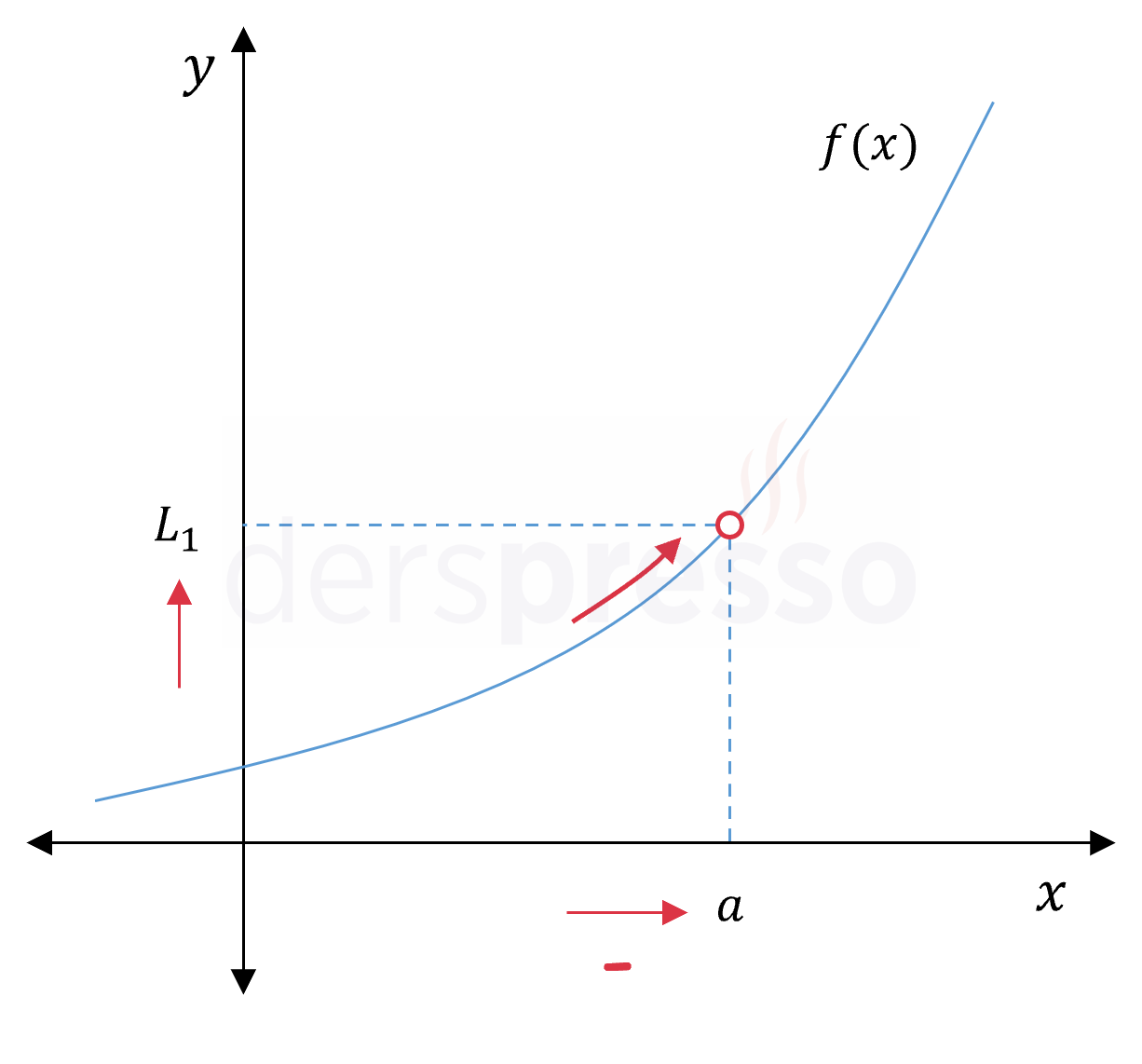
Soldan limitin iki farklı gösterimi aşağıdaki gibidir. Bu gösterimlerde \( a \) değerinin üstüne konan negatif işareti, \( a \) değerine \( x \) ekseninin negatif tarafından (soldan) yaklaştığımızı gösterir.
\( a, L_1 \in \mathbb{R} \) olmak üzere,
\( \lim\limits_{x \to a^-} f(x) = L_1 \)
\( f(a^-) = L_1 \)
Yukarıda tanımladığımız \( f \) fonksiyonunun \( 2 \) noktası için soldan limiti:
\( \lim\limits_{x \to 2^-} f(x) = f(2^-) = 4 \)
Sağdan Limit
Bir \( f \) fonksiyonunda \( x \) değişkenine bir \( a \) değerine \( x \gt a \) olmak koşulu ile sınırsız yaklaşan (ama hiçbir zaman \( x = a \) olmayan) değerler verdiğimizde \( f(x) \) değerleri bir \( L_2 \) değerine sınırsız yaklaşıyorsa ve yakın kalıyorsa, bu \( L_2 \) değerine \( f \) fonksiyonunun \( a \) noktası için sağdan limiti denir.
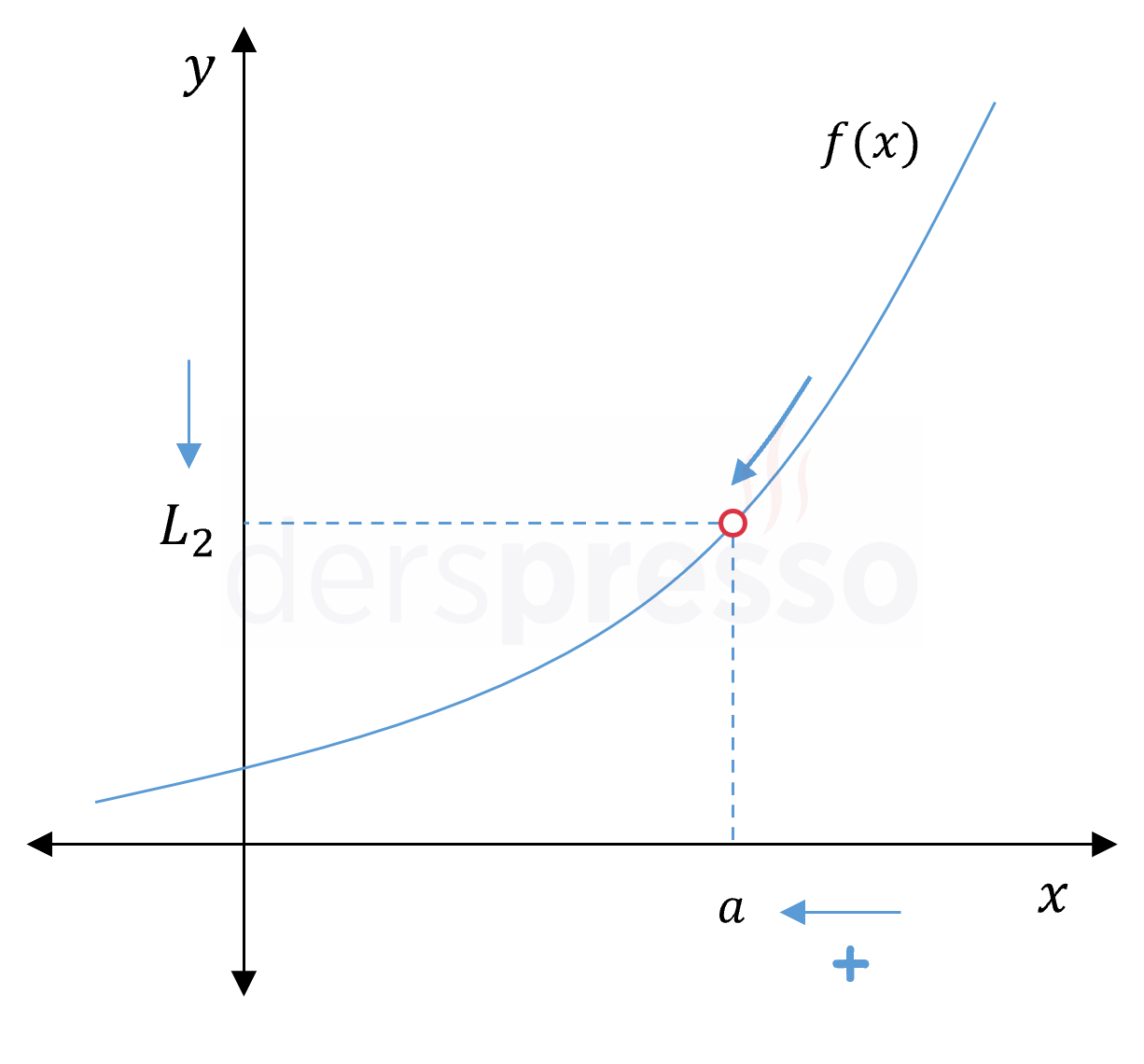
Sağdan limitin iki farklı gösterimi aşağıdaki gibidir. Bu gösterimlerde \( a \) değerinin üstüne konan pozitif işareti, \( a \) değerine \( x \) ekseninin pozitif tarafından (sağdan) yaklaştığımızı gösterir.
\( a, L_2 \in \mathbb{R} \) olmak üzere,
\( \lim\limits_{x \to a^+} f(x) = L_2 \)
\( f(a^+) = L_2 \)
Yukarıda tanımladığımız \( f \) fonksiyonunun \( 2 \) noktası için sağdan limiti:
\( \lim\limits_{x \to 2^+} f(x) = f(2^+) = 4 \)
Bir fonksiyonun bir noktadaki soldan ve sağdan limitlerine ayrı ayrı tek taraflı limit denir.
İki Taraflı Limit
Bir fonksiyonun bir noktadaki soldan ve sağdan limitleri birer reel sayı olarak tanımlı ve birbirine eşitse fonksiyonun o noktada iki taraflı limiti vardır ve soldan ve sağdan limit değerine eşittir.
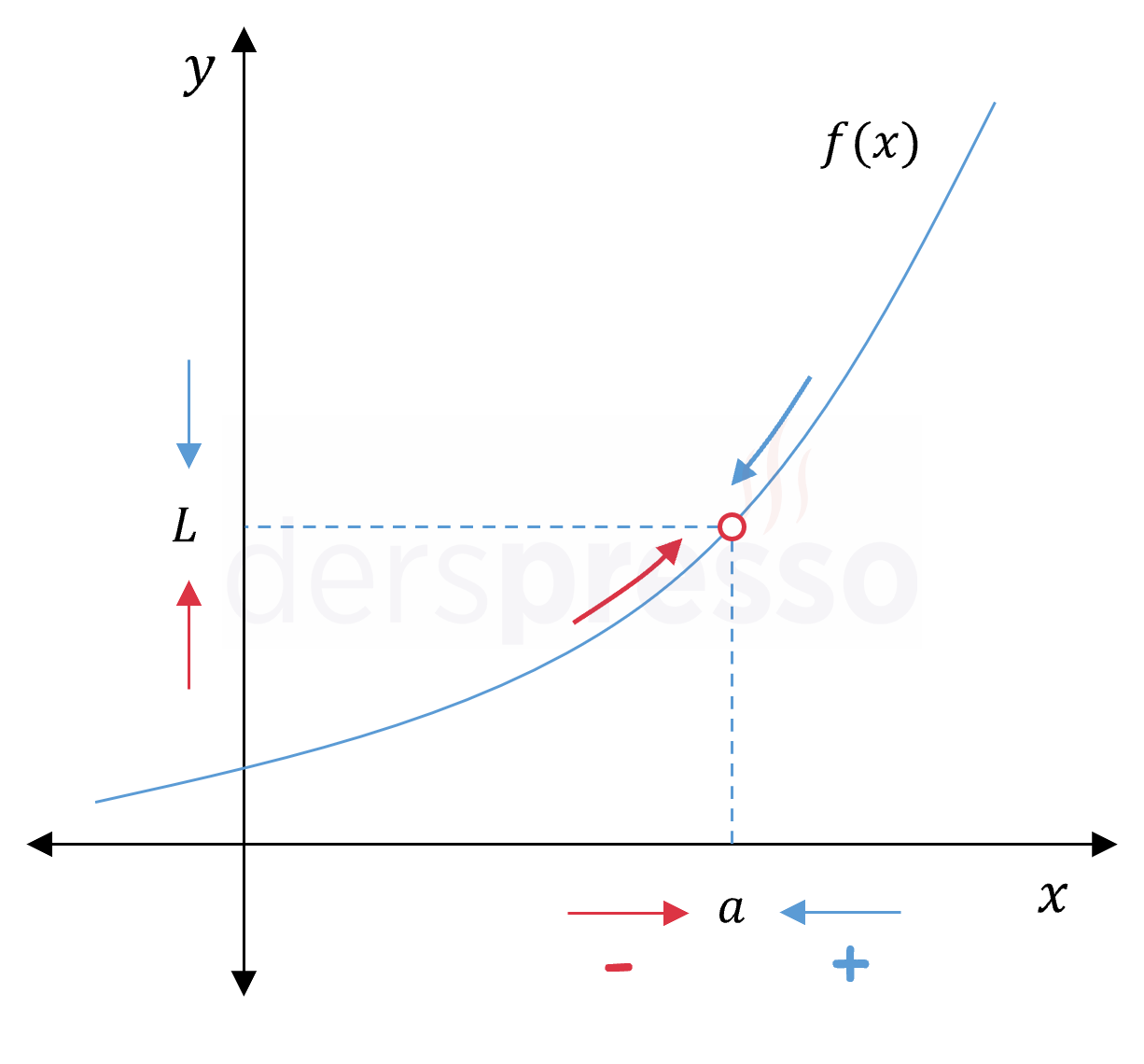
\( a, L \in \mathbb{R} \) olmak üzere,
\( \lim\limits_{x \to a^-} f(x) = \lim\limits_{x \to a^+} f(x) = L \) ise,
\( \lim\limits_{x \to a} f(x) = L \)
Bir fonksiyonun iki taraflı limitinde limiti hesaplanan değerin üstüne pozitif ya da negatif işareti konmaz.
Bir fonksiyonun belirli bir noktadaki limitinden bahsediliyorsa ve soldan ya da sağdan limit olduğu belirtilmemişse iki taraflı limit anlaşılmalıdır.
Bir fonksiyonun bir noktadaki limiti ile ilgili önemli bazı noktalar aşağıdaki gibidir.
- Bir fonksiyonun limiti bir aralık için değil, belirli bir nokta için hesaplanır.
- Bir noktada limitin tanımlı olması için fonksiyonun o noktada reel sayı bir \( L \) değerine yaklaşması gerekir. Fonksiyon değerinin sonsuza gittiği durumlar (sonsuz limit) gerçek bir limit teşkil etmez.
- Fonksiyonun bir noktadaki soldan ve sağdan limit değerleri birbirine eşit değilse ya da ikisinden biri tanımlı değilse fonksiyonun o noktada (iki taraflı) limiti yoktur.
- Bir fonksiyonun bir noktada limitinin olmaması soldan ve sağdan limitlerinin tanımsız olması anlamına gelmez. Soldan ve sağdan limitler o noktadaki limit değerinden bağımsız olarak tanımlı olabilirler.
- Limit bir fonksiyonun belirli bir \( x \) değeri civarında nasıl davrandığı ile ilgilenir, fonksiyonun o noktadaki değeri ya da tanımlı olup olmaması ile ilgilenmez. Dolayısıyla fonksiyonun bir \( x \) noktası için limitinin olması için fonksiyonun o noktada tanımlı olması ya da o noktadaki fonksiyon değerinin soldan/sağdan limit değerine eşit olması gerekli değildir.
Önümüzdeki bölümlerde detaylı inceleyeceğimiz üzere, aşağıdaki durumlarda soldan ve sağdan limitler farklı sonuç verebilir, dolayısıyla bir noktadaki limit değerini bulmak için her iki tek taraflı limitin de incelenmesi gerekir.
- Parçalı fonksiyonların geçiş noktaları
- Mutlak değerli fonksiyonların kritik noktaları
- Bir fonksiyonda dikey asimptot oluşan noktalar
Burada yaptığımız tanımı limitin "pratik" tanımı olarak adlandırdık, limitin standart ve en doğru tanımı olan epsilon-delta tanımından önümüzdeki bölümde bahsedeceğiz.
Uç Noktalarda Limit
Belirli bir \( [a, b) \) aralığında tanımlı bir fonksiyonun tanım aralığının uç noktalarında tek taraflı limitler sadece fonksiyonun tanımlı olduğu yönlerde, yani \( x = a \) noktasında sadece sağdan, \( x = b \) noktasında ise sadece soldan tanımlıdır.
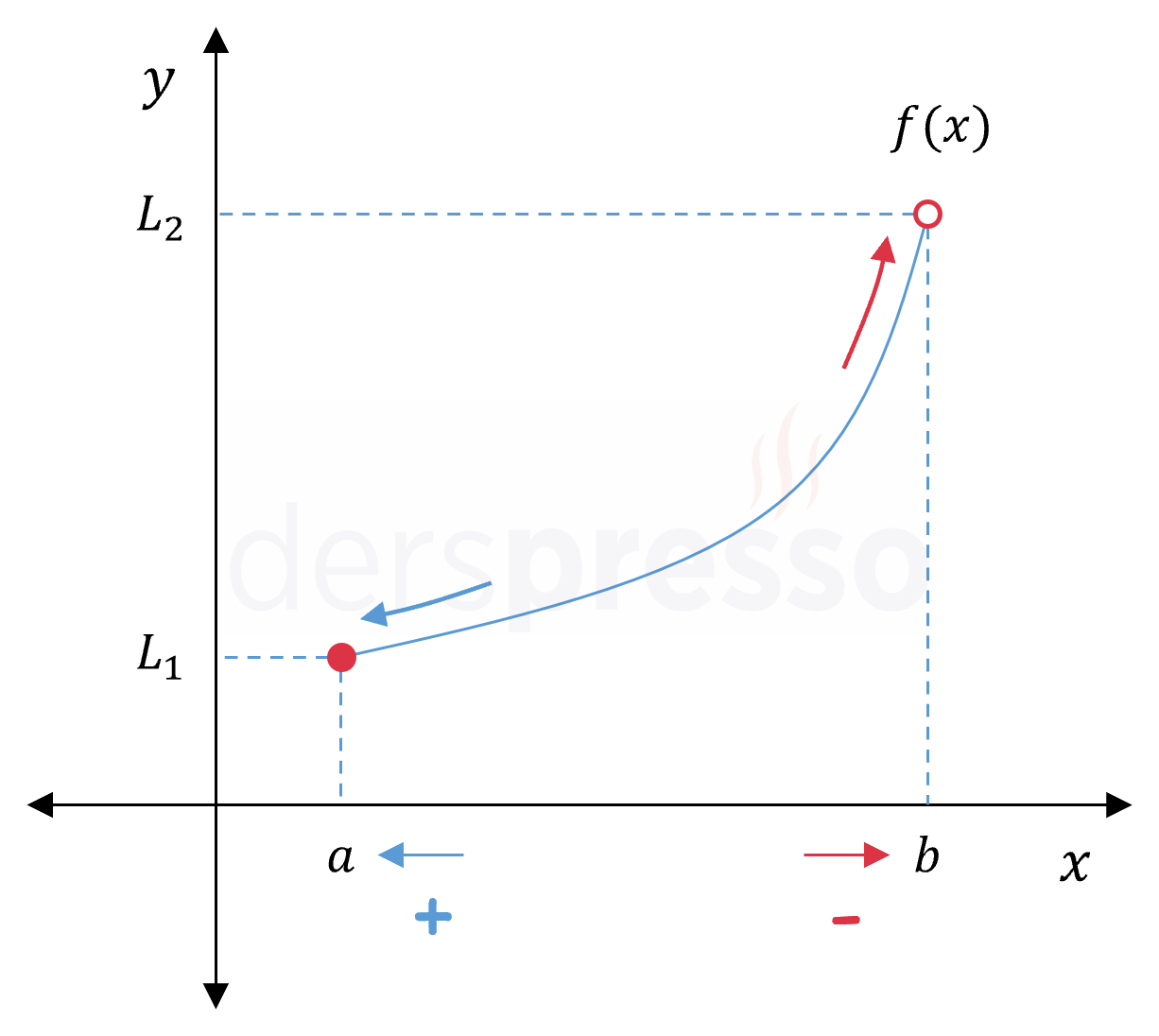
İki taraflı limit soldan ve sağdan limitlerin tanımlı ve eşit olmasını gerektirdiği için, uç noktalarda iki taraflı limit tanımlı değildir.
\( f: [a, b) \to \mathbb{R} \) olmak üzere,
\( \lim\limits_{x \to a^+} f(x) = L_1 \)
\( \lim\limits_{x \to a^-} f(x) \) ve \( \lim\limits_{x \to a} f(x) \) tanımsızdır.
\( \lim\limits_{x \to b^-} f(x) = L_2 \)
\( \lim\limits_{x \to b^+} f(x) \) ve \( \lim\limits_{x \to b} f(x) \) tanımsızdır.
Bir noktada limitin olması için fonksiyonun o noktada tanımlı olma koşulu olmadığı için, fonksiyonun tanımlı olduğu aralığın açık, kapalı ya da yarı açık olmasının uç noktalardaki limit açısından bir önemi yoktur.
\( a, b \in \mathbb{R} \) olmak üzere,
\( \lim\limits_{x \to 4^-} {f(x)} = 6a + 3 \)
\( \lim\limits_{x \to 4^+} {f(x)} = 7b - 2 \)
\( \lim\limits_{x \to 4} {f(x)} = 12 \)
olduğuna göre, \( ab \) çarpımı kaçtır?
Çözümü GösterFonksiyonun \( x = 4 \) noktasında iki taraflı limiti tanımlı olduğuna göre, bu noktadaki soldan ve sağdan limitler de tanımlı ve iki taraflı limit değerine eşit olmalıdır.
\( \lim\limits_{x \to 4^-} f(x) = \lim\limits_{x \to 4^+} f(x) = \lim\limits_{x \to 4} f(x) \)
\( 6a + 3 = 7b - 2 = 12 \)
\( 6a + 3 = 12 \)
\( a = \dfrac{3}{2} \)
\( 7b - 2 = 12 \)
\( b = 2 \)
\( ab = \frac{3}{2} \cdot 2 = 3 \) bulunur.
\( a, b \in \mathbb{R} \) olmak üzere,
\( \lim\limits_{x \to 2} {f(x)} = 11 \)
\( \lim\limits_{x \to 3^-} {f(x - 1)} = 5a - 4 \)
\( \lim\limits_{x \to 1^+} {f(x + 1)} = 2b + 3 \)
olduğuna göre, \( a + b \) toplamı kaçtır?
Çözümü GösterFonksiyonun \( x = 2 \) noktasında iki taraflı limiti tanımlı olduğuna göre, bu noktadaki soldan ve sağdan limitler de tanımlı ve iki taraflı limit değerine eşit olmalıdır.
\( \lim\limits_{x \to 2^-} f(x) = f(2^-) = 11 \)
\( \lim\limits_{x \to 2^+} f(x) = f(2^+) = 11 \)
Soruda verilen soldan limit ifadesini düzenleyelim.
\( x \to 3^- \) iken \( x - 1 \to 2^- \) olur.
Buna göre verilen ifade \( f \) fonksiyonunun \( x = 2 \) noktasındaki soldan limitidir.
\( \lim\limits_{x \to 3^-} f(x - 1) = f(2^-) \)
\( = \lim\limits_{x \to 2^-} f(x) = 5a - 4 \)
Soruda verilen sağdan limit ifadesini düzenleyelim.
\( x \to 1^+ \) iken \( x + 1 \to 2^+ \) olur.
Buna göre verilen ifade \( f \) fonksiyonunun \( x = 2 \) noktasındaki sağdan limitidir.
\( \lim\limits_{x \to 1^+} f(x + 1) = f(2^+) \)
\( = \lim\limits_{x \to 2^+} f(x) = 2b + 3 \)
Bu iki ifadeyi \( f \) fonksiyonunun \( x = 2 \) noktasındaki iki taraflı limitine eşitleyelim.
\( f(2^-) = 5a - 4 = 11 \)
\( a = 3 \)
\( f(2^+) = 2b + 3 = 11 \)
\( b = 4 \)
\( a + b = 3 + 4 = 7 \) bulunur.
Reel sayılar kümesinde tanımlı \( f \) fonksiyonu için,
\( \lim\limits_{x \to 1^+} f(5 - x) = 5 \)
\( \lim\limits_{x \to 3^+} f(x + 1) = 7 \)
olduğuna göre, aşağıdaki ifadelerden hangileri doğrudur?
I. \( \lim\limits_{x \to 4} f(x) \) tanım değildir.
II. \( \lim\limits_{x \to 2^+} f(x + 2) = 7 \)
III. \( \lim\limits_{x \to 3^-} f(7 - x) = 5 \)
Çözümü Göster\( x \to 1^+ \) iken \( 5 - x \to 4^- \) olur.
Buna göre verilen birinci ifade \( f \) fonksiyonunun \( x = 4 \) noktasındaki soldan limitidir.
\( \lim\limits_{x \to 1^+} f(5 - x) = f(4^-) \)
\( = \lim\limits_{x \to 4^-} f(x) = 5 \)
\( x \to 3^+ \) iken \( x + 1 \to 4^+ \) olur.
Buna göre verilen ikinci ifade \( f \) fonksiyonunun \( x = 4 \) noktasındaki sağdan limitidir.
\( \lim\limits_{x \to 3^+} f(x + 1) = f(4^+) \)
\( = \lim\limits_{x \to 4^+} f(x) = 7 \)
Bu bilgiler doğrultusunda soruda verilen öncülleri kontrol edelim.
I. öncül:
\( x = 4 \) noktasındaki soldan ve sağdan limitler tanımlı, ancak farklı olduğu için bu noktada iki taraflı limit tanımlı değildir.
\( f(4^-) \ne f(4^+) \)
I. öncül doğrudur.
II. öncül:
\( x \to 2^+ \) iken \( x + 2 \to 4^+ \) olur.
Buna göre verilen ifade \( f \) fonksiyonunun \( x = 4 \) noktasındaki sağdan limitidir.
\( f(4^+) = 7 \) olduğu için II. öncül doğrudur.
III. öncül:
\( x \to 3^- \) iken \( 7 - x \to 4^+ \) olur.
Buna göre verilen ifade \( f \) fonksiyonunun \( x = 4 \) noktasındaki sağdan limitidir.
\( f(4^+) = 7 \) olduğu için III. öncül yanlıştır.
Buna göre I. ve II. öncüller doğrudur.

Yukarıda \( f \) fonksiyonunun grafiği verilmiştir.
\( g \) ve \( h \) fonksiyonları, \( f \) fonksiyonu kullanılarak aşağıdaki şekilde tanımlanmıştır.
\( g(x) = f(x) - \lim\limits_{t \to x^+} f(t) \)
\( h(x) = f(x) + \lim\limits_{t \to x^-} f(t) \)
Buna göre, \( (h \circ g \circ f)(0) \) kaçtır?
Çözümü Göster\( (h \circ g \circ f)(0) = h(g(f(0))) \)
Bileşke fonksiyonu içten dışa doğru çözelim.
\( f(0) = -2 \)
\( h(g(f(0))) = h(g(-2)) \)
\( g(-2) \) değerini bulalım.
\( g(-2) = f(-2) - \lim\limits_{t \to -2^+} f(t) \)
\( = 3 - 3 = 0 \)
\( h(g(-2)) = h(0) \)
\( h(0) \) değerini bulalım.
\( h(0) = f(0) + \lim\limits_{t \to 0^-} f(t) \)
\( = -2 + 3 = 1 \) bulunur.