Bileşke Fonksiyonların Limiti
Bu bölümde aşağıdaki ve benzer formdaki bileşke fonksiyonların limitini hesaplamak için kullanabileceğimiz yöntemleri inceleyeceğiz.
| Dıştaki Fonksiyon | Bileşke Fonksiyon |
|---|---|
| \( f(x) = \sqrt{x} \) | \( (f \circ g)(x) = \sqrt{g(x)} \) |
| \( f(x) = \sin{x} \) | \( (f \circ g)(x) = \sin{g(x)} \) |
| \( f(x) = e^x \) | \( (f \circ g)(x) = e^{g(x)} \) |
| \( f(x) = \log{x} \) | \( (f \circ g)(x) = \log{g(x)} \) |
| \( f(x) = \abs{x} \) | \( (f \circ g)(x) = \abs{g(x)} \) |
\( f \) ve \( g \) fonksiyonları arasındaki \( f \circ g \) bileşke fonksiyonunun \( a \) noktasındaki limitini bulmak istiyor olalım ve içteki \( g \) fonksiyonunun \( a \) noktasındaki limitinin \( b \) reel sayısı olarak tanımlı olduğunu varsayalım.

\( b \in \mathbb{R} \) olmak üzere,
\( \lim\limits_{x \to a} g(x) = b \)
\( \lim\limits_{x \to a} (f \circ g)(x) = \lim\limits_{x \to a} {f(g(x))} = ? \)
Dıştaki \( f \) fonksiyonu \( b \) noktasında sürekli ise \( f \circ g \) bileşke fonksiyonunun \( a \) noktasındaki limiti, \( f \) fonksiyonunun \( b \) noktasındaki fonksiyon değerine eşit olur.
\( f \) fonksiyonu \( b \) noktasında sürekli ise,
\( \lim\limits_{x \to a} (f \circ g)(x) = \lim\limits_{x \to a} {f(g(x))} \)
\( = f(\lim\limits_{x \to a} g(x)) = f(b) \)
Bir diğer ifadeyle, \( f \) fonksiyonu \( b \) noktasında sürekli ise \( \lim\limits_{x \to a} {f(g(x))} \) ifadesinde limit işlemini \( f(\lim\limits_{x \to a} g(x)) \) şeklinde parantez içine alabiliriz ve \( f(b) \) değerini hesaplayarak limit değerini bulabiliriz.
\( f(x) = x^2 - 2x + 5 \)
\( g(x) = \sqrt[3]{x^2 + 2} \) olduğuna göre,
\( \lim\limits_{x \to 5} (f \circ g)(x) \) limitinin değerini bulalım.
\( g \) tek dereceli köklü fonksiyonu tüm reel sayılarda tanımlı ve sürekli olduğu için limit değerini doğrudan yerine koyma yöntemi ile bulabiliriz.
\( \lim\limits_{x \to 5} {g(x)} = g(5) = \sqrt[3]{5^2 + 2} = 3 \)
\( f \) polinom fonksiyonu tüm reel sayılarda tanımlı ve sürekli olduğu için \( g \) fonksiyonunun limit değeri olan \( x = 3 \) noktasında süreklidir.
Buna göre bileşke fonksiyon limit kuralı ile limit işlemini parantez içine alabiliriz.
\( \lim\limits_{x \to 5} (f \circ g)(x) = \lim\limits_{x \to 5} {f(g(x))} \)
\( = f(\lim\limits_{x \to 5} {g(x)}) = f(3) \)
\( f \) fonksiyonunda \( x = 3 \) yazalım.
\( = 3^2 - 2(3) + 5 = 8 \)
\( g \) fonksiyonunun \( a \) noktasındaki limiti bir reel sayı olarak tanımlı değilse birkaç özel durum hariç (\( f \) bir sabit fonksiyon gibi) \( f \circ g \) bileşke fonksiyonunun bu noktadaki limiti de tanımsız olur.
\( f \) fonksiyonu \( b \) noktasında sürekli değilse yukarıdaki limit kuralı geçerli değildir, ancak \( f \circ g \) bileşke fonksiyonunun \( a \) noktadaki limiti yine de tanımlı olabilir. Bu durumda bileşke fonksiyonun limitini bulmak için aşağıdaki yöntemler kullanılabilir.
- \( f \circ g \) bileşke fonksiyonunun tanımı bulunur ve fonksiyonun \( a \) noktasındaki limiti hesaplanır.
- Aşağıda bahsedeceğimiz yöntemle \( g \) fonksiyonunun \( a \) noktasındaki ve \( f \) fonksiyonunun \( b \) noktasındaki tek taraflı limitleri incelenir.
Süreklilik Koşulu
Yukarıda bahsettiğimiz süreklilik koşulunun neden gerekli olduğunu, \( f \) fonksiyonunun \( b \) noktasında sürekli olmadığı bir örnek üzerinde gösterelim. Bu örnekte \( f \) fonksiyonu \( x = 2 \) noktası hariç sabit fonksiyon, \( g \) ise birim fonksiyondur.

\( g \) birim fonksiyon olduğu için \( f \circ g \) bileşke fonksiyonu \( f \) fonksiyonuna eşit olur. Verilen grafiklerde görülebileceği üzere, \( \lim\limits_{x \to 2} (f \circ g)(x)) = 3 \) olmakta ve bu limit değeri \( f(\lim\limits_{x \to 2} {g(x)}) = f(2) = 5 \) değerinden farklı olmaktadır.
Farklı Fonksiyonlarla Bileşke
Bileşke fonksiyon limit kuralı farklı fonksiyonlara aşağıda örneklerini verdiğimiz şekilde uygulanabilir.
Üstel Fonksiyonla Bileşke
Üstel fonksiyonun üssünün bir fonksiyon olduğu durumda bileşke fonksiyon limit kuralı aşağıdaki şekilde uygulanabilir. Üstel fonksiyonlar tüm reel sayılarda sürekli olduğu için, \( g \) fonksiyonunun limiti tanımlı olduğu sürece süreklilik koşulu sağlanmış olur.
\( \lim\limits_{x \to a} g(x) = b \) olmak üzere,
\( \lim\limits_{x \to a} e^{g(x)} = e^{\lim\limits_{x \to a} g(x)} = e^b \)
\( \lim\limits_{x \to 3} 5^{\sqrt{3x}} = 5^{\lim\limits_{x \to 3} \sqrt{3x}} \)
\( = 5^3 = 125 \)
İSPATI GÖSTER
Üstel fonksiyonlar tüm reel sayılarda sürekli olduğu için dıştaki fonksiyonun sürekli olduğunu kabul ederek bileşke fonksiyon limit kuralını kullanabiliriz.
\( \lim\limits_{x \to a} g(x) = b \) olmak üzere,
\( \lim\limits_{x \to a} (f \circ g)(x) = \lim\limits_{x \to a} {f(g(x))} \)
\( = f(\lim\limits_{x \to a} g(x)) = f(b) \)
\( f \) fonksiyonunu \( f(x) = e^x \) şeklinde tanımlayarak bileşke fonksiyonu yazalım.
\( (f \circ g)(x) = f(g(x)) = e^{g(x)} \)
Yukarıdaki limit ifadesini buna göre düzenleyelim.
\( \lim\limits_{x \to a} e^{g(x)} = e^{\lim\limits_{x \to a} g(x)} = e^b \)
Bu kural \( e \) dışında herhangi bir tabana da uygulanabilir.
Logaritma Fonksiyonuyla Bileşke
Logaritma fonksiyonunun içinin bir fonksiyon olduğu durumda bileşke fonksiyon limit kuralı aşağıdaki şekilde uygulanabilir. Logaritma fonksiyonu pozitif reel sayılarda sürekli olduğu için, \( g \) fonksiyonunun limiti pozitif reel sayı olarak tanımlı olduğu sürece süreklilik koşulu sağlanmış olur.
\( \lim\limits_{x \to a} g(x) = b \) olmak üzere,
\( \lim\limits_{x \to a} (\ln{g(x)}) = \ln(\lim\limits_{x \to a} g(x)) = \ln{b} \)
\( \lim\limits_{x \to 125} (\log_5{\sqrt{5x}}) = \log_5(\lim\limits_{x \to 125} \sqrt{5x}) \)
\( = \log_5{25} = 2 \)
İSPATI GÖSTER
Logaritma fonksiyonu pozitif reel sayılarda sürekli olduğu için dıştaki fonksiyonun sürekli olduğu durum için paylaştığımız bileşke fonksiyon limit kuralını kullanabiliriz.
\( \lim\limits_{x \to a} g(x) = b \) olmak üzere,
\( \lim\limits_{x \to a} (f \circ g)(x) = \lim\limits_{x \to a} {f(g(x))} \)
\( = f(\lim\limits_{x \to a} g(x)) = f(b) \)
\( f \) fonksiyonunu \( f(x) = \ln{x} \) şeklinde tanımlayarak bileşke fonksiyonu yazalım.
\( (f \circ g)(x) = f(g(x)) = \ln{g(x)} \)
Yukarıdaki limit ifadesini buna göre düzenleyelim.
\( \lim\limits_{x \to a} (\ln{g(x)}) = \ln(\lim\limits_{x \to a} g(x)) = \ln{b} \)
Bu kural \( e \) dışında herhangi bir logaritma tabanına da uygulanabilir.
Mutlak Değer Fonksiyonuyla Bileşke
Mutlak değer fonksiyonunun içinin bir fonksiyon olduğu durumda bileşke fonksiyon limit kuralı aşağıdaki şekilde uygulanabilir. Mutlak değer fonksiyonu tüm reel sayılarda sürekli olduğu için, \( g \) fonksiyonunun limiti reel sayı olarak tanımlı olduğu sürece süreklilik koşulu sağlanmış olur.
\( \lim\limits_{x \to a} g(x) = b \) olmak üzere,
\( \lim\limits_{x \to a} \abs{g(x)} = \abs{\lim\limits_{x \to a} g(x)} = \abs{b} \)
\( \lim\limits_{x \to 8} \abs{\sqrt{2x} - x^2} = \abs{\lim\limits_{x \to 8} (\sqrt{2x} - x^2)} \)
\( = \abs{\sqrt{16} - 64} = 60 \)
Tek Taraflı Limit
\( f \) fonksiyonu \( b \) noktasında sürekli değilse yukarıda bahsettiğimiz limit kuralı geçerli değildir, bu durumda bileşke fonksiyonun limitini bulmak için tek taraflı limitleri incelememiz gerekebilir.
Tek taraflı limitleri kullanarak bileşke fonksiyonun limitini bulmak için aşağıdaki yöntem kullanılabilir.
- \( a \) noktasına soldan yaklaşırken \( g \) fonksiyonunun \( b \) limit değerine hangi yönden (aşağıdan ya da yukarıdan) yaklaştığına bakılır (\( \lim\limits_{x \to a^-} {g(x)} = b^- \) ya da \( \lim\limits_{x \to a^-} {g(x)} = b^+ \)).
- Daha sonra \( f \) fonksiyonunun \( b \) noktasında bu yöndeki tek taraflı limiti incelenir (\( \lim\limits_{x \to b^-} {f(x)} \) ya da \( \lim\limits_{x \to b^+} {f(x)} \)).
- Elde edilen limit değeri bileşke fonksiyonun \( a \) noktasındaki soldan limit değerini verir (\( \lim\limits_{x \to a^-} (f \circ g)(x) \)).
- Benzer adımlar \( a \) noktasındaki sağdan limit için tekrarlanır. Soldan ve sağdan limitler tanımlı ve birbirine eşitse bileşke fonksiyonun \( a \) noktasındaki limiti tanımlıdır ve bulunan limit değerine eşittir.
Bu yöntemde tek taraflı limiti hesaplarken, içteki fonksiyonun yaklaştığı limit değerine ek olarak bu değere hangi yönden (aşağıdan ya da yukarıdan) yaklaştığını takip etmemiz ve dıştaki fonksiyonun ilgili nokta ve yöndeki tek yönlü limitini hesaplamamız gerekir.
Tek taraflı limit hesaplarken limit değerine olan yaklaşım (fonksiyonun limiti alınan nokta civarında sabit değer aldığı durum hariç) dört şekilde olabilir.
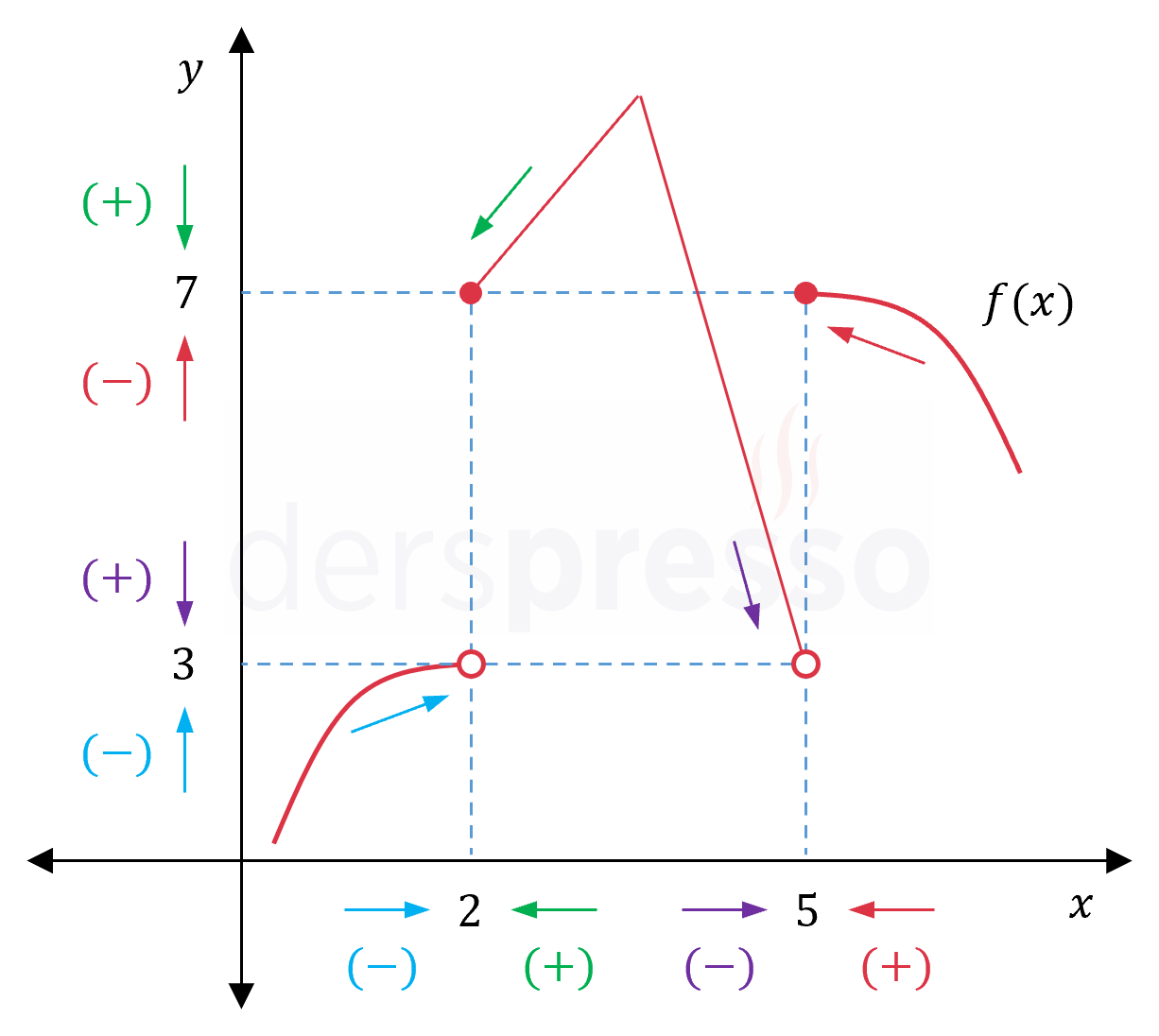
| Renk | Limit | \( x \) Değerine Yaklaşım | Limit Değerine Yaklaşım |
|---|---|---|---|
| Mavi oklar | \( \lim\limits_{x \to 2^-} {f(x)} = 3^- \) | \( x \); \( 1.9, 1.99, 1.999 \) şeklinde artan değerler alarak \( x = 2 \) noktasına negatif taraftan/soldan yaklaşır. | \( f(x) \); \( 2.9, 2.99, 2.999 \) şeklinde artan değerler alarak \( 3 \) limit değerine negatif taraftan/aşağıdan yaklaşır. |
| Yeşil oklar | \( \lim\limits_{x \to 2^+} {f(x)} = 7^+ \) | \( x \); \( 2.1, 2.01, 2.001 \) şeklinde azalan değerler alarak \( x = 2 \) noktasına pozitif taraftan/sağdan yaklaşır. | \( f(x) \); \( 7.1, 7.01, 7.001 \) şeklinde azalan değerler alarak \( 7 \) limit değerine pozitif taraftan/yukarıdan yaklaşır. |
| Mor oklar | \( \lim\limits_{x \to 5^-} {f(x)} = 3^+ \) | \( x \); \( 4.9, 4.99, 4.999 \) şeklinde artan değerler alarak \( x = 5 \) noktasına negatif taraftan/soldan yaklaşır. | \( f(x) \); \( 3.1, 3.01, 3.001 \) şeklinde azalan değerler alarak \( 3 \) limit değerine pozitif taraftan/yukarıdan yaklaşır. |
| Kırmızı oklar | \( \lim\limits_{x \to 5^+} {f(x)} = 7^- \) | \( x \); \( 5.1, 5.01, 5.001 \) şeklinde azalan değerler alarak \( x = 5 \) noktasına pozitif taraftan/sağdan yaklaşır. | \( f(x) \); \( 6.9, 6.99, 6.999 \) şeklinde artan değerler alarak \( 7 \) limit değerine negatif taraftan/aşağıdan yaklaşır. |
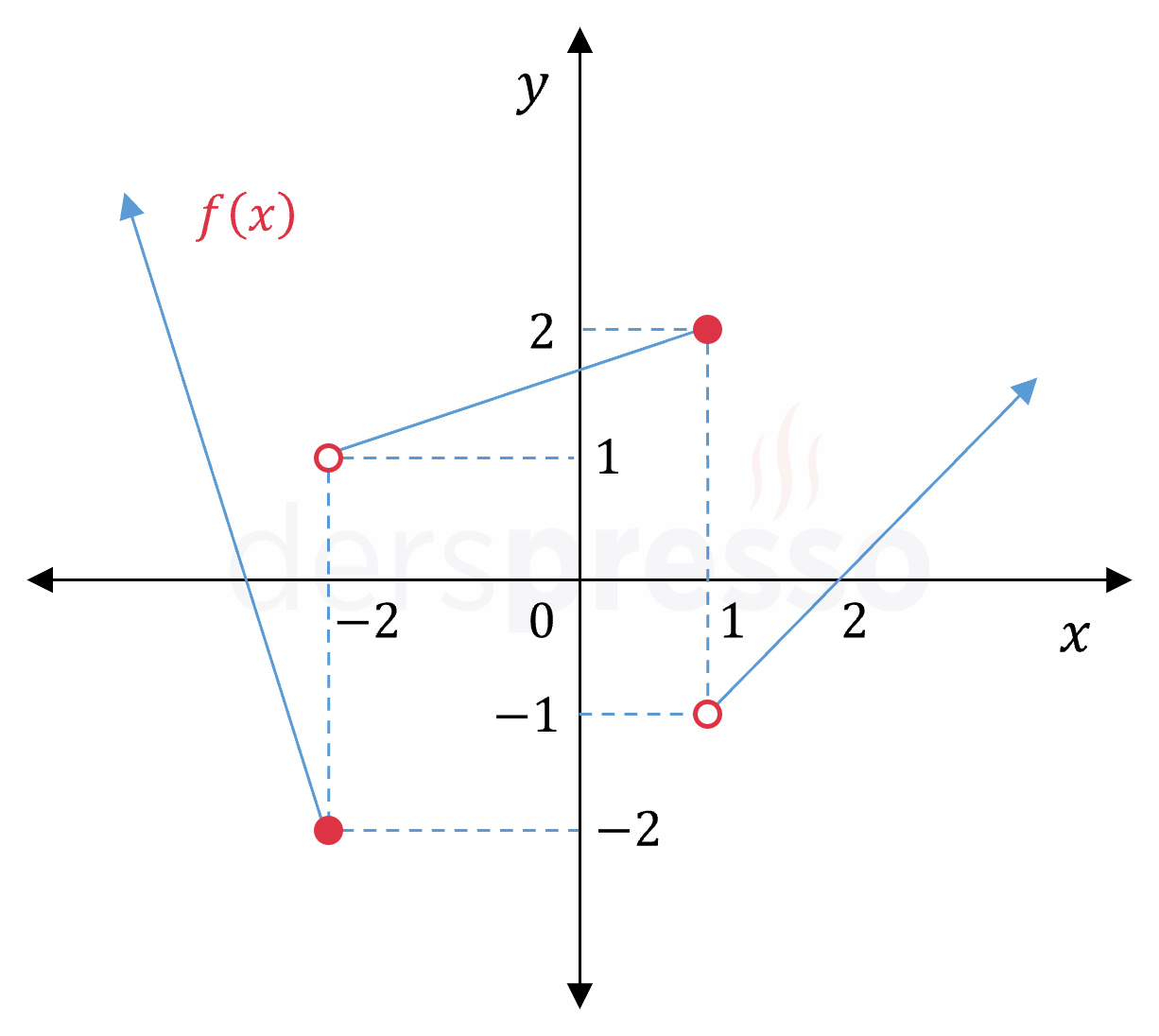
Yukarıda verilen grafiğe göre,
\( \lim\limits_{x \to -2^+} (f \circ f \circ f)(x) \) limitinin değerini bulalım.
\( \lim\limits_{x \to -2^+} (f \circ f \circ f)(x) = \lim\limits_{x \to -2^+} {f(f(f(x)))} \)
Önce en içteki \( f \) fonksiyonunun \( x \to -2^+ \) iken limitini bulalım.
Aşağıdaki grafikte yeşil okla gösterildiği üzere, \( x \to -2^+ \) iken \( f(x) \to 1^- \) olur.
\( \lim\limits_{x \to -2^+} {f(x)} = 1^- \)
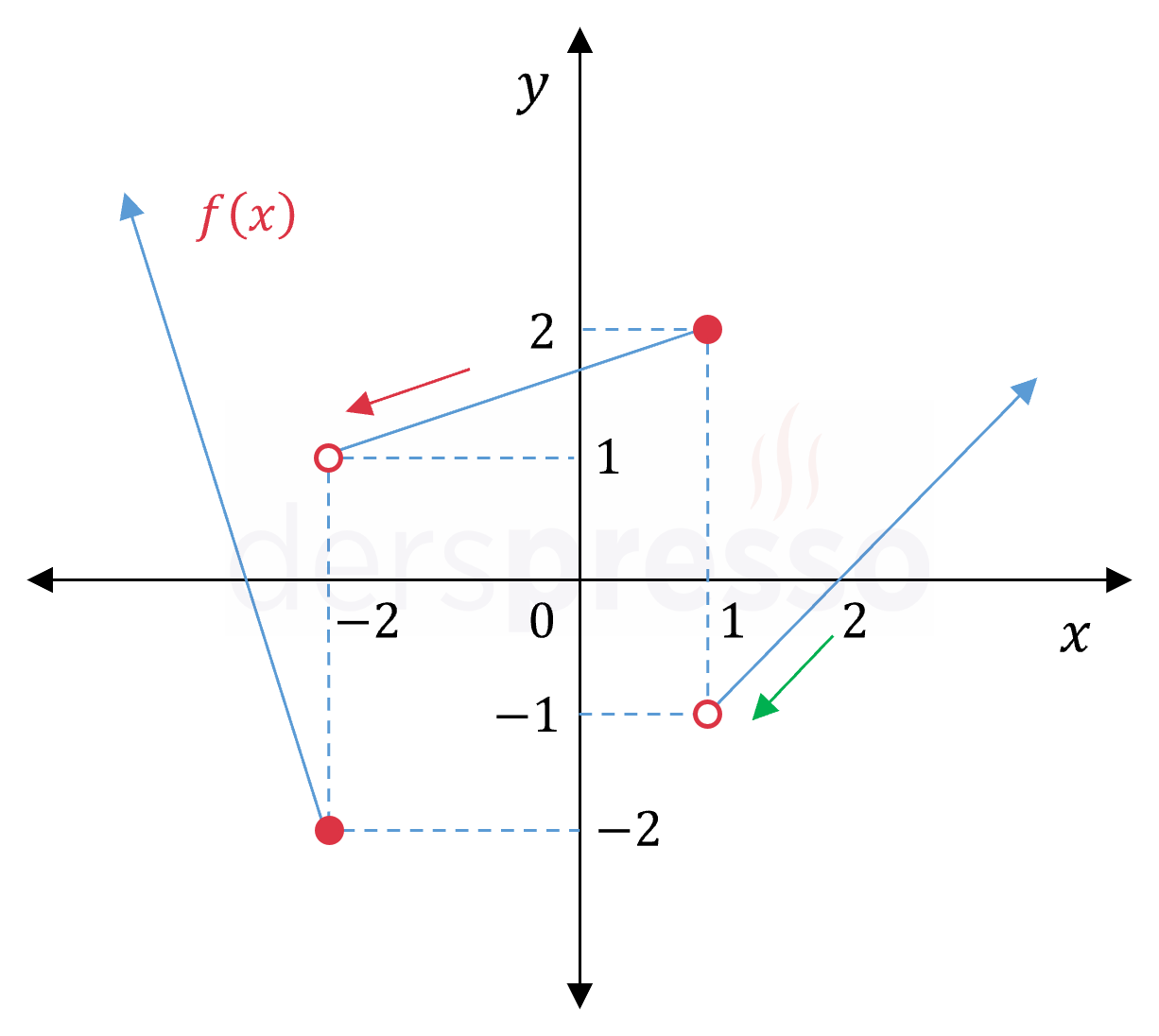
Şimdi ortadaki \( f \) fonksiyonunun \( x \to 1^- \) iken limitini bulalım.
Yukarıdaki grafikte mavi okla gösterildiği üzere, \( x \to 1^- \) iken \( f(x) \to -2^- \) olur.
\( \lim\limits_{x \to 1^-} {f(x)} = -2^- \)
Şimdi en dıştaki \( f \) fonksiyonunun \( x \to -2^- \) iken limitini bulalım.
Yukarıdaki grafikte mor okla gösterildiği üzere, \( x \to -2^- \) iken \( f(x) \to -3^+ \) olur.
\( \lim\limits_{x \to -2^-} {f(x)} = -3^+ \)
Buna göre istenen limit değeri \( -3 \) olarak bulunur.
\( \lim\limits_{x \to -2^+} (f \circ f \circ f)(x) = -3 \)
Fonksiyonun limiti alınan nokta civarında sabit değer aldığı durumda ise fonksiyon limit değerine aşağıdan ya da yukarıdan değil, sabit değer alarak yaklaşır, dolayısıyla aşağıdaki örnekteki gibi durumları dikkate almamız gerekir.
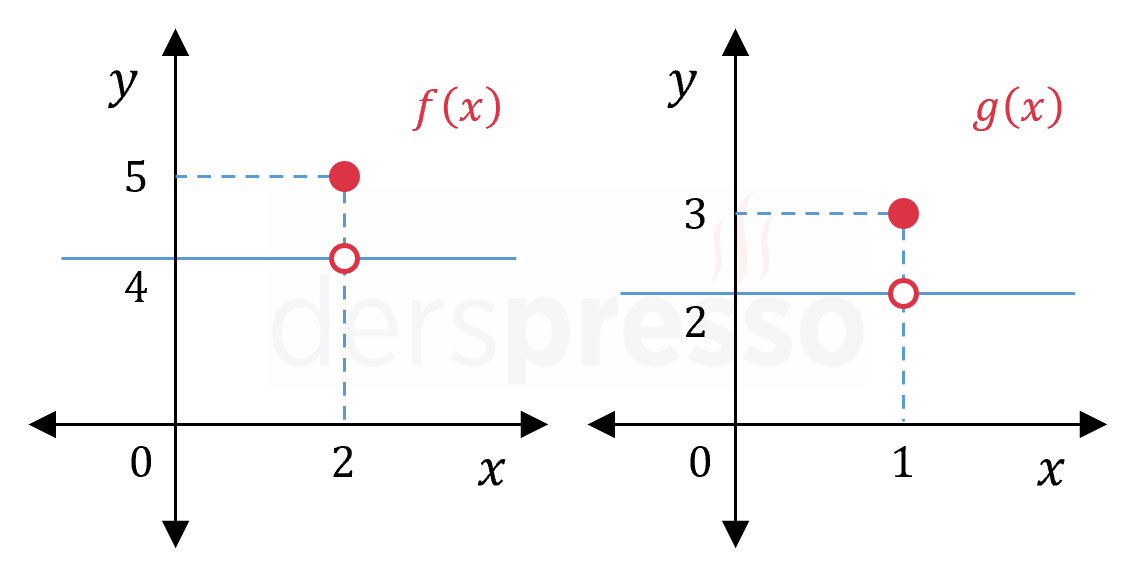
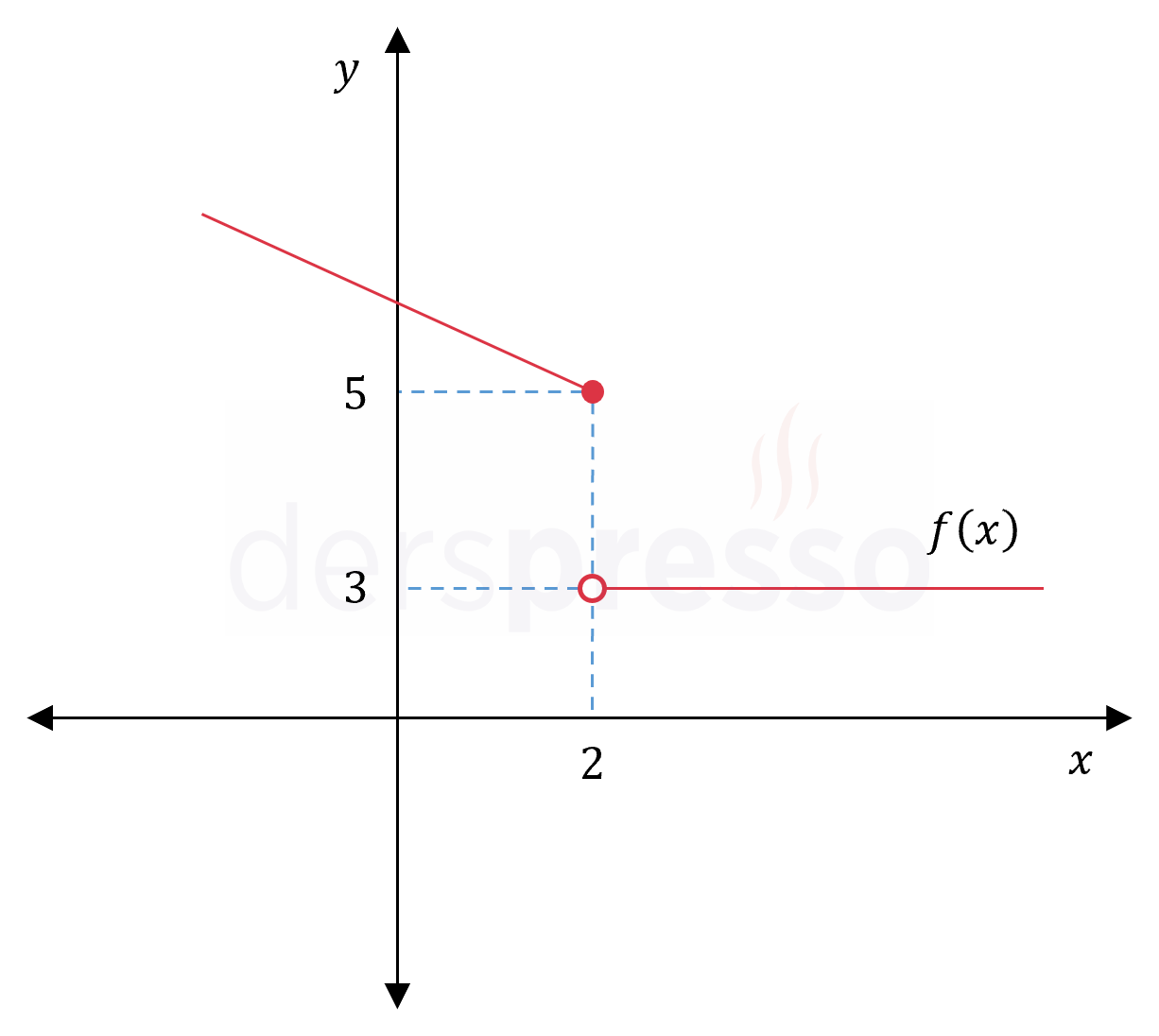
Yukarıda verilen grafiklere göre,
\( \lim\limits_{x \to 1^+} (f \circ g)(x) \) limitinin değerini bulalım.
İlk önce \( g \) fonksiyonunun \( x = 1 \) noktasındaki sağdan limitini bulalım.
\( \lim\limits_{x \to 1^+} g(x) = 2 \)
Şimdi de \( f \) fonksiyonunun bulduğumuz \( x = 2 \) noktasındaki sağdan limitini bulalım.
\( \lim\limits_{x \to 2^+} f(x) = 4 \)
Buna göre \( f \circ g \) bileşke fonksiyonunun \( x = 1 \) noktasındaki sağdan limitinin 4 olduğunu düşünebiliriz, ancak aşağıda göstereceğimiz üzere gerçek limit değeri 5'tir.
Verilen grafikleri kullanarak \( f \circ g \) fonksiyon tanımını yazalım.
\( (f \circ g)(x) = \begin{cases} 4 & x = 1 \\ 5 & x \ne 1 \end{cases} \)
Bu tanımı kullanarak bileşke fonksiyon grafiğini çizelim.
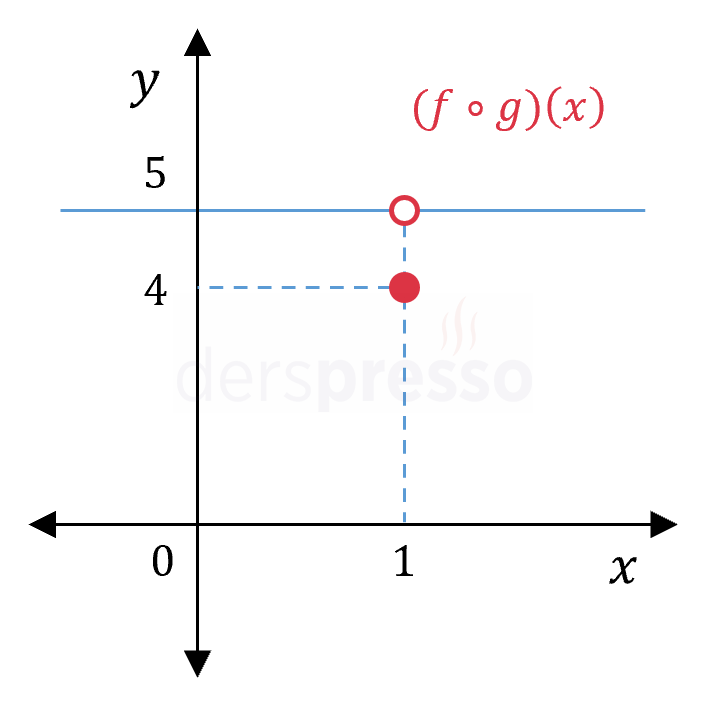
Bileşke fonksiyon grafiğini incelediğimizde, \( x = 1 \) noktasındaki limit değerinin 4 değil 5 olduğunu görürüz.
\( \lim\limits_{x \to 1^+} (f \circ g)(x) = 5 \ne 4 \)
Bunun sebebi, \( g \) fonksiyonu \( x = 1 \) noktasına sağdan yaklaşırken artarak ya da azalarak değil, sabit şekilde 2 değerini alması, \( f \) fonksiyonunun da \( x = 2 \) noktasındaki değerinin 5 olmasıdır.
Aşağıdaki limitleri hesaplayınız.
(a) \( \lim\limits_{x \to \frac{\pi}{5}} {\sin\left( \dfrac{5x}{3} - \dfrac{\pi}{6} \right)} \)
(b) \( \lim\limits_{x \to \frac{\pi}{3}} {\sqrt{\cos{x}}} \)
(c) \( \lim\limits_{x \to -3} {e^{2x^2}} \)
Çözümü Göster(a) seçeneği:
\( \lim\limits_{x \to \frac{\pi}{5}} {\sin\left( \dfrac{5x}{3} - \dfrac{\pi}{6} \right)} \)
İçteki doğrusal fonksiyon tüm reel sayılarda tanımlı ve sürekli olduğu için limit değerini doğrudan yerine koyma yöntemi ile bulabiliriz.
\( \lim\limits_{x \to \frac{\pi}{5}} \left( \dfrac{5x}{3} - \dfrac{\pi}{6} \right) = \dfrac{5 \cdot \frac{\pi}{5}}{3} - \dfrac{\pi}{6} = \dfrac{\pi}{6} \)
Dıştaki sinüs fonksiyonu tüm reel sayılarda tanımlı ve sürekli olduğu için içteki fonksiyonun limit değeri olan \( x = \frac{\pi}{6} \) noktasında süreklidir.
Buna göre bileşke fonksiyon limit kuralı ile limit işlemini sinüs içine alabiliriz.
\( \lim\limits_{x \to \frac{\pi}{5}} {\sin\left( \dfrac{5x}{3} - \dfrac{\pi}{6} \right)} = \sin{\lim\limits_{x \to \frac{\pi}{5}} \left( \dfrac{5x}{3} - \dfrac{\pi}{6} \right)} \)
\( = \sin{\dfrac{\pi}{6}} = \dfrac{1}{2} \)
(b) seçeneği:
\( \lim\limits_{x \to \frac{\pi}{3}} {\sqrt{\cos{x}}} \)
İçteki kosinüs fonksiyonu tüm reel sayılarda tanımlı ve sürekli olduğu için limit değerini doğrudan yerine koyma yöntemi ile bulabiliriz.
\( \lim\limits_{x \to \frac{\pi}{3}} {\cos{x}} = \cos{\dfrac{\pi}{3}} = \dfrac{1}{2} \)
Dıştaki karekök fonksiyonu sıfır ve pozitif reel sayılarda tanımlı ve sürekli olduğu için içteki fonksiyonun limit değeri olan \( x = \frac{1}{2} \) noktasında süreklidir.
Buna göre bileşke fonksiyon limit kuralı ile limit işlemini karekök içine alabiliriz.
\( \lim\limits_{x \to \frac{\pi}{3}} {\sqrt{\cos{x}}} = \sqrt{\lim\limits_{x \to \frac{\pi}{3}} {\cos{x}}} \)
\( = \sqrt{\dfrac{1}{2}} = \dfrac{\sqrt{2}}{2} \)
(c) seçeneği:
\( \lim\limits_{x \to -3} {e^{2x^2}} \)
İçteki kuvvet fonksiyonu tüm reel sayılarda tanımlı ve sürekli olduğu için limit değerini doğrudan yerine koyma yöntemi ile bulabiliriz.
\( \lim\limits_{x \to -3} (2x^2) = 2(-3)^2 = 18 \)
Dıştaki üstel fonksiyon tüm reel sayılarda tanımlı ve sürekli olduğu için içteki fonksiyonun limit değeri olan \( x = 18 \) noktasında süreklidir.
Buna göre bileşke fonksiyon limit kuralı ile limit işlemini üstel fonksiyonun üssüne alabiliriz.
\( \lim\limits_{x \to -3} {e^{2x^2}} = e^{\lim\limits_{x \to -3} (2x^2)} \)
\( = e^{18} \)
Aşağıdaki limitleri hesaplayınız.
(a) \( \lim\limits_{x \to 16} {\sqrt[3]{2\sqrt{x}}} \)
(b) \( \lim\limits_{x \to \frac{\pi}{4}} {\ln{\tan{x}}} \)
(c) \( \lim\limits_{x \to 3} {\abs{x^2 - 6x + 2}} \)
Çözümü Göster(a) seçeneği:
\( \lim\limits_{x \to 16} {\sqrt[3]{2\sqrt{x}}} \)
İçteki karekök fonksiyonu sıfır ve pozitif reel sayılarda tanımlı ve sürekli olduğu için limit değerini doğrudan yerine koyma yöntemi ile bulabiliriz.
\( \lim\limits_{x \to 16} (2\sqrt{x}) = 2\sqrt{16} = 8 \)
Dıştaki küpkök fonksiyonu tüm reel sayılarda tanımlı ve sürekli olduğu için içteki fonksiyonun limit değeri olan \( x = 8 \) noktasında süreklidir.
Buna göre bileşke fonksiyon limit kuralı ile limit işlemini kök içine alabiliriz.
\( \lim\limits_{x \to 16} {\sqrt[3]{2\sqrt{x}}} = \sqrt[3]{\lim\limits_{x \to 16} (2\sqrt{x})} \)
\( = \sqrt[3]{8} = 2 \)
(b) seçeneği:
\( \lim\limits_{x \to \frac{\pi}{4}} {\ln{\tan{x}}} \)
İçteki tanjant fonksiyonu \( (-\frac{\pi}{2}, \frac{\pi}{2}) \) aralığında tanımlı ve sürekli olduğu için limit değerini doğrudan yerine koyma yöntemi ile bulabiliriz.
\( \lim\limits_{x \to \frac{\pi}{4}} {\tan{x}} = \tan{\dfrac{\pi}{4}} = 1 \)
Dıştaki logaritma fonksiyonu pozitif reel sayılarda tanımlı ve sürekli olduğu için içteki fonksiyonun limit değeri olan \( x = 1 \) noktasında süreklidir.
Buna göre bileşke fonksiyon limit kuralı ile limit işlemini logaritma içine alabiliriz.
\( \lim\limits_{x \to \frac{\pi}{4}} {\ln{\tan{x}}} = \ln{\lim\limits_{x \to \frac{\pi}{4}} {\tan{x}}} \)
\( = \ln{1} = 0 \)
(c) seçeneği:
\( \lim\limits_{x \to 3} {\abs{x^2 - 6x + 2}} \)
İçteki polinom fonksiyonu tüm reel sayılarda tanımlı ve sürekli olduğu için limit değerini doğrudan yerine koyma yöntemi ile bulabiliriz.
\( \lim\limits_{x \to 3} (x^2 - 6x + 2) = 3^2 - 6(3) + 2 = -7 \)
Dıştaki mutlak değer fonksiyonu tüm reel sayılarda tanımlı ve sürekli olduğu için içteki fonksiyonun limit değeri olan \( x = -7 \) noktasında süreklidir.
Buna göre bileşke fonksiyon limit kuralı ile limit işlemini mutlak değer içine alabiliriz.
\( \lim\limits_{x \to 3} {\abs{x^2 - 6x + 2}} = \abs{\lim\limits_{x \to 3} (x^2 - 6x + 2)} \)
\( = \abs{-7} = 7 \)
\( \lim\limits_{x \to 4} 81^{\frac{x - 3}{\sqrt[3]{x^2 + 10x + 8}}} \) limitinin değeri kaçtır?
Çözümü GösterÜstel fonksiyonlar tüm reel sayılarda tanımlı ve sürekli olduğu için limit işlemini üsse alabiliriz.
\( \lim\limits_{x \to 4} 81^{\frac{x - 3}{\sqrt[3]{x^2 + 10x + 8}}} = 81^{\lim\limits_{x \to 4} {\frac{x - 3}{\sqrt[3]{x^2 + 10x + 8}}}} \)
Aşağıda göstereceğimiz üzere, üsteki pay ve paydadaki ifadelerin limiti tanımlı ve paydadaki ifadenin limiti sıfırdan farklı olduğu için limit bölme kuralını kullanabiliriz.
\( = 81^{\frac{\lim\limits_{x \to 4} (x - 3)}{\lim\limits_{x \to 4} {\sqrt[3]{x^2 + 10x + 8}}}} \)
Küpkök fonksiyonu tüm reel sayılarda, dolayısıyla \( x = 4 \) noktasında tanımlı ve sürekli olduğu için bileşke fonksiyon limit kuralı ile limit işlemini kök içine alabiliriz.
\( = 81^{\frac{\lim\limits_{x \to 4} (x - 3)}{\sqrt[3]{\lim\limits_{x \to 4} (x^2 + 10x + 8)}}} \)
Polinom fonksiyonlarının bir noktadaki limit değeri o noktadaki fonksiyon değerine eşittir.
\( = 81^{\frac{4 - 3}{\sqrt[3]{4^2 + 10(4) + 8}}} \)
\( = 81^{\frac{1}{\sqrt[3]{64}}} \)
\( = 81^{\frac{1}{4}} \)
\( = \sqrt[4]{81} = 3 \) bulunur.
\( \lim\limits_{x \to 4} f(x) = 2 \)
\( \lim\limits_{x \to 4} g(x) = 1 \) olduğuna göre,
\( \lim\limits_{x \to 4} \dfrac{e^{f(x)} - 1}{\sin(\pi g(x) - \frac{3\pi}{4})} \) limitinin değeri kaçtır?
Çözümü GösterPaydaki ifadenin limitini bulalım.
\( \lim\limits_{x \to 4} (e^{f(x)} - 1) = \lim\limits_{x \to 4} {e^{f(x)}} - \lim\limits_{x \to 4} {1} \)
Üstel fonksiyonlar tüm reel sayılarda tanımlı ve sürekli olduğu için bileşke fonksiyon limit kuralını kullanabiliriz.
\( = e^{\lim\limits_{x \to 4} f(x)} - 1 = e^2 - 1 \)
Paydadaki ifadenin limitini bulalım.
\( \lim\limits_{x \to 4} (\sin(\pi g(x) - \frac{3\pi}{4})) \)
Sinüs fonksiyonu tüm reel sayılarda tanımlı ve sürekli olduğu için bileşke fonksiyon limit kuralını kullanabiliriz.
\( = \sin(\lim\limits_{x \to 4} (\pi g(x) - \frac{3\pi}{4})) \)
\( = \sin(\pi \lim\limits_{x \to 4} g(x) - \lim\limits_{x \to 4} \frac{3\pi}{4})) \)
\( = \sin(\pi(1) - \frac{3\pi}{4}) \)
\( = \sin{\dfrac{\pi}{4}} = \dfrac{\sqrt{2}}{2} \)
Pay ve paydadaki ifadelerin limiti tanımlı ve paydadaki ifadenin limiti sıfırdan farklı olduğu için limit bölme kuralını kullanabiliriz.
\( \lim\limits_{x \to 4} \dfrac{e^{f(x)} - 1}{\sin(\pi g(x) - \frac{3\pi}{4})} \)
\( = \dfrac{\lim\limits_{x \to 4} (e^{f(x)} - 1)}{\lim\limits_{x \to 4} (\sin(\pi g(x) - \frac{3\pi}{4}))} \)
\( = \dfrac{e^2 - 1}{\frac{\sqrt{2}}{2}} \)
\( = \sqrt{2}(e^2 - 1) \) bulunur.
\( g(x)= \begin{cases} x^2 - 2 & x \le 5 \\ 2x - 5 & x \gt 5 \end{cases} \)
Yukarıdaki \( f \) fonksiyonunun grafiği ve \( g \) parçalı fonksiyonunun tanımına göre,
\( \lim\limits_{x \to 2^-} (g \circ f)(x) \) limitinin değeri kaçtır?
Çözümü Göster\( (g \circ f)(x) = g(f(x)) \)
Önce içteki \( f \) fonksiyonunun \( x \to 2^- \) iken limitini bulalım.
Verilen grafiğe göre, \( x \to 2^- \) iken \( f(x) \to 5^+ \) olur.
\( \lim\limits_{x \to 2^-} {f(x)} = 5^+ \)
Şimdi dıştaki \( g \) fonksiyonunun \( x \to 5^+ \) iken limitini bulalım.
\( x \to 5^+ \) iken \( x \ge 5 \) olduğundan \( g \) parçalı fonksiyonunun ikinci tanımı kullanılır.
\( = 2(5) - 5 = 5 \)
\( \lim\limits_{x \to 2^-} (g \circ f)(x) = 5 \) bulunur.
\( \lim\limits_{x \to -3} \dfrac{\abs{x^3 + 27}}{\abs{x + 3}} \) limitinin sonucu kaçtır?
Çözümü GösterPaydaki ifadeyi çarpanlarına ayıralım.
\( \lim\limits_{x \to -3} \dfrac{\abs{x^3 + 27}}{\abs{x + 3}} = \lim\limits_{x \to -3} \dfrac{\abs{(x + 3)(x^2 - 3x + 9)}}{\abs{x + 3}} \)
İki ifadenin çarpımının mutlak değeri, mutlak değerlerinin çarpımına eşittir.
\( = \lim\limits_{x \to -3} \dfrac{\abs{x + 3}\abs{x^2 - 3x + 9}}{\abs{x + 3}} \)
\( = \lim\limits_{x \to -3} {\abs{x^2 - 3x + 9}} \)
Mutlak değer içindeki polinom fonksiyonunun tüm reel sayılarda limiti tanımlıdır, mutlak değer fonksiyonu da tüm reel sayılarda süreklidir.
Buna göre bileşke fonksiyon limit kuralı ile limit işlemini mutlak değer içine alabiliriz.
\( = \abs{\lim\limits_{x \to -3} (x^2 - 3x + 9)} \)
Polinom fonksiyonunun bir noktadaki limiti o noktadaki fonksiyon değerine eşittir.
\( = \abs{(-3)^2 - 3(-3) + 9} \)
\( = \abs{27} = 27 \) bulunur.
\( \lim\limits_{x \to 1} \dfrac{\ln(x^2 - x + e^3)}{3^{\log_4(2x - 1)}} \) limitinin değeri kaçtır?
Çözümü GösterAşağıda göstereceğimiz üzere, pay ve paydadaki ifadelerin limiti tanımlı ve paydadaki ifadenin limiti sıfırdan farklı olduğu için limit bölme kuralını kullanabiliriz.
\( \lim\limits_{x \to 1} {\dfrac{\ln(x^2 - x + e^3)}{3^{\log_4(2x - 1)}}} = \dfrac{\lim\limits_{x \to 1} {\ln(x^2 - x + e^3)}}{\lim\limits_{x \to 1} {3^{\log_4(2x - 1)}}} \)
Önce paydaki ifadenin limitini bulalım.
Payda logaritma içindeki ifadenin limitini bulalım.
\( \lim\limits_{x \to 1} (x^2 - x + e^3) \)
Polinom fonksiyonunun bir noktadaki limit değeri o noktadaki fonksiyon değerine eşittir.
\( = 1^2 - 1 + e^3 = e^3 \)
Logaritma fonksiyonu pozitif reel sayılarda, dolayısıyla \( x = e^3 \) noktasında sürekli olduğu için bileşke fonksiyon limit kuralı ile limit işlemini logaritma içine alabiliriz.
\( = \dfrac{\ln{\lim\limits_{x \to 1} (x^2 - x + e^3)}}{\lim\limits_{x \to 1} {3^{\log_4(2x - 1)}}} \)
\( = \dfrac{\ln{e^3}}{\lim\limits_{x \to 1} {3^{\log_4(2x - 1)}}} \)
\( = \dfrac{3}{\lim\limits_{x \to 1} {3^{\log_4(2x - 1)}}} \)
Şimdi paydadaki ifadenin limitini bulalım.
Üstel fonksiyon tüm reel sayılarda tanımlı ve sürekli olduğu için bileşke fonksiyon limit kuralı ile limit işlemini üsse alabiliriz.
\( = \dfrac{3}{3^{\lim\limits_{x \to 1} {\log_4(2x - 1)}}} \)
Logaritma içindeki ifadenin limitini bulalım.
\( \lim\limits_{x \to 1} (2x - 1) \)
Polinom fonksiyonunun bir noktadaki limit değeri o noktadaki fonksiyon değerine eşittir.
\( = 2(1) - 1 = 1 \)
Logaritma fonksiyonu pozitif reel sayılarda, dolayısıyla \( x = 1 \) noktasında sürekli olduğu için bileşke fonksiyon limit kuralı ile limit işlemini logaritma içine alabiliriz.
\( = \dfrac{3}{3^{\log_4{\lim\limits_{x \to 1} (2x - 1)}}} \)
\( = \dfrac{3}{3^{\log_4{1}}} \)
\( = \dfrac{3}{3^0} \)
\( = \dfrac{3}{1} = 3 \) bulunur.
\( k \in \mathbb{R} \) olmak üzere,
\( \lim\limits_{x \to 5} \dfrac{\log_4(x^2 + 5x + 14)}{\sqrt{x^2 - 8x + k + 12}} = 1 \)
olduğuna göre, \( k \) kaçtır?
Çözümü GösterPay ve paydadaki ifadelerin birbirine bölümünün limiti 1'e eşit olduğuna göre, bu iki ifadenin limiti tanımlıdır ve birbirine eşittir.
\( \lim\limits_{x \to 5} {\log_4(x^2 + 5x + 14)} = \lim\limits_{x \to 5} {\sqrt{x^2 - 8x + k + 12}} \)
Önce eşitliğin sol tarafındaki logaritma fonksiyonunun limitini bulalım.
Logaritma içindeki ifadenin limitini bulalım.
\( \lim\limits_{x \to 5} (x^2 + 5x + 14) \)
Polinom fonksiyonunun bir noktadaki limit değeri o noktadaki fonksiyon değerine eşittir.
\( = 5^2 + 5(5) + 14 = 64 \)
Logaritma fonksiyonu tüm pozitif reel sayılarda, dolayısıyla \( x = 64 \) noktasında sürekli olduğu için bileşke fonksiyon limit kuralı ile limit işlemini logaritma içine alabiliriz.
\( \lim\limits_{x \to 5} {\log_4(x^2 + 5x + 14)} = \log_4{\lim\limits_{x \to 5} (x^2 + 5x + 14)} \)
\( = \log_4{64} = 3 \)
Eşitliğin sağ tarafını 3'e eşitleyelim.
\( \lim\limits_{x \to 5} {\sqrt{x^2 - 8x + k + 12}} = 3 \)
Karekök fonksiyonu sıfır ve pozitif reel sayılarda tanımlı ve sürekli olduğu için bileşke fonksiyon limit kuralı ile limit işlemini kök içine alabiliriz.
\( \sqrt{\lim\limits_{x \to 5} (x^2 - 8x + k + 12)} = 3 \)
Polinom fonksiyonunun bir noktadaki limit değeri o noktadaki fonksiyon değerine eşittir.
\( \sqrt{5^2 - 8(5) + k + 12} = 3 \)
\( \sqrt{k - 3} = 3 \)
\( k - 3 = 9 \)
\( k = 12 \) bulunur.