Limitte Tanımsızlık ve Belirsizlik
Limit tanımına göre, bir fonksiyonun bir noktada limitinin tanımlı olabilmesi için bu noktada soldan ve sağdan limitler birer reel sayı olarak tanımlı ve birbirine eşit olmalıdır.
Bir fonksiyonun belirli bir noktadaki limiti tanımlı olabildiği gibi, aşağıda detaylandıracağımız üzere tanımsızlık ve belirsizlik durumları da oluşabilir. Bu bölümde karşılaşabileceğimiz farklı tanımsızlık durumlarını özetleyip, limit konusunun önemli bir alt başlığı olan belirsizlik durumlarına giriş yapacağız.
Tanımsızlık
Belirli bir noktada limit dört şekilde tanımsız olabilir.
Soldan ve Sağdan Limitler Tanımlı Ancak Farklı
Bu tanımsızlık durumunda soldan ve sağdan limitler reel sayı olarak tanımlıdır, ancak birbirinden farklıdır.
\( L_1, L_2 \in \mathbb{R} \) olmak üzere,
\( \lim_{x \to a^-} f(x) = L_1 \) ve
\( \lim_{x \to a^+} f(x) = L_2 \) olmak üzere,
\( L_1 \ne L_2 \) ise,
\( \lim_{x \to a} f(x) \) limiti tanımsızdır.
Bu tip tanımsızlık en çok parçalı fonksiyonlarda karşımıza çıkmaktadır. Parçalı fonksiyonların farklı aralıklarında farklı fonksiyon tanımları söz konusu olduğu için, kritik noktaların solunda ve sağında fonksiyonların yaklaştıkları değerler farklı olabilmektedir.
Ayrıca özel fonksiyonlar bölümünde gördüğümüz taban ve tavan fonksiyonlarında \( x \)'in tam sayı değerlerinde ve işaret fonksiyonunda \( x = 0 \) noktasında soldan ve sağdan limitler tanımlı, ancak farklıdır, dolayısıyla bu noktalarda limit tanımsızdır.
Soldan ve/veya Sağdan Limit Sonsuz
Sonsuz bir reel sayı değere karşılık gelmediği için, soldan ve sağdan limitlerin en az birinin pozitif ya da negatif sonsuz olduğu durumda bu noktadaki limit tanımsız olur. Soldan ve sağdan limitlerin ikisinin de pozitif ya da negatif sonsuz olması o noktada limiti tanımlı yapmaz, limitin tanımlı olması için bu iki limit birer reel sayı olarak tanımlı ve birbirine eşit olmalıdır.
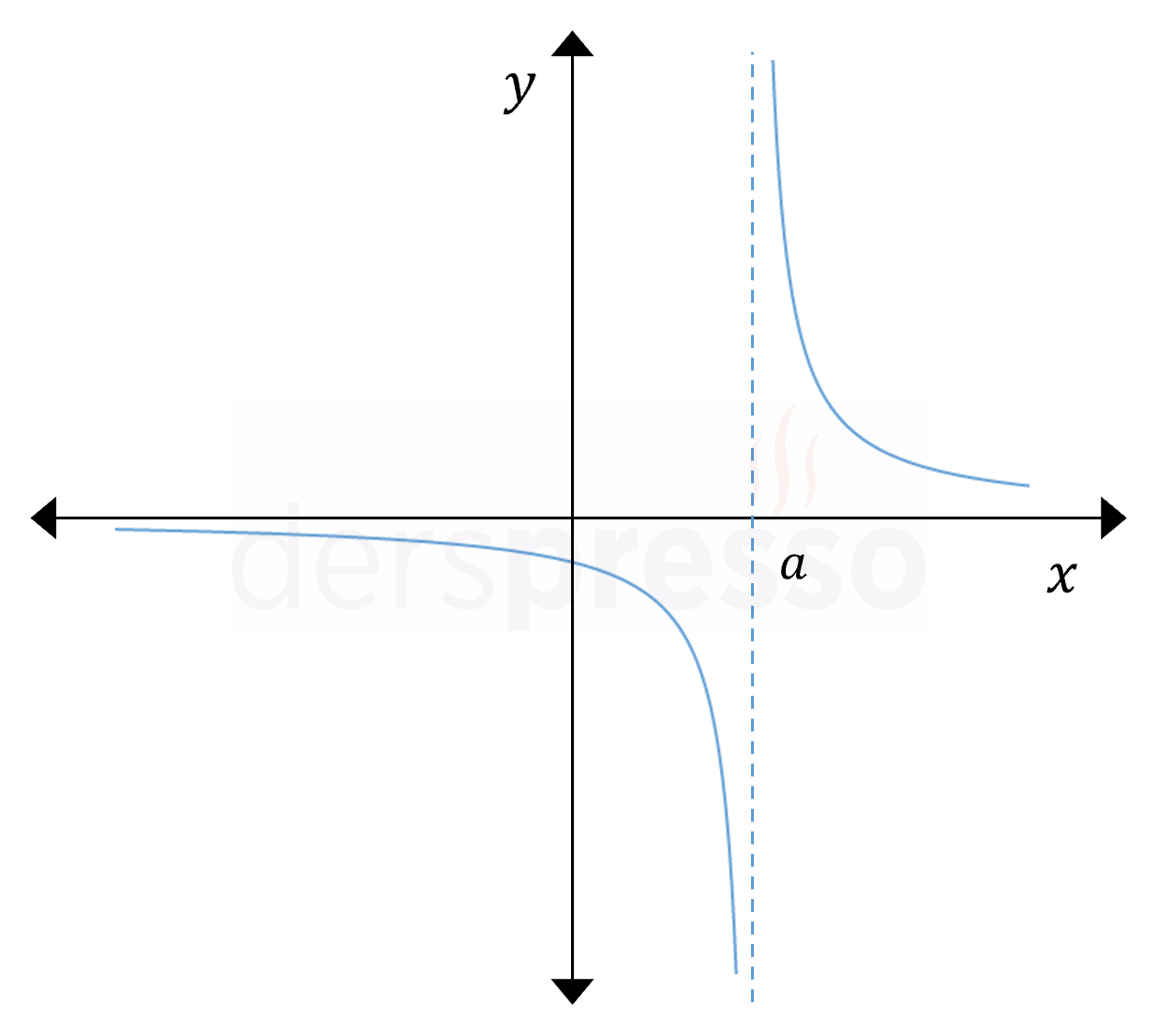
\( \lim_{x \to a^-} f(x) = \pm \infty \) ve/veya
\( \lim_{x \to a^+} f(x) = \pm \infty \) ise,
\( \lim_{x \to a} f(x) \) limiti tanımsızdır.
Bu tip tanımsızlığın karşımıza çıktığı durumlardan biri rasyonel fonksiyonlarda payın limitinin sıfırdan farklı bir reel sayı, paydanın limitinin de sıfır olduğu durumdur. Bu durum belirsizlik durumlarından farklı olup bu tanımsızlığı gidermek için yapabileceğimiz ek bir işlem yoktur.
\( c \in \mathbb{R}, \quad c \ne 0 \) olmak üzere,
\( \lim_{x \to a} \dfrac{f(x)}{g(x)} \) limitinde,
\( \lim_{x \to a} f(x) = c \) ve
\( \lim_{x \to a} g(x) = 0 \) ise,
\( \lim_{x \to a} \dfrac{f(x)}{g(x)} \) limiti tanımsızdır.
\( \lim_{x \to 2} \dfrac{x + 2}{x - 2} \) \( = \dfrac{2 + 2}{2 - 2} \) \( = \dfrac{4}{0} \Longrightarrow \) Tanımsız
İSPATI GÖSTER
İspat için çelişkiyle ispat yöntemini kullanalım.
\( c, L \in \mathbb{R}, \quad c \ne 0 \)
\( \lim_{x \to a} f(x) = c \)
\( \lim_{x \to a} g(x) = 0 \) olmak üzere,
\( \lim_{x \to a} \frac{f(x)}{g(x)} \) limitinin bir reel sayı olarak tanımlı olduğunu varsayalım.
\( \lim_{x \to a} \dfrac{f(x)}{g(x)} = L \)
\( f \) fonksiyonunu iki fonksiyonun çarpımı şeklinde yazalım.
\( \lim_{x \to a} f(x) = \lim_{x \to a} (\dfrac{f(x)}{g(x)} \cdot g(x)) = c \)
Limit çarpma kuralı gereği, bu limit ifadesini tanımlı olduğunu bildiğimiz/varsaydığımız iki limit ifadesinin çarpımı şeklinde yazabiliriz.
\( \lim_{x \to a} \dfrac{f(x)}{g(x)} \cdot \lim_{x \to a} g(x) = c \)
Yukarıdaki limit değerlerini bu eşitlikte yerine koyalım.
\( L \cdot 0 = c \)
\( L \) reel sayısı ile 0'ın çarpımı sıfırdan farklı \( c \) reel sayısı olamayacağı için bir çelişki elde etmiş olduk.
Buna göre en başta yaptığımız varsayım doğru olamaz, dolayısıyla aşağıdaki limit tanımsızdır.
\( \lim_{x \to a} \dfrac{f(x)}{g(x)} \Longrightarrow \) Tanımsız
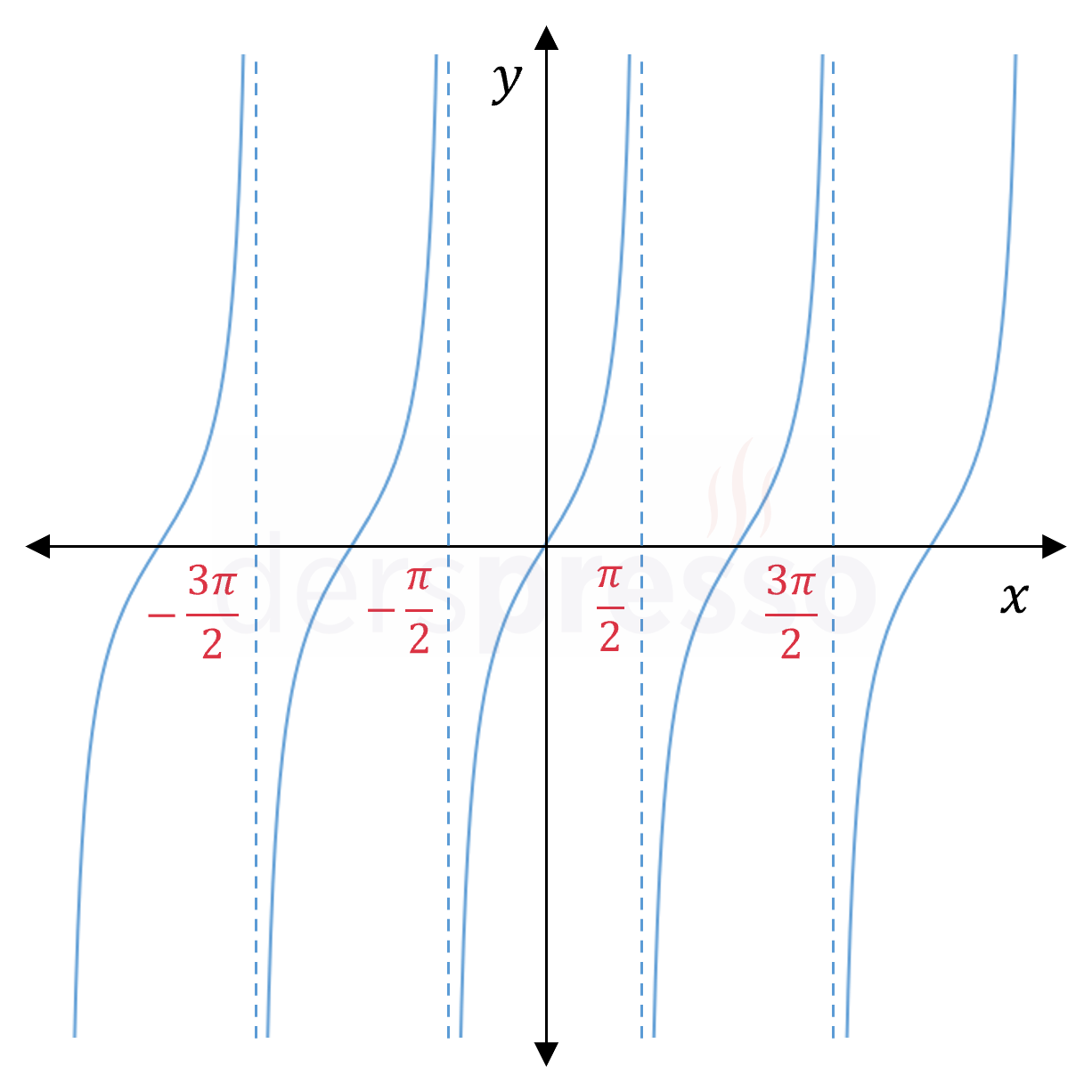
Bu tip tanımsızlıkla karşılaşabileceğimiz bir diğer durum tanjant ve kotanjant fonksiyonlarının tanımsız olduğu noktalardır.
\( x \) açısının esas ölçüsü \( \frac{\pi}{2} \) ya da \( \frac{3\pi}{2} \) ise,
\( \lim_{x \to \frac{\pi}{2}} \tan{x} \quad \) limiti tanımsızdır.
\( x \) açısının esas ölçüsü \( 0 \) ya da \( \pi \) ise,
\( \lim_{x \to 0} \cot{x} \quad \) limiti tanımsızdır.
Bu tanımsızlık durumunda fonksiyon grafiğinde dikey asimptot oluşur. Aşağıda tanjant fonksiyon grafiği üzerinde bu dikey asimptotlar gösterilmiştir (mavi kesikli çizgiler).
Belirli Bir Değere Yaklaşmayan Limit
Bazı fonksiyonlar limiti alınan noktaya yaklaşırken salınım (osilasyon) hareketi yapar ve fonksiyonun yaklaştığı değer kesin bir reel sayı olarak ifade edilemez. Bu tip fonksiyonların soldan ve sağdan limitleri tanımsızdır, dolayısıyla bu noktadaki limit de tanımsızdır.
Böyle bir fonksiyonun grafiği ve denklemi aşağıda verilmiştir.
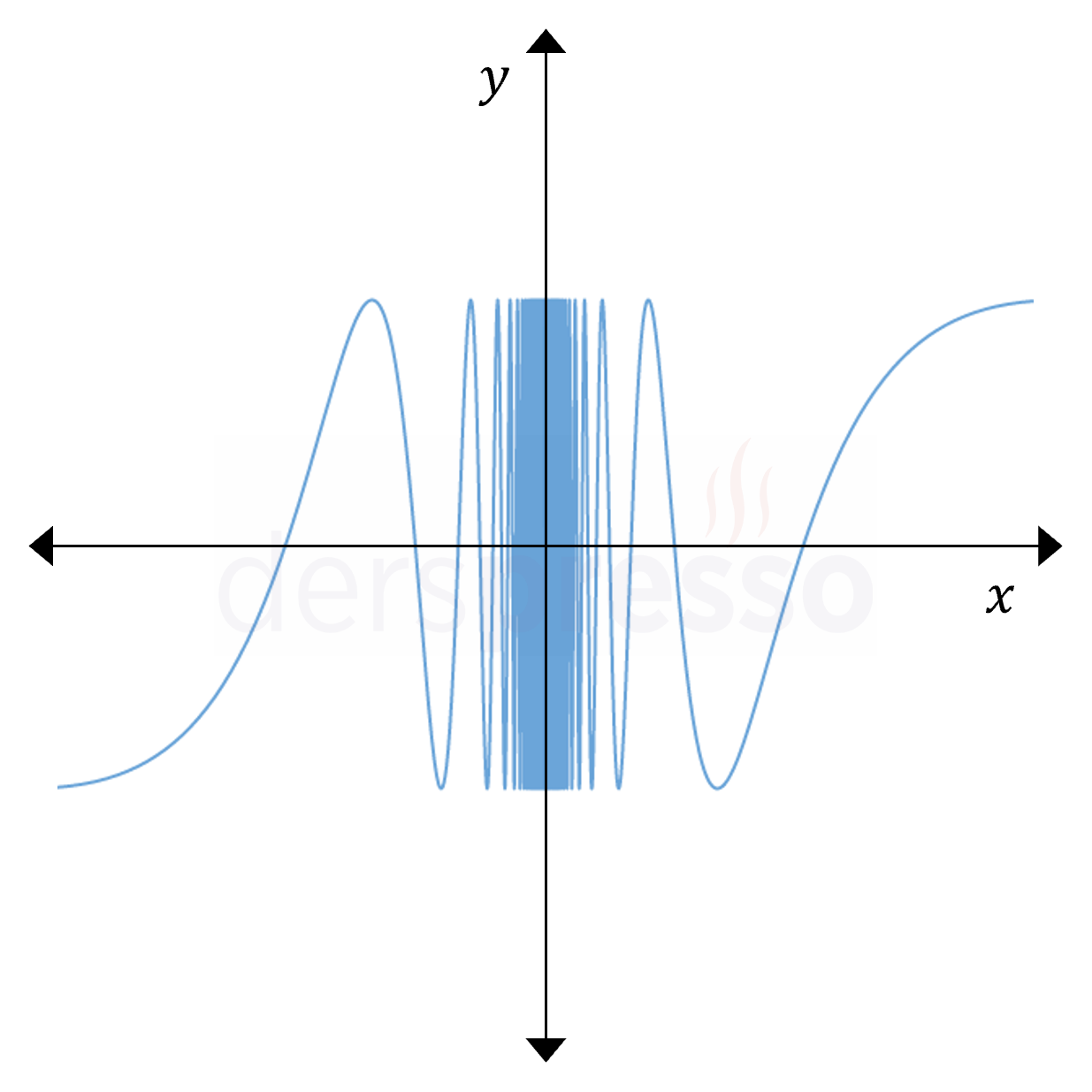
Aşağıdaki limitler tanımsızdır.
\( \lim_{x \to 0^-} \sin{\frac{1}{x}} \)
\( \lim_{x \to 0^+} \sin{\frac{1}{x}} \)
\( \lim_{x \to 0} \sin{\frac{1}{x}} \)
Uç Noktalarda Limit
Belirli bir \( [a, b) \) aralığında tanımlı bir fonksiyonun tanım aralığının uç noktalarında tek taraflı limitler sadece fonksiyonun tanımlı olduğu yönlerde, yani \( x = a \) noktasında sadece sağdan, \( x = b \) noktasında ise sadece soldan tanımlıdır. İki taraflı limit soldan ve sağdan limitlerin tanımlı ve eşit olmasını gerektirdiği için, uç noktalarda iki taraflı limit tanımlı değildir.
\( f: [a, b) \to \mathbb{R} \) olmak üzere,
\( \lim_{x \to a^+} f(x) = L_1 \)
\( \lim_{x \to a^-} f(x) \) ve \( \lim_{x \to a} f(x) \) tanımsızdır.
\( \lim_{x \to b^-} f(x) = L_2 \)
\( \lim_{x \to b^+} f(x) \) ve \( \lim_{x \to b} f(x) \) tanımsızdır.
Tanımsız Olmayan Durumlar
Rasyonel fonksiyonlarda payın limitinin sıfır, paydanın limitinin sıfırdan farklı bir reel sayı olduğu durumlarda limit tanımlıdır ve değeri sıfırdır. Aşağıdaki örnekte elde ettiğimiz \( \frac{0}{5} = 0 \) limit değeri tanımlı bir değerdir ve diğer tanımsızlık ve belirsizlik durumları ile karıştırılmamalıdır.
\( \lim_{x \to 3} \dfrac{x - 3}{x + 2} \) \( = \dfrac{3 - 3}{3 + 2} \) \( = \dfrac{0}{5} = 0 \)
Belirsizlik
Matematiksel işlemlerde sonucu tanımlı olan ama değerini belirleyemediğimiz ifadeler belirsiz olarak adlandırılırlar.
İki fonksiyondan oluşan bir ifadede bu fonksiyonların limitleri ayrı ayrı \( 0 \), \( 1 \) ya da \( \pm\infty \) olarak bulunuyorsa ve tüm ifadenin limiti için aşağıdaki 7 sonuçtan biri elde ediliyorsa bir belirsizlik durumu söz konusudur.
\( \dfrac{0}{0}, \quad \dfrac{\infty}{\infty}, \quad \) \( \infty - \infty, \quad 0 \cdot \infty, \quad \) \( \infty^0, \quad 0^0, \quad 1^\infty \)
Belirsizlik durumları tanımsızlık gibi fonksiyonun o noktada limitinin olmadığı anlamına gelmeyebilir. Bir belirsizlik durumunu ortadan kaldırmak ve fonksiyonun o noktada bir limiti varsa bu limit değerini bulmak için kullanabileceğimiz yöntemleri önümüzdeki bölümlerde inceleyeceğiz.
\( f(x) = 5x^2 - 7x + k \)
\( g(x) = 8x^2 - 9x + 2 \) fonksiyonları verilmiştir.
\( \lim_{x \to 2} \dfrac{f(x)}{g(x)} = 2 \) olduğuna göre, \( k \) kaçtır?
Çözümü Göster\( f(2) = 5(2)^2 - 7(2) + k \)
\( = 6 + k \)
\( g(2) = 8(2)^2 - 9(2) + 2 \)
\( = 32 - 18 + 2 = 16 \)
Limiti alınan ifadenin paydası sıfırdan farklı ve limit değeri tanımlı olduğu için bir belirsizlik söz konusu değildir.
\( \dfrac{f(2)}{g(2)} = 2 \)
\( \dfrac{6 + k}{16} = 2 \)
\( k = 26 \) bulunur.
Aşağıdaki limitlerin sonucunu bulunuz.
(a) \( \lim\limits_{x \to 8} \dfrac{x^2 - 64}{x - 7} \)
(b) \( \lim\limits_{x \to 8} \dfrac{x^2 - 63}{x - 8} \)
(c) \( \lim\limits_{x \to 8} \dfrac{x^2 - 64}{x - 8} \)
Çözümü Göster(a) seçeneği:
\( \lim\limits_{x \to 8} \dfrac{x^2 - 64}{x - 7} \)
\( x = 8 \) değeri limit içindeki rasyonel fonksiyonun paydasını sıfır yapmadığı için fonksiyon bu noktada tanımlı ve süreklidir, dolayısıyla doğrudan yerine koyma yöntemi ile limiti hesaplayabiliriz.
\( \lim\limits_{x \to 8} \dfrac{x^2 - 64}{x - 7} = \dfrac{8^2 - 64}{8 - 7} \)
\( = \dfrac{0}{1} = 0 \)
(b) seçeneği:
\( \lim\limits_{x \to 8} \dfrac{x^2 - 63}{x - 8} \) limitinde,
\( \lim\limits_{x \to 8} (x^2 - 63) = 8^2 - 63 = 1 \)
ve
\( \lim\limits_{x \to 8} (x - 8) = 8 - 8 = 0 \)
olduğu için \( \frac{1}{0} \) ifadesi bir belirsizlik değil tanımsızlık ifade eder.
Bu noktadaki soldan limiti hesaplayalım.
\( \lim\limits_{x \to 8^-} \dfrac{x^2 - 63}{x - 8} \)
\( x \to 8^- \) iken \( x - 8 \to 0^- \) olur.
\( = \dfrac{1}{0^-} = -\infty \)
Bu noktadaki sağdan limiti hesaplayalım.
\( \lim\limits_{x \to 8^+} \dfrac{x^2 - 63}{x - 8} \)
\( x \to 8^+ \) iken \( x - 8 \to 0^+ \) olur.
\( = \dfrac{1}{0^+} = +\infty \)
İfadenin limiti soldan ve sağdan aynı reel sayı değere yaklaşmadığı için tanımlı değildir.
(c) seçeneği:
\( \lim\limits_{x \to 8} \dfrac{x^2 - 64}{x - 8} \) limitinde,
\( \lim\limits_{x \to 8} (x^2 - 64) = 8^2 - 64 = 0 \)
ve
\( \lim\limits_{x \to 8} (x - 8) = 8 - 8 = 0 \)
olduğu için \( \frac{0}{0} \) belirsizliği vardır.
Belirsizliği gidermek için çarpanlara ayırma ve sadeleştirme yöntemini kullanalım (belirsizlik giderme yöntemlerini önümüzdeki bölümlerde inceleyeceğiz).
\( \lim\limits_{x \to 8} \dfrac{x^2 - 64}{x - 8} = \lim\limits_{x \to 8} \dfrac{(x - 8)(x + 8)}{x - 8} \)
\( = \lim\limits_{x \to 8} (x + 8) \)
Doğrusal fonksiyonlar tüm reel sayılarda sürekli olduğundan ifadenin limitini doğrudan yerine koyma yöntemiyle hesaplayabiliriz.
\( = 8 + 8 = 16 \)
\( \lim\limits_{x \to 16} \dfrac{4 + \sqrt{x}}{16 - x} \) limitinin sonucunu bulunuz.
Çözümü Göster\( \lim\limits_{x \to 16} \dfrac{4 + \sqrt{x}}{16 - x} \) limitinde,
\( \lim\limits_{x \to 16} (4 + \sqrt{x}) = 4 + \sqrt{16} = 8 \)
ve
\( \lim\limits_{x \to 16} (16 - x) = 16 - 16 = 0 \)
olduğu için \( \frac{8}{0} \) ifadesi bir belirsizlik değil tanımsızlık ifade eder.
Bu noktadaki soldan limiti hesaplayalım.
\( \lim\limits_{x \to 16^-} \dfrac{4 + \sqrt{x}}{16 - x} \)
\( x \to 16^- \) iken \( 16 - x \to 0^+ \) olur.
\( = \dfrac{8}{0^+} = +\infty \)
Bu noktadaki sağdan limiti hesaplayalım.
\( \lim\limits_{x \to 16^+} \dfrac{4 + \sqrt{x}}{16 - x} \)
\( x \to 16^+ \) iken \( 16 - x \to 0^- \) olur.
\( = \dfrac{8}{0^-} = -\infty \)
İfadenin limiti soldan ve sağdan aynı reel sayı değere yaklaşmadığı için tanımlı değildir.