Parçalı Fonksiyon
Tanım kümesinin farklı aralıklarında farklı tanımlara sahip olan fonksiyonlara parçalı fonksiyon denir. Bir parçalı fonksiyonun farklı tanıma sahip olduğu alt aralıklara fonksiyonun dalları ya da parçaları denir.
Aşağıda üç parçadan oluşan örnek bir parçalı \( f \) fonksiyonunun grafiği verilmiştir. Bu grafiğe göre fonksiyonun tanımı mavi ile işaretli \( (-\infty, -3) \) aralığında \( f(x) = 3 \), kırmızı ile işaretli \( [-3, 2) \) aralığında \( f(x) = -x \), yeşil ile işaretli \( [2, \infty) \) aralığında ise \( f(x) = x \) olmaktadır.
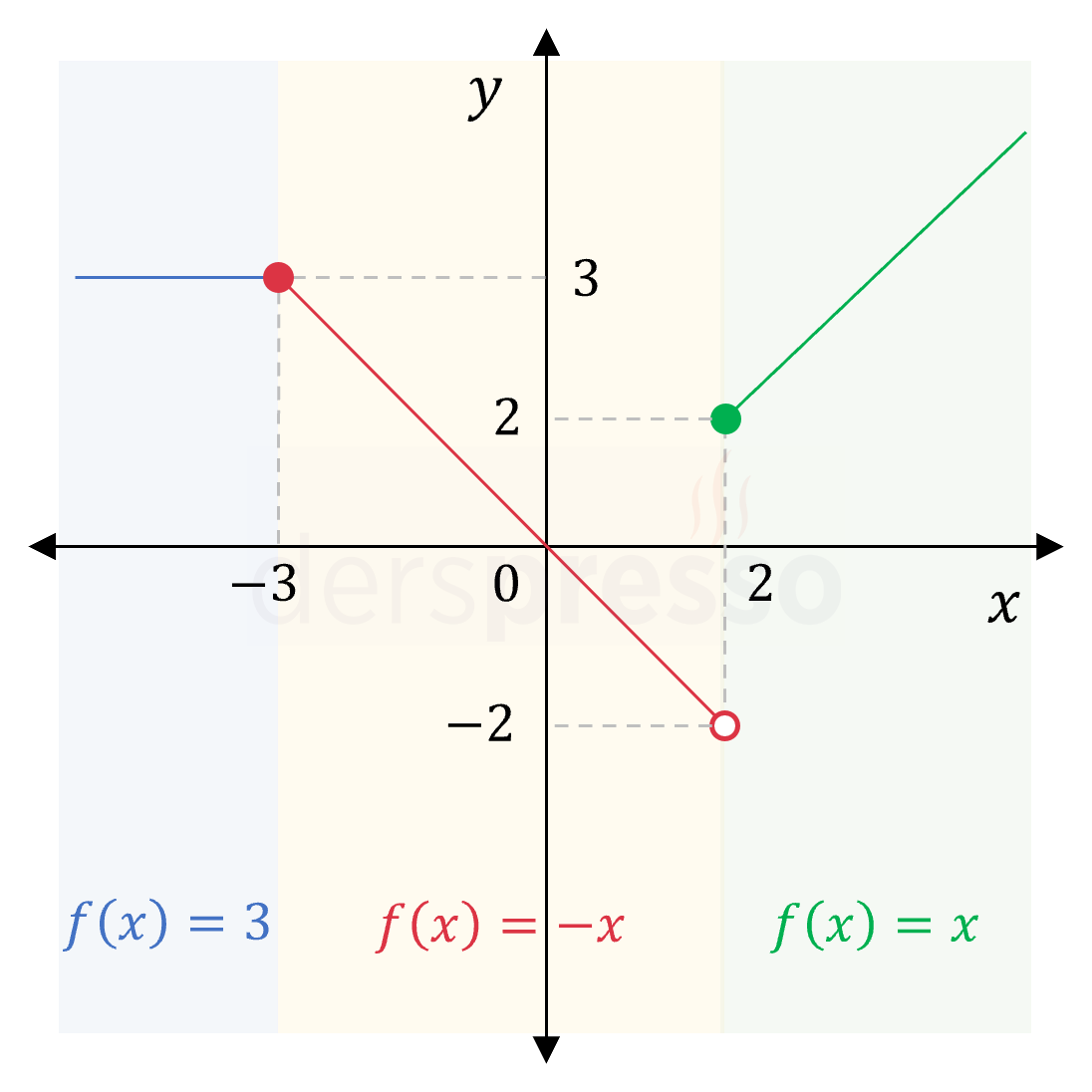
Yukarıda grafiği verilen \( f \) fonksiyonunun tanımı aşağıdaki gibidir. Bu gösterimde bir parantez açılarak fonksiyonun parçaları her satırda o parçaya ait fonksiyon tanımı ve parçanın tanımlı olduğu aralık olacak şekilde alt alta listelenir.
\( f(x) = \begin{cases} 3 & x \lt -3 \\ -x & -3 \le x \lt 2 \\ x & 2 \le x \end{cases} \)
Bir parçalı fonksiyonun belirli bir \( x \) değeri için değerini bulmak için, öncelikle bu \( x \) değerinin fonksiyonun hangi parçasına karşılık geldiği belirlenir.
\( x = -4 \) birinci aralıkta olduğu için \( f(x) = 3 \) tanımı geçerlidir.
\( f(-4) = 3 \)
\( x = -1 \) ikinci aralıkta olduğu için \( f(x) = -x \) tanımı geçerlidir.
\( f(-1) = -(-1) = 1 \)
\( x = 5 \) üçüncü aralıkta olduğu için \( f(x) = x \) tanımı geçerlidir.
\( f(5) = 5 \)
Bir parçalı fonksiyonun tanımının değiştiği noktalara fonksiyonun sınır noktaları denir. Tanımladığımız parçalı \( f \) fonksiyonu için bu sınır noktaları \( x = -3 \) ve \( x = 2 \) noktalarıdır. İleriki bölümlerde göreceğimiz üzere, parçalı fonksiyonlar limit, süreklilik ve türev gibi açılardan incelenirken sınır noktalarının özel olarak ele alınması gerekmektedir.
Bir parçalı fonksiyonun parçaları belirli bir aralık için tanımlanabileceği gibi tek bir değer için de tanımlanabilir. Aşağıdaki parçalı fonksiyonun \( x = 2 \) noktasındaki \( g(x) = 4 \) tanımı buna örnek olarak verilebilir.
\( g(x) = \begin{cases} -2x - 3 & x \lt 2 \\ 4 & x = 2 \\ 3x + 2 & 2 \lt x \end{cases} \)
Bir parçalı fonksiyonun grafiği çizilirken her parça sadece tanımlı olduğu aralıkta çizilmeli, farklı parçaların grafikleri belirli \( x \) değerlerinde ya da aralıklarında çakışmamalıdır.
Parçalı fonksiyonların tanım ve görüntü kümeleri ile ilgili üç önemli nokta aşağıdaki gibidir.
- Bir parçalı fonksiyonun parçalarının tanım aralıkları birbirinden ayrık olmalı, yani kesişim kümeleri boş küme olmalıdır.
- Bir parçalı fonksiyonun tanım kümesi, fonksiyonun parçalarının tanım aralıklarının birleşim kümesine eşittir.
- Bir parçalı fonksiyonun görüntü kümesi, fonksiyonun parçalarının görüntülerinin birleşim kümesine eşittir.
Mutlak değer içindeki ifadenin işaretine göre iki farklı tanıma sahip olan mutlak değer fonksiyonu bir parçalı fonksiyon olarak aşağıdaki şekilde tanımlanabilir.
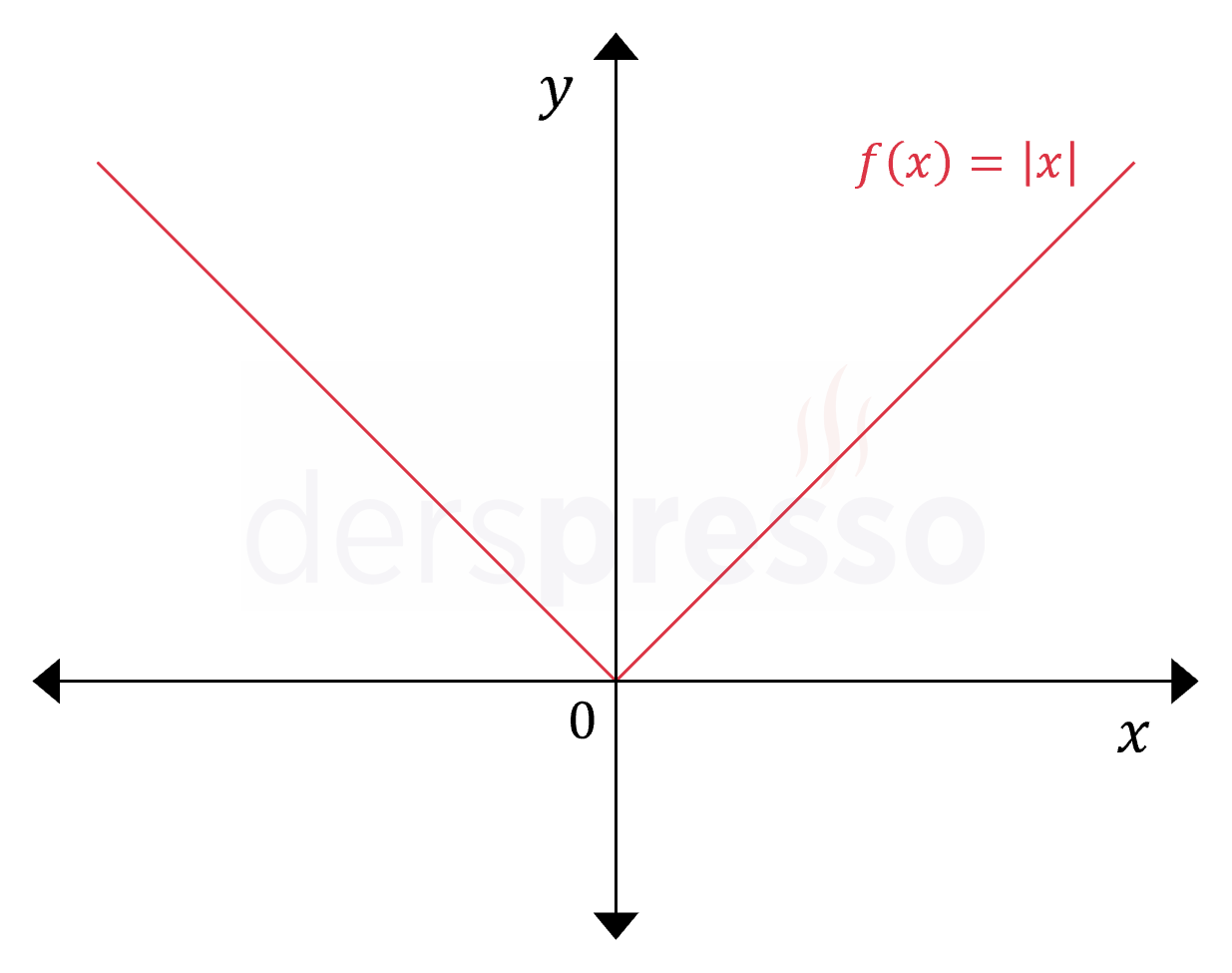
\( f(x) = \abs{x} = \begin{cases} x & x \ge 0 \\ -x & x \lt 0 \end{cases} \)
\( f(4) = 4 = \abs{4} \)
\( f(-4) = -(-4) = 4 = \abs{-4} \)
Önümüzdeki bölümlerde göreceğimiz özel tanımlı bir fonksiyon olan işaret fonksiyonunun parçalı fonksiyon tanımı ve grafiği de aşağıdaki gibidir.
\( g(x) = \sgn(x) = \begin{cases} 1 & x \gt 0 \\ 0 & x = 0 \\ -1 & x \lt 0 \end{cases} \)
\( g(4) = 1 \)
\( g(-4) = -1 \)
\( f(x)= \begin{cases} x^2 + 4 & x \lt -1 \\ 2x + 5 & x \ge -1 \end{cases} \)
olduğuna göre, \( \dfrac{f(-2)}{f(2)} \) kaçtır?
Çözümü Göster\( x = -2 \) parçalı fonksiyonun birinci aralığında tanımlıdır ve \( f(x) = x^2 + 4 \) tanımına karşılık gelir.
\( f(-2) = (-2)^2 + 4 = 8 \)
\( x = 2 \) parçalı fonksiyonun ikinci aralığında tanımlıdır ve \( f(x) = 2x + 5 \) tanımına karşılık gelir.
\( f(2) = 2(2) + 5 = 9 \)
\( \dfrac{f(-2)}{f(2)} = \dfrac{8}{9} \) olarak bulunur.
\( f: \mathbb{Z} \to \mathbb{Z} \) olmak üzere,
\( f(x)= \begin{cases} x^2 - 2 & x \bmod{3} = 0 \\ x + 2 & x \bmod{3} = 1 \\ x^2 + 2 & x \bmod{3} = 2 \end{cases} \)
olduğuna göre, \( f(4) + f(5) + f(6) \) ifadesinin değeri kaçtır?
Çözümü GösterParçalı fonksiyon tanımına göre, \( x \) 3 ile tam bölünüyorsa birinci tanım, 1 kalanını veriyorsa ikinci tanım, 2 kalanını veriyorsa üçüncü tanım geçerlidir.
4 3'e bölündüğünde 1 kalanını verdiği için ikinci tanım geçerlidir.
\( f(4) = 4 + 2 = 6 \)
5 3'e bölündüğünde 2 kalanını verdiği için üçüncü tanım geçerlidir.
\( f(5) = 5^2 + 2 = 27 \)
6 3'e tam bölündüğü için birinci tanım geçerlidir.
\( f(6) = 6^2 - 2 = 34 \)
Buna göre, \( f(4) + f(5) + f(6) = 6 + 27 + 34 = 67 \) bulunur.
\( f \) fonksiyonu \( x \) sayısı 4'ten büyük olduğunda \( x + f(x - 2) \), 4 ya da 4'ten küçük olduğunda \( 3x \) şeklinde tanımlanıyor.
Buna göre \( f(11) \) kaçtır?
Çözümü GösterFonksiyonu parçalı fonksiyon şeklinde yazalım.
\( f(x) = \begin{cases} 3x & x \le 4 \\ x + f(x - 2) & x \gt 4 \end{cases} \)
\( f(11) = 11 + f(9) \)
\( f(9) = 9 + f(7) \)
\( f(7) = 7 + f(5) \)
\( f(5) = 5 + f(3) \)
\( f(3) = 3 \cdot 3 = 9 \)
Yukarıdaki ifadeleri taraf tarafa topladığımızda \( f(11) \) dışındaki fonksiyon terimleri birbirini götürür.
\( f(11) = 11 + 9 + 7 + 5 + 9 = 41 \) bulunur.
\( f(x) = \begin{cases} x^2 - x + 1 & x \lt 3 \\ x^2 + x + 1 & x \ge 3 \end{cases} \)
\( g(x) = \begin{cases} 3x & x \le 1 \\ 8 - 7x & x \gt 1 \end{cases} \)
olduğuna göre, \( (f + g)(x) \) fonksiyonunun tanımını bulunuz.
Çözümü Gösterİki ya da daha fazla fonksiyon arasında yapılan işlemin sonucunun tanım kümesi, işlemin terimi olan fonksiyonların tanım kümelerinin kesişim kümesine eşittir.
Daha rahat işlem yapmak için parçalı fonksiyonları tanım aralıkları aynı olacak şekilde düzenleyelim.
\( f(x) = \begin{cases} x^2 - x + 1 & x \le 1 \\ x^2 - x + 1 & 1 \lt x \lt 3 \\ x^2 + x + 1 & x \ge 3 \end{cases} \)
\( g(x) = \begin{cases} 3x & x \le 1 \\ 8 - 7x & 1 \lt x \lt 3 \\ 8 - 7x & x \ge 3 \end{cases} \)
Fonksiyonların ortak tanım aralıkları arasında toplama işlemi yaparak \( f + g \) fonksiyonunu bulalım.
\( (f + g)(x) = \begin{cases} x^2 + 2x + 1 & x \le 1 \\ x^2 - 8x + 9 & 1 \lt x \lt 3 \\ x^2 - 6x + 9 & x \ge 3 \end{cases} \)
\( = \begin{cases} (x + 1)^2 & x \le 1 \\ x^2 - 8x + 9 & 1 \lt x \lt 3 \\ (x - 3)^2 & x \ge 3 \end{cases} \)
\( f(x) = \begin{cases} 2x & x \le 1 \\ x^{2} & x \gt 1 \end{cases} \)
\( g(x) = \begin{cases} 3x - 2 & x \lt 0 \\ x - 1 & x \ge 0 \end{cases} \)
olduğuna göre, \( (f \cdot g)(x) \) fonksiyonunu bulunuz.
Çözümü GösterBirinci fonksiyonun tanımının değiştiği sınır noktası \( x = 1 \), ikinci fonksiyonun tanımının değiştiği sınır noktası \( x = 0 \) olur.
İki fonksiyonun bu sınır noktaları birlikte değerlendirildiğinde aşağıdaki tablodaki gibi üç aralık oluşur.
Buna göre \( (f \cdot g)(x) \) fonksiyonunu aşağıdaki şekilde yazabiliriz.
\( (f \cdot g)(x) = \begin{cases} 6x^{2} - 4x & x \lt 0 \\ 2x^{2} - 2x & 0 \le x \le 1 \\ x^{3} - x^{2} & x \gt 1 \end{cases} \)
\( f(x)= \begin{cases} 5x - 2 & x \lt 1 \\ 2x + 1 & x \ge 1 \end{cases} \)
\( g(x)= \begin{cases} 2x + 4 & x \le 3 \\ 6x - 1 & x \gt 3 \end{cases} \)
olduğuna göre, \( (g \circ f)(1) \) kaçtır?
Çözümü Göster\( (g \circ f)(1) = g(f(1)) \)
\( x = 1 \) değeri \( f \) parçalı fonksiyonunun ikinci aralığında tanımlıdır ve \( f(x) = 2x + 1 \) tanımına karşılık gelir.
\( f(1) = 2(1) + 1 = 3 \)
\( (g \circ f)(1) = g(f(1)) = g(3) \)
\( x = 3 \) değeri \( g \) parçalı fonksiyonun birinci aralığında tanımlıdır ve \( g(x) = 2x + 4 \) tanımına karşılık gelir.
\( g(3) = 2(3) + 4 = 10 \)
\( (g \circ f)(1) = g(3) = 10 \) bulunur.
\( f(x) = \begin{cases} 3x - 4 & x \ge 0 \\ x + 1 & x \lt 0 \end{cases} \)
olduğuna göre, \( f(x + 2) \) fonksiyonunun tanımı nedir?
Çözümü Göster\( x \) yerine \( x + 2 \) yazalım.
\( f(x + 2) = \begin{cases} 3(x + 2) - 4 & x + 2 \ge 0 \\ (x + 2) + 1 & x + 2 \lt 0 \end{cases} \)
\( f(x + 2) = \begin{cases} 3x + 2 & x \ge -2 \\ x + 3 & x \lt -2 \end{cases} \)
\( f(x) = \begin{cases} 1 & x = 0 \\ \dfrac{f^2(\frac{x}{2})}{5} & x \text{ (sıfır hariç) çift ise,} \\ kf(x - 1) & x \text{ tek ise} \end{cases} \)
\( f(3) = 25 \) olduğuna göre, \( k \) sayısı kaçtır?
Çözümü GösterVerilen parçalı fonksiyon \( x \) değerinin sıfır, tek ya da çift olmasına göre üç farklı tanıma sahiptir.
Öncelikle \( f(0) \) değerini kullanarak \( f(1) \) değerini bulalım.
\( f(1) = k \cdot f(0) = k \)
Şimdi \( f(1) \) değerini kullanarak \( f(2) \) değerini bulalım.
\( f(2) = \dfrac{f^2(\frac{2}{2})}{5} = \dfrac{f^2(1)}{5} \)
\( = \dfrac{k^2}{5} \)
Şimdi de \( f(2) \) değerini kullanarak \( f(3) \) değerini bulalım.
\( f(3) = k \cdot f(2) = k \cdot \dfrac{k^2}{5} \)
\( = \dfrac{k^3}{5} \)
Bulduğumuz değeri \( f(3) = 25 \) değerine eşitleyelim.
\( \dfrac{k^3}{5} = 25 \)
\( k^3 = 125 \)
\( k = 5 \) bulunur.
\( f(n) = \begin{cases} 2n & n \text{ tek ise} \\ n + 5 & n \text{ çift ise} \end{cases} \)
\( f(f(f(k))) = 30 \) olduğuna göre, \( k \) tam sayısı kaça eşittir?
Çözümü Göster\( k \) değerini bulmak için \( f(f(f(k))) = 30 \) ifadesini dıştan içe doğru inceleyelim.
\( f(f(k)) = a, \quad f(a) = 30 \)
\( f(a) = 30 \) yapan \( a \) değerini bulmak için iki fonksiyon tanımını ayrı ayrı 30'a eşitleyelim.
\( n \) tek ise:
\( 2a = 30 \Rightarrow a = 15 \)
\( n \) çift ise:
\( n + 5 = 30 \Rightarrow a = 25 \)
\( a = 25 \) çift sayı olmadığı için \( a = 15 \) bulunur.
\( f(f(k)) = a = 15 \)
\( f(k) = b, \quad f(b) = 15 \)
\( f(b) = 15 \) yapan \( b \) değerini bulmak için iki fonksiyon tanımını ayrı ayrı 15'e eşitleyelim.
\( n \) tek ise:
\( 2b = 15 \Rightarrow b = 7,5 \)
\( n \) çift ise:
\( b + 5 = 15 \Rightarrow b = 10 \)
\( b = 7,5 \) tek sayı olmadığı için \( b = 10 \) bulunur.
\( f(k) = b = 10 \)
\( f(k) = 10 \) yapan \( k \) değerini bulmak için iki fonksiyon tanımını ayrı ayrı 10'a eşitleyelim.
\( n \) tek ise:
\( 2k = 10 \Rightarrow k = 5 \)
\( n \) çift ise:
\( k + 5 = 10 \Rightarrow k = 5 \)
Buna göre \( k = 5 \) bulunur.