Doğrusal Fonksiyon
Birinci dereceden \( f(x) = ax + b \) formundaki fonksiyonlara doğrusal fonksiyon denir.
\( a, b \in \mathbb{R}, \quad a \ne 0 \) olmak üzere,
\( f: A \to B \)
\( f(x) = ax + b \) ise,
\( f \) bir doğrusal fonksiyondur.
Bazı kaynaklarda \( a = 0 \) olması durumunda oluşan sabit fonksiyonlar da doğrusal kabul edilir. Biz burada doğrusal fonksiyonları derecesi bir olan polinom fonksiyonları olarak tanımlıyoruz.
Doğrusal fonksiyonun en geniş tanım ve görüntü kümesi tüm reel sayılardır.
| Fonksiyon | Tanım Kümesi | Görüntü Kümesi |
|---|---|---|
| Doğrusal fonksiyon (\( a \ne 0 \)) | \( \mathbb{R} \) | \( \mathbb{R} \) |
Tüm doğrusal fonksiyonların grafiği (yukarıda yaptığımız \( a \ne 0 \) tanımına göre) eğimi sıfırdan farklı birer doğrudur. Analitik geometride gördüğümüz gibi \( a \) katsayısı doğrunun eğimini verir.

\( f(x) = x \) doğrusal fonksiyonuna birim fonksiyon da denir.
Doğrusal fonksiyonlar birebir ve örtendir.
\( f(x) = (a - 3)x^3 + (b + 2)x^2 + ax + 4 \) bir doğrusal fonksiyon olduğuna göre, \( ab \) çarpımı kaçtır?
Çözümü Göster\( f(x) \) fonksiyonu doğrusal olduğu için sadece birinci dereceden \( x \)'li terim ve sabit terim içerebilir.
Bu durumda \( x^3 \) ve \( x^2 \)'li terimlerin katsayıları sıfır olmalıdır.
\( a - 3 = 0 \Longrightarrow a = 3 \)
\( b + 2 = 0 \Longrightarrow b = -2 \)
\( ab = 3(-2) = -6 \) bulunur.
Aşağıdaki öncüllerden hangileri doğrudur?
I. Her doğrusal fonksiyon sabit fonksiyondur.
II. Her sabit fonksiyon birim fonksiyondur.
III. Her birim fonksiyon doğrusal fonksiyondur.
IV. Her doğrusal fonksiyon birim fonksiyondur.
Çözümü GösterDoğrusal fonksiyonlar \( f(x) = ax + b \) formundadır.
Birim fonksiyon \( f(x) = x \) formundadır.
Sabit fonksiyonlar \( f(x) = c \) formundadır.
I. öncül:
Doğrusal fonksiyonlar sadece \( a = 0 \) olduğunda sabit fonksiyon olur.
I. öncül yanlıştır.
II. öncül:
Birim fonksiyonda bir \( x \) değerinin görüntüsü kendisidir, sabit fonksiyonda ise sabit bir değerdir.
II. öncül yanlıştır.
III. öncül:
Birim fonksiyonu \( f(x) = 1x + 0 \) şeklinde yazabiliriz, dolayısıyla birim fonksiyon aynı zamanda doğrusaldır.
III. öncül doğrudur.
IV. öncül:
Doğrusal fonksiyonlar sadece \( a = 1 \) ve \( b = 0 \) olduğunda birim fonksiyon olur.
IV. öncül yanlıştır.
Buna göre sadece III. öncül doğrudur.
\( f \) doğrusal bir fonksiyon olmak üzere,
\( f(-3) = -15 \) ve \( f(2) = 5 \) olduğuna göre, \( f(6) \) kaçtır?
Çözümü GösterDenklemi iki yöntemle çözebiliriz.
1. yöntem:
\( f(x) = ax + b \) olarak kabul edelim.
\( f(-3) = -3a + b = -15 \)
\( f(2) = 2a + b = 5 \)
İkinci denklemden birinci denklemi taraf tarafa çıkaralım.
\( 2a - (-3a) = 5 - (-15) \)
\( a = 4 \)
\( b = -3 \)
\( f \) fonksiyonunun tanımı aşağıdaki gibi olur.
\( f(x) = 4x - 3 \)
\( f(6) = 4(6) - 3 = 21 \)
2. yöntem:
Doğrusal bir fonksiyonda ortalama değişim oranı (eğim) tüm doğru boyunca sabittir.
\( x \) değeri \( 2 - (-3) = 5 \) birim arttığında \( f(x) \) değeri \( 5 - (-15) = 20 \) birim artmıştır.
Buna göre \( x \) değeri 1 birim arttığında \( f(x) \) değeri 4 birim artmaktadır. Bu da doğrunun eğiminin 4 olduğu anlamına gelir.
Fonksiyon \( x = 2 \)'den \( x = 6 \)'ya 4 birim arttığında \( f(x) \) değeri \( 4 \cdot 4 = 16 \) birim artacaktır.
\( f(6) = f(2) + 16 = 21 \)
\( f \) bir doğrusal fonksiyondur.
\( f(x) + f(x + 2) = 6x + 14 \) olduğuna göre, \( f(2) \) kaçtır?
Çözümü Göster\( f \) fonksiyonunun denklemini aşağıdaki şekilde yazalım.
\( f(x) = ax + b \)
\( f(x) + f(x + 2) = 6x + 14 \)
\( ax + b + a(x + 2) + b = 6x + 14 \)
\( 2ax + 2a + 2b = 6x + 14 \)
\( ax + a + b = 3x + 7 \)
İki polinomun eşitliğinde dereceleri aynı terimlerin katsayıları birbirine eşittir.
\( a = 3 \)
\( a + b = 7 \Longrightarrow b = 4 \)
Buna göre fonksiyon tanımı aşağıdaki gibi olur.
\( f(x) = 3x + 4 \)
\( f(2) = 3(2) + 4 = 10 \) bulunur.

Yukarıda doğrusal \( f \) fonksiyonunun grafiği verilmiştir.
\( f(3) + 8 = f(5) \) olduğuna göre, \( f(9) \) kaçtır?
Çözümü Göster\( f \) fonksiyonunun denklemini aşağıdaki şekilde yazalım.
\( f(x) = ax + b \)
Soruda verilen eşitliği kullanarak \( a \) katsayısını bulalım.
\( f(3) = 3a + b \)
\( f(5) = 5a + b \)
\( 3a + b + 8 = 5a + b \)
\( a = 4 \)
\( f(x) = 4x + b \)
Verilen grafiğe göre fonksiyon \( (2, 0) \) noktasından geçmektedir.
\( f(2) = 0 \)
\( 4(2) + b = 0 \)
\( b = -8 \)
\( f(x) = 4x - 8 \)
\( f(9) \) değerini bulalım.
\( f(9) = 4(9) - 8 = 28 \) bulunur.
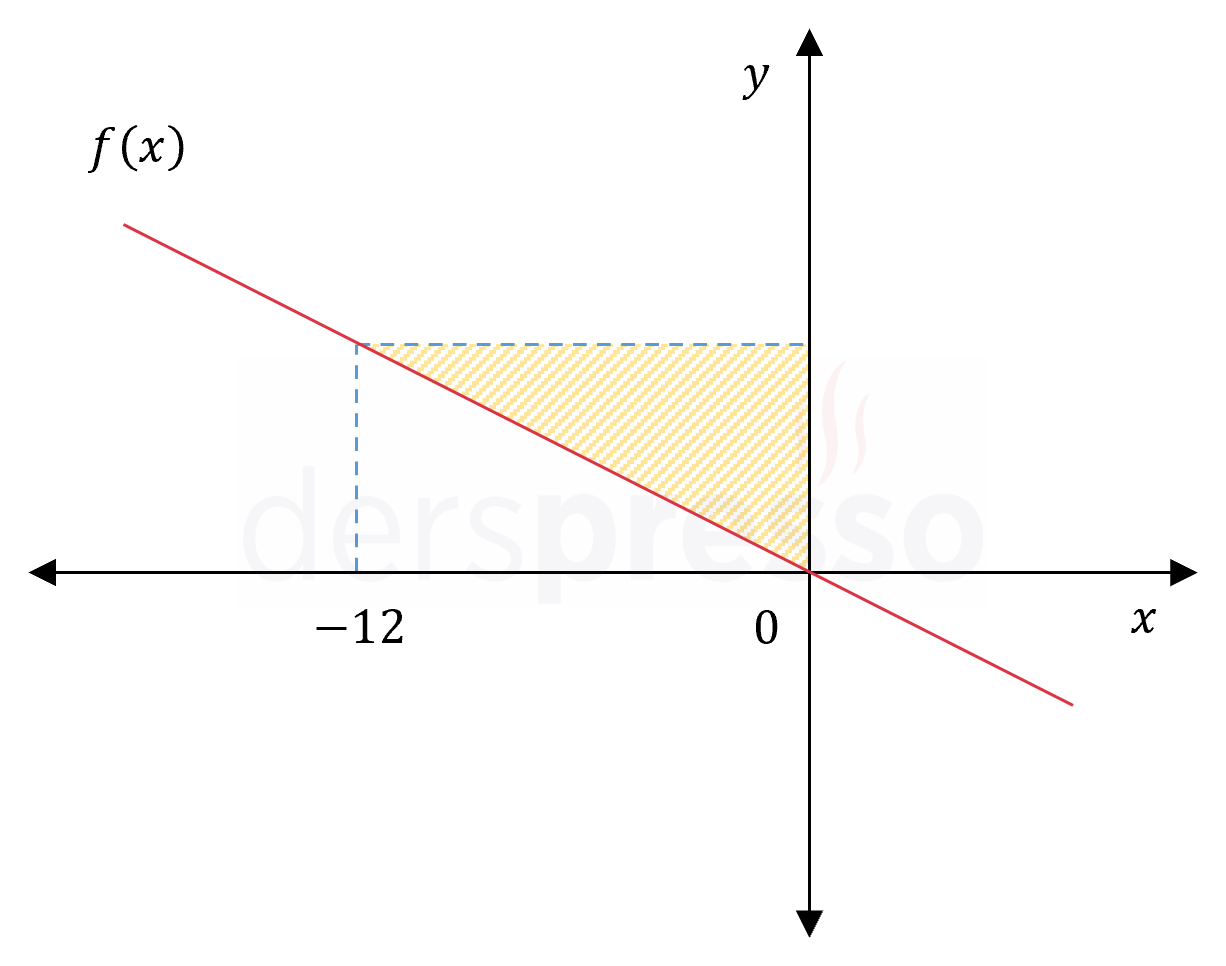
Yukarıda doğrusal \( f \) fonksiyonunun grafiği verilmiştir.
\( f(9) = -3 \) olduğuna göre, taralı bölgenin alanı kaçtır?
Çözümü Göster\( f \) bir doğrusal fonksiyondur.
\( f \) fonksiyonu orijinden geçtiğine göre denklemi sabit terim içermez.
\( f(x) = ax \)
Soruda verilen noktayı kullanarak \( a \) katsayısını bulalım.
\( f(9) = a(9) = -3 \)
\( a = -\dfrac{1}{3} \)
\( f(x) = -\dfrac{1}{3}x \)
Fonksiyonun \( x = -12 \) noktasındaki değerini bulalım.
\( f(-12) = -\dfrac{1}{3}(-12) = 4 \)
Taralı bölgenin oluşturduğu üçgenin alanını hesaplayalım.
\( A = \dfrac{12 \cdot 4}{2} = 24 \) bulunur.
\( f \) bir doğrusal fonksiyondur.
\( f(x) = (a - 2)x^2 - (b + 2)x + c + 3 \)
\( f(a) = -2 \) ve \( f(3) = 6 \) olduğuna göre, \( c \) kaçtır?
Çözümü GösterDoğrusal fonksiyonların denklemi \( f(x) = ax + b \) formundadır, dolayısıyla \( x^2 \)'li terim içermezler.
\( a - 2 = 0 \Longrightarrow a = 2 \)
\( f(a) = f(2) = -2 \)
\( f(x) = -(b + 2)x + c + 3 \)
\( f(x) \) fonksiyonunda \( x = 2 \) ve \( x = 3 \) yazalım.
\( f(2) = -(b + 2)2 + c + 3 = -2 \)
\( -2b + c = -1 \)
\( f(3) = -(b + 2)3 + c + 3 = 6 \)
\( -3b + c = 9 \)
Birinci denklemden ikinci denklemi taraf tarafa çıkaralım.
\( b = -10 \)
Bu değeri birinci denklemde yerine koyalım.
\( -2(-10) + c = -1 \)
\( c = -21 \) bulunur.
\( f \) ve \( g \) reel sayılar kümesinde tanımlı doğrusal fonksiyonlardır.
\( f \) fonksiyonu \( x \) eksenini \( (5, 0) \) noktasında, \( g \) fonksiyonu da \( y \) eksenini \( (0, 2) \) noktasında kesmektedir.
\( h(x) \) birim fonksiyon olup, \( h(x) = 4f(x) - 5g(x) \) eşitliği verilmektedir.
Buna göre \( f(4) + g(3) \) toplamı kaçtır?
Çözümü Göster\( f \) bir doğrusal fonksiyondur.
\( f(x) = ax + b \)
\( f \) fonksiyonu \( x \) eksenini \( (5, 0) \) noktasında keser.
\( f(5) = a(5) + b = 0 \)
\( b = -5a \)
\( f(x) = ax - 5a \)
\( g \) bir doğrusal fonksiyondur.
\( g(x) = cx + d \)
\( g \) fonksiyonu \( y \) eksenini \( (0, 2) \) noktasında keser.
\( g(0) = c(0) + d = 2 \)
\( d = 2 \)
\( g(x) = cx + 2 \)
\( h \) birim fonksiyondur
\( h(x) = x \)
\( h \) fonksiyonu için aşağıdaki eşitlik veriliyor.
\( h(x) = 4f(x) - 5g(x) \)
\( x = 4(ax - 5a) - 5(cx + 2) \)
\( x = 4ax - 20a - 5cx - 10 \)
\( x = (4a - 5c)x - 20a - 10 \)
İki polinomun eşitliğinde aynı dereceli terimlerin katsayıları birbirine eşittir.
\( 4a - 5c = 1 \)
\( -20a - 10 = 0 \)
\( a = -\dfrac{1}{2} \)
\( c = -\dfrac{3}{5} \)
Buna göre fonksiyonların tanımı aşağıdaki gibi olur.
\( f(x) = -\dfrac{1}{2}x + \dfrac{5}{2} \)
\( g(x) = -\dfrac{3}{5}x + 2 \)
Soruda istenen değerleri bulalım.
\( f(4) = -\dfrac{1}{2}(4) + \dfrac{5}{2} = \dfrac{1}{2} \)
\( g(3) = -\dfrac{3}{5}(3) + 2 = \dfrac{1}{5} \)
\( f(4) + g(3) = \dfrac{1}{2} + \dfrac{1}{5} = \dfrac{7}{10} \) bulunur.