Fonksiyonun Sol ve Sağ Tersi
\( f: A \to B \) şeklinde bir fonksiyon tanımlayalım. \( I_A \) fonksiyonu \( A \) kümesinde tanımlı, \( I_B \) fonksiyonu da \( B \) kümesinde tanımlı birim fonksiyonlardır.
Her \( a \in A \) ve \( b \in B \) için,
\( I_A(a) = a \)
\( I_B(b) = b \)
\( f \) fonksiyonunun sol ve sağ tersi olan fonksiyonlar aşağıdaki şekilde tanımlanır.
Bir Fonksiyonun Sol Tersi
\( g: B \to A \) olmak üzere,
\( g \circ f = I_A \) ise,
\( g \) fonksiyonuna \( f \) fonksiyonunun sol tersi denir.
Bu tanımı sağlayan bir \( f \) fonksiyonu ve sol tersi olan (ancak sağ tersi olmayan) \( g \) fonksiyonu için küme ve Venn şema gösterimleri aşağıda verilmiştir.
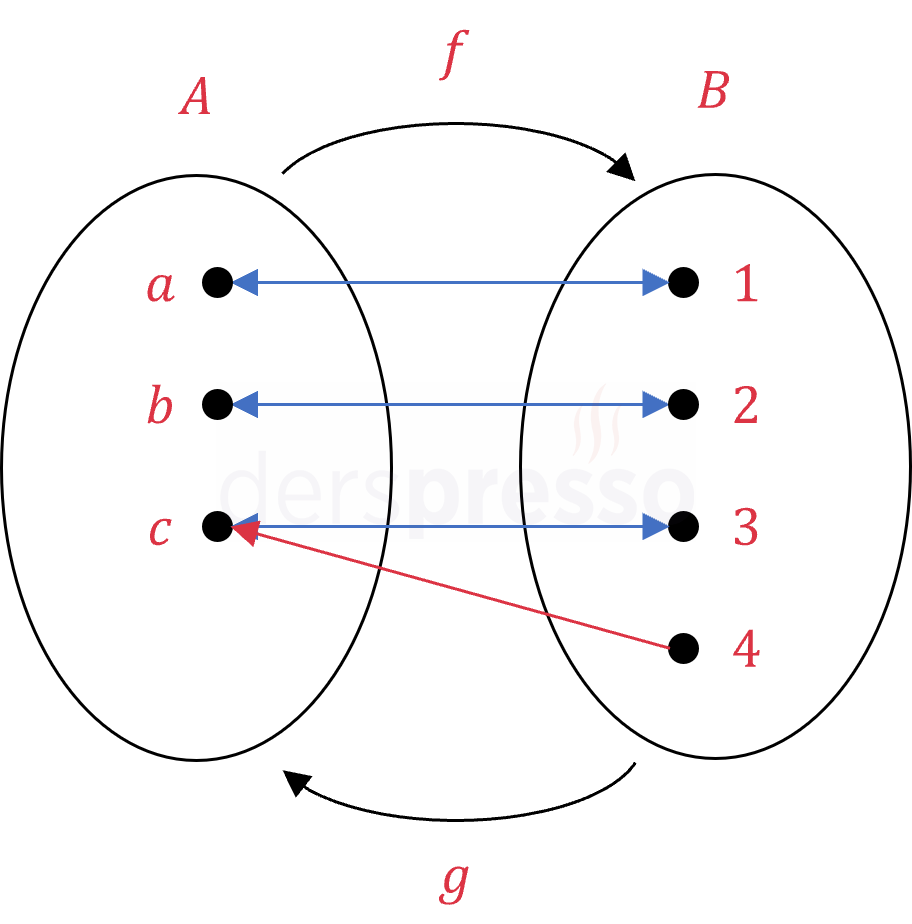
\( f = \{(a, 1), (b, 2), (c, 3)\} \)
\( g = \{(1, a), (2, b), (3, c), (4, c)\} \)
\( g \circ f = \{(a, a), (b, b), (c, c)\} \)
Bir fonksiyonun sol tersinin tanımlı olması için gerekli ve yeterli koşul fonksiyonun birebir olmasıdır.
Bir \( f: A \to B \) fonksiyonu tanımlayalım.
Önce \( f \) fonksiyonunun sol tersi olan bir fonksiyon varsa \( f \) fonksiyonunun birebir olduğunu gösterelim.
\( g: B \to A \) fonksiyonunun \( f \) fonksiyonunun sol tersi olduğunu kabul edelim.
\( a_1, a_2 \in A \) olsun.
\( f \) fonksiyonunun birebir olduğunu göstermek için \( f(a_1) = f(a_2) \) olduğunu kabul edelim.
Eşitliğin iki tarafının \( g \) fonksiyonuna göre görüntüsü de birbirine eşit olur.
\( g(f(a_1)) = g(f(a_2)) \)
\( (g \circ f)(a_1) = (g \circ f)(a_2) \)
\( g \) fonksiyonu \( f \) fonksiyonunun sol tersi ise tanım gereği \( g \circ f = I_A \) olur.
\( I_A(a_1) = I_A(a_2) \)
\( a_1 = a_2 \)
Buna göre \( f \) fonksiyonu birebirdir.
Şimdi \( f \) fonksiyonu birebir ise sol tersi olan bir fonksiyonun var olduğunu gösterelim.
\( f \) fonksiyonunun birebir olduğunu kabul edelim.
\( g: B \to A \) şeklinde tanımlı ve \( f \) fonksiyonunun sol tersi olan bir fonksiyon bulunduğunu gösterelim.
\( b \in B \) olsun.
\( b \) elemanı iki farklı durumda olabilir.
Durum 1: \( b \in f(A) \)
\( f \) birebir olduğu için \( f(a) = b \) olan benzersiz bir \( a \in A \) elemanı vardır.
Tanımlayacağımız \( g \) fonksiyonu bu \( b \) elemanını bu \( a \) elemanı ile eşlesin.
Durum 2: \( b \not\in f(A) \)
Herhangi bir \( a_1 \in A \) elemanı seçelim.
Tanımlayacağımız \( g \) fonksiyonu bu \( b \) elemanını seçtiğimiz bu sabit \( a_1 \) elemanı ile eşlesin.
\( b \not\in f(A) \) olduğu için bu tanımlama \( g \circ f = I_A \) eşitliğini bozmayacaktır.
Buna göre \( f \) fonksiyonunun sol tersi olan bir \( g \) fonksiyonunu aşağıdaki şekilde tanımlayabiliriz.
Bir Fonksiyonun Sağ Tersi
\( h: B \to A \) olmak üzere,
\( f \circ h = I_B \) ise,
\( h \) fonksiyonuna \( f \) fonksiyonunun sağ tersi denir.
Bu tanımı sağlayan bir \( f \) fonksiyonu ve sağ tersi olan (ancak sol tersi olmayan) \( h \) fonksiyonu için küme ve Venn şema gösterimleri aşağıda verilmiştir.
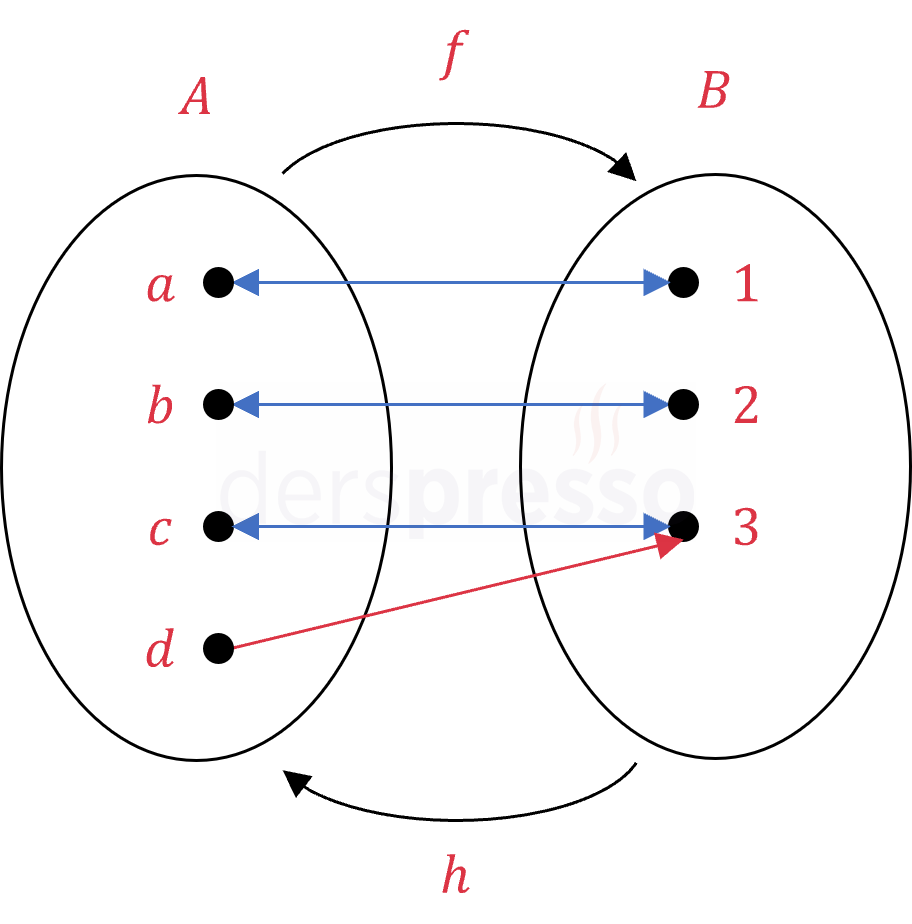
\( f = \{(a, 1), (b, 2), (c, 3), (d, 3)\} \)
\( h = \{(1, a), (2, b), (3, c)\} \)
\( f \circ h = \{(1, 1), (2, 2), (3, 3)\} \)
Bir fonksiyonun sağ tersinin tanımlı olması için gerekli ve yeterli koşul fonksiyonun örten olmasıdır.
Bir \( f: A \to B \) fonksiyonu tanımlayalım.
Önce \( f \) fonksiyonunun sağ tersi olan bir fonksiyon varsa \( f \) fonksiyonunun örten olduğunu gösterelim.
\( h: B \to A \) fonksiyonunun \( f \) fonksiyonunun sağ tersi olduğunu kabul edelim.
\( b \in B \) olsun.
\( h \) fonksiyonu \( f \) fonksiyonunun sağ tersi olduğu için tanım gereği \( f \circ h = I_B \) olur.
\( (f \circ h)(b) = b \)
\( f(h(b)) = b \)
Dolayısıyla \( b \) elemanı en az bir \( a \in A \) elemanının \( f \) fonksiyonuna göre görüntüsüdür.
Buna göre \( f \) fonksiyonu örtendir.
Şimdi \( f \) fonksiyonu örten ise sağ tersi olan bir fonksiyonun var olduğunu gösterelim.
\( f \) fonksiyonunun örten olduğunu kabul edelim.
\( h: B \to A \) şeklinde tanımlı ve \( f \) fonksiyonunun sağ tersi olan bir fonksiyon bulunduğunu gösterelim.
\( b \in B \) olsun.
\( f \) fonksiyonu örten olduğu için \( f(a) = b \) olan en az bir \( a \in A \) vardır.
\( b \) elemanı iki farklı durumda olabilir.
Durum 1: \( f(a) = b \) olan tek bir \( a \in A \) elemanı vardır.
Tanımlayacağımız \( h \) fonksiyonu bu \( b \) elemanını bu \( a \) elemanı ile eşlesin.
Durum 2: \( f(a) = b \) olan birden fazla \( a \in A \) elemanı vardır.
Bu elemanlar arasından herhangi bir \( a_1 \in A \) seçelim.
Tanımlayacağımız \( h \) fonksiyonu bu \( b \) elemanını seçtiğimiz bu \( a_1 \) elemanı ile eşlesin.
Yukarıdaki şekilde tanımlayacağımız \( h \) fonksiyonu \( f \) fonksiyonunun sağ tersi olur.
Bir Fonksiyonun Tersi
Bir fonksiyonun hem sol tersi hem de sağ tersi tanımlı ise bu fonksiyonun ters fonksiyonu tanımlıdır.
\( g, h: B \to A \) olmak üzere,
\( g \) fonksiyonu \( f \) fonksiyonun sol tersi olsun.
\( g \circ f = I_A \)
\( h \) fonksiyonu \( f \) fonksiyonun sağ tersi olsun.
\( f \circ h = I_B \)
Bu durumda \( f \) fonksiyonun ters fonksiyonu tanımlıdır ve bu iki fonksiyona eşittir.
\( g = h = f^{-1} \)
Buna göre bir fonksiyonun tersinin tanımlı olması için fonksiyonun sol ve sağ tersi tanımlı olmalı, dolayısıyla fonksiyon hem birebir hem de örten olmalıdır.
Bir \( f \) fonksiyonunun tersi \( g \) fonksiyonu ise \( g \) fonksiyonun tersi de \( f \) fonksiyonudur.
\( f^{-1} = g \Longleftrightarrow f = g^{-1} \)