Fonksiyon Sayısı
Bağıntı konusunda \( A \) kümesinden \( B \) kümesine tanımlanabilecek bağıntı sayısını aşağıdaki formülle hesaplamıştık.
\( s(A) = n, \quad s(B) = k \) olmak üzere,
\( A \)'dan \( B \)'ye bağıntı sayısı \( = 2^{s(A \times B)} = 2^{n \cdot k} \)
4 elemanlı \( A \) kümesinden 5 elemanlı \( B \) kümesine tanımlanabilecek bağıntı sayısı:
Bağıntı sayısı \( = 2^{4 \cdot 5} \)
\( A \) kümesinden \( B \) kümesine tanımlanabilecek fonksiyon sayısı ise aşağıdaki formülle hesaplanır.
\( s(A) = n, \quad s(B) = k \) olmak üzere,
\( A \)'dan \( B \)'ye fonksiyon sayısı \( = k^n \)
4 elemanlı \( A \) kümesinden 5 elemanlı \( B \) kümesine tanımlanabilecek fonksiyon sayısı:
Fonksiyon sayısı \( = 5^4 \)
İSPATI GÖSTER
\( n \) elemanlı \( A \) kümesinden \( k \) elemanlı \( B \) kümesine tanımlı bir bağıntının fonksiyon olabilmesi için, \( A \) kümesinin her elemanı \( B \) kümesinin tek bir elemanı ile eşlenmelidir.
\( A \) kümesinin birinci elemanının \( B \) kümesinde eşlenebileceği \( k \) farklı eleman/seçenek vardır. Benzer şekilde, \( A \) kümesinin ikinci elemanının da \( B \) kümesinde eşlenebileceği \( k \) farklı seçenek vardır. Aynı durum \( A \) kümesinin \( n \) elemanının tümü için geçerlidir.
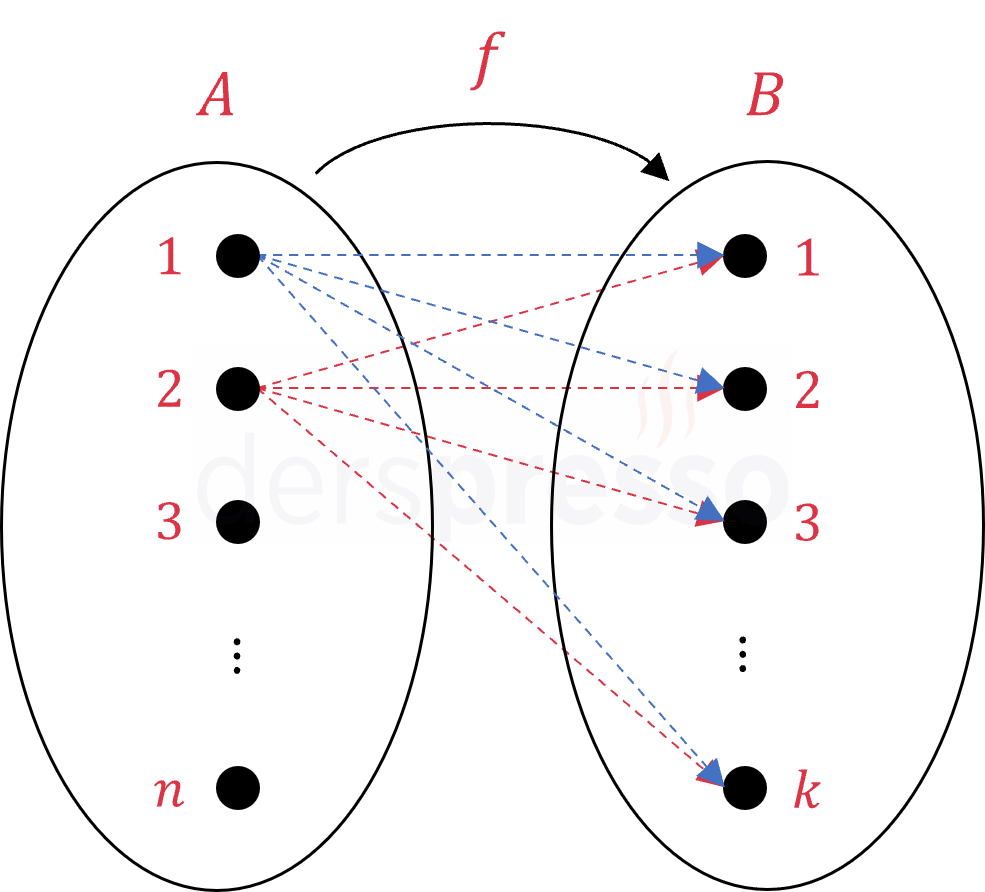
\( A \) kümesinin her elemanı için yapılacak bu eşlemeler birbirinden bağımsız seçimler olduğu için (bir eleman için yapılan eşleme diğer bir elemanın eşlenebileceği seçenek sayısını değiştirmediği için), çarpma kuralını kullanarak toplam farklı eşleme sayısını \( k^n \) olarak buluruz.
Fonksiyon sayısı \( = \underbrace{k \cdot k \cdot \ldots \cdot k}_\text{n adet} = k^n \)
\( A = \{2, 3, 5, 7\} \)
\( B = \{d, e, f\} \)
\( A \)'dan \( B \)'ye tanımlanabilecek fonksiyon sayısı, \( B \)'den \( A \)'ya tanımlanabilecek fonksiyon sayısından kaç fazladır?
Çözümü Göster\( s(A) = 4, \quad s(B) = 3 \)
\( A \)'dan \( B \)'ye \( 3^4 = 81 \) fonksiyon tanımlanabilir.
\( B \)'den \( A \)'ya \( 4^3 = 64 \) fonksiyon tanımlanabilir.
Buna göre cevap \( 81 - 64 = 17 \) olarak bulunur.
\( A = \{ -1, 0, 1, 2 \} \)
\( B = \{ x, y, z, t \} \) olmak üzere,
\( A \)'dan \( B \)'ye \( f(0) = x \) koşulunu sağlayan kaç \( f \) fonksiyonu yazılabilir?
Çözümü GösterHerhangi ek bir koşul olmadan \( A \)'dan \( B \)'ye yazılabilecek fonksiyon sayısı \( s(B)^{s(A)} = 4^4 = 256 \) olur.
\( f(0) = x \) koşulu ile \( A \) kümesindeki bir elemanın \( B \) kümesindeki bir elemanla eşlemesini yapmış oluruz, dolayısıyla \( A \) kümesinden bir eleman eksilmiş olur.
Kalan 3 elemanlı kümeden 4 elemanlı \( B \) kümesine tanımlanabilecek fonksiyon sayısını bulalım.
\( s(B)^{s(A) - 1} = 4^3 = 64 \) bulunur.
\( A = \{ 3, 4, 5 \} \)
\( B = \{ 4, 5, 6, 7 \} \)
\( f: A \to B \) olduğuna göre,
Her \( m \in A \) için, \( m + f(m) \le 9 \) koşulunu sağlayan kaç farklı fonksiyon yazılabilir?
Çözümü Göster\( A \) kümesindeki "3" elemanı \( B \) kümesindeki "4", "5", "6" elemanları ile eşlendiğinde verilen koşul sağlanır.
\( A \) kümesindeki "4" elemanı \( B \) kümesindeki "4", "5" elemanları ile eşlendiğinde verilen koşul sağlanır.
\( A \) kümesindeki "5" elemanı \( B \) kümesindeki "4" elemanı ile eşlendiğinde verilen koşul sağlanır.
\( A \) kümesindeki her elemanın eşlemesi birbirinden bağımsız olaylar olduğu için bu farklı durumları çarparak toplam fonksiyon sayısını bulabiliriz.
\( 3 \cdot 2 \cdot 1 = 6 \) farklı fonksiyon yazılabilir.
\( A = \{ 2, 3, 4, 9, 15 \} \) olmak üzere,
\( A \) kümesi üzerinde tanımlı ve en az bir \( a \in A \) için \( f(a) = \sqrt{a} \) koşulunu sağlayan kaç farklı \( f \) fonksiyonu yazılabilir?
Çözümü Göster5 elemanlı \( A \) kümesi üzerinde tanımlı bir fonksiyonda tanım kümesindeki her elemanın değer kümesinde eşlenebileceği 5 seçenek vardır, dolayısıyla \( A \) kümesi üzerinde \( 5^5 = 3125 \) farklı fonksiyon tanımlanabilir.
Soruda en az bir \( a \in A \) için \( f(a) = \sqrt{a} \) koşulunu sağlayan fonksiyonların sayısı istenmektedir.
\( f(a) = \sqrt{a} \) koşulu iki durumda sağlanır.
\( f(4) = \sqrt{4} = 2 \)
\( f(9) = \sqrt{9} = 3 \)
\( f(4) = \sqrt{4} = 2 \) koşulunu sağlayan fonksiyon sayısını bulmak için, önce "4" elemanını "2" elemanı ile eşlediğimizi varsayalım. Bu durumda tanım kümesinin kalan 4 elemanı ile değer kümesinin 5 elemanı arasında \( 5^4 = 625 \) farklı fonksiyon tanımlanabilir.
Benzer şekilde, \( f(9) = \sqrt{9} = 3 \) koşulunu sağlayan fonksiyon sayısını bulmak için, önce "9" elemanını "3" elemanı ile eşlediğimizi varsayalım. Bu durumda tanım kümesinin kalan 4 elemanı ile değer kümesinin 5 elemanı arasında \( 5^4 = 625 \) farklı fonksiyon tanımlanabilir.
Bulduğuz ilk 625 fonksiyon \( f(9) = \sqrt{9} = 3 \) koşulunu sağlayan fonksiyonları, ikinci 625 fonksiyon \( f(4) = \sqrt{4} = 2 \) koşulunu sağlayan fonksiyonları da içermektedir.
Hem \( f(4) = \sqrt{4} = 2 \) hem de \( f(9) = \sqrt{9} = 3 \) koşulunu sağlayan fonksiyon sayısını bulmak için, önce "4" ve "9" elemanlarını sırasıyla "2" ve "3" elemanları ile eşlediğimizi varsayalım. Bu durumda tanım kümesinin kalan 3 elemanı ile değer kümesinin 5 elemanı arasında \( 5^3 = 125 \) farklı fonksiyon tanımlanabilir.
İstenen fonksiyon sayısını bulmak için bulduğumuz fonksiyon sayılarının toplamından her iki toplamda da sayılan fonksiyonların sayısını çıkaralım.
\( 625 + 625 - 125 = 1125 \) bulunur.
\( A = \{ 2, 3, 4 \} \)
\( B = \{ 1, 5, 7, 9, 10 \} \) kümeleri veriliyor.
\( f: A \to B \) olmak üzere,
\( x + x^2 + xf(x) + f(x) \) ifadesini çift sayı yapan kaç farklı fonksiyon yazılabilir?
Çözümü Gösterİfadeyi gruplara ayırma yöntemi ile çarpanlarına ayıralım.
\( x + x^2 + xf(x) + f(x) = x(1 + x) + f(x)(x + 1) \)
\( = (x + 1)(x + f(x)) \)
Çarpımın sonucu çift olduğuna göre, çarpanlardan en az biri çift olmalıdır.
\( A \) kümesinden \( B \) kümesine tanımlı bir fonksiyon, \( A \) kümesinin her elemanını \( B \) kümesinin sadece bir elemanı ile eşler.
İfadeyi \( A \) kümesinin her elemanı için ayrı ayrı inceleyelim.
Durum 1: \( x = 2 \)
İfadede yerine koyalım.
\( (2 + 1)(2 + f(2)) = 3(2 + f(2)) \)
3 tek sayı olduğu için \( 2 + f(2) \) çift sayı olmalıdır.
İki sayının toplamı çift ise bu sayıların ya ikisi de tektir ya da ikisi de çifttir, dolayısıyla \( f(2) \) çift sayı olmalıdır.
\( f(2) = 10 \)
Bu durumda yazılabilecek tek bir fonksiyon vardır.
Durum 2: \( x = 3 \)
İfadede yerine koyalım.
\( (3 + 1)(3 + f(3)) = 4(3 + f(3)) \)
4 çift sayı olduğu için sonuç daima çifttir.
\( f(3) \) tüm değerleri alabilir.
\( f(3) \in \{ 1, 5, 7, 9, 10 \} \)
Bu durumda yazılabilecek 5 fonksiyon vardır.
Durum 3: \( x = 4 \)
İfadede yerine koyalım.
\( (4 + 1)(4 + f(4)) = 5(4 + f(4)) \)
5 tek sayı olduğu için \( 4 + f(4) \) çift sayı olmalıdır.
İki sayının toplamı çift ise bu sayıların ya ikisi de tektir ya da ikisi de çifttir, dolayısıyla \( f(4) \) çift sayı olmalıdır.
\( f(4) = 10 \)
Bu durumda yazılabilecek tek bir fonksiyon vardır.
\( A \) kümesindeki her elemanın eşlemesi birbirinden bağımsız olaylar olduğu için toplam fonksiyon sayısını bu farklı durumları çarparak bulabiliriz.
\( 1 \cdot 5 \cdot 1 = 5 \) farklı fonksiyon yazılabilir.