Bağıntı Tanımı
Konu tekrarı için: Sıralı İkili | Kartezyen Çarpımı
\( A \) ve \( B \) kümelerinin kartezyen çarpımını; birinci bileşeni \( A \) kümesinin, ikinci bileşeni \( B \) kümesinin elemanı olmak üzere yazılabilecek tüm sıralı ikililerin kümesi olarak tanımlamıştık.
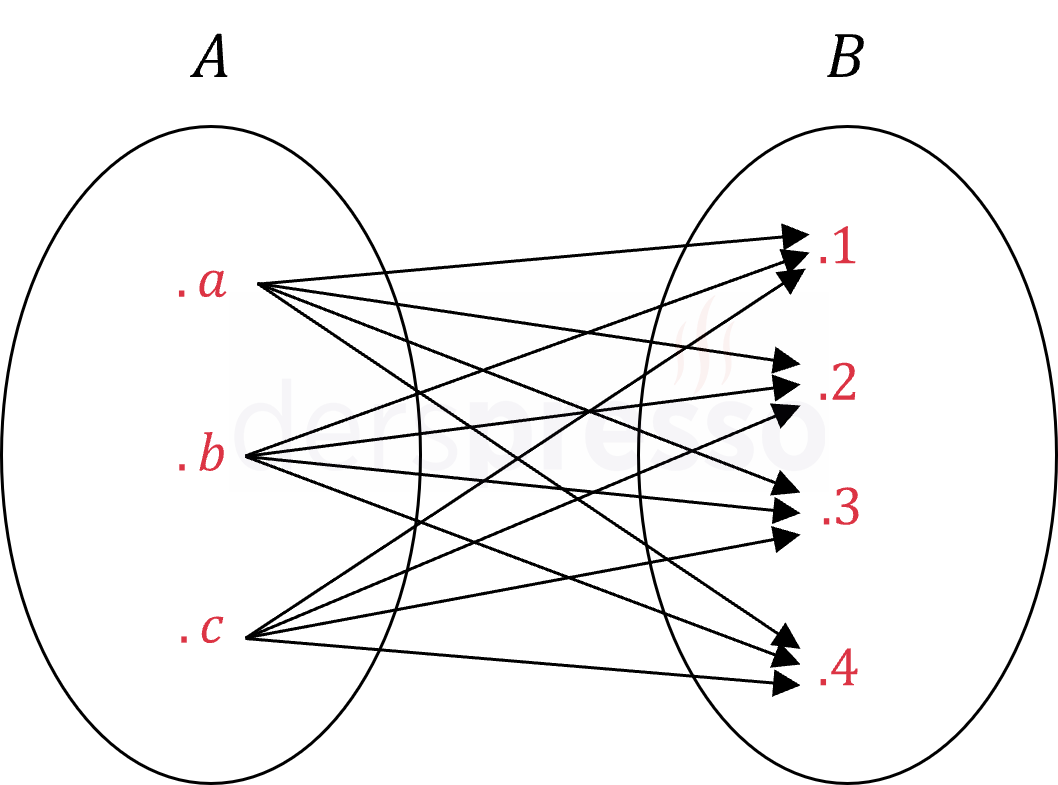
\( A \times B = \{(x, y) \mid x \in A \land y \in B\} \)
\( \textcolor{red}{A = \{a, b, c\}} \)
\( \textcolor{blue}{B = \{1, 2, 3, 4\}} \)
\( \textcolor{red}{A} \times \textcolor{blue}{B} = \{(\textcolor{red}{a}, \textcolor{blue}{1}), (\textcolor{red}{a}, \textcolor{blue}{2}), (\textcolor{red}{a}, \textcolor{blue}{3}), (\textcolor{red}{a}, \textcolor{blue}{4}), (\textcolor{red}{b}, \textcolor{blue}{1}), (\textcolor{red}{b}, \textcolor{blue}{2}), (\textcolor{red}{b}, \textcolor{blue}{3}), (\textcolor{red}{b}, \textcolor{blue}{4}), (\textcolor{red}{c}, \textcolor{blue}{1}), (\textcolor{red}{c}, \textcolor{blue}{2}), (\textcolor{red}{c}, \textcolor{blue}{3}), (\textcolor{red}{c}, \textcolor{blue}{4})\} \)
\( A \) ve \( B \) boş kümeden farklı iki küme olmak üzere, \( A \times B \) kartezyen çarpımının her bir alt kümesine \( A \)'dan \( B \)'ye (ya da \( A \) ile \( B \) arasında) bir bağıntı denir. Bağıntılar genellikle \( R \), \( S \), \( T \) harfleri ile gösterilir.
\( R \), \( A \)'dan \( B \)'ye bir bağıntı olmak üzere,
\( R \subseteq A \times B \)
Yukarıdaki \( A \) ve \( B \) kümeleri arasında tanımlı bazı bağıntılar aşağıdaki gibidir.
\( R_1 = \{(a, 1) \} \)
\( R_2 = \{(b, 2), (b, 3), (c, 4) \} \)
\( R_3 = \{(a, 1), (a, 2), (b, 1), (b, 3), (c, 2), (c, 4) \} \)
\( A \times B \) kartezyen çarpımının alt kümeleri boş küme ve kartezyen çarpımının kendisini de içerdiği için iki küme arasında birer bağıntı olurlar. Bunlardan birinciye boş bağıntı, ikinciye evrensel bağıntı denir.
Boş bağıntı:
\( R_4 = \emptyset \)
Evrensel bağıntı:
\( R_5 = A \times B \)
İleriki bölümlerde göreceğimiz üzere, matematiğin en önemli yapılarından olan fonksiyonlar belirli koşulları sağlayan birer bağıntıdır.
\( A \times B \) kartezyen çarpımı \( B \times A \) kartezyen çarpımına eşit olmadığı için bir bağıntının hangi kümeden hangi kümeye tanımlandığı önemlidir.
\( A \) kümesinin kendisiyle kartezyen çarpımının (\( A \times A \)) bir alt kümesi olan bağıntıya \( A \) kümesinde ya da \( A \) üzerinde tanımlı bağıntı denir.
\( A = \{a, b, c\} \)
\( A \times A = \{(a, a), (a, b), \ldots, (c, c)\} \)
\( A \) kümesinde tanımlı bazı bağıntılar aşağıdaki gibidir.
\( R_1 = \{(a, b)\} \)
\( R_2 = \{(a, a), (b, b), (c, c)\} \)
\( R_3 = \{(a, c), (b, a), (b, c), (c, b)\} \)
Her \( x \in A \) için \( (x, x) \) ikililerinden oluşan bağıntıya \( A \) üzerinde tanımlı birim bağıntı denir. \( A \) üzerinde tanımlı birim bağıntı \( I_A \) ile gösterilir.
\( I_A = \{(x, x) \mid x \in A\} \)
\( I_N \) doğal sayılarda tanımlı birim bağıntı olmak üzere,
\( I_N = \{(0, 0), (1, 1), (2, 2), \ldots\} \)
Bir bağıntı iki kümenin elemanları arasında bir ilişki kurar. Örneğin \( (x, y) \) ikilisi bir \( R \) bağıntısının elemanı ise \( x \) ve \( y \) elemanları arasında \( R \) bağıntısı bağlamında bir ilişki bulunduğunu söyleriz. Bu ilişkinin varlığı ya da yokluğu aşağıdaki şekillerde gösterilir.
\( (x, y) \in R, \quad (x, y) \notin R \)
\( x \sim y, \quad x \not\sim y \)
\( xRy, \quad x\cancel{R}y \)
\( R = \{(x, y) \mid x, y \in \mathbb{Z}; x^2 = y\} \)
\( (3, 9) \in R, \quad (3, 7) \notin R \)
\( 3 \sim 9, \quad 3 \not\sim 9 \)
\( 3R9, \quad 3\cancel{R}9 \)
Aşağıdaki matematiksel ilişkiler birer bağıntıdır.
| Konu | Bağıntı örnekleri |
|---|---|
| Eşitlik, denklik |
\( 2 = 2 \) \( 23 \equiv 43 \pmod{5} \) |
| Eşitsizlik |
\( 3 \lt 5, \quad 7 \le 7 \) \( 11 \gt 9, \quad 4 \ge 0 \) |
| Kümeler |
\( 3 \in A, \quad -2 \notin \mathbb{N} \) \( \mathbb{Z^+} \subset \mathbb{Z} \) |
| Bölünebilme |
\( 3 \mid 9, \quad 4 \not\mid 9 \) |
| Geometri |
\( d_1 \parallel d_2, \quad d_3 \perp d_4 \) \( \overset{\triangle}{ABC} \sim \overset{\triangle}{DEF} \) \( \overset{\triangle}{ABC} \cong \overset{\triangle}{DEF} \) |
Bir bağıntının iki küme arasında kurduğu ilişki matematiksel olmak zorunda değildir. Matematiksel olmayan bağıntılara aşağıdaki gibi örnekler verebiliriz.
- Öğrenciler ve üye oldukları kulüpler
- Bir sosyal medya platformunda kimin kimi takip ettiği bilgisi
- Bir operatörün müşterileri ve cep telefonu numaraları
- Bir üniversitedeki öğrenciler ve aldıkları dersler
- Ülkeler ve komşuları
Tanım ve Görüntü Kümesi
Bir bağıntının elemanlarının birinci bileşenlerinin oluşturduğu kümeye tanım kümesi, ikinci bileşenlerinin oluşturduğu kümeye ise görüntü kümesi denir.
\( A = \{a, b, c, d, e, f \} \)
\( B = \{1, 2, 3, 4, 5 \} \)
\( R \), \( A \)'dan \( B \)'ye bir bağıntı olmak üzere,
\( R = \{(a, 2), (a, 3), (b, 3), (d, 1), (d, 4)\} \)
Tanım kümesi \( = \{a, b, d\} \)
Görüntü kümesi \( = \{1, 2, 3, 4\} \)
Bağıntı Sayısı
\( A \) kümesinden \( B \) kümesine tanımlanabilecek toplam bağıntı sayısının formülünü vermeden önce iki konuyu hatırlayalım.
Öncelikle, \( A \times B \) kartezyen çarpımının eleman sayısı bu iki kümenin eleman sayılarının çarpımına eşittir. Bunun sebebi, kartezyen çarpım kümesinde birinci kümenin her elemanının ikinci kümenin her elemanı ile eşleniyor olmasıdır.
\( s(A \times B) = s(A) \cdot s(B) \)
İkinci olarak, \( n \) elemanlı bir kümenin alt kümelerinin sayısı \( 2^n \) formülü ile bulunur. Bu formülün mantığını alt küme konusunda açıklamıştık.
\( A \) kümesinden \( B \) kümesine tanımlanabilecek toplam bağıntı sayısı, \( A \times B \) kartezyen çarpımının alt küme sayısına eşittir. Yukarıda paylaştığımız iki noktayı buraya uyguladığımızda aşağıdaki formülü elde ederiz.
\( A \to B \) bağıntı sayısı \( = A \times B \) kümesinin alt küme sayısı
\( = 2^{s(A \times B)} = 2^{s(A) \cdot s(B)} \)
\( s(A) = 3, \quad s(B) = 4 \)
\( s(A \times B) = s(A) \cdot s(B) = 12 \)
\( A \to B \) bağıntı sayısı \( = 2^{12} = 4.096 \)
\( A \) kümesi üzerinde tanımlanabilecek bağıntıların sayısı 512 olduğuna göre, \( A \) kümesinin eleman sayısı kaçtır?
Çözümü Göster\( A \) kümesinden \( B \) kümesine tanımlanabilecek bağıntı sayısı \( 2^{s(A) \cdot s(B)} \) formülü ile bulunur.
Buna göre \( A \) kümesi üzerinde tanımlanabilecek bağıntı sayısı \( 2^{s(A) \cdot s(A)} \) olur.
\( 2^{s(A) \cdot s(A)} = 512 = 2^9 \)
\( s(A) \cdot s(A) = 9 \)
\( s(A) = 3 \)
Buna göre \( A \) kümesinin eleman sayısı 3'tür.
\( A = \{x \mid 2 \le x \lt 10, x \in \mathbb{Z}\} \)
olduğuna göre, \( A \) kümesi üzerinde kaç bağıntı tanımlanabilir?
Çözümü GösterVerilen tanıma göre, \( A \) kümesi \( [2, 10) \) yarı açık aralığındaki tam sayılardan oluşur.
\( A = \{2, 3, 4, 5, 6, 7, 8, 9\} \)
\( s(A) = 8 \)
\( A \) kümesi üzerinde tanımlanabilecek bağıntı sayısı \( 2^{s(A) \cdot s(A)} \) formülü ile bulunur.
Buna göre \( A \) kümesi üzerinde \( 2^{8 \cdot 8} = 2^{64} \) farklı bağıntı tanımlanabilir.
Pozitif tam sayılar kümesinde tanımlı aşağıdaki bağıntı veriliyor.
\( R = \{(x, y) \mid 5x + 2y = 40; x, y \in \mathbb{Z^+}\} \)
Buna göre \( R \) bağıntısının eleman sayısı kaçtır?
Çözümü GösterBağıntı tanımındaki eşitlikte \( y \) değişkenini yalnız bırakalım.
\( 2y = 40 - 5x \)
\( y = 20 - \dfrac{5x}{2} \)
\( y \) değişkenini pozitif tam sayı yapan \( x \) pozitif tam sayı değerleri aşağıdaki gibidir.
\( x \in \{2, 4, 6\} \)
\( x \) değişkeni bu değerleri aldığında \( y \) değişkeni aşağıdaki değerleri alır.
\( x = 2 \Longrightarrow y = 15 \)
\( x = 4 \Longrightarrow y = 10 \)
\( x = 6 \Longrightarrow y = 5 \)
Buna göre \( R \) bağıntısı aşağıdaki sıralı ikililerden oluşur.
\( R = \{(2, 15), (4, 10), (6, 5)\} \)
\( R \) bağıntısı üç elemanlıdır.
\( A = \{x, y\} \)
\( B = \{2, 4, 6, 8 \} \) olmak üzere,
\( A \) kümesinden \( B \) kümesine,
(a) Kaç bağıntı tanımlanabilir?
(b) En az 6 elemanlı kaç bağıntı tanımlanabilir?
(c) En fazla 3 elemanlı kaç bağıntı tanımlanabilir?
Çözümü Göster\( s(A) = 2, \quad s(B) = 4 \)
\( s(A \times B) = 2 \cdot 4 = 8 \)
8 elemanlı \( A \times B \) kartezyen çarpım kümesinin her bir alt kümesi, \( A \) kümesinden \( B \) kümesine bir bağıntıdır.
(a) seçeneği:
\( A \times B \) kümesi 8 elemanlıdır, dolayısıyla \( A \) kümesinden \( B \) kümesine \( 2^8 = 256 \) bağıntı tanımlanabilir.
(b) seçeneği:
\( n \) elemanlı bir kümenin \( k \) elemanlı alt kümelerinin sayısı \( C(n, k) \) formülü ile bulunur.
En az 6 elemanlı bağıntılar, \( A \times B \) kümesinin 6, 7 ve 8 elemanlı alt kümelerinden oluşur.
\( C(8, 6) + C(8, 7) + C(8, 8) = 28 + 8 + 1 = 37 \)
(c) seçeneği:
En fazla 3 elemanlı bağıntılar, \( A \times B \) kümesinin 0, 1, 2 ve 3 elemanlı alt kümelerinden oluşur.
\( C(8, 0) + C(8, 1) + C(8, 2) + C(8, 3) = 1 + 8 + 28 + 56 = 93 \)