Bağıntı Gösterim Yöntemleri
Sıralı ikililerden oluşan birer küme olan bağıntılar; kümelerde olduğu gibi liste, ortak özellik ve Venn şeması yöntemleri ile gösterilebilir.
Liste Yöntemi
Bu yöntemde bağıntının elemanları küme parantezleri içinde ve virgülle ayrılarak listelenir.
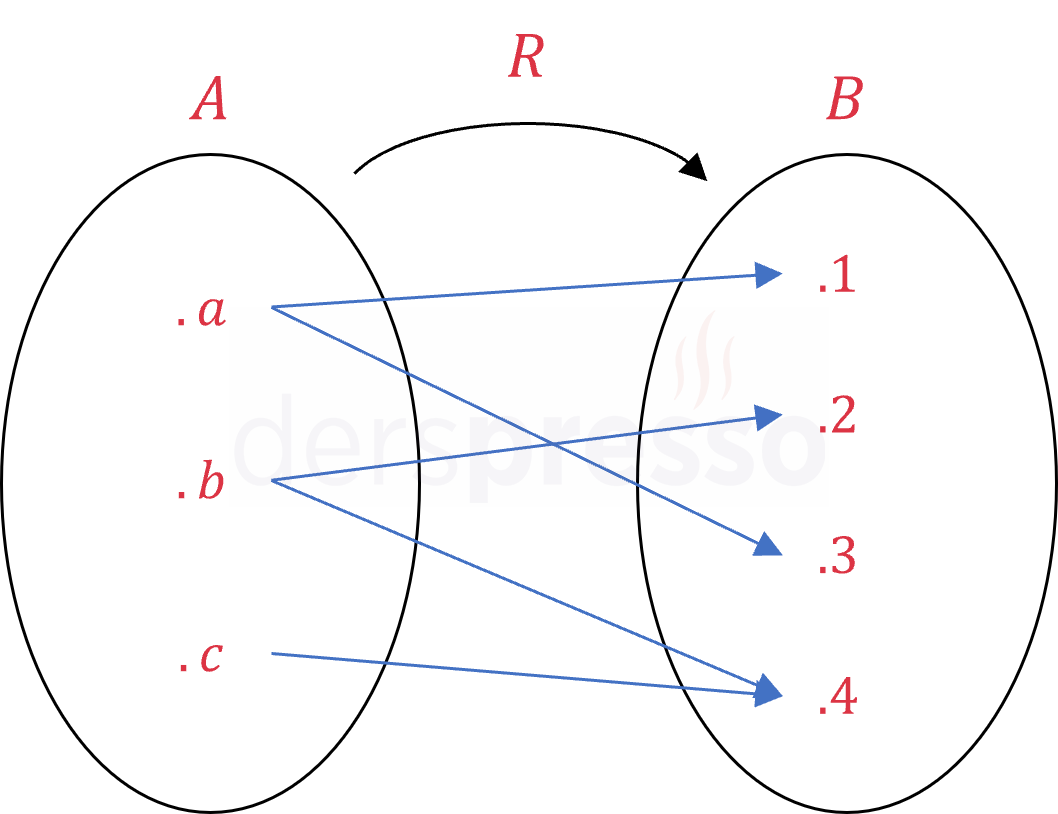
\( R = \{(a, 2), (b, 3), (e, 7)\} \)
Ortak Özellik Yöntemi
Bu yöntemde bağıntının elemanları matematiksel ya da sözel bir ifade ile tanımlanır.
\( A = \{1, 2, \ldots, 99\} \) olmak üzere,
\( R_1 = \{(a, a) \mid a \in A \} \)
\( R_1 = \{(1, 1), (2, 2), \ldots, (99, 99)\} \)
\( R_2 = \{(x, y) \mid x, y \in \mathbb{Z^+}, \text{y x'ten büyük en küçük asal sayı} \} \)
\( R_2 = \{(1, 2), (2, 3), (3, 5), (4, 5), \ldots\} \)
Venn Şeması
Bu yöntemde bağıntının üzerinde tanımlı olduğu kümeler bir Venn şemasında gösterilir ve bağıntının elemanı olan sıralı ikililerin birinci bileşeninden ikinci bileşenine birer ok çizilir.
Grafik Yöntemi
Bu yöntemde bağıntının tanım kümesi kartezyen düzleminin yatay ekseniyle, görüntü kümesi de dikey ekseniyle eşlenir ve her kümenin elemanları eksenler üzerinde işaretlenir. Daha sonra bağıntının elemanı olan sıralı ikililer grafik üzerinde işaretlenir.
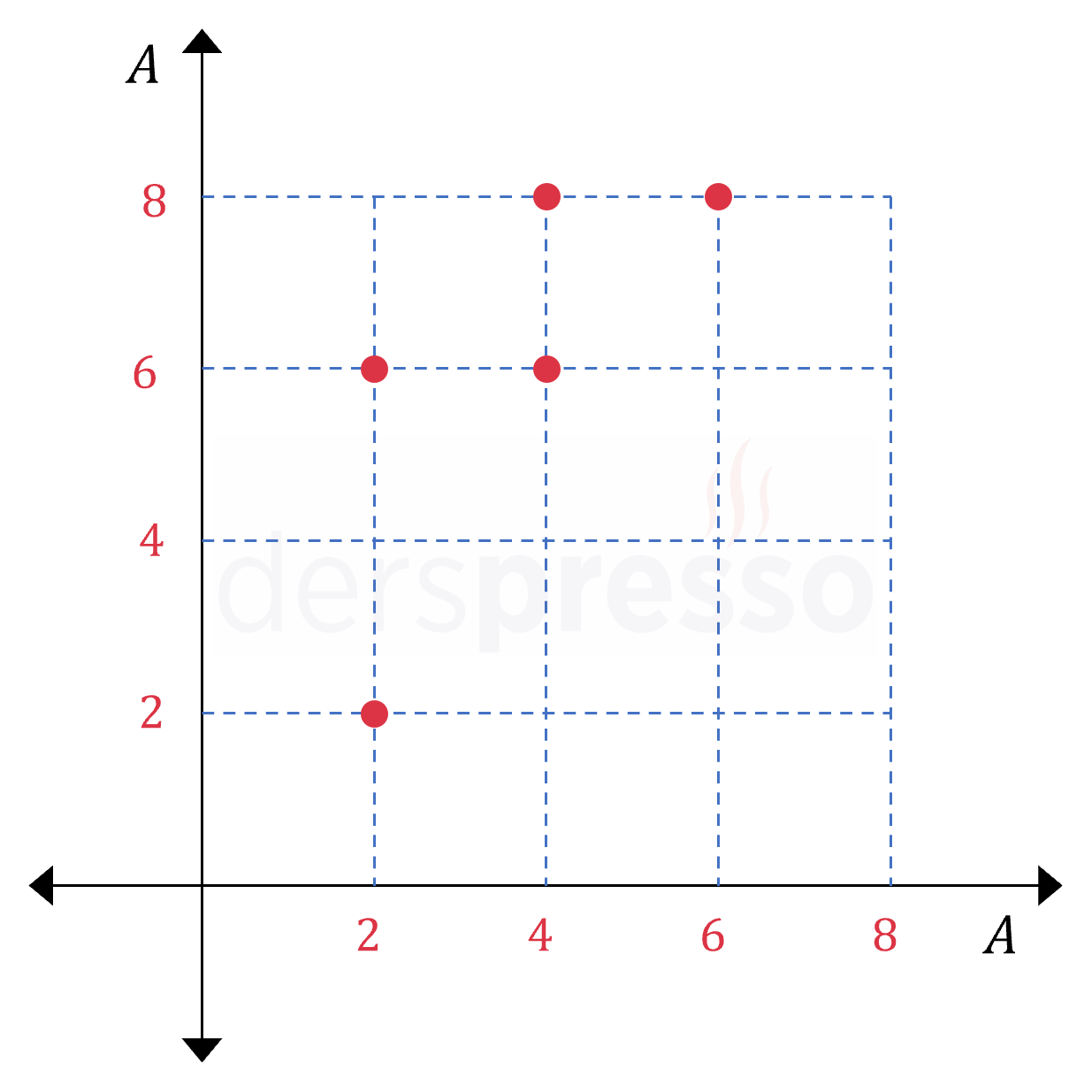
Aşağıda \( A \) kümesi üzerinde tanımlı \( R \) bağıntısının grafiği verilmiştir.
\( A = \{2, 4, 6, 8\} \)
\( R = \{(2, 2), (2, 6), (4, 6), (4, 8), (6, 8)\} \)
\( A = \{1, 3, 5, 7\} \) kümesinde tanımlı olan,
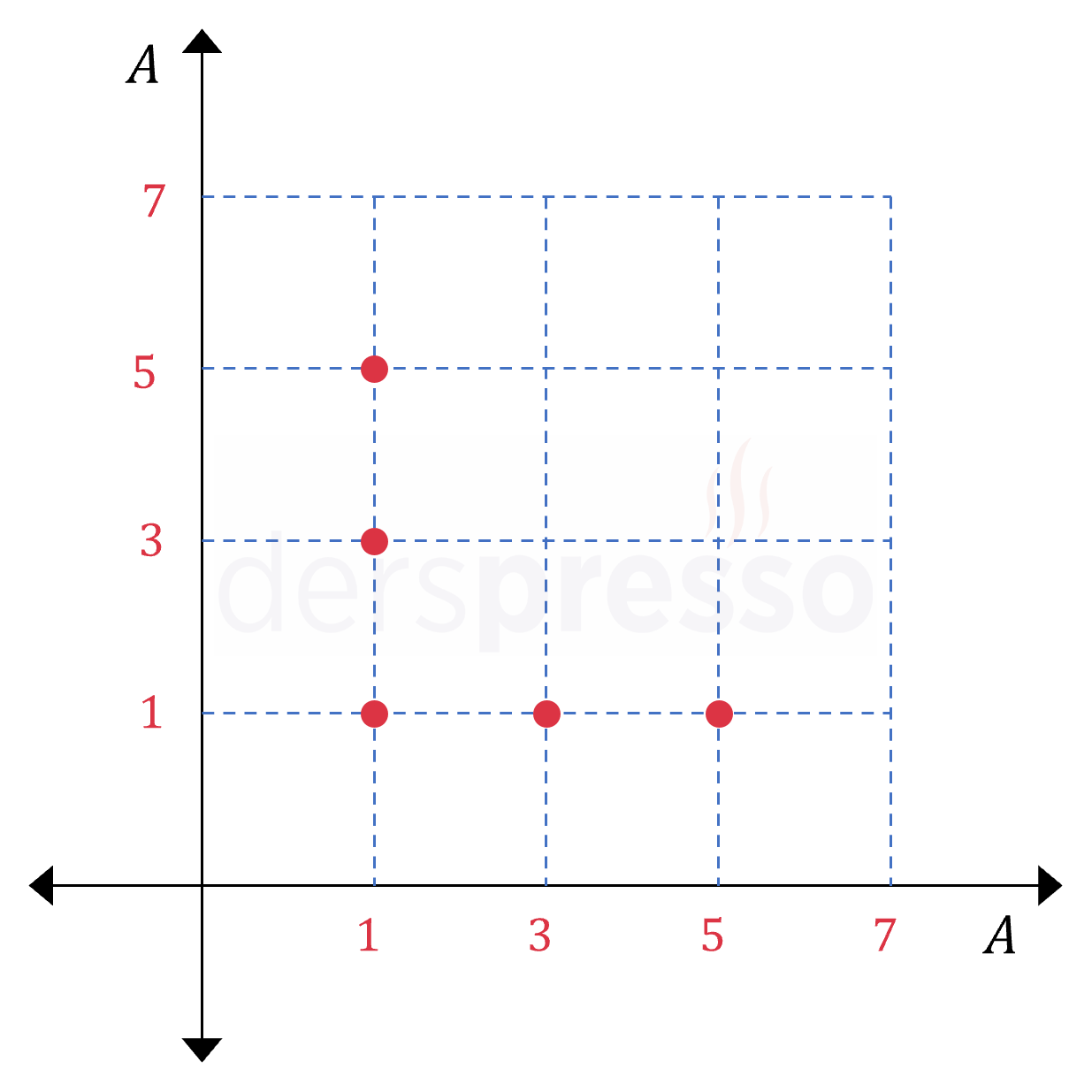
bileşenlerinin çarpımı 7'den küçük olan sıralı ikililerden oluşan bağıntıyı liste yöntemi, Venn şeması ve grafik yöntemleri ile gösterelim.
Liste yöntemiyle gösterim:
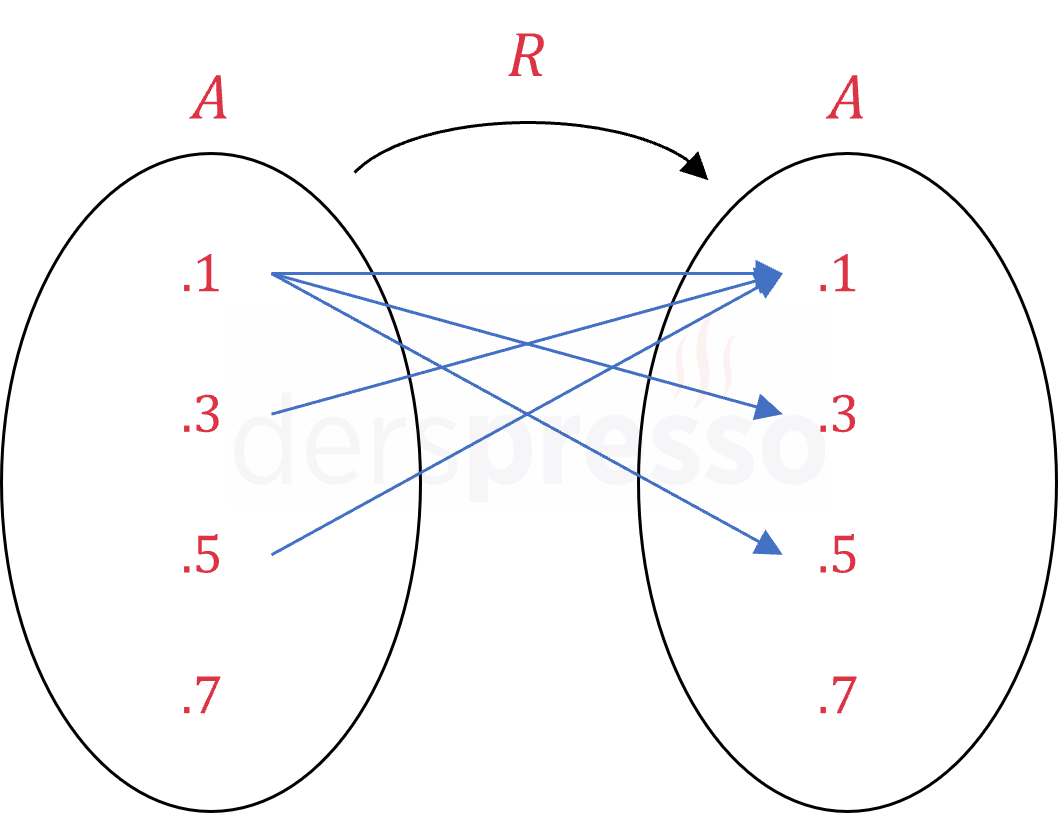
\( R = \{(1, 1), (1, 3), (1, 5), (3, 1), (5, 1)\} \)
Ortak özellik yöntemiyle gösteri:
\( R = \{(x, y) \mid x \cdot y \lt 7, x, y \in A\} \)
Venn şemasıyla gösterimi:
Grafik yöntemiyle gösterim:
Yukarıda bahsettiğimiz yöntemler dışında bağıntılar tablo ve yönlü graf (digraf) yöntemleri ile de gösterilebilir.
\( B = \{1, 2, 3, \ldots 15\} \) kümesinde tanımlı olan,
\( R = \{(a, b) \mid a \cdot b = 15; a, b \in B\} \)
bağıntısını liste yöntemiyle gösterin.
Çözümü GösterVerilen tanıma göre, \( R \) bağıntısı bileşenleri \( B \) kümesinin elemanı olan ve bileşenlerinin çarpımı 15 olan sıralı ikililerden oluşur.
Buna göre \( R \) bağıntısı aşağıdaki gibi olur.
\( R = \{(1, 15), (3, 5), (5, 3), (15, 1)\} \)
\( A = \{a, b, c, d, e\} \)
\( R = \{(x, y): x \text{ sesli harf}; y \text{ sessiz harf}; x, y \in A \} \) bağıntısı veriliyor.
\( R \) ve \( R^{-1} \) bağıntılarını liste ve grafik yöntemleriyle gösterin.
Çözümü Göster\( A \) üzerinde tanımlı olan ve birinci bileşeni sesli harflerden, ikinci bileşeni sessiz harflerden oluşan \( R \) bağıntısını yazalım.
\( R = \{ a, e \} \times \{ b, c, d \} \)
\( = \{(a, b), (a, c), (a, d), (e, b), (e, c), (e, d)\} \)
\( R^{-1} \) bağıntısı, \( R \) bağıntısının elemanlarının bileşenlerinin yerleri değiştirilerek buluur.
\( R^{-1} = \{(b, a), (c, a), (d, a), (b, e), (c, e), (d, e)\} \)
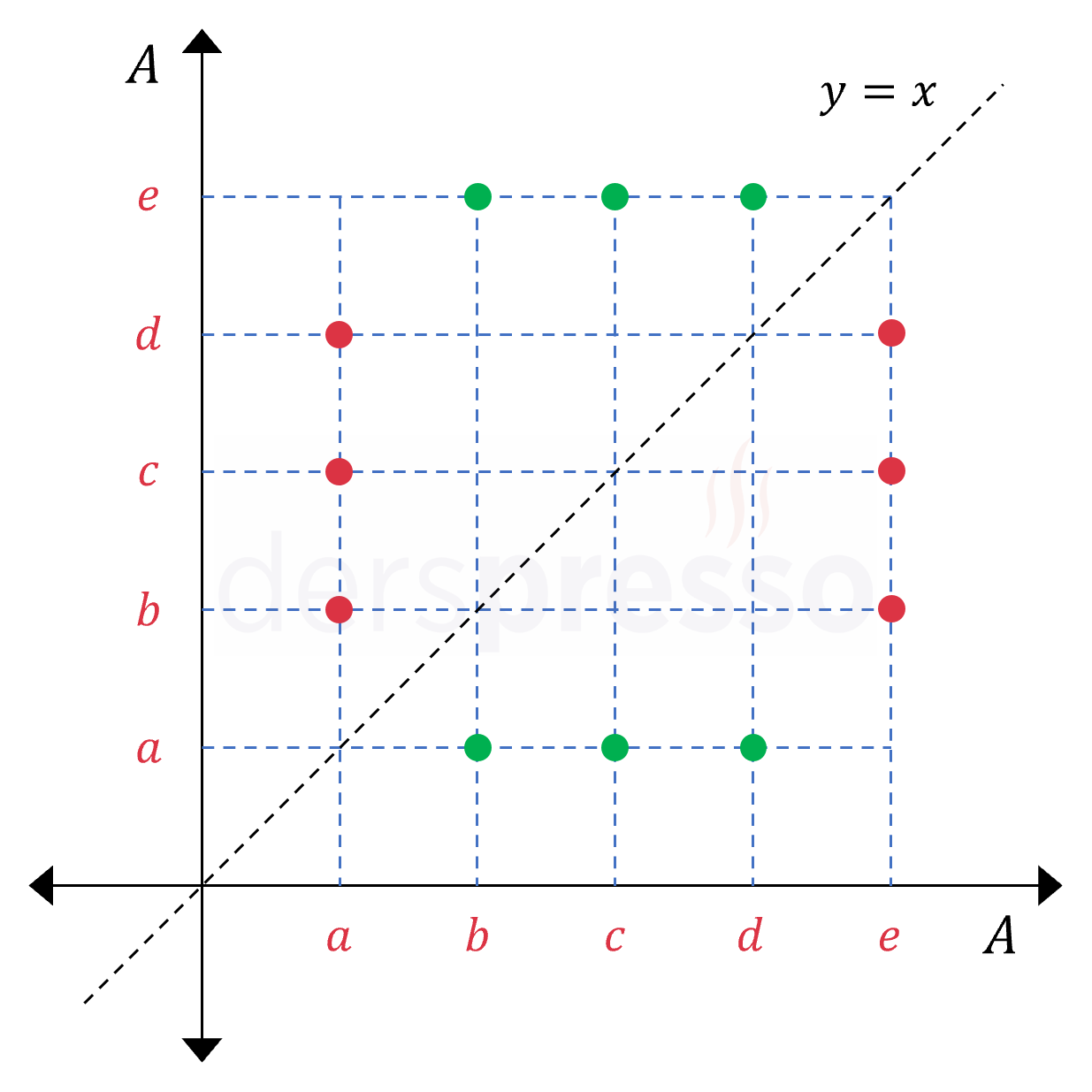
Bağıntıların grafik gösterimi aşağıdaki gibidir. Bu grafikte kırmızı noktalar \( R \) bağıntısına, yeşil noktalar \( R^{-1} \) bağıntısına aittir.
Bir bağıntının kendisinin ve tersinin grafiklerinin 1. açıortay doğrusuna göre simetrik olduklarını bu grafikte görebiliriz.