Türevlenebilirliğin Grafik Yorumu
Konu tekrarı için: Süreksizlik Tipleri
Denklemi verilen bir fonksiyonun belirli bir noktada türevlenebilir olup olmadığı türevin limit tanımı ile bulunabilir. Bu bölümde grafiği verilen bir fonksiyonun belirli bir noktada ya da aralıkta türevlenebilir olup olmadığını inceleyeceğiz.
Türevlenebilir Noktalar
Bir fonksiyonun uç nokta olmayan (açık bir aralıktaki) bir noktada soldan ve sağdan türevleri tanımlı ve birbirine eşitse fonksiyon bu noktada türevlenebilirdir. Bir diğer ifadeyle, bu noktaya soldan ve sağdan yaklaşırken fonksiyona çizilen teğet doğruların eğimleri aynı reel sayı değere yaklaşır.
Bir fonksiyon bir noktada türevlenebilir ise o noktada süreklidir. Karşıt ters ifadeyle, bir fonksiyon bir noktada sürekli değilse o noktada türevlenebilir değildir.
| Grafik | Açıklama |
|---|---|
|
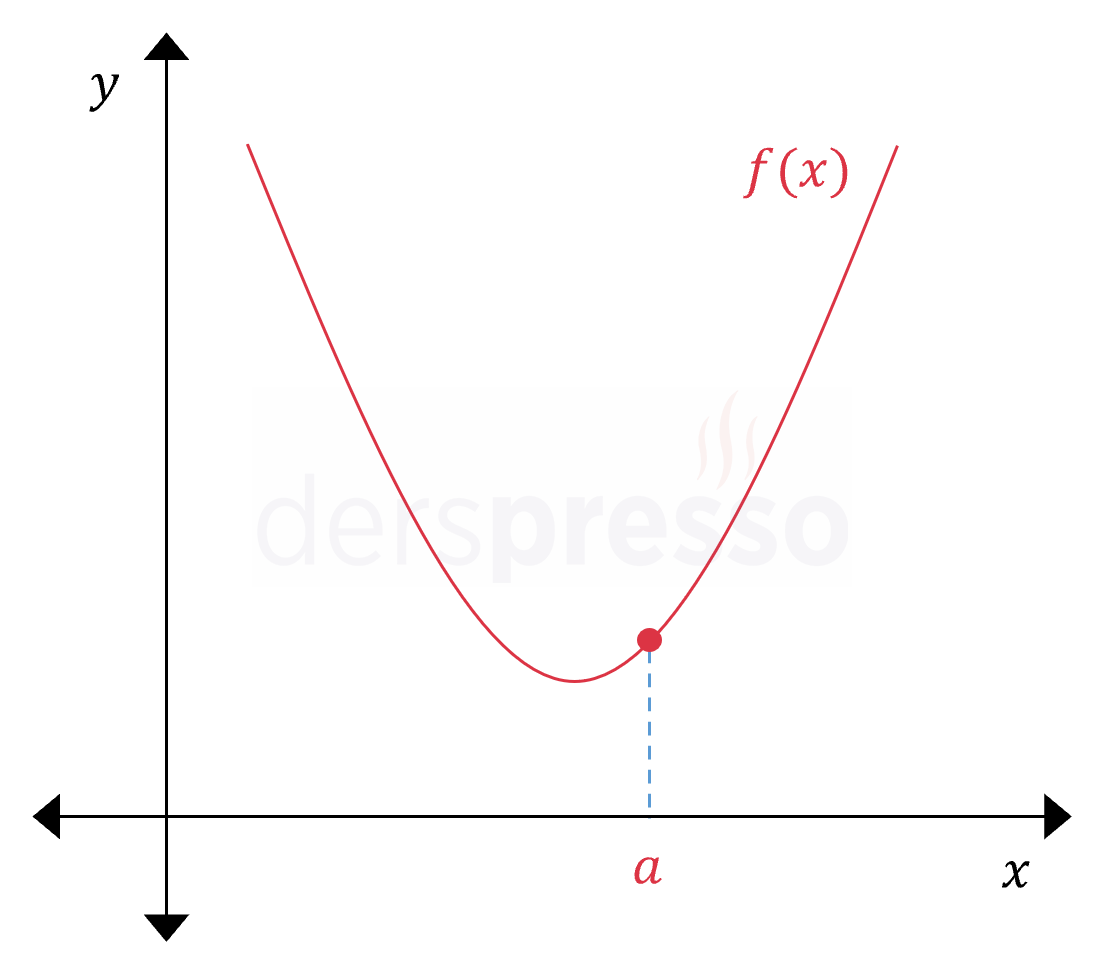
Fonksiyon \( x = a \) noktasında süreklidir, soldan ve sağdan türevler tanımlıdır ve birbirine eşittir. \( f'(a) = f'(a^-) = f'(a^+) \) Buna göre fonksiyon bu noktada türevlenebilirdir. |
|
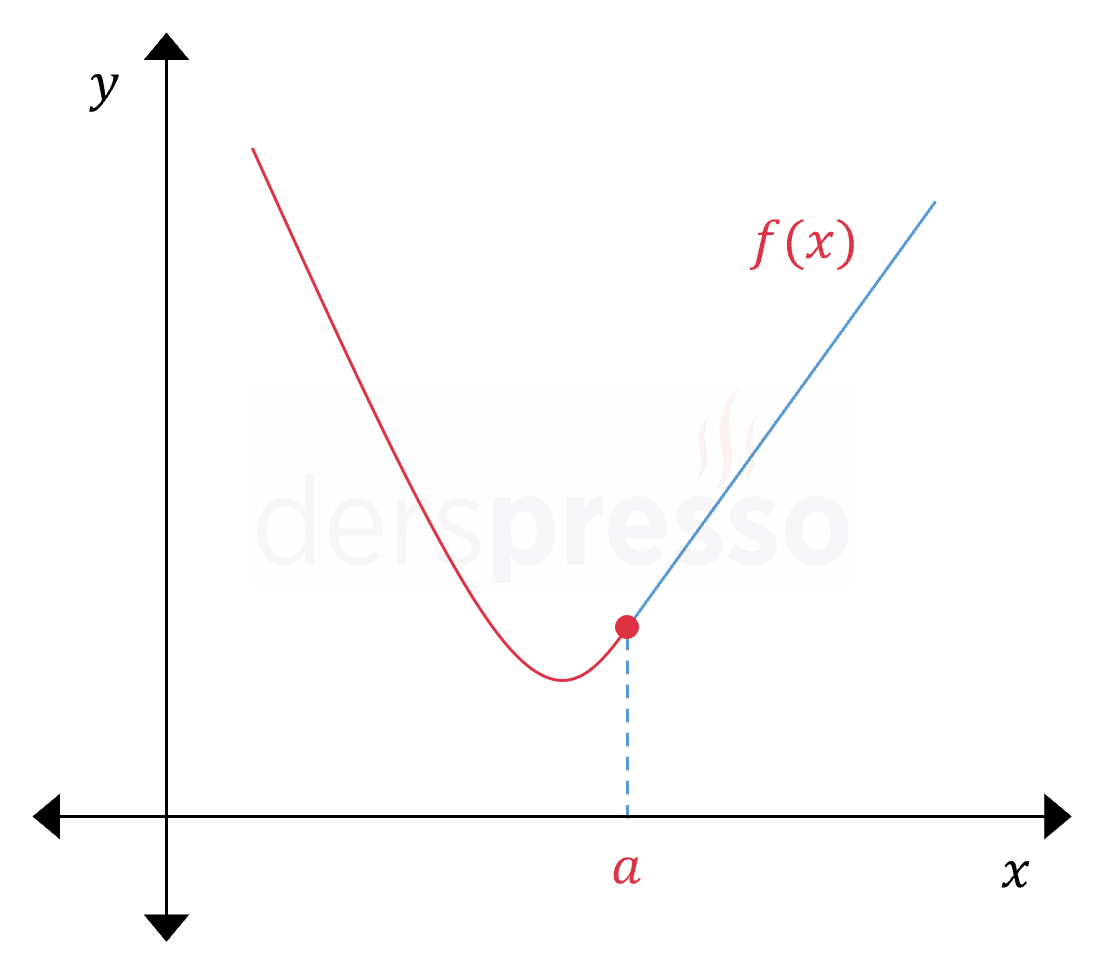
Fonksiyon \( x = a \) noktasında süreklidir, soldan ve sağdan türevler tanımlıdır ve (bu noktanın hemen solunda ve sağında eğimlerin aynı değere yaklaştığını varsayarak) birbirine eşittir. \( f'(a) = f'(a^-) = f'(a^+) \) Buna göre fonksiyon bu noktada türevlenebilirdir. |
Bir fonksiyon bir uç noktada aşağıdaki iki koşul sağlanıyorsa türevlenebilirdir.
- Fonksiyon bu noktada soldan (ya da sağdan) süreklidir.
- Fonksiyonun bu noktada soldan (ya da sağdan) türevi tanımlıdır. Bir diğer ifadeyle, bu noktaya soldan (ya da sağdan) yaklaşırken fonksiyona çizilen teğet doğruların eğimleri bir reel sayı değere yaklaşır.
Türevlenebilir Olmayan Noktalar
Bir fonksiyon bir noktada üç sebeple türevlenebilir olmayabilir.
- Süreksizlik
- Keskin könüş
- Dikey teğet
Süreksizlik
Bir noktada süreklilik bölümünde incelediğimiz kaldırılabilir, sıçrama, sonsuz ve salınım süreksizlik tiplerinden herhangi biri varsa fonksiyon o noktada türevlenebilir değildir.
| Grafik | Açıklama |
|---|---|
|
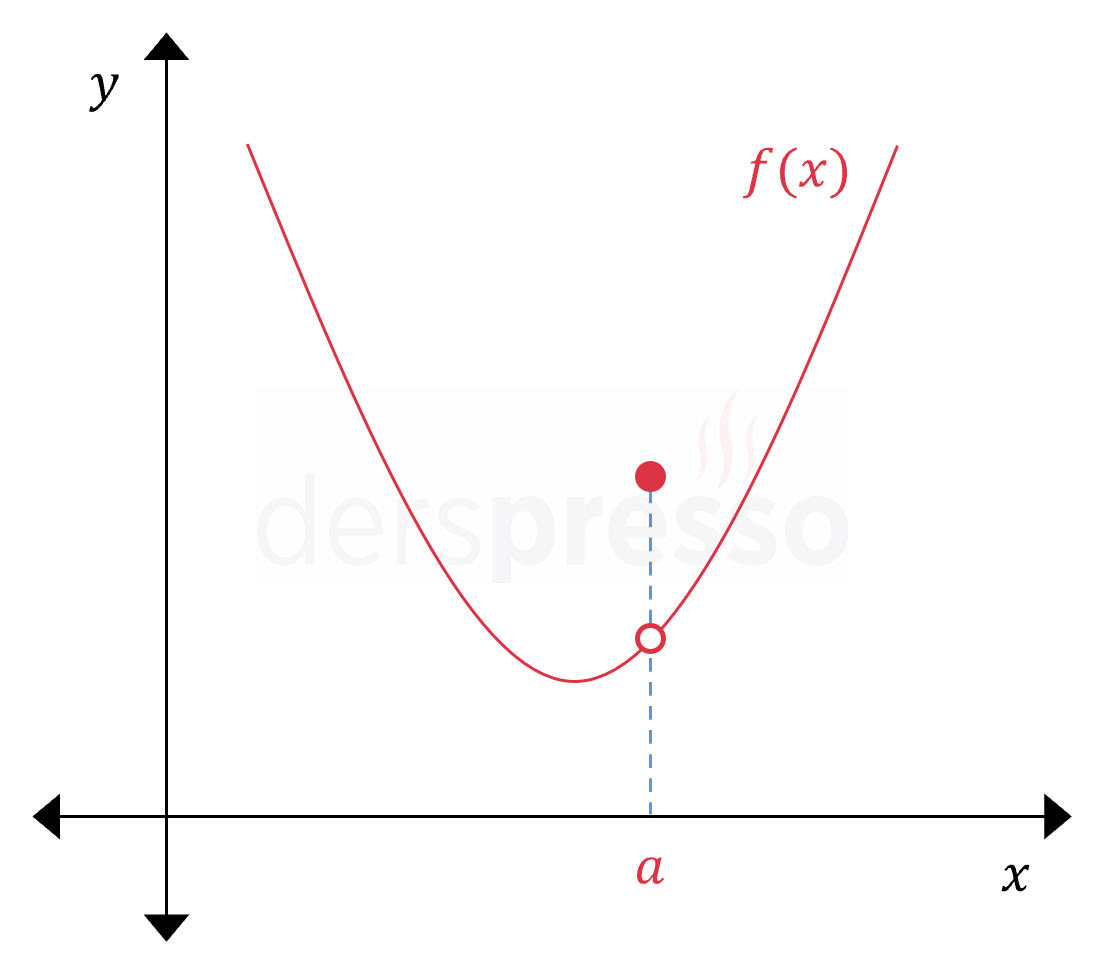
Kaldırılabilir süreksizlik Bu süreksizlik tipinde türevin limit tanımı soldan ve sağdan pozitif/negatif sonsuz sonucu verir. Soldan ve sağdan türev değerleri birer reel sayı olarak tanımlı olmadığı için fonksiyon bu noktada türevlenebilir değildir. |
|
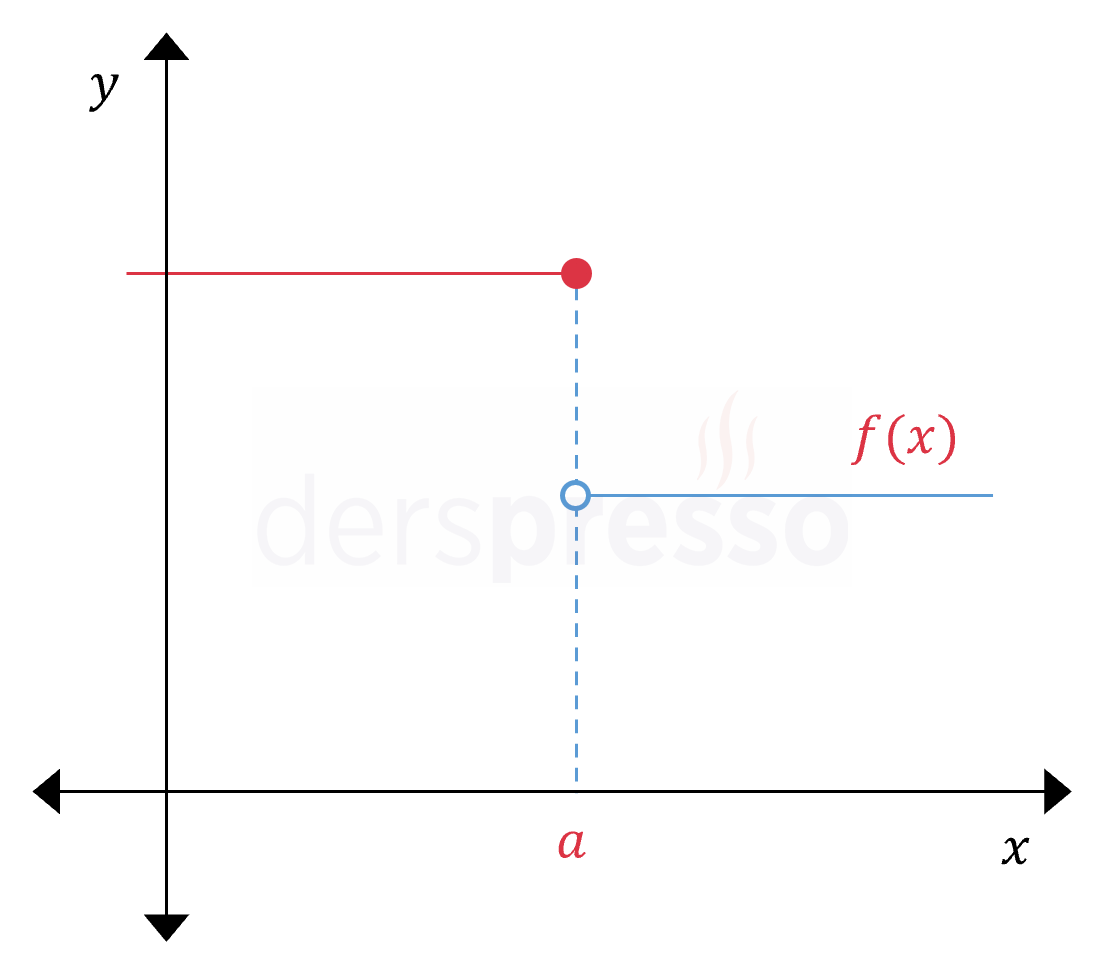
Sıçrama süreksizliği Bu süreksizlik tipinde türevin limit tanımı soldan ya da sağdan (fonksiyonun tanımsız olduğu tarafta) pozitif/negatif sonsuz sonucu verir. Soldan ya da sağdan türev değeri bir reel sayı olarak tanımlı olmadığı için fonksiyon bu noktada türevlenebilir değildir. |
|
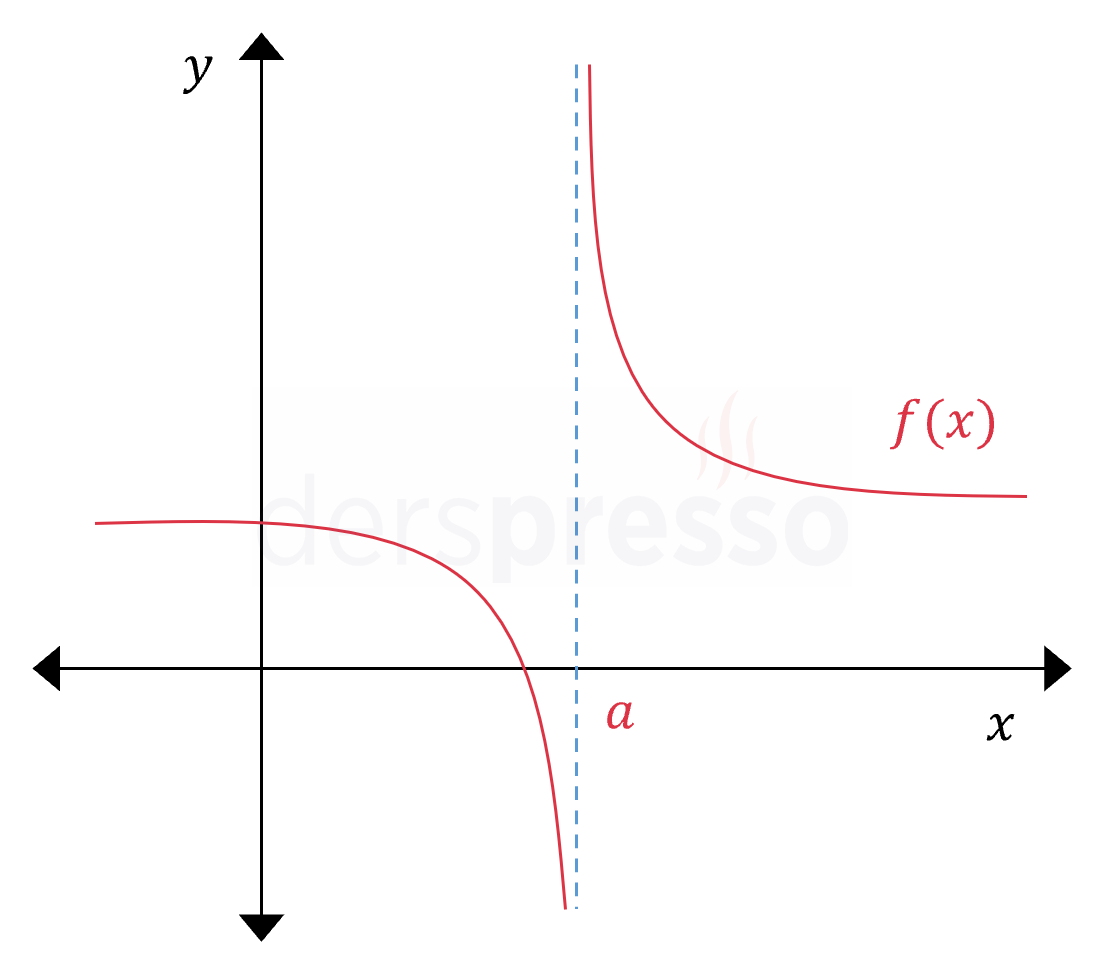
Sonsuz süreksizlik Fonksiyon bu noktada tanımlı olmadığı için türevlenebilir de değildir. |
|
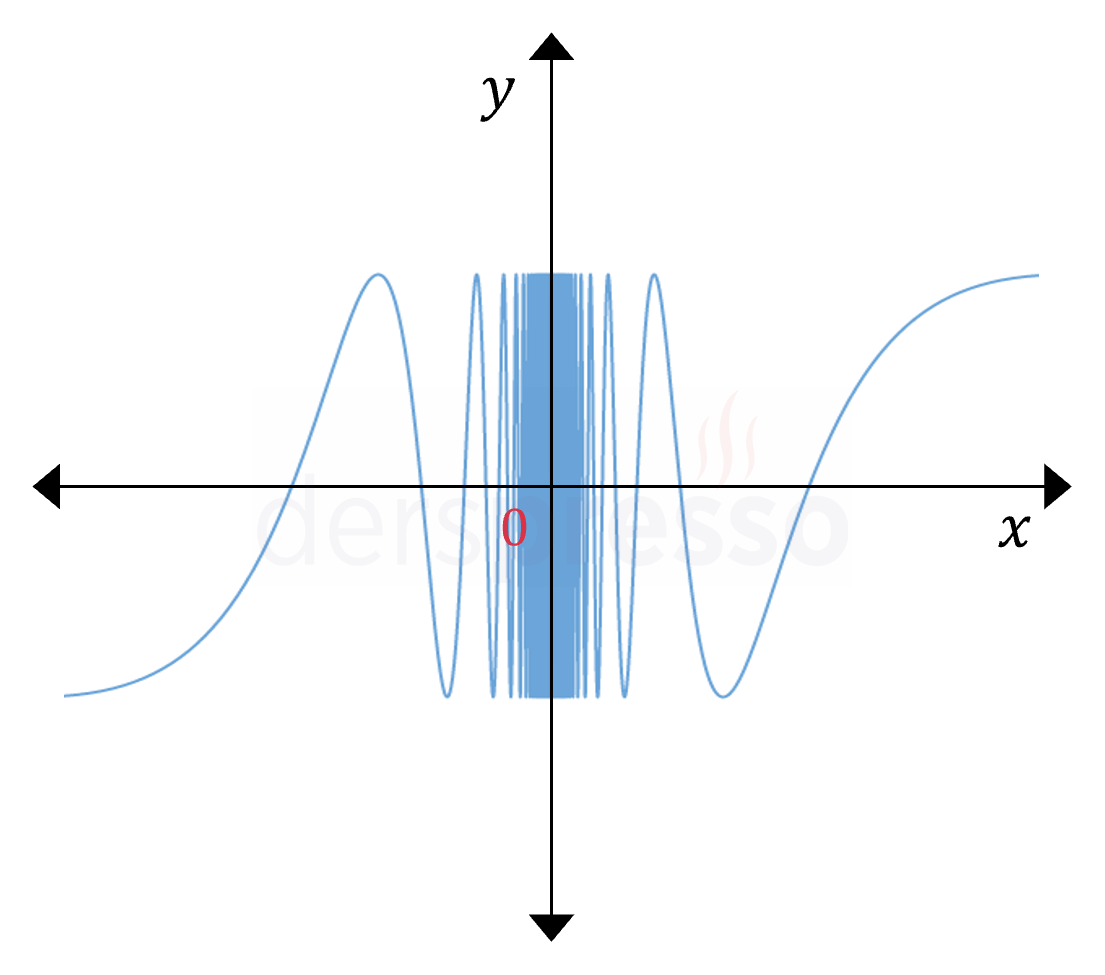
Salınım süreksizliği Bu süreksizlik tipinde türevin limit tanımı soldan ve sağdan bir reel sayı sonuç vermez. Soldan ve sağdan türev değerleri birer reel sayı olarak tanımlı olmadığı için fonksiyon bu noktada türevlenebilir değildir. |
Keskin Dönüş
Bir fonksiyon bir noktada sürekli olsa da bu noktaya soldan ve sağdan yaklaşırken fonksiyona çizilen teğet doğrular aynı eğim değerine yaklaşmayabilir. Bu durumda fonksiyon grafiğinde keskin dönüşler (sivri uç, köşe vb.) oluşur.
| Grafik | Açıklama |
|---|---|
|
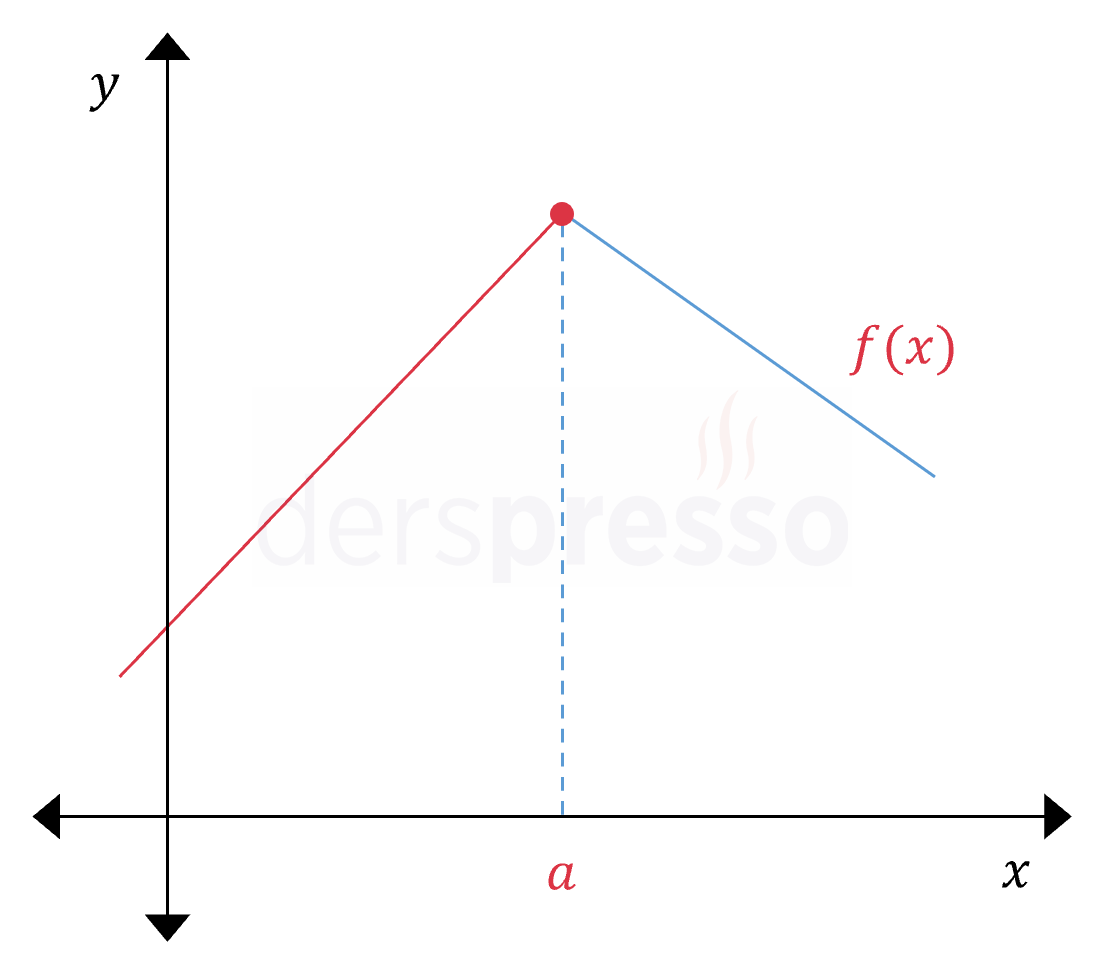
Fonksiyon \( x = a \) noktasında süreklidir, soldan ve sağdan türevler tanımlıdır, ancak birbirine eşit değildir (bu noktanın solunda ve sağında eğimler farklı değerlere yaklaşır). \( f'(a^-) \ne f'(a^+) \) Buna göre fonksiyon bu noktada türevlenebilir değildir. |
|
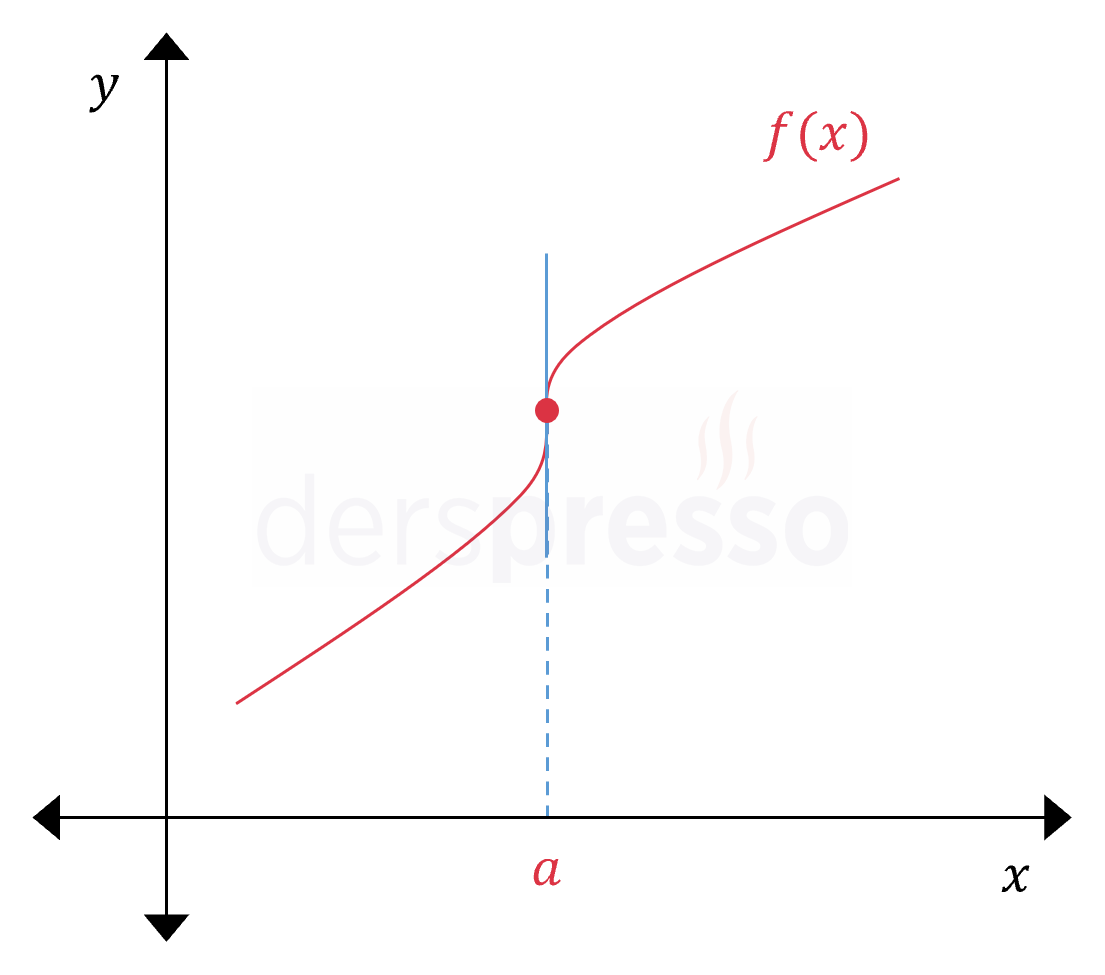
Fonksiyon \( x = a \) noktasında süreklidir, soldan ve sağdan türevler tanımlıdır, ancak birbirine eşit değildir (bu noktanın solunda ve sağında eğimler farklı değerlere yaklaşır). \( f'(a^-) \ne f'(a^+) \) Buna göre fonksiyon bu noktada türevlenebilir değildir. |
Dikey Teğet
Bir noktadaki teğet doğrunun eğim açısının 90° olduğu durumda eğim değeri tanımsız olduğu için (\( m = \tan{90°} \)) türev bir reel değere sahip olmaz, dolayısıyla fonksiyon böyle bir noktada türevlenebilir değildir.
| Grafik | Açıklama |
|---|---|
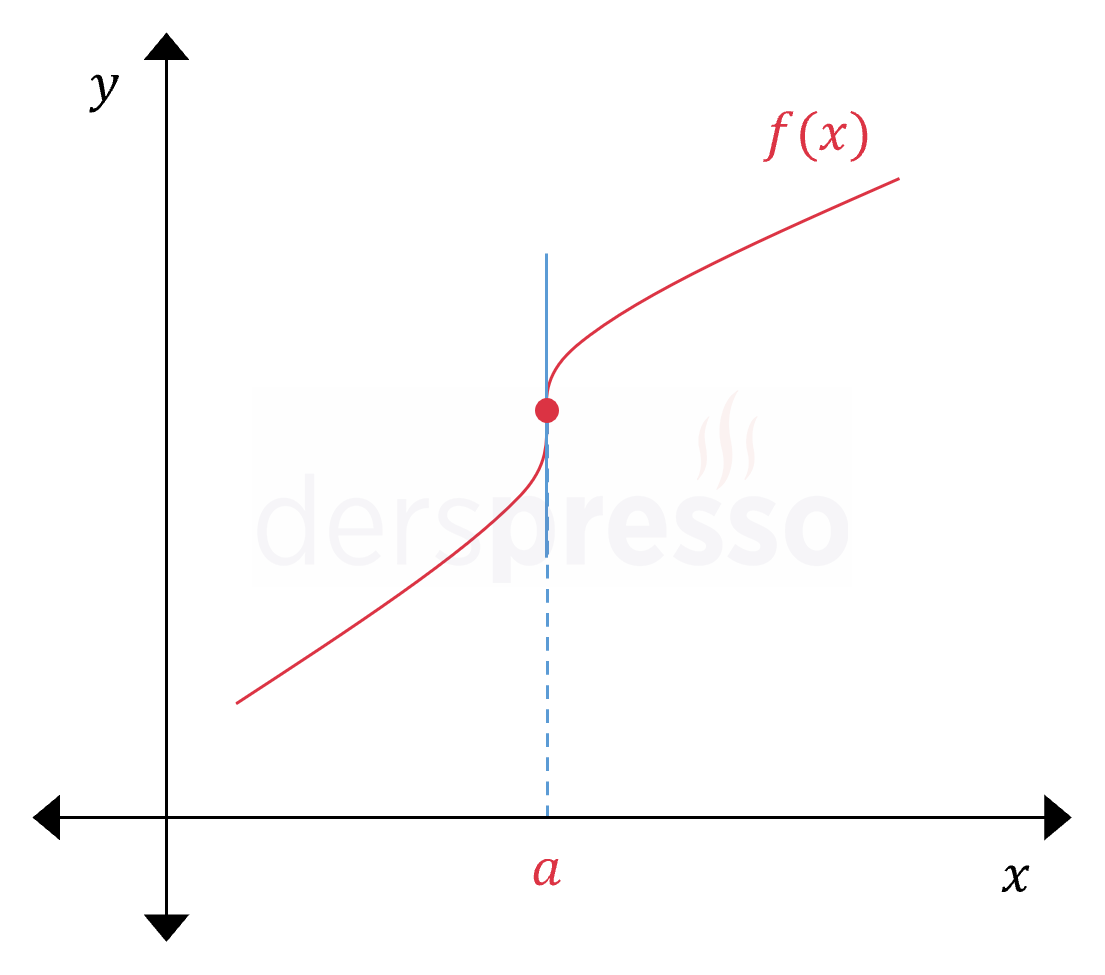
|
Fonksiyon \( x = a \) noktasında süreklidir, ancak fonksiyona bu noktada teğet olan doğru dikey olduğu için eğimi tanımsızdır, dolayısıyla fonksiyon bu noktada soldan ve sağdan türevlenebilir değildir. \( f'(a^-) \) ve \( f'(a^+) \): tanımsız Buna göre fonksiyon bu noktada türevlenebilir değildir. |
Türev Grafiğinde Süreksizlik
Bir fonksiyonun bir noktada türevlenebilir olması için o noktada soldan ve sağdan türevlerinin tanımlı ve birbirine eşit olması gerektiğini belirttik. Buna göre bir türev fonksiyon grafiği belirli bir noktada tanımlı ise grafik bu noktada soldan ve sağdan bu tanımlı türev değerine yaklaşmalıdır, dolayısıyla türev grafiği bu noktada sürekli olmalıdır.
Bu bilgi doğrultusunda bir fonksiyonun türevinin grafiği aşağıdaki birinci ve ikinci şekilde olabilirken üçüncü şekilde olamaz.
| Grafik | Açıklama |
|---|---|
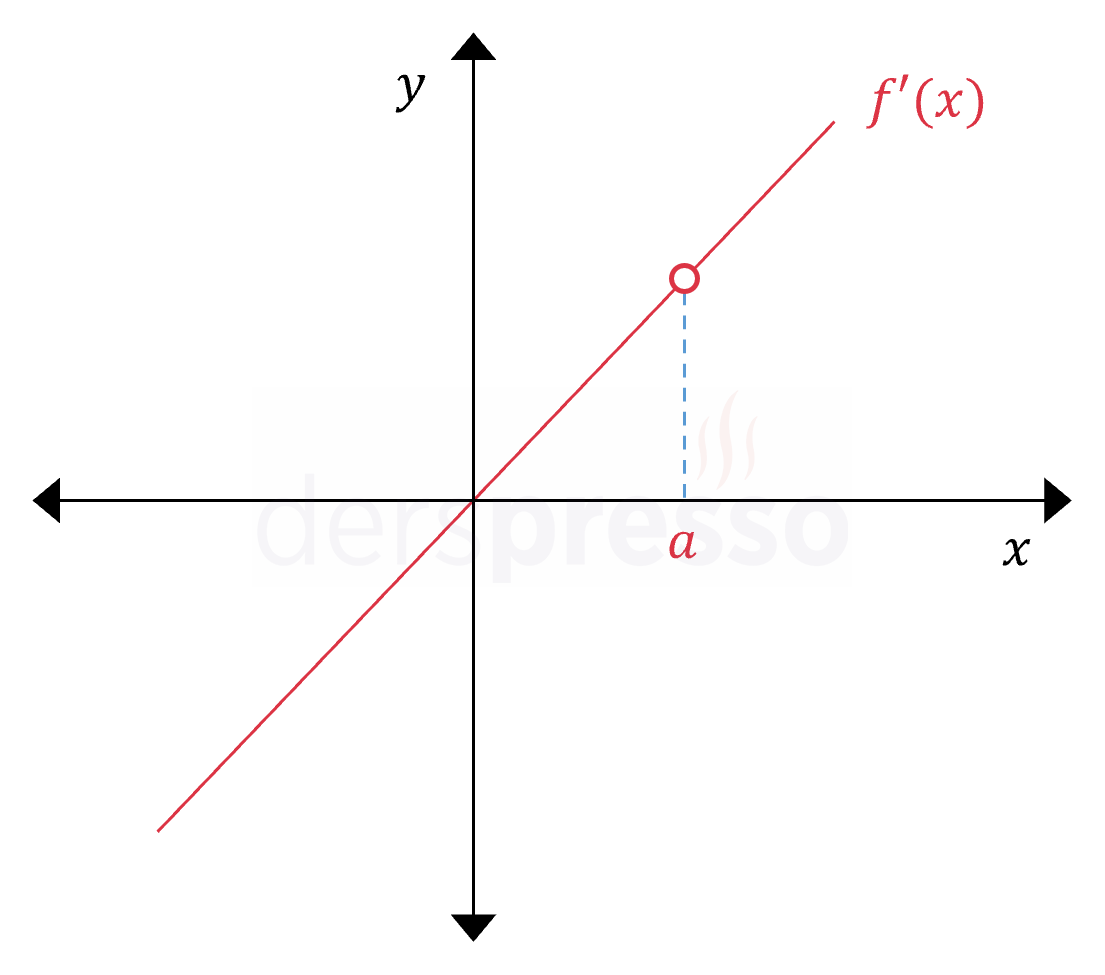
|
Türev fonksiyonu \( x = a \) noktasında tanımsız olduğu için türev grafiği bu noktada limitli ama süreksiz olabilir. Örneğin yanda verilen grafik \( x = a \) noktasında tanımsız olan \( f(x) = \dfrac{x^2(x - a)}{x - a} \) fonksiyonunun türev grafiği olabilir. |
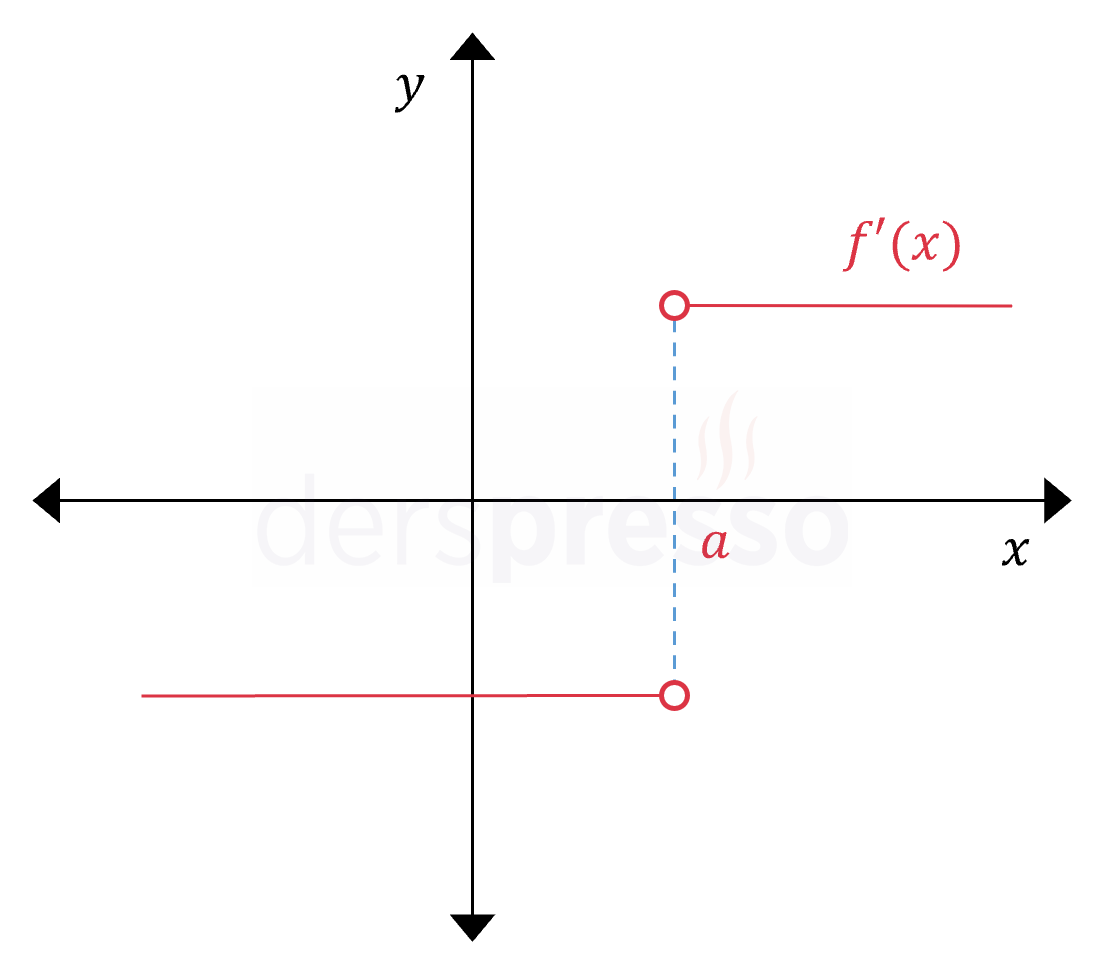
|
Türev fonksiyonu \( x = a \) noktasında tanımsız olduğu için türev grafiği bu noktada hem limitsiz hem de süreksiz olabilir. Örneğin yanda verilen grafik \( f(x) = \abs{x - a} \) fonksiyonunun türev grafiği olabilir. |
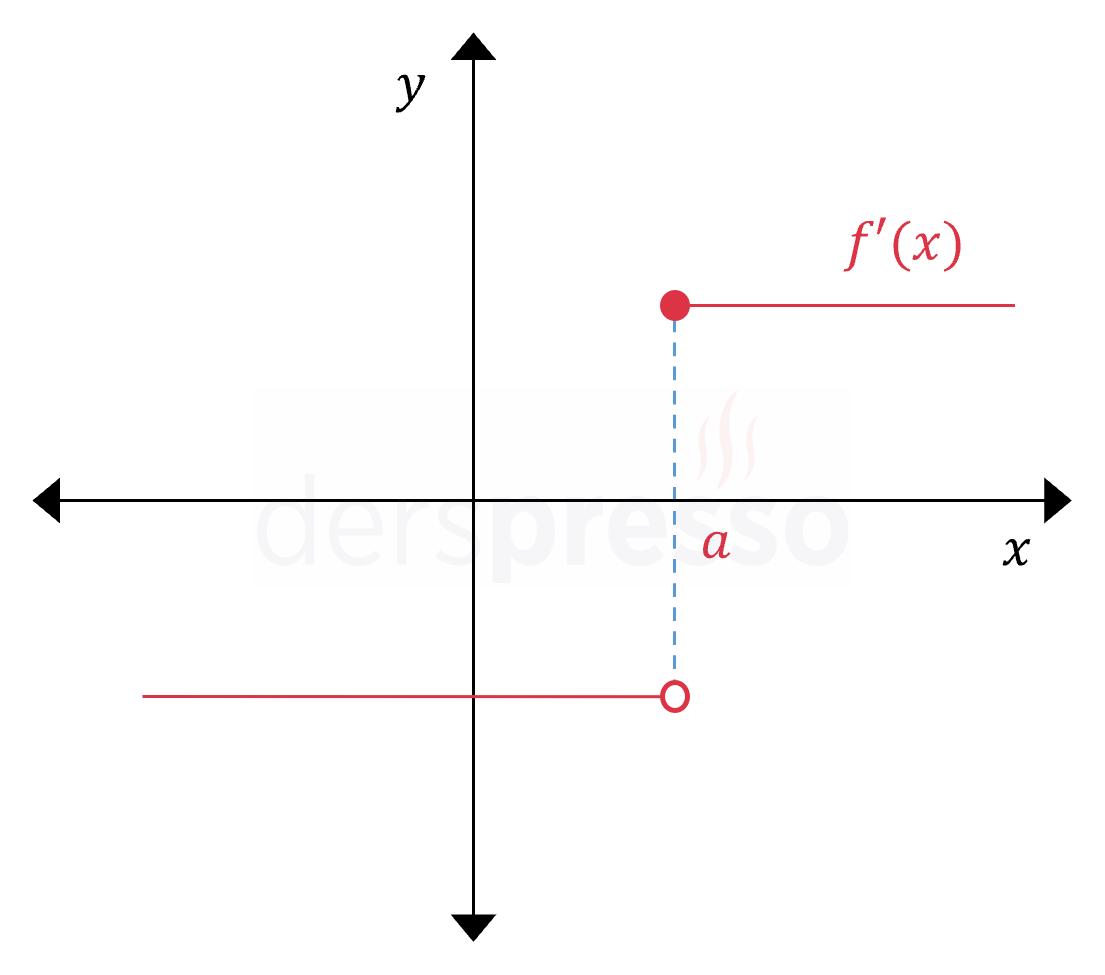
|
Türev fonksiyonu \( x = a \) noktasında tanımlı olduğu için aynı zamanda sürekli olmalıdır. Bunun sebebi, türev grafiği \( x = a \) noktasında tanımlı ise soldan ve sağdan türev değerlerinin de aynı tanımlı değere yaklaşması gerekir. Buna göre yanda verilen grafik bir fonksiyonun türev grafiği olamaz. |
Bir fonksiyon açık bir aralıkta bulunan bir noktada türevlenebilir ise bu nokta için aşağıdaki ifadelerden hangileri kesinlikle doğrudur?
- Limiti tanımlıdır.
- Tanımlıdır.
- Süreklidir.
- Soldan ve sağdan türevleri birbirine eşittir.
Bir fonksiyon açık bir aralıkta bulunan bir noktada türevlenebilir ise bu noktada soldan ve sağdan türevleri tanımlıdır ve birbirine eşittir.
Bir fonksiyon bir noktada türevlenebilir ise bu noktada süreklidir.
Bir fonksiyon açık bir aralıkta bulunan bir noktada sürekli ise soldan ve sağdan limit değerleri ve fonksiyon değeri tanımlı ve birbirine eşittir.
Buna göre verilen ifadelerin tümü kesinlikle doğrudur.
Aşağıda grafiği verilen \( f \) fonksiyonu verilen aralıkta kaç noktada türevlenebilir değildir?
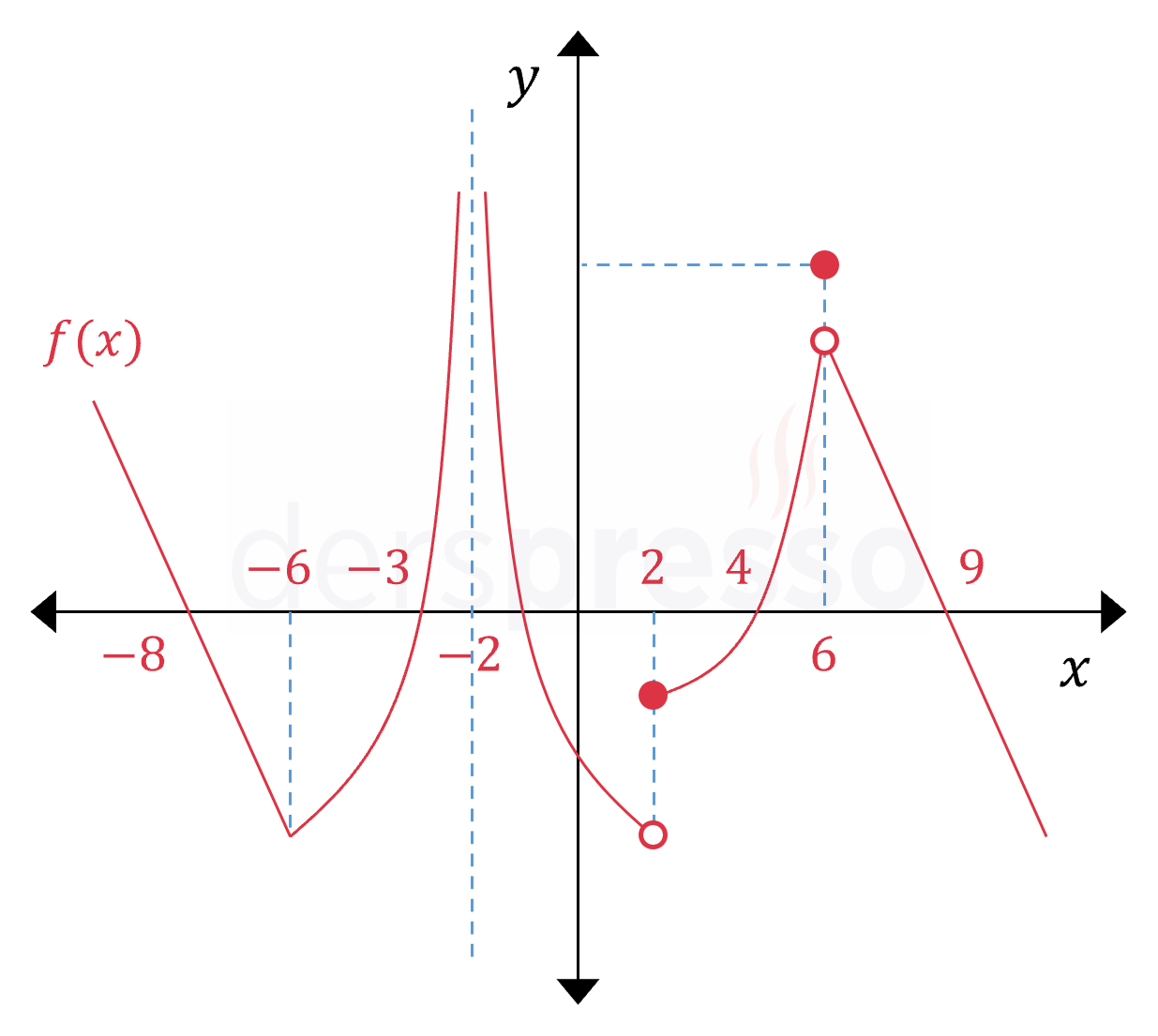
Fonksiyon;
\( x = -6 \) noktasında soldan ve sağdan türev değerleri eşit olmadığı için,
\( x = -2 \) noktasında sonsuz süreksizlik tipinde süreksiz olduğu için,
\( x = 2 \) noktasında sıçrama süreksizliği tipinde süreksiz olduğu için,
\( x = 6 \) noktasında kaldırılabilir süreksizlik tipinde süreksiz olduğu için,
türevlenebilir değildir.
Buna göre fonksiyon verilen aralıkta 4 noktada türevlenebilir değildir.
Aşağıda grafiği verilen \( f \) fonksiyonu verilen aralıkta kaç noktada türevlenebilir değildir?
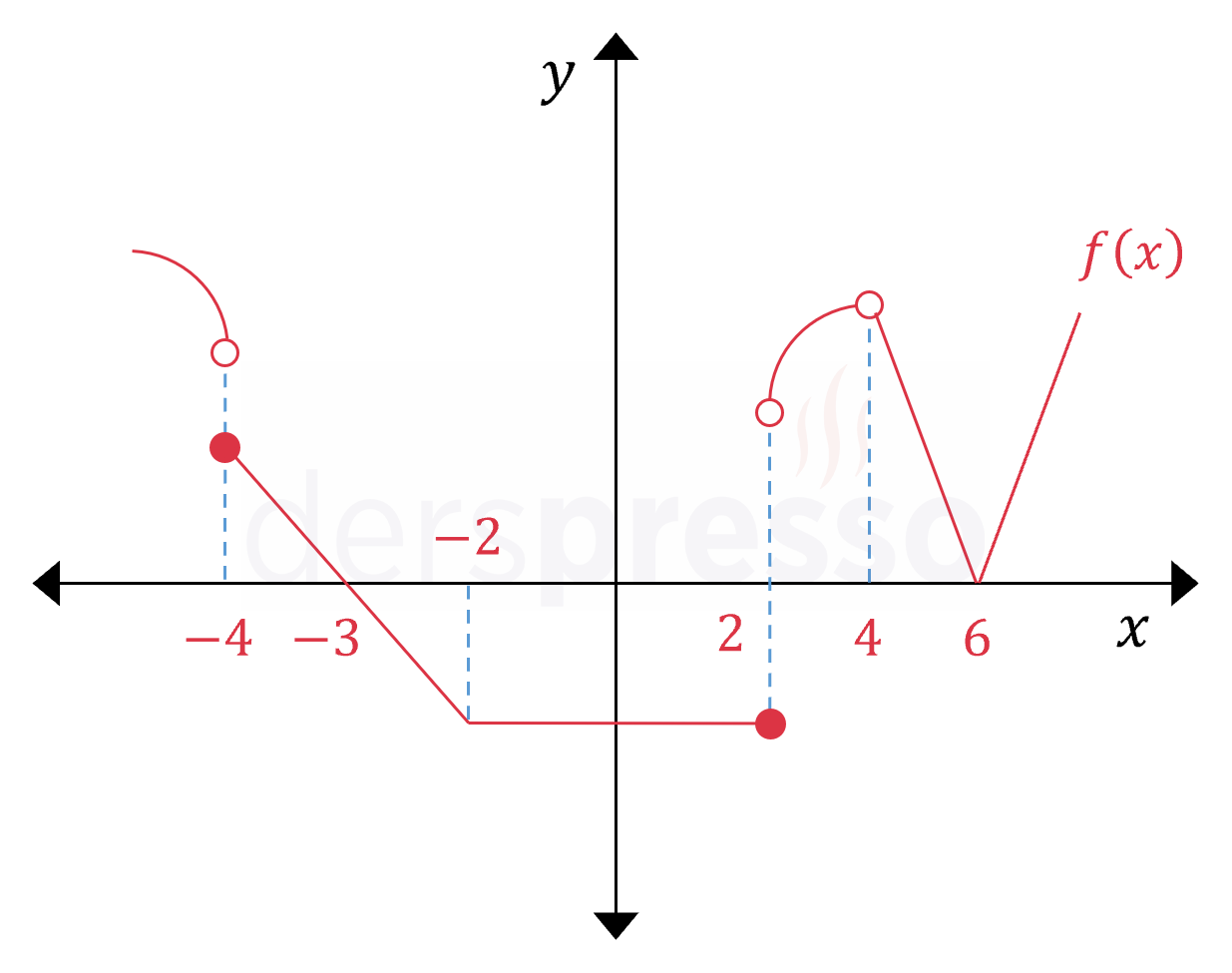
Fonksiyon;
\( x = -4 \) noktasında sıçrama süreksizliği tipinde süreksiz olduğu için,
\( x = -2 \) noktasında soldan ve sağdan türev değerleri eşit olmadığı için,
\( x = 2 \) noktasında sıçrama süreksizliği tipinde süreksiz olduğu için,
\( x = 4 \) noktasında tanımsız olduğu için,
\( x = 6 \) noktasında soldan ve sağdan türev değerleri eşit olmadığı için,
türevlenebilir değildir.
Buna göre fonksiyon verilen aralıkta 5 noktada türevlenebilir değildir.
Aşağıda grafiği verilen fonksiyonun \( x \in \{-6, -2, 2, 6\} \) noktalarında türevlenebilirliğini inceleyin.
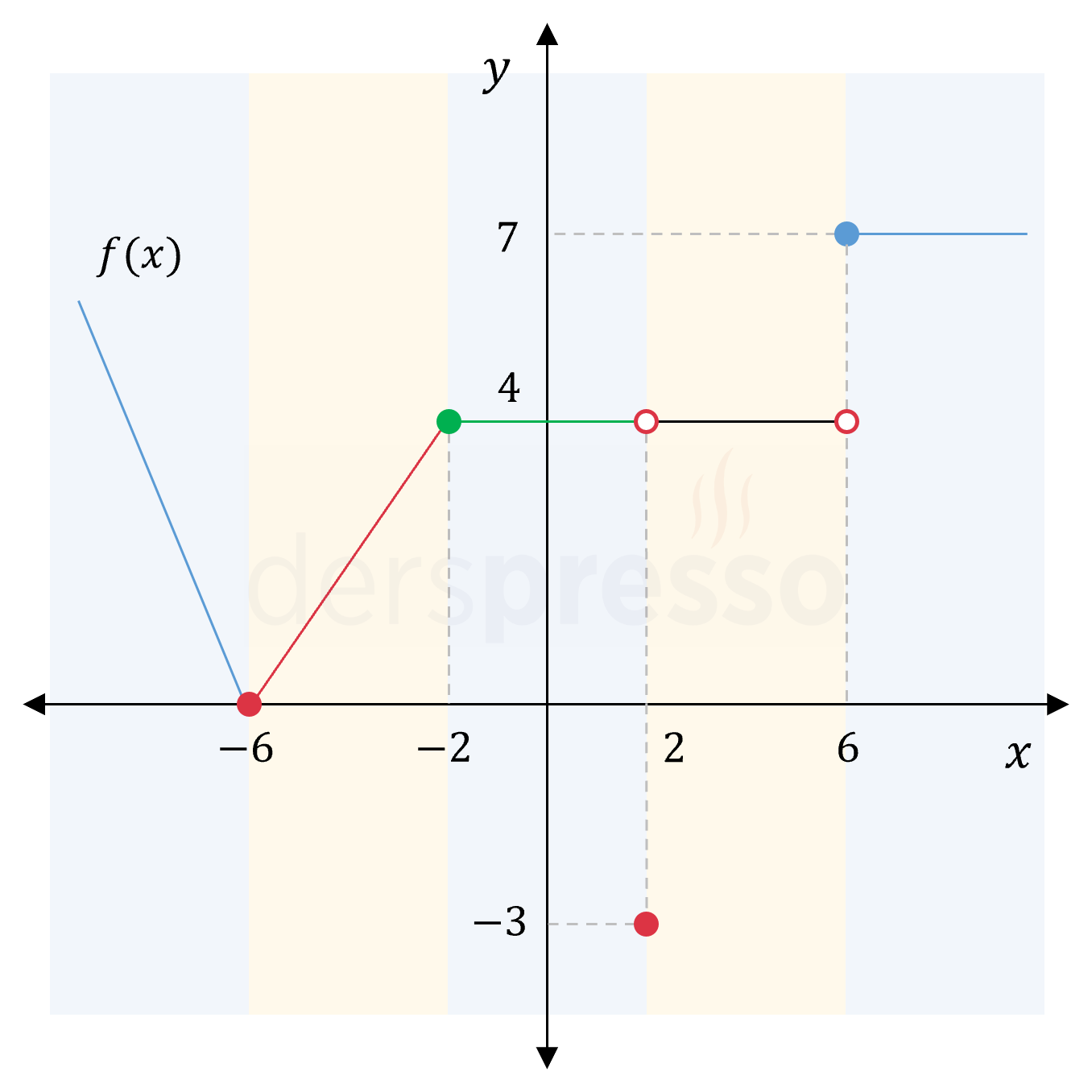
Bir fonksiyonun bir noktada türevlenebilir olması için bu noktadaki soldan ve sağdan türevler birer reel sayı olarak tanımlı ve birbirine eşit olmalıdır. Türevlenebilirlik tanımı sürekliliği de içerdiği için, bir noktada sürekli olmayan bir fonksiyon o noktada türevlenebilir de değildir.
Fonksiyon \( x = -6 \) noktasında süreklidir, ancak soldan ve sağdan türevler birbirine eşit değildir. Bu yüzden fonksiyon bu noktada türevlenebilir değildir.
Fonksiyon \( x = -2 \) noktasında süreklidir, ancak soldan ve sağdan türevler eşit değildir. Bu yüzden fonksiyon bu noktada türevlenebilir değildir.
Fonksiyonun \( x = 2 \) noktasında soldan ve sağdan limit değerleri eşit olsa da bu noktadaki fonksiyon değeri farklı olduğu için fonksiyon bu noktada süreksizdir. Bu yüzden fonksiyon bu noktada türevlenebilir değildir.
Fonksiyonun \( x = 6 \) noktasında soldan ve sağdan limit değerleri eşit olmadığı için fonksiyon bu noktada süreksizdir. Bu yüzden fonksiyon bu noktada türevlenebilir değildir.
\( g(x) = \dfrac{1}{x^2 - 2x + a} \) fonksiyonunun tüm reel sayılarda türevlenebilir olabilmesi için \( a \) sayısının alabileceği en küçük tam sayı değeri nedir?
Çözümü GösterRasyonel fonksiyonlar paydalarını sıfır yapan \( x \) değerleri dışındaki tüm noktalarda sürekli ve türevlenebilirdir.
Buna göre verilen rasyonel fonksiyonda sürekliliği ve türevlenebilirliği bozabilecek tek durum paydanın sıfır olma durumudur.
Paydanın hiçbir \( x \) değerinde sıfır olmaması için ikinci derece ifadenin diskriminantı sıfırdan küçük olmalıdır (ifadeyi sıfır yapan reel kök bulunmamalıdır).
\( \Delta = (-2)^2 - 4(1)(a) \lt 0 \)
\( 4a \gt 4 \)
\( a \gt 1 \)
Buna göre \( a \)'nın alabileceği en küçük tam sayı değeri 2 olur.