Trigonometrik Fonksiyonların Türevi
Bu bölümde trigonometrik ve ters trigonometrik fonksiyonların türev alma kurallarını inceleyeceğiz.
Trigonometrik Fonksiyonlar
Trigonometrik fonksiyonların türevlenebilir oldukları aralıklarda türev alma kuralları aşağıdaki gibidir.
\( f(x) = \sin{x} \)
\( f'(x) = \cos{x} \)
İSPATI GÖSTER
Türev fonksiyonunun limit tanımını yazalım.
\( f'(x) = \lim\limits_{h \to 0} \dfrac{f(x + h) - f(x)}{h} \)
\( f(x) = \sin{x} \)
\( f(x + h) = \sin(x + h) \)
\( f'(x) = \lim\limits_{h \to 0} \dfrac{\sin(x + h) - \sin{x}}{h} \)
\( \sin(x + h) \) ifadesine sinüs toplam formülünü uygulayalım.
\( \sin(x + h) = \sin{x}\cos{h} + \cos{x}\sin{h} \)
\( = \lim\limits_{h \to 0} \dfrac{\sin{x}\cos{h} + \cos{x}\sin{h} - \sin{x}}{h} \)
Terimleri düzenleyelim.
\( = \lim\limits_{h \to 0} \left( \dfrac{\sin{x}\cos{h} - \sin{x}}{h} + \dfrac{\cos{x}\sin{h}}{h} \right) \)
\( = \lim\limits_{h \to 0} \left( \sin{x}\dfrac{\cos{h} - 1}{h} + \cos{x}\dfrac{\sin{h}}{h} \right) \)
Toplama limit kuralı ile iki terimin toplamının limitini terimlerin limitinin toplamı şeklinde yazalım.
\( = \lim\limits_{h \to 0} \sin{x}\dfrac{\cos{h} - 1}{h} + \lim\limits_{h \to 0} \cos{x}\dfrac{\sin{h}}{h} \)
\( x \) cinsinden olan ifadeleri limitin dışına alalım.
\( = \sin{x}\lim\limits_{h \to 0} \dfrac{\cos{h} - 1}{h} + \cos{x}\lim\limits_{h \to 0} \dfrac{\sin{h}}{h} \)
Trigonometrik ifadelerin limiti bölümünde aşağıdaki iki limiti ispatlarıyla tanımlamıştık.
\( \lim\limits_{x \to 0} \dfrac{\sin{x}}{x} = 1 \)
\( \lim\limits_{x \to 0} \dfrac{1 - \cos{x}}{x} = 0 \)
Bu limit değerlerini yerine koyalım.
\( = \sin{x} \cdot 0 + \cos{x} \cdot 1 \)
\( = \cos{x} \)
Buna göre, \( f(x) = \sin{x} \) fonksiyonunun türevi \( f'(x) = \cos{x} \) fonksiyonudur.
\( f(x) = \cos{x} \)
\( f'(x) = -\sin{x} \)
İSPATI GÖSTER
Türev fonksiyonunun limit tanımını yazalım.
\( f'(x) = \lim\limits_{h \to 0} \dfrac{f(x + h) - f(x)}{h} \)
\( f(x) = \cos{x} \)
\( f(x + h) = \cos(x + h) \)
\( f'(x) = \lim\limits_{h \to 0} \dfrac{\cos(x + h) - \cos{x}}{h} \)
\( \cos(x + h) \) ifadesine kosinüs toplam formülünü uygulayalım.
\( \cos(x + h) = \cos{x}\cos{h} - \sin{x}\sin{h} \)
\( = \lim\limits_{h \to 0} \dfrac{\cos{x}\cos{h} - \sin{x}\sin{h} - \cos{x}}{h} \)
Terimleri düzenleyelim.
\( = \lim\limits_{h \to 0} \left( \dfrac{\cos{x}\cos{h} - \cos{x}}{h} - \dfrac{\sin{x}\sin{h}}{h} \right) \)
\( = \lim\limits_{h \to 0} \left( \cos{x}\dfrac{\cos{h} - 1}{h} - \sin{x}\dfrac{\sin{h}}{h} \right) \)
Toplama limit kuralı ile iki terimin toplamının limitini terimlerin limitinin toplamı şeklinde yazalım.
\( = \lim\limits_{h \to 0} \cos{x}\dfrac{\cos{h} - 1}{h} - \lim\limits_{h \to 0} \sin{x}\dfrac{\sin{h}}{h} \)
\( x \) cinsinden olan ifadeleri limitin dışına alalım.
\( = \cos{x}\lim\limits_{h \to 0} \dfrac{\cos{h} - 1}{h} - \sin{x}\lim\limits_{h \to 0} \dfrac{\sin{h}}{h} \)
Trigonometrik ifadelerin limiti bölümünde aşağıdaki iki limiti ispatlarıyla tanımlamıştık.
\( \lim\limits_{x \to 0} \dfrac{\sin{x}}{x} = 1 \)
\( \lim\limits_{x \to 0} \dfrac{1 - \cos{x}}{x} = 0 \)
Bu limit değerlerini yerine koyalım.
\( = \cos{x} \cdot 0 - \sin{x} \cdot 1 \)
\( = -\sin{x} \)
Buna göre, \( f(x) = \cos{x} \) fonksiyonunun türevi \( f'(x) = -\sin{x} \) fonksiyonudur.
\( f(x) = \tan{x} \)
\( f'(x) = \sec^2{x} = 1 + \tan^2{x} \)
İSPATI GÖSTER
\( f(x) = \tan{x} = \dfrac{\sin{x}}{\cos{x}} \)
\( f'(x) = \left( \dfrac{\sin{x}}{\cos{x}} \right)' \)
Türev bölme kuralı ile ifadenin türevini alalım.
\( = \dfrac{(\sin{x})'\cos{x} - \sin{x}(\cos{x})'}{\cos^2{x}} \)
\( = \dfrac{\cos{x}\cos{x} + \sin{x}\sin{x}}{\cos^2{x}} \)
\( = \dfrac{\cos^2{x} + \sin^2{x}}{\cos^2{x}} \)
Paydaki ifade Pisagor özdeşliğine göre 1'e eşittir.
\( = \dfrac{1}{\cos^2{x}} \)
Kosinüs fonksiyonunun çarpmaya göre tersi sekant fonksiyonudur.
\( = \sec^2{x} \)
Buna göre, \( f(x) = \tan{x} \) fonksiyonunun türevi \( f'(x) = \sec^2{x} \) fonksiyonudur.
Pisagor özdeşliğine göre \( f'(x) = \sec^2{x} \) fonksiyonu aşağıdaki şekilde de yazılabilir.
\( f'(x) = \sec^2{x} = 1 + \tan^2{x} \)
\( f(x) = \cot{x} \)
\( f'(x) = -\csc^2{x} = -(1 + \cot^2{x}) \)
İSPATI GÖSTER
\( f(x) = \cot{x} = \dfrac{\cos{x}}{\sin{x}} \)
\( f'(x) = \left( \dfrac{\cos{x}}{\sin{x}} \right)' \)
Türev bölme kuralı ile ifadenin türevini alalım.
\( = \dfrac{(\cos{x})'\sin{x} - \cos{x}(\sin{x})'}{\sin^2{x}} \)
\( = \dfrac{-\sin{x}\sin{x} - \cos{x}\cos{x}}{\sin^2{x}} \)
\( = \dfrac{-(\sin^2{x} + \cos^2{x})}{\sin^2{x}} \)
Paydaki parantez içindeki ifade Pisagor özdeşliğine göre 1'e eşittir.
\( = \dfrac{-1}{\sin^2{x}} \)
Sinüs fonksiyonunun çarpmaya göre tersi kosekant fonksiyonudur.
\( = -\csc^2{x} \)
Buna göre, \( f(x) = \cot{x} \) fonksiyonunun türevi \( f'(x) = -\csc^2{x} \) fonksiyonudur.
Pisagor özdeşliğine göre \( f'(x) = -\csc^2{x} \) fonksiyonu aşağıdaki şekilde de yazılabilir.
\( f'(x) = -\csc^2{x} = -(1 + \cot^2{x}) \)
\( f(x) = \sec{x} \)
\( f'(x) = \tan{x}\sec{x} \)
İSPATI GÖSTER
\( f(x) = \sec{x} = \dfrac{1}{\cos{x}} \)
\( f'(x) = \left( \dfrac{1}{\cos{x}} \right)' \)
Türev bölme kuralı ile ifadenin türevini alalım.
\( = \dfrac{(1)'\cos{x} - 1(\cos{x})'}{\cos^2{x}} \)
\( = \dfrac{0 + \sin{x}}{\cos^2{x}} \)
\( = \dfrac{\sin{x}}{\cos{x}\cos{x}} \)
İfadeye aşağıdaki iki dönüşümü uygulayalım.
\( \dfrac{\sin{x}}{\cos{x}} = \tan{x} \)
\( \dfrac{1}{\cos{x}} = \sec{x} \)
\( = \tan{x}\sec{x} \)
Buna göre, \( f(x) = \sec{x} \) fonksiyonunun türevi \( f'(x) = \tan{x}\sec{x} \) fonksiyonudur.
\( f(x) = \csc{x} \)
\( f'(x) = -\cot{x}\csc{x} \)
İSPATI GÖSTER
\( f(x) = \csc{x} = \dfrac{1}{\sin{x}} \)
\( f'(x) = \left( \dfrac{1}{\sin{x}} \right)' \)
Türev bölme kuralı ile ifadenin türevini alalım.
\( = \dfrac{(1)'\sin{x} - 1(\sin{x})'}{\sin^2{x}} \)
\( = \dfrac{0 - \cos{x}}{\sin^2{x}} \)
\( = \dfrac{-\cos{x}}{\sin{x}\sin{x}} \)
İfadeye aşağıdaki iki dönüşümü uygulayalım.
\( \dfrac{\cos{x}}{\sin{x}} = \cot{x} \)
\( \dfrac{1}{\sin{x}} = \csc{x} \)
\( = -\cot{x}\csc{x} \)
Buna göre, \( f(x) = \csc{x} \) fonksiyonunun türevi \( f'(x) = -\cot{x}\csc{x} \) fonksiyonudur.
Ters Trigonometrik Fonksiyonlar
Ters trigonometrik fonksiyonların türevlenebilir oldukları aralıklarda türev alma kuralları aşağıdaki gibidir.
\( f(x) = \arcsin{x} \)
\( f'(x) = \dfrac{1}{\sqrt{1 - x^2}} \)
İSPATI GÖSTER
\( f(x) = y = \arcsin{x} \)
Arc sinüs fonksiyonu, sinüs değeri \( x \) olan bir açının ölçüsünü \( y \) değeri olarak verir.
\( y \) ve \( x \) arasındaki ilişki aşağıdaki dik üçgende gösterilmiştir.
Bu üçgende \( y \) açısının komşu kenarını Pisagor teoreminden aşağıdaki şekilde bulabiliriz.
\( x^2 + a^2 = 1^2 \)
\( a = \sqrt{1 - x^2} \)
Yukarıdaki \( y \) fonksiyonunun tersini alalım. Elde ettiğimiz fonksiyon, ölçüsü \( y \) olan açının sinüs trigonometrik oranını \( x \) olarak verir.
\( \sin{y} = x \)
Bu eşitliğin taraflarının \( x \)'e göre türevini alalım. Zincir kuralı gereği, \( x \) değişkenine bağlı olan \( y \) fonksiyonunun türevini \( \frac{dy}{dx} \) ile de çarpmamız gerekir.
\( \dfrac{d}{dx} (\sin{y}) = \dfrac{d}{dx} (x) \)
\( \cos{y} \dfrac{dy}{dx} = 1 \)
\( \dfrac{dy}{dx} = \dfrac{1}{\cos{y}} \)
\( \cos{y} \) yerine yukarıdaki dik üçgendeki karşılığını yazalım.
\( f'(x) = \dfrac{dy}{dx} = \dfrac{1}{\sqrt{1 - x^2}} \)
Buna göre, \( f(x) = \arcsin{x} \) fonksiyonunun türevi \( f'(x) = \dfrac{1}{\sqrt{1 - x^2}} \) fonksiyonudur.
\( f(x) = \arccos{x} \)
\( f'(x) = -\dfrac{1}{\sqrt{1 - x^2}} \)
İSPATI GÖSTER
\( f(x) = y = \arccos{x} \)
Arc kosinüs fonksiyonu, kosinüs değeri \( x \) olan bir açının ölçüsünü \( y \) değeri olarak verir.
\( y \) ve \( x \) arasındaki ilişki aşağıdaki dik üçgende gösterilmiştir.
Bu üçgende \( y \) açısının karşı kenarını Pisagor teoreminden aşağıdaki şekilde bulabiliriz.
\( x^2 + a^2 = 1^2 \)
\( a = \sqrt{1 - x^2} \)
Yukarıdaki \( y \) fonksiyonunun tersini alalım. Elde ettiğimiz fonksiyon, ölçüsü \( y \) olan açının kosinüs trigonometrik oranını \( x \) olarak verir.
\( \cos{y} = x \)
Bu eşitliğin taraflarının \( x \)'e göre türevini alalım. Zincir kuralı gereği, \( x \) değişkenine bağlı olan \( y \) fonksiyonunun türevini \( \frac{dy}{dx} \) ile de çarpmamız gerekir.
\( \dfrac{d}{dx} (\cos{y}) = \dfrac{d}{dx} (x) \)
\( -\sin{y} \dfrac{dy}{dx} = 1 \)
\( \dfrac{dy}{dx} = -\dfrac{1}{\sin{y}} \)
\( \sin{y} \) yerine yukarıdaki dik üçgendeki karşılığını yazalım.
\( f'(x) = \dfrac{dy}{dx} = -\dfrac{1}{\sqrt{1 - x^2}} \)
Buna göre, \( f(x) = \arccos{x} \) fonksiyonunun türevi \( f'(x) = -\dfrac{1}{\sqrt{1 - x^2}} \) fonksiyonudur.
\( f(x) = \arctan{x} \)
\( f'(x) = \dfrac{1}{1 + x^2} \)
İSPATI GÖSTER
\( f(x) = y = \arctan{x} \)
Arc tanjant fonksiyonu, tanjant değeri \( x \) olan bir açının ölçüsünü \( y \) değeri olarak verir.
\( y \) ve \( x \) arasındaki ilişki aşağıdaki dik üçgende gösterilmiştir.
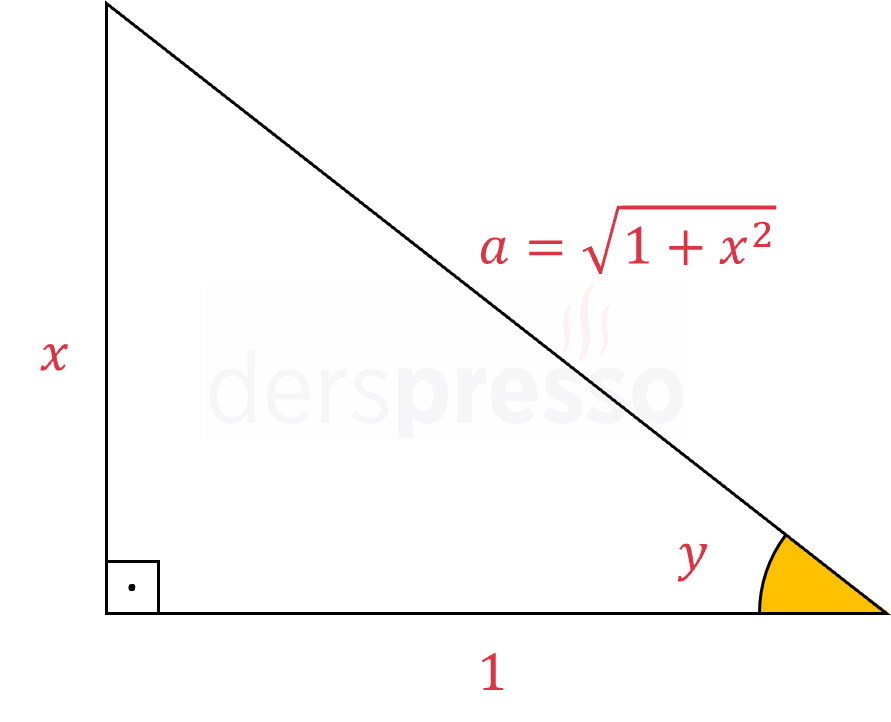
Bu üçgende hipotenüsü Pisagor teoreminden aşağıdaki şekilde bulabiliriz.
\( 1^2 + x^2 = a^2 \)
\( a = \sqrt{1 + x^2} \)
Yukarıdaki \( y \) fonksiyonunun tersini alalım. Elde ettiğimiz fonksiyon, ölçüsü \( y \) olan açının tanjant trigonometrik oranını \( x \) olarak verir.
\( \tan{y} = x \)
Bu eşitliğin taraflarının \( x \)'e göre türevini alalım. Zincir kuralı gereği, \( x \) değişkenine bağlı olan \( y \) fonksiyonunun türevini \( \frac{dy}{dx} \) ile de çarpmamız gerekir.
\( \dfrac{d}{dx} (\tan{y}) = \dfrac{d}{dx} (x) \)
\( \sec^2{y} \dfrac{dy}{dx} = 1 \)
\( \dfrac{dy}{dx} = \dfrac{1}{\sec^2{y}} \)
\( \sec^2{y} \) yerine yukarıdaki dik üçgendeki karşılığını yazalım.
\( f'(x) = \dfrac{dy}{dx} = \dfrac{1}{1 + x^2} \)
Buna göre, \( f(x) = \arctan{x} \) fonksiyonunun türevi \( f'(x) = \dfrac{1}{1 + x^2} \) fonksiyonudur.
\( f(x) = \arccot{x} \)
\( f'(x) = -\dfrac{1}{1 + x^2} \)
İSPATI GÖSTER
\( f(x) = y = \arccot{x} \)
Arc kotanjant fonksiyonu, kotanjant değeri \( x \) olan bir açının ölçüsünü \( y \) değeri olarak verir.
\( y \) ve \( x \) arasındaki ilişki aşağıdaki dik üçgende gösterilmiştir.
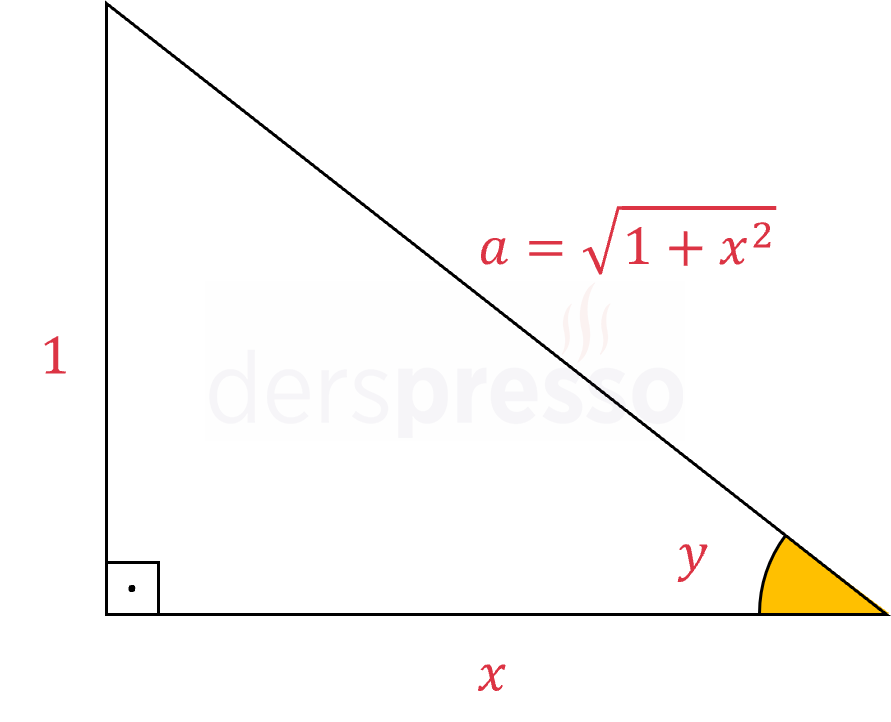
Bu üçgende hipotenüsü Pisagor teoreminden aşağıdaki şekilde bulabiliriz.
\( 1^2 + x^2 = a^2 \)
\( a = \sqrt{1 + x^2} \)
Yukarıdaki \( y \) fonksiyonunun tersini alalım. Elde ettiğimiz fonksiyon, ölçüsü \( y \) olan açının kotanjant trigonometrik oranını \( x \) olarak verir.
\( \cot{y} = x \)
Bu eşitliğin taraflarının \( x \)'e göre türevini alalım. Zincir kuralı gereği, \( x \) değişkenine bağlı olan \( y \) fonksiyonunun türevini \( \frac{dy}{dx} \) ile de çarpmamız gerekir.
\( \dfrac{d}{dx} (\cot{y}) = \dfrac{d}{dx} (x) \)
\( -\csc^2{y} \dfrac{dy}{dx} = 1 \)
\( \dfrac{dy}{dx} = -\dfrac{1}{\csc^2{y}} \)
\( \csc^2{y} \) yerine yukarıdaki dik üçgendeki karşılığını yazalım.
\( f'(x) = \dfrac{dy}{dx} = -\dfrac{1}{1 + x^2} \)
Buna göre, \( f(x) = \arccot{x} \) fonksiyonunun türevi \( f'(x) = -\dfrac{1}{1 + x^2} \) fonksiyonudur.
\( f(x) = \arcsec{x} \)
\( f'(x) = \dfrac{1}{\abs{x}\sqrt{x^2 - 1}} \)
İSPATI GÖSTER
\( f(x) = y = \arcsec{x} \)
Arc sekant fonksiyonu, sekant değeri \( x \) olan bir açının ölçüsünü \( y \) değeri olarak verir.
\( y \) ve \( x \) arasındaki ilişki aşağıdaki dik üçgende gösterilmiştir.
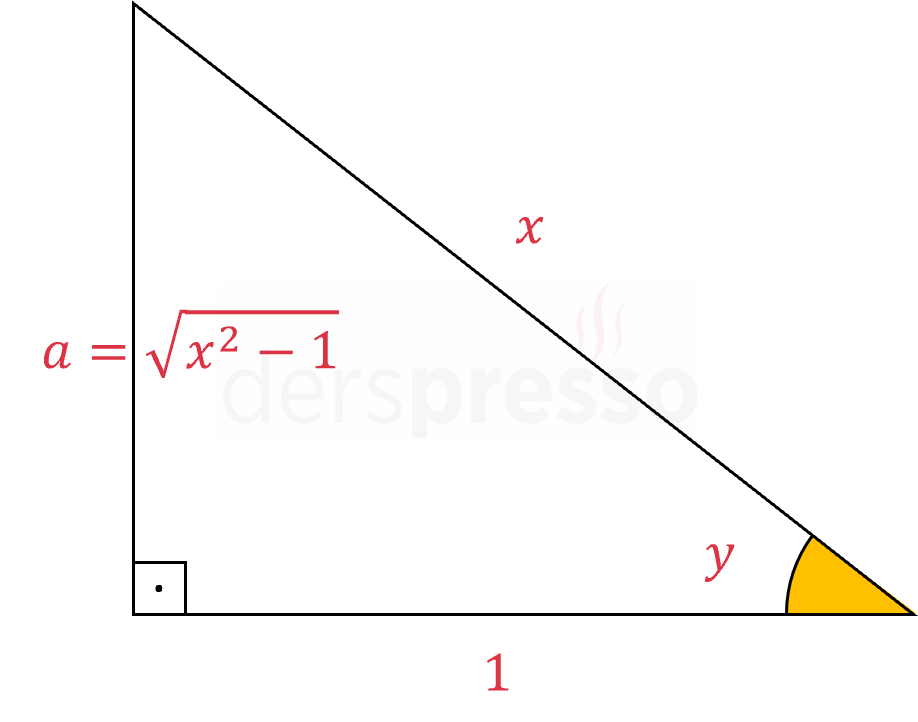
Bu üçgende \( y \) açısının karşı kenarını Pisagor teoreminden aşağıdaki şekilde bulabiliriz.
\( a^2 + 1^2 = x^2 \)
\( a = \sqrt{x^2 - 1} \)
Yukarıdaki \( y \) fonksiyonunun tersini alalım. Elde ettiğimiz fonksiyon, ölçüsü \( y \) olan açının sekant trigonometrik oranını \( x \) olarak verir.
\( \sec{y} = x \)
Bu eşitliğin taraflarının \( x \)'e göre türevini alalım. Zincir kuralı gereği, \( x \) değişkenine bağlı olan \( y \) fonksiyonunun türevini \( \frac{dy}{dx} \) ile de çarpmamız gerekir.
\( \dfrac{d}{dx} (\sec{y}) = \dfrac{d}{dx} (x) \)
\( \tan{y}\sec{y} \dfrac{dy}{dx} = 1 \)
\( \dfrac{dy}{dx} = \dfrac{1}{\tan{y}\sec{y}} \)
\( \tan{y} \) ve \( \sec{y} \) yerine yukarıdaki dik üçgendeki karşılıklarını yazalım.
\( \dfrac{dy}{dx} = \dfrac{1}{\sqrt{x^2 - 1} \cdot x} \)
Arc sekant fonksiyonu tanım aralığı gereği girdi olarak hem pozitif hem de negatif trigonometrik değer alabilir, ancak aşağıdaki grafikte de görebileceğimiz gibi her iki durumda da fonksiyon grafiği artandır (mavi grafik), dolayısıyla türevi/eğimi her zaman pozitiftir. Bu yüzden arcsec türev fonksiyonunda \( x \) değişkeninin mutlak değeri alınır.
\( f'(x) = \dfrac{dy}{dx} = \dfrac{1}{\abs{x}\sqrt{x^2 - 1}} \)
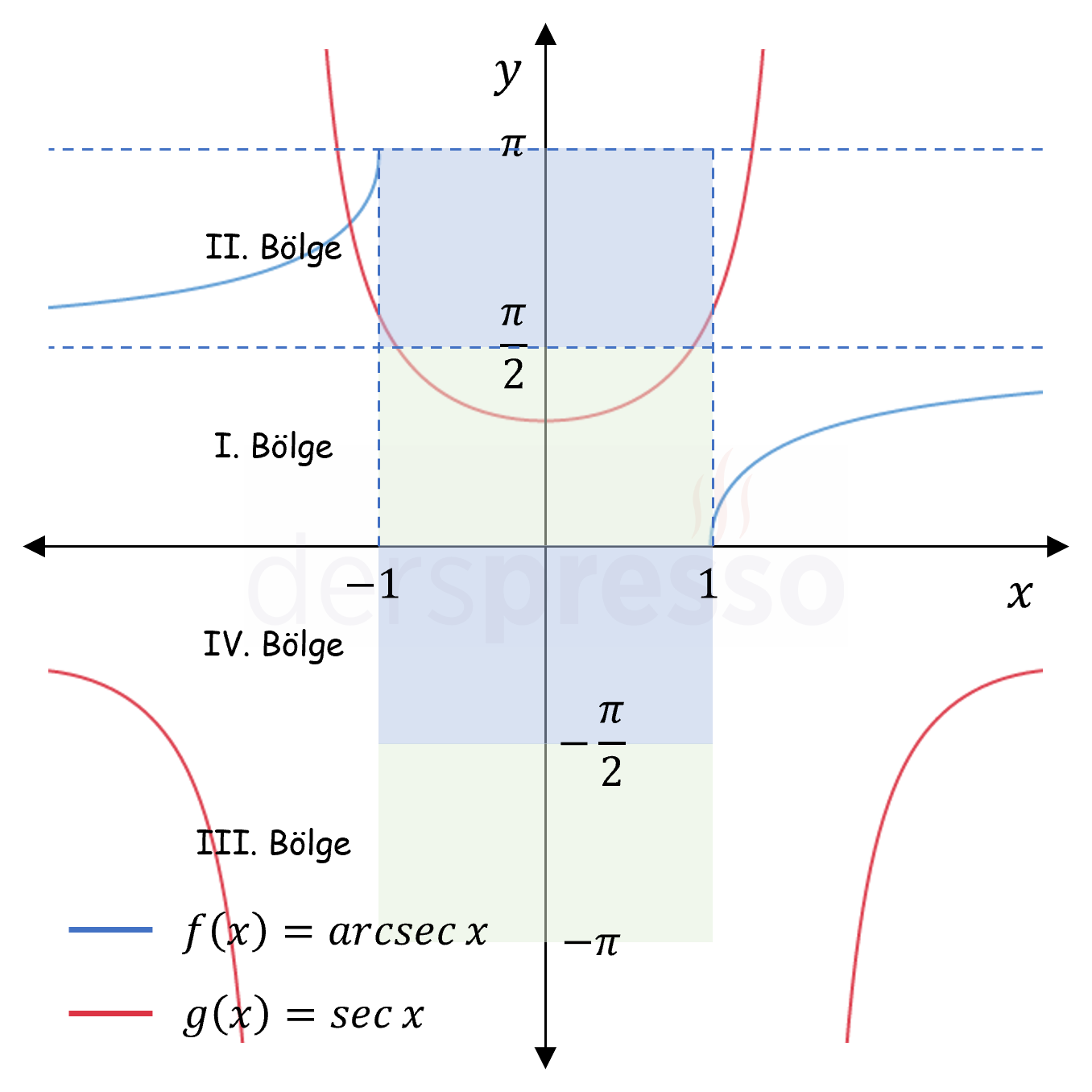
Buna göre, \( f(x) = \arcsec{x} \) fonksiyonunun türevi \( f'(x) = \dfrac{1}{\abs{x}\sqrt{x^2 - 1}} \) fonksiyonudur.
\( f(x) = \arccsc{x} \)
\( f'(x) = -\dfrac{1}{\abs{x}\sqrt{x^2 - 1}} \)
İSPATI GÖSTER
\( f(x) = y = \arccsc{x} \)
Arc kosekant fonksiyonu, kosekant değeri \( x \) olan bir açının ölçüsünü \( y \) değeri olarak verir.
\( y \) ve \( x \) arasındaki ilişki aşağıdaki dik üçgende gösterilmiştir.
Bu üçgende \( y \) açısının komşu kenarını Pisagor teoreminden aşağıdaki şekilde bulabiliriz.
\( a^2 + 1^2 = x^2 \)
\( a = \sqrt{x^2 - 1} \)
Yukarıdaki \( y \) fonksiyonunun tersini alalım. Elde ettiğimiz fonksiyon, ölçüsü \( y \) olan açının kosekant trigonometrik oranını \( x \) olarak verir.
\( \csc{y} = x \)
Bu eşitliğin taraflarının \( x \)'e göre türevini alalım. Zincir kuralı gereği, \( x \) değişkenine bağlı olan \( y \) fonksiyonunun türevini \( \frac{dy}{dx} \) ile de çarpmamız gerekir.
\( \dfrac{d}{dx} (\csc{y}) = \dfrac{d}{dx} (x) \)
\( -\cot{y}\csc{y} \dfrac{dy}{dx} = 1 \)
\( \dfrac{dy}{dx} = -\dfrac{1}{\cot{y}\csc{y}} \)
\( \cot{y} \) ve \( \csc{y} \) yerine yukarıdaki dik üçgendeki karşılıklarını yazalım.
\( \dfrac{dy}{dx} = -\dfrac{1}{\sqrt{x^2 - 1} \cdot x} \)
Arc kosekant fonksiyonu tanım aralığı gereği girdi olarak hem pozitif hem de negatif trigonometrik değer alabilir, ancak aşağıdaki grafikte de görebileceğimiz gibi her iki durumda da fonksiyon grafiği azalandır (mavi grafik), dolayısıyla türevi/eğimi her zaman negatiftir. Bu yüzden arccsc türev fonksiyonunun işareti zaten negatif olduğu için \( x \) değişkeninin mutlak değeri alınır.
\( f'(x) = \dfrac{dy}{dx} = -\dfrac{1}{\abs{x}\sqrt{x^2 - 1}} \)
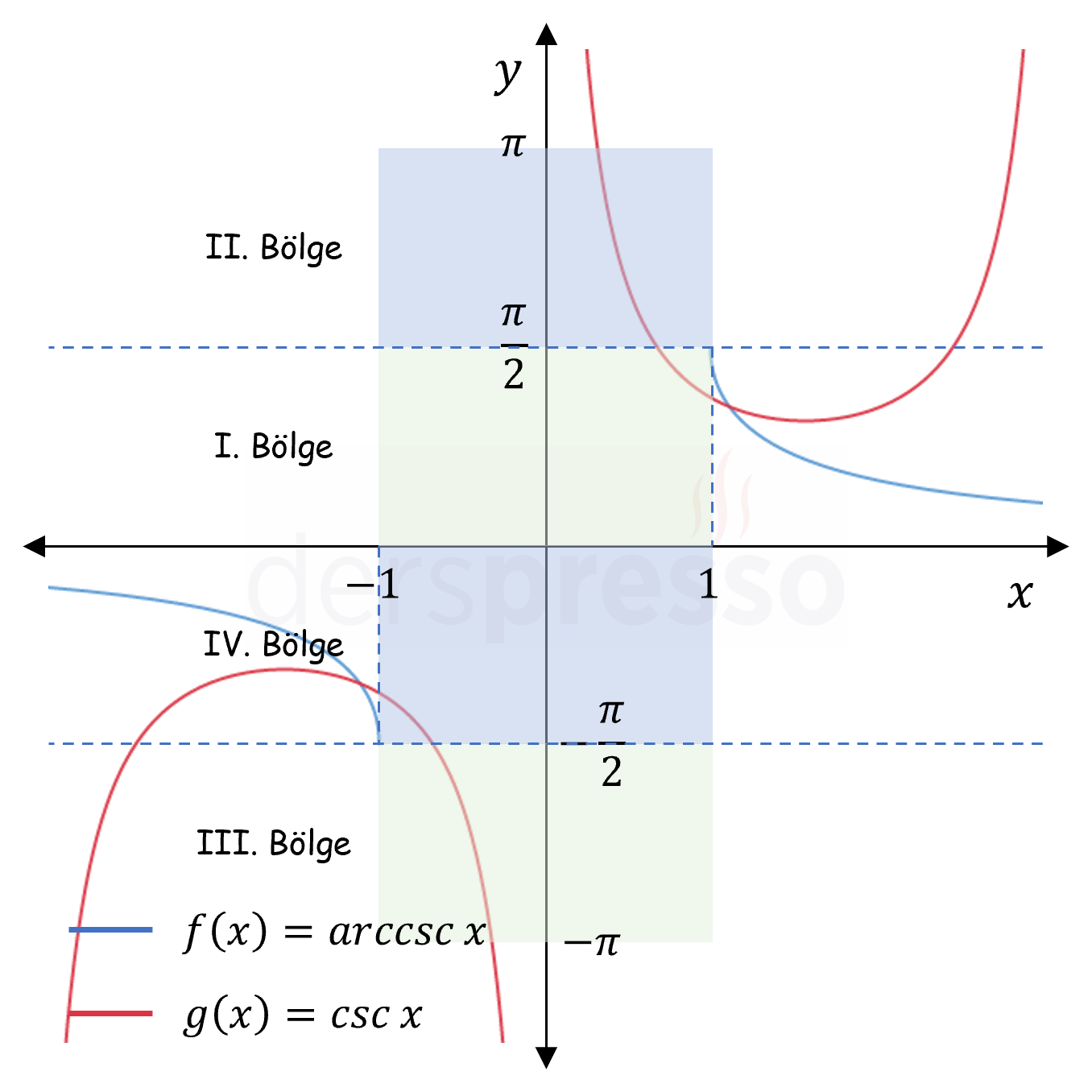
Buna göre, \( f(x) = \arccsc{x} \) fonksiyonunun türevi \( f'(x) = -\dfrac{1}{\abs{x}\sqrt{x^2 - 1}} \) fonksiyonudur.
Aşağıdaki fonksiyonların türevlerini bulunuz.
(a) \( f(x) = \sin(11x) \)
(b) \( g(x) = \cos(5x^2) \)
(c) \( h(x) = \cot(x^3 - 2x) \)
Çözümü Göster(a) seçeneği:
\( f(x) = \sin(11x) \)
Zincir kuralını kullanarak bileşke fonksiyonun türevini alalım.
\( f'(x) = (\sin(11x))' \)
\( = \cos(11x) \cdot (11x)' \)
\( = \cos(11x) \cdot 11 \)
\( = 11\cos(11x) \)
(b) seçeneği:
\( g(x) = \cos(5x^2) \)
Zincir kuralını kullanarak bileşke fonksiyonun türevini alalım.
\( g'(x) = (\cos(5x^2))' \)
\( = -\sin(5x^2) \cdot (5x^2)' \)
\( = -\sin(5x^2) \cdot 10x \)
\( = -10x\sin(5x^2) \)
(c) seçeneği:
\( h(x) = \cot(x^3 - 2x) \)
Zincir kuralını kullanarak bileşke fonksiyonun türevini alalım.
\( h'(x) = (\cot(x^3 - 2x))' \)
\( = -\csc^2(x^3 - 2x) \cdot (x^3 - 2x)' \)
\( = -\csc^2(x^3 - 2x) \cdot (3x^2 - 2) \)
\( = -(3x^2 - 2)\csc^2(x^3 - 2x) \)
Aşağıdaki fonksiyonların türevini bulunuz.
(a) \( f(x) = 3\cot(4x) - 2\sec(3x) \)
(b) \( g(x) = 2\sec^3(5x) \)
(c) \( h(x) = 16\csc^3{\dfrac{x}{4}} \)
Çözümü Göster(a) seçeneği:
\( f(x) = 3\cot(4x) - 2\sec(3x) \)
Zincir kuralını kullanarak bileşke fonksiyonun türevini alalım.
\( f'(x) = (3\cot(4x) - 2\sec(3x))' \)
\( = (-3\csc^2(4x))(4x)' - 2\tan(3x)\sec(3x)(3x)' \)
\( = -3\csc^2(4x)(4) - 2\tan(3x)\sec(3x)(3) \)
\( = -12\csc^2(4x) - 6\tan(3x)\sec(3x) \)
(b) seçeneği:
\( g(x) = 2\sec^3(5x) \)
Zincir kuralını kullanarak bileşke fonksiyonun türevini alalım.
\( g'(x) = (2\sec^3(5x))' \)
\( = 2 \cdot 3\sec^2(5x)(\sec(5x))' \)
\( = 6\sec^2(5x)\tan(5x)\sec(5x)(5x)' \)
\( = 6\sec^2(5x)\tan(5x)\sec(5x)(5) \)
\( = 30\sec^3(5x)\tan(5x) \)
(c) seçeneği:
\( h(x) = 16\csc^3{\dfrac{x}{4}} \)
Zincir kuralını kullanarak bileşke fonksiyonun türevini alalım.
\( h'(x) = (16\csc^3{\dfrac{x}{4}})' \)
\( = 16 \cdot 3\csc^2{\dfrac{x}{4}}(\csc{\dfrac{x}{4}})' \)
\( = 48\csc^2{\dfrac{x}{4}}(-\cot{\dfrac{x}{4}}\csc{\dfrac{x}{4}})(\dfrac{x}{4})' \)
\( = -48\csc^3{\dfrac{x}{4}}\cot{\dfrac{x}{4}}(\dfrac{1}{4}) \)
\( = -12\csc^3{\dfrac{x}{4}}\cot{\dfrac{x}{4}} \)
Aşağıdaki fonksiyonların türevini bulunuz.
(a) \( f(x) = 5\sin(\tan{x}) \)
(b) \( g(x) = 4\cos(\sqrt[4]{x^5}) \)
(c) \( h(x) = (4\sin(2x) - 2\cos(4x))^3 \)
Çözümü Göster(a) seçeneği:
\( f(x) = 5\sin(\tan{x}) \)
Zincir kuralını kullanarak bileşke fonksiyonun türevini alalım.
\( f'(x) = (5\sin(\tan{x}))' \)
\( = 5\cos(\tan{x})(\tan{x})' \)
\( = 5\cos(\tan{x})\sec^2{x} \)
(b) seçeneği:
\( g(x) = 4\cos(\sqrt[4]{x^5}) \)
Zincir kuralını kullanarak bileşke fonksiyonun türevini alalım.
\( g'(x) = (4\cos(\sqrt[4]{x^5}))' \)
\( = -4\sin(\sqrt[4]{x^5})(\sqrt[4]{x^5})' \)
\( = -4\sin(\sqrt[4]{x^5})(\dfrac{5}{4}\sqrt[4]{x}) \)
\( = -5\sin(\sqrt[4]{x^5})\sqrt[4]{x} \)
(c) seçeneği:
\( h(x) = (4\sin(2x) - 2\cos(4x))^3 \)
Zincir kuralını kullanarak bileşke fonksiyonun türevini alalım.
\( h'(x) = 3(4\sin(2x) - 2\cos(4x))^2(4\sin(2x) - 2\cos(4x))' \)
\( = 3(4\sin(2x) - 2\cos(4x))^2(4\cos(2x)(2x)' - (-2\sin(4x))(4x)') \)
\( = 3(4\sin(2x) - 2\cos(4x))^2(4\cos(2x)(2) + 2\sin(4x)(4)) \)
\( = 3(4\sin(2x) - 2\cos(4x))^2(8\cos(2x) + 8\sin(4x)) \)
\( = 24(4\sin(2x) - 2\cos(4x))^2(\cos(2x) + \sin(4x)) \)
\( \lim\limits_{h \to 0} \dfrac{\tan(5(x + h)) - \tan(5x)}{h} \) limitinin değerini türevin limit tanımını kullanarak bulunuz.
Çözümü GösterTürev fonksiyonunun limit tanımını yazalım.
\( f'(x) = \lim\limits_{h \to 0} \dfrac{f(x + h) - f(x)}{h} \)
Bu tanımda \( f(x) = \tan(5x) \) kullandığımızda verilen ifadenin elde edildiği görülebilir.
Buna göre verilen ifade, \( f(x) = \tan(5x) \) fonksiyonunun türevinin limit tanımıdır.
Zincir kuralını kullanarak bileşke fonksiyonun türevini alalım.
\( f'(x) = \sec^2(5x)(5x)' \)
\( = 5\sec^2(5x) \) bulunur.
Aşağıdaki fonksiyonların türevini bulunuz.
(a) \( f(x) = (\sin{x})^2\sin(x^2) \)
(b) \( g(x) = \dfrac{1 + \sin(6x)}{1 - \cos(3x)} \)
(c) \( h(x) = \dfrac{\sec^2{x}}{\tan{x}} \)
Çözümü Göster(a) seçeneği:
\( f(x) = (\sin{x})^2\sin(x^2) \)
Çarpma ve zincir kurallarını kullanarak fonksiyonun türevini alalım.
\( f'(x) = [(\sin{x})^2]'\sin(x^2) + (\sin{x})^2[\sin(x^2)]' \)
\( = 2\sin{x}(\sin{x})'\sin(x^2) + (\sin{x})^2\cos(x^2)(x^2)' \)
\( = 2\sin{x}\cos{x}\sin(x^2) + (\sin{x})^2\cos(x^2)2x \)
Sinüs iki kat açı formülünü kullanalım.
\( = \sin(2x)\sin(x^2) + 2x(\sin{x})^2\cos(x^2) \)
(b) seçeneği:
\( g(x) = \dfrac{1 + \sin(6x)}{1 - \cos(3x)} \)
Bölme kuralını kullanarak fonksiyonun türevini alalım.
\( g'(x) = \dfrac{(1 + \sin(6x))'(1 - \cos(3x)) - (1 + \sin(6x))(1 - \cos(3x))'}{(1 - \cos(3x))^2} \)
\( = \dfrac{\cos(6x)(6x)'(1 - \cos(3x)) - (1 + \sin(6x))\sin(3x)(3x)'}{(1 - \cos(3x))^2} \)
\( = \dfrac{6\cos(6x)(1 - \cos(3x)) - 3\sin(3x)(1 + \sin(6x))}{(1 - \cos(3x))^2} \)
(c) seçeneği:
\( h(x) = \dfrac{\sec^2{x}}{\tan{x}} \)
Bölme kuralını kullanarak fonksiyonun türevini alalım.
\( h'(x) = \dfrac{(\sec^2{x})'\tan{x} - \sec^2{x}(\tan{x})'}{\tan^2{x}} \)
\( = \dfrac{2\sec{x}(\sec{x})'\tan{x} - \sec^2{x}\sec^2{x}}{\tan^2{x}} \)
\( = \dfrac{2\sec{x}\tan{x}\sec{x}\tan{x} - \sec^2{x}\sec^2{x}}{\tan^2{x}} \)
\( = \dfrac{2\sec^2{x}\tan^2{x} - \sec^4{x}}{\tan^2{x}} \)
\( = \dfrac{2\frac{1}{\cos^2{x}}\frac{\sin^2{x}}{\cos^2{x}} - \frac{1}{\cos^4{x}}}{\frac{\sin^2{x}}{\cos^2{x}}} \)
\( = \dfrac{\frac{2\sin^2{x} - 1}{\cos^4{x}}}{\frac{\sin^2{x}}{\cos^2{x}}} \)
\( = \dfrac{2\sin^2{x} - 1}{\cos^2{x}\sin^2{x}} \)
İfadeyi sadeleştirmek için payı ve paydayı 4 ile çarpalım.
\( = \dfrac{4(2\sin^2{x} - 1)}{4\cos^2{x}\sin^2{x}} \)
\( = \dfrac{4(2\sin^2{x} - 1)}{(2\cos{x}\sin{x})^2} \)
Payda kosinüs iki kat açı formülünü, paydada sinüs iki kat açı formülünü kullanalım.
\( = \dfrac{-4\cos(2x)}{\sin^2(2x)} \)
\( = \dfrac{-4\cos(2x)}{\sin(2x)\sin(2x)} \)
\( = -4\cot(2x)\csc(2x) \)
Aşağıdaki fonksiyonların belirtilen noktalardaki türev değerini bulunuz.
(a) \( f(x) = x\sin{x} \quad (x = \pi) \)
(b) \( g(x) = \sqrt{x\tan{x}} \quad (x = \frac{\pi}{4}) \)
(c) \( h(x) = \tan^2{x} - \cot^2{x} \quad (x = \frac{\pi}{4}) \)
Çözümü Göster(a) seçeneği:
\( f(x) = x\sin{x} \)
Çarpma kuralını kullanarak fonksiyonun türevini bulalım.
\( f'(x) = (x)'\sin{x} + x(\sin{x})' \)
\( = \sin{x} + x\cos{x} \)
\( f'(\pi) \) değerini bulmak için \( x = \pi \) koyalım.
\( f'(\pi) = \sin{\pi} + \pi\cos{\pi} \)
\( = 0 + \pi(-1) = -\pi \)
(b) seçeneği:
\( g(x) = \sqrt{x\tan{x}} \)
Zincir kuralını kullanarak bileşke fonksiyonun türevini alalım.
\( g'(x) = (\sqrt{x\tan{x}})' \)
\( = \dfrac{(x\tan{x})'}{2\sqrt{x\tan{x}}} \)
Çarpma kuralı ile paydaki ifadenin türevini alalım.
\( = \dfrac{(x)'\tan{x} + x(\tan{x})'}{2\sqrt{x\tan{x}}} \)
\( = \dfrac{\tan{x} + x\sec^2{x}}{2\sqrt{x\tan{x}}} \)
\( g'(\frac{\pi}{4}) \) değerini bulmak için \( x = \frac{\pi}{4} \) koyalım.
\( g'(\frac{\pi}{4}) = \dfrac{\tan{\frac{\pi}{4}} + \frac{\pi}{4}\sec^2{\frac{\pi}{4}}}{2\sqrt{\frac{\pi}{4}\tan{\frac{\pi}{4}}}} \)
\( = \dfrac{1 + \frac{\pi}{4}(\sqrt{2})^2}{2\sqrt{\frac{\pi}{4}(1)}} \)
\( = \dfrac{2 + \pi}{2\sqrt{\pi}} \)
(c) seçeneği:
\( h(x) = \tan^2{x} - \cot^2{x} \)
\( h'(x) = (\tan^2{x} - \cot^2{x})' \)
\( = (\tan^2{x})' - (\cot^2{x})' \)
\( = 2\tan{x}(\tan{x})' - 2\cot{x}(\cot{x})' \)
\( = 2\tan{x}\sec^2{x} - 2\cot{x}(-\csc^2{x}) \)
\( = 2\tan{x}\sec^2{x} + 2\cot{x}\csc^2{x} \)
\( h'(\frac{\pi}{4}) \) değerini bulmak için \( x = \frac{\pi}{4} \) koyalım.
\( h'(\frac{\pi}{4}) = 2\tan{\frac{\pi}{4}}\sec^2{\frac{\pi}{4}} + 2\cot{\frac{\pi}{4}}\csc^2{\frac{\pi}{4}} \)
\( = 2(1)(\sqrt{2})^2 + 2(1)(\sqrt{2})^2 \)
\( = 4 + 4 = 8 \)
\( f(x) = \cos(\sin(2x)) \) fonksiyonunun türevi nedir?
Çözümü GösterZincir kuralını kullanarak fonksiyonun türevini alalım.
\( f'(x) = (\cos(\sin(2x)))' \)
\( = -\sin(\sin(2x))(\sin(2x))' \)
\( = -\sin(\sin(2x))\cos(2x)(2x)' \)
\( = -\sin(\sin(2x))\cos(2x)(2) \)
\( = -2\sin(\sin(2x))\cos(2x) \)
\( \lim\limits_{h \to 0} \dfrac{4\sin(2x + 2h) - 8\sin{x}\cos{x}}{h} \) limitinin değerini türevin limit tanımını kullanarak bulunuz.
Çözümü GösterVerilen ifadeyi düzenleyelim.
\( \lim\limits_{h \to 0} \dfrac{4\sin(2(x + h)) - 4(2\sin{x}\cos{x})}{h} = \lim\limits_{h \to 0} \dfrac{4\sin(2(x + h)) - 4\sin(2x)}{h} \)
Türev fonksiyonunun limit tanımını yazalım.
\( f'(x) = \lim\limits_{h \to 0} \dfrac{f(x + h) - f(x)}{h} \)
Bu tanımda \( f(x) = 4\sin(2x) \) kullandığımızda verilen ifadenin elde edildiği görülebilir.
Buna göre verilen ifade, \( f(x) = 4\sin(2x) \) fonksiyonunun türevinin limit tanımıdır.
Zincir kuralını kullanarak bileşke fonksiyonun türevini alalım.
\( f'(x) = 4\cos(2x)(2x)' \)
\( = 8\cos(2x) \) bulunur.
\( y = \sqrt{\sin{\sqrt{2x}}} \) fonksiyonunun türevi nedir?
Çözümü GösterZincir kuralını kullanarak fonksiyonun türevini alalım.
\( y' = (\sqrt{\sin{\sqrt{2x}}})' \)
\( = \dfrac{(\sin{\sqrt{2x}})'}{2\sqrt{\sin{\sqrt{2x}}}} \)
\( = \dfrac{\cos{\sqrt{2x}}(\sqrt{2x})'}{2\sqrt{\sin{\sqrt{2x}}}} \)
\( = \dfrac{\cos{\sqrt{2x}}(2x)'}{2\sqrt{\sin{\sqrt{2x}}}(2\sqrt{2x})} \)
\( = \dfrac{\cos{\sqrt{2x}(2)}}{4\sqrt{\sin{\sqrt{2x}}}\sqrt{2x}} \)
\( = \dfrac{\cos{\sqrt{2x}}}{2\sqrt{\sin{\sqrt{2x}}}\sqrt{2x}} \)
\( f(x) = \tan(\sin^2(3x)) \) olduğuna göre, \( f'(x) \) nedir?
Çözümü GösterZincir kuralını kullanarak fonksiyonun türevini alalım.
\( f'(x) = (\tan(\sin^2(3x)))' \)
\( = \sec^2(\sin^2(3x))(\sin^2(3x))' \)
\( = \sec^2(\sin^2(3x))2\sin(3x)(\sin(3x))' \)
\( = 2\sec^2(\sin^2(3x))\sin(3x)\cos(3x)(3x)' \)
\( = 2\sec^2(\sin^2(3x))\sin(3x)\cos(3x)(3) \)
\( = 6\sec^2(\sin^2(3x))\sin(3x)\cos(3x) \)
Sinüs iki kat açı formülünü kullanalım.
\( = 3\sec^2(\sin^2(3x))\sin(6x) \) bulunur.
\( f(x) = \cos{x}\cos(2x)\cos(4x)\cos(8x) \)
olduğuna göre, \( f'(\frac{\pi}{6}) \) kaçtır?
Çözümü GösterFonksiyonun payını ve paydasını \( 16\sin{x} \) ile genişletelim.
\( f(x) = \dfrac{16\sin{x}\cos{x}\cos(2x)\cos(4x)\cos(8x)}{16\sin{x}} \)
Paya arka arkaya sinüs iki kat açı formülünü uygulayalım.
\( \sin(2x) = 2\sin{x}\cos{x} \)
\( = \dfrac{8\sin(2x)\cos(2x)\cos(4x)\cos(8x)}{16\sin{x}} \)
\( = \dfrac{4\sin(4x)\cos(4x)\cos(8x)}{16\sin{x}} \)
\( = \dfrac{2\sin(8x)\cos(8x)}{16\sin{x}} \)
\( = \dfrac{\sin(16x)}{16\sin{x}} \)
Bölme kuralı ile fonksiyonun türevini alalım.
\( f'(x) = \dfrac{(\sin(16x))'(16\sin{x}) - \sin(16x)(16\sin{x})'}{[16\sin{x}]^2} \)
\( = \dfrac{16\cos(16x)(16x)'\sin{x} - \sin(16x)(16\cos{x})}{256(\sin{x})^2} \)
\( = \dfrac{16\cos(16x)(16)\sin{x} - 16\sin(16x)\cos{x}}{256(\sin{x})^2} \)
\( = \dfrac{16\cos(16x)\sin{x} - \sin(16x)\cos{x}}{16(\sin{x})^2} \)
\( x = \frac{\pi}{6} \) yazarak bu noktadaki türev değerini bulalım.
\( f'(\frac{\pi}{6}) = \dfrac{16\cos(16 \cdot \frac{\pi}{6})\sin{\frac{\pi}{6}} - \sin(16 \cdot \frac{\pi}{6})\cos{\frac{\pi}{6}}}{16(\sin{\frac{\pi}{6}})^2} \)
\( = \dfrac{16\cos{\frac{8\pi}{3}}\sin{\frac{\pi}{6}} - \sin{\frac{8\pi}{3}}\cos{\frac{\pi}{6}}}{16(\sin{\frac{\pi}{6}})^2} \)
\( = \dfrac{16(-\frac{1}{2})\frac{1}{2} - \frac{\sqrt{3}}{2}\frac{\sqrt{3}}{2}}{16(\frac{1}{2})^2} \)
\( = \dfrac{-4 - \frac{3}{4}}{4} = -\dfrac{19}{16} \) bulunur.