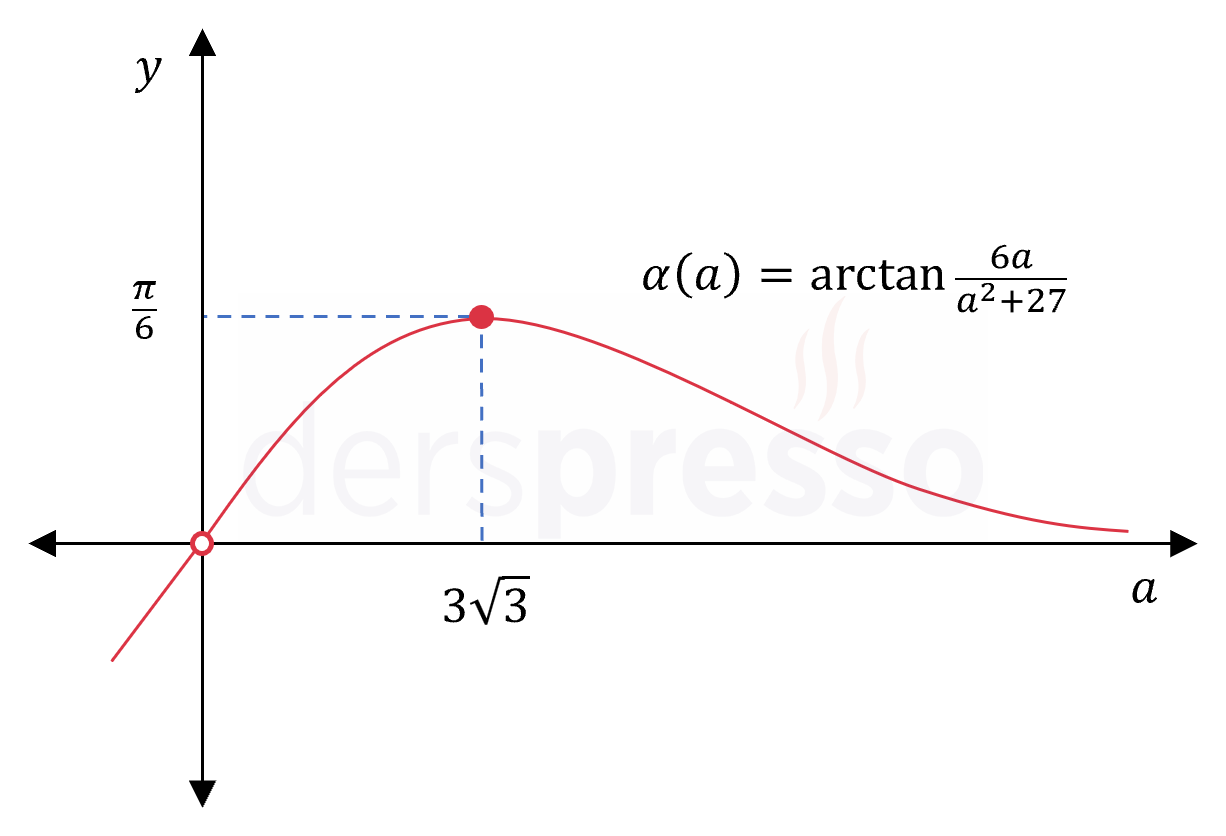
Minimum - Maksimum Problemleri
Minimum - maksimum problemleri (bir diğer adıyla optimizasyon problemleri), pek çok olası çözüm arasından en iyi çözümü bulmayı hedefleyen problemlerdir. Bu "en iyi çözüm" bazı problemlerde amaç fonksiyonu olarak adlandırılan bir fonksiyonun belirli bir aralıkta alabileceği en küçük değer iken, diğerlerinde en büyük değerdir.
Bu tip problemler mutlak minimum ve maksimum problemlerinin gerçek hayat uygulamaları olarak düşünülebilir, dolayısıyla bu konuya başlarken hem kapalı hem de açık aralıkta tanımlı fonksiyonların mutlak minimum ve maksimum noktalarının ve değerlerinin bulunma yöntemlerine iyi düzeyde hakim olmak önemlidir.
Bu bölümde tek bir bağımsız değişkene bağlı olan ya da tek bir bağımsız değişkene indirgenebilen minimum - maksimum problemlerini inceleyeceğiz.
Minimum - maksimum problemlerinin çözümünde aşağıdaki üç adımlı yöntem kullanılabilir.
Adım 1: Problem tanımı
Tüm bağımsız değişkenler tanımlanır.
En küçük/en büyük değeri bulunmak istenen değişken tanımlanır.
Bu aşamada değişkenleri ve aralarındaki ilişkileri gösteren bir şekil çizilebilir.
Adım 2: Amaç fonksiyonu
En küçük/en büyük değeri bulunmak istenen değişkeni temsil eden amaç fonksiyonu yazılır.
Değişkenlerin ve amaç fonksiyonunun tanım aralıkları belirlenir.
Değişkenler arasındaki kısıtlar matematiksel olarak ifade edilir.
Bu kısıtlar kullanılarak tüm değişkenler tek bir değişken cinsinden ifade edilir ve amaç fonksiyonunda yerine konduğunda tek bir değişkene bağlı amaç fonksiyonu elde edilir.
Adım 3: Problem çözümü
Amaç fonksiyonunun tanımlı olduğu aralıkta alabileceği en büyük/en küçük değer ve bu değeri aldığı nokta bulunur.
Bu aşamada çoğu zaman mutlak minimum/maksimum nokta bulma yöntemleri kullanılır.
Bu adımlar uygulanırken aşağıdaki noktalara dikkat edilmelidir.
- Değişkenlerin tanım aralıkları problemde verilebileceği gibi, fiziksel büyüklüklerin doğasından gelen ve özellikle belirtilmeyen bazı kısıtların da probleme dahil edilmesi gerekebilir (uzunluk pozitiftir gibi).
- En iyi çözümü veren değişken değerleri tanım aralıkları ile kontrol edilmeli, tanım aralığı dışında kalan değerler çözüme dahil edilmemelidir.
Minimum - maksimum problemlerinin çözümünü bir örnek üzerinde gösterelim.

Bir kenarı boyunca duvar örülü olan bir arsanın bir bölümü tel ile çevrilerek dikdörtgen şeklinde bir bahçe oluşturulmak isteniyor.
Toplam 300 m tel bulunduğuna ve duvar boyunca tel çekilmesine gerek olmadığına göre, oluşturulabilecek en büyük alanlı bahçe kaç metrekare olur?
1. Problem tanımı:
\( a \): Bahçenin duvara paralel kenarının uzunluğu
\( b \): Bahçenin duvara dik kenarının uzunluğu
\( A \): Bahçenin alanı
Problemde bahçenin alanının en büyük değeri istenmektedir.
2. Amaç fonksiyonu:
Bahçenin alanını aşağıdaki formülle bulabiliriz.
\( A = ab \)
Bahçenin kenar uzunlukları ve alanı pozitif büyüklüklerdir.
\( a, b, A \in \mathbb{R^+} \)
Amaç fonksiyonunu tek bir değişken cinsinden yazabilmek için değişkenler arasında bir ilişki kurmaya çalışalım.
Bahçenin üç kenarında kullanılabilecek toplam tel uzunluğu 300 m'dir.
\( a + 2b = 300 \)
Bu eşitlikte \( a \) değişkenini yalnız bırakalım.
\( a = 300 - 2b \)
\( a \) değerini alan formülünde yerine koyduğumuzda sadece \( b \) değişkenine bağlı olan amaç fonksiyonunu elde ederiz.
\( A = ab \)
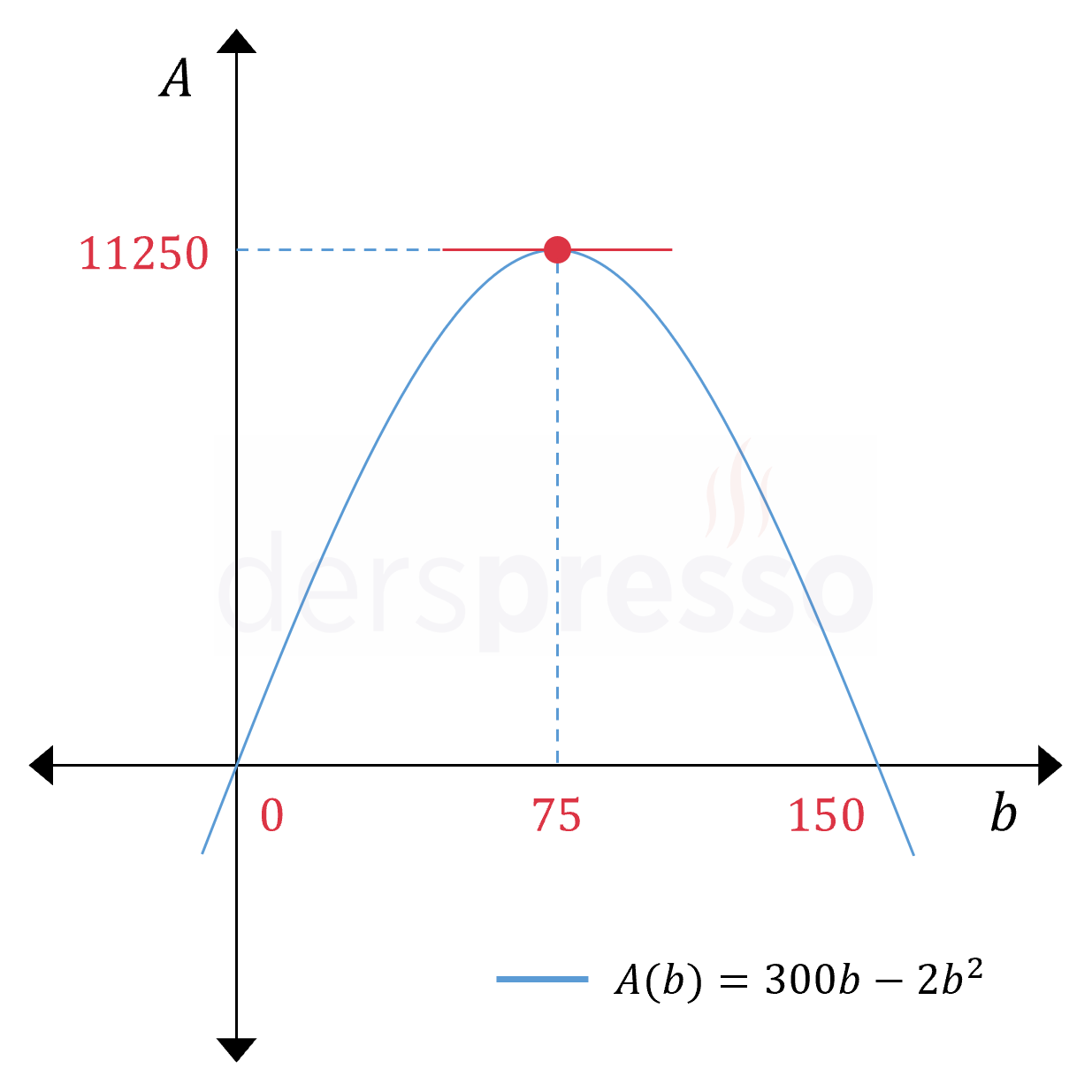
\( A(b) = (300 - 2b)b \)
\( = 300b - 2b^2 \)
\( a \in \mathbb{R^+} \) bilgisini kullanarak \( b \) tanım aralığını bulalım.
\( a = 300 - 2b \gt 0 \)
\( b \lt 150 \)
Buna göre en büyük değerini bulmak istediğimiz amaç fonksiyonu aşağıdaki gibidir.
\( A: (0, 150) \to \mathbb{R^+} \)
\( A(b) = 300b - 2b^2 \)
3. Problem çözümü:
\( A \) fonksiyonu açık bir aralıkta tanımlıdır ve bir polinom fonksiyonu olduğu için süreklidir.
\( A \) fonksiyonu negatif başkatsayılı (kolları aşağı yönlü) bir parabol olduğu için (eğer tanım aralığı bu noktayı içeriyorsa) en büyük değerini birinci türevinin sıfır olduğu tepe noktasında alır.
\( A'(b) = 300 - 4b \)
Tepe noktasını bulmak için birinci türevi sıfıra eşitleyelim.
\( 300 - 4b = 0 \)
\( b = 75 \)
Tepe noktası fonksiyonun tanım aralığında olduğu için \( A \) fonksiyonu en büyük değerini bu noktada alır ve fonksiyonun uç noktalarını kontrol etmemize gerek yoktur.
Fonksiyonun tepe noktasındaki değerini bulalım.
\( A(75) = 300(75) - 2(75)^2 \)
\( = 11250 \) metrekare bulunur.
Amaç fonksiyonunun grafiği, bulduğumuz noktalar ve değerleri aşağıdaki şekilde gösterilmiştir.
Minimum - maksimum problemlerinin çözümünü diğer bir örnek üzerinde gösterelim.
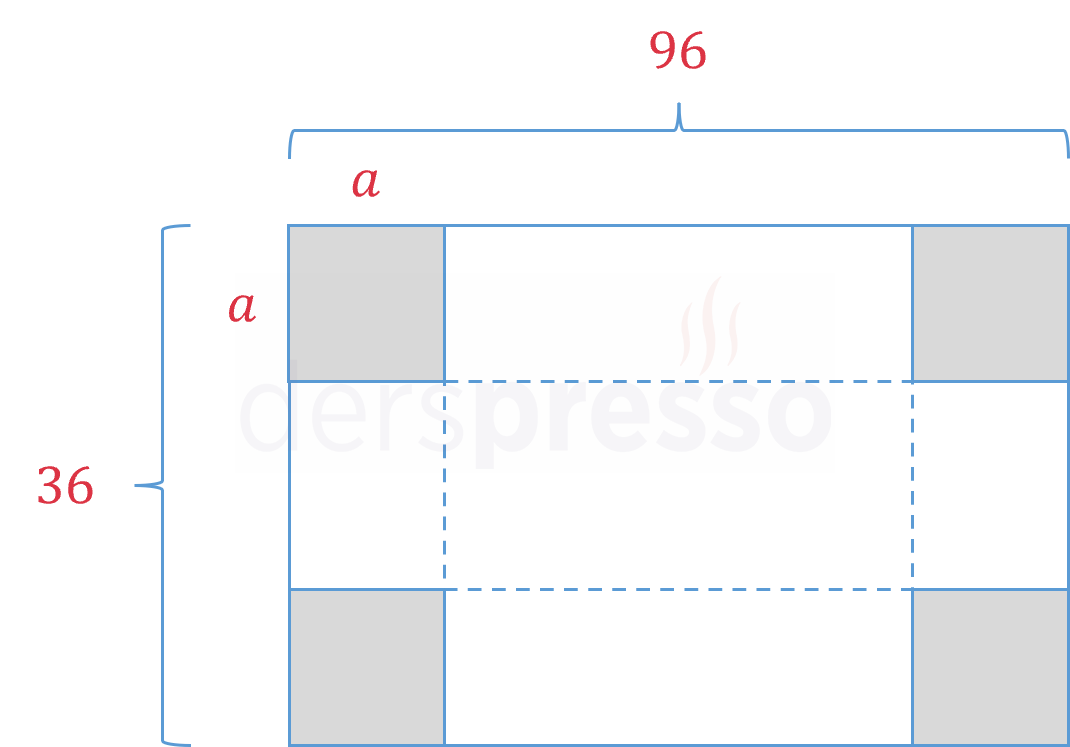
Kenar uzunlukları 36 cm ve 96 cm olan dikdörtgen şeklindeki bir kartonun köşelerinden kenarları \( a \) cm uzunluğunda kareler kesilip geriye kalan kartonun yan yüzleri katlanarak dikdörtgen prizma şeklinde üstü açık bir kutu yapılacaktır.
En büyük hacimli kutu oluşturulmak istendiğine göre, \( a \) uzunluğu kaç cm olmalıdır?
1. Problem tanımı:
\( a \): Kesilen kare parçaların bir kenar uzunluğu
\( V \): Oluşturulan kutunun hacmi
Problemde kartonun köşeleri kesildikten sonra oluşan kutunun hacminin en büyük değeri istenmektedir.
2. Amaç fonksiyonu:
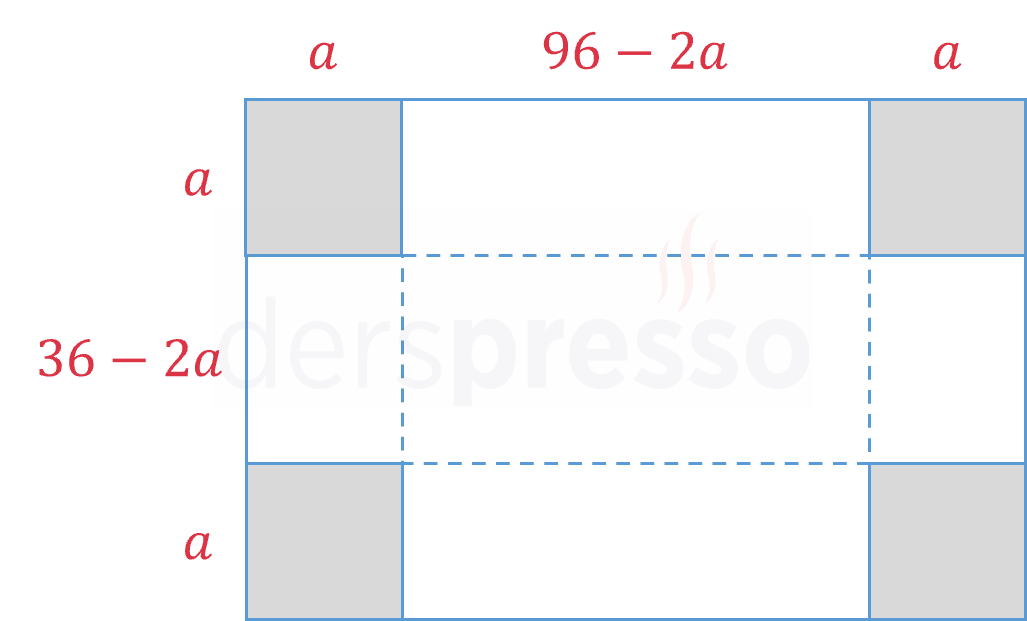
Köşeler kesildikten sonra elde edilen kartonun kenar uzunlukları aşağıdaki gibi olur.
Kutunun hacmini aşağıdaki formülle bulabiliriz.
V = Taban uzunluğu x Taban genişliği x Yükseklik
Taban uzunluğu \( = 96 - 2a \)
Taban genişliği \( = 36 - 2a \)
Yükseklik \( = a \)
Kesilecek kenar uzunluğu ve hacim pozitif büyüklüklerdir.
\( a, V \in \mathbb{R^+} \)
\( a \) değişkeni cinsinden hacim aşağıdaki şekilde ifade edilebilir.
\( V(a) = (96 - 2a)(36 - 2a)a \)
\( = 4a^3 - 264a^2 + 3456a \)
Kesilen parçaların bir kenar uzunluğu kartonun kısa kenarının uzunluğundan küçük olmalıdır.
\( 2a \lt 36 \)
\( a \lt 18 \)
Buna göre en büyük değerini bulmak istediğimiz amaç fonksiyonu aşağıdaki gibidir.
\( V: (0, 18) \to \mathbb{R^+} \)
\( V(a) = 4a^3 - 264a^2 + 3456a \)
3. Problem çözümü:
\( V \) fonksiyonu açık bir aralıkta tanımlıdır ve bir polinom fonksiyonu olduğu için süreklidir.
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
\( V'(a) = 12a^2 - 528a + 3456 \)
Fonksiyonun tanım aralığı içinde birinci türevinin sıfır olduğu iç noktaları bulalım.
\( 12a^2 - 528a + 3456 = 0 \)
\( 12(a^2 - 44a - 288) = 0 \)
\( 12(a - 8)(a - 36) \)
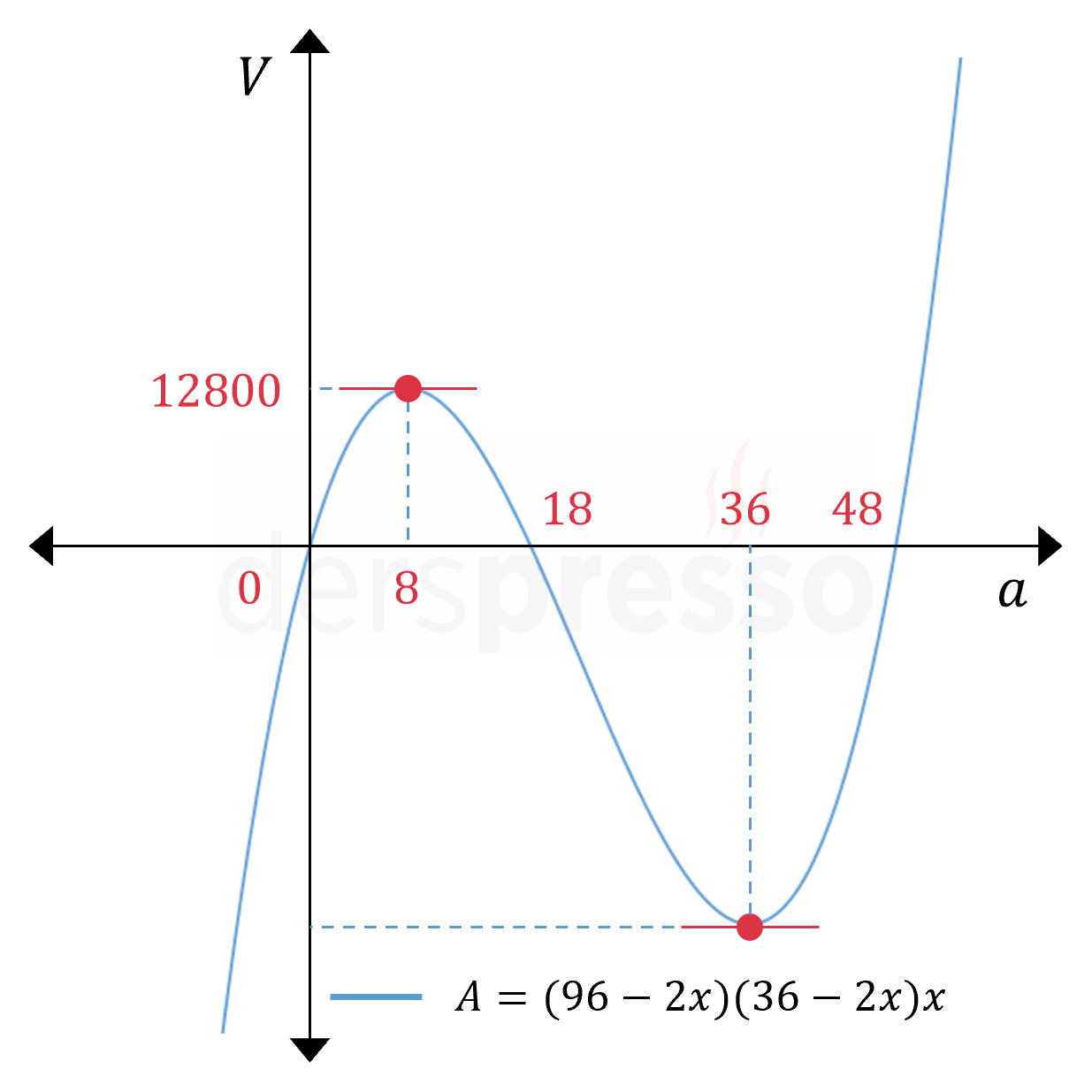
\( a = 8 \)
Fonksiyonun birinci türevinin tanımsız olduğu iç nokta yoktur.
Kritik nokta: \( a = 8 \)
Fonksiyonun kritik noktadaki değerini bulalım.
\( V(8) = (96 - 2(8))(36 - 2(8))8 \)
\( = 80 \cdot 20 \cdot 8 = 12800 \)
Fonksiyonun açık uç noktalarındaki limitini bulalım.
\( \lim\limits_{x \to 0^+} [(96 - 2a)(36 - 2a)a] \)
\( = (96 - 2(0))(36 - 2(0))0 = 0 \)
\( \lim\limits_{x \to 18^-} [(96 - 2a)(36 - 2a)a] \)
\( = (96 - 2(18))(36 - 2(18))18 = 0 \)
Buna göre fonksiyon açık uç noktaları civarında \( 12800 \) değerinden daha büyük bir değer almaz.
Bu değerleri karşılaştırdığımızda fonksiyonun tanım aralığındaki en büyük değeri olarak \( a = 8 \) noktasında aldığı \( 12800 \text{ cm}^3 \) değeri bulunur.
Amaç fonksiyonunun grafiği, bulduğumuz noktalar ve değerleri aşağıdaki şekilde gösterilmiştir.
\( x \ge 0 \), \( y \ge 0 \)
\( x + y = 80 \)
olduğuna göre, \( x^3y \) çarpımının alabileceği en büyük değer kaçtır?
Çözümü GösterAdım 1: Problem tanımı
Problemde aşağıdaki çarpımın en büyük değeri istenmektedir.
\( A = x^3y \)
Adım 2: Amaç fonksiyonu
Amaç fonksiyonunu tek bir değişken cinsinden yazabilmek için \( x \) ve \( y \) değişkenleri arasında verilen ilişkiyi kullanalım.
\( x + y = 80 \)
\( y = 80 - x \)
\( y \) değişenini çarpımda yerine koyduğumuzda sadece \( x \) değişkenine bağlı olan amaç fonksiyonunu elde ederiz.
\( A = x^3y \)
\( = x^3(80 - x) \)
\( = 80x^3 - x^4 \)
\( y \ge 0 \) bilgisini kullanarak \( x \) tanım aralığını bulalım.
\( y = 80 - x \ge 0 \)
\( x \le 80 \)
Buna göre en büyük değerini bulmak istediğimiz amaç fonksiyonu aşağıdaki gibidir.
\( A: [0, 80] \to \mathbb{R^+} \)
\( A(x) = 80x^3 - x^4 \)
Adım 3: Problem çözümü
\( A \) fonksiyonu kapalı bir aralıkta tanımlıdır ve bir polinom fonksiyonu olduğu için süreklidir.
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
\( A'(x) = 240x^2 - 4x^3 \)
Fonksiyonun tanım kümesi içinde birinci türevinin sıfır olduğu iç noktaları bulalım.
\( 240x^2 - 4x^3 = 0 \)
\( 4x^2(60 - x) = 0 \)
\( x = 60 \)
Fonksiyonun tanım kümesi içinde birinci türevinin tanımsız olduğu iç nokta yoktur.
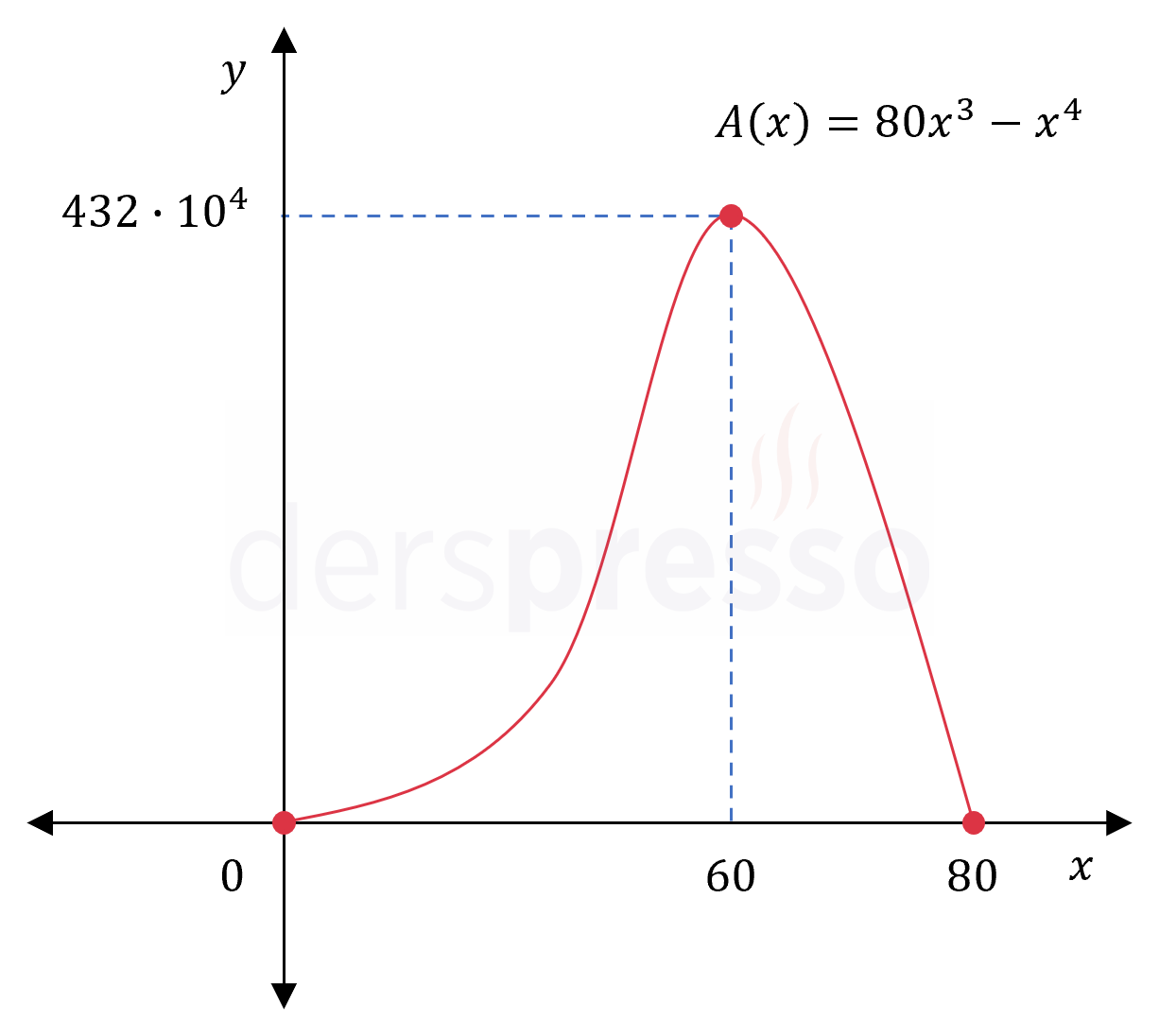
Kritik nokta: \( x = 60 \)
Fonksiyonun kritik noktadaki değerini bulalım.
\( A(60) = 80(60)^3 - (60)^4 = 60^3(80 - 60) \)
\( = 60^3(20) = 432 \cdot 10^4 \)
Fonksiyonun kapalı uç noktalarındaki değerini bulalım.
\( A(0) = 80(0)^3 - (0)^4 = 0 \)
\( A(80) = 80(80)^3 - (80)^4 = 0 \)
Bu değerleri karşılaştırdığımızda fonksiyon tanım aralığındaki en büyük değeri \( x = 60 \) noktasında \( 432 \cdot 10^4 \) olarak alır.
Amaç fonksiyonunun grafiği, bulduğumuz noktalar ve değerleri aşağıdaki şekilde gösterilmiştir.
Bir traktör üreticisi günde \( x \) adet traktör üretmektedir. Traktörün birim maliyeti üretim adedi cinsinden aşağıdaki formülle hesaplanıyor.
\( m(x) = x^3 + \dfrac{1875}{x} - 100 \)
Buna göre birim maliyetin en az olması için üretici günde kaç adet traktör üretmelidir?
Çözümü GösterAdım 1: Problem tanımı
\( x \): Bir günde üretilen traktör adedi
Birim maliyetin en küçük olduğu üretim adedi istenmektedir.
Adım 2: Amaç fonksiyonu
Üretilen traktör sayısı pozitif bir tam sayıdır.
\( x \in \mathbb{Z^+} \)
Maliyet pozitif bir büyüklüktür.
\( m \in \mathbb{R^+} \)
Buna göre en küçük değerini bulmak istediğimiz amaç fonksiyonu aşağıdaki gibidir.
\( m: [1, \infty) \to \mathbb{R^+} \)
\( m(x) = x^3 + \dfrac{1875}{x} - 100 \)
Adım 3: Problem çözümü
\( m \) fonksiyonu açık bir aralıkta tanımlıdır ve bir rasyonel fonksiyon içerdiği için paydayı sıfır yapan ve tanım aralığı dışındaki \( x = 0 \) noktası hariç süreklidir.
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
\( m'(x) = 3x^2 - \dfrac{1875}{x^2} \)
\( = \dfrac{3x^4 - 1875}{x^2} \)
Fonksiyonun tanım kümesi içinde birinci türevinin sıfır olduğu iç noktaları bulalım.
\( \dfrac{3x^4 - 1875}{x^2} = 0 \)
\( 3x^4 - 1875 = 0 \)
\( 3(x - 5)(x + 5)(x^2 + 25) = 0 \)
\( x = 5 \)
Fonksiyonun tanım aralığı içinde birinci türevinin tanımsız olduğu iç nokta yoktur.
Kritik nokta: \( x = 5 \)
Fonksiyonun kritik noktadaki değerini bulalım.
\( m(5) = 5^3 + \dfrac{1875}{5} - 100 = 400 \)
Fonksiyonun kapalı uç noktasındaki değerini bulalım.
\( m(1) = 1^3 + \dfrac{1875}{1} - 100 = 1776 \)
Fonksiyonun açık uç noktasındaki limitini bulalım.
\( \lim\limits_{x \to \infty} (x^3 + \dfrac{1875}{x} - 100) = \infty + 0 - 100 = \infty \)
Bu değerleri karşılaştırdığımızda fonksiyon tanım aralığındaki en küçük değeri \( x = 5 \) noktasında alır.
Dolayısıyla üretici ortalama maliyetin en az olması için günde \( 5 \) adet traktör üretmelidir.
Amaç fonksiyonunun grafiği, bulduğumuz noktalar ve değerleri aşağıdaki şekilde gösterilmiştir.

Bir firma günde en az 100 en fazla 400 litre sirke üretiyor ve ürettiği tüm sirkeyi satıyor. Firmanın günlük kârı aşağıdaki formülle hesaplanıyor.
\( k(x) = \dfrac{(x - 100)^3}{3000} - \dfrac{(x - 10)}{10} + 500 \)
\( x \) bir günde üretilen sirke hacmi olduğuna göre, firma en yüksek kârı elde edebilmek için günde kaç litre sirke üretmelidir?
Çözümü GösterAdım 1: Problem tanımı
\( x \): Bir günde üretilen litre cinsinden sirke miktarı
Problemde kârın en yüksek değerini aldığı litre cinsinden üretim miktarı istenmektedir.
Adım 2: Amaç fonksiyonu
Hacim pozitif bir büyüklüktür.
\( x \in \mathbb{R^+} \)
Buna göre en büyük değerini bulmak istediğimiz amaç fonksiyonu aşağıdaki gibidir.
\( k: [100, 400] \to \mathbb{R^+} \)
\( k(x) = \dfrac{(x - 100)^3}{3000} - \dfrac{x - 10}{10} + 500 \)
Adım 3: Problem çözümü
\( k \) fonksiyonu kapalı bir aralıkta tanımlıdır ve bir polinom fonksiyonu olduğu için süreklidir.
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
\( k'(x) = \dfrac{(x - 100)^2}{1000} - \dfrac{1}{10} \)
\( = \dfrac{(x - 100)^2 - 100}{1000} \)
Fonksiyonun tanım kümesi içinde birinci türevinin sıfır olduğu iç noktaları bulalım.
\( \dfrac{(x - 100)^2 - 100}{1000} = 0 \)
\( (x - 100)^2 - 100 = 0 \)
\( (x - 100)^2 = 100 \)
\( x - 100 = \pm 10 \)
\( x \) değişkeni \( [100, 400] \) aralığında tanımlıdır.
\( x = 110 \)
Fonksiyonun tanım kümesi içinde birinci türevinin tanımsız olduğu iç nokta yoktur.
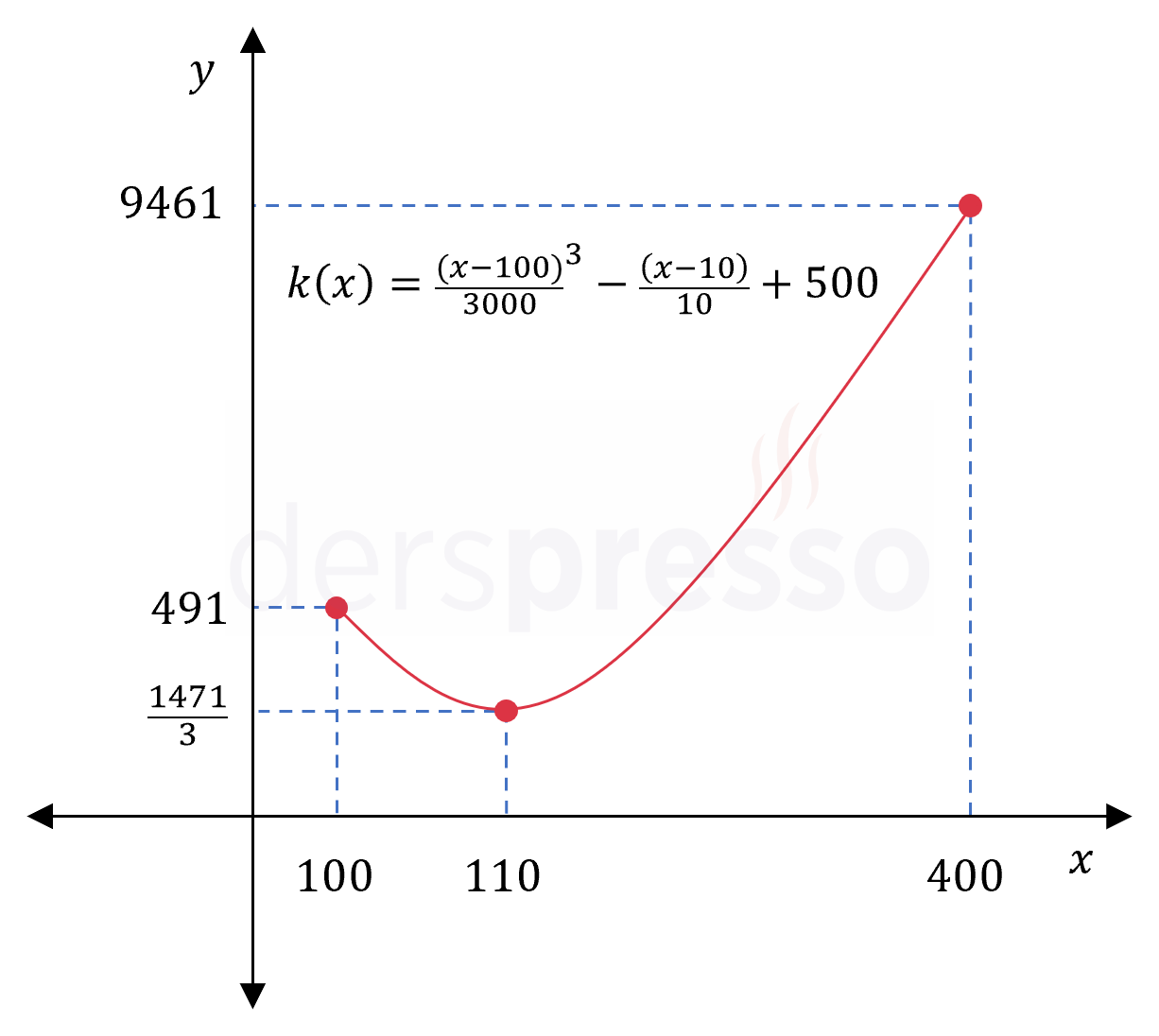
Kritik nokta: \( x = 110 \)
Fonksiyonun kritik noktadaki değerini bulalım.
\( k(110) = \dfrac{(110 - 100)^3}{3000} - \dfrac{110 - 10}{10} + 500 = \dfrac{1471}{3} \)
Fonksiyonun kapalı uç noktalarındaki değerini bulalım.
\( k(100) = \dfrac{(100 - 100)^3}{3000} - \dfrac{100 - 10}{10} + 500 = 491 \)
\( k(400) = \dfrac{(400 - 100)^3}{3000} - \dfrac{400 - 10}{10} + 500 = 9461 \)
Bu değerleri karşılaştırdığımızda fonksiyon tanım aralığındaki en büyük değeri olarak \( x = 400 \) noktasında aldığı \( 9461 \) TL değeri bulunur.
Dolayısıyla firma kârın en yüksek olması için günde 400 litre sirke üretmelidir.
Amaç fonksiyonunun grafiği, bulduğumuz noktalar ve değerleri aşağıdaki şekilde gösterilmiştir.
Bir ayakkabı firması günde \( x \) adet ayakkabı üretmektedir. Bir adet ayakkabının satış fiyatı \( 136 - 0,1x \) fonksiyonu ile belirlenirken, bir günde üretilen ayakkabıların toplam maliyeti \( 100 + 0,2x \) fonksiyonu ile hesaplanmaktadır.
Firma ürettiği her ayakkabıyı satabildiğine göre, en yüksek kârı elde edebilmek için bir günde üretmesi gereken ayakkabı adedi kaçtır?
Çözümü GösterAdım 1: Problem tanımı
\( x \): Bir günde üretilen ayakkabı adedi
\( G \): Bir günde satılan ayakkabıdan elde edilen toplam gelir
\( M \): Bir günde satılan ayakkabının toplam maliyeti
\( K \): Firmanın günlük kârı
Problemde ayakkabı satışından en yüksek kârın elde edildiği günlük ayakkabı üretim adedi istenmektedir.
Adım 2: Amaç fonksiyonu
Bir günde üretilen ayakkabı adedi ile bir adet ayakkabının satış fiyatının çarpımı, bir günde elde edilen toplam geliri verir.
\( G = x(136 - 0,1x) \)
Bir günde üretilen ayakkabıların toplam maliyeti soruda verilmiştir.
\( M = 100 + 0,2x \)
Firmanın günlük kârı, bir güne ait toplam gelir ile toplam maliyetin farkına eşittir.
\( K = x(136 - 0,1x) - (100 + 0,2x) \)
\( K = -0,1x^2 + (135,8)x - 100 \)
Üretilen ayakkabı adedi pozitif bir tam sayıdır.
\( x \in \mathbb{Z^+} \)
Birim satış fiyatı pozitif bir büyüklüktür.
\( 136 - 0,1x \gt 0 \)
\( x \lt 1360 \)
Toplam maliyet pozitif bir büyüklüktür.
\( M \in \mathbb{R^+} \)
\( 100 + 0,2x \gt 0 \)
\( x \gt -500 \)
Bulduğumuz \( x \) değer aralıklarının kesişim kümesini bulalım.
\( 0 \lt x \lt 1360 \)
Buna göre en büyük değerini bulmak istediğimiz amaç fonksiyonu aşağıdaki gibidir.
\( K: [1, 1360) \to \mathbb{R} \)
\( K(x) = -0,1x^2 + (135,8)x - 100 \)
Adım 3: Problem çözümü
\( K \) fonksiyonu açık bir aralıkta tanımlıdır ve bir polinom fonksiyonu olduğu için süreklidir.
\( K \) fonksiyonu negatif başkatsayılı (kolları aşağı yönlü) bir parabol olduğu için (eğer tanım aralığı bu noktayı içeriyorsa) en büyük değerini birinci türevinin sıfır olduğu tepe noktasında alır.
\( K'(x) = -0,2x + 135,8 \)
Tepe noktasını bulmak için birinci türevi sıfıra eşitleyelim.
\( -0,2x + 135,8 = 0 \)
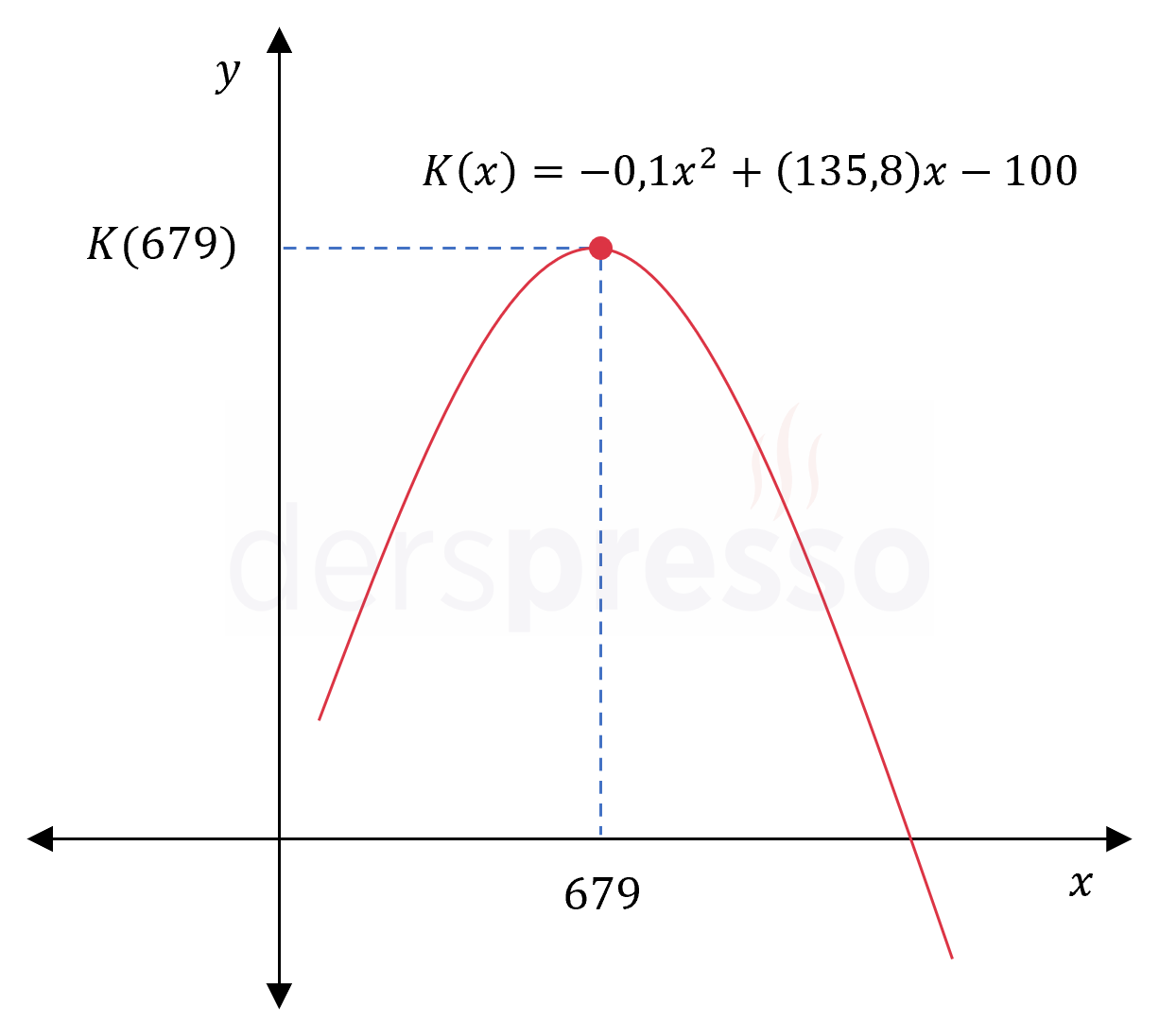
\( x = 679 \)
Tepe noktası fonksiyonun tanım aralığında olduğu için \( K \) fonksiyonu en büyük değerini bu noktada alır ve fonksiyonun uç noktalarını kontrol etmemize gerek yoktur.
Dolayısıyla firma en yüksek kârı günde \( x = 679 \) adet ayakkabı ürettiğinde elde eder.
Amaç fonksiyonunun grafiği, bulduğumuz noktalar ve değerleri aşağıdaki şekilde gösterilmiştir.
\( y = \dfrac{x^2}{2} \) parabol grafiği üzerinde \( A(6, 0) \) noktasına en yakın olan nokta hangisidir?
Çözümü GösterAdım 1: Problem tanımı
\( P(x, y) \): Parabol üzerindeki herhangi bir nokta
\( d \): \( A \) ve \( P \) noktaları arasındaki uzaklık
Problemde \( A \) noktasının parabole uzaklığının en küçük olduğu nokta istenmektedir.
Adım 2: Amaç fonksiyonu
İki nokta arasındaki uzaklık formülünü kullanalım.
\( d = \sqrt{(x - 6)^2 + (y - 0)^2} \)
\( = \sqrt{(x - 6)^2 + y^2} \)
Bir karekök ifadesi en küçük değerini kök içindeki ifade en küçük değerini aldığında alır.
O halde bir \( D \) fonksiyonu tanımlayalım ve işlemlerimizi bu fonksiyon üzerinden yapalım.
\( D = (x - 6)^2 + y^2 \)
\( D \) fonksiyonu en küçük değerini aldığında soruda istenen \( d \) uzaklığı da en küçük değerini alacaktır.
Uzaklık pozitif bir büyüklüktür.
\( d, D \in \mathbb{R^+} \)
Amaç fonksiyonunu tek bir değişken cinsinden yazabilmek için \( x \) ve \( y \) değişkenleri arasında bir ilişki kurmaya çalışalım.
\( P(x, y) \) noktası parabol üzerinde olduğu için parabol denklemini sağlar.
\( P(x, y = \dfrac{x^2}{2}) \)
Bulduğumuz \( y \) değerini formülde yerine koyduğumuzda sadece \( x \) değişkenine bağlı olan amaç fonksiyonunu elde ederiz.
\( D = (x - 6)^2 + (\dfrac{x^2}{2})^2 \)
\( = x^2 - 12x + 36 + \dfrac{x^4}{4} \)
Buna göre en küçük değerini bulmak istediğimiz amaç fonksiyonu aşağıdaki gibidir.
\( D: \mathbb{R} \to \mathbb{R^+} \)
\( D(x) = \dfrac{x^4}{4} + x^2 - 12x + 36 \)
Adım 3: Problem çözümü
\( D \) fonksiyonu açık bir aralıkta tanımlıdır ve bir polinom fonksiyonu olduğu için süreklidir.
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
\( D'(x) = x^3 + 2x - 12 \)
Fonksiyonun tanım kümesi içinde birinci türevinin sıfır olduğu iç noktaları bulalım.
\( x^3 + 2x - 12 = 0 \)
\( (x - 2)(x^2 + 2x + 6) = 0 \)
\( x^2 + 2x + 6 = 0 \) denkleminin deltasını hesaplayalım.
\( \Delta = b^2 - 4ac \)
\( = 2^2 - 4(1)(6) = -20 \lt 0 \)
İkinci çarpanın reel kökü yoktur.
\( x = 2 \)
Fonksiyonun tanım kümesi içinde birinci türevinin tanımsız olduğu iç nokta yoktur.
Kritik nokta: \( x = 2 \)
Fonksiyonun kritik noktadaki değerini bulalım.
\( D(2) = \dfrac{2^4}{4} + 2^2 - 12(2) + 36 = 20 \)
Fonksiyonun açık uç noktalarındaki limitini bulalım.
\( \lim\limits_{x \to -\infty} (\dfrac{x^4}{4} + x^2 - 12x + 36) = \infty \)
\( \lim\limits_{x \to \infty} (\dfrac{x^4}{4} + x^2 - 12x + 36) = \infty \)
Bu değerleri karşılaştırdığımızda fonksiyon tanım aralığındaki en küçük değeri \( x = 2 \) noktasında alır.
Dolayısıyla \( d \) uzaklığı da tanım kümesi içinde en küçük değerini \( x = 2 \) noktasında alır.
\( x = 2 \) için \( y \) değerini bulalım.
\( y = \dfrac{x^2}{2} = \dfrac{2^2}{2} = 2 \)
Buna göre parabol grafiği üzerinde \( A(6, 0) \) noktasına en yakın olan nokta \( P(2, 2) \) noktasıdır.
Amaç fonksiyonunun grafiği, bulduğumuz noktalar ve değerleri aşağıdaki şekilde gösterilmiştir.


Şekildeki gibi iki kenarı \( x \) ve \( y \) eksenleri üzerinde ve bir köşesi \( f(x) = 2 - x^2 \) eğrisi üzerinde olan dikdörtgenlerden çevresi en büyük olan dikdörtgenin alanı nedir?
Çözümü GösterAdım 1: Problem tanımı
\( C \): Dikdörtgenin çevresi
\( (a, 2 - a^2) \): Dikdörtgenin \( f \) fonksiyonu üzerinde bulunan köşesinin koordinatları
Problemde dikdörtgenin çevresinin en büyük değeri istenmektedir.
Adım 2: Amaç fonksiyonu
Fonksiyonun \( x \) eksenini kestiği noktayı bulalım.
\( 0 = 2 - x^2 \)
\( x = \sqrt{2} \)
Birinci bölgede bir dikdörtgen oluşması için \( a \) değer aralığı aşağıdaki gibi olmalıdır.
\( a \in (0, \sqrt{2}) \)
Çevre pozitif bir büyüklüktür.
\( C \in \mathbb{R^+} \)
Fonksiyon grafiği ve dikdörtgen aşağıdaki şekildeki gibidir.

Dikdörtgenin çevresini aşağıdaki formülle bulabiliriz.
\( C = 2a + 2(2 - a^2) \)
\( = -2a^2 + 2a + 4 \)
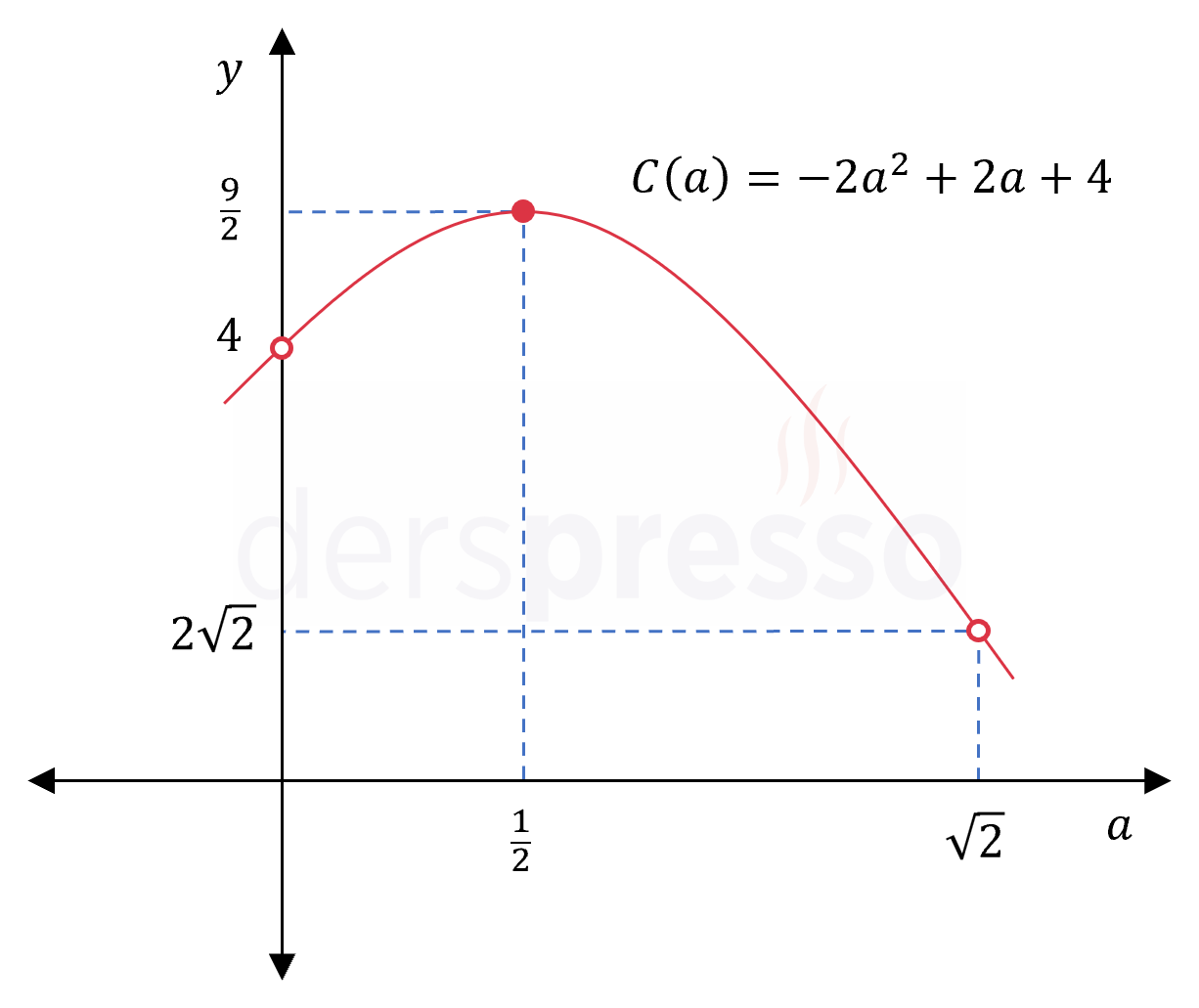
Buna göre en büyük değerini bulmak istediğimiz amaç fonksiyonu aşağıdaki şekilde tanımlanır.
\( C: (0, \sqrt{2}) \to (0, \infty) \)
\( C(a) = -2a^2 + 2a + 4 \)
Adım 3: Problem çözümü
\( C \) fonksiyonu açık bir aralıkta tanımlıdır ve polinom fonksiyonu olduğu için süreklidir.
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
\( C'(a) = -4a + 2 \)
Fonksiyonun tanım kümesi içinde birinci türevinin sıfır olduğu iç noktaları bulalım.
\( -4a + 2 = 0 \)
\( a = \dfrac{1}{2} \)
Fonksiyonun birinci türevinin tanımsız olduğu iç nokta yoktur.
Kritik nokta: \( a = \dfrac{1}{2} \)
Fonksiyonun kritik noktadaki değerini bulalım.
\( C\left( \dfrac{1}{2} \right) = -2\left( \dfrac{1}{2} \right)^2 + 2\left( \dfrac{1}{2} \right) + 4 \)
\( = \dfrac{9}{2} \)
Fonksiyonun açık uç noktalarındaki limitini bulalım.
\( \lim\limits_{a \to 0^+} (-2a^2 + 2a + 4) = -2(0)^2 + 2(0) + 4 = 4 \)
\( \lim\limits_{a \to \sqrt{2}^-} (-2a^2 + 2a + 4) = -2(\sqrt{2})^2 + 2(\sqrt{2}) + 4 = 2\sqrt{2} \)
Buna göre amaç fonksiyonu açık uç noktaları civarında \( \frac{9}{2} \) değerinden daha büyük bir değer almaz.
Bu değerleri karşılaştırdığımızda amaç fonksiyonunun tanım aralığındaki en büyük değeri olarak \( a = \frac{1}{2} \) noktasında aldığı \( \frac{9}{2} \) değeri bulunur.
Dikdörtgenin çevresinin en büyük olduğu \( a = \frac{1}{2} \) değeri için dikdörtgenin alanını bulalım.
\( A = a(2 - a^2) = \dfrac{1}{2}\left( 2 - \left( \dfrac{1}{2} \right)^2 \right) = \dfrac{7}{8} \)
Amaç fonksiyonunun grafiği, bulduğumuz noktalar ve değerleri aşağıdaki şekilde gösterilmiştir.
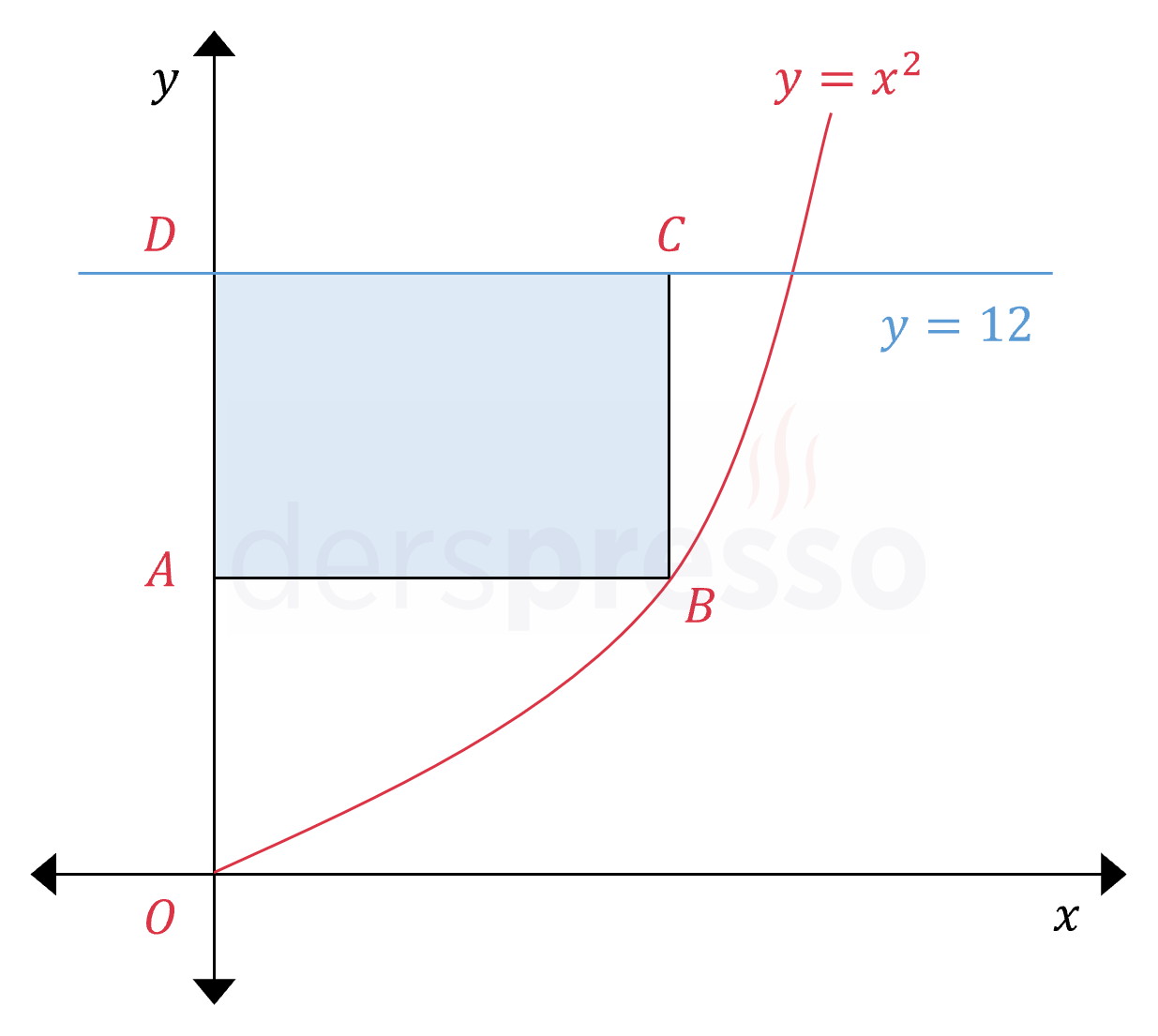
Şekildeki \( ABCD \) dikdörtgeninin \( [AD] \) kenarı \( y \) ekseni, \( [DC] \) kenarı \( y = 12 \) doğrusu, \( B \) köşesi de \( y = x^2 \) parabolü üzerindedir.
Buna göre \( ABCD \) dikdörtgeninin alanı en fazla kaç birimkare olabilir?
Çözümü GösterAdım 1: Problem tanımı
\( a \): Dikdörtgenin genişliği
\( \abs{AB} = \abs{DC} = a \)
\( b \): Dikdörtgenin yüksekliği
\( \abs{AD} = \abs{BC} = b \)
\( A \): Dikdörtgenin alanı
Problemde \( ABCD \) dikdörtgeninin alanının en büyük değeri istenmektedir.
Adım 2: Amaç fonksiyonu
Dikdörtgenin alanını aşağıdaki formülle bulabiliriz.
\( A = ab \)
Dikdörtgenin genişliği, yüksekliği ve alanı pozitif büyüklüklerdir.
\( a, b, A \in \mathbb{R^+} \)
Amaç fonksiyonunu tek bir değişken cinsinden yazabilmek için değişkenler arasında bir ilişki kurmaya çalışalım.
\( y = x^2 \) parabolü üzerindeki \( B \) noktasının \( a \) cinsinden koordinatlarını yazalım.
\( B(a, a^2) \)
\( B \) noktasının ordinat değeri ile dikdörtgenin yüksekliğinin toplamı, \( y = 12 \) doğrusunun ordinatına eşittir.
\( a^2 + b = 12 \)
Bu eşitlikte \( b \) değişkenini yalnız bırakalım.
\( b = 12 - a^2 \)
\( b \) değerini alan formülünde yerine koyduğumuzda sadece \( a \) değişkenine bağlı olan amaç fonksiyonunu elde ederiz.
\( A = ab \)
\( A(a) = a(12 - a^2) \)
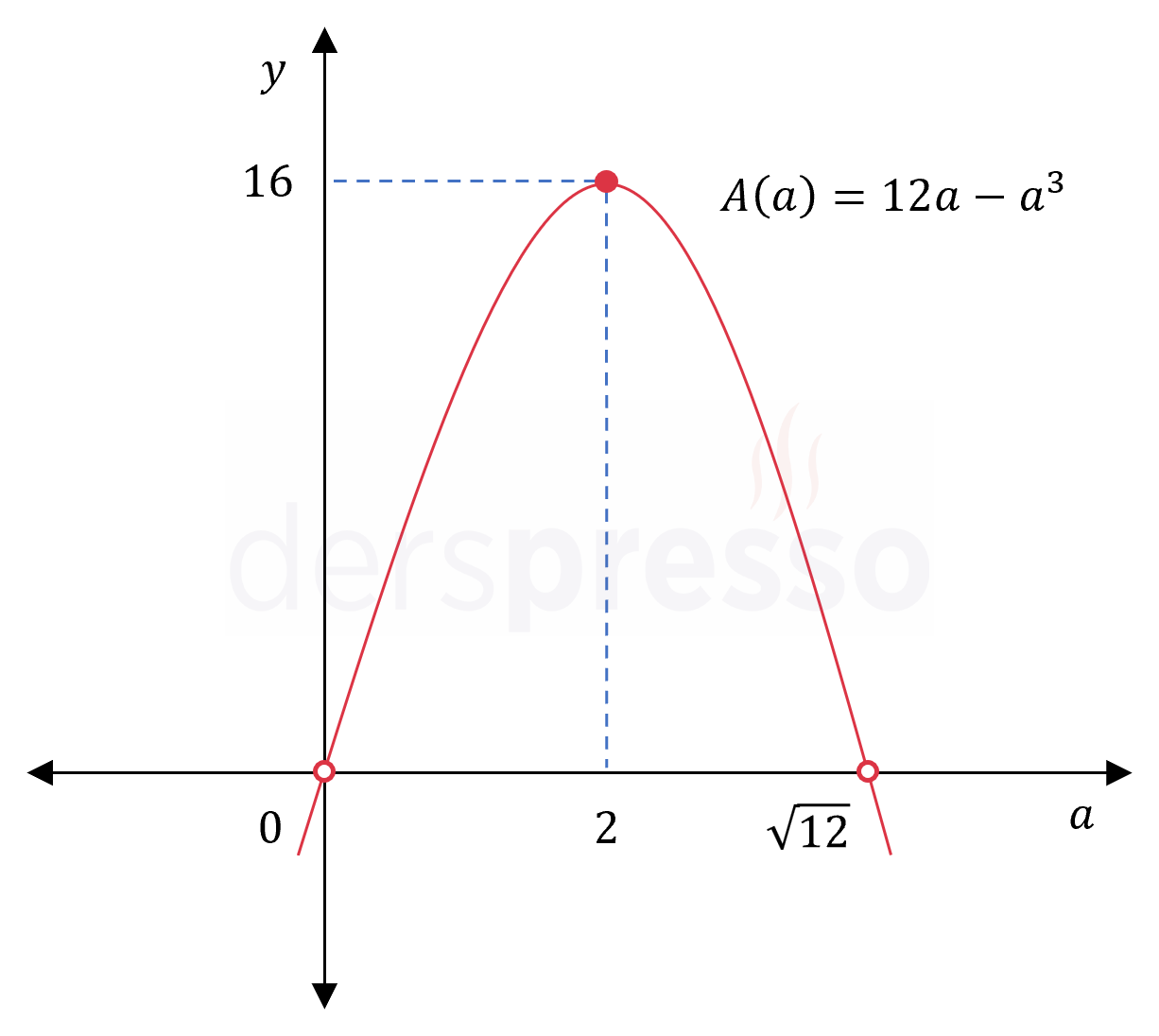
\( = 12a - a^3 \)
Belirtilen bölgede bir dikdörtgen oluşması için, \( a \) uzunluğu \( y = 12 \) doğrusu ile parabolün kesiştiği noktanın apsis değerinden küçük olmalıdır.
\( a \lt \sqrt{12} \)
Buna göre en büyük değerini bulmak istediğimiz amaç fonksiyonu aşağıdaki gibidir.
\( A: (0, \sqrt{12}) \to \mathbb{R^+} \)
\( A(a) = 12a - a^3 \)
Adım 3: Problem çözümü
\( A \) fonksiyonu açık bir aralıkta tanımlıdır ve bir polinom fonksiyonu olduğu için süreklidir.
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
\( A'(a) = 12 - 3a^2 \)
Fonksiyonun tanım aralığı içinde birinci türevinin sıfır olduğu iç noktaları bulalım.
\( 3(2 - a)(2 + a) = 0 \)
\( a = 2 \)
Fonksiyonun birinci türevinin tanımsız olduğu iç nokta yoktur.
Kritik nokta: \( a = 2 \)
Fonksiyonun kritik noktadaki değerini bulalım.
\( A(2) = 12(2) - 2^3 = 16 \)
Fonksiyonun açık uç noktalarındaki limitini bulalım.
\( \lim\limits_{x \to 0^+} (12a - a^3) = 12(0) - 0^3 = 0 \)
\( \lim\limits_{x \to \sqrt{12}^-} (12a - a^3) = 12(\sqrt{12}) - (\sqrt{12})^3 = 0 \)
Buna göre amaç fonksiyonu açık uç noktaları civarında \( 16 \) değerinden daha büyük bir değer almaz.
Bu değerleri karşılaştırdığımızda amaç fonksiyonunun tanım aralığındaki en büyük değeri olarak \( a = 2 \) noktasında aldığı \( 16 \) birimkare değeri bulunur.
Amaç fonksiyonunun grafiği, bulduğumuz noktalar ve değerleri aşağıdaki şekilde gösterilmiştir.

Selin, aile fotoğraflarını bastıracak ve fotoğrafa uygun bir çerçeve alacaktır. Çerçevenin alt ve üst kenarları ile fotoğraf arasındaki mesafe 5 cm, yan kenarları ile fotoğraf arasındaki mesafe 2,5 cm olacaktır. Selin, fotoğrafın kapladığı alanın 32 cm\( ^2 \) olmasını istemektedir.
Buna göre çerçeve ile fotoğrafın kapladığı toplam alanın en küçük değeri kaç cm\( ^2 \) olur?
Çözümü GösterAdım 1: Problem tanımı
\( x \): Fotoğrafın yüksekliği
\( y \): Fotoğrafın genişliği
\( F \): Fotoğrafın alanı
\( x + 10 \): Çerçevenin yüksekliği
\( y + 5 \): Çerçevenin genişliği
\( A \): Çerçeve ile fotoğrafın kapladığı toplam alan
Problemde çerçeve ile fotoğrafın kapladığı toplam alanın en küçük değeri istenmektedir.
Adım 2: Amaç fonksiyonu
Toplam alanı ve fotoğrafın alanını aşağıdaki iki formülle bulabiliriz.
\( A = (x + 10)(y + 5) \)
\( F = xy \)
Uzunluk ve alan pozitif büyüklüklerdir.
\( x, y, F, A \in \mathbb{R^+} \)
Amaç fonksiyonunu tek bir değişken cinsinden yazabilmek için \( x \) ve \( y \) değişkenleri arasında bir ilişki kurmaya çalışalım.
Fotoğrafın alanı soruda verilmiştir.
\( 32 = xy \)
\( y = \dfrac{32}{x} \)
Bulduğumuz \( y \) değerini alan formülünde yerine koyduğumuzda sadece \( x \) değişkenine bağlı olan amaç fonksiyonunu elde ederiz.
\( A = (x + 10)(\dfrac{32}{x} + 5) \)
\( = 5x + \dfrac{320}{x} + 82 \)
Buna göre en küçük değerini bulmak istediğimiz amaç fonksiyonu aşağıdaki gibidir.
\( A: (0, \infty) \to \mathbb{R^+} \)
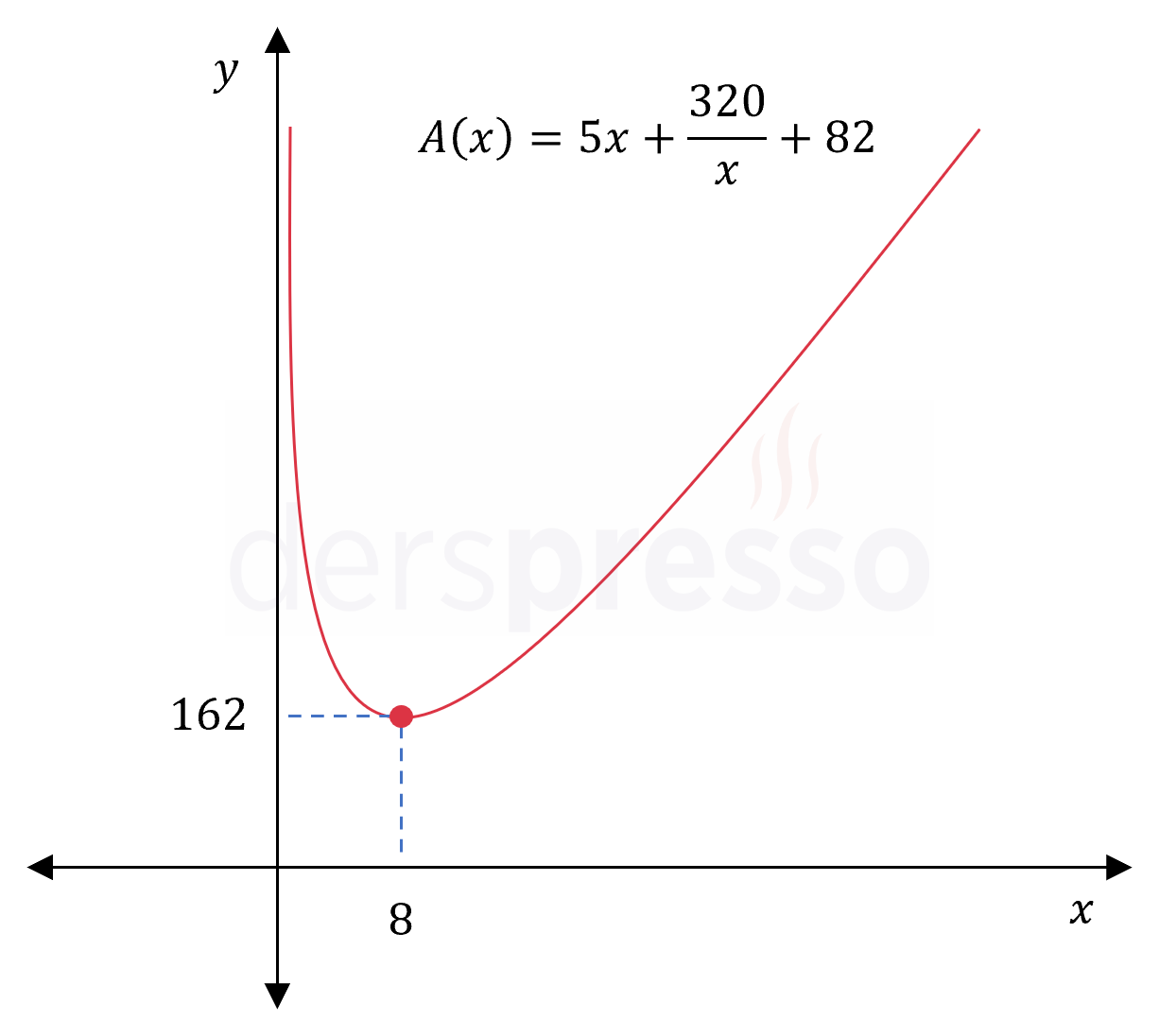
\( A(x) = 5x + \dfrac{320}{x} + 82 \)
Adım 3: Problem çözümü
\( A \) fonksiyonu açık bir aralıkta tanımlıdır ve bir rasyonel fonksiyon içerdiği için paydayı sıfır yapan ve tanım aralığı dışındaki \( x = 0 \) noktası hariç süreklidir.
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
\( A'(x) = 5 - \dfrac{320}{x^2} \)
Fonksiyonun tanım kümesi içinde birinci türevinin sıfır olduğu iç noktaları bulalım.
\( 5 - \dfrac{320}{x^2} = 0 \)
\( \dfrac{5x^2 - 320}{x^2} = 0 \)
\( 5x^2 - 320 = 0 \)
\( 5(x - 8)(x + 8) = 0 \)
\( x = 8 \)
Fonksiyonun tanım kümesi içinde birinci türevinin tanımsız olduğu iç nokta yoktur.
Kritik nokta: \( x = 8 \)
Fonksiyonun kritik noktadaki değerini bulalım.
\( A(8) = 5(8) + \dfrac{320}{8} + 82 = 162 \)
Fonksiyonun açık uç noktalarındaki limitini bulalım.
\( \lim\limits_{x \to 0^+} (5x + \dfrac{320}{x} + 82) = 5(0) + \dfrac{320}{0^+} + 82 = \infty \)
\( \lim\limits_{x \to \infty} (5x + \dfrac{320}{x} + 82) = \infty \)
Bu değerleri karşılaştırdığımızda fonksiyonun tanım aralığındaki en küçük değeri olarak \( x = 8 \) noktasında aldığı \( 162 \) cm\( ^2 \) değeri bulunur.
Amaç fonksiyonunun grafiği, bulduğumuz noktalar ve değerleri aşağıdaki şekilde gösterilmiştir.
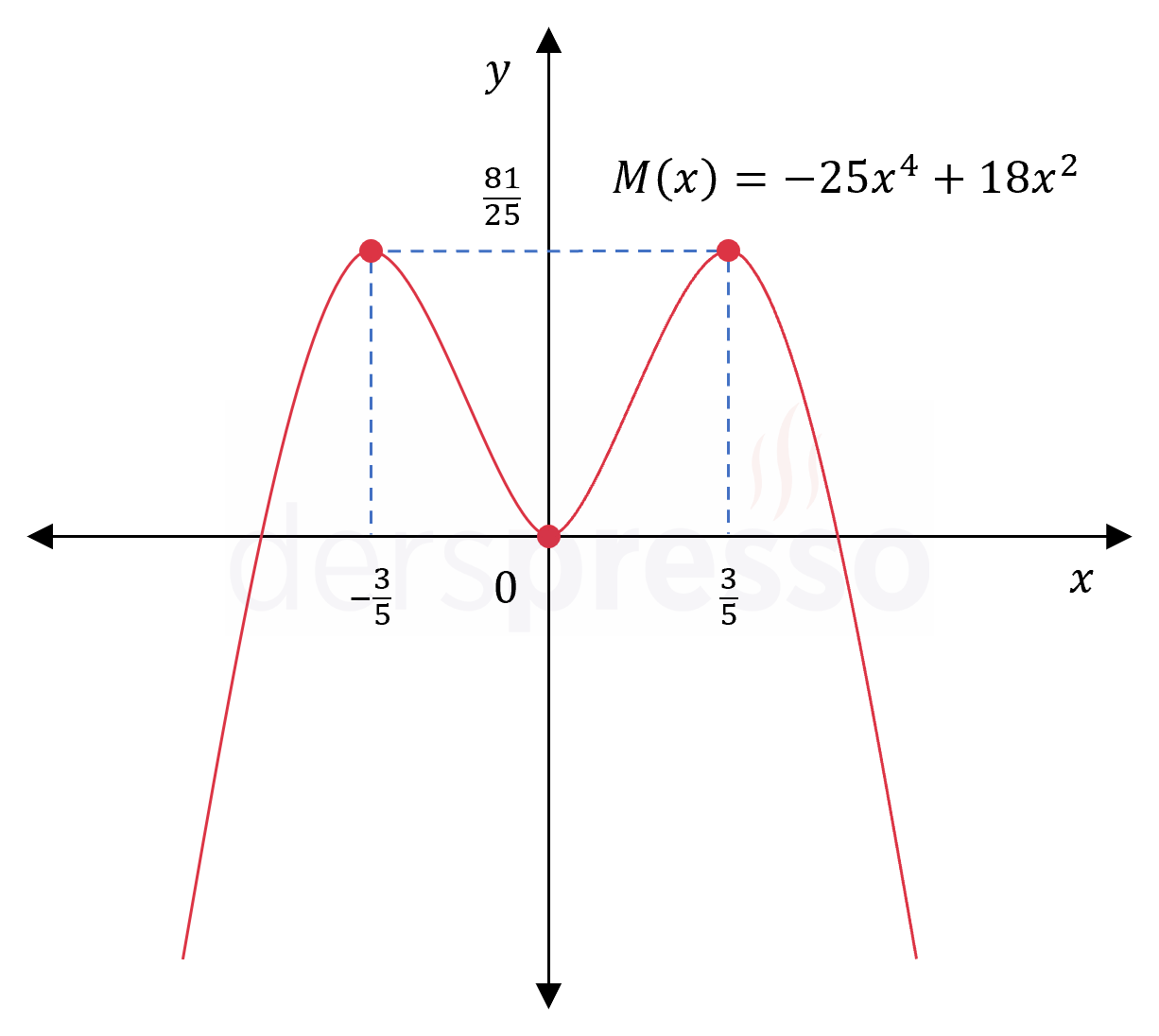
\( f(x) = -5x^5 + 6x^3 + 350 \) fonksiyonunun grafiğine teğet olan doğruların eğimi hangi nokta(lar)da en büyük değerini alır?
Çözümü GösterAdım 1: Problem tanımı
\( (x, f(x)) \): Fonksiyon grafiği üzerinde bir nokta
Problemde teğet doğrunun eğiminin en büyük değeri istenmektedir.
Adım 2: Amaç fonksiyonu
Bir fonksiyonun birinci türevinin bir noktadaki değeri fonksiyona o noktada teğet olan doğrunun eğimini verir.
\( f'(x) = -25x^4 + 18x^2 \)
\( f'(x) \) fonksiyonu bir polinom fonksiyonudur ve tüm reel sayılarda tanımlıdır.
Buna göre en büyük değerini bulmak istediğimiz amaç fonksiyonu aşağıdaki gibidir.
\( M: \mathbb{R} \to \mathbb{R} \)
\( M(x) = f'(x) = -25x^4 + 18x^2 \)
Adım 3: Problem çözümü
\( M \) fonksiyonu açık bir aralıkta tanımlıdır ve bir polinom fonksiyonu olduğu için süreklidir.
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
\( M'(x) = -100x^3 + 36x \)
Fonksiyonun tanım kümesi içinde birinci türevinin sıfır olduğu iç noktaları bulalım.
\( -100x^3 + 36x = 0 \)
\( 4x(9 - 25x^2) = 0 \)
\( 4x(3 - 5x)(3 + 5x) = 0 \)
\( x \in \{ -\frac{3}{5}, 0, \frac{3}{5} \} \)
Fonksiyonun tanım aralığı içinde birinci türevinin tanımsız olduğu iç nokta yoktur.
Kritik nokta: \( x \in \{ -\frac{3}{5}, 0, \frac{3}{5} \}\)
Fonksiyonun kritik noktalardaki değerini bulalım.
\( f(-\dfrac{3}{5}) = -25(-\dfrac{3}{5})^4 + 18(-\dfrac{3}{5})^2 = \dfrac{81}{25} \)
\( f(0) = -25(0)^4 + 18(0)^2 = 0 \)
\( f(\dfrac{3}{5}) = -25(\dfrac{3}{5})^4 + 18(\dfrac{3}{5})^2 = \dfrac{81}{25} \)
Fonksiyonun açık uç noktalarındaki limitini bulalım.
\( \lim\limits_{x \to -\infty} (-25x^4 + 18x^2) = -\infty \)
\( \lim\limits_{x \to \infty} (-25x^4 + 18x^2) = -\infty \)
Bu değerleri karşılaştırdığımızda amaç fonksiyonu tanım aralığındaki en büyük eğim değerini \( x = \pm \frac{3}{5} \) noktalarında \( \frac{81}{25} \) olarak alır.
Amaç fonksiyonunun grafiği, bulduğumuz noktalar ve değerleri aşağıdaki şekilde gösterilmiştir.
Çevresi 60 birim olan bir ikizkenar üçgenin alanı en fazla kaç birimkare olabilir?
Çözümü GösterAdım 1: Problem tanımı
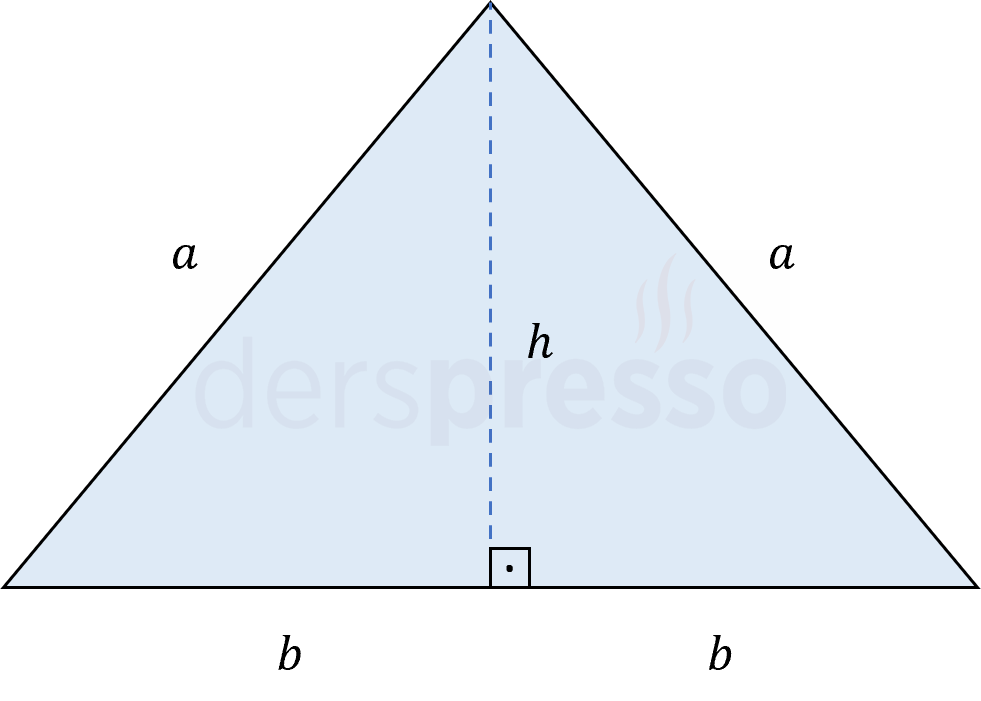
\( a \): Üçgenin yan kenarlarının uzunluğu
\( 2b \): Üçgenin taban uzunluğu
\( h \): Üçgenin yüksekliği
\( A \): Üçgenin alanı
\( C \): Üçgenin çevresi
Problemde ikizkenar üçgenin alanının en büyük değeri istenmektedir.
Adım 2: Amaç fonksiyonu
İkizkenar üçgeninin alanını aşağıdaki formülle bulabiliriz
\( A = \dfrac{2bh}{2} = bh \)
Uzunluk, alan ve çevre pozitif büyüklüklerdir.
\( a, b, h, A, C \in \mathbb{R^+} \)
Amaç fonksiyonunu tek bir değişken cinsinden yazabilmek için değişkenler arasında bir ilişki kurmaya çalışalım.
Üçgenin çevre formülünü yazalım
\( C = 2a + 2b \)
Üçgenin çevre uzunluğu soruda verilmiştir.
\( 60 = 2a + 2b \)
\( a = 30 - b \)
Üçgenin yüksekliği, tabanı ve yan kenarının oluşturduğu üçgende Pisagor teoremini uygulayalım.
\( h^2 + b^2 = a^2 \)
\( h = \sqrt{a^2 - b^2} \)
Bulduğumuz \( a \) değerini formülde yerine koyalım.
\( h = \sqrt{(30 - b)^2 - b^2} \)
\( = \sqrt{900 - 60b} \)
\( h \) değerini alan formülünde yerine koyduğumuzda sadece \( b \) değişkenine bağlı olan amaç fonksiyonunu elde ederiz.
\( A = bh \)
\( = b\sqrt{900 - 60b} \)
\( = \sqrt{900b^2 - 60b^3} \)
Bir karekök ifadesi en büyük değerini kök içindeki ifade en büyük değerini aldığında alır.
O halde bir \( f \) fonksiyonu tanımlayalım ve işlemlerimizi bu fonksiyon üzerinden yapalım.
\( f(b) = 900b^2 - 60b^3 \)
\( f \) fonksiyonu en büyük değerini aldığında soruda istenen \( A \) alanı da en büyük değerini alacaktır.
\( A \in \mathbb{R^+} \) bilgisini kullanarak \( b \) tanım aralığını bulalım.
\( A = \sqrt{900b^2 - 60b^3} \gt 0 \)
\( 900b^2 - 60b^3 \gt 0 \)
\( 60b^2(15 - b) \gt 0 \)
\( 0 \lt b \lt 15 \)
Buna göre en büyük değerini bulmak istediğimiz amaç fonksiyonu aşağıdaki şekilde tanımlanır.
\( f: (0, 15) \to \mathbb{R^+} \)
\( f(b) = 900b^2 - 60b^3 \)
Adım 3: Problem çözümü
\( f \) fonksiyonu açık bir aralıkta tanımlıdır ve bir polinom fonksiyonu olduğu için süreklidir.
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
\( f'(b) = 1800b - 180b^2 \)
Fonksiyonun tanım kümesi içinde birinci türevinin sıfır olduğu iç noktaları bulalım.
\( 1800b - 180b^2 = 0 \)
\( 180b(10 - b) = 0 \)
Fonksiyon \( b = 0 \) noktasında tanımlı değildir.
\( b = 10 \)
Fonksiyonun tanım kümesi içinde birinci türevinin tanımsız olduğu iç nokta yoktur.
Kritik nokta: \( b = 10 \)
Fonksiyonun kritik noktadaki değerini bulalım.
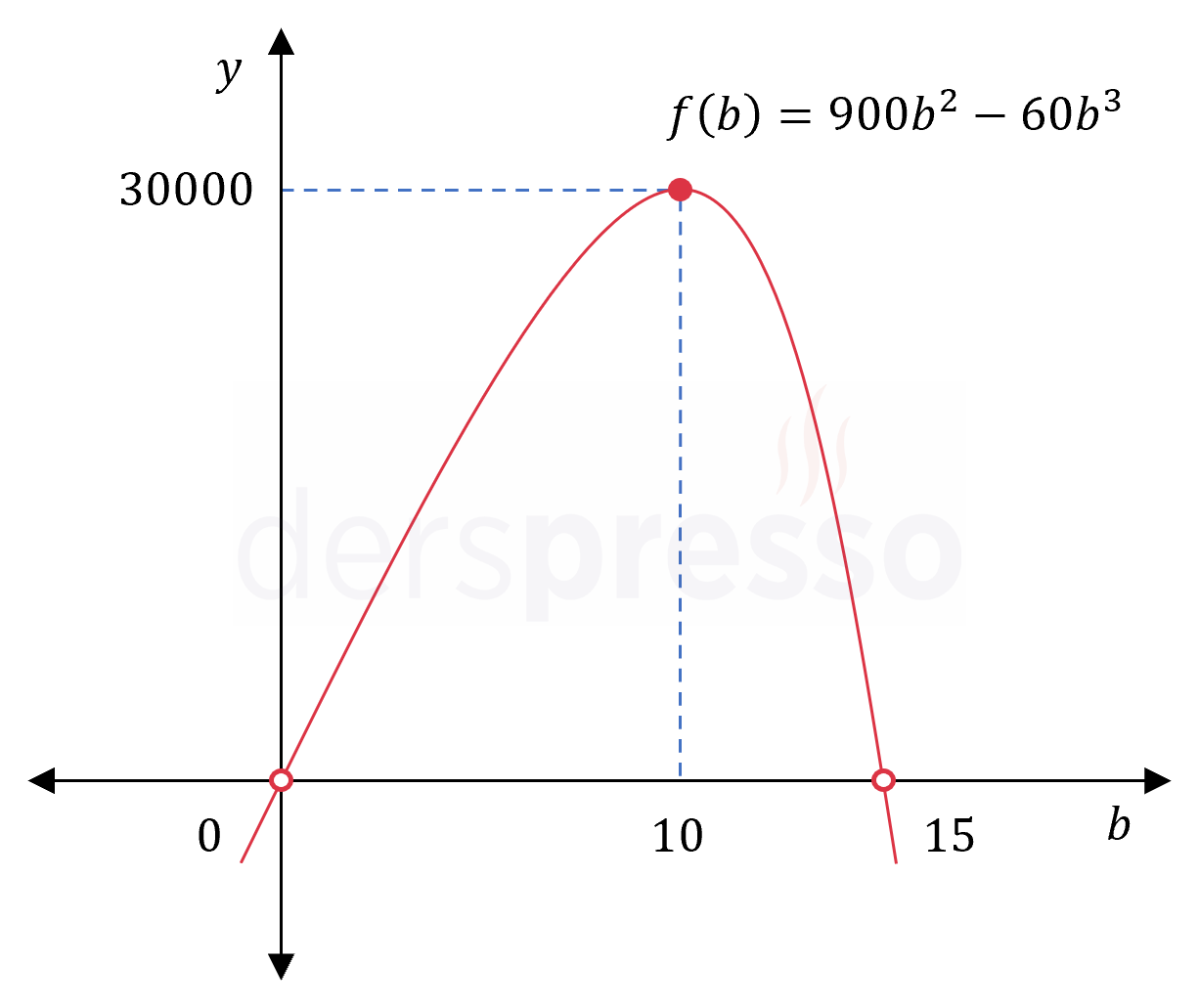
\( f(10) = 900(10)^2 - 60(10)^3 = 30000 \)
Fonksiyonun açık uç noktalarındaki değerini bulalım.
\( \lim\limits_{x \to 0^+} (900b^2 - 60b^3) = 900(0)^2 - 60(0)^3 = 0 \)
\( \lim\limits_{x \to 15^-} (900b^2 - 60b^3) = 900(15)^2 - 60(15)^3 = 0 \)
Buna göre fonksiyon açık uç noktaları civarında 30000 değerinden daha büyük bir değer almaz.
Bu değerleri karşılaştırdığımızda \( f \) fonksiyonu tanım kümesi içindeki en büyük değerini \( b = 10 \) noktasında alır.
Dolayısıyla \( A \) alanı da en büyük değerini \( b = 10 \) noktasında alır.
\( b = 10 \) için \( A \) değerini bulalım.
\( A = \sqrt{f(10)} \)
\( = \sqrt{30000} = 100\sqrt{3} \) birimkare bulunur.
Amaç fonksiyonunun grafiği, bulduğumuz noktalar ve değerleri aşağıdaki şekilde gösterilmiştir.
Denklemi \( \frac{x^2}{25} + \frac{y^2}{16} = 1 \) olan bir elipsin içine yerleştirilecek, kenarları eksenlere paralel olan ve alanı en büyük olan dikdörtgenin alanı nedir?
Çözümü GösterAdım 1: Problem tanımı
Verilen denklem merkezi orijin olan ve eksenleri \( (5, 0), (-5, 0), (0, 4), (0, -4) \) noktalarında kesen bir elips belirtir.
Elipsin ve içine yerleştirilen dikdörtgenin koordinat düzlemindeki görüntüsü aşağıdaki gibidir.
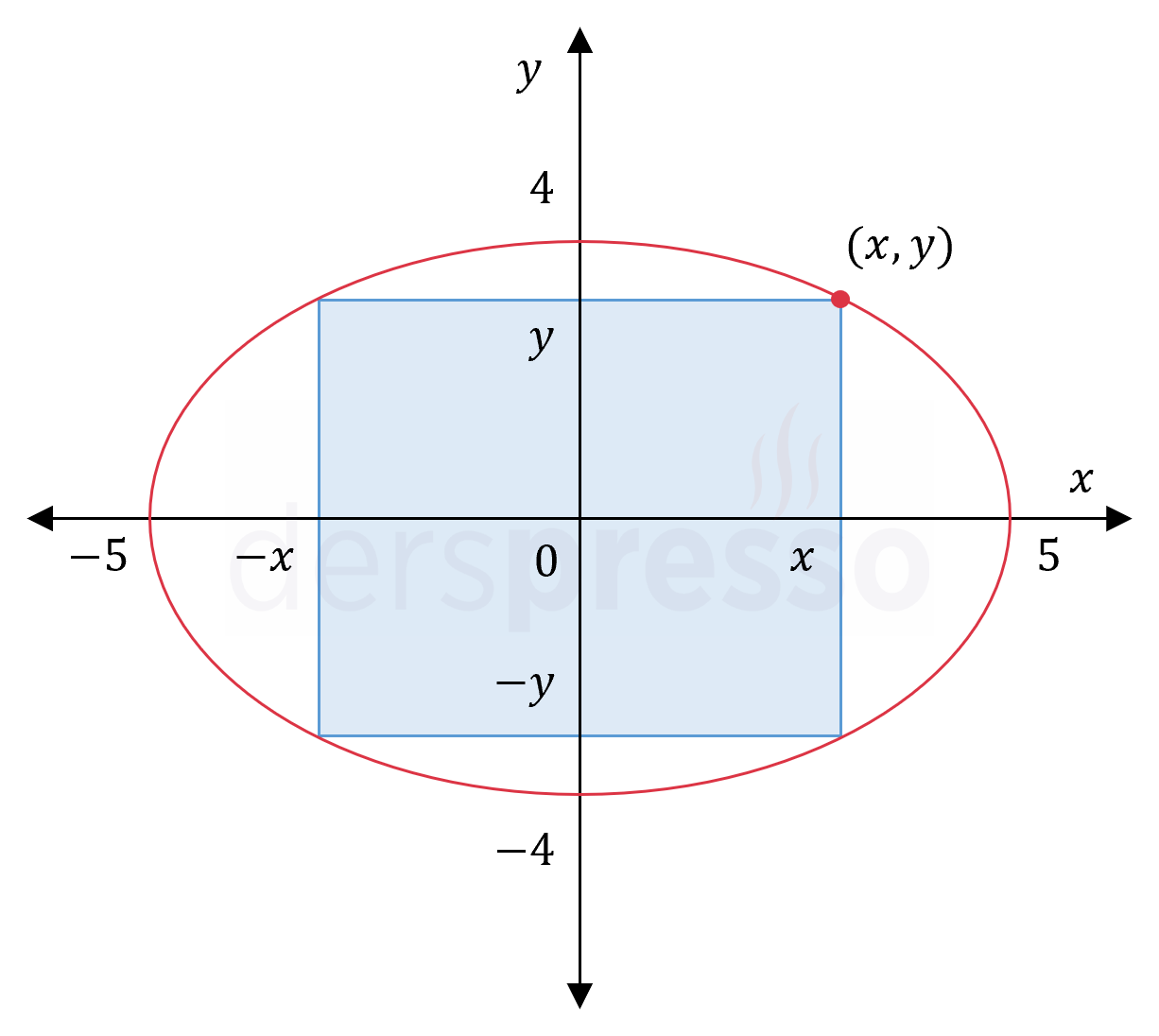
\( (x, y) \): Dikdörtgenin birinci bölgede kalan köşesinin koordinatları
\( 2x \): Dikdörtgenin genişliği
\( 2y \): Dikdörtgenin yüksekliği
\( A \): Dikdörtgenin alanı
Problemde dikdörtgenin alanının en büyük değeri istenmektedir.
Adım 2: Amaç fonksiyonu
Dikdörtgenin alanını aşağıdaki formülle bulabiliriz.
\( A = (2x)(2y) = 4xy \)
Uzunluk ve alan pozitif büyüklüklerdir.
\( x, y, A \in \mathbb{R^+} \)
Amaç fonksiyonunu tek bir değişken cinsinden yazabilmek için \( x \) ve \( y \) değişkenleri arasında bir ilişki kurmaya çalışalım.
Dikdörtgenin köşesi elips üzerinde bir noktadır ve elips denklemini sağlar.
\( (x, y) \) noktasının koordinatlarını \( x \) cinsinden yazalım.
\( \dfrac{x^2}{25} + \dfrac{y^2}{16} = 1 \)
\( y^2 = 16(1 - \dfrac{x^2}{25}) \)
\( y = \sqrt{16(1 - \dfrac{x^2}{25})} \)
\( = \dfrac{4}{5}\sqrt{25 - x^2} \)
\( y \) değerini alan formülünde yerine koyduğumuzda sadece \( x \) değişkenine bağlı olan amaç fonksiyonunu elde ederiz.
\( A = 4xy \)
\( = 4x \cdot \dfrac{4}{5}\sqrt{25 - x^2} \)
\( = \dfrac{16x}{5} \sqrt{25 - x^2} \)
Elipsin içinde bir dikdörtgen oluşması için dikdörtgenin genişliği elipsin yatay eksen uzunluğundan küçük olmalıdır.
\( 2x \lt 10 \)
\( x \lt 5 \)
Buna göre en büyük değerini bulmak istediğimiz amaç fonksiyonu aşağıdaki gibidir.
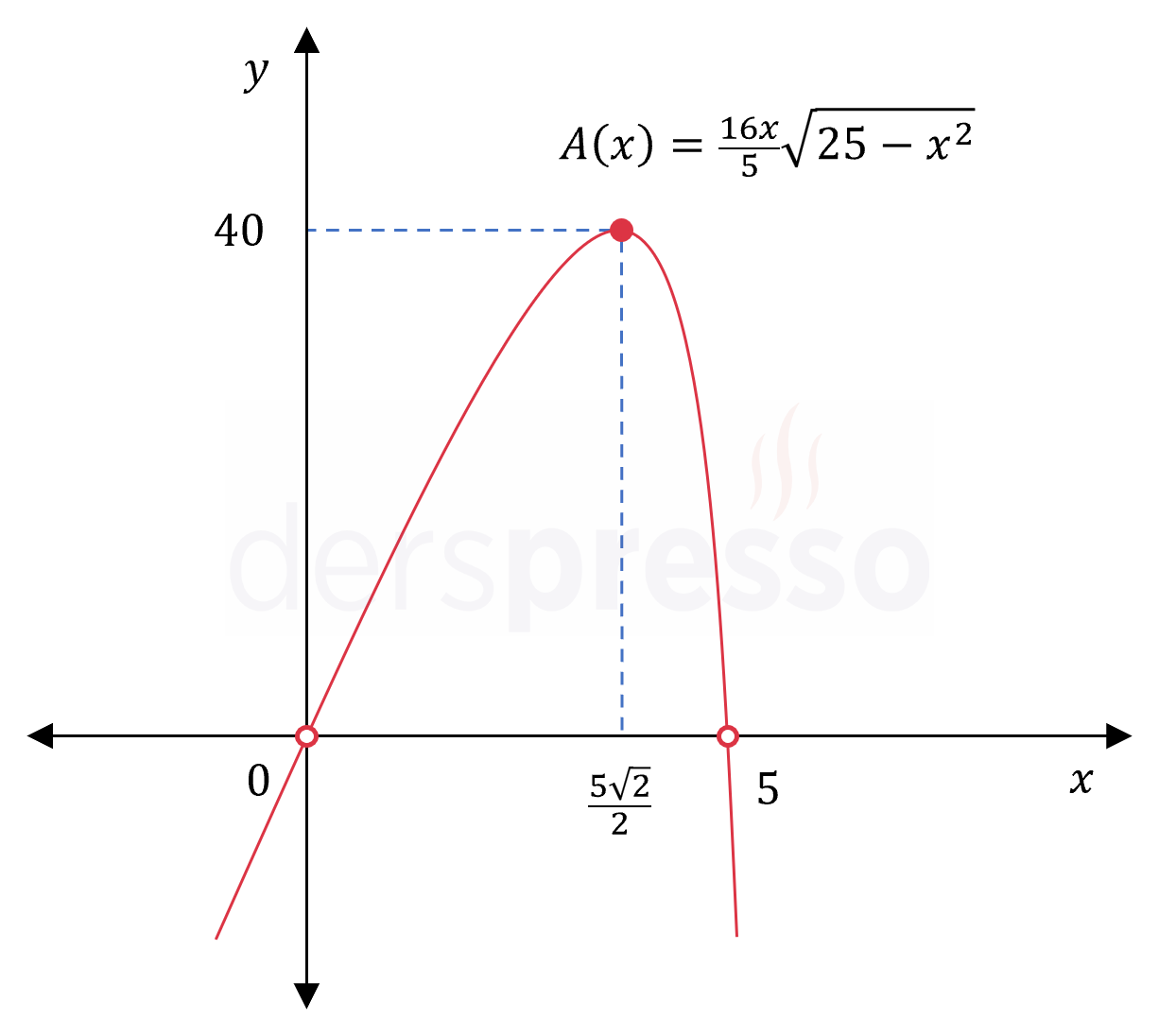
\( A: (0, 5) \to \mathbb{R^+} \)
\( A(x) = \dfrac{16x}{5}\sqrt{25 - x^2} \)
Adım 3: Problem çözümü
\( A \) fonksiyonu açık bir aralıkta tanımlıdır ve iki sürekli fonksiyonun çarpımından oluştuğu için tanım kümesi içinde süreklidir.
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
\( A'(x) = \dfrac{16}{5}(\sqrt{25 - x^2} - \dfrac{x^2}{\sqrt{25 - x^2}}) \)
\( = \dfrac{16(25 - 2x^2)}{5\sqrt{25 - x^2}} \)
Fonksiyonun tanım kümesi içinde birinci türevinin sıfır olduğu iç noktaları bulalım.
\( \dfrac{16(25 - 2x^2)}{5\sqrt{25 - x^2}} = 0 \)
\( 25 - 2x^2 = 0 \)
\( x = \dfrac{5\sqrt{2}}{2} \)
Fonksiyonun tanım kümesi içinde birinci türevinin tanımsız olduğu iç nokta yoktur.
Kritik nokta: \( x = \frac{5\sqrt{2}}{2}\)
Fonksiyonun kritik noktadaki değerini bulalım.
\( A(\dfrac{5\sqrt{2}}{2}) = \dfrac{16(\frac{5\sqrt{2}}{2})}{5}\sqrt{25 - (\frac{5\sqrt{2}}{2})^2} \)
\( = 8\sqrt{2}\dfrac{5}{\sqrt{2}} = 40 \)
Fonksiyonun açık uç noktalarındaki limitini bulalım.
\( \lim\limits_{x \to 0^+} {\dfrac{16x}{5}\sqrt{25 - x^2}} = \dfrac{16(0)}{5}\sqrt{25 - 0^2} = 0 \)
\( \lim\limits_{x \to 5^-} {\dfrac{16x}{5}\sqrt{25 - x^2}} = \dfrac{16(5)}{5}\sqrt{25 - (5^-)^2} = 0 \)
Bu değerleri karşılaştırdığımızda fonksiyonun tanım aralığındaki en büyük değeri olarak \( x = \frac{5\sqrt{2}}{2} \) noktasında aldığı \( 40 \) birimkare değeri bulunur.
Amaç fonksiyonunun grafiği, bulduğumuz noktalar ve değerleri aşağıdaki şekilde gösterilmiştir.

Zehra'nın gittiği seramik kursunda öğretmen tüm sınıftan hacmi \( 288\pi \) cm\(^3 \) olan üstü açık dik koni şeklinde bir vazo yapmalarını istiyor.
Zehra elindeki kil miktarı sınırlı olduğundan vazoyu mümkün olan en az miktarda kil kullanarak yapmak istiyor. Buna göre, vazonun yüksekliği (\( h \)) kaç cm olmalıdır?
Çözümü GösterAdım 1: Problem tanımı
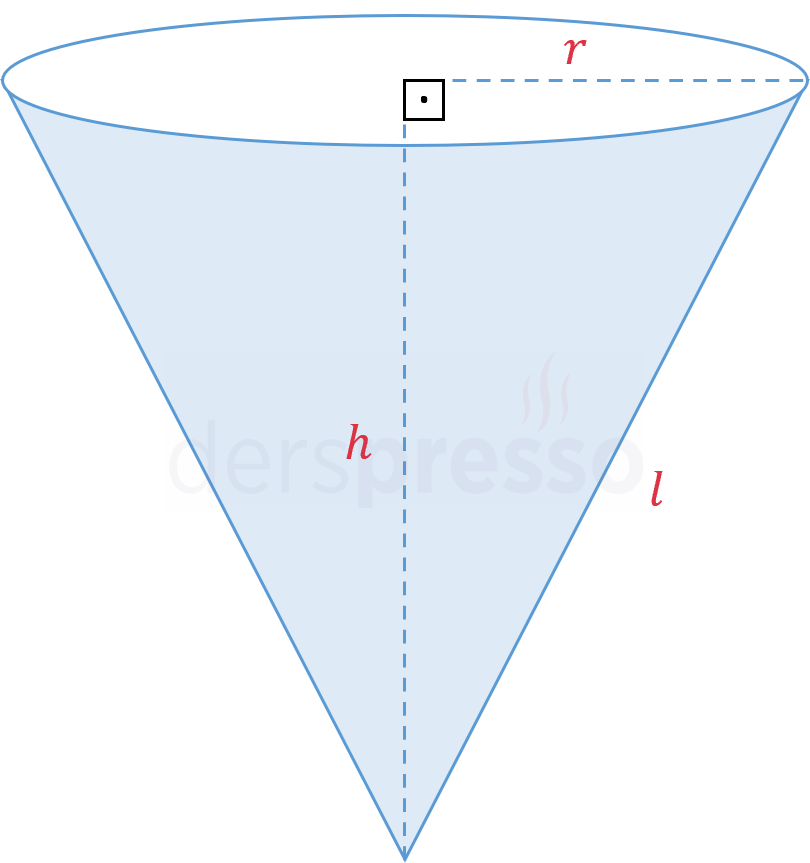
\( r \): Koninin taban yarıçapı
\( h \): Koninin yüksekliği
\( l \): Koninin yan yüz yüksekliği
\( A \): Koninin yüzey alanı
\( V \): Koninin hacmi
Zehra en az miktarda kil kullanmak istemektedir, bu da vazonun yüzey alanının en küçük değeri alması ile mümkün olur.
Problemde vazonun yüzey alanını en küçük yapan \( h \) değeri istenmektedir.
Adım 2: Amaç fonksiyonu
Koninin yüzey alanını aşağıdaki formülle bulabiliriz.
Yüzey alanını hesaplarken koninin üst tabanının açık olduğunu dikkate almalıyız.
\( A = \pi rl \)
Uzunluk, alan ve hacim pozitif büyüklüklerdir.
\( r, h, l, A, V \in \mathbb{R^+} \)
Amaç fonksiyonunu tek bir değişken cinsinden yazabilmek için değişkenler arasında bir ilişki kurmaya çalışalım.
Koninin hacim formülünü yazalım.
\( V = \dfrac{1}{3} \pi r^2h \)
Koninin hacmi soruda verilmiştir.
\( 288\pi = \dfrac{1}{3} \pi r^2h \)
Hacim formülünde \( r \) değişkenini yalnız bırakalım.
\( r = \sqrt{\dfrac{864}{h}} \)
Koninin yüksekliği, taban yarıçapı ve yan yüz yüksekliğinin oluşturduğu üçgende Pisagor teoremini uygulayalım.
\( l^2 = h^2 + r^2 \)
Bulduğumuz \( r \) değerini formülde yerine koyalım.
\( l^2 = h^2 + \dfrac{864}{h} \)
\( l = \sqrt{h^2 + \dfrac{864}{h}} \)
\( = \sqrt{\dfrac{h^3 + 864}{h}} \)
Bulduğumuz değerleri yüzey alanı formülünde yerine koyduğumuzda sadece \( h \) değişkenine bağlı olan amaç fonksiyonunu elde ederiz.
\( A = \pi rl \)
\( = \pi \sqrt{\dfrac{864}{h}} \sqrt{\dfrac{h^3 + 864}{h}} \)
\( = \dfrac{12\sqrt{6}\pi}{h} \sqrt{h^3 + 864} \)
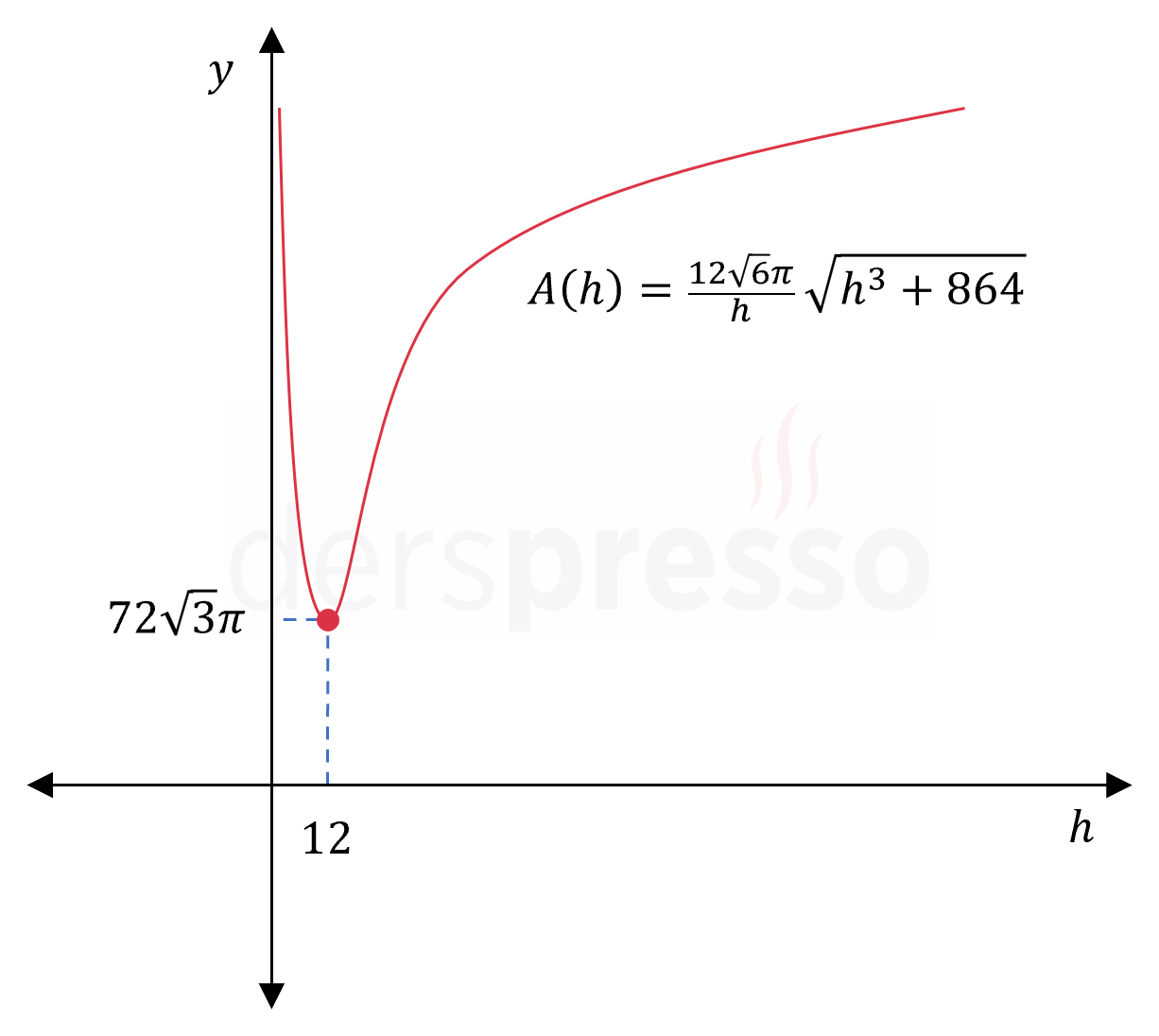
Buna göre en küçük değerini bulmak istediğimiz amaç fonksiyonu aşağıdaki şekilde tanımlanır.
\( A: (0, \infty) \to \mathbb{R^+} \)
\( A(h) = \dfrac{12\sqrt{6}\pi}{h} \sqrt{h^3 + 864} \)
Adım 3: Problem çözümü
\( A \) fonksiyonu açık bir aralıkta tanımlıdır ve iki sürekli fonksiyonun çarpımından oluştuğu için tanım kümesi içinde süreklidir.
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
\( A'(h) = -\dfrac{12\sqrt{6}\pi}{h^2} \sqrt{h^3 + 864} + \dfrac{3h^2}{2\sqrt{h^3 + 864}} \cdot \dfrac{12\sqrt{6}\pi}{h} \)
\( = \dfrac{12\sqrt{6}\pi}{h}\left( -\dfrac{\sqrt{h^3 + 864}}{h} + \dfrac{3h^2}{2\sqrt{h^3 + 864}} \right) \)
\( = \dfrac{12\sqrt{6}\pi}{h} \cdot \dfrac{-2(h^3 + 864) + 3h^3}{2h\sqrt{h^3 + 864}} \)
\( = \dfrac{6\sqrt{6}\pi(h^3 - 1728)}{h^2\sqrt{h^3 + 864}} \)
Fonksiyonun tanım kümesi içinde birinci türevinin sıfır olduğu iç noktaları bulalım.
\( \dfrac{6\sqrt{6}\pi(h^3 - 1728)}{h^2\sqrt{h^3 + 864}} = 0 \)
\( h^3 - 1728 = 0 \)
\( h = 12 \)
Fonksiyonun birinci türevinin tanımsız olduğu iç nokta yoktur.
Kritik nokta: \( h = 12 \)
Fonksiyonun kritik noktadaki değerini bulalım.
\( A(12) = \dfrac{12\sqrt{6}\pi}{12} \sqrt{12^3 + 864} \)
\( = 72\sqrt{3}\pi \)
Fonksiyonun açık uç noktalarındaki limitini bulalım.
\( \lim\limits_{h \to 0^+} \left( \dfrac{12\sqrt{6}\pi}{h} \sqrt{h^3 + 864} \right) = \dfrac{12\sqrt{6}\pi}{0^+} \sqrt{0^3 + 864} = \infty \)
\( \lim\limits_{h \to \infty} \left( \dfrac{12\sqrt{6}\pi}{h} \sqrt{h^3 + 864} \right) = \lim\limits_{h \to \infty} {12\sqrt{6}\pi \sqrt{\dfrac{h^3 + 864}{h^2}}} = \infty \)
Bu değerleri karşılaştırdığımızda fonksiyonun tanım aralığındaki en küçük değeri olarak \( h = 12 \) noktasında aldığı \( 72\sqrt{3}\pi \) cm\(^2 \) değeri bulunur.
Dolayısıyla Zehra'nın vazoyu en az miktarda kil kullanarak yapabilmesi için vazonun yüksekliği \( h = 12 \) cm olmalıdır.
Amaç fonksiyonunun grafiği, bulduğumuz noktalar ve değerleri aşağıdaki şekilde gösterilmiştir.
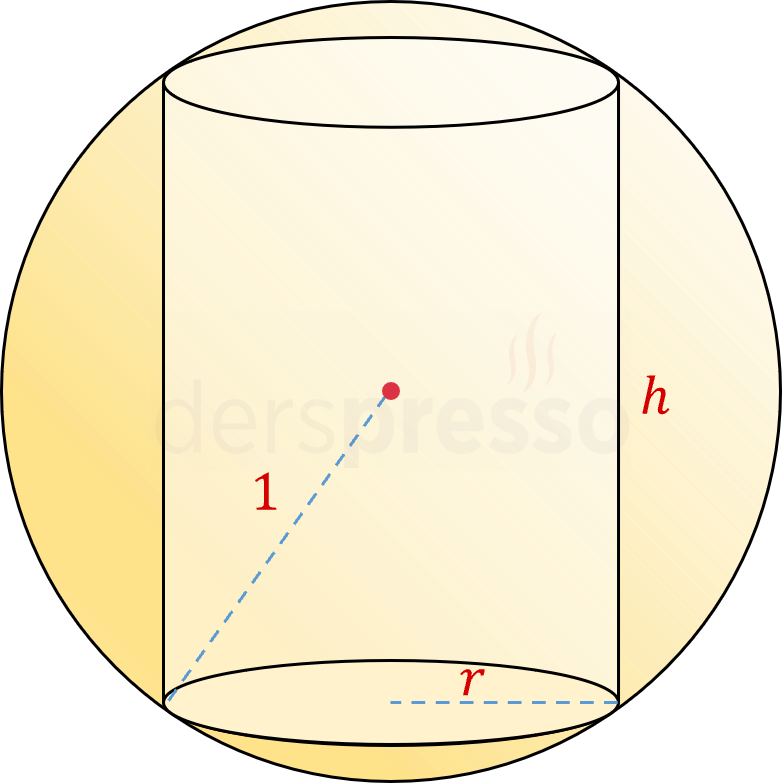
Yarıçapı 1 birim olan bir kürenin içine yerleştirilebilecek en büyük hacimli dik silindirin hacmi nedir?
Çözümü GösterAdım 1: Problem tanımı
Kürenin ve içine yerleştirilen silindirin iki boyutlu görüntüsü aşağıdaki gibidir.

\( r \): Silindirin taban yarıçapı
\( h \): Silindirin yüksekliği
\( V \): Silindirin hacmi
Problemde silindirin hacminin en büyük değeri istenmektedir.
Adım 2: Amaç fonksiyonu
Silindirin hacmini aşağıdaki formülle bulabiliriz.
\( V = \pi r^2h \)
Uzunluk ve hacim pozitif büyüklüklerdir.
\( r, h, V \in \mathbb{R^+} \)
Amaç fonksiyonunu tek bir değişken cinsinden yazabilmek için değişkenler arasında bir ilişki kurmaya çalışalım.
Silindirin yüksekliğinin yarısı ve taban yarıçapı, hipotenüsü kürenin yarıçapı olan bir dik üçgen oluştururlar.
Bu üçgene Pisagor teoremini uygulayalım.
\( r^2 + (\frac{h}{2})^2 = 1 \)
Bu eşitlikte \( h \) değişkenini yalnız bırakalım.
\( h = 2\sqrt{1 - r^2} \)
\( h \) değerini hacim formülünde yerine koyduğumuzda sadece \( r \) değişkenine bağlı olan amaç fonksiyonunu elde ederiz.
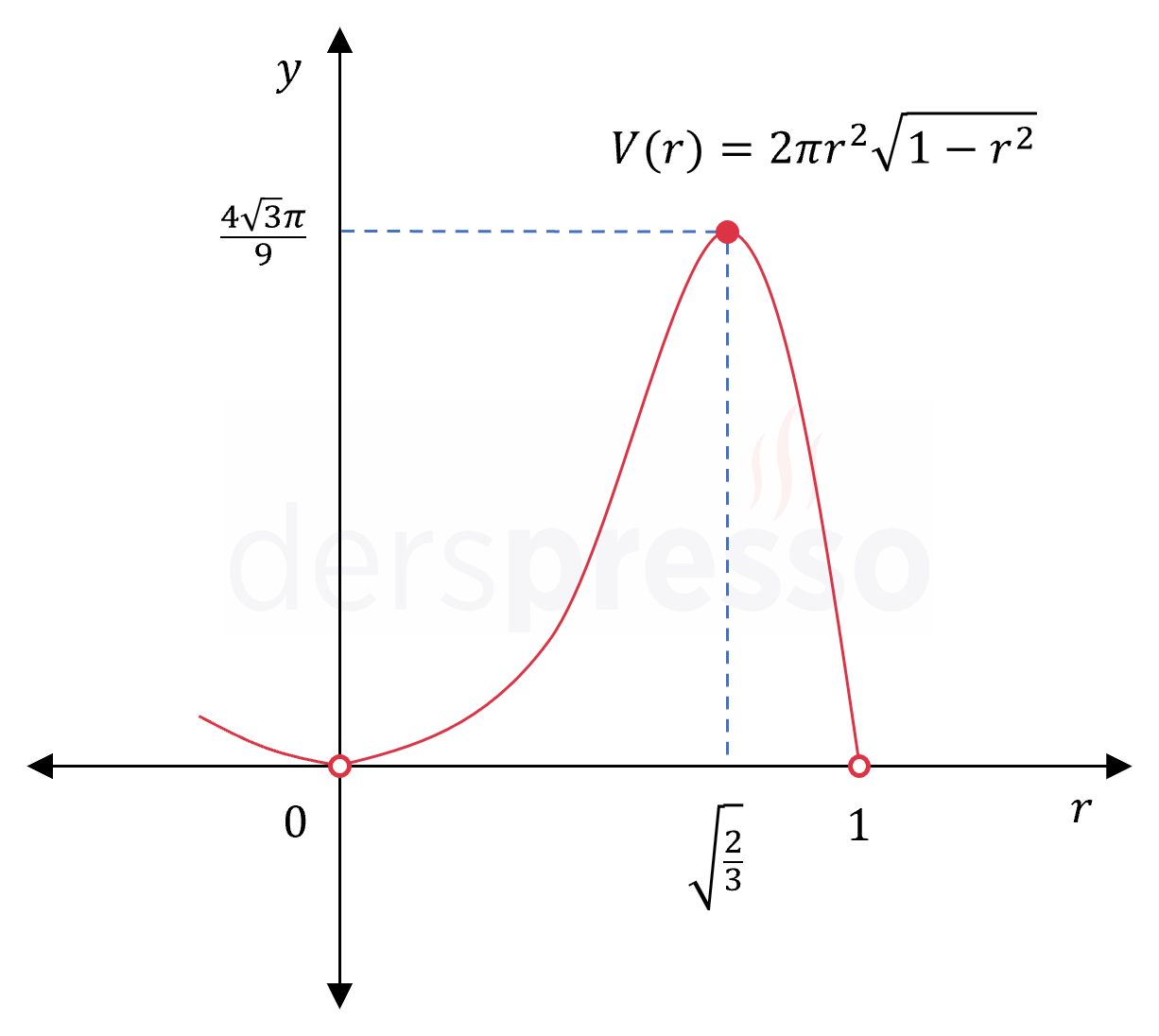
\( V(r) = 2\pi r^2\sqrt{1 - r^2} \)
Kürenin içinde bir silindirin oluşması için taban yarıçapı kürenin yarıçapından küçük olmalıdır.
\( r \lt 1 \)
Buna göre en büyük değerini bulmak istediğimiz amaç fonksiyonu aşağıdaki gibidir.
\( V: (0, 1) \to \mathbb{R^+} \)
\( V(r) = 2\pi r^2\sqrt{1 - r^2} \)
Adım 3: Problem çözümü
\( V \) fonksiyonu açık bir aralıkta tanımlıdır ve iki sürekli fonksiyonun (kuvvet ve karekök) çarpımından oluştuğu için tanım kümesi içinde süreklidir.
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
\( V'(r) = 2\pi\left( 2r\sqrt{1 - r^2} - \dfrac{r^3}{\sqrt{1 - r^2}} \right) \)
Fonksiyonun tanım aralığı içinde birinci türevinin sıfır olduğu iç noktaları bulalım.
\( 2\pi\left( 2r\sqrt{1 - r^2} - \dfrac{r^3}{\sqrt{1 - r^2}}\right) = 0 \)
\( 2r\sqrt{1 - r^2} = \dfrac{r^3}{\sqrt{1 - r^2}} \)
\( r \gt 0 \) olduğu için \( r \) çarpanları sadeleşir.
\( 2(1 - r^2) = r^2 \)
\( (r - \sqrt{\frac{2}{3}})(r + \sqrt{\frac{2}{3}}) = 0 \)
\( r = \sqrt{\frac{2}{3}} \)
Fonksiyonun tanım aralığı içinde birinci türevinin tanımsız olduğu iç nokta yoktur.
Kritik nokta: \( r = \sqrt{\frac{2}{3}} \)
Fonksiyonun kritik noktadaki değerini bulalım.
\( V(\sqrt{\frac{2}{3}}) = 2\pi (\sqrt{\frac{2}{3}})^2\sqrt{1 - (\sqrt{\frac{2}{3}})^2} \)
\( = 2\pi \cdot \dfrac{2}{3} \cdot \sqrt{1 - \frac{2}{3}} \)
\( = \dfrac{4\sqrt{3}\pi}{9} \)
Fonksiyonun açık uç noktalarındaki limitini bulalım.
\( \lim\limits_{x \to 0^+} (2\pi r^2\sqrt{1 - r^2}) = 2\pi 0^2\sqrt{1 - 0^2} = 0 \)
\( \lim\limits_{x \to 1^-} (2\pi r^2\sqrt{1 - r^2}) = 2\pi 1^2\sqrt{1 - 1^2} = 0 \)
Buna göre fonksiyon açık uç noktaları civarında \( \frac{4\sqrt{3}\pi}{9} \) değerinden daha büyük bir değer almaz.
Bu değerleri karşılaştırdığımızda fonksiyonun tanım aralığındaki en büyük değeri olarak \( r = \sqrt{\frac{2}{3}} \) noktasında aldığı \( \frac{4\sqrt{3}\pi}{9} \) birimküp değeri bulunur.
Amaç fonksiyonunun grafiği, bulduğumuz noktalar ve değerleri aşağıdaki şekilde gösterilmiştir.
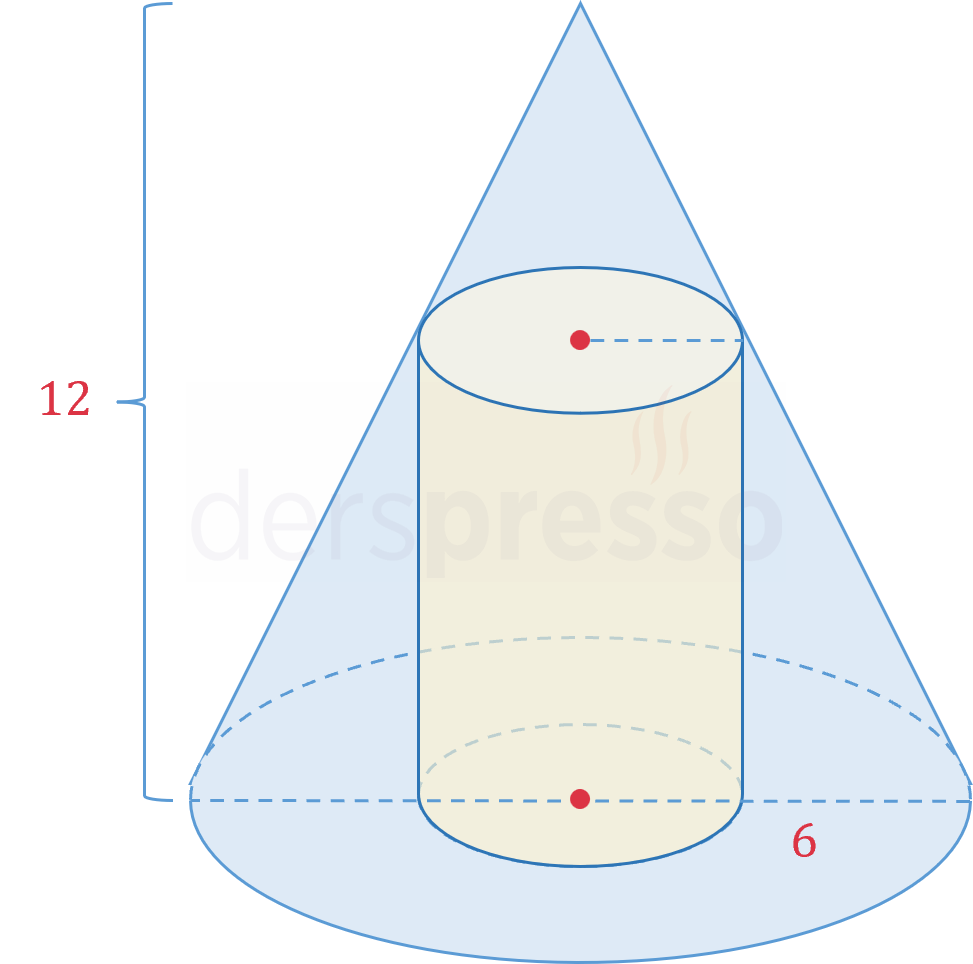
Yarıçapı 6 cm, yüksekliği 12 cm olan bir dik dairesel koninin içine yerleştirilebilecek en büyük hacimli dik dairesel silindirin hacmi nedir?
Çözümü GösterAdım 1: Problem tanımı
\( r \): Silindirin taban yarıçapı
\( h \): Silindirin yüksekliği
\( V \): Silindirin hacmi
Problemde silindirin hacminin en büyük değeri istenmektedir.
Adım 2: Amaç fonksiyonu
Silindirin hacmini aşağıdaki formülle bulabiliriz.
\( V = \pi r^2h \)
Uzunluk ve hacim pozitif büyüklüklerdir.
\( r, h, V \in \mathbb{R^+} \)
Amaç fonksiyonunu tek bir değişken cinsinden yazabilmek için \( r \) ve \( h \) değişkenleri arasında bir ilişki kurmaya çalışalım.
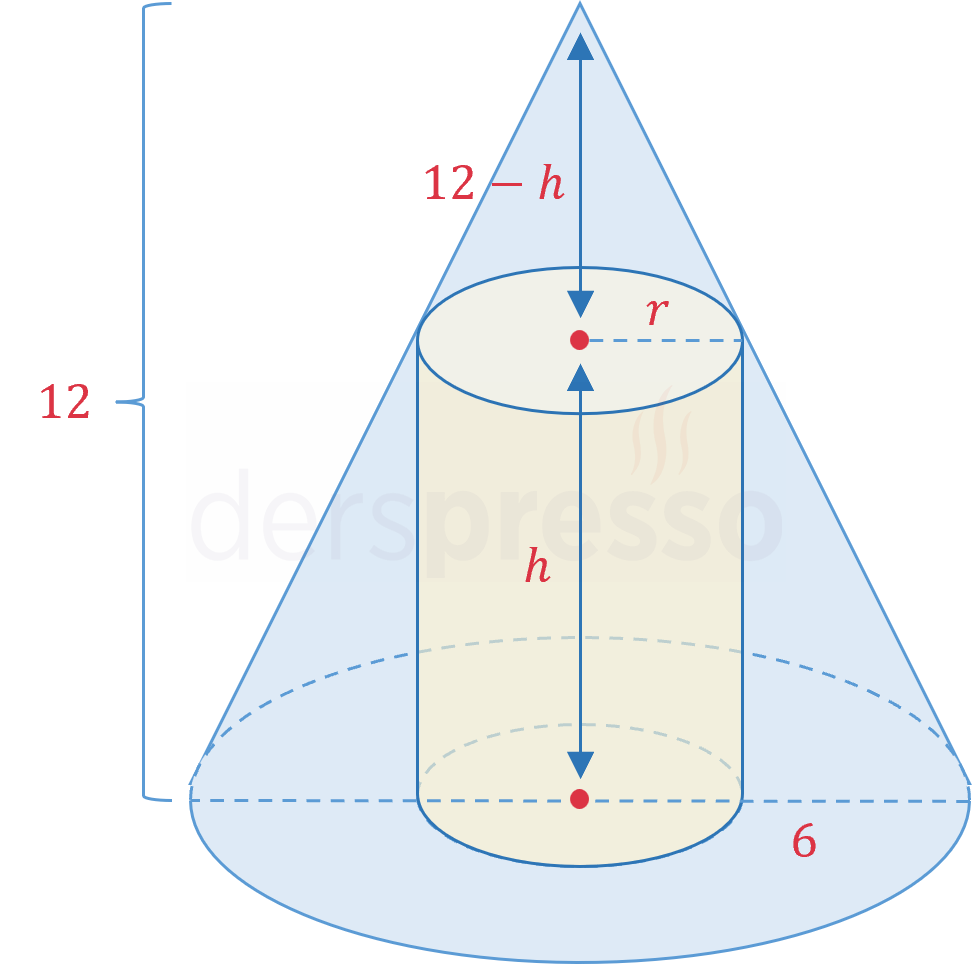
Koninin silindirin üstünde kalan kısmı ile bütününün kesitleri arasında üçgen benzerliği kullanalım.
\( \dfrac{12 - h}{r} = \dfrac{12}{6} \)
Bu eşitlikte \( h \) değişkenini yalnız bırakalım.
\( h = 12 - 2r \)
\( h \) değerini hacim formülünde yerine koyduğumuzda sadece \( r \) değişkenine bağlı olan amaç fonksiyonunu elde ederiz
\( V = \pi r^2h \)
\( = \pi r^2(12 - 2r) \)
\( = 12\pi r^2 - 2\pi r^3 \)
Koninin içinde bir silindirin oluşabilmesi için taban yarıçapı koninin yarıçapından küçük olmalıdır.
\( r \lt 6 \)
Buna göre en büyük değerini bulmak istediğimiz amaç fonksiyonu aşağıdaki gibidir.
\( V: (0, 6) \to \mathbb{R^+} \)
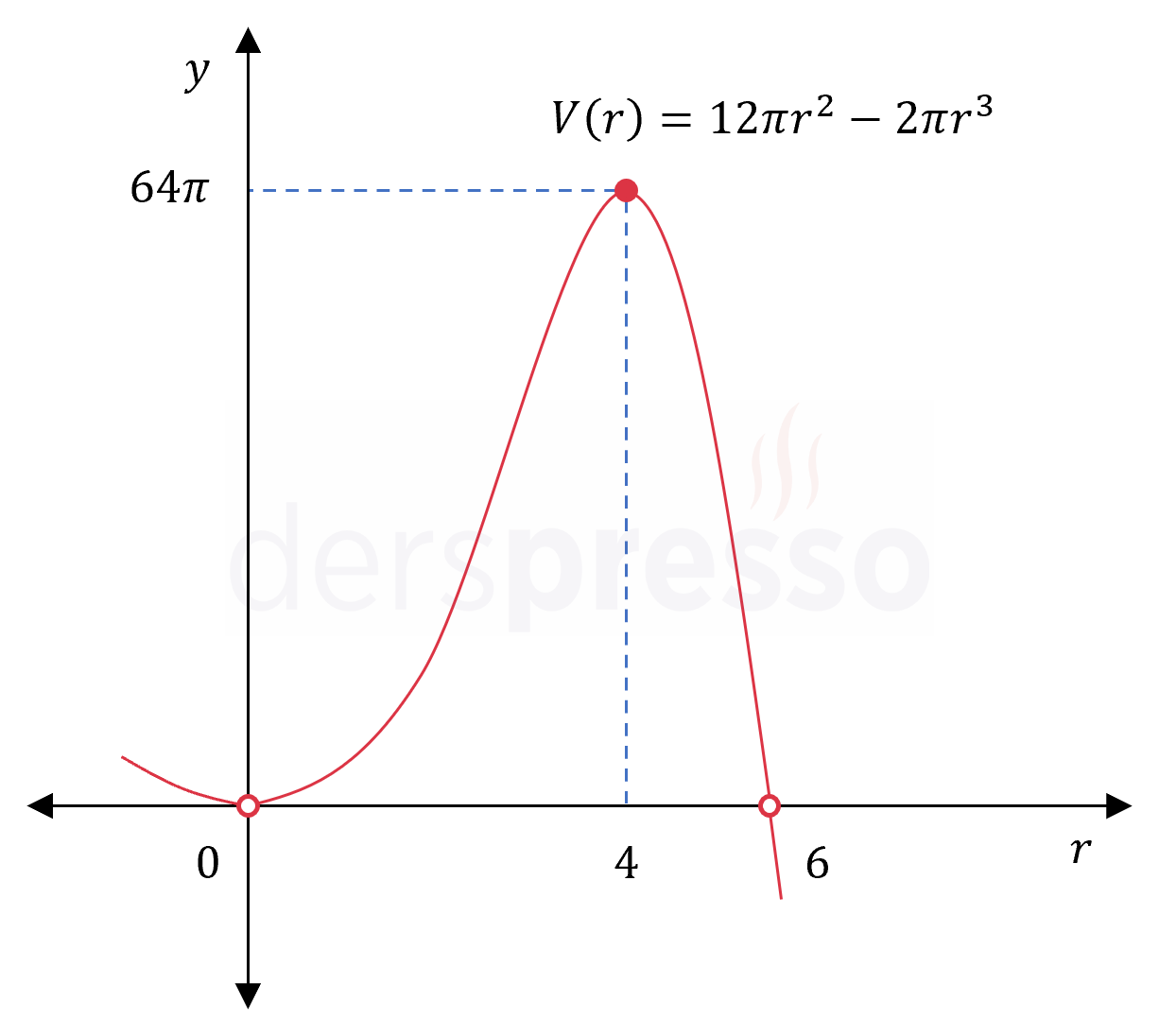
\( V(r) = 12\pi r^2 - 2\pi r^3 \)
Adım 3: Problem çözümü
\( V \) fonksiyonu açık bir aralıkta tanımlıdır ve bir polinom fonksiyonu olduğu için süreklidir.
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
\( V'(r) = 24\pi r - 6\pi r^2 \)
Fonksiyonun tanım kümesi içinde birinci türevinin sıfır olduğu iç noktaları bulalım.
\( 24\pi r - 6\pi r^2 = 0 \)
\( 6\pi r(4 - r) = 0 \)
\( r = 4 \)
Fonksiyonun tanım kümesi içinde birinci türevinin tanımsız olduğu iç nokta yoktur.
Kritik nokta: \( r = 4 \)
Fonksiyonun kritik noktadaki değerini bulalım.
\( V(4) = 12\pi (4)^2 - 2\pi (4)^3 = 64\pi \)
Fonksiyonun açık uç noktalarındaki limitini bulalım.
\( \lim\limits_{x \to 0^+} (12\pi r^2 - 2\pi r^3) = 12\pi (0)^2 - 2\pi (0)^3 = 0 \)
\( \lim\limits_{x \to 6^-} (12\pi r^2 - 2\pi r^3) = 12\pi (6)^2 - 2\pi (6)^3 = 0 \)
Bu değerleri karşılaştırdığımızda fonksiyonun tanım aralığındaki en büyük değeri olarak \( r = 4 \) noktasında aldığı \( 64\pi \) cm\( ^3 \) değeri bulunur.
Amaç fonksiyonunun grafiği, bulduğumuz noktalar ve değerleri aşağıdaki şekilde gösterilmiştir.
Yapılacak kare prizma şeklindeki bir heykelin alt ve üst yüzeylerinin malzemeleri metrekare başına 50 TL, yan yüzeylerinin malzemeleri ise metrekare başına 100 TL'dir. Heykelin tabanının bir kenar uzunluğu en az 1 en fazla 4 metre olacaktır.
Buna göre, 10800 TL bütçe ile yapılabilecek en büyük hacimli heykelin yüksekliği nedir?
Çözümü GösterAdım 1: Problem tanımı
\( a \): Prizmanın kare tabanının bir kenar uzunluğu
\( h \): Prizmanın yüksekliği
\( A \): Prizmanın yüzey alanı
\( V \): Prizmanın hacmi
\( M \): Prizmanın maliyeti
Problemde heykelin hacmini en büyük yapan \( h \) yüksekliği istenmektedir.
Adım 2: Amaç fonksiyonu
Kare prizmanın hacmini aşağıdaki formülle bulabiliriz.
\( V = a^2h \)
Uzunluk, alan, hacim ve maliyet pozitif büyüklüklerdir.
\( a, h, A, V, M \in \mathbb{R^+} \)
Amaç fonksiyonunu tek bir değişken cinsiden yazabilmek için değişkenler arasında bir ilişki kurmaya çalışalım.
Heykelin maliyeti, prizmanın yüzey alanında kullanılan malzemelerin toplam maliyetidir.
Prizmanın alanı, alt ve üst yüzeylerin alanları ile 4 yan yüzeyin alanları toplamına eşittir.
\( A = 2a^2 + 4ah \)
Birim maliyetler, prizmanın üst ve alt yüzeyleri için 50 TL, yan yüzeyleri için 100 TL'dir.
\( M = (50)2a^2 + (100)4ah \)
\( = 100a^2 + 400ah \)
Prizmanın toplam maliyeti soruda verilmiştir.
\( 10800 = 100a^2 + 400ah \)
\( 108 = a^2 + 4ah \)
\( h \) değişkenini yalnız bırakalım.
\( h = \dfrac{108 - a^2}{4a} \)
\( h \) değerini hacim formülünde yerine koyduğumuzda sadece \( a \) değişkenine bağlı olan amaç fonksiyonunu elde ederiz.
\( V = a^2 \cdot \dfrac{108 - a^2}{4a} \)
\( = \dfrac{108a - a^3}{4} \)
Prizmanın tabanının bir kenar uzunluğu \( (a) \) en az 1 en fazla 4 metredir.
\( 1 \le a \le 4 \)
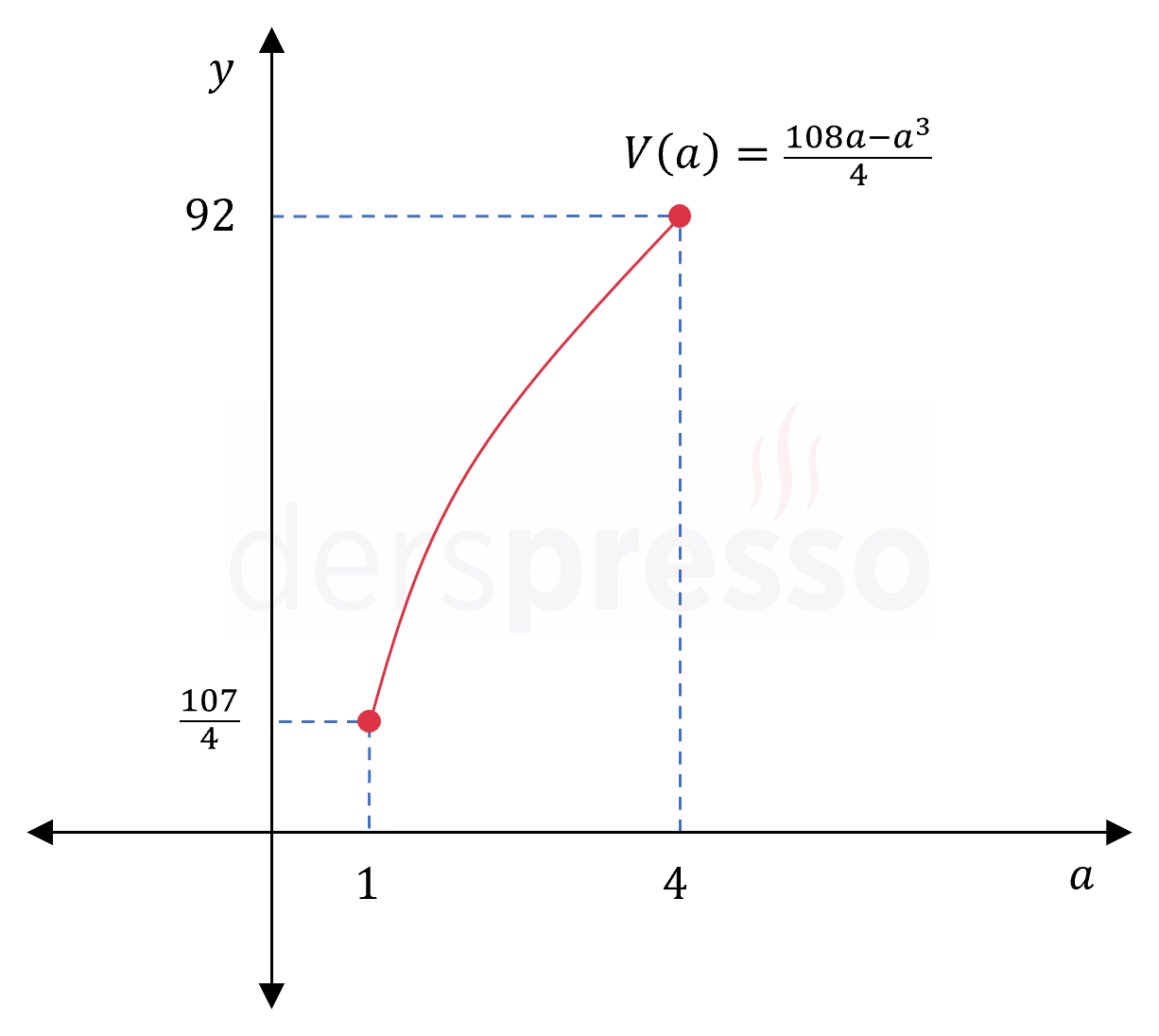
Buna göre en küçük değerini bulmak istediğimiz amaç fonksiyonu aşağıdaki şekilde tanımlanır.
\( V: [1, 4] \to \mathbb{R^+} \)
\( V(a) = \dfrac{108a - a^3}{4} \)
Adım 3: Problem çözümü
\( V \) fonksiyonu kapalı bir aralıkta tanımlıdır ve bir polinom fonksiyonu olduğu için süreklidir.
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
\( V'(x) = \dfrac{108 - 3a^2}{4} \)
Fonksiyonun tanım kümesi içinde birinci türevinin sıfır olduğu iç noktaları bulalım.
\( \dfrac{108 - 3a^2}{4} = 0 \)
\( \dfrac{3(36 - a^2)}{4} = 0 \)
\( a = \pm 6 \)
Fonksiyonun tanım kümesi \( [1, 4] \) aralığı olduğu için birinci türevinin sıfır olduğu iç nokta yoktur.
Fonksiyonun birinci türevinin tanımsız olduğu iç nokta yoktur.
Kritik noktalar: \( a \in \emptyset \)
Fonksiyonun kapalı uç noktalarındaki değerini bulalım.
\( V(1) = \dfrac{108(1) - 1^3}{4} = \dfrac{107}{4} \)
\( V(4) = \dfrac{108(4) - 4^3}{4} = 92 \)
Bu değerleri karşılaştırdığımızda \( V \) fonksiyonunun tanım kümesi içindeki en büyük değeri olarak \( a = 4 \) noktasında aldığı \( 92 \) m\(^3 \) değeri bulunur.
\( a = 4 \) için \( h \) değerini bulalım.
\( h = \dfrac{108 - 4^2}{4(4)} \)
\( = \dfrac{23}{4} \) m bulunur.
Amaç fonksiyonunun grafiği, bulduğumuz noktalar ve değerleri aşağıdaki şekilde gösterilmiştir.
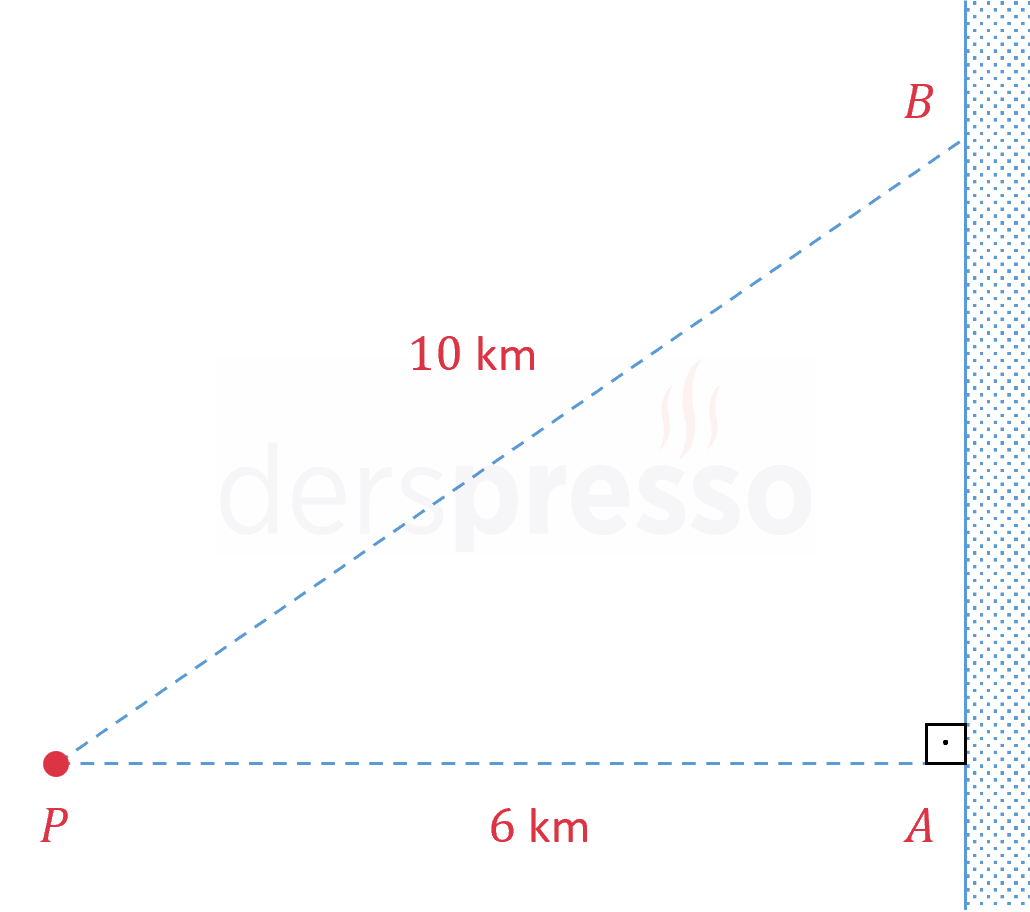
Saatte 3 km hızla yüzen ve 5 km hızla koşan Ceren, denizde sahile 6 km uzaklıkta olduğu anda bulunduğu noktadan 10 km uzaklıktaki kafedeki toplantısına geç kaldığını fark ediyor.
Ceren sahilde hangi noktaya kadar yüzüp o noktadan kafeye koşarsa toplantıya en kısa sürede varır?
Çözümü GösterAdım 1: Problem tanımı
\( P \): Ceren'in denizde bulunduğu nokta
\( A \): Ceren'in denizde bulunduğu noktanın kıyıya en yakın noktası
\( B \): Ceren'in toplantısının olacağı nokta
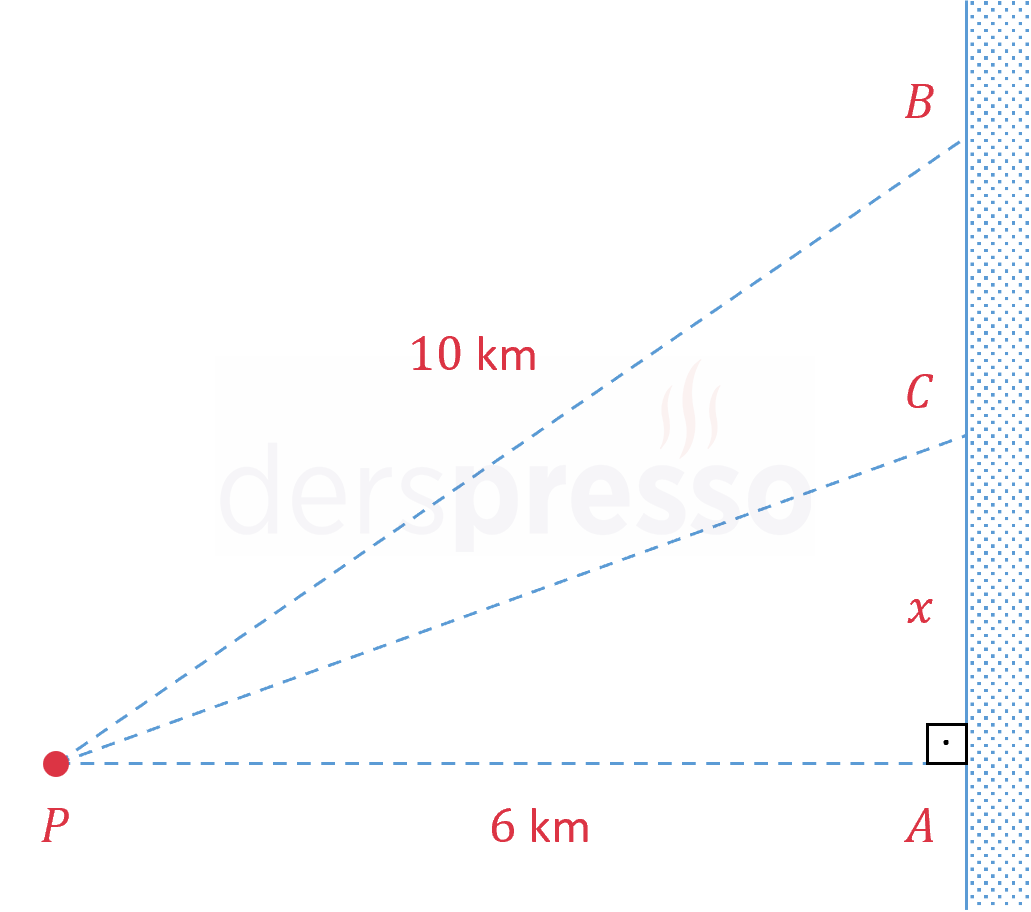
\( C \): Ceren'in yüzerek sahile çıkacağı nokta
\( \abs{PC} \): Ceren'in yüzeceği mesafe
\( \abs{CB} \): Ceren'in koşacağı mesafe
\( t_1 \): Ceren'in yüzdüğü süre
\( t_2 \): Ceren'in koştuğu süre
\( t \): Ceren'in yüzdüğü + koştuğu toplam süre
Problemde Ceren'in yüzdüğü + koştuğu toplam sürenin en küçük değeri istenmektedir.
Adım 2: Amaç fonksiyonu
Pisagor teoreminden \( \abs{AB} \) uzaklığını bulalım.
\( \abs{AB}^2 + 6^2 = 10^2 \)
\( \abs{AB} = 8 \)
\( \abs{AC} \) uzaklığına \( x \) diyelim.
\( \abs{AB} = \abs{AC} + \abs{CB} \)
\( 8 = x + \abs{CB} \)
\( \abs{CB} = 8 - x \)
O halde Ceren'in sahile çıktığı nokta ile kafe arasındaki uzaklık \( 8 - x \) olur.
Ceren'in koştuğu mesafe: \( 8 - x \) km
Pisagor teoremini kullanarak \( \abs{PC} \) uzaklığını bulalım.
\( \abs{PC}^2 = x^2 + 6^2 \)
\( \abs{PC} = \sqrt{x^2 + 36} \)
Ceren'in yüzdüğü mesafe: \( \sqrt{x^2 + 36} \) km
Hız denklemini yazalım.
Yol = Hız x Zaman
Ceren'in yüzdüğü yolun hız denklemini yazalım.
Ceren'in yüzme hızı: 3 km/sa
\( \sqrt{x^2 + 36} = 3t_1 \)
\( t_1 = \dfrac{\sqrt{x^2 + 36}}{3} \)
Ceren'in koştuğu yolun hız denklemini yazalım.
Ceren'in koşma hızı: 5 km/sa
\( 8 - x = 5t_2 \)
\( t_2 = \dfrac{8 - x}{5} \)
Toplam geçen süreyi bulalım.
\( T = t_1 + t_2 \)
\( = \dfrac{\sqrt{x^2 + 36}}{3} + \dfrac{8 - x}{5} \)
Süre ve uzaklık pozitif büyüklüklerdir.
\( T, x \in \mathbb{R^+} \)
\( x \), \( \abs{AB} \) uzunluğundan büyük olamaz.
\( x \in [0, 8] \)
Buna göre en küçük değerini bulmak istediğimiz amaç fonksiyonu aşağıdaki gibidir.
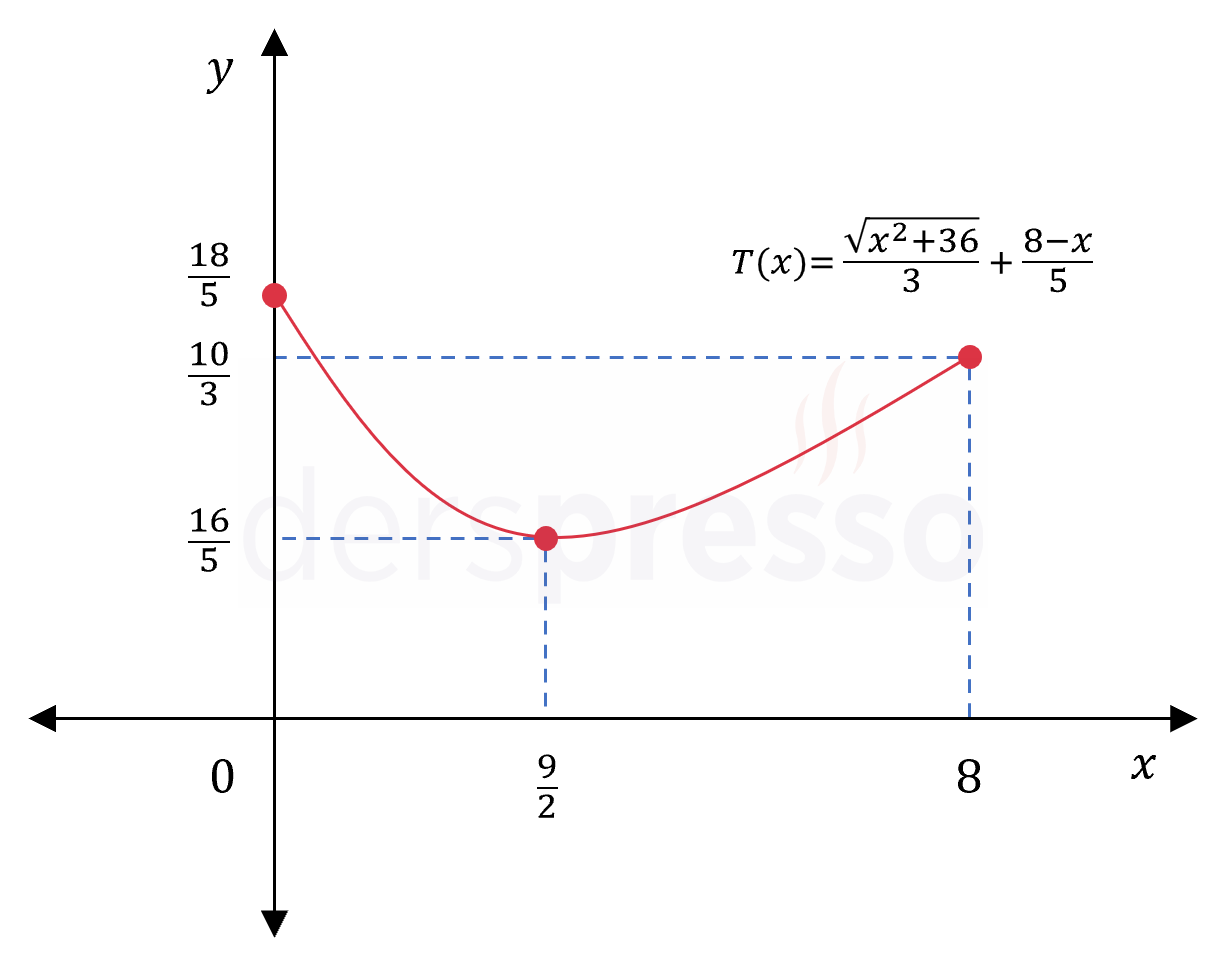
\( T: [0, 8] \to \mathbb{R^+} \)
\( T(x) = \dfrac{\sqrt{x^2 + 36}}{3} + \dfrac{8 - x}{5} \)
Adım 3: Problem çözümü
\( T \) fonksiyonu kapalı bir aralıkta tanımlıdır ve iki sürekli fonksiyonun toplamından oluştuğu için tanım kümesi içinde süreklidir.
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
\( T'(x) = \dfrac{x}{3\sqrt{x^2 + 36}} - \dfrac{1}{5} \)
Fonksiyonun tanım kümesi içinde birinci türevinin sıfır olduğu iç noktaları bulalım.
\( \dfrac{x}{3\sqrt{x^2 + 36}} - \dfrac{1}{5} = 0 \)
\( \dfrac{5x - 3\sqrt{x^2 + 36}}{15\sqrt{x^2 + 36}} = 0 \)
\( 5x - 3\sqrt{x^2 + 36} = 0 \)
\( 5x = 3\sqrt{x^2 + 36} \)
Eşitliğin iki tarafının da karesini alalım.
\( 25x^2 = 9x^2 + 324 \)
\( 16x^2 = 324 \)
\( x^2 = \dfrac{81}{4} \)
\( x = \dfrac{9}{2} \)
Fonksiyonun tanım aralığı içinde birinci türevinin tanımsız olduğu iç nokta yoktur.
Kritik nokta: \( x = \frac{9}{2} \)
Fonksiyonun kritik noktadaki değerini bulalım.
\( T(\dfrac{9}{2}) = \dfrac{\sqrt{(\frac{9}{2})^2 + 36}}{3} + \dfrac{8 - \frac{9}{2}}{5} = \dfrac{16}{5} \)
Fonksiyonun kapalı uç noktalarındaki değerini bulalım.
\( f(0) = \dfrac{\sqrt{0^2 + 36}}{3} + \dfrac{8 - 0}{5} = \dfrac{18}{5} \)
\( f(8) = \dfrac{\sqrt{8^2 + 36}}{3} + \dfrac{8 - 8}{5} = \dfrac{10}{3} \)
Bu değerleri karşılaştırdığımızda fonksiyonun tanım aralığındaki en küçük değeri olarak \( x = \frac{9}{2} \) noktasında aldığı \( \frac{16}{5} \) değeri bulunur.
O halde Ceren, toplantıya en kısa sürede varabilmek için \( x = \frac{9}{2} \) olan noktaya kadar yüzmeli, o noktadan kafeye kadar koşmalıdır.
Amaç fonksiyonunun grafiği, bulduğumuz noktalar ve değerleri aşağıdaki şekilde gösterilmiştir.

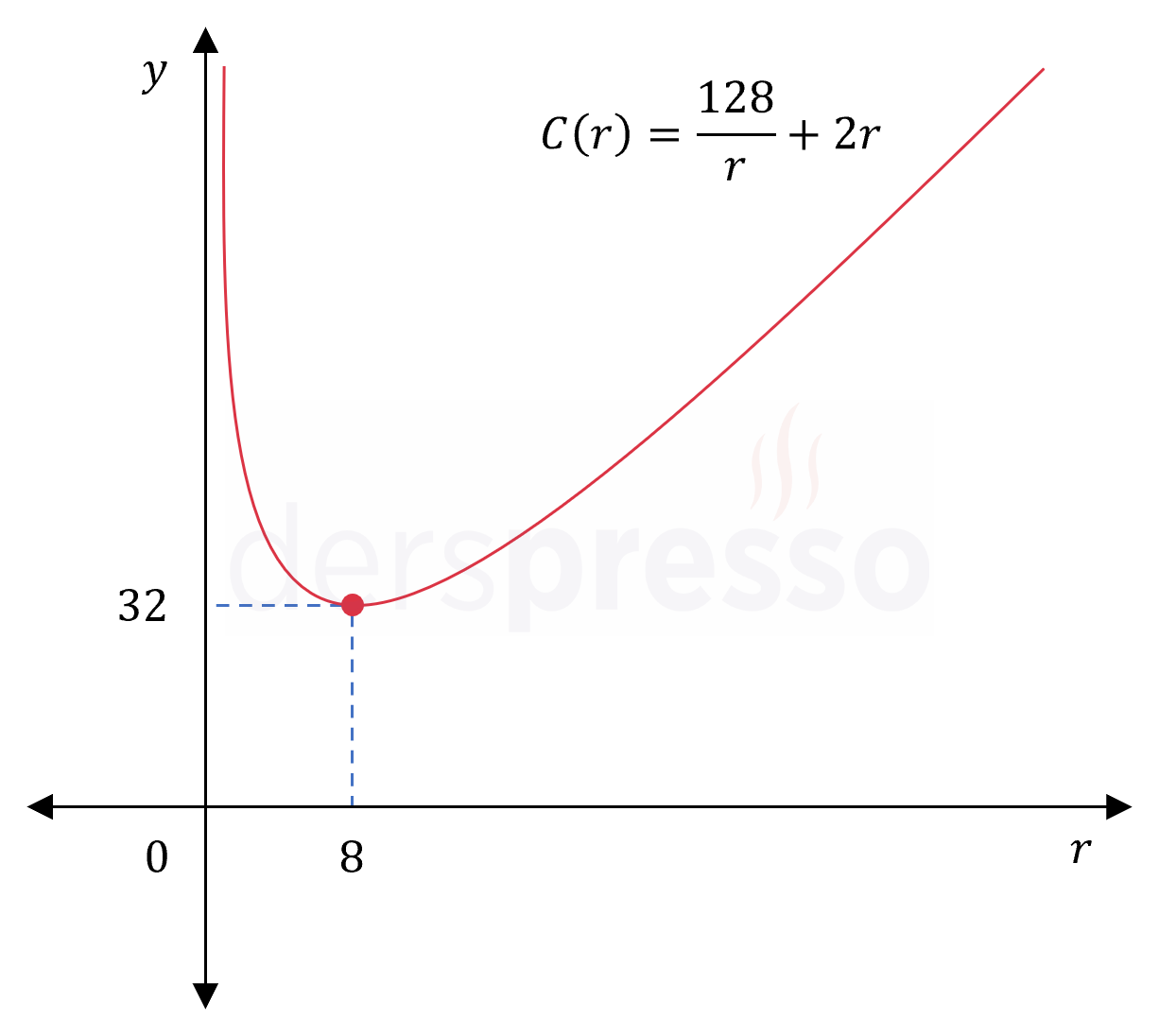
Alanı 64 cm\( ^2 \) olan bir daire diliminin çevresi en az kaç santimetre olabilir?
Çözümü GösterAdım 1: Problem tanımı

\( r \): Daire diliminin yarıçapı
\( x \): Daire diliminin merkez açısı (radyan)
\( a \): Daire diliminin yay uzunluğu
\( A \): Daire diliminin alanı
\( C \): Daire diliminin çevresi
Problemde daire diliminin çevresinin en küçük değeri istenmektedir.
Adım 2: Amaç fonksiyonu
Merkez açısının ölçüsü radyan cinsinden verilen daire diliminin yay uzunluğu ve alanı aşağıdaki iki formülle hesaplanır.
\( a = rx \)
\( A = \dfrac{r^2x}{2} \)
Daire diliminin çevresini aşağıdaki formülle bulabiliriz.
\( C = a + 2r \)
\( = rx + 2r \)
Uzunluk, açı, çevre ve alan pozitif büyüklüklerdir.
\( r, a, x, C, A \in \mathbb{R^+} \)
Amaç fonksiyonunu tek bir değişken cinsiden yazabilmek için değişkenler arasında bir ilişki kurmaya çalışalım.
Daire diliminin alanı verilmiştir.
\( A = 64 \) cm\( ^2 \)
Bu değeri alan formülünde yerine koyalım.
\( 64 = \dfrac{r^2x}{2} \)
\( rx \) ifadesini yalnız bırakalım.
\( rx = \dfrac{128}{r} = a \)
Bulduğumuz değeri çevre formülünde yerine koyduğumuzda sadece \( r \) değişkenine bağlı olan amaç fonksiyonunu elde ederiz.
\( C = \dfrac{128}{r} + 2r \)
Buna göre en küçük değerini bulmak istediğimiz amaç fonksiyonu aşağıdaki şekilde tanımlanır.
\( C: (0, \infty) \to \mathbb{R^+} \)
\( C(r) = \dfrac{128}{r} + 2r \)
Adım 3: Problem çözümü
\( C \) fonksiyonu açık bir aralıkta tanımlıdır ve bir rasyonel fonksiyon içerdiği için paydayı sıfır yapan ve tanım aralığı dışındaki \( r = 0 \) noktası hariç süreklidir.
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
\( C'(r) = -\dfrac{128}{r^2} + 2 \)
Fonksiyonun tanım aralığı içinde birinci türevinin sıfır olduğu iç noktaları bulalım.
\( -\dfrac{128}{r^2} + 2 = 0 \)
\( r^2 = 64 \)
\( r = 8 \)
Fonksiyonun tanım aralığı içinde birinci türevinin tanımsız olduğu iç nokta yoktur.
Kritik nokta: \( x = 8 \)
Fonksiyonun kritik noktadaki değerini bulalım.
\( C(8) = \dfrac{128}{8} + 2(8) = 32 \)
Fonksiyonun açık uç noktalarındaki limitini bulalım.
\( \lim\limits_{x \to 0^+} \left( \dfrac{128}{r} + 2r \right) = \infty + 0 = \infty \)
\( \lim\limits_{x \to \infty} \left( \dfrac{128}{r} + 2r \right) = 0 + \infty = \infty \)
Bu değerleri karşılaştırdığımızda \( C \) fonksiyonun tanım aralığındaki en küçük değeri olarak \( r = 8 \) noktasında aldığı \( 32 \) cm değeri bulunur.
Amaç fonksiyonunun grafiği, bulduğumuz noktalar ve değerleri aşağıdaki şekilde gösterilmiştir.

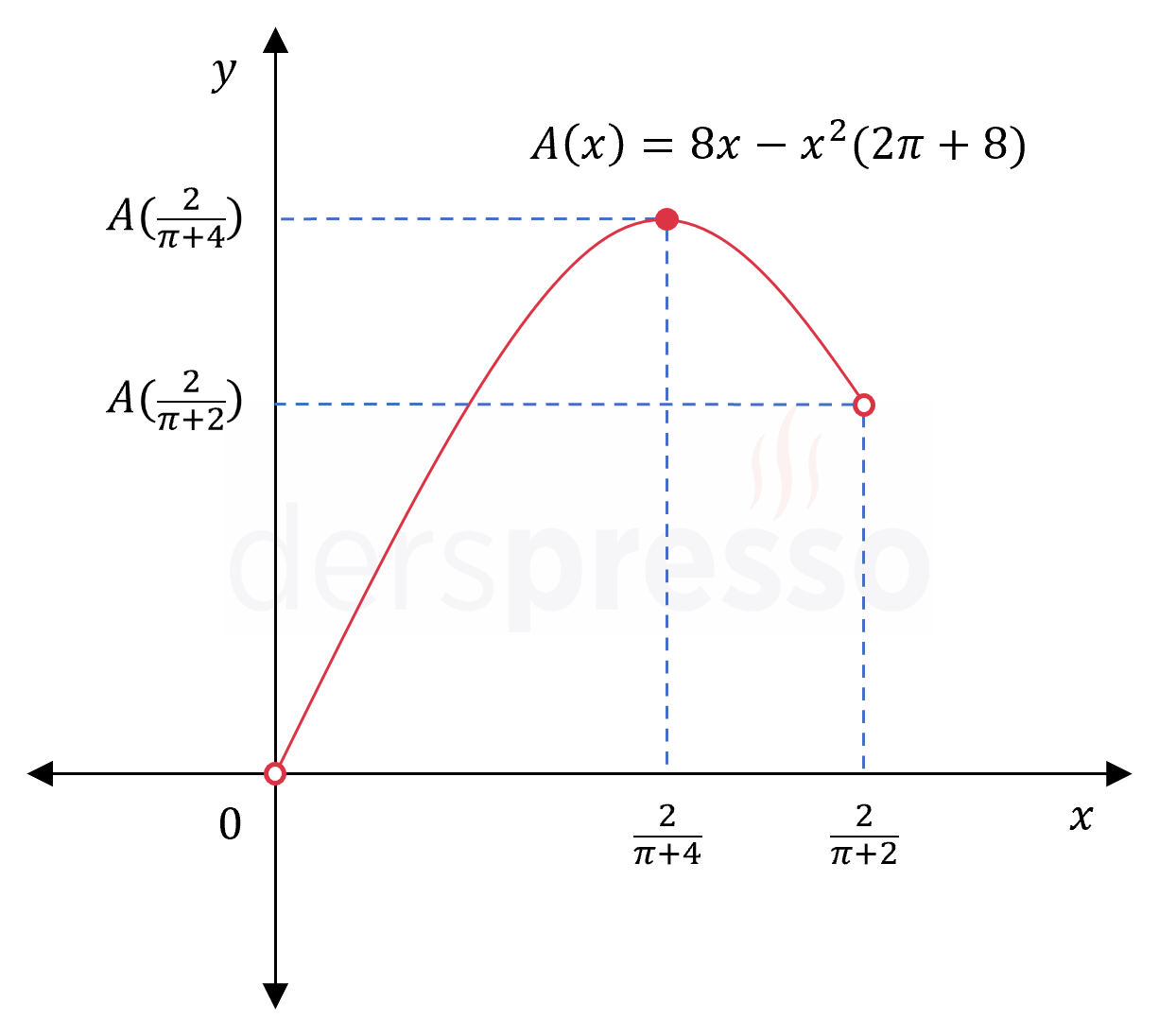
Yarım daire ve dikdörtgenden oluşan şekildeki gibi bir pencerenin çevresi 4 m'dir. Bu pencerenin önüne bir saksı bitkisi konmak istenmektedir. Bitkinin aldığı ışık miktarı pencerenin alanı ile doğru orantılıdır.
Bitkinin en çok miktarda ışık alması için pencerenin yarım daire kısmının yarıçapı kaç metre olmalıdır?
Çözümü GösterAdım 1: Problem tanımı
\( 2x \): Yarım dairenin yarıçapı
\( y \): Dikdörtgenin yüksekliği
\( C_1 \): Pencerenin yarım daire kısmının çevresi
\( C_2 \): Pencerenin dikdörtgen kısmının çevresi
\( C \): Pencerenin toplam çevresi
\( A_1 \): Pencerenin yarım daire kısmının alanı
\( A_2 \): Pencerenin dikdörtgen kısmının alanı
\( A \): Pencerenin toplam alanı
Bitkinin en fazla ışığı alması istenmektedir, bu da pencerenin alanının en büyük değeri ile mümkün olur.
Problemde pencerenin alanını en büyük yapan yarıçap değeri istenmektedir.
Adım 2: Amaç fonksiyonu
Yarım dairenin ve dikdörtgenin alanını aşağıdaki iki formülle bulabiliriz.
\( A_1 = \dfrac{\pi (2x)^2}{2} = 2\pi x^2 \)
\( A_2 = 4xy \)
\( A = A_1 + A_2 \)
\( A = 2\pi x^2 + 4xy \)
Uzunluk, yarıçap, çevre ve alan pozitif büyüklüklerdir.
\( x, y, C, A \in \mathbb{R^+} \)
Amaç fonksiyonunu tek bir değişken cinsinden yazabilmek için değişkenler arasında bir ilişki kurmaya çalışalım.
Yarım dairenin ve dikdörtgenin çevre formülünü yazalım.
\( C_1 = \dfrac{2\pi \cdot 2x}{2} \)
\( = 2\pi x \)
\( C_2 = 4x + 2y \)
\( C = C_1 + C_2 \)
\( = 2\pi x + 4x + 2y \)
Pencerenin çevre uzunluğu soruda verilmiştir.
\( 4 = 2\pi x + 4x + 2y \)
\( y \) değişkenini yalnız bırakalım.
\( y = 2 - \pi x - 2x \)
\( y \) değerini alan formülünde yerine koyduğumuzda sadece \( x \) değişkenine bağlı olan amaç fonksiyonunu elde ederiz.
\( A = 2\pi x^2 + 4x(2 - \pi x - 2x) \)
\( = 8x - x^2(2\pi + 8) \)
\( y \in \mathbb{R^+} \) bilgisini kullanarak \( x \) tanım aralığını bulalım.
\( y = 2 - \pi x - 2x \gt 0 \)
\( 2 - x(\pi + 2) \gt 0 \)
\( x \lt \dfrac{2}{\pi + 2} \)
Buna göre en büyük değerini bulmak istediğimiz amaç fonksiyonu aşağıdaki gibidir.
\( A: (0, \frac{2}{\pi + 2}) \to \mathbb{R^+} \)
\( A(x) = 8x - x^2(2\pi + 8) \)
Adım 3: Problem çözümü
\( A \) fonksiyonu ikinci dereceden bir polinom fonksiyondur ve tanım kümesi içinde süreklidir.
\( A \) fonksiyonu negatif başkatsayılı (kolları aşağı yönlü) bir parabol olduğu için (eğer tanım aralığı bu noktayı içeriyorsa) en büyük değerini birinci türevinin sıfır olduğu tepe noktasında alır.
\( A'(x) = 8 - 2x(2\pi + 8) \)
Tepe noktasını bulmak için birinci türevi sıfıra eşitleyelim.
\( 8 - 2x(2\pi + 8) = 0 \)
\( x = \dfrac{2}{\pi + 4} \)
Tepe noktası fonksiyonun tanım aralığında olduğu için \( A \) fonksiyonu en büyük değerini bu noktada alır ve fonksiyonun uç noktalarını kontrol etmemize gerek yoktur.
Dolayısıyla pencerenin alanı en büyük değerini \( x = \frac{2}{\pi + 4} \) olduğunda alır.
Problemde pencerenin alanını en büyük yapan yarım dairenin yarıçap değeri istenmektedir.
\( 2x = 2 \cdot \dfrac{2}{\pi + 4} \)
\( = \dfrac{4}{\pi + 4} \) bulunur.
Amaç fonksiyonunun grafiği, bulduğumuz noktalar ve değerleri aşağıdaki şekilde gösterilmiştir.

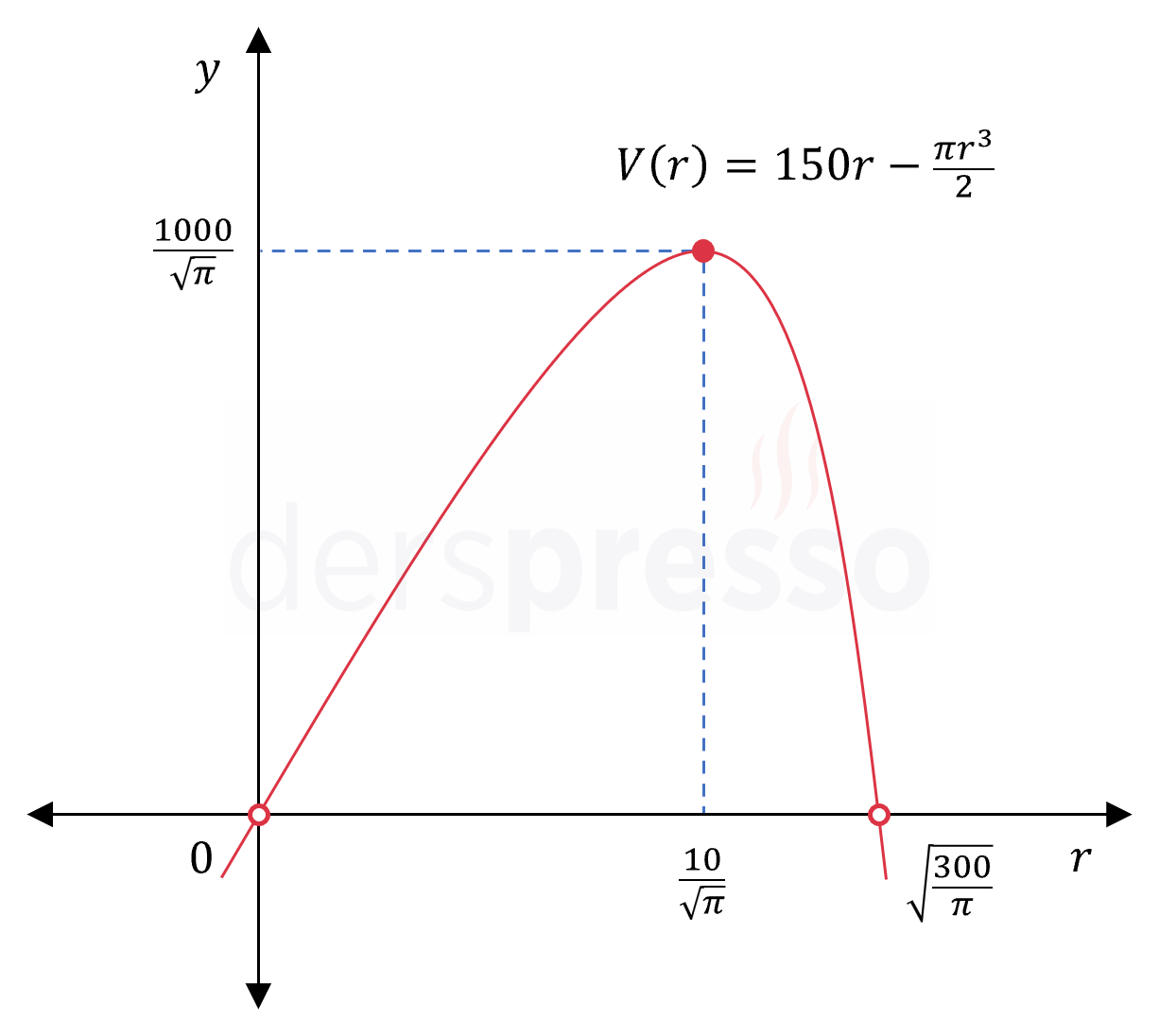
Üst tabanı açık olan dik dairesel silindir şeklindeki vazonun toplam yüzey alanı 300 cm\(^2 \)'dir.
Buna göre vazonun hacminin alabileceği en büyük değer kaçtır?
Çözümü GösterAdım 1: Problem tanımı
\( r \): Silindirin taban yarıçapı
\( h \): Silindirin yüksekliği
\( A \): Silindirin yüzey alanı
\( V \): Silindirin hacmi
Problemde vazonun hacminin en büyük değeri istenmektedir.
Adım 2: Amaç fonksiyonu
Silindirin hacmini aşağıdaki formülle bulabiliriz.
\( V = \pi r^2h \)
Uzunluk, alan ve hacim pozitif büyüklüklerdir.
\( r, h, A, V \in \mathbb{R^+} \)
Amaç fonksiyonunu tek bir değişken cinsinden yazabilmek için değişkenler arasında bir ilişki kurmaya çalışalım.
Silindirin yüzey alan formülünü yazalım.
Yüzey alanını hesaplarken silindirin üst tabanının açık olduğunu dikkate almalıyız.
\( A = \pi r^2 + 2\pi rh \)
Silindirin yüzey alanı soruda verilmiştir.
\( 300 = \pi r^2 + 2\pi rh \)
Alan formülünde \( h \) değişkenini yalnız bırakalım.
\( h = \dfrac{300 - \pi r^2}{2\pi r} \)
\( h \) değerini hacim formülünde yerine koyduğumuzda sadece \( r \) değişkenine bağlı olan amaç fonksiyonunu elde ederiz.
\( V = \pi r^2h \)
\( = \pi r^2 \cdot \dfrac{300 - \pi r^2}{2\pi r} \)
\( = 150r - \dfrac{\pi r^3}{2} \)
\( h \in \mathbb{R^+} \) bilgisini kullanarak \( r \) tanım aralığını bulalım.
\( h = \dfrac{300 - \pi r^2}{2\pi r} \gt 0 \)
\( 300 - \pi r^2 \gt 0 \)
\( \dfrac{300}{\pi} \gt r^2 \)
\( 0 \lt r \lt \sqrt{\dfrac{300}{\pi}} \)
Buna göre en büyük değerini bulmak istediğimiz amaç fonksiyonu aşağıdaki gibidir.
\( V: (0, \sqrt{\frac{300}{\pi}}) \to \mathbb{R^+} \)
\( V(r) = 150r - \dfrac{\pi r^3}{2} \)
Adım 3: Problem çözümü
\( V \) fonksiyonu açık bir aralıkta tanımlıdır ve bir polinom fonksiyonu olduğu için süreklidir.
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
\( V'(r) = 150 - \dfrac{3\pi r^2}{2} \)
\( = \dfrac{300 - 3\pi r^2}{2} \)
Fonksiyonun tanım kümesi içinde birinci türevinin sıfır olduğu iç noktaları bulalım.
\( \dfrac{300 - 3\pi r^2}{2} = 0 \)
\( \dfrac{3(10 - \sqrt{\pi}r)(10 + \sqrt{\pi}r)}{2} = 0 \)
\( r = \dfrac{10}{\sqrt{\pi}} \)
Fonksiyonun tanım kümesi içinde birinci türevinin tanımsız olduğu iç nokta yoktur.
Kritik nokta: \( r = \frac{10}{\sqrt{\pi}} \)
Fonksiyonun kritik noktadaki değerini bulalım.
\( V(\dfrac{10}{\sqrt{\pi}}) = 150 \cdot \dfrac{10}{\sqrt{\pi}} - \dfrac{\pi(\frac{10}{\sqrt{\pi}})^3}{2} \)
\( = \dfrac{1000}{\sqrt{\pi}} \)
Fonksiyonun açık uç noktalarındaki değerini bulalım.
\( \lim\limits_{x \to 0^+} (150r - \dfrac{\pi r^3}{2}) = 150(0) - \dfrac{\pi (0)^3}{2} = 0 \)
\( \lim\limits_{x \to \sqrt{\frac{300}{\pi}}^-} (150r - \dfrac{\pi r^3}{2}) = 150(\sqrt{\frac{300}{\pi}}) - \dfrac{\pi (\sqrt{\frac{300}{\pi}})^3}{2} \)
\( = \dfrac{300(\sqrt{\frac{300}{\pi}}) - \pi (\sqrt{\frac{300}{\pi}})^3}{2} \)
\( = \dfrac{\sqrt{\frac{300}{\pi}}(300 - \pi (\frac{300}{\pi}))}{2} \)
\( = \dfrac{\sqrt{\frac{300}{\pi}}(300 - 300)}{2} = 0 \)
Bu değerleri karşılaştırdığımızda fonksiyonun tanım aralığındaki en büyük değeri olarak \( r = \frac{10}{\sqrt{\pi}} \) noktasında aldığı \( \frac{1000}{\sqrt{\pi}} \) cm\(^3 \) değeri bulunur.
Amaç fonksiyonunun grafiği, bulduğumuz noktalar ve değerleri aşağıdaki şekilde gösterilmiştir.
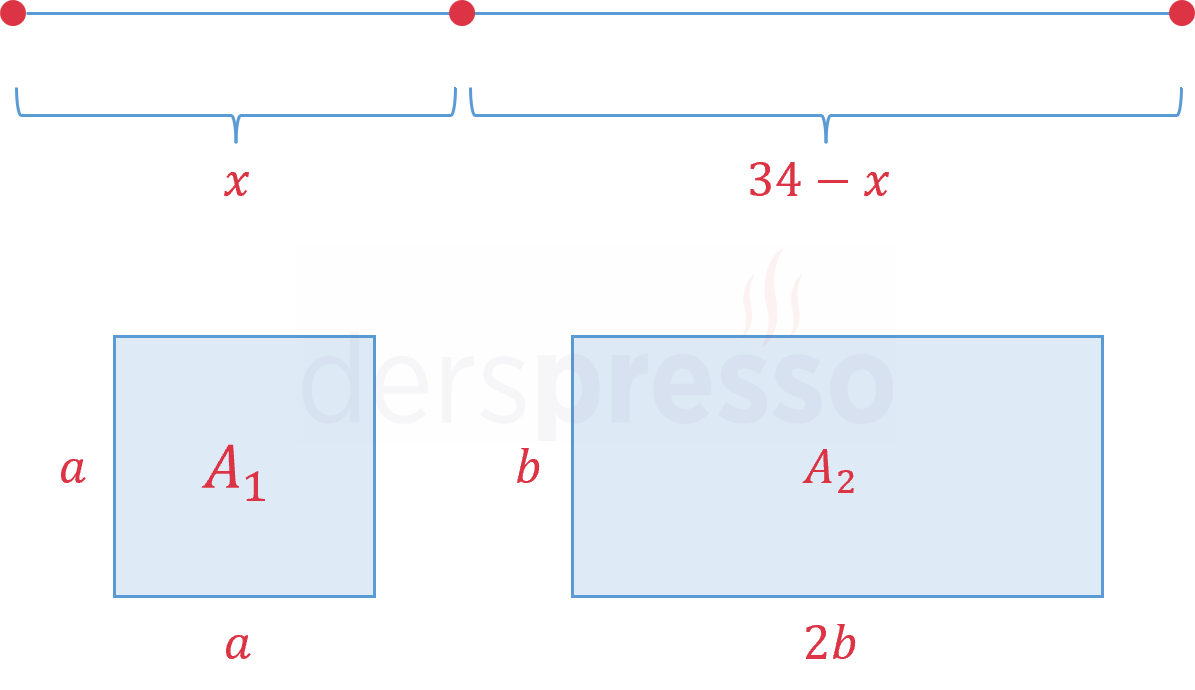
34 cm uzunluğundaki bir tel parçası, biri kare diğeri kenar uzunluklarının oranı \( \frac{1}{2} \) olan bir dikdörtgen oluşturacak şekilde iki parçaya bölünmek isteniyor.
Oluşan şekillerin alanlarının toplamı en az kaç olabilir?
Çözümü GösterAdım 1: Problem tanımı
\( A_1 \) : Karenin alanı
\( A_2 \) : Dikdörtgenin alanı
\( A \) : Toplam alan
\( a \): Karenin bir kenar uzunluğu
\( b \): Dikdörtgenin kısa kenar uzunluğu
\( 2b \): Dikdörtgenin uzun kenar uzunluğu
\( x \): Kareyi oluşturan telin uzunluğu, dolayısıyla karenin çevresi
\( 34 - x \): Dikdörtgeni oluşturan telin uzunluğu, dolayısıyla dikdörtgenin çevresi
Problemde kare ve dikdörtgenin toplam alanının en küçük değeri istenmektedir.
Adım 2: Amaç fonksiyonu
Karenin alan formülünü yazalım.
\( A_1 = a^2 \)
Dikdörtgenin alan formülünü yazalım.
\( A_2 = b \cdot 2b = 2b^2 \)
\( A = A_1 + A_2 \)
\( = a^2 + 2b^2 \)
Uzunluk ve alan pozitif büyüklüklerdir.
\( a, b, x, A \in \mathbb{R^+} \)
Amaç fonksiyonunu tek bir değişken cinsinden yazabilmek için değişkenler arasında bir ilişki kurmaya çalışalım.
Karenin çevre formülünü kullanarak \( a \) değişkenini \( x \) cinsinden yazalım.
\( 4a = x \)
\( a = \dfrac{x}{4} \)
Dikdörtgenin çevre formülünü kullanarak \( b \) değişkenini \( x \) cinsinden yazalım.
\( 34 - x = 2(2b + b) = 6b \)
\( b = \dfrac{34 - x}{6} \)
Bulduğumuz değerleri alan formülünde yerine koyalım .
\( A = (\dfrac{x}{4})^2 + 2(\dfrac{34 - x}{6})^2 \)
\( = \dfrac{x^2}{16} + \dfrac{(34 - x)^2}{18} \)
\( x \) uzunluğundaki tel büyük telin bir parçasıdır.
\( 0 \le x \le 34 \)
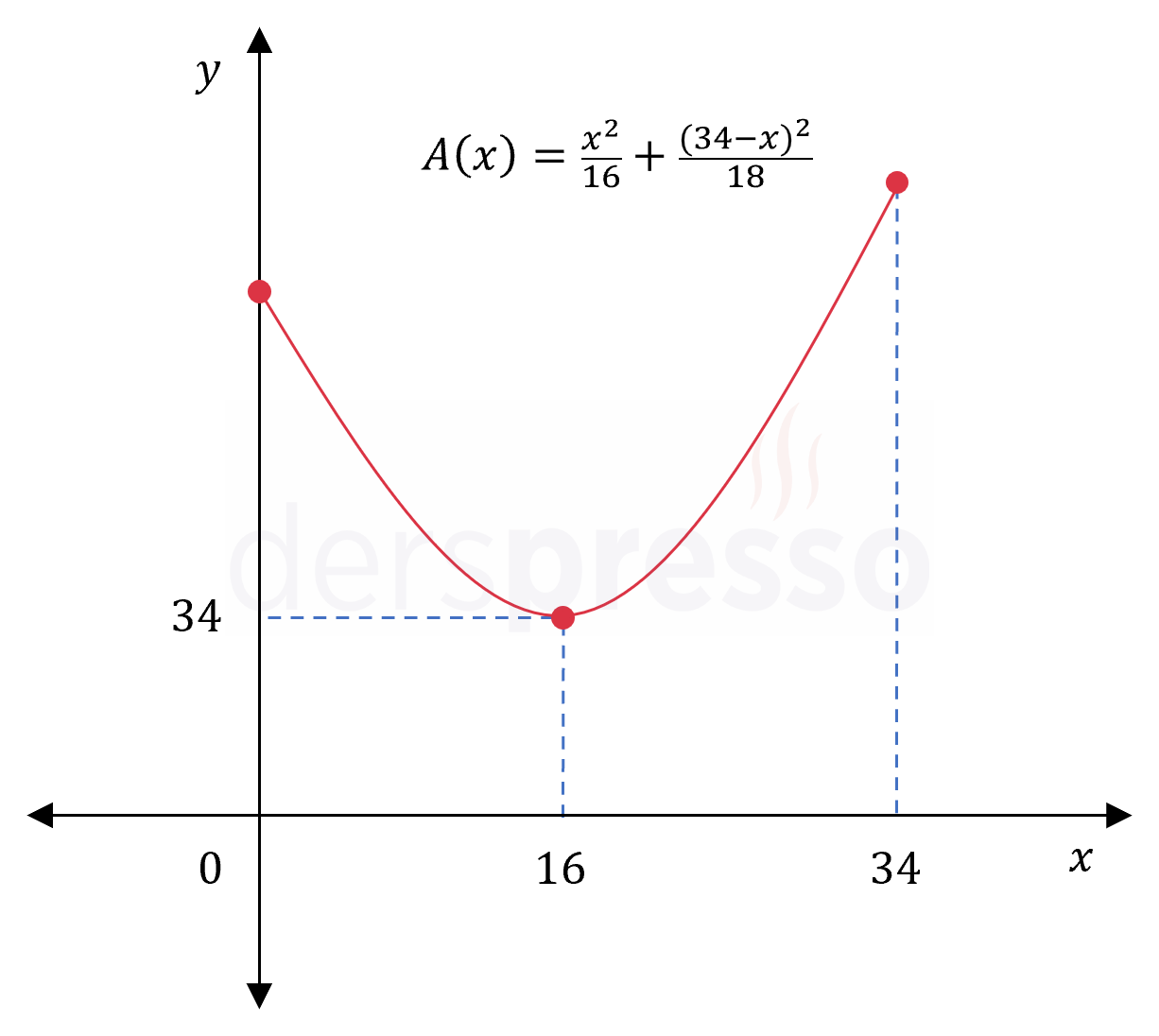
Buna göre en küçük değerini bulmak istediğimiz amaç fonksiyonu aşağıdaki gibidir.
\( A: [0, 34] \to \mathbb{R^+} \)
\( A(x) = \dfrac{x^2}{16} + \dfrac{(34 - x)^2}{18} \)
Adım 3: Problem çözümü
\( A \) fonksiyonu ikinci dereceden bir polinom fonksiyonudur ve tanım kümesi içinde süreklidir.
\( A \) fonksiyonu pozitif başkatsayılı (kolları yukarı yönlü) bir parabol olduğu için (eğer tanım aralığı bu noktayı içeriyorsa) en küçük değerini birinci türevinin sıfır olduğu tepe noktasında alır.
\( A'(x) = \dfrac{x}{8} - \dfrac{34 - x}{9} \)
Tepe noktasını bulmak için birinci türevi sıfıra eşitleyelim.
\( \dfrac{x}{8} - \dfrac{34 - x}{9} = 0 \)
\( x = 16 \)
Tepe noktası fonksiyonun tanım aralığında olduğu için \( A \) fonksiyonu en küçük değerini bu noktada alır ve fonksiyonun uç noktalarını kontrol etmemize gerek yoktur.
Buna göre \( A \) fonksiyonu tanım kümesi içinde en küçük değerini \( x = 16 \) noktasında alır.
\( x = 16 \) için toplam alanı bulalım.
\( A(16) = \dfrac{16^2}{16} + \dfrac{(34 - 16)^2}{18} \)
\( = 34 \)
Buna göre fonksiyonun tanım aralığındaki en küçük değeri olarak \( x = 16 \) noktasında aldığı \( 34 \) değeri bulunur.
Dolayısıyla oluşan şekillerin toplam alanının en küçük değeri 34 cm\(^2 \) olarak bulunur.
Amaç fonksiyonunun grafiği, bulduğumuz noktalar ve değerleri aşağıdaki şekilde gösterilmiştir.
\( x \) ekseni, \( y \) ekseni ve \( f(x) = -\ln{x} \) eğrisine teğet olan bir doğru ile sınırlandırılmış olan ve birinci bölgede bulunan üçgenler içinde alanı en büyük olan üçgenin alanı nedir?
Çözümü GösterAdım 1: Problem tanımı
\( A \): Üçgenin alanı
Dik üçgenin hipotenüsü \( f \) fonksiyonunun bir noktasındaki teğetidir ve teğet noktası fonksiyon denklemini sağlar.
\( (a, -\ln{a}) \): Üçgenin hipotenüsünün \( f \) fonksiyonuna teğet olduğu noktanın koordinatları
Problemde üçgenin alanının en büyük değeri istenmektedir.
Adım 2: Amaç fonksiyonu
Alan pozitif bir büyüklüktür.
\( A \in \mathbb{R^+} \)
Bir fonksiyonun birinci türevinin bir noktadaki değeri fonksiyona o noktada teğet olan doğrunun eğimini verir.
\( f'(x) = -\dfrac{1}{x} \)
\( f'(a) = -\dfrac{1}{a} \)
\( (x_1, y_1) \) noktasından geçen ve eğimi \( m \) olan doğrunun denklemi aşağıdaki formülle bulunur.
\( y - y_1 = m(x - x_1) \)
\( y - (-\ln{a}) = -\dfrac{1}{a}(x - a) \)
\( y = 1 -\dfrac{x}{a} - \ln{a} \)
Teğet doğrunun (hipotenüsün) eksenleri kestiği noktaları bulalım.
\( x = 0 \) için:
\( y = 1 -\dfrac{0}{a} - \ln{a} \)
\( = 1 - \ln{a} \)
\( (0, 1 - \ln{a}) \)
\( y = 0 \) için:
\( 0 = 1 -\dfrac{x}{a} - \ln{a} \)
\( x = a - a\ln{a} \)
\( (a - a\ln{a}, 0) \)
\( f \) fonksiyonunun ve üçgenin koordinat düzlemindeki görüntüsü aşağıdaki gibidir.
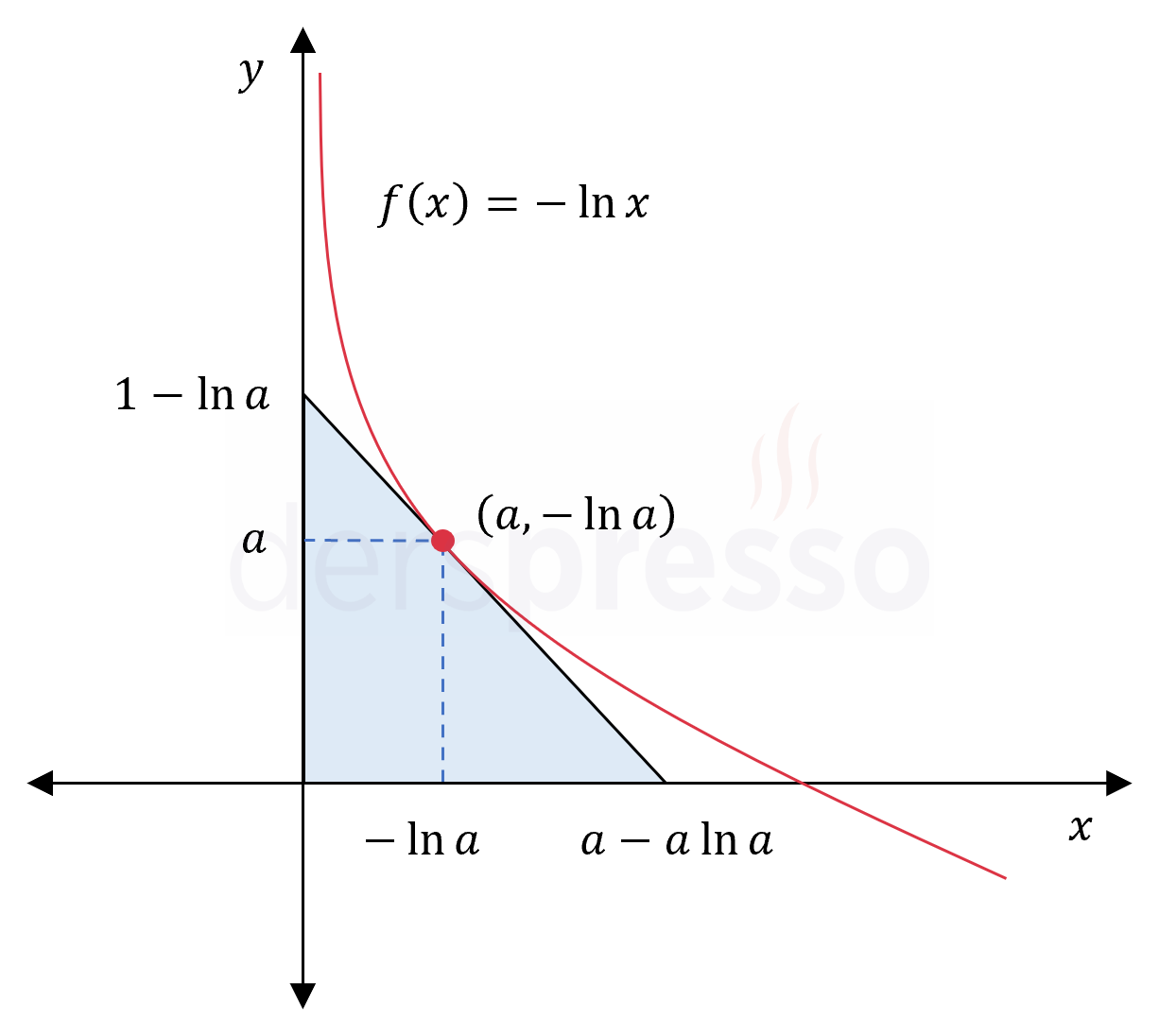
Üçgenin alanı taban ile yüksekliğin çarpımının yarısına eşittir.
\( A = \dfrac{(a - a\ln{a})(1 - \ln{a})}{2} \)
\( = \dfrac{a(1 - \ln{a})^2}{2} \)
Üçgenin birinci bölgede olması için teğet doğru \( y \) eksenini pozitif tarafta kesmelidir.
\( 1 - \ln{a} \gt 0 \)
\( \ln{a} \lt 1 \)
\( a \lt e \)
Üçgenin birinci bölgede olması için teğet doğru \( x \) eksenini pozitif tarafta kesmelidir.
\( a - a\ln{a} \gt 0 \)
\( a(1 - \ln{a}) \gt 0 \)
\( 0 \lt a \lt e \)
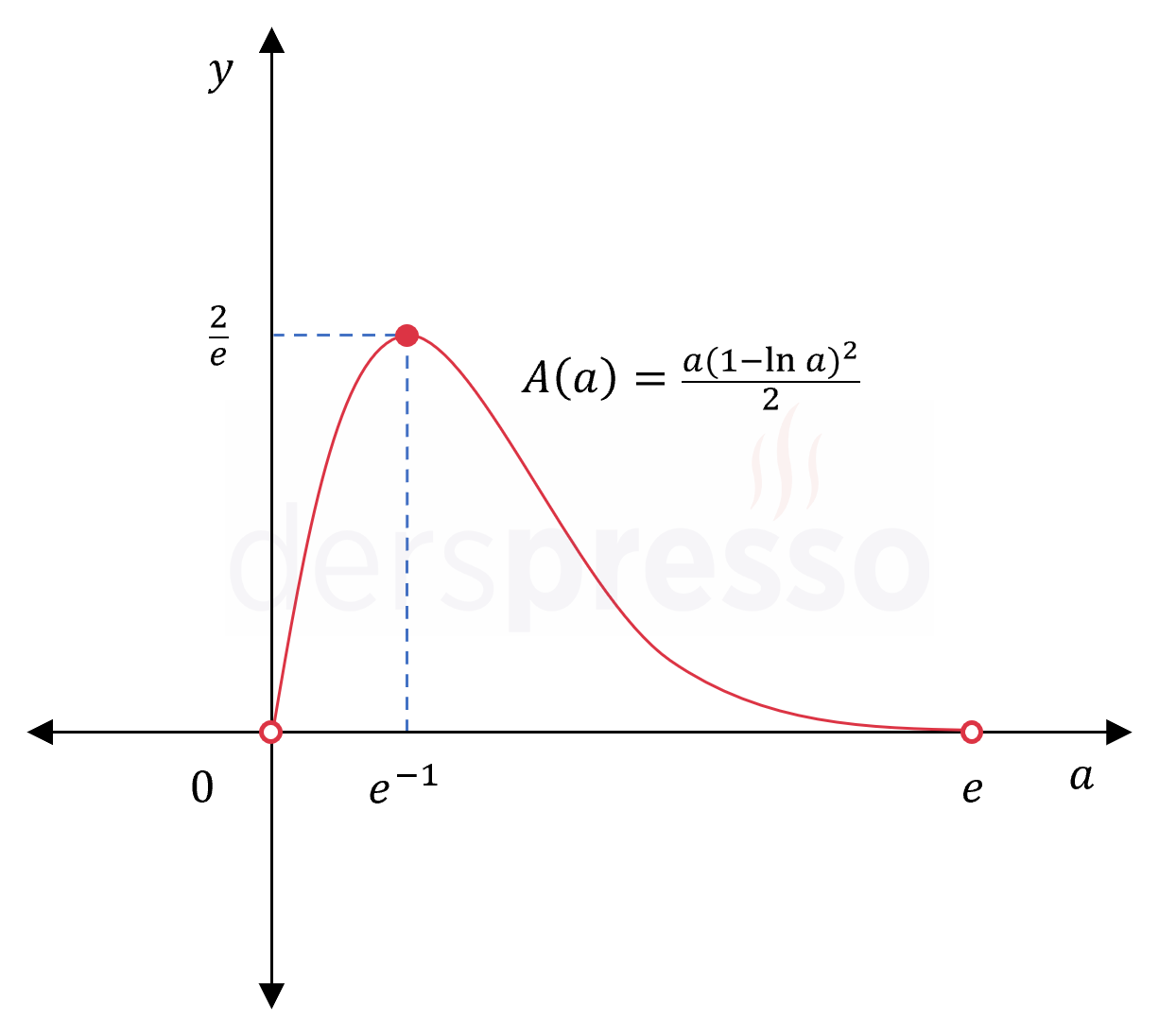
Buna göre en küçük ve en büyük değerini bulmak istediğimiz amaç fonksiyonu aşağıdaki şekilde tanımlanır.
\( A: (0, e) \to (0, \infty) \)
\( A(a) = \dfrac{a(1 - \ln{a})^2}{2} \)
Adım 3: Problem çözümü
\( A \) fonksiyonu açık bir aralıkta tanımlıdır ve sürekli fonksiyonların çarpımından oluştuğu için tanım kümesi içinde süreklidir.
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
\( A'(a) = \dfrac{(1 - \ln{a})^2 + 2a(1 - \ln{a})(-\frac{1}{a})}{2} \)
\( = \dfrac{\ln^2{a} -1}{2} \)
Fonksiyonun tanım kümesi içinde birinci türevinin sıfır olduğu iç noktaları bulalım.
\( \dfrac{\ln^2{a} - 1}{2} = 0 \)
\( \dfrac{(\ln{a} - 1)(\ln{a} + 1)}{2} = 0 \)
Bu eşitlik iki durumda sağlanır.
Durum 1:
\( \ln{a} - 1 = 0 \)
\( \ln{a} = 1 \)
\( a = e \)
Bu değer amaç fonksiyonunun tanım kümesi içinde değildir.
Durum 2:
\( \ln{a} + 1 = 0 \)
\( \ln{a} = -1 \)
\( a = e^{-1} \)
Fonksiyonun birinci türevinin tanımsız olduğu iç nokta yoktur.
Kritik nokta: \( a = e^{-1} \)
Fonksiyonun kritik noktadaki değerini bulalım.
\( A(e^{-1}) = \dfrac{e^{-1}(1 - \ln{e^{-1}})^2}{2} = \dfrac{e^{-1}(1 + 1)^2}{2} \)
\( = \dfrac{2}{e} \)
Fonksiyonun açık uç noktalarındaki limitini bulalım.
\( \lim\limits_{a \to 0^+} {\dfrac{a(1 - \ln{a})^2}{2}} = \dfrac{1}{2} \lim\limits_{a \to 0^+} {\dfrac{(1 - \ln{a})^2}{\frac{1}{a}}} \)
Bu limit ifadesinde \( \frac{\infty}{\infty} \) belirsizliği vardır.
İfadeye L'Hospital kuralını uygulayalım.
\( = \dfrac{1}{2} \lim\limits_{a \to 0^+} {\dfrac{2(1 - \ln{a})(-\frac{1}{a})}{-\frac{1}{a^2}}} = \lim\limits_{a \to 0^+} {\dfrac{1 - \ln{a}}{\frac{1}{a}}} \)
Bu limit ifadesinde \( \frac{\infty}{\infty} \) belirsizliği vardır.
İfadeye tekrar L'Hospital kuralını uygulayalım.
\( = \lim\limits_{a \to 0^+} {\dfrac{\frac{1}{a}}{\frac{1}{a^2}}} = \lim\limits_{a \to 0^+} {a} = 0 \)
\( \lim\limits_{a \to e^-} {\dfrac{a(1 - \ln{a})^2}{2}} = {\dfrac{e(1 - \ln{e})^2}{2}} = 0 \)
Buna göre amaç fonksiyonu açık uç noktaları civarında \( \frac{2}{e} \) değerinden daha büyük bir değer almaz.
Bu değerleri karşılaştırdığımızda amaç fonksiyonunun tanım aralığındaki en büyük değeri olarak \( a = e^{-1} \) noktasında aldığı \( \frac{2}{e} \) değeri bulunur.
Amaç fonksiyonunun grafiği, bulduğumuz noktalar ve değerleri aşağıdaki şekilde gösterilmiştir.
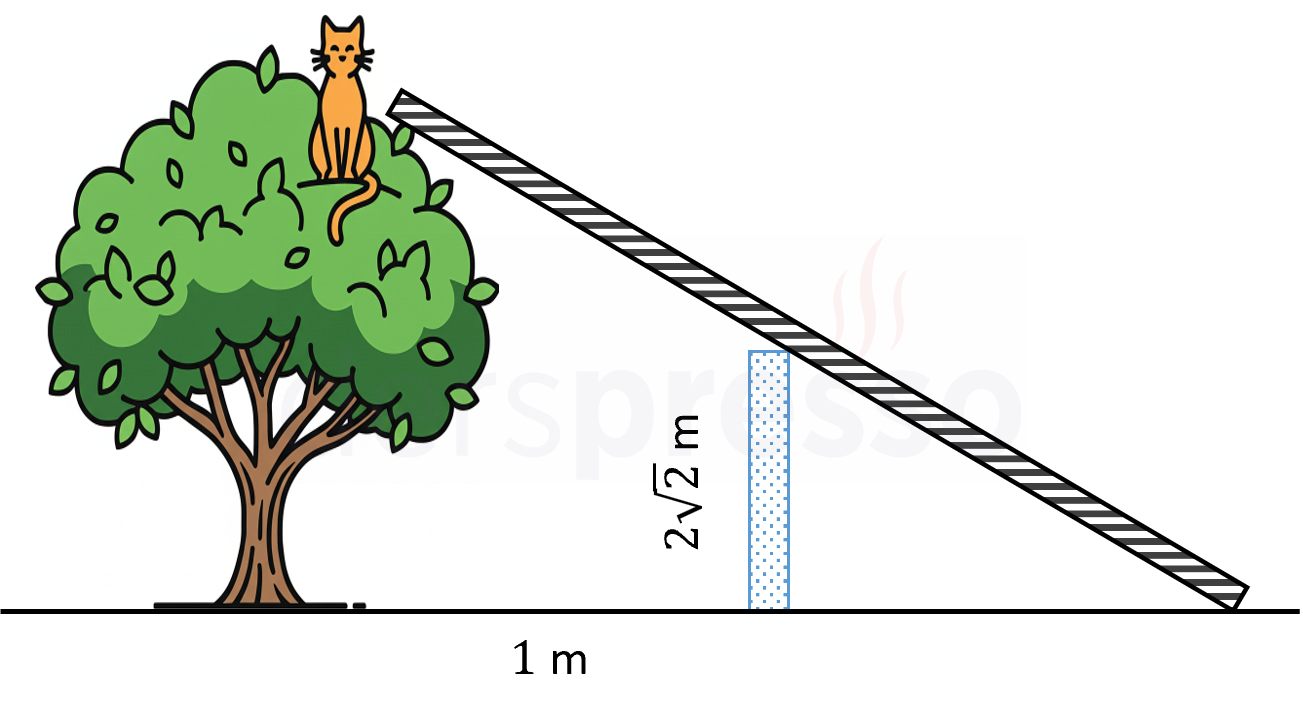
Bir itfaiyeci merdiveniyle birlikte ağaçta mahsur kalan bir kediyi kurtarmak için gelmiştir. Ağacın 1 metre ilerisinde \( 2\sqrt{2} \) metre yüksekliğinde bir duvar bulunmaktadır ve itfaiyeci merdiveni bu duvara şekildeki gibi yaslayarak ağaca ulaşmayı hedeflemektedir.
Buna göre merdivenin uzunluğu en az kaç metre olmalıdır?
Çözümü GösterAdım 1: Problem tanımı

\( x \): Merdivenin yere temas ettiği noktanın duvara olan uzaklığı
\( y \): Merdivenin ağaca temas ettiği noktanın yerden yüksekliği
\( d \): Merdivenin uzunluğu
Problemde merdivenin uzunluğunun en küçük değeri istenmektedir.
Adım 2: Amaç fonksiyonu
Ağaç, merdiven ve yerin oluşturduğu üçgene Pisagor teoremini uygulayalım.
\( d^2 = y^2 + (x + 1)^2 \)
\( d = \sqrt{y^2 + (x + 1)^2} \)
Bir karekök ifadesi en küçük değerini kök içindeki ifade en küçük değerini aldığında alır.
O halde bir \( D \) fonksiyonu tanımlayalım ve işlemlerimizi bu fonksiyon üzerinden yapalım.
\( D(x, y) = y^2 + (x + 1)^2 \)
\( D \) fonksiyonu en küçük değerini aldığında soruda istenen \( d \) uzaklığı da en küçük değerini alacaktır.
Uzunluk pozitif bir büyüklüktür.
\( x, y, d, D \in \mathbb{R^+} \)
Amaç fonksiyonunu tek bir değişken cinsinden yazabilmek için \( x \) ve \( y \) değişkenleri arasında bir ilişki kurmaya çalışalım.
Ağaç, merdiven ve yerin oluşturduğu üçgen ile duvar, merdiven ve yerin oluşturduğu üçgen benzer üçgenlerdir.
\( \dfrac{x}{2\sqrt{2}} = \dfrac{x + 1}{y} \)
Bu eşitlikte \( y \) değişkenini yalnız bırakalım.
\( y = \dfrac{2\sqrt{2}(x + 1)}{x} \)
\( y \) değerini denklemde yerine koyduğumuzda sadece \( x \) değişkenine bağlı olan amaç fonksiyonunu elde ederiz.
\( D(x, y) = y^2 + (x + 1)^2 \)
\( D(x) = (\dfrac{2\sqrt{2}(x + 1)}{x})^2 + (x + 1)^2 \)
\( = \dfrac{x^4 + 2x^3 + 9x^2 + 16x + 8}{x^2} \)
Buna göre en küçük değerini bulmak istediğimiz amaç fonksiyonu aşağıdaki gibidir.
\( D: (0, \infty) \to \mathbb{R^+} \)
\( D(x) = \dfrac{x^4 + 2x^3 + 9x^2 + 16x + 8}{x^2} \)
Adım 3: Problem çözümü
\( D \) fonksiyonu açık bir aralıkta tanımlıdır ve bir rasyonel fonksiyon olduğu için paydayı sıfır yapan ve tanım aralığı dışındaki \( x = 0 \) noktası hariç süreklidir.
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
\( D'(x) = \dfrac{(4x^3 + 6x^2 + 18x + 16)x^2 - 2x(x^4 + 2x^3 + 9x^2 + 16x + 8)}{x^4} \)
\( = \dfrac{2x^5 + 2x^4 - 16x^2 - 16x}{x^4} \)
\( = \dfrac{2(x + 1)(x^3 - 8)}{x^3} \)
\( = \dfrac{2(x + 1)(x - 2)(x^2 + 2x + 4)}{x^3} \)
Fonksiyonun tanım kümesi içinde birinci türevinin sıfır olduğu iç noktaları bulalım.
\( 2(x + 1)(x - 2)(x^2 + 2x + 4) = 0 \)
\( x = 2 \)
Fonksiyonun tanım kümesi içinde birinci türevinin tanımsız olduğu iç nokta yoktur.
Kritik nokta: \( x = 2 \)
Fonksiyonun kritik noktadaki değerini bulalım.
\( D(2) = \dfrac{2^4 + 2(2)^3 + 9(2)^2 + 16(2) + 8}{2^2} = 27 \)
Fonksiyonun açık uç noktalarındaki limitini bulalım.
\( \lim\limits_{x \to 0^+} {\dfrac{x^4 + 2x^3 + 9x^2 + 16x + 8}{x^2}} = \dfrac{0^4 + 2(0)^3 + 9(0)^2 + 16(0) + 8}{(0^+)^2} = \infty \)
\( \lim\limits_{x \to \infty} {\dfrac{x^4 + 2x^3 + 9x^2 + 16x + 8}{x^2}} = \infty \)
Bu değerleri karşılaştırdığımızda \( D \) fonksiyonu tanım kümesi içindeki en küçük değerini \( x = 2 \) noktasında alır.
Dolayısıyla \( d \) uzunluğu da en küçük değerini \( x = 2 \) noktasında alır.
\( x = 2 \) için \( d \) değerini bulalım.
\( d = \sqrt{D(2)} \)
\( = \sqrt{27} = 3\sqrt{3} \) metre bulunur.
Amaç fonksiyonunun grafiği, bulduğumuz noktalar ve değerleri aşağıdaki şekilde gösterilmiştir.

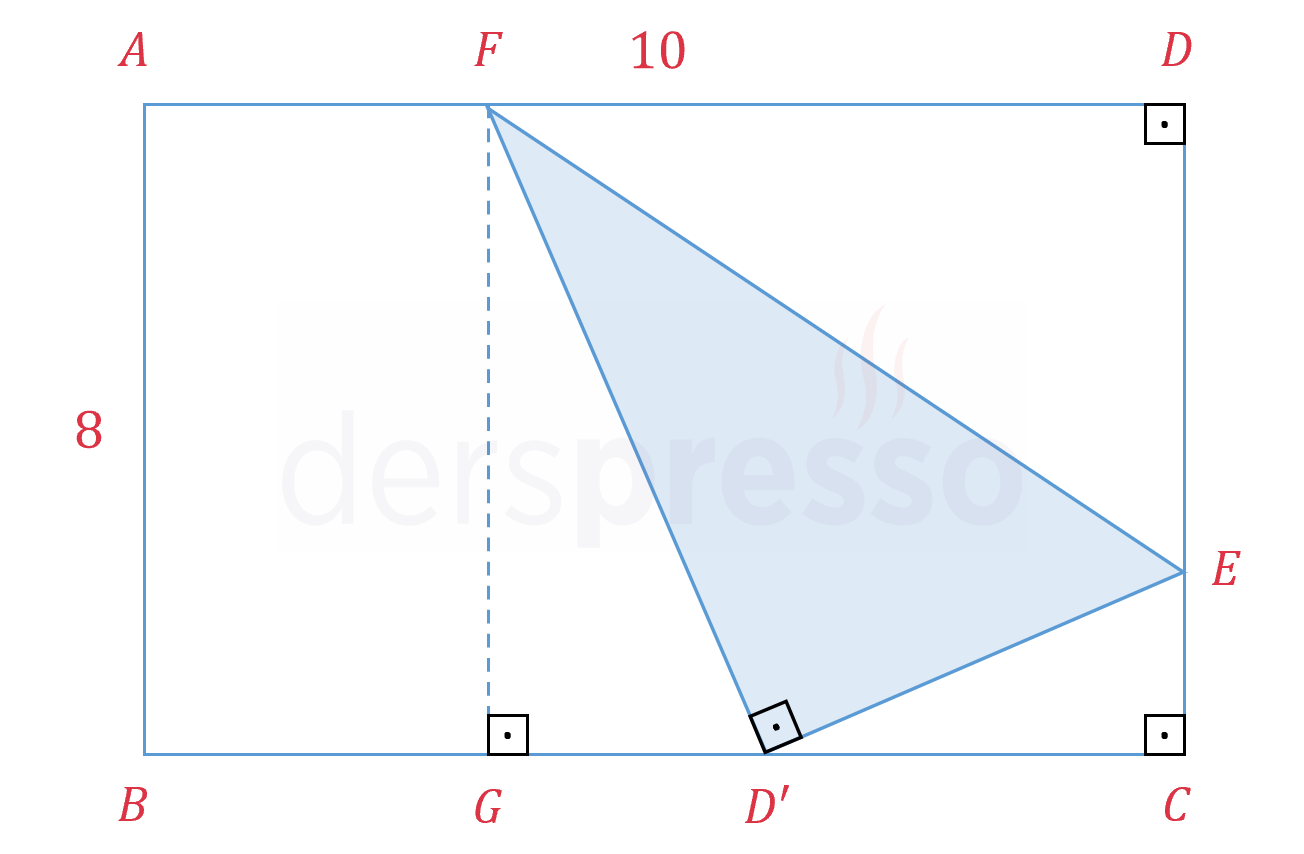
Kenar uzunlukları 8 ve 10 cm olan dikdörtgen şeklindeki bir kağıt şekildeki gibi \( D \) köşesi \( [BC] \) kenarı üzerinde bir \( D' \) noktasına gelecek şekilde katlanıyor.
\( [FE] \) katlama çizgisinin uzunluğunun en küçük değeri kaçtır?
Çözümü GösterAdım 1: Problem tanımı
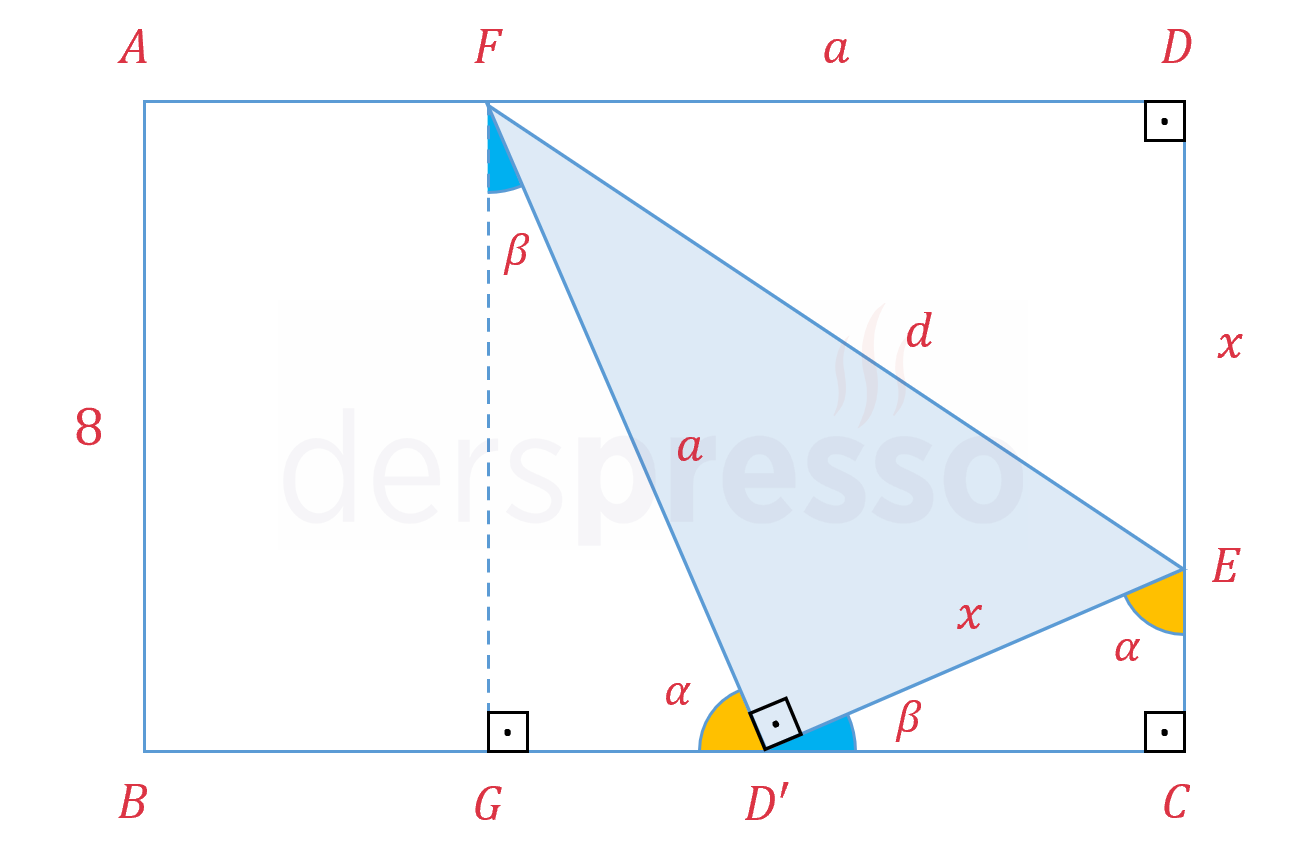
\( a \): Kağıdın katlanan parçasının uzun kenar uzunluğu
\( x \): Kağıdın katlanan parçasının kısa kenar uzunluğu
\( \abs{DE} = \abs{D'E} = x \)
\( \abs{FD} = \abs{FD'} = a \)
\( \alpha = m(\widehat{GD'F}) \)
\( \beta = m(\widehat{GFD'}) \)
\( \alpha \) ve \( \beta \) tümler açılardır.
\( \alpha = m(\widehat{CED'}) \)
\( \beta = m(\widehat{CD'E}) \)
\( d \): Katlama çizgisinin uzunluğu
Problemde katlama çizgisinin uzunluğunun en küçük değeri istenmektedir.
Adım 2: Amaç fonksiyonu
\( FDE \) üçgenine Pisagor teoremini uygulayalım.
\( d^2 = a^2 + x^2 \)
\( d = \sqrt{a^2 + x^2} \)
Bir karekök ifadesi en küçük değerini kök içindeki ifade en küçük değerini aldığında alır.
O halde bir \( D \) fonksiyonu tanımlayalım ve işlemlerimizi bu fonksiyon üzerinden yapalım.
\( D = a^2 + x^2 \)
\( D \) en küçük değeri aldığında soruda istenen \( d \) uzunluğu da en küçük değerini alacaktır.
Uzunluk ve açı pozitif büyüklüklerdir.
\( d, a, x, \alpha, \beta \in \mathbb{R^+} \)
Amaç fonksiyonunu tek bir değişken cinsinden yazabilmek için \( x \) ve \( a \) değişkenleri arasında bir ilişki kurmaya çalışalım.
\( ECD' \) üçgenine Pisagor teoremini uygulayalım.
\( \abs{D'C}^2 = x^2 - (8 - x)^2 \)
\( \abs{D'C} = \sqrt{16x - 64} \)
Tüm açıları aynı olan \( ECD' \) ve \( D'GF \) üçgenleri benzer üçgenlerdir.
\( \overset{\triangle}{ECD'} \sim \overset{\triangle}{D'GF} \)
\( \dfrac{\abs{ED'}}{\abs{CD'}} = \dfrac{\abs{D'F}}{\abs{GF}} \)
\( \dfrac{x}{\sqrt{16x - 64}} = \dfrac{a}{8} \)
Bu eşitlikte \( a \) değişkenini yalnız bırakalım.
\( a = \dfrac{8x}{\sqrt{16x - 64}} \)
\( a \) değerini denklemde yerine koyduğumuzda sadece \( x \) değişkenine bağlı olan amaç fonksiyonunu elde ederiz.
\( D = (\dfrac{8x}{\sqrt{16x - 64}})^2 + x^2 \)
\( = \dfrac{x^3}{x - 4} \)
\( x \) uzunluğu dikdörtgenin kısa kenarının bir parçasıdır.
\( x \lt 8 \)
\( a \) uzunluğu dikdörtgenin uzun kenarının bir parçasıdır.
\( a = \dfrac{8x}{\sqrt{16x - 64}} \lt 10 \)
\( \dfrac{64x^2}{16x - 64} \lt 100 \)
\( 64x^2 - 1600x + 6400 \lt 0 \)
\( x^2 - 25x + 100 \lt 0 \)
\( (x - 5)(x - 20) \lt 0 \)
\( 5 \lt x \lt 20 \)
Bu aralık ile \( x \lt 8 \) aralığının kesişimi amaç fonksiyonunun tanım kümesini verir.
Buna göre en küçük değerini bulmak istediğimiz amaç fonksiyonu aşağıdaki gibidir.
\( D: (5, 8) \to \mathbb{R^+} \)
\( D(x) = \dfrac{x^3}{x - 4} \)
Adım 3: Problem çözümü
\( D \) fonksiyonu açık bir aralıkta tanımlıdır ve bir rasyonel fonksiyon olduğu için paydayı sıfır yapan ve tanım aralığı dışındaki \( x = 4 \) noktası hariç süreklidir.
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
\( D'(x) = \dfrac{3x^2(x - 4) - x^3}{(x - 4)^2} \)
\( = \dfrac{2x^3 - 12x^2}{(x - 4)^2} \)
Fonksiyonun tanım kümesi içinde birinci türevinin sıfır olduğu iç noktaları bulalım.
\( \dfrac{2x^2(x - 6)}{(x - 4)^2} = 0 \)
\( x = 6 \)
Fonksiyonun tanım kümesi içinde birinci türevinin tanımsız olduğu iç nokta yoktur.
Kritik nokta: \( x = 6 \)
Fonksiyonun kritik noktadaki değerini bulalım.
\( D(6) = \dfrac{6^3}{6 - 4} = 108 \)
Fonksiyonun açık uç noktalarındaki limitini bulalım.
\( \lim\limits_{x \to 5^+} {\dfrac{x^3}{x - 4}} = \dfrac{5^3}{5 - 4} = 125 \)
\( \lim\limits_{x \to 8^-} {\dfrac{x^3}{x - 4}} = \dfrac{8^3}{8 - 4} = 128 \)
Bu değerleri karşılaştırdığımızda fonksiyonun tanım aralığındaki en küçük değeri olarak \( x = 6 \) noktasında aldığı \( 108 \) değeri bulunur.
\( x = 6 \) için katlama çizgisinin uzunluğunu bulalım.
\( d = \sqrt{D(6)} \)
\( = \sqrt{\dfrac{6^3}{6 - 4}} = 6\sqrt{3} \) cm bulunur.
Amaç fonksiyonunun grafiği, bulduğumuz noktalar ve değerleri aşağıdaki şekilde gösterilmiştir.
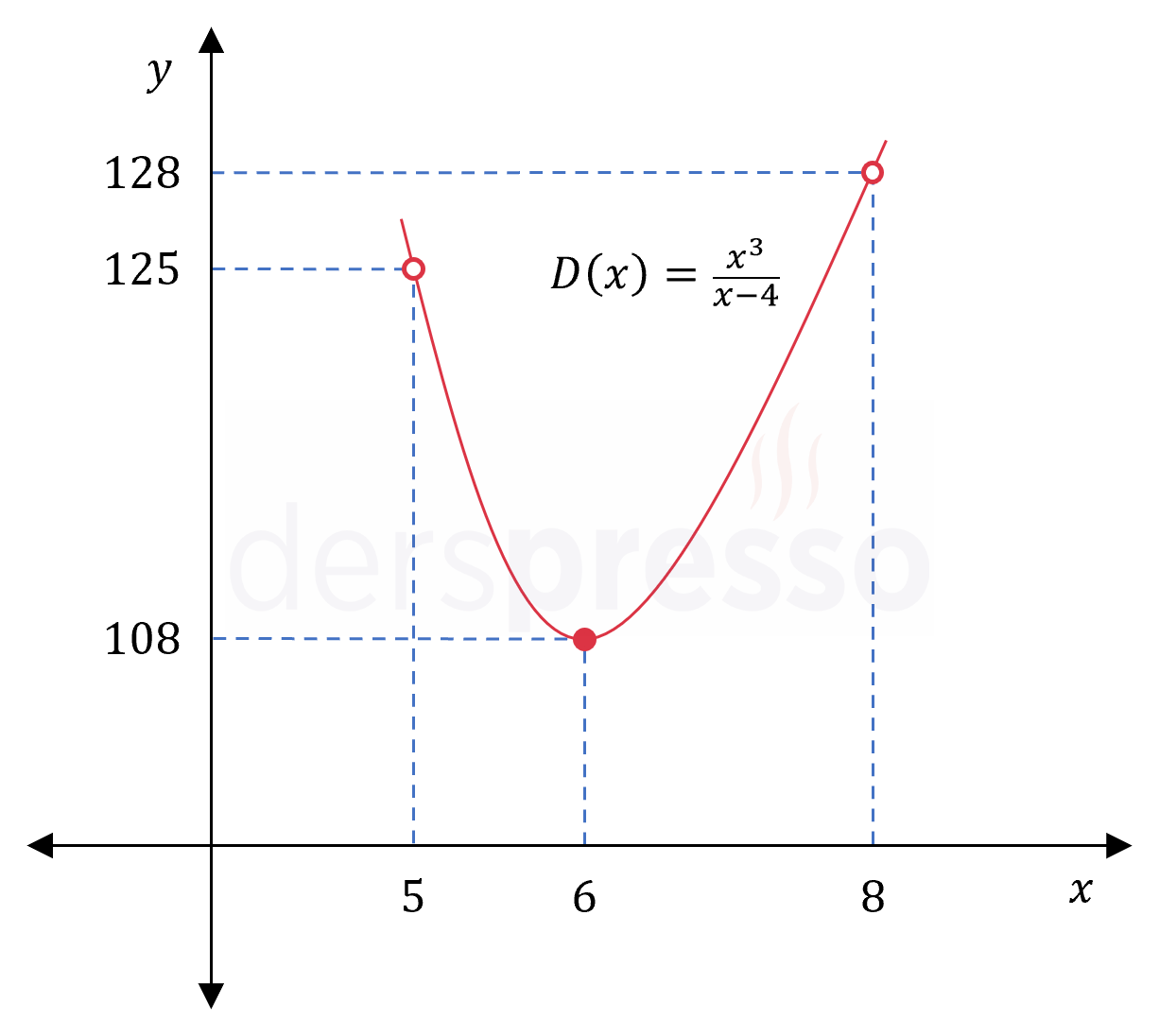
Yüzey alanı 1800 cm\(^2 \) ve kenar uzunlukları şekildeki gibi olan dik üçgen prizmanın hacminin alabileceği en büyük değer kaçtır?
Çözümü GösterAdım 1: Problem tanımı
\( x, y \): Prizmanın kenar uzunluklarında kullanılan değişkenler
\( A \): Prizmanın yüzey alanı
\( V \): Prizmanın hacmi
Problemde dik üçgen prizmanın hacminin en büyük değeri istenmektedir.
Adım 2: Amaç fonksiyonu
Dik üçgen prizmanın hacmini aşağıdaki formülle bulabiliriz.
V = Taban alanı x Yükseklik
\( V = \dfrac{3x \cdot 4x}{2} \cdot 2y \)
\( = 12x^2y \)
Uzunluk, alan ve hacim pozitif büyüklüklerdir.
\( x, y, A, V \in \mathbb{R^+} \)
Amaç fonksiyonunu tek bir değişken cinsinden yazabilmek için değişkenler arasında bir ilişki kurmaya çalışalım.
Prizmanın alan formülünü yazalım.
\( A = \text{2 üçgen yüz} + \text{3 dikdörtgen yüz} \)
\( = 2 \cdot \dfrac{3x \cdot 4x}{2} + (3x \cdot 2y + 4x \cdot 2y + 5x \cdot 2y) \)
\( = 12x^2 + 6xy + 8xy + 10xy \)
\( = 12x^2 + 24xy \)
Prizmanın alanı soruda verilmiştir.
\( 1800 = 12x^2 + 24xy \)
\( 150 = x^2 + 2xy \)
Alan formülünde \( xy \) çarpımını yalnız bırakalım.
\( xy = \dfrac{150 - x^2}{2} \)
\( xy \) değerini hacim formülünde yerine koyduğumuzda sadece \( x \) değişkenine bağlı olan amaç fonksiyonunu elde ederiz.
\( V = 12x^2y \)
\( = 12x \cdot xy \)
\( = 12x \cdot \dfrac{150 - x^2}{2} \)
\( = 900x - 6x^3 \)
\( x, y \in \mathbb{R^+} \) bilgisini kullanarak \( x \) tanım aralığını bulalım.
\( xy \gt 0 \)
\( xy = \dfrac{150 - x^2}{2} \gt 0 \)
\( 150 - x^2 \gt 0 \)
\( 0 \lt x \lt 5\sqrt{6} \)
Buna göre en büyük değerini bulmak istediğimiz amaç fonksiyonu aşağıdaki gibidir.
\( V: (0, 5\sqrt{6}) \to \mathbb{R^+} \)
\( V(x) = 900x - 6x^3 \)
Adım 3: Problem çözümü
\( V \) fonksiyonu açık bir aralıkta tanımlıdır ve bir polinom fonksiyonu olduğu için süreklidir.
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
\( V'(r) = 900 - 18x^2 \)
Fonksiyonun tanım kümesi içinde birinci türevinin sıfır olduğu iç noktaları bulalım.
\( 900 - 18x^2 = 0 \)
\( 18(5\sqrt{2} - x)(5\sqrt{2} + x) = 0 \)
\( x = 5\sqrt{2} \)
Fonksiyonun tanım kümesi içinde birinci türevinin tanımsız olduğu iç nokta yoktur.
Kritik nokta: \( x = 5\sqrt{2} \)
Fonksiyonun kritik noktadaki değerini bulalım.
\( V(5\sqrt{2}) = 900(5\sqrt{2}) - 6(5\sqrt{2})^3 \)
\( = 4500\sqrt{2} - 1500\sqrt{2} \)
\( = 3000\sqrt{2} \)
Fonksiyonun açık uç noktalarındaki değerini bulalım.
\( \lim\limits_{x \to 0^+} (900x - 6x^3) = 900(0) - 6(0)^3 = 0 \)
\( \lim\limits_{x \to 5\sqrt{6}} (900x - 6x^3) = 900(5\sqrt{6}) - 6(5\sqrt{6})^3 \)
\( = 6 \cdot 5\sqrt{6}(150 - (5\sqrt{6})^2) \)
\( = 30\sqrt{6}(150 - 150) = 0 \)
Bu değerleri karşılaştırdığımızda fonksiyonun tanım aralığındaki en büyük değeri olarak \( x = 5\sqrt{2} \) noktasında aldığı \( 3000\sqrt{2} \) cm\(^3 \) değeri bulunur.
Amaç fonksiyonunun grafiği, bulduğumuz noktalar ve değerleri aşağıdaki şekilde gösterilmiştir.
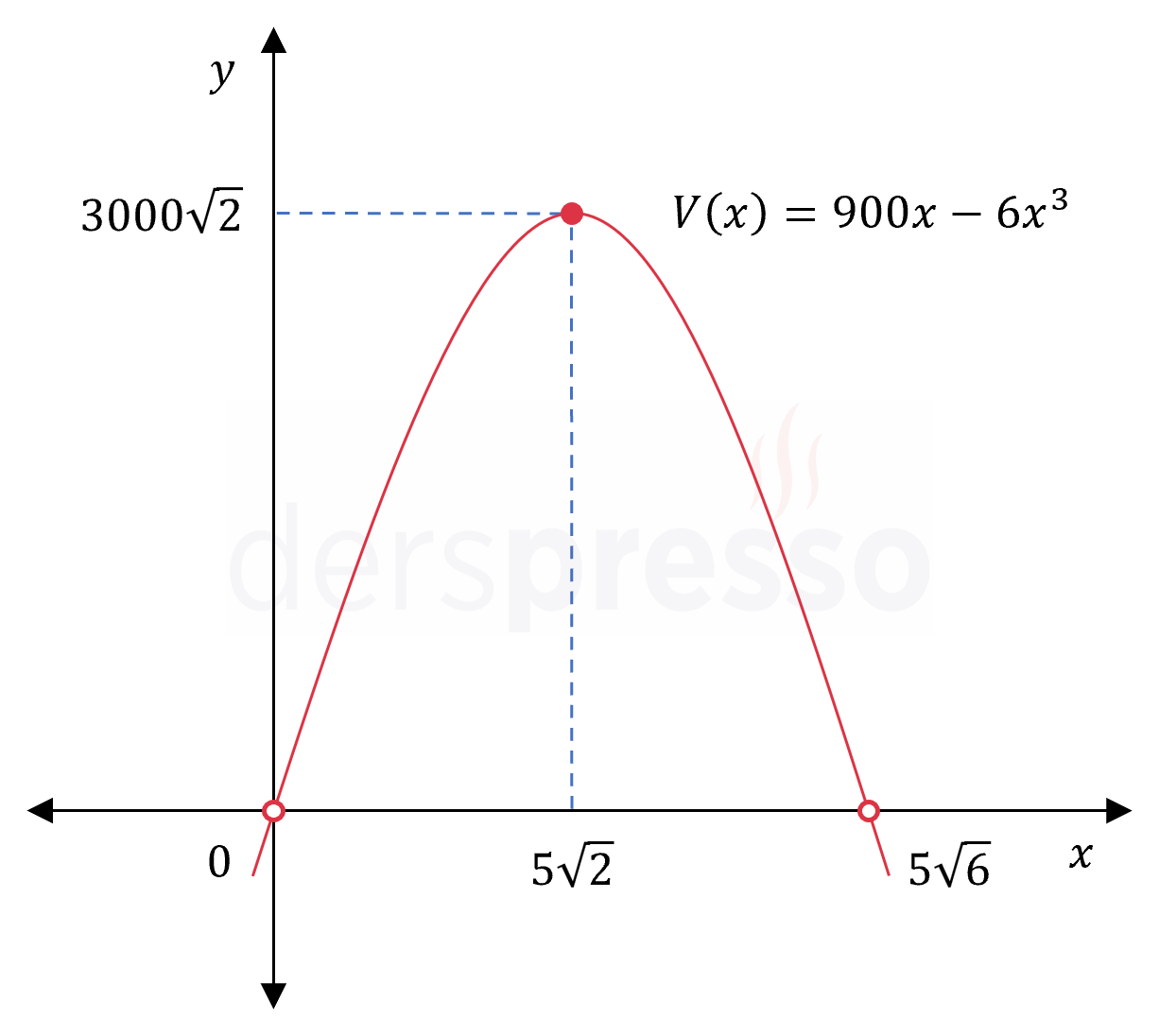

Kütleleri 64 kg ve 1 kg olan iki noktasal cisim aralarında 9 metre olacak şekilde yerleştiriliyor. Bu iki kütleyi birleştiren doğru parçası üzerine bir test parçacığı yerleştirilecektir. Bu test parçacığı ile 64 kg kütleli cisim arasındaki uzaklık \( x \) metre olmak üzere, test parçacığına etki eden net çekim kuvvetinin büyüklüğü aşağıdaki formülle modelleniyor.
\( f(x) = \abs{\dfrac{64}{x^2} - \dfrac{1}{(9 - x)^2}} \)
Parçacığa uygulanan net çekim kuvvetinin büyüklüğünün en az ve en çok olduğu \( x \) değerleri nedir?
Çözümü GösterAdım 1: Problem tanımı
\( x \): Parçacığın 64 kg kütleli cisme olan uzaklığı
Problemde parçacığa uygulanan net çekim kuvvetinin büyüklüğünün en az ve en çok olduğu değerler için parçacığın konumu istenmektedir.
Adım 2: Amaç fonksiyonu
Uzaklık pozitif bir büyüklüktür.
\( x \in \mathbb{R^+} \)
Test parçacığının 64 kg kütleli cisme olan uzaklığı, iki cismin arasındaki mesafeden küçük olmalıdır.
\( x \lt 9 \)
Mutlak değer fonksiyonunu parçalı fonksiyon şeklinde yazalım.
Fonksiyonun kritik noktalarını bulmak için mutlak değer ifadesinin içini sıfıra eşitleyelim.
\( \dfrac{64}{x^2} - \dfrac{1}{(9 - x)^2} = 0 \)
\( \dfrac{64}{x^2} = \dfrac{1}{(9 - x)^2} \)
Eşitliğin taraflarını karekök içine alalım.
\( \sqrt{\dfrac{64}{x^2}} = \sqrt{\dfrac{1}{(9 - x)^2}} \)
\( \dfrac{8}{x} = \dfrac{1}{9 - x} \)
\( x = 8 \)
\( f(x) = \begin{cases} \dfrac{64}{x^2} - \dfrac{1}{(9 - x)^2} & 0 \lt x \lt 8 \\ \dfrac{1}{(9 - x)^2} - \dfrac{64}{x^2} & 8 \le x \lt 9 \end{cases} \)
Buna göre en küçük ve en büyük değerini bulmak istediğimiz amaç fonksiyonu aşağıdaki şekilde tanımlanır.
\( f: (0, 9) \to [0, \infty) \)
\( f(x) = \begin{cases} \dfrac{64}{x^2} - \dfrac{1}{(9 - x)^2} & 0 \lt x \lt 8 \\ \dfrac{1}{(9 - x)^2} - \dfrac{64}{x^2} & 8 \le x \lt 9 \end{cases} \)
Adım 3: Problem çözümü
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
\( f \) parçalı fonksiyonunun \( x = 8 \) geçiş noktasında sürekli olup olmadığını bulalım.
\( x = 8 \) noktasındaki soldan limiti bulalım.
\( \lim\limits_{x \to 8^-} \left( \dfrac{64}{x^2} - \dfrac{1}{(9 - x)^2} \right) = \dfrac{64}{8^2} - \dfrac{1}{(9 - 8)^2} = 0 \)
\( x = 8 \) noktasındaki sağdan limiti bulalım.
\( \lim\limits_{x \to 8^+} \left( \dfrac{1}{(9 - x)^2} - \dfrac{64}{x^2} \right) = \dfrac{1}{(9 - 8)^2} - \dfrac{64}{8^2} = 0 \)
\( x = 8 \) noktasındaki fonksiyon değerini bulalım.
\( f(8) = \dfrac{1}{(9 - 8)^2} - \dfrac{64}{8^2} = 0 \)
Buna göre bu noktada soldan ve sağdan limitler ve fonksiyon değeri birer reel sayı olarak tanımlı ve birbirine eşittir, dolayısıyla fonksiyon \( x = 8 \) noktasında süreklidir.
\( f(8^-) = f(8^+) = f(8) \)
Sürekliliğini gösterdiğimiz bu noktadaki türevlenebilirliği kontrol edelim.
Fonksiyonun \( x = 8 \) noktasındaki soldan türevini bulalım.
\( f'(x) = -\dfrac{128}{x^3} - \dfrac{2}{(9 - x)^3} \)
\( f'(8^-) = -\dfrac{128}{8^3} - \dfrac{2}{(9 - 8)^3} = -\dfrac{9}{4} \)
Fonksiyonun \( x = 8 \) noktasındaki sağdan türevini bulalım.
\( f'(x) = \dfrac{2}{(9 - x)^3} + \dfrac{128}{x^3} \)
\( f'(8^+) = \dfrac{2}{(9 - 8)^3} + \dfrac{128}{8^3} = \dfrac{9}{4} \)
Buna göre bu noktada soldan ve sağdan türevler birbirine eşit değildir, dolayısıyla fonksiyonun \( x = 8 \) noktasında türevi tanımsızdır.
\( f'(x) = \begin{cases} -\dfrac{128}{x^3} - \dfrac{2}{(9 - x)^3} & 0 \lt x \lt 8 \\ \text{Tanımsız} & x = 8 \\ \dfrac{2}{(9 - x)^3} + \dfrac{128}{x^3} & 8 \lt x \lt 9 \end{cases} \)
Fonksiyonun tanım kümesi içinde birinci türevinin sıfır olduğu iç noktaları bulalım.
\( 0 \lt x \lt 8 \) için:
\( -\dfrac{128}{x^3} - \dfrac{2}{(9 - x)^3} = 0 \)
\( -\dfrac{64}{x^3} = \dfrac{1}{(9 - x)^3} \)
Eşitliğin taraflarının küpkökünü alalım.
\( \sqrt[3]{-\dfrac{64}{x^3}} = \sqrt[3]{\dfrac{1}{(9 - x)^3}} \)
\( -\dfrac{4}{x} = \dfrac{1}{9 - x} \)
Fonksiyonun tanım aralığı içinde bu denklemi sağlayan bir \( x \) değeri yoktur.
\( 8 \lt x \lt 9 \) için:
\( \dfrac{2}{(9 - x)^3} + \dfrac{128}{x^3} = 0 \)
\( \dfrac{1}{(9 - x)^3} = -\dfrac{64}{x^3} \)
Eşitliğin taraflarının küpkökünü alalım.
\( \sqrt[3]{\dfrac{1}{(9 - x)^3}} = \sqrt[3]{-\dfrac{64}{x^3}} \)
\( \dfrac{1}{9 - x} = -\dfrac{4}{x} \)
Fonksiyonun tanım aralığı içinde bu denklemi sağlayan bir \( x \) değeri yoktur.
Fonksiyonun \( x = 8 \) noktasında birinci türevi tanımsızdır.
Kritik nokta: \( x = 8 \)
Fonksiyonun kritik noktadaki değerini bulalım.
\( f(8) = \dfrac{1}{(9 - 8)^2} - \dfrac{64}{8^2} = 0 \)
Fonksiyonun açık uç noktalarındaki limitini bulalım.
\( \lim\limits_{x \to 0^+} \left( \dfrac{64}{x^2} - \dfrac{1}{(9 - x)^2} \right) = \dfrac{64}{(0^+)^2} - \dfrac{1}{(9 - 0)^2} = \infty \)
\( \lim\limits_{x \to 9^-} \left( \dfrac{1}{(9 - x)^2} - \dfrac{64}{x^2} \right) = \dfrac{1}{(9 - 9^-)^2} - \dfrac{64}{9^2} = \infty \)
Buna göre amaç fonksiyonunun aldığı bir mutlak maksimum değer yoktur.
Bu değerleri karşılaştırdığımızda amaç fonksiyonunun tanım aralığındaki en küçük değeri olarak \( x = 8 \) noktasında aldığı \( 0 \) değeri bulunur.
Dolayısıyla parçacığa uygulanan net çekim kuvvetinin büyüklüğünün en az olması için parçacık, 64 kg kütleli cisimden 8 metre uzağa yerleştirilmelidir.
Amaç fonksiyonunun grafiği, bulduğumuz noktalar ve değerleri aşağıdaki şekilde gösterilmiştir.
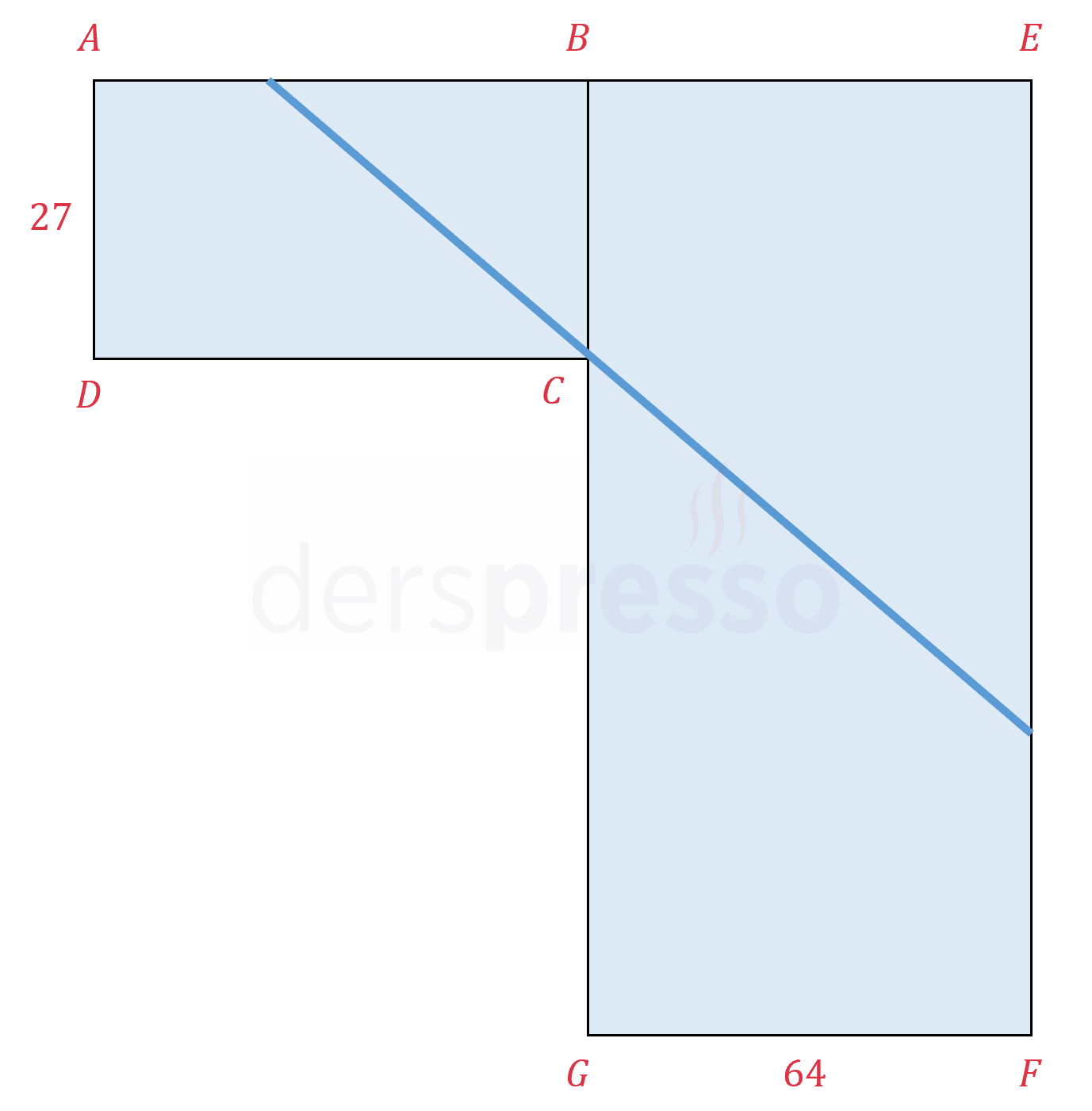
Genişlikleri sırasıyla 27 cm ve 64 cm olan \( ABCD \) ve \( BEFG \) dikdörtgenleri şekildeki gibi yerleştiriliyor.
Bir ucu \( [AB] \) kenarına, diğer ucu \( [EF] \) kenarına değen ve \( C \) noktasından geçen en kısa doğru parçasının uzunluğu kaçtır?
Çözümü GösterAdım 1: Problem tanımı
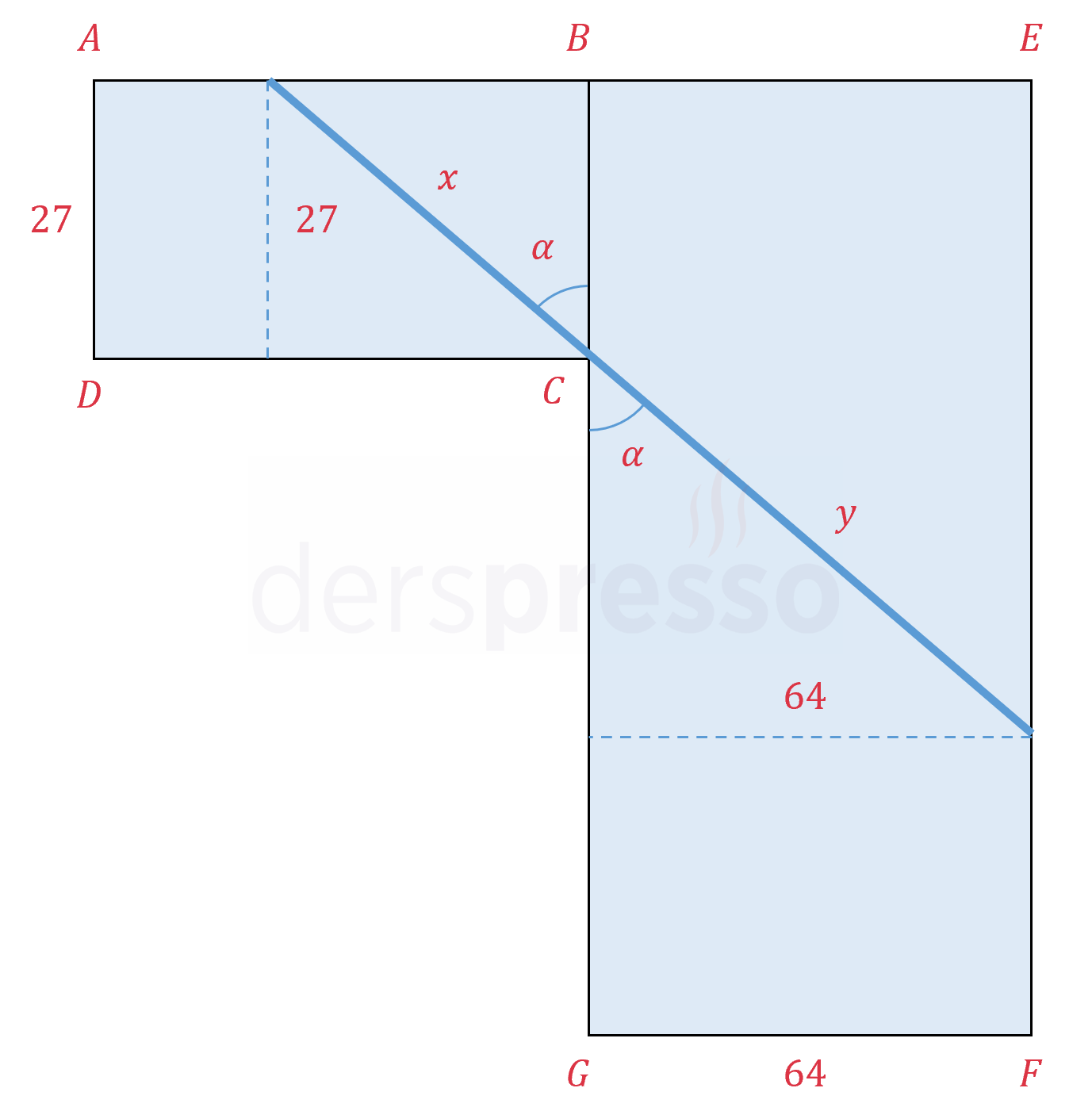
\( \alpha \): Doğru parçasının \( [BC] \) kenarı ile yaptığı açı
\( x \): Doğru parçasının \( ABCD \) dikdörtgeninin içerisinde kalan uzunluğu
\( y \): Doğru parçasının \( BEFG \) dikdörtgeninin içerisinde kalan uzunluğu
\( L \): Doğru parçasının uzunluğu
Problemde doğru parçasının uzunluğunun en küçük değeri istenmektedir.
Adım 2: Amaç fonksiyonu
Uzunluk ve açı pozitif büyüklüklerdir.
\( x, y, L, \alpha \in \mathbb{R^+} \)
Amaç fonksiyonunu tek bir değişken cinsinden yazabilmek için değişkenler arasında bir ilişki kurmaya çalışalım.
\( L \) uzunluğu \( x \) ve \( y \) uzunluklarının toplamına eşittir.
\( L = x + y \)
\( x \) ve \( y \) uzunluklarının trigonometrik eşitliklerini yazalım.
\( x = 27\sec{\alpha} \)
\( y = 64\csc{\alpha} \)
\( L = 27\sec{\alpha} + 64\csc{\alpha} \)
\( \alpha \) açısı dikdörtgenin kenarı ile doğru parçası arasındaki açıdır. Bu nedenle dikdörtgenin bir iç açısından küçüktür.
\( 0 \lt \alpha \lt \dfrac{\pi}{2} \)
Buna göre en küçük değerini bulmak istediğimiz amaç fonksiyonu aşağıdaki gibidir.
\( L: (0, \frac{\pi}{2}) \to \mathbb{R^+} \)
\( L(\alpha) = 27\sec{\alpha} + 64\csc{\alpha} \)
Adım 3: Problem çözümü
\( L \) fonksiyonu açık bir aralıkta tanımlıdır ve iki sürekli fonksiyonun toplamından oluştuğu için tanım kümesi içinde süreklidir.
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
\( L'(\alpha) = 27\tan{\alpha}\sec{\alpha} - 64\cot{\alpha}\csc{\alpha} \)
Fonksiyonun tanım kümesi içinde birinci türevinin sıfır olduğu iç noktaları bulalım.
\( 27\tan{\alpha}\sec{\alpha} - 64\cot{\alpha}\csc{\alpha} = 0 \)
\( 27\dfrac{\sin{\alpha}}{\cos{\alpha}} \cdot \dfrac{1}{\cos{\alpha}} = 64\dfrac{\cos{\alpha}}{\sin{\alpha}} \cdot \dfrac{1}{\sin{\alpha}} \)
\( \dfrac{\sin^3{\alpha}}{\cos^3{\alpha}} = \dfrac{64}{27} \)
\( \tan^3{\alpha} = \dfrac{64}{27} \)
\( \tan{\alpha} = \dfrac{4}{3} \)
\( \alpha = \arctan{\dfrac{4}{3}} \)
Fonksiyonun tanım kümesi içinde birinci türevinin tanımsız olduğu iç nokta yoktur.
Kritik nokta: \( \alpha = \arctan{\frac{4}{3}} \)
Fonksiyonun kritik noktadaki değerini bulalım.
\( \alpha = \arctan{\frac{4}{3}} \) için \( L \) değerini bulalım.
\( \tan{\alpha} = \frac{4}{3} \) değerini kullanarak bir dik üçgen yardımıyla \( \sec{\alpha} \) ve \( \csc{\alpha} \) değerlerini bulalım.

\( \sec{\alpha} = \dfrac{5}{3} \)
\( \csc{\alpha} = \dfrac{5}{4} \)
\( L(\alpha) = 27 \sec{\alpha} + 64 \csc{\alpha} \)
\( = 27 \cdot \dfrac{5}{3} + 64 \cdot \dfrac{5}{4} = 125 \)
Fonksiyonun açık uç noktalarındaki limitini bulalım.
\( \lim\limits_{x \to 0^+} (27 \sec{\alpha} + 64 \csc{\alpha}) = 27 \sec{0} + 64 \csc{0^+} \)
\( = 27 \dfrac{1}{\cos{0}} + 64 \dfrac{1}{\sin{0^+}} \)
\( = 27 \cdot 1 + 64 \dfrac{1}{0^+} = \infty \)
\( \lim\limits_{x \to \frac{\pi}{2}^-} (27 \sec{\alpha} + 64 \csc{\alpha}) = 27 \sec{\frac{\pi}{2}^-} + 64 \csc{\frac{\pi}{2}} \)
\( = 27 \dfrac{1}{\cos{\frac{\pi}{2}^-}} + 64 \dfrac{1}{\sin{\frac{\pi}{2}}} \)
\( = 27 \dfrac{1}{0^+} + 64 \cdot 1 = \infty \)
Bu değerleri karşılaştırdığımızda fonksiyonun tanım aralığındaki en küçük değeri olarak \( \alpha = \arctan{\frac{4}{3}} \) noktasında aldığı \( 125 \) cm değeri bulunur.
Amaç fonksiyonunun grafiği, bulduğumuz noktalar ve değerleri aşağıdaki şekilde gösterilmiştir.
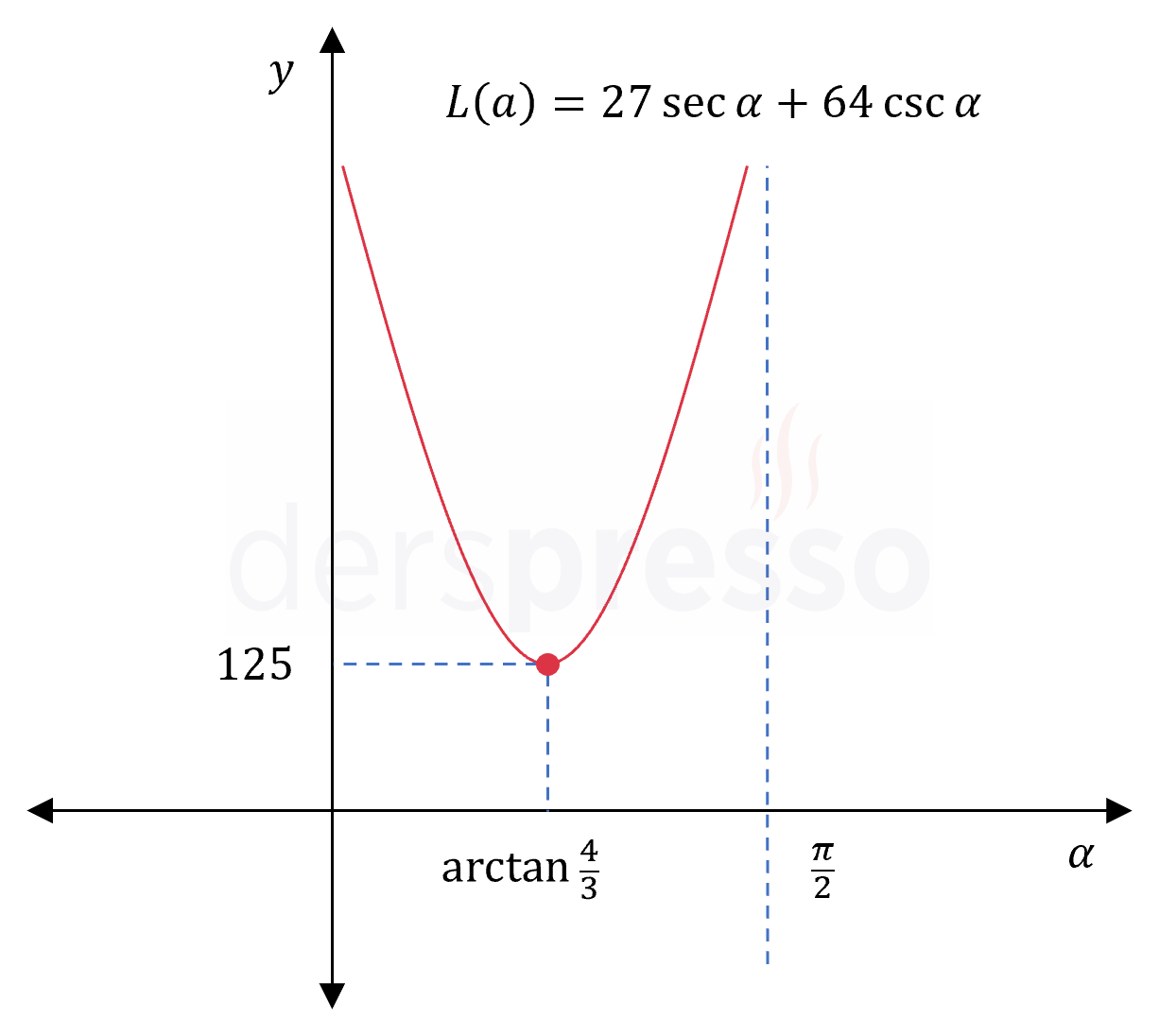
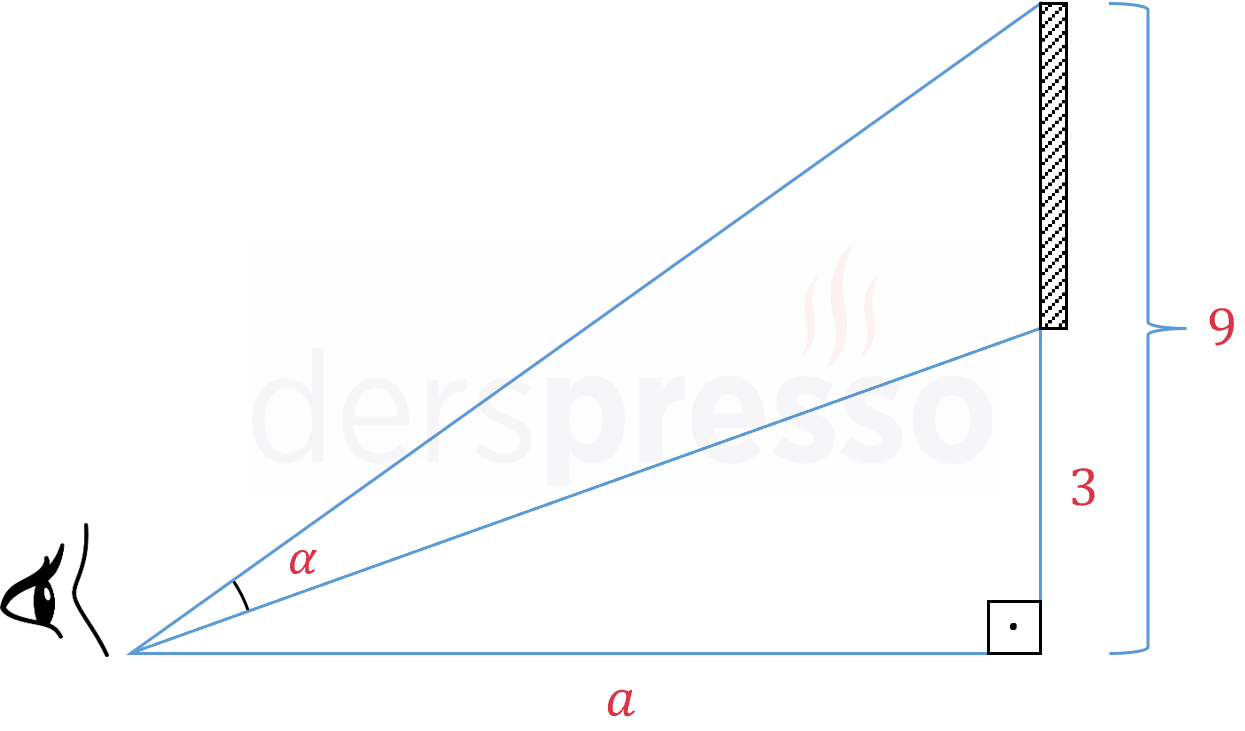
Bir sinema salonunda zemin seviyesinde oturan bir seyirci perdede oynayan filmi izlemektedir. Perdenin en alt noktası zeminden 3 metre, en üst noktası ise 9 metre yüksektedir.
Seyircinin perdeyi görüş açısı olan \( \alpha \) değerinin en büyük olması için, seyircinin perdenin bulunduğu duvara olan \( a \) uzaklığı kaç metre olmalıdır?
Çözümü GösterAdım 1: Problem tanımı
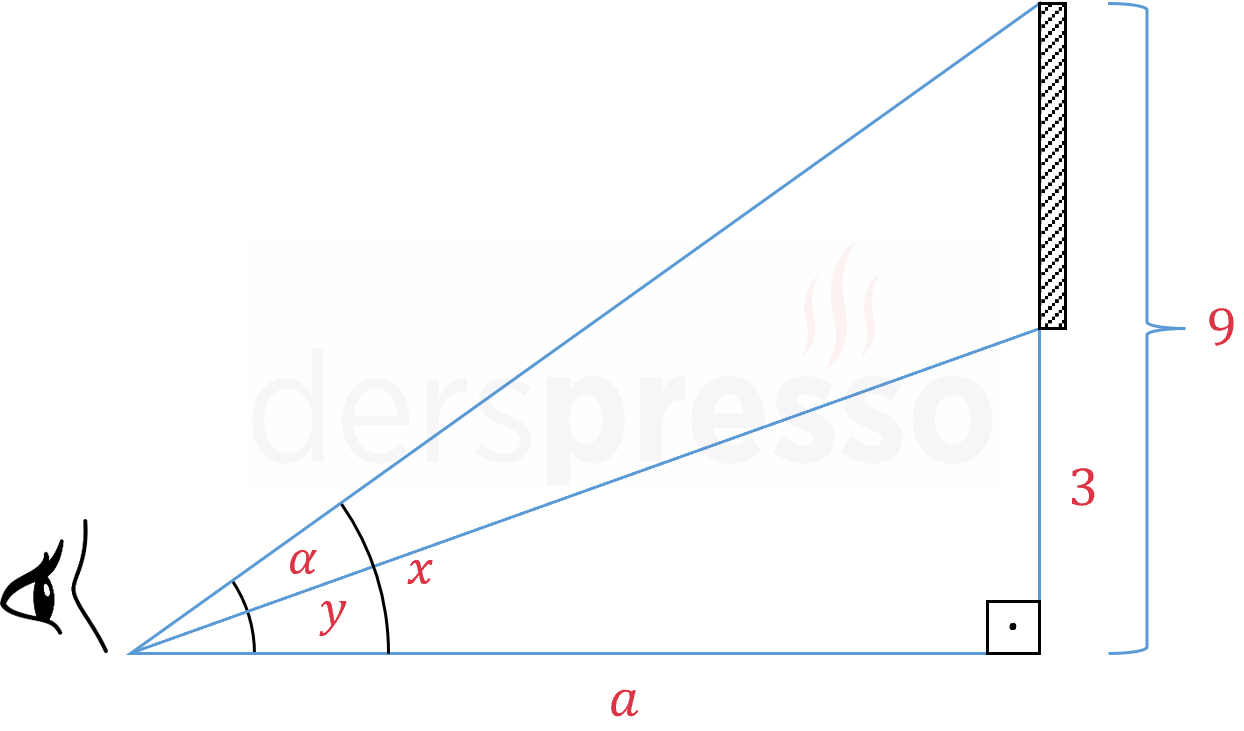
\( a \): Seyirci ile duvar arasındaki mesafe
\( x \): Perdenin en üst noktası ile zemin arasını gören açı
\( y \): Perdenin en alt noktası ile zemin arasını gören açı
\( \alpha \): Seyircinin perdeyi görüş açısı
Problemde \( \alpha \) açısını en büyük yapan \( a \) değeri istenmektedir.
Adım 2: Amaç fonksiyonu
Uzaklık ve açı pozitif büyüklüklerdir.
\( a, x, y, \alpha \in \mathbb{R^+} \)
Amaç fonksiyonunu tek bir değişken cinsinden yazabilmek için değişkenler arasında bir ilişki kurmaya çalışalım.
\( \alpha \) açısı \( x \) ve \( y \) açılarının farkına eşittir.
\( \alpha = x - y \)
Eşitliğin taraflarının tanjantını alalım.
\( \tan{\alpha} = \tan(x - y) \)
Tanjant fark formülünü kullanalım.
\( \tan{\alpha} = \dfrac{\tan{x} - \tan{y}}{1 + \tan{x}\tan{y}} \)
\( \tan{x} = \dfrac{9}{a}, \quad \tan{y} = \dfrac{3}{a} \)
\( \tan{\alpha} = \dfrac{\frac{9}{a} - \frac{3}{a}}{1 + \frac{9}{a} \cdot \frac{3}{a}} \)
\( \tan{\alpha} = \dfrac{6a}{a^2 + 27} \)
Bu eşitlikte \( \alpha \) açısını yalnız bıraktığımızda sadece \( a \) değişkenine bağlı olan amaç fonksiyonunu elde ederiz.
\( \alpha(a) = \arctan{\dfrac{6a}{a^2 + 27}} \)
\( a \) herhangi bir pozitif reel sayı değeri alabilir.
Buna göre en büyük değerini bulmak istediğimiz amaç fonksiyonu aşağıdaki gibidir.
\( \alpha: (0, \infty) \to \mathbb{R^+} \)
\( \alpha(a) = \arctan{\dfrac{6a}{a^2 + 27}} \)
Adım 3: Problem çözümü
\( \alpha \) fonksiyonu açık bir aralıkta tanımlıdır ve arctan fonksiyonu tüm reel sayılarda süreklidir.
Fonksiyonun kritik noktaları birinci türevin sıfır ya da tanımsız olduğu iç noktalardır.
\( \alpha'(a) = \left( \arctan{\dfrac{6a}{a^2 + 27}} \right)' \)
\( \arctan{x} \) fonksiyonunun türevini hatırlayalım.
\( (\arctan{x})' = \dfrac{1}{1 + x^2} \)
\( \alpha'(a) = \dfrac{1}{1 + (\frac{6a}{a^2 + 27})^2} \cdot \left( \dfrac{6a}{a^2 + 27} \right)' \)
Türev bölme kuralını kullanalım.
\( \alpha'(a) = \dfrac{1}{1 + (\frac{6a}{a^2 + 27})^2} \cdot \dfrac{6(a^2 + 27) - 6a \cdot 2a}{(a^2 + 27)^2} \)
\( \alpha'(a) = \dfrac{1}{1 + (\frac{6a}{a^2 + 27})^2} \cdot \dfrac{6(27 - a^2)}{(a^2 + 27)^2} \)
\( \alpha'(a) = \dfrac{1}{1 + (\frac{6a}{a^2 + 27})^2} \cdot \dfrac{6(3\sqrt{3} - a)(3\sqrt{3} + a)}{(a^2 + 27)^2} \)
Fonksiyonun tanım aralığı içinde birinci türevinin sıfır olduğu iç noktaları bulalım.
Paydadaki ifadeler her \( a \) değeri için pozitif olduğu için payı sıfıra eşitleyebiliriz.
\( 6(3\sqrt{3} - a)(3\sqrt{3} + a) = 0 \)
\( a = 3\sqrt{3} \)
Fonksiyonun birinci türevinin tanımsız olduğu iç nokta yoktur.
Kritik nokta: \( a = 3\sqrt{3} \)
Fonksiyonun kritik noktadaki değerini bulalım.
\( \alpha(3\sqrt{3}) = \arctan{\dfrac{6(3\sqrt{3})}{(3\sqrt{3})^2 + 27}} \)
\( = \arctan{\dfrac{\sqrt{3}}{3}} = \dfrac{\pi}{6} \)
Fonksiyonun açık uç noktalarındaki limitini bulalım.
\( \lim\limits_{x \to 0^+} {\arctan{\dfrac{6a}{a^2 + 27}}} = \arctan{\dfrac{6(0)}{0^2 + 27}} \)
\( = \arctan{0} = 0 \)
\( \lim\limits_{x \to \infty} {\arctan{\dfrac{6a}{a^2 + 27}}} = \arctan{0} = 0 \)
Buna göre fonksiyon açık uç noktaları civarında \( \frac{\pi}{6} \) değerinden daha büyük bir değer almaz.
Bu değerleri karşılaştırdığımızda fonksiyonun tanım aralığındaki en büyük değeri olarak \( a = 3\sqrt{3} \) noktasında aldığı \( \frac{\pi}{6} \) değeri bulunur.
Amaç fonksiyonunun grafiği, bulduğumuz noktalar ve değerleri aşağıdaki şekilde gösterilmiştir.