Türevin Tanımı
Konu tekrarı için: Limit Tanımı | Anlık Değişim Oranı
Bir fonksiyonun belirli bir noktadaki anlık değişim oranına fonksiyonun o noktadaki türevi denir. Önceki bölümde gördüğümüz üzere, bir noktadaki türevin tanımı fonksiyona o noktada teğet olan doğrunun eğimini veren limit ifadesine dayanır.
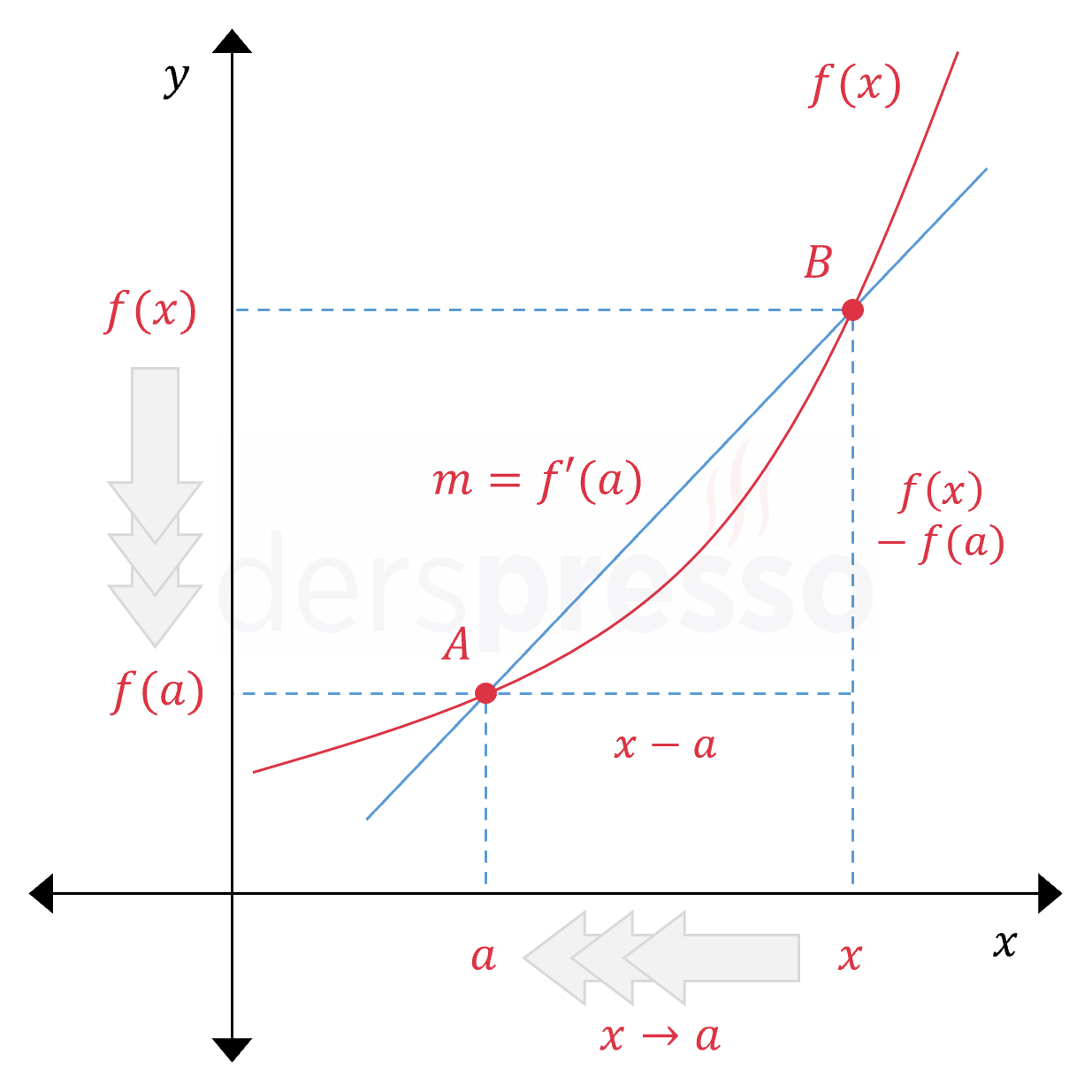
\( x = a \) noktası \( f \) fonksiyonunun tanım kümesi içindeki bir açık aralıkta bir nokta olmak üzere,
\( \lim\limits_{x \to a} \dfrac{f(x) - f(a)}{x - a} = L \)
limiti bir reel sayı olarak tanımlı ise bu limit değerine fonksiyonun \( x = a \) noktasındaki türevi denir ve \( f'(a) \) ile gösterilir.
\( f'(a) = L \)
\( f(x) = \sqrt{2x - 3} \) fonksiyonunun \( x = 2 \) noktasındaki türev değerini veren limit ifadesi:
\( f'(2) = \lim\limits_{x \to 2} \dfrac{f(x) - f(2)}{x - 2} \)
\( = \lim\limits_{x \to 2} \dfrac{\sqrt{2x - 3} - \sqrt{2(2) - 3}}{x - 2} \)
\( = \lim\limits_{x \to 2} \dfrac{\sqrt{2x - 3} - 1}{x - 2} \)
Bir fonksiyon için belirli bir noktada yukarıdaki limit bir reel sayı olarak tanımlı ise fonksiyonun bu noktada türevlenebilir olduğunu, aksi takdirde türevlenebilir olmadığını söyleriz.
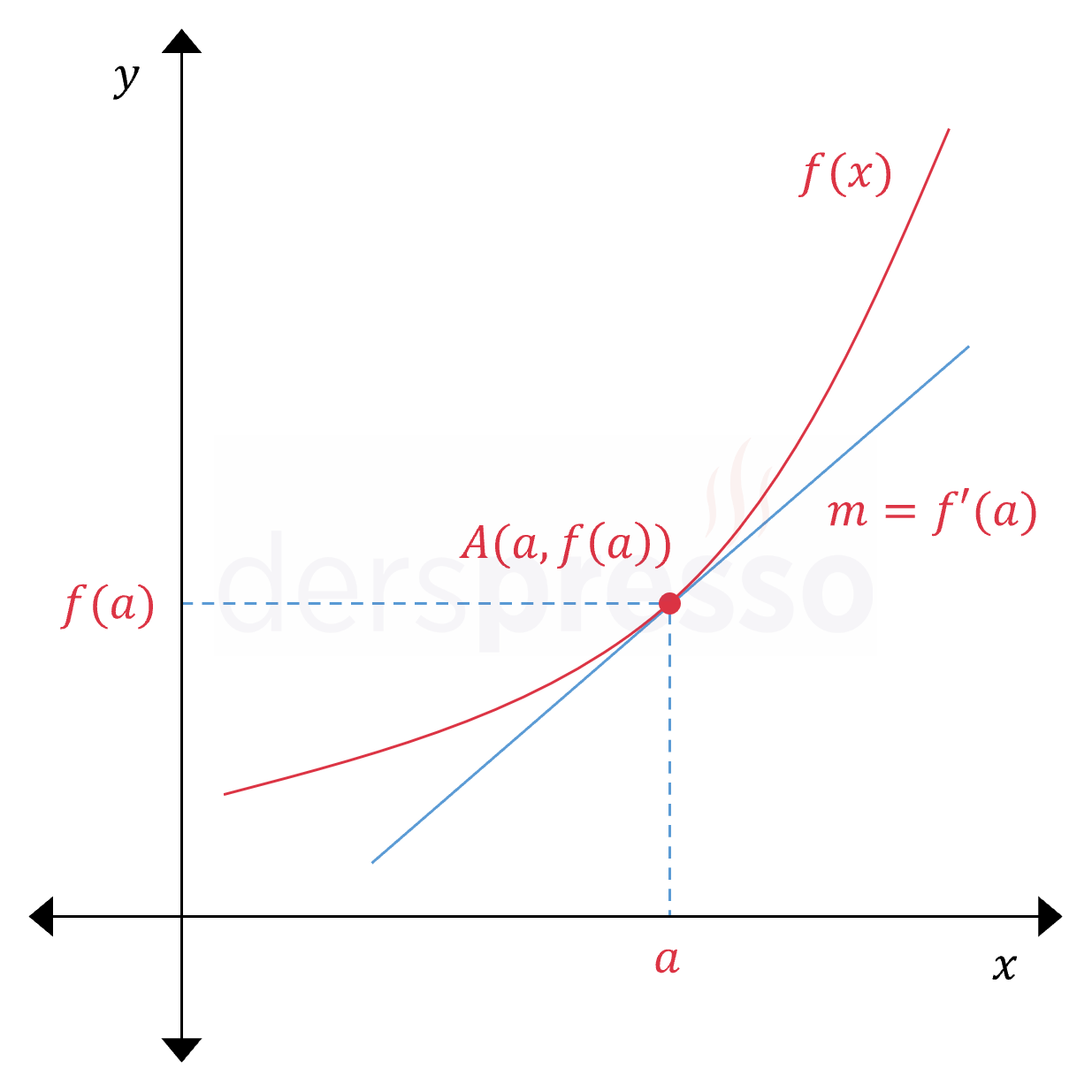
Bir fonksiyonun belirli bir noktadaki türev değeri, fonksiyon grafiğine o noktada çizilen teğet doğrunun eğimine eşittir. Buna göre \( f \) fonksiyonunun grafiğine \( (a, f(a)) \) noktasında çizilen teğet doğrunun eğimi \( f'(a) \) olur.
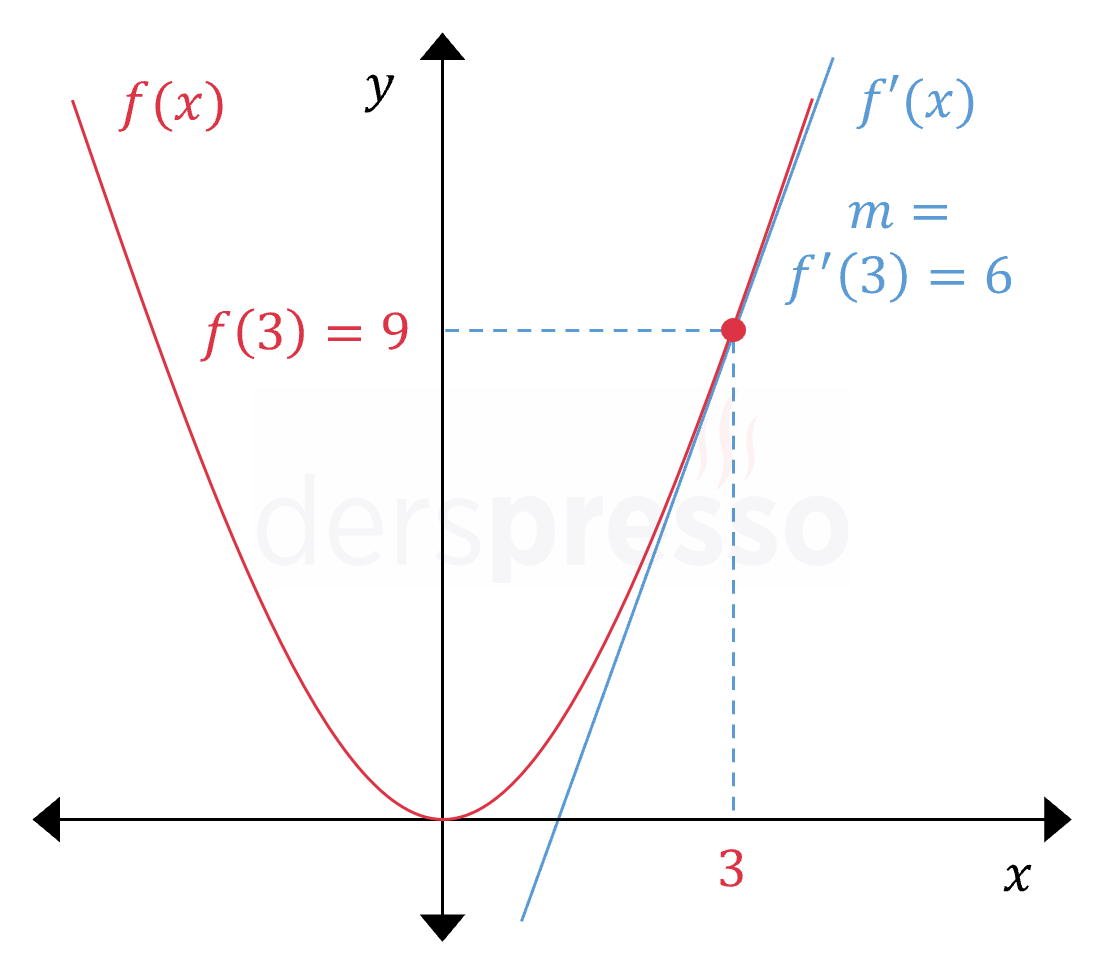
\( f(x) = x^2 \) fonksiyonunun \( x = 3 \) noktasındaki türev değerini türevin limit tanımını kullanarak bulalım.
\( x = 3 \) noktasındaki teğet doğru parabolü \( (3, f(3)) = (3, 9) \) noktasında keser.
Teğet doğrunun eğimini türevin limit tanımını kullanarak bulalım.
\( f'(3) = \lim\limits_{x \to 3} \dfrac{x^2 - 3^2}{x - 3} \)
\( = \lim\limits_{x \to 3} \dfrac{(x - 3)(x + 3)}{x - 3} \)
\( = \lim\limits_{x \to 3} (x + 3) = 3 + 3 = 6 \)
Yukarıdaki örnekteki \( f \) fonksiyon grafiğine \( x = 3 \) noktasında çizilen teğet doğrunun denklemini bulalım.
Bir noktası ve eğimi bilinen doğru denklemini kullanalım.
\( y - y_0 = m(x - x_0) \)
Teğet doğru \( (x_0, y_0) = (3, f(3)) \) noktasından geçer ve eğimi \( m = f'(3) \) olur.
\( y - f(3) = f'(3)(x - 3) \)
\( y - 9 = 6(x - 3) \)
\( y = 6x - 9 \)
\( f \) fonksiyonunun ve teğet doğrunun grafikleri aşağıdaki gibidir.
Türevin limit tanımında \( x \)'in \( a \)'ya yaklaşması, \( x \) ve \( a \) arasındaki uzaklığın sıfıra yaklaşması şeklinde de yorumlanabilir. Tanımda \( h \) sıfıra yaklaşacak şekilde \( h = x - a \) dönüşümü yapıldığında türevin daha sık kullanılan ikinci limit tanımı elde edilir.
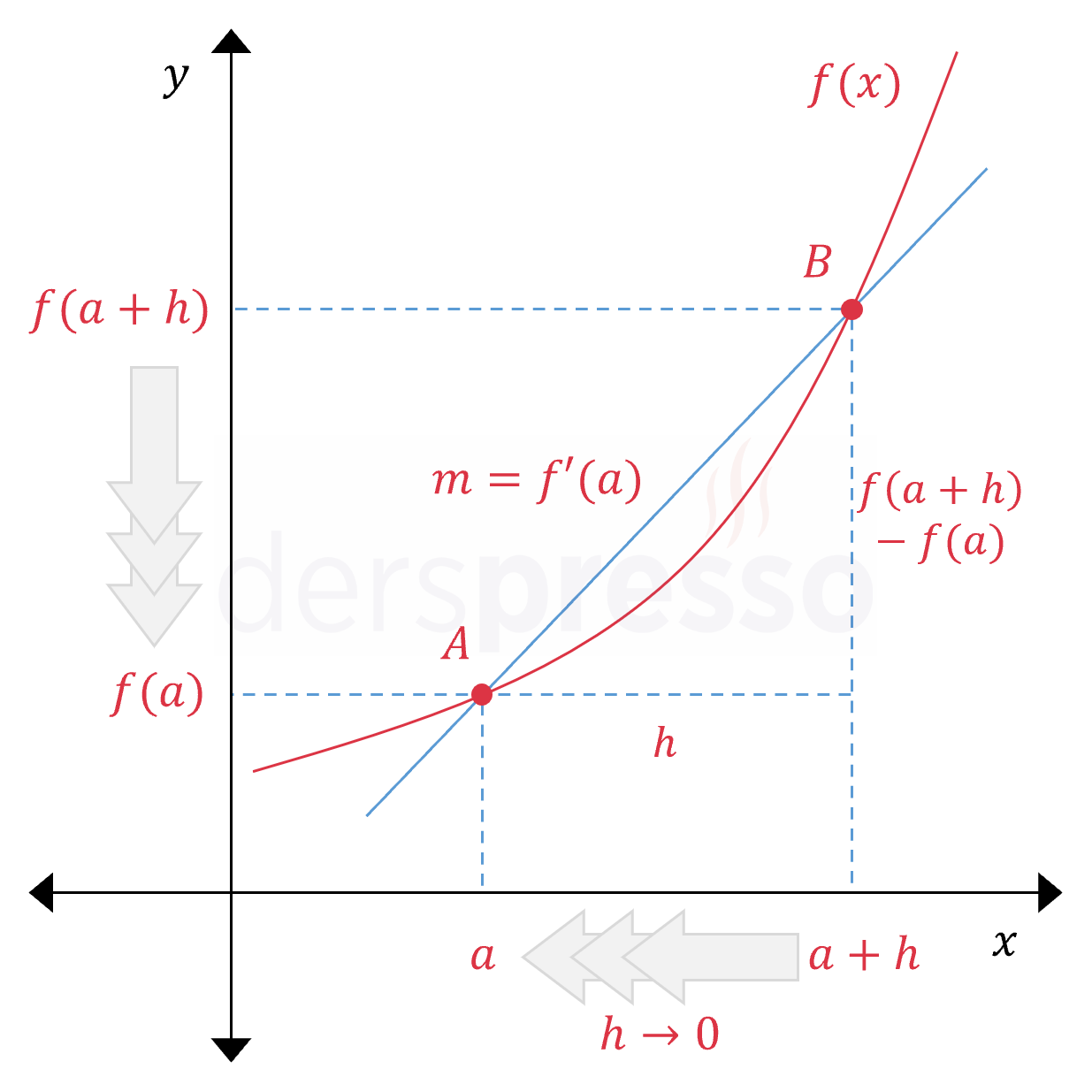
\( f'(a) = \lim\limits_{x \to a} \dfrac{f(x) - f(a)}{x - a} \)
\( h = x - a \) dönüşümü yapalım.
\( x \to a \) iken \( h = x - a \to 0 \) olur.
\( f'(a) = \lim\limits_{h \to 0} \dfrac{f(a + h) - f(a)}{h} \)
\( f(x) = e^{3x} \) fonksiyonunun \( x = 1 \) noktasındaki türev değerini veren limit ifadesi:
\( f'(1) = \lim\limits_{h \to 0} \dfrac{f(1 + h) - f(1)}{h} \)
\( = \lim\limits_{h \to 0} \dfrac{e^{3(1 + h)} - e^{3}}{h} \)
\( f(x) = x^4 - 2x + 3 \) için \( x = 2 \) noktasındaki türev değerini türevin limit tanımını kullanarak hesaplayın.
Çözümü GösterBir noktadaki türevin limit tanımını yazalım.
\( f'(a) = \lim\limits_{h \to 0} \dfrac{f(a + h) - f(a)}{h} \)
\( f'(2) = \lim\limits_{h \to 0} \dfrac{f(2 + h) - f(2)}{h} \)
Paydaki ifadeyi bulalım.
\( f(2 + h) - f(2) = (2 + h)^4 - 2(2 + h) + 3 - (2^4 - 2(2) + 3) \)
\( = 2^4 + 4(2)^3h + 6(2)^2h^2 + 4(2)h^3 + h^4 - 4 - 2h + 3 - 16 + 4 - 3 \)
\( = 16 + 32h + 24h^2 + 8h^3 + h^4 - 2h - 16 \)
\( = h^4 + 8h^3 + 24h^2 + 30h \)
Bu ifadeyi türevin limit tanımında yerine koyalım.
\( f'(2) = \lim\limits_{h \to 0} \dfrac{h^4 + 8h^3 + 24h^2 + 30h}{h} \)
\( = \lim\limits_{h \to 0} (h^3 + 8h^2 + 24h + 30) \)
Limiti alınan polinom ifadesi tüm reel sayılarda sürekli olduğu için doğrudan yerine koyma yöntemi ile limitini bulabiliriz.
\( = 0^3 + 8(0)^2 + 24(0) + 30 = 30 \) bulunur.
Türev Fonksiyonu
Yukarıda paylaştığımız iki limit tanımı kullanılarak bir fonksiyonun belirli bir noktadaki türev değeri bulunabilir. Bu tanımda \( a \) yerine \( x \) yazıldığında, fonksiyonun herhangi bir noktadaki türev değerini veren türev fonksiyonu elde edilir.
\( f'(x) = \lim\limits_{h \to 0} \dfrac{f(x + h) - f(x)}{h} \)
Bir fonksiyonun türevi de bir fonksiyondur ve bir noktadaki değeri ana fonksiyonun grafiğine o noktada çizilen teğet doğrunun eğimini verir.
Türev Fonksiyonunun Tanım Kümesi
Türev fonksiyonunun tanım kümesi, ana fonksiyonun tanım kümesi içinde türev tanımındaki limitin tanımlı olduğu noktalar kümesidir, dolayısıyla türev fonksiyonunun tanım kümesi ana fonksiyonun tanım kümesinin bir alt kümesidir.
\( f \) ve \( f' \) fonksiyonlarının tanım kümeleri sırasıyla \( A_1 \) ve \( A_2 \) ise,
\( A_2 \subseteq A_1 \)
\( f(x) = x^2 - 2x + 3 \) için türev fonksiyonunu ve \( f'(-2) \), \( f'(1) \) ve \( f'(3) \) türev değerlerini türevin limit tanımını kullanarak bulalım.
Türev fonksiyonunun limit tanımını yazalım.
\( f'(x) = \lim\limits_{h \to 0} \dfrac{f(x + h) - f(x)}{h} \)
Paydaki ifadeyi bulalım.
\( f(x + h) - f(x) = (x + h)^2 \) \( - 2(x + h) + 3 \) \( - (x^2 - 2x + 3) \)
\( = x^2 + 2xh + h^2 \) \( - 2x - 2h + 3 \) \( - x^2 + 2x - 3 \)
\( = 2xh + h^2 - 2h \)
Bu ifadeyi türevin limit tanımında yerine koyalım.
\( f'(x) = \lim\limits_{h \to 0} \dfrac{2xh + h^2 - 2h}{h} \)
\( = \lim\limits_{h \to 0} (2x + h - 2) \)
Limit toplama kuralı ile limiti terimlere dağıtabiliriz.
\( = \lim\limits_{h \to 0} (2x) + \lim\limits_{h \to 0} {h} - \lim\limits_{h \to 0} {2} \)
Bu limit ifadelerinde \( x \) sabit terimdir.
\( = 2x + \lim\limits_{h \to 0} {h} - 2 \)
\( h \) sıfıra giderken \( h \) ifadesinin limiti sıfırdır.
\( = 2x - 2 \)
Buna göre \( f \) fonksiyonunun türev fonksiyonu \( f'(x) = 2x - 2 \) olur.
Bu fonksiyonu kullanarak istenen noktalardaki türev değerini bulalım.
\( f'(-2) = 2(-2) - 2 = -6 \)
\( f'(1) = 2(1) - 2 = 0 \)
\( f'(3) = 2(3) - 2 = 4 \)
\( f \) fonksiyonunun grafiği, verilen noktalarda çizilen teğet doğrular ve eğimleri aşağıdaki şekilde gösterilmiştir.
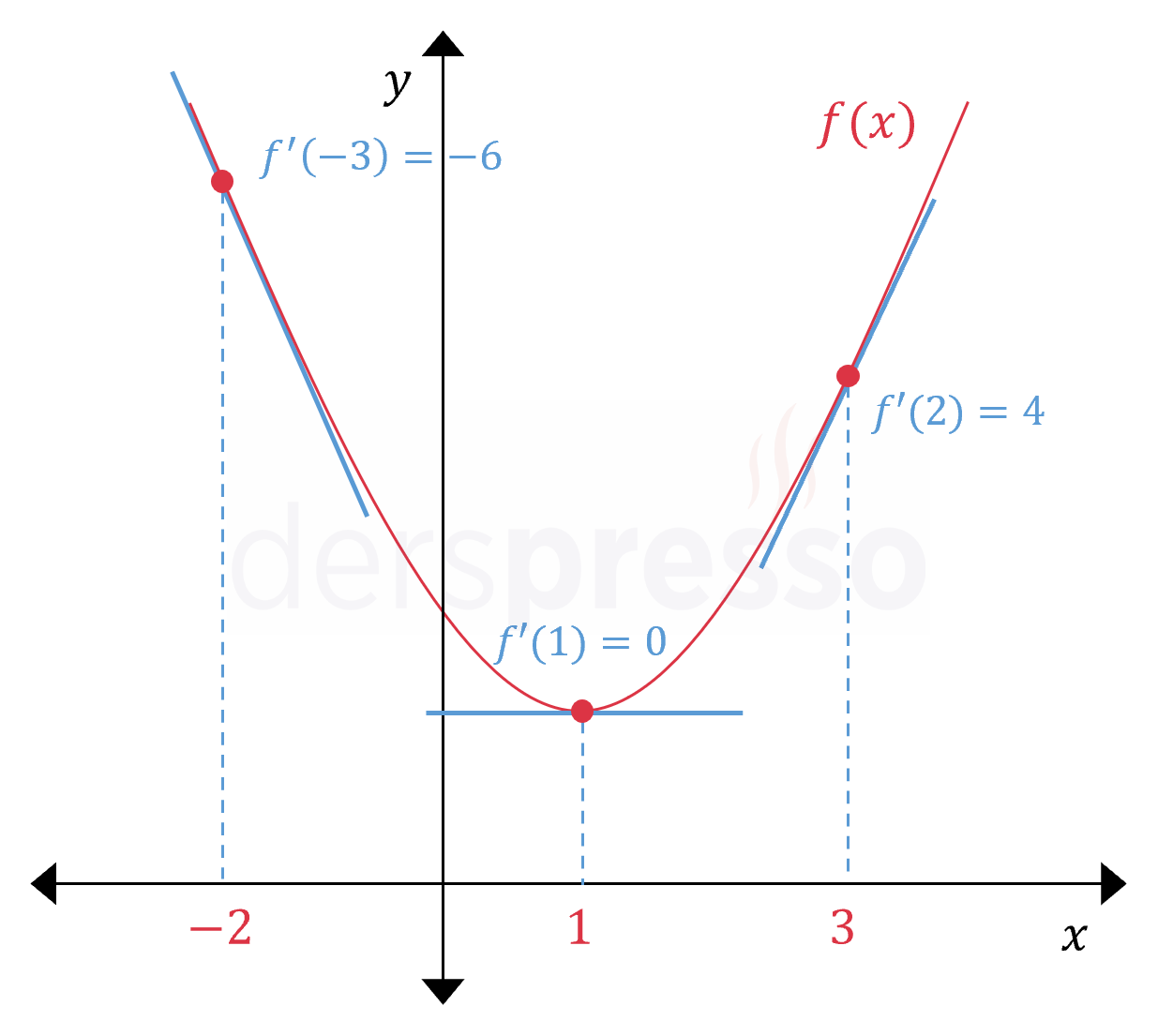
Verilen üç noktada da türev birer reel sayı olarak tanımlı olduğu için fonksiyon bu üç noktada türevlenebilirdir.
\( f(x) = x^3 + 2x \) için türev fonksiyonunu türevin limit tanımını kullanarak bulun.
Çözümü GösterTürev fonksiyonunun limit tanımını yazalım.
\( f'(x) = \lim\limits_{h \to 0} \dfrac{f(x + h) - f(x)}{h} \)
Paydaki ifadeyi bulalım.
\( f(x + h) - f(x) = (x + h)^3 + 2(x + h) - (x^3 + 2x) \)
\( = x^3 + 3x^2h + 3xh^2 + h^3 + 2x + 2h - x^3 - 2x \)
\( = 3x^2h + 3xh^2 + h^3 + 2h \)
Bu ifadeyi türevin limit tanımında yerine koyalım.
\( f'(x) = \lim\limits_{h \to 0} \dfrac{3x^2h + 3xh^2 + h^3 + 2h}{h} \)
\( = \lim\limits_{h \to 0} (3x^2 + 3xh + h^2 + 2) \)
Limit toplama kuralı ile limiti terimlere dağıtabiliriz.
\( = \lim\limits_{h \to 0} (3x^2) + \lim\limits_{h \to 0} (3xh) + \lim\limits_{h \to 0} {h^2} + \lim\limits_{h \to 0} {2} \)
Bu limit ifadelerinde \( x \) sabit terimdir.
\( = 3x^2 + 3x\lim\limits_{h \to 0} {h} + \lim\limits_{h \to 0} {h^2} + 2 \)
\( h \) sıfıra giderken \( h \) ve \( h^2 \) ifadelerinin limiti sıfırdır.
\( = 3x^2 + 2 \) bulunur.
Türevin Gösterimleri
Aşağıdaki gösterimlerin tümü \( y = f(x) \) fonksiyonunun türevi için kullanılabilir.
\( y' = f'(x) = \dfrac{dy}{dx} = \dfrac{df(x)}{dx} \) \( = \dfrac{d}{dx}(f(x)) \)
\( \frac{dy}{dx} \) gösterimindeki \( d \) sembolü bir değişken değildir ve pay ve paydaki \( d \)'ler birbirini götürmez. Ortalama değişim oranını hesaplarken kullandığımız \( \Delta y \) ve \( \Delta x \) ifadeleri belirli bir aralıkta \( y \) ve \( x \) değişkenlerindeki değişimi ifade ederken, \( dy \) ve \( dx \) ifadeleri bu aralık sıfıra yaklaşırkenki değişimleri ifade eder.
\( \dfrac{dy}{dx} = \lim\limits_{\Delta x \to 0} \dfrac{\Delta y}{\Delta x} \)
Bir ifadenin türevi aşağıdaki şekillerde de gösterilebilir.
\( (x^3 + 2x)' = \dfrac{d}{dx}(x^3 + 2x) \)
Türev her zaman belirli bir değişkene göre alınır. Bir fonksiyonda türevin hangi değişkene göre alındığı açık ise \( y' \) gösterimi kullanılabilir, aksi takdirde \( \frac{dy}{dx} \) gösterimi ile türevin hangi değişkene göre alındığı belirtilmelidir.
\( y = tx^2 - 5tx \) ise,
\( \dfrac{dy}{dx} \): \( x \) değişkenine göre türev
\( \dfrac{dy}{dt} \): \( t \) değişkenine göre türev
Bir fonksiyonun bir \( x = a \) noktasındaki türev değeri aşağıdaki şekillerde gösterilebilir.
\( f'(a) = \dfrac{dy}{dx} |_{x = a} \)
Soldan ve Sağdan Türev
Limit ve süreklilikte olduğu gibi, bir fonksiyonun bir noktada soldan ve sağdan türevleri de tanımlanabilir.
\( \lim\limits_{h \to 0^-} \dfrac{f(a + h) - f(a)}{h} = L_1 \)
limiti bir reel sayı olarak tanımlı ise bu limit değerine fonksiyonun \( x = a \) noktasındaki soldan türevi denir ve \( f'(a^-) \) ile gösterilir.
\( f'(a^-) = L_1 \)
\( \lim\limits_{h \to 0^+} \dfrac{f(a + h) - f(a)}{h} = L_2 \)
limiti bir reel sayı olarak tanımlı ise bu limit değerine fonksiyonun \( x = a \) noktasındaki sağdan türevi denir ve \( f'(a^+) \) ile gösterilir.
\( f'(a^+) = L_2 \)
Bir fonksiyon için belirli bir noktada yukarıdaki soldan limit bir reel sayı olarak tanımlı ise fonksiyonun bu noktada soldan türevlenebilir olduğunu, aksi takdirde soldan türevlenebilir olmadığını söyleriz.
Benzer şekilde, bir fonksiyon için belirli bir noktada yukarıdaki sağdan limit bir reel sayı olarak tanımlı ise fonksiyonun bu noktada sağdan türevlenebilir olduğunu, aksi takdirde sağdan türevlenebilir olmadığını söyleriz.
Bir fonksiyonun \( x = a \) noktasındaki soldan (sağdan) türev değeri, bu nokta ile solundaki (sağındaki) ikinci bir noktayı birleştiren kesen doğrunun eğiminin, iki nokta arasındaki uzaklık sıfıra giderken yaklaştığı değeri ifade eder.
\( f(x) = \abs{x} \) fonksiyonunun \( x = 0 \) noktasındaki soldan ve sağdan türev değerlerini bulalım.
Fonksiyon grafiği aşağıdaki gibidir.
Soldan türevi bulalım.
\( f'(0^-) = \lim\limits_{h \to 0^-} \dfrac{f(0 + h) - f(0)}{h} \)
\( = \lim\limits_{h \to 0^-} \dfrac{\abs{0 + h} - \abs{0}}{h} \)
\( h \to 0^- \) iken \( \abs{0 + h} \) ifadesi negatif olur.
\( = \lim\limits_{h \to 0^-} \dfrac{-h - 0}{h} = -1 \)
Sağdan türevi bulalım.
\( f'(0^+) = \lim\limits_{h \to 0^+} \dfrac{f(0 + h) - f(0)}{h} \)
\( = \lim\limits_{h \to 0^+} \dfrac{\abs{0 + h} - \abs{0}}{h} \)
\( h \to 0^+ \) iken \( \abs{0 + h} \) ifadesi pozitif olur.
\( = \lim\limits_{h \to 0^+} \dfrac{h - 0}{h} = 1 \)
Soldan ve sağdan türevler birer reel sayı olarak tanımlı olduğu için fonksiyon bu noktada hem soldan hem de sağdan türevlenebilirdir.
Ancak önümüzdeki bölümde göreceğimiz üzere, soldan ve sağdan türev değerleri tanımlı olsa da birbirine eşit olmadığı için fonksiyon bu noktada türevlenebilir değildir.
\( f(x) = 5x^2 + 4x + 17 \) için türev fonksiyonunu türevin limit tanımını kullanarak bulun.
Çözümü GösterTürev fonksiyonunun limit tanımını yazalım.
\( f'(x) = \lim\limits_{h \to 0} \dfrac{f(x + h) - f(x)}{h} \)
Paydaki ifadeyi bulalım.
\( f(x + h) - f(x) = 5(x + h)^2 + 4(x + h) + 17 - (5x^2 + 4x + 17) \)
\( = 5x^2 + 10xh + 5h^2 + 4x + 4h + 17 - 5x^2 - 4x - 17 \)
\( = 10xh + 5h^2 + 4h \)
Bu ifadeyi türevin limit tanımında yerine koyalım.
\( f'(x) = \lim\limits_{h \to 0} \dfrac{10xh + 5h^2 + 4h}{h} \)
\( = \lim\limits_{h \to 0} (10x + 5h + 4) \)
Limit toplama kuralı ile limiti terimlere dağıtabiliriz.
\( = \lim\limits_{h \to 0} (10x) + \lim\limits_{h \to 0} (5h) + \lim\limits_{h \to 0} {4} \)
Birinci limit ifadesinde \( x \) sabit terimdir.
\( = 10x + 5\lim\limits_{h \to 0} {h} + 4 \)
\( h \) sıfıra giderken \( h \) ifadesinin limiti sıfırdır.
\( = 10x + 4 \) bulunur.
\( f(x) = x^3 - 2x^2 + 3x - 5 \) için türev fonksiyonunu türevin limit tanımını kullanarak bulun.
Çözümü GösterTürev fonksiyonunun limit tanımını yazalım.
\( f'(x) = \lim\limits_{h \to 0} \dfrac{f(x + h) - f(x)}{h} \)
Paydaki ifadeyi bulalım.
\( f(x + h) - f(x) = (x + h)^3 - 2(x + h)^2 + 3(x + h) - 5 - (x^3 - 2x^2 + 3x - 5) \)
\( = x^3 + 3x^2h + 3xh^2 + h^3 - 2x^2 - 4xh - 2h^2 + 3x + 3h - 5 - x^3 + 2x^2 - 3x + 5 \)
\( = 3x^2h + 3xh^2 + h^3 - 4xh - 2h^2 + 3h \)
Bu ifadeyi türevin limit tanımında yerine koyalım.
\( f'(x) = \lim\limits_{h \to 0} \dfrac{3x^2h + 3xh^2 + h^3 - 4xh - 2h^2 + 3h}{h} \)
\( = \lim\limits_{h \to 0} (3x^2 + 3xh + h^2 - 4x - 2h + 3) \)
Limit toplama kuralı ile limiti terimlere dağıtabiliriz.
\( = \lim\limits_{h \to 0} (3x^2) + \lim\limits_{h \to 0} (3xh) + \lim\limits_{h \to 0} {h^2} - \lim\limits_{h \to 0} (4x) - \lim\limits_{h \to 0} (2h) + \lim\limits_{h \to 0} {3} \)
Bu limit ifadelerinde \( x \) sabit terimdir.
\( = 3x^2 + 3x\lim\limits_{h \to 0} {h} + \lim\limits_{h \to 0} {h^2} - 4x - 2\lim\limits_{h \to 0} {h} + 3 \)
\( h \) sıfıra giderken \( h \) ve \( h^2 \) ifadelerinin limiti sıfırdır.
\( = 3x^2 - 4x + 3 \) bulunur.
\( f: \mathbb{R} - \{-4\} \to \mathbb{R} \) olmak üzere,
\( f(x) = \dfrac{x - 4}{x + 4} \) için türev fonksiyonunu türevin limit tanımını kullanarak bulun.
Çözümü GösterTürev fonksiyonunun limit tanımını yazalım.
\( f'(x) = \lim\limits_{h \to 0} \dfrac{f(x + h) - f(x)}{h} \)
Paydaki ifadeyi bulalım.
\( f(x + h) - f(x) = \dfrac{x + h - 4}{x + h + 4} - \dfrac{x - 4}{x + 4} \)
\( = \dfrac{(x + h - 4)(x + 4) - (x - 4)(x + h + 4)}{(x + h + 4)(x + 4)} \)
\( = \dfrac{[(x - 4)(x + 4) + h(x + 4)] - [(x - 4)(x + 4) + h(x - 4)]}{(x + h + 4)(x + 4)} \)
\( = \dfrac{(x^2 - 16) + h(x + 4) - (x^2 - 16) - h(x - 4)}{(x + h + 4)(x + 4)} \)
\( = \dfrac{h(x + 4) - h(x - 4)}{(x + h + 4)(x + 4)} \)
\( = \dfrac{hx + 4h - hx + 4h}{(x + h + 4)(x + 4)} \)
\( = \dfrac{8h}{(x + h + 4)(x + 4)} \)
Bu ifadeyi türevin limit tanımında yerine koyalım.
\( f'(x) = \lim\limits_{h \to 0} \dfrac{\frac{8h}{(x + h + 4)(x + 4)}}{h} \)
\( = \lim\limits_{h \to 0} \dfrac{8}{(x + h + 4)(x + 4)} \)
Bu limit ifadesinde \( x \) sabit terimdir.
Limiti alınan rasyonel fonksiyon ifadesi paydayı sıfır yapan \( h \) değerleri hariç tüm reel sayılarda sürekli olduğu için doğrudan yerine koyma yöntemi ile limitini bulabiliriz.
\( = \dfrac{8}{(x + 0 + 4)(x + 4)} \)
\( = \dfrac{8}{(x + 4)^2} \) bulunur.
\( f(x) = \dfrac{1}{1 + x^2} \) için türev fonksiyonunu türevin limit tanımını kullanarak bulun.
Çözümü GösterTürev fonksiyonunun limit tanımını yazalım.
\( f'(x) = \lim\limits_{h \to 0} \dfrac{f(x + h) - f(x)}{h} \)
Paydaki ifadeyi bulalım.
\( f(x + h) - f(x) = \dfrac{1}{1 + (x + h)^2} - \dfrac{1}{1 + x^2} \)
\( = \dfrac{1 + x^2 - 1 - (x + h)^2}{(1 + (x + h)^2)(1 + x^2)} \)
\( = \dfrac{x^2 - (x^2 + 2xh + h^2)}{(1 + (x + h)^2)(1 + x^2)} \)
\( = \dfrac{-2xh - h^2}{(1 + (x + h)^2)(1 + x^2)} \)
Bu ifadeyi türevin limit tanımında yerine koyalım.
\( f'(x) = \lim\limits_{h \to 0} \dfrac{\frac{-2xh - h^2}{(1 + (x + h)^2)(1 + x^2)}}{h} \)
\( = \lim\limits_{h \to 0} \dfrac{-2x - h}{(1 + (x + h)^2)(1 + x^2)} \)
Bu limit ifadesinde \( x \) sabit terimdir.
Limiti alınan rasyonel fonksiyon ifadesi paydayı sıfır yapan \( h \) değerleri hariç tüm reel sayılarda sürekli olduğu için doğrudan yerine koyma yöntemi ile limitini bulabiliriz.
\( = \dfrac{-2x - 0}{(1 + (x + 0)^2)(1 + x^2)} \)
\( = \dfrac{-2x}{(1 + x^2)^2} \) bulunur.
\( f: \mathbb{R} - \{-3\} \to \mathbb{R} \) olmak üzere,
\( f(x) = \dfrac{x^2}{x + 3} \) için türev fonksiyonunu türevin limit tanımını kullanarak bulun.
Çözümü GösterTürev fonksiyonunun limit tanımını yazalım.
\( f'(x) = \lim\limits_{h \to 0} \dfrac{f(x + h) - f(x)}{h} \)
Paydaki ifadeyi bulalım.
\( f(x + h) - f(x) = \dfrac{(x + h)^2}{x + h + 3} - \dfrac{x^2}{x + 3} \)
\( = \dfrac{(x^2 + 2xh + h^2)(x + 3) - x^2(x + h + 3)}{(x + h + 3)(x + 3)} \)
\( = \dfrac{x^3 + 3x^2 + 2x^2h + 6xh + xh^2 + 3h^2 - x^3 - x^2h - 3x^2}{(x + h + 3)(x + 3)} \)
\( = \dfrac{x^2h + 6xh + xh^2 + 3h^2}{(x + h + 3)(x + 3)} \)
Bu ifadeyi türevin limit tanımında yerine koyalım.
\( f'(x) = \lim\limits_{h \to 0} \dfrac{\frac{x^2h + 6xh + xh^2 + 3h^2}{(x + h + 3)(x + 3)}}{h} \)
\( = \lim\limits_{h \to 0} \dfrac{x^2 + 6x + xh + 3h}{(x + h + 3)(x + 3)} \)
Bu limit ifadesinde \( x \) sabit terimdir.
Limiti alınan rasyonel fonksiyon ifadesi paydayı sıfır yapan \( h \) değerleri hariç tüm reel sayılarda sürekli olduğu için doğrudan yerine koyma yöntemi ile limitini bulabiliriz.
\( = \dfrac{x^2 + 6x + x(0) + 3(0)}{(x + 0 + 3)(x + 3)} \)
\( = \dfrac{x^2 + 6x}{(x + 3)^2} \)
\( = \dfrac{x(x + 6)}{(x + 3)^2} \) bulunur.
\( f \) tüm reel sayılarda türevlenebilir bir fonksiyondur.
\( \lim\limits_{h \to 0} \dfrac{f(x + h) - f(x - h)}{h} \) limitinin eşitini \( f'(x) \) cinsinden bulunuz.
Çözümü GösterTürev fonksiyonunun limit tanımını yazalım.
\( f'(x) = \lim\limits_{h \to 0} \dfrac{f(x + h) - f(x)}{h} \)
İfadeyi \( f'(x) \) limit tanımına benzetmek için ifadenin payına \( f(x) \) ekleyip çıkaralım.
\( = \lim\limits_{h \to 0} \dfrac{f(x + h) - f(x) + f(x) - f(x - h)}{h} \)
\( = \lim\limits_{h \to 0} \dfrac{f(x + h) - f(x)}{h} - \lim\limits_{h \to 0} \dfrac{f(x - h) - f(x)}{h} \)
Birinci limit ifadesi \( f'(x) \)'in limit tanımıdır.
\( = f'(x) - \lim\limits_{h \to 0} \dfrac{f(x - h) - f(x)}{h} \)
Limit ifadesini düzenleyelim.
\( = f'(x) - \lim\limits_{h \to 0} \dfrac{f(x + (-h)) - f(x)}{h} \)
\( = f'(x) + \lim\limits_{h \to 0} \dfrac{f(x + (-h)) - f(x)}{-h} \)
Limit iki yönlü bir işlem olduğu için \( h \) sıfıra giderkenki limit ile \( -h \) sıfıra giderkenki limit birbirine eşittir.
\( = f'(x) + f'(x) = 2f'(x) \) olarak bulunur.
\( f(x) = \sqrt{1 + x^2} \) için türev fonksiyonunu türevin limit tanımını kullanarak bulun.
Çözümü GösterTürev fonksiyonunun limit tanımını yazalım.
\( f'(x) = \lim\limits_{h \to 0} \dfrac{f(x + h) - f(x)}{h} \)
\( = \lim\limits_{h \to 0} \dfrac{\sqrt{1 + (x + h)^2} - \sqrt{1 + x^2}}{h} \)
Payı ve paydayı, payın eşleniği ile çarpalım.
\( = \lim\limits_{h \to 0} \dfrac{(\sqrt{1 + (x + h)^2} - \sqrt{1 + x^2})(\sqrt{1 + (x + h)^2} + \sqrt{1 + x^2})}{h(\sqrt{1 + (x + h)^2} + \sqrt{1 + x^2})} \)
\( = \lim\limits_{h \to 0} \dfrac{(\sqrt{1 + (x + h)^2})^2 - (\sqrt{1 + x^2})^2}{h(\sqrt{1 + (x + h)^2} + \sqrt{1 + x^2})} \)
\( = \lim\limits_{h \to 0} \dfrac{1 + (x + h)^2 - (1 + x^2)}{h(\sqrt{1 + (x + h)^2} + \sqrt{1 + x^2})} \)
\( = \lim\limits_{h \to 0} \dfrac{1 + x^2 + 2xh + h^2 - 1 - x^2}{h(\sqrt{1 + (x + h)^2} + \sqrt{1 + x^2})} \)
\( = \lim\limits_{h \to 0} \dfrac{2xh + h^2}{h(\sqrt{1 + (x + h)^2} + \sqrt{1 + x^2})} \)
\( = \lim\limits_{h \to 0} \dfrac{2x + h}{\sqrt{1 + (x + h)^2} + \sqrt{1 + x^2}} \)
Bu limit ifadesinde \( x \) sabit terimdir.
Doğrudan yerine koyma yöntemi ile ifadenin limitini bulalım.
\( = \dfrac{2x + 0}{\sqrt{1 + (x + 0)^2} + \sqrt{1 + x^2}} \)
\( = \dfrac{2x}{\sqrt{1 + x^2} + \sqrt{1 + x^2}} \)
\( = \dfrac{2x}{2\sqrt{1 + x^2}} \)
\( = \dfrac{x}{\sqrt{1 + x^2}} \) bulunur.
\( f(x) = \sin(3x + 1) \) için türev fonksiyonunu türevin limit tanımını kullanarak bulun.
Çözümü GösterTürev fonksiyonunun limit tanımını yazalım.
\( f'(x) = \lim\limits_{h \to 0} \dfrac{f(x + h) - f(x)}{h} \)
\( = \lim\limits_{h \to 0} \dfrac{\sin(3(x + h) + 1) - \sin(3x + 1)}{h} \)
\( = \lim\limits_{h \to 0} \dfrac{\sin(3x + 1 + 3h) - \sin(3x + 1)}{h} \)
Sinüs toplam formülünü kullanalım.
\( \sin(a + b) = \sin{a}\cos{b} + \cos{a}\sin{b} \)
\( a = 3x + 1 \) ve \( b = 3h \) alalım.
\( = \lim\limits_{h \to 0} \dfrac{\sin(3x + 1)\cos(3h) + \sin(3h)\cos(3x + 1) - \sin(3x + 1)}{h} \)
\( = \lim\limits_{h \to 0} \dfrac{\sin(3x + 1)(\cos(3h) - 1) + \cos(3x + 1)\sin(3h)}{h} \)
Limit toplama kuralı ile ifadeyi iki limitin toplamı şeklinde yazalım.
\( = \lim\limits_{h \to 0} \dfrac{\sin(3x + 1)(\cos(3h) - 1)}{h} + \lim\limits_{h \to 0} \dfrac{\cos(3x + 1)\sin(3h)}{h} \)
\( h \) içermeyen ifadeleri limitin dışına birer sabit olarak alabiliriz.
\( = \sin(3x + 1)\lim\limits_{h \to 0} \dfrac{\cos(3h) - 1}{h} + \cos(3x + 1)\lim\limits_{h \to 0} \dfrac{\sin(3h)}{h} \)
Her iki limit ifadesinde payı ve paydayı 3 ile çarpalım.
\( = \sin(3x + 1)\lim\limits_{h \to 0} \dfrac{3\cos(3h) - 3}{3h} + \cos(3x + 1)\lim\limits_{h \to 0} \dfrac{3\sin(3h)}{3h} \)
\( = 3\sin(3x + 1)\lim\limits_{h \to 0} \dfrac{\cos(3h) - 1}{3h} + 3\cos(3x + 1)\lim\limits_{h \to 0} \dfrac{\sin(3h)}{3h} \)
İspatlarını trigonometrik fonksiyonların limiti bölümünde verdiğimiz bazı trigonometrik ifadelerin limit değerlerini kullanalım.
\( \lim\limits_{x \to 0} \dfrac{1 - \cos{x}}{x} = 0, \quad \lim\limits_{x \to 0} \dfrac{\sin{x}}{x} = 1 \)
\( = 3\sin(3x + 1) \cdot 0 + 3\cos(3x + 1) \cdot 1 \)
\( = 3\cos(3x + 1) \) bulunur.
\( \sgn{} \) işaret fonksiyonu olmak üzere,
\( f(x) = \sgn(x^2 - x - 6) \) için \( f'(1) \) ve \( f'(3) \) değerlerini türevin limit tanımını kullanarak hesaplayın.
Çözümü Göster\( \sgn{x} \) işaret fonksiyonu \( x \) sayısı pozitif ise \( +1 \), negatif ise \( -1 \), sıfır ise 0 değeri veren bir parçalı fonksiyondur.
İkinci dereceden ifadeyi çarpanlarına ayıralım.
\( f(x) = \sgn((x + 2)(x - 3)) \)
Pozitif başkatsayılı ve birbirinden farklı iki reel kökü olan ikinci dereceden bir ifade kök değerlerinde sıfır, köklerin arasındaki aralıkta negatif, dışındaki aralıkta pozitif olur.
Fonksiyonu parçalı fonksiyon şeklinde yazalım.
\( f(x) = \begin{cases} 0 & x = -2 \text{ veya } x = 3 \\ -1 & -2 \lt x \lt 3 \\ 1 & x \lt -2 \text{ veya } x \gt 3 \end{cases} \)
1. nokta: \( f'(1) \)
\( x = 1 \) noktasındaki soldan türevi bulalım.
Fonksiyon \( (-2, 3) \) aralığında \( f(x) = -1 \) şeklinde sabit fonksiyondur.
\( f'(1^-) = \lim\limits_{x \to 1^-} \dfrac{f(x) - f(1)}{x - 1} \)
\( = \lim\limits_{x \to 1^-} \dfrac{-1 - (-1)}{x - 1} \)
\( = \lim\limits_{x \to 1^-} \dfrac{0}{x - 1} \)
Payı 0 olan bu limit ifadesi bir belirsizlik ifade etmez ve sonucu 0'dır.
\( = 0 \)
\( x = 1 \) noktasındaki sağdan türevi bulalım.
\( f'(1^+) = \lim\limits_{x \to 1^+} \dfrac{f(x) - f(1)}{x - 1} \)
\( = \lim\limits_{x \to 1^+} \dfrac{-1 - (-1)}{x - 1} \)
\( = \lim\limits_{x \to 1^+} \dfrac{0}{x - 1} \)
\( = 0 \)
\( f'(1^-) = f'(1^+) \) olduğundan fonksiyonun \( x = 1 \) noktasında türevi tanımlıdır ve bulduğumuz limit değerine eşittir.
\( f'(1) = 0 \)
2. nokta: \( f'(3) \)
\( x = 3 \) noktasındaki soldan türevi bulalım.
Fonksiyonun bu noktanın solunda ve sağında farklı tanımları vardır ve bu noktadaki değeri \( f(3) = 0 \)'dır.
\( f'(3^-) = \lim\limits_{x \to 3^-} \dfrac{f(x) - f(3)}{x - 3} \)
\( = \lim\limits_{x \to 3^-} \dfrac{-1 - 0}{x - 3} \)
\( = \lim\limits_{x \to 3^-} \dfrac{-1}{x - 3} \)
Bu limit bir belirsizlik değil, tanımsızlık ifade eder. Fonksiyon \( x \to 3^- \) iken pozitif sonsuza gider, dolayısıyla soldan limit tanımlı değildir.
\( = +\infty \)
\( x = 3 \) noktasındaki sağdan türevi bulalım.
\( f'(3^+) = \lim\limits_{x \to 3^+} \dfrac{f(x) - f(3)}{x - 3} \)
\( = \lim\limits_{x \to 3^+} \dfrac{1 - 0}{x - 3} \)
\( = \lim\limits_{x \to 3^+} \dfrac{1}{x - 3} \)
Bu limit bir belirsizlik değil, tanımsızlık ifade eder. Fonksiyon \( x \to 3^+ \) iken pozitif sonsuza gider, dolayısıyla sağdan limit tanımlı değildir.
\( = +\infty \)
Soldan ve sağdan limitler tanımlı olmadığı için bu noktada fonksiyonun türevi tanımlı değildir.
\( f \) tüm reel sayılarda türevlenebilir bir fonksiyondur.
\( \lim\limits_{h \to 0} \dfrac{f(-1) - f(8h - 1)}{2h} \) limitinin eşitini bulunuz.
Çözümü Göster\( f \) fonksiyonunun \( x = -1 \) noktasındaki türevinin limit tanımını yazalım.
\( f'(-1) = \lim\limits_{h \to 0} \dfrac{f(-1 + h) - f(-1)}{h} \)
Soruda verilen limit ifadesini düzenleyelim.
\( \lim\limits_{h \to 0} \dfrac{-(f(-1 + 8h) - f(-1))}{2h} \)
İfadenin payını ve paydasını 4 ile çarpalım.
\( = \lim\limits_{h \to 0} \dfrac{-4(f(-1 + 8h) - f(-1))}{8h} \)
\( = -4\lim\limits_{h \to 0} \dfrac{f(-1 + 8h) - f(-1)}{8h} \)
\( u = 8h \) şeklinde değişken değiştirelim.
\( h \to 0 \) iken \( u = 8h \to 0 \) olur.
\( = -4\lim\limits_{u \to 0} \dfrac{f(-1 + u) - f(-1)}{u} \)
Limit ifadesi \( f \) fonksiyonunun \( x = -1 \) noktasındaki türevinin tanımıdır.
\( = -4f'(-1) \) bulunur.
\( f \) tüm reel sayılarda türevlenebilir bir fonksiyondur.
\( \lim\limits_{x \to 1} \dfrac{f(x) - f(2 - x)}{x - 1} \) limitinin eşitini bulunuz.
Çözümü Göster\( x - 1 = h \) şeklinde değişken değiştirelim.
\( x = 1 + h \)
\( x \to 1 \) iken \( x - 1 \to 0 \) olur.
\( x - 1 \to 0 \) iken \( h \to 0 \) olur.
\( \lim\limits_{x \to 1} \dfrac{f(x) - f(2 - x)}{x - 1} = \lim\limits_{h \to 0} \dfrac{f(1 + h) - f(2 - (1 + h))}{h} \)
\( = \lim\limits_{h \to 0} \dfrac{f(1 + h) - f(1 - h)}{h} \)
İfadeyi \( f'(1) \) limit tanımına benzetmek için ifadenin payına \( f(1) \) ekleyip çıkaralım.
\( = \lim\limits_{h \to 0} \dfrac{f(1 + h) - f(1) + f(1) - f(1 - h)}{h} \)
\( = \lim\limits_{h \to 0} \dfrac{f(1 + h) - f(1)}{h} - \lim\limits_{h \to 0} \dfrac{f(1 - h) - f(1)}{h} \)
Birinci limit ifadesi \( f'(1) \)'in limit tanımıdır.
\( = f'(1) + \lim\limits_{h \to 0} \dfrac{f(1 + (-h)) - f(1)}{-h} \)
Limit iki yönlü bir işlem olduğu için \( h \) sıfıra giderkenki limit ile \( -h \) sıfıra giderkenki limit birbirine eşittir.
\( = f'(1) + f'(1) = 2f'(1) \) olarak bulunur.
\( f \) tüm reel sayılarda türevlenebilir bir fonksiyon olmak üzere,
\( 4 \le f'(x) \le 7 \) ve \( f(0) = 12 \) olduğuna göre,
\( f(-5) \) ifadesinin alabileceği en küçük değer kaçtır?
Çözümü GösterBir fonksiyonun birinci türevi belirli bir \( x \) değeri için \( y \) değerindeki anlık değişimi verir.
Fonksiyonun birinci türevinin \( [4, 7] \) aralığında olduğu biliniyor. \( f(0) = 12 \) ise \( f(-5) \) değerinin en küçük değerini alması için fonksiyon değeri \( [-5, 0] \) aralığında maksimum miktarda artmış olmalıdır, yani birinci türev bu aralıkta en büyük değerini almalıdır.
Birinci türevin alabileceği en büyük değer olan \( f'(x) = 7 \) değerini \( [-5, 0] \) aralığındaki ortalama değişim oranı olarak kabul edelim.
Ort. Değişim Oranı \( = \dfrac{f(0) - f(-5)}{0 - (-5)} \)
\( 7 = \dfrac{12 - f(-5)}{5} \)
\( 12 - f(-5) = 35 \)
\( f(-5) = -23 \)
Buna göre \( f(-5) \) ifadesinin alabileceği en küçük değer \( -23 \) olur.