Türev Grafik Yorumu
Bu bölümde bazı örnek fonksiyonların ve türevlerinin grafiklerini inceleyeceğiz.
Doğrusal Fonksiyon
Aşağıda azalan bir doğrusal fonksiyonun ve türevlerinin denklem ve grafikleri verilmiştir.
\( f(x) = -2x + 2 \)
\( f'(x) = -2 \)
\( f''(x) = 0 \)
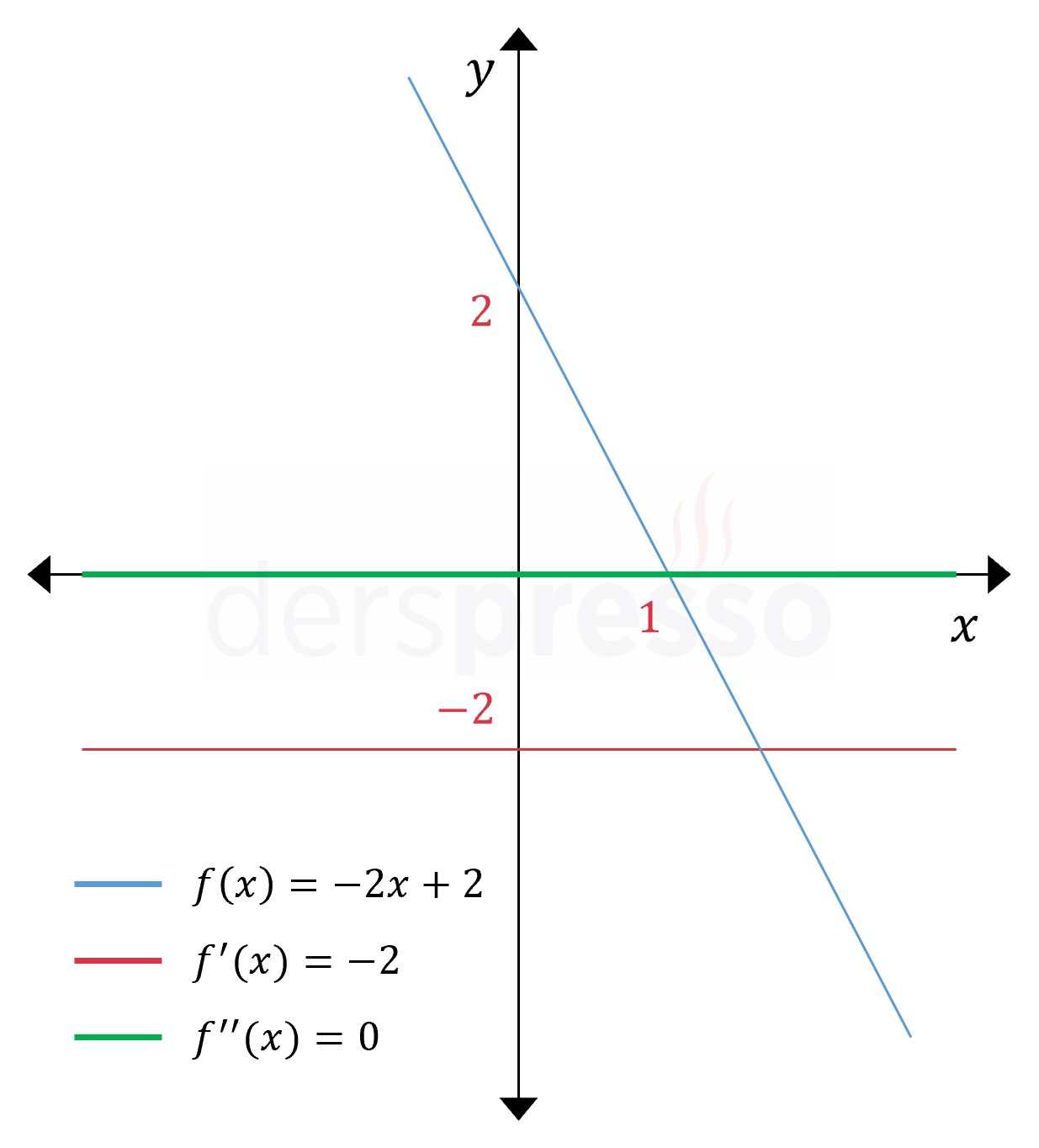
Bu fonksiyon ve türevleri ile ilgili aşağıdaki yorumlar yapılabilir.
- Ana fonksiyonun değeri doğrusal bir şekilde azalır.
- Ana fonksiyonun eğimi negatif ve sabit olduğu için birinci türev de sabit ve negatiftir.
- Birinci türevin eğimi sabit olduğu için ikinci türev sıfırdır.
- Ana fonksiyonun artan bir doğrusal fonksiyon olması durumunda, birinci türev fonksiyonu pozitif değere sahip sabit fonksiyon olur.
Parabol
Aşağıda pozitif başkatsayılı (kolları yukarı bakan) bir parabolün ve türevlerinin denklem ve grafikleri verilmiştir.
\( f(x) = x^2 - 2x + 4 \)
\( f'(x) = 2x - 2 \)
\( f''(x) = 2 \)
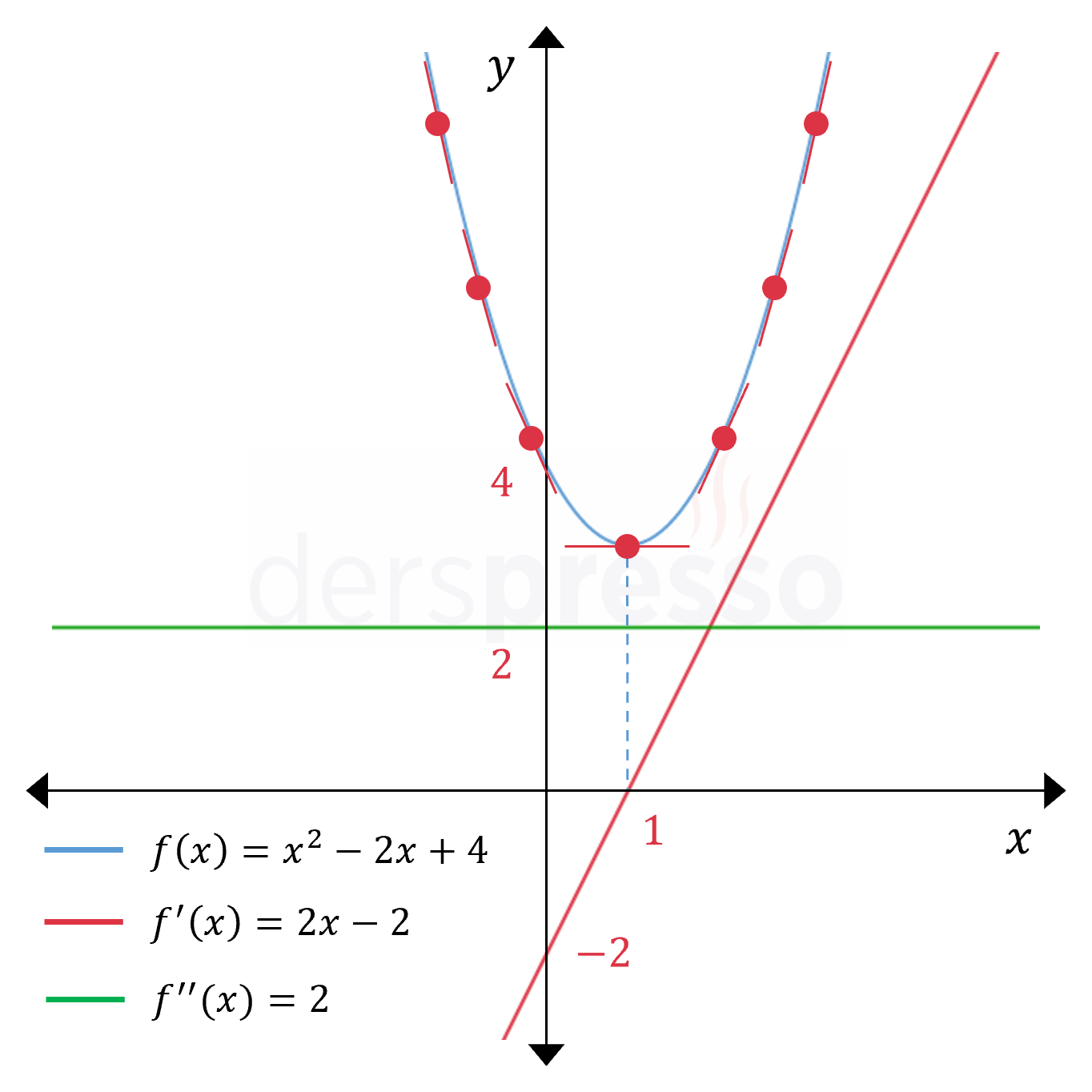
Bu fonksiyon ve türevleri ile ilgili aşağıdaki yorumlar yapılabilir.
- Ana fonksiyon ikinci dereceden bir polinom fonksiyonu (parabol), birinci türev birinci dereceden bir polinom fonksiyonu (doğru), ikinci türev sıfırıncı dereceden bir polinom fonksiyonudur (sabit fonksiyon).
- Ana fonksiyon \( (-\infty, 1) \) aralığında azalandır, dolayısıyla birinci türev bu aralıkta negatiftir.
- Ana fonksiyon \( x = 1 \) noktasında bir yerel minimum değerine ulaşır, dolayısıyla birinci türev bu noktada sıfır olur.
- Ana fonksiyon \( (1, \infty) \) aralığında artandır, dolayısıyla birinci türev bu aralıkta pozitiftir.
- Ana fonksiyonun eğimi tüm tanım aralığında artmaktadır, dolayısıyla birinci türevi artan, ikinci türevi pozitiftir.
- \( x = 1 \) noktası aynı zamanda mutlak minimum noktasıdır. Fonksiyon değeri pozitif sonsuza gittiği için mutlak maksimum noktası yoktur.
3. Dereceden Polinom Fonksiyonu
Aşağıda pozitif başkatsayılı üçüncü dereceden bir polinom fonksiyonunun ve türevlerinin denklem ve grafikleri verilmiştir.
\( f(x) = x^3 - 3x^2 + 6 \)
\( f'(x) = 3x^2 - 6x \)
\( f''(x) = 6x - 6 \)
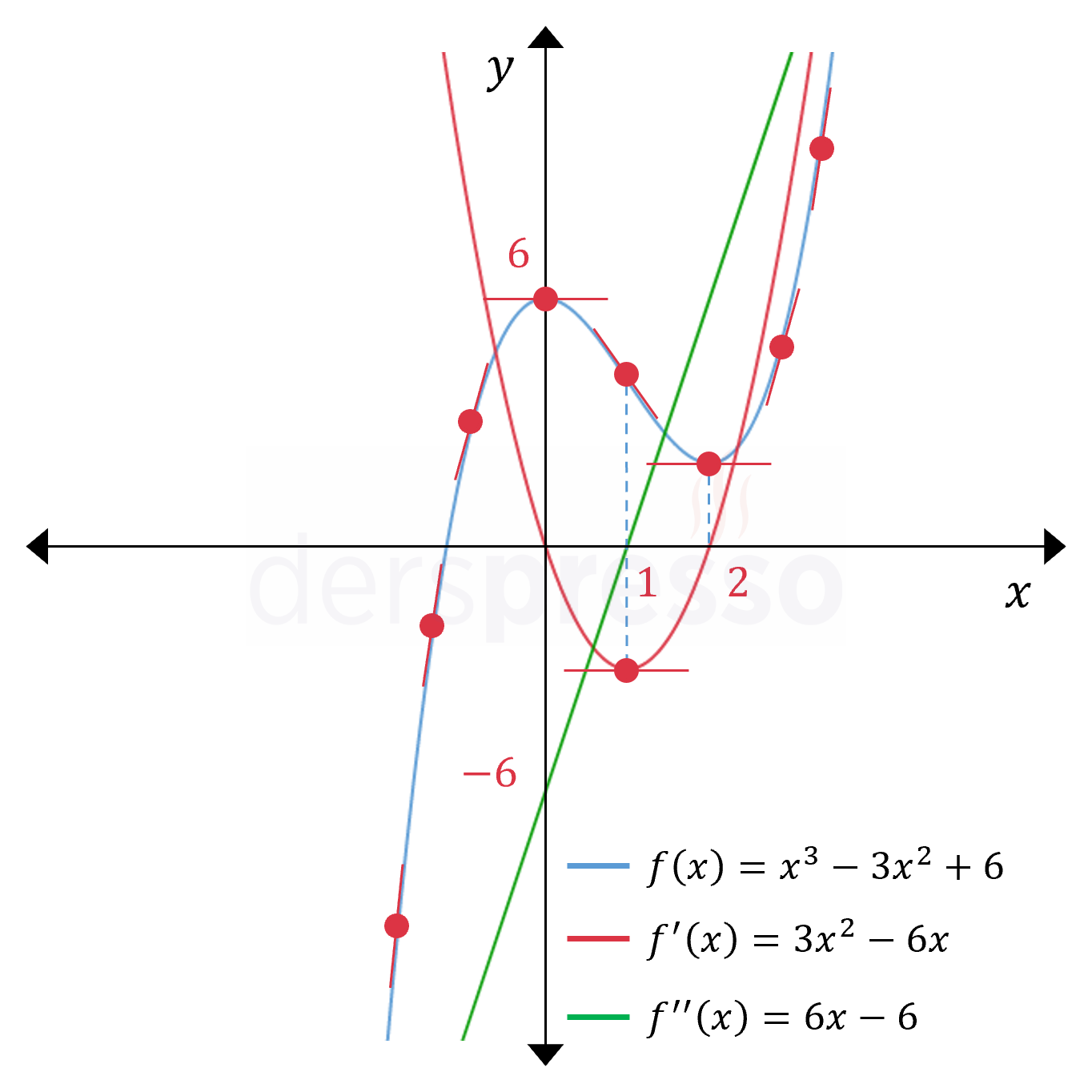
Bu fonksiyon ve türevleri ile ilgili aşağıdaki yorumlar yapılabilir.
- Ana fonksiyon üçüncü dereceden bir polinom fonksiyonu, birinci türev ikinci dereceden bir polinom fonksiyonu (parabol), ikinci türev birinci dereceden bir polinom fonksiyonudur (doğru).
- Ana fonksiyon \( (-\infty, 0) \) ve \( (2, \infty) \) aralıklarında artandır, dolayısıyla birinci türev bu aralıkta pozitiftir.
- Ana fonksiyon \( (0, 2) \) aralığında azalandır, dolayısıyla birinci türev bu aralıkta negatiftir.
- Ana fonksiyon \( x = 0 \) noktasında bir yerel maksimum değerine, \( x = 2 \) noktasında bir yerel minimum değerine ulaşır, dolayısıyla birinci türev bu noktalarda sıfır olur.
- Ana fonksiyonun eğimi \( (-\infty, 1) \) aralığında azalır, dolayısıyla bu aralıkta birinci türev azalandır ve ikinci türev negatiftir.
- Ana fonksiyonun eğimi \( (1, \infty) \) aralığında artar, dolayısıyla bu aralıkta birinci türev artandır ve ikinci türev pozitiftir.
- Ana fonksiyonun eğimi \( x = 1 \) noktasında azalırken artmaya başladığı ve grafik konkavdan konvekse geçtiği için bu nokta bir büküm noktasıdır ve ikinci türev sıfırdır.
- Fonksiyon değeri negatif ve pozitif sonsuza gittiği için mutlak minimum ve maksimum noktaları yoktur.
Sinüs Fonksiyonu
Aşağıda sinüs fonksiyonunun ve türevlerinin denklem ve grafikleri verilmiştir.
\( f(x) = \sin{x} \)
\( f'(x) = \cos{x} \)
\( f''(x) = -\sin{x} \)
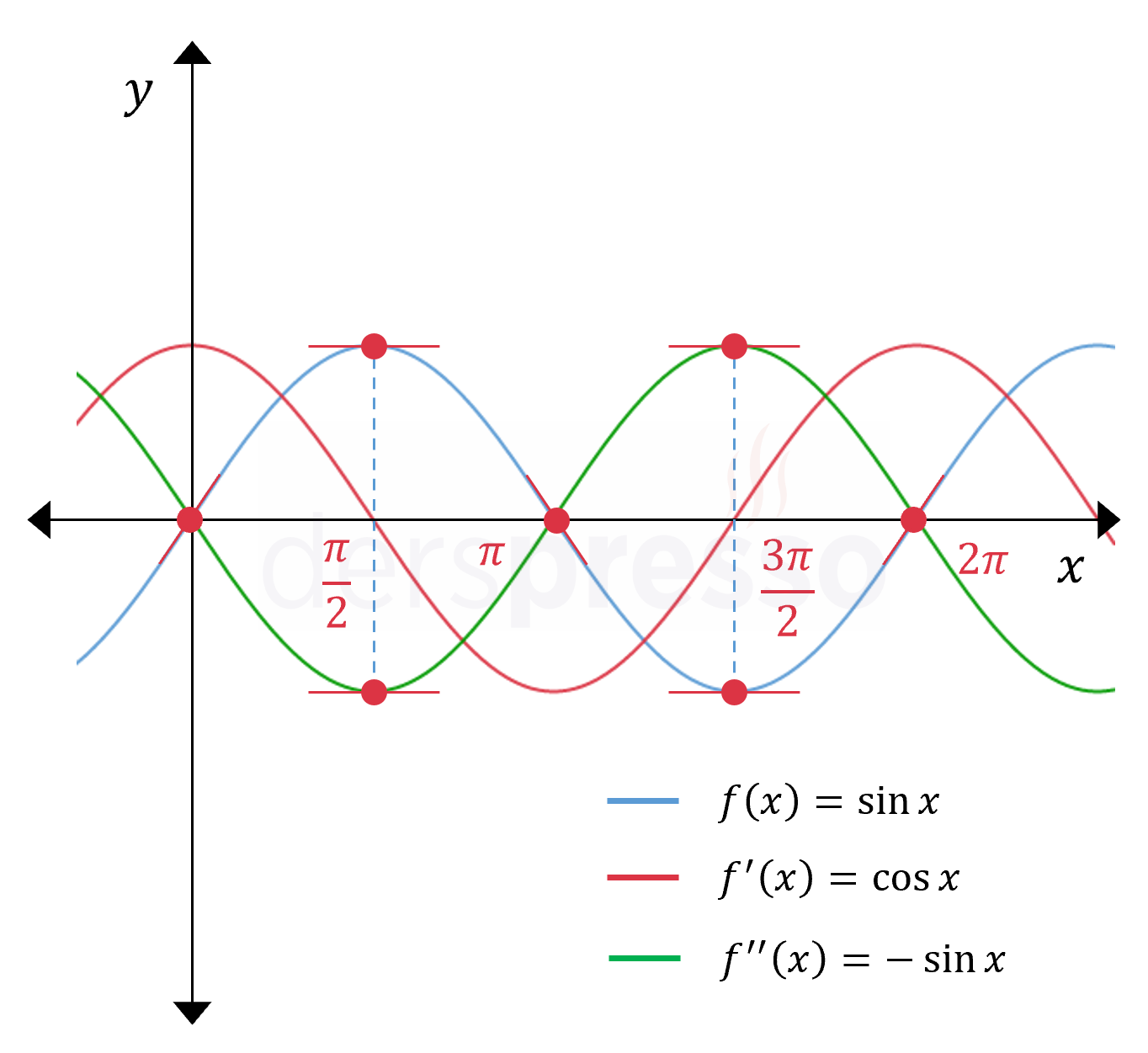
Bu fonksiyon ve türevleri ile ilgili aşağıdaki yorumlar yapılabilir.
- Ana fonksiyonun \( x = \frac{\pi}{2} \)'deki yerel maksimum ve \( x = \frac{3\pi}{2} \)'deki yerel minimum noktalarında birinci türev sıfırdır.
- Ana fonksiyonun eğimi \( x = 0 \) ve \( x = 2\pi \) noktalarında artarken azalmaya, \( x = \pi \) noktasında ise azalırken artmaya başlamıştır, dolayısıyla bu noktalar birer büküm noktasıdır. Bu noktalarda birinci türev yerel minimum ya da maksimum değerlerine ulaşmıştır, ikinci türev ise sıfırdır.
- Yerel minimum ve maksimum noktaları aynı zamanda birer mutlak minimum ve maksimum noktasıdır.
Logaritma Fonksiyonu
Aşağıda doğal logaritma fonksiyonunun ve türevlerinin denklem ve grafikleri verilmiştir.
\( f(x) = \ln{x} \)
\( f'(x) = \dfrac{1}{x} \)
\( f''(x) = -\dfrac{1}{x^2} \)
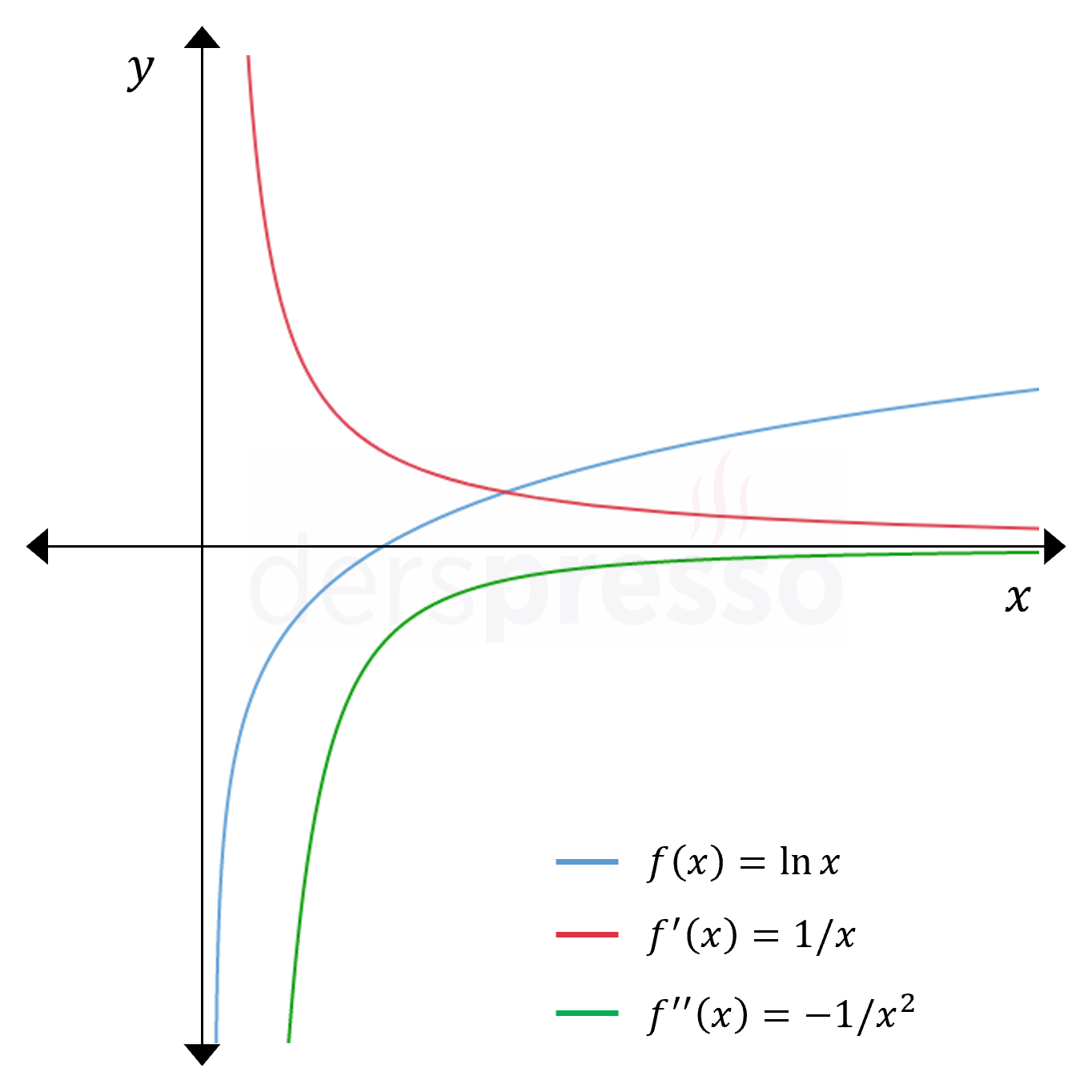
Bu fonksiyon ve türevleri ile ilgili aşağıdaki yorumlar yapılabilir.
- Ana fonksiyonun değeri tüm tanım aralığında artış hızı azalarak artar.
- Ana fonksiyonun eğimi pozitiftir ve azalmaktadır, dolayısıyla birinci türev de pozitif ve azalandır.
- Birinci türevin eğimi negatiftir ve sıfıra yaklaşmaktadır, bu yüzden ikinci türev de negatiftir ve sıfıra yaklaşmaktadır.
- Fonksiyonun yerel veya mutlak minimum ve maksimum noktası yoktur.
Tek/Çift Fonksiyonların Türevi
Bir tek fonksiyonun türevi çift fonksiyondur.
\( f(x) = x^5 - 4x^3 + 2x \)
\( f'(x) = 5x^4 - 12x^2 + 2 \)
\( g(x) = \sin{x} \)
\( g'(x) = \cos{x} \)
Bir çift fonksiyonun türevi tek fonksiyondur.
\( f(x) = 5x^4 - 12x^2 + 2 \)
\( f'(x) = 20x^3 - 24x \)
\( g(x) = \cos{x} \)
\( g'(x) = -\sin{x} \)
\( f: \mathbb{R} \to \mathbb{R} \) olmak üzere,
\( f(x) = \dfrac{4x^2}{3} + 4x \) fonksiyonuna üzerindeki \( K(a, b) \) noktasından teğet çiziliyor, çizilen bu teğet \( x \) ekseniyle pozitif yönde \( 135° \)'lik açı yapmaktadır.
Buna göre, \( b \) kaçtır?
Çözümü GösterBir doğrunun eğimi o doğrunun \( x \) ekseniyle yaptığı pozitif yönlü açının tanjantına eşittir.
\( f'(a) = \tan{135°} = -1 \)
\( f \) fonksiyonunun türevini bulalım.
\( f'(x) = \dfrac{8x}{3} + 4 \)
\( x = a \) yazarak fonksiyonun \( a \) noktasındaki türev değerini bulalım.
\( f'(a) = \dfrac{8a}{3} + 4 = -1 \)
\( 8a + 12 = -3 \)
\( a = -\dfrac{15}{8} \)
\( K \) noktasının ordinat değerini bulmak için fonksiyonda \( x = a = -\frac{15}{8} \) yazalım.
\( f(-\dfrac{15}{8}) = \dfrac{4}{3} \cdot \dfrac{15^2}{8^2} - \dfrac{4 \cdot 15}{8} \)
\( = -\dfrac{45}{16} \) bulunur.
\( f \) reel sayılarda türevlenebilen bir fonksiyondur.
\( f(x + 1) + f(5 - 3x) = x^3 + 6x - 4 \) eşitliği veriliyor.
Buna göre, \( g(x) = \dfrac{4x^3}{5} \cdot f(x + 1) \) fonksiyonunun grafiğine \( x = 1 \) apsisli noktadan çizilen teğetin eğimi kaçtır?
Çözümü GösterVerilen birinci eşitliğin türevini alalım.
\( f'(x + 1) \cdot (x + 1)' + f'(5 - 3x) \cdot (5 - 3x)' = (x^3 + 6x - 4)' \)
\( f'(x + 1) \cdot 1 + f'(5 - 3x) \cdot (-3) = 3x^2 + 6 \)
\( x = 1 \) yazalım.
\( f'(2) - 3f'(2) = 9 \)
\( f'(2) = -\dfrac{9}{2} \)
Verilen birinci eşitlikte \( x = 1 \) yazalım.
\( f(1 + 1) + f(5 - 3(1)) = 1^3 + 6(1) - 4 \)
\( f(2) + f(2) = 3 \)
\( f(2) = \dfrac{3}{2} \)
\( g \) fonksiyonunun türevini alalım.
\( g'(x) = \dfrac{12x^2}{5} \cdot f(x + 1) + \dfrac{4x^3}{5} \cdot f'(x + 1) \)
\( x = 1 \) yazalım.
\( g'(1) = \dfrac{12}{5} \cdot f(2) + \dfrac{4}{5} \cdot f'(2) \)
Yukarıda bulduğumuz \( f(2) \) ve \( f'(2) \) değerlerini yerine koyalım.
\( = \dfrac{12}{5} \cdot \dfrac{3}{2} + \dfrac{4}{5} \cdot \dfrac{-9}{2} \)
\( = 0 \) bulunur.