Süreksizlik Tipleri
Bir fonksiyonun belirli bir noktadaki süreksizliği dört farklı şekilde olabilir.
Kaldırılabilir Süreksizlik
Kaldırılabilir süreksizlikte fonksiyonun bir noktadaki soldan ve sağdan limitleri birer reel sayı olarak tanımlıdır ve birbirine eşittir, dolayısıyla fonksiyonun bu noktada limiti vardır, ancak fonksiyon değeri limit değerinden farklıdır.
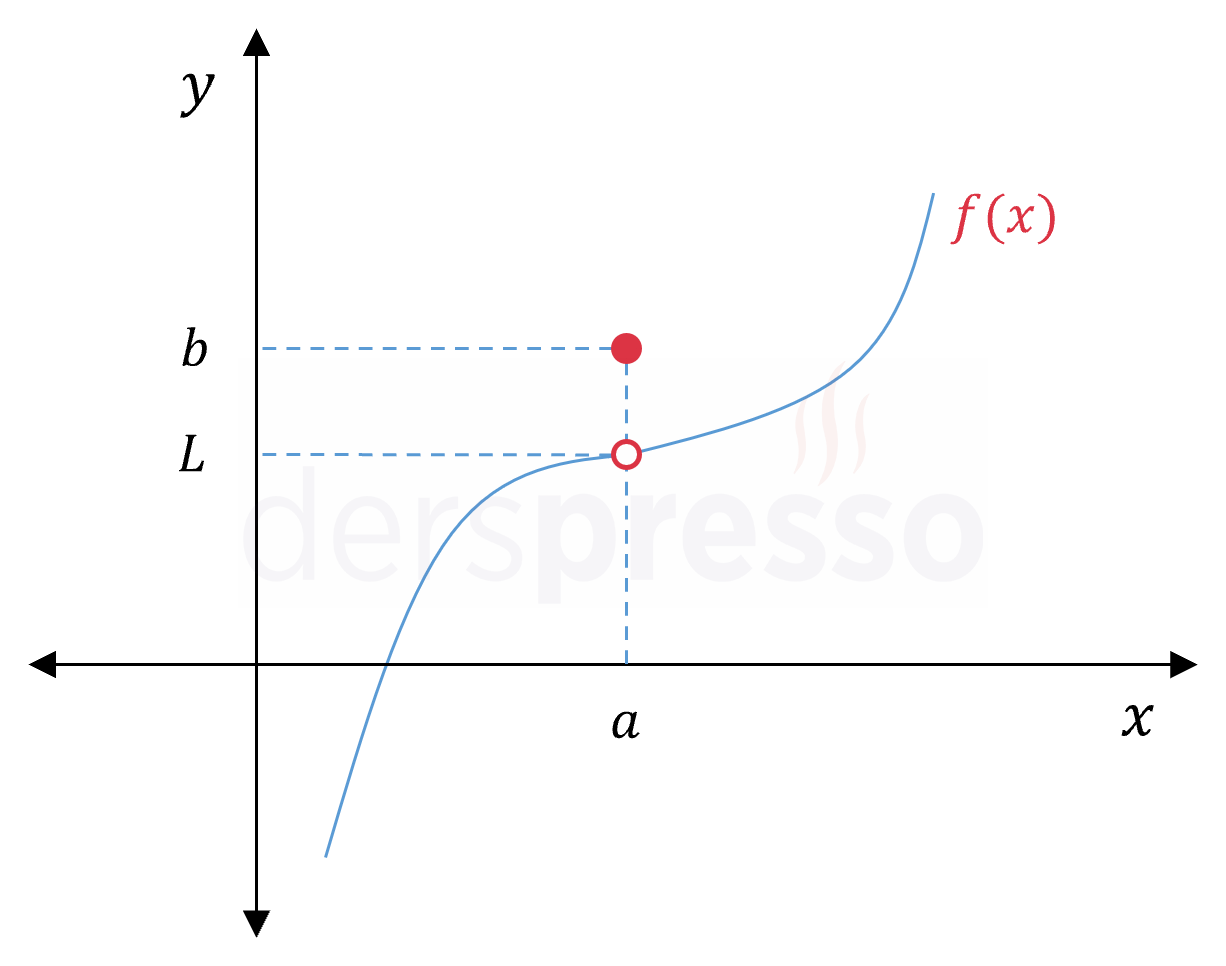
\( L, b \in \mathbb{R} \) olmak üzere,
\( \lim\limits_{x \to a^-} f(x) = \lim\limits_{x \to a^+} f(x) = L \) ve
\( f(a) = b \ne L \) ise,
\( f \) fonksiyonu için \( x = a \) noktasında kaldırılabilir süreksizlik vardır.
Bir fonksiyon parçalı bir fonksiyona dönüştürülerek ve kaldırılabilir süreksizlik olan noktasında fonksiyon değeri limit değerine eşitlenerek bu süreksizlik giderilebilir. Örneğin yukarıdaki grafikteki süreksizlik aşağıda bu şekilde giderilmiştir.
\( \lim\limits_{x \to a^-} f(x) = \lim\limits_{x \to a^+} f(x) = L \) olmak üzere,
\( g(x) = \begin{cases} f(x) & x \ne a \\ L & x = a \end{cases} \)
Sıçrama Süreksizliği
Sıçrama süreksizliğinde fonksiyonun bir noktadaki soldan ve sağdan limitleri birer reel sayı olarak tanımlıdır, ancak birbirinden farklıdır, dolayısıyla fonksiyonun bu noktada limiti tanımsızdır. Fonksiyon bu noktada herhangi bir değer alabilir.
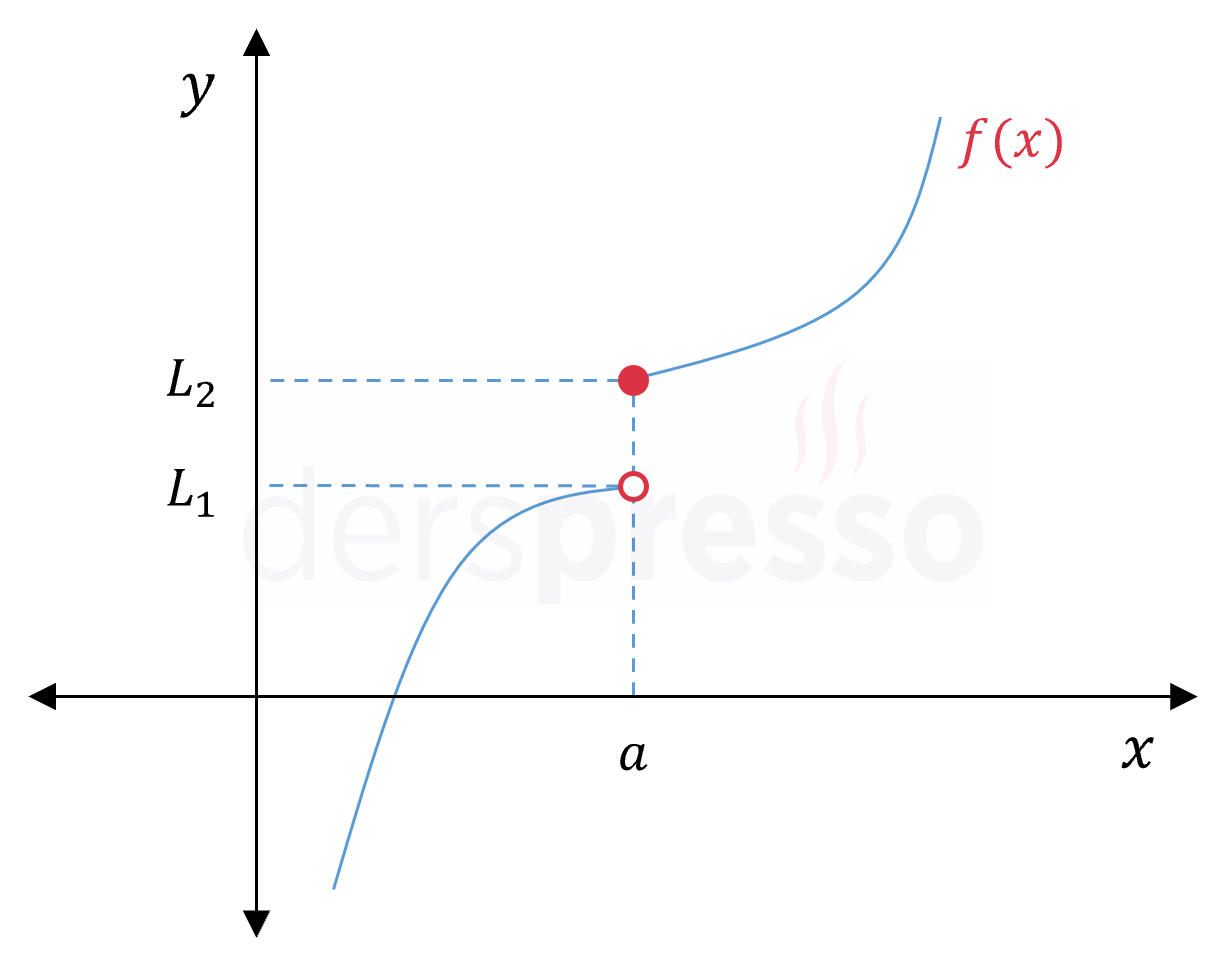
\( L_1, L_2 \in \mathbb{R} \) olmak üzere,
\( \lim\limits_{x \to a^-} f(x) = L_1 \)
\( \lim\limits_{x \to a^+} f(x) = L_2 \) ve
\( L_1 \ne L_2 \) ise,
\( f \) fonksiyonu için \( x = a \) noktasında sıçrama süreksizliği vardır.
Sonsuz Süreksizlik
Sonsuz süreksizlikte fonksiyonun bir noktadaki soldan ve sağdan limitlerinden en azından biri pozitif ya da negatif sonsuza gider. Fonksiyon bu noktada tanımsızdır.
\( \lim\limits_{x \to a^-} f(x) = \pm \infty \) ve/veya
\( \lim\limits_{x \to a^+} f(x) = \pm \infty \) ise,
\( f \) fonksiyonu için \( x = a \) noktasında sonsuz süreksizlik vardır.
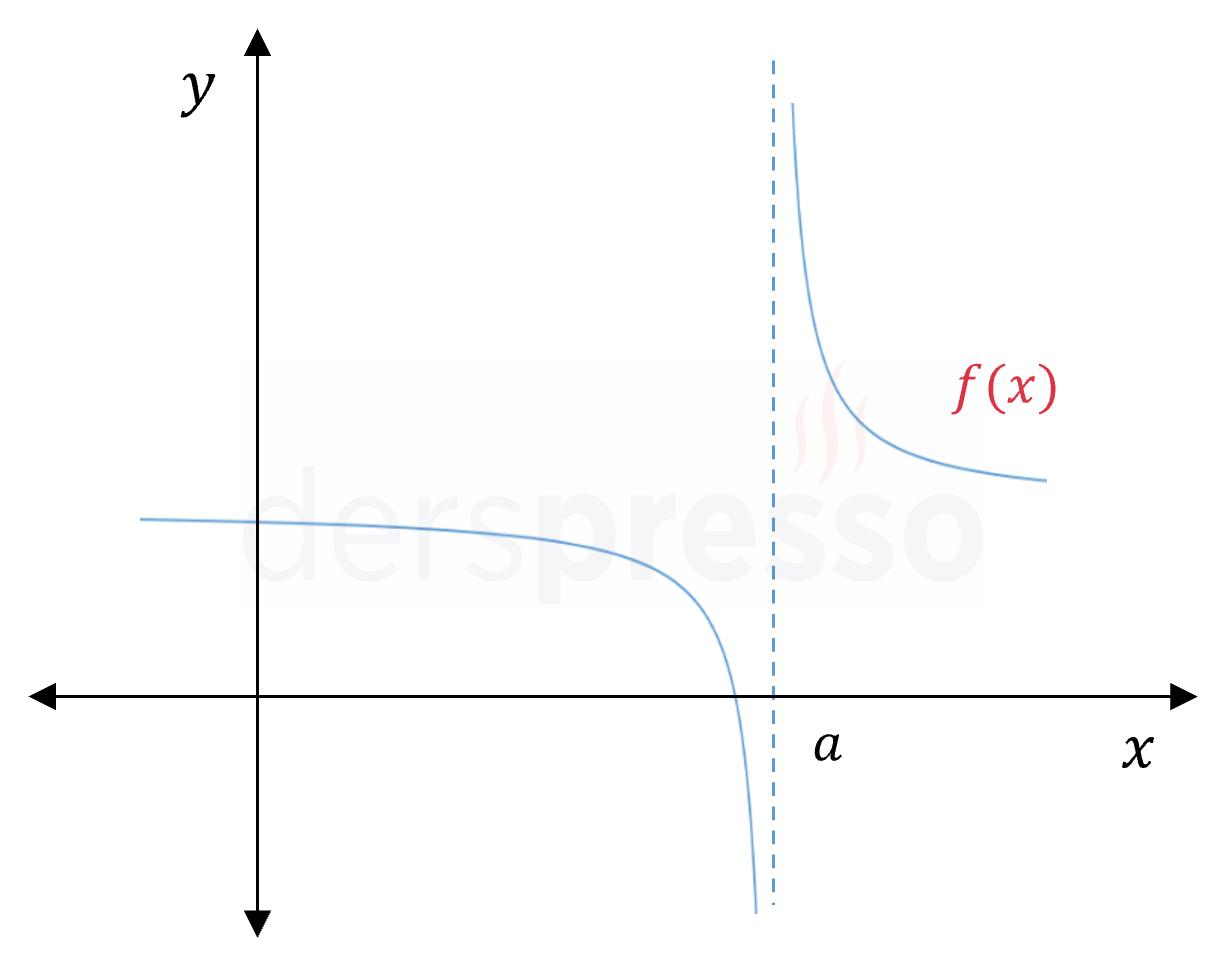
Sonsuz süreksizlik genellikle fonksiyonları tanımsız yapan değerlerde oluşur. Bunlara örnek olarak rasyonel fonksiyonlarda sadece paydayı sıfır yapan \( x \) değerleri ve tanjant/kotanjant fonksiyonlarını tanımsız yapan değerler verilebilir.
- \( \tan{x} \) fonksiyonunda \( \{ \ldots, \frac{\pi}{2}, \frac{3\pi}{2}, \ldots \} \) noktaları
- \( \cot{x} \) fonksiyonunda \( \{ \ldots, 0, \pi, \ldots \} \) noktaları
- \( f(x) = \frac{g(x)}{h(x)} \) biçimindeki fonksiyonlarda \( g(x) \ne 0, h(x) = 0 \) koşullarını sağlayan noktalar
Salınım (Osilasyon) Süreksizliği
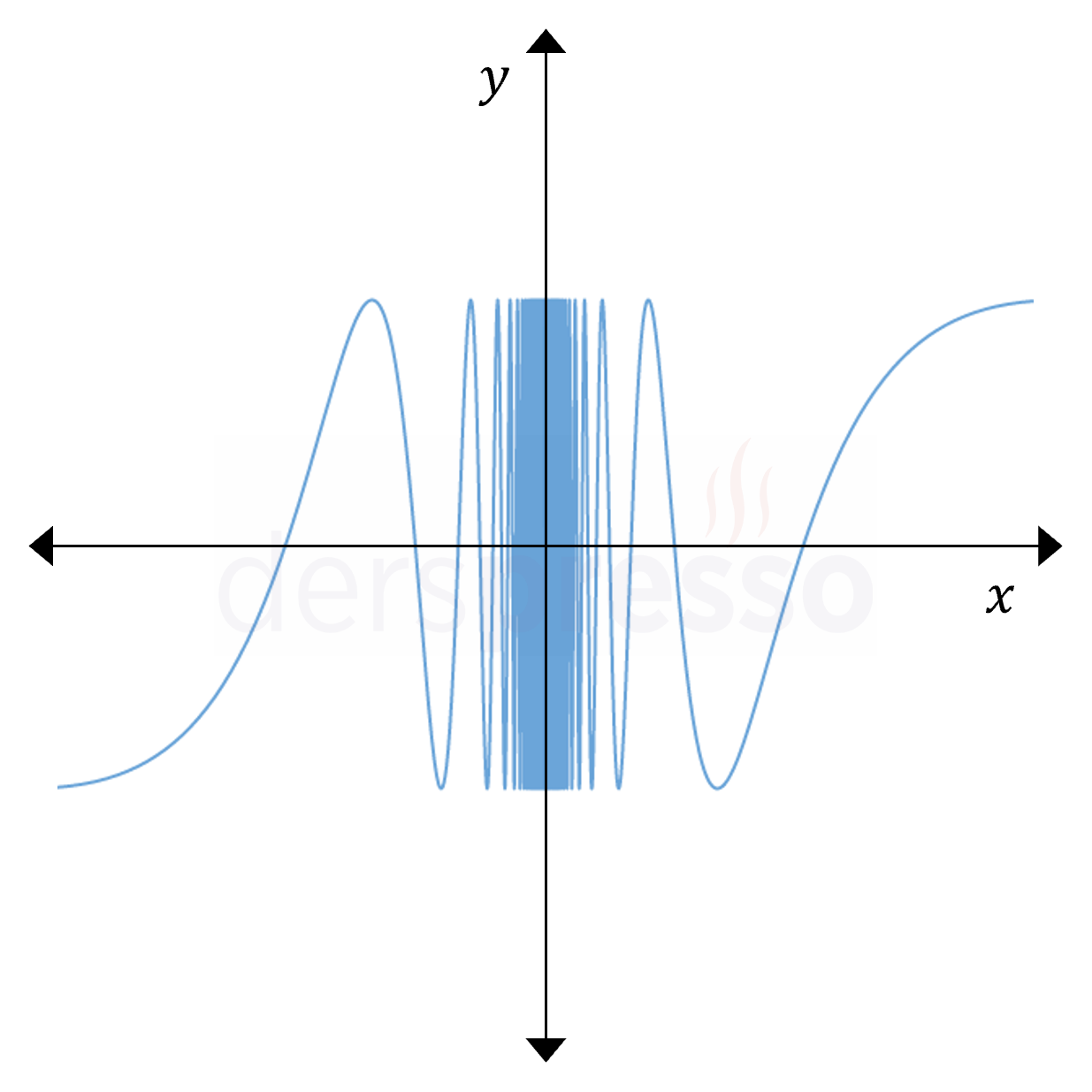
Bazı fonksiyonlar belirli bir noktaya yaklaşırken salınım (osilasyon) hareketi yapar ve fonksiyonun yaklaştığı değer belirli bir reel sayı olarak ifade edilemez. Bu tip noktalarda soldan, sağdan ve iki yönlü limitler tanımsızdır, dolayısıyla fonksiyonlar bu noktalarda süreksizdir.
Böyle bir fonksiyonun grafiği ve denklemi aşağıda verilmiştir.
\( f(x) = \sin{\dfrac{1}{x}} \)
\( \lim\limits_{x \to 0^-} f(x) \Longrightarrow \) Tanımsız
\( \lim\limits_{x \to 0^+} f(x) \Longrightarrow \) Tanımsız
\( f \) fonksiyonu için \( x = 0 \) noktasında salınım (osilasyon) süreksizliği vardır.
\( \lim\limits_{x \to 3} \dfrac{x - 3}{\abs{2x - 6}} \) fonksiyonunun süreksizlik tipini bulunuz.
Çözümü Göster\( \lim\limits_{x \to 3} \dfrac{x - 3}{\abs{2x - 6}} = \lim\limits_{x \to 3} \dfrac{x - 3}{2\abs{x - 3}} \)
\( = \dfrac{1}{2} \lim\limits_{x \to 3} \dfrac{x - 3}{\abs{x - 3}} \)
İfadenin soldan limitini bulalım.
\( \lim\limits_{x \to 3^-} \dfrac{x - 3}{\abs{x - 3}} \)
\( x \to 3^- \) iken \( x \lt 3 \) olduğu için \( \abs{x - 3} = 3 - x \) olur.
\( = \lim\limits_{x \to 3^-} \dfrac{x - 3}{3 - x} = -1 \)
İfadenin sağdan limitini bulalım.
\( \lim\limits_{x \to 3^+} \dfrac{x - 3}{\abs{x - 3}} \)
\( x \to 3^+ \) iken \( x \gt 3 \) olduğu için \( \abs{x - 3} = x - 3 \) olur.
\( = \lim\limits_{x \to 3^+} \dfrac{x - 3}{x - 3} = 1 \)
Soldan ve sağdan limitler tanımlıdır, ancak birbirine eşit değildir. Bu nedenle \( x = 3 \) noktasında sıçrama süreksizliği vardır.
\( \lim\limits_{x \to 12} \dfrac{x}{x - 12} \) fonksiyonunun süreksizlik tipini bulunuz.
Çözümü Gösterİfadenin soldan limitini bulalım.
\( \lim\limits_{x \to 12^-} \dfrac{x}{x - 12} \)
\( x \to 12^- \) iken \( x - 12 \) sıfıra soldan yaklaşır.
\( = -\infty \)
İfadenin sağdan limitini bulalım.
\( \lim\limits_{x \to 12^+} \dfrac{x}{x - 12} \)
\( x \to 12^+ \) iken \( x - 12 \) sıfıra sağdan yaklaşır.
\( = +\infty \)
Soldan ve sağdan limitler sonsuza gittiği için \( x = 12 \) noktasında sonsuz süreksizliği vardır.
\( \lim\limits_{x \to 0} \cos{\dfrac{1}{x}} \) fonksiyonunun süreksizlik tipini bulunuz.
Çözümü Göster\( \frac{1}{x} \) ifadesi \( x \) sıfıra soldan yaklaşırken negatif sonsuza, \( x \) sıfıra sağdan yaklaşırken pozitif sonsuza gider. Kosinüs fonksiyonu periyodik bir fonksiyon olduğu için \( \frac{1}{x} \) ifadesi sonsuza giderken \( \cos{\frac{1}{x}} \) ifadesi periyodik hareketine devam eder ve belirli bir değere yaklaşmaz.
Bu yüzden fonksiyonun \( x = 0 \) noktasında limiti yoktur ve bu noktada salınım süreksizliği vardır.
\( \lim\limits_{x \to 4} \dfrac{2 - \sqrt{x}}{4 - x} \) fonksiyonunun süreksizlik tipini bulunuz.
Çözümü Göster\( \lim\limits_{x \to 4} \dfrac{2 - \sqrt{x}}{4 - x} = \lim\limits_{x \to 4} \dfrac{2- \sqrt{x}}{(2 - \sqrt{x})(2 + \sqrt{x})} \)
Pay ve paydadaki ortak çarpanları sadeleştirelim.
\( = \lim\limits_{x \to 4} \dfrac{1}{2 + \sqrt{x}} \)
Yerine koyma yöntemi ile limit değerini bulalım.
\( = \dfrac{1}{2 + \sqrt{4}} = \dfrac{1}{4} \)
Limiti alınan ifade \( x = 4 \) noktasında tanımsızdır, ancak limitteki belirsizlik çarpanlara ayırma yöntemi ile giderilebilmektedir. İfade bu noktada tanımsız olsa da limiti tanımlı olduğu için \( x = 4 \) noktasında kaldırılabilir süreksizlik vardır.