Sürekliliğin Epsilon-Delta Tanımı
Konu tekrarı için: Limitin Epsilon-Delta Tanımı
Giriş bölümünde sürekliliğin limit tanımını vermiştik. Bu bölümde limitin epsilon-delta tanımına benzer bir tanım olan sürekliliğin epsilon-delta tanımından bahsedeceğiz.
Sürekliliğin epsilon-delta tanımı aşağıdaki gibidir.
\( f: A \to \mathbb{R}, \quad a, L \in \mathbb{R} \),
\( A \) reel sayılar kümesinde tanımlı, \( a \) noktasını içeren açık bir aralık olmak üzere,
her \( \varepsilon \gt 0 \) değeri için aşağıdaki koşullu önermeyi sağlayan bir \( \delta \gt 0 \) değeri bulunabiliyorsa \( f \) fonksiyonu \( a \) noktasında süreklidir.
Her \( x \in A \) değeri için,
\( \abs{x - a} \lt \delta \Longrightarrow \abs{f(x) - f(a)} \lt \varepsilon \)
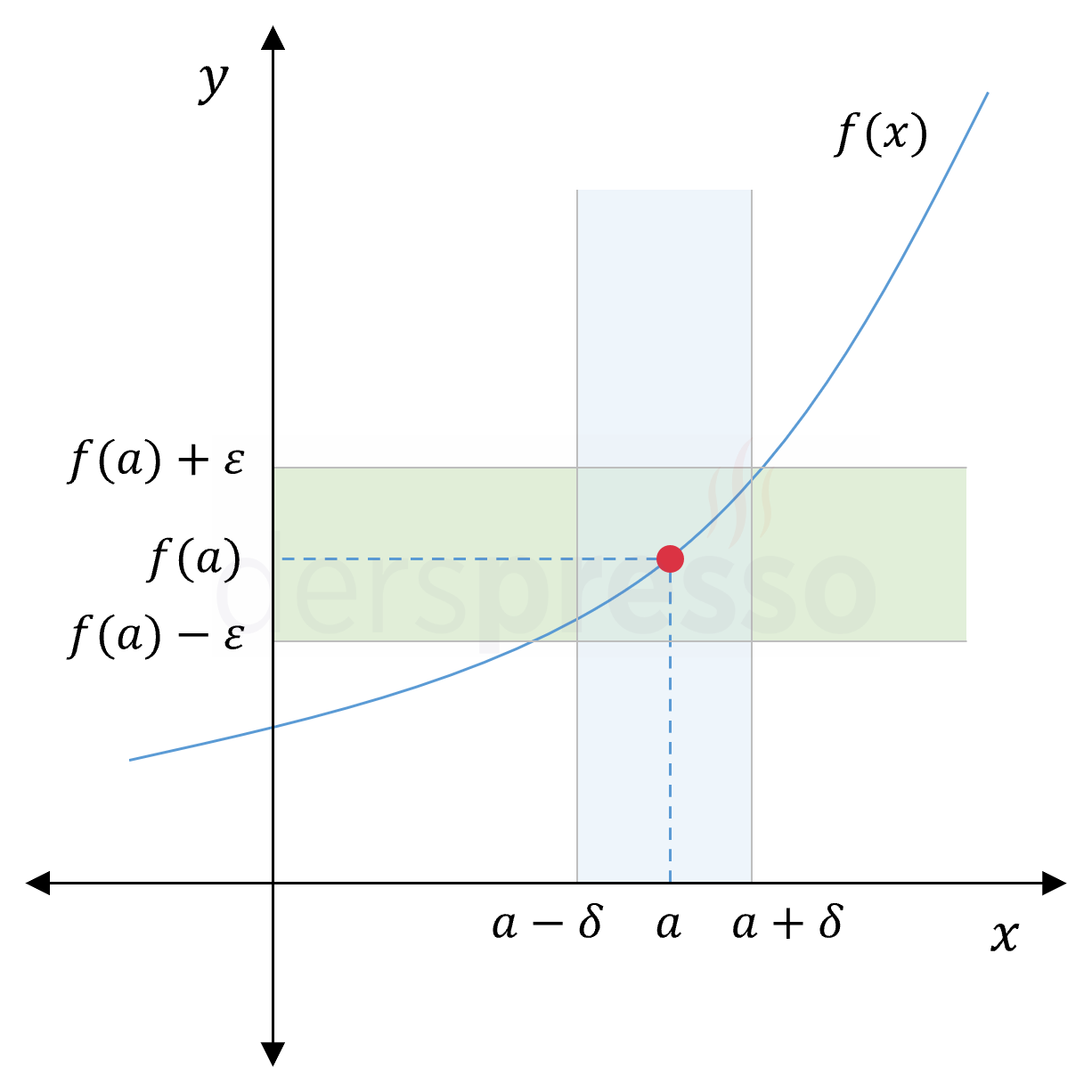
Birbirine çok benzer tanımlar olmakla birlikte, sürekliliğin ve limitin epsilon-delta tanımları arasında aşağıdaki gibi bir fark vardır.
- Limit tanımında \( a \) noktasının tanım kümesinin bir elemanı olma zorunluluğu yoktur ve nokta \( 0 \lt \abs{x - a} \lt \delta \) eşitsizliği ile tanımdaki koşulun dışında tutulur.
- Süreklilik tanımında \( a \) noktası tanım kümesinin bir elemanıdır ve \( \abs{x - a} \lt \delta \) eşitsizliği ile tanımdaki koşula dahil edilir.
Bu tanımdaki \( \delta \) değeri \( \varepsilon \) değerine bağlı olan ve \( \varepsilon \) cinsinden ifade edilen bir değişkendir, bu yüzden soru ve ispatlarda \( \delta = \delta(\varepsilon) \) şeklinde de ifade edilebilir.
\( f(x) = 2x + 6 \) fonksiyonunun \( x = 4 \) noktasında sürekli olduğunu epsilon-delta tanımını kullanarak gösterelim.
Fonksiyonun sürekliliğini epsilon-delta tanımına göre gösterebilmek için aşağıdaki koşulun her durumda sağlandığı bir \( \delta \) değerini \( \varepsilon \) cinsinden ifade edebilmemiz gerekir.
\( \varepsilon \gt 0 \) ve \( \delta \gt 0 \) olmak üzere, fonksiyonun tanım kümesindeki her \( x \) değeri için,
\( \abs{x - a} \lt \delta \Longrightarrow \abs{f(x) - f(a)} \lt \varepsilon \)
koşulunu sağlayan \( \delta \) değerini \( \varepsilon \) cinsinden bulmaya çalışalım.
Soruda verilen bilgileri bu koşullu önermede yerine koyalım.
\( f(4) = 2(4) + 6 = 14 \) olmak üzere,
\( \abs{x - 4} \lt \delta \Longrightarrow \abs{(2x + 6) - 14} \lt \varepsilon \)
İkinci önermeyi aşağıdaki gibi düzenleyelim.
\( \abs{(2x + 6) - 14} \lt \varepsilon \)
\( \abs{2x - 8} \lt \varepsilon \)
\( \abs{2(x - 4)} \lt \varepsilon \)
\( 2\abs{x - 4} \lt \varepsilon \)
\( \abs{x - 4} \lt \dfrac{\varepsilon}{2} \)
Amacımız fonksiyonun tanım kümesindeki her \( x \) değeri için tanımdaki koşullu önermeyi sağlayacak \( \delta \) değerini \( \varepsilon \) cinsinden ifade etmekti. Elde ettiğimiz \( \abs{x - 4} \lt \frac{\varepsilon}{2} \) eşitsizliğinin \( \abs{x - 4} \lt \delta \) eşitsizliği ile benzer olduğunu görüyoruz, dolayısıyla \( \delta = \frac{\varepsilon}{2} \) olarak seçtiğimiz durumda yukarıdaki koşullu önermenin her zaman sağlanacağını söyleyebiliriz.
\( \delta = \frac{\varepsilon}{2} \) olarak seçtiğimiz durumda, fonksiyonun tanım kümesindeki her \( x \) değeri için,
\( \abs{x - 4} \lt \delta \Longrightarrow \abs{(2x + 6) - 14} \lt \varepsilon \)
koşullu önermesi sağlanır. Bu yüzden fonksiyon \( x = 4 \) noktasında süreklidir.
Tek Taraflı Süreklilik
Sürekliliğin epsilon-delta tanımını tek taraflı sürekliliğe küçük değişikliklerle aşağıdaki şekilde uyarlayabiliriz.
Sağdan Süreklilik
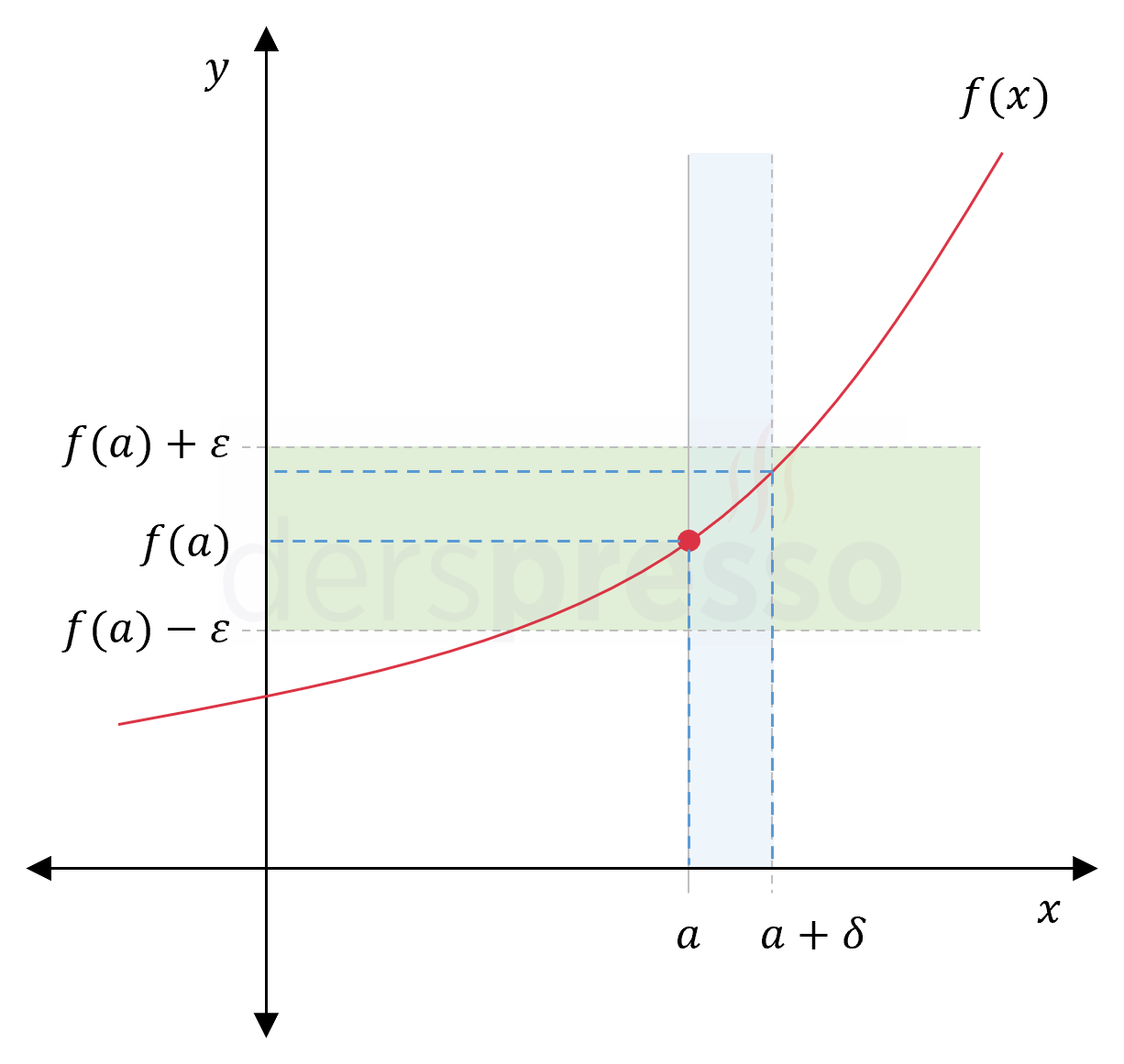
Sağdan sürekliliğin epsilon-delta tanımında, \( x \) \( a \)'ya sağdan yaklaştığı için \( \abs{x - a} \lt \delta \) eşitsizliği yerine \( a \le x \lt a + \delta \) kullanılır.
Yukarıda tanımını yaptığımız \( f \) fonksiyonu için,
her \( \varepsilon \gt 0 \) değeri için aşağıdaki koşullu önermeyi sağlayan bir \( \delta \gt 0 \) değeri bulunabiliyorsa \( f \) fonksiyonu \( a \) noktasında sağdan süreklidir.
Her \( x \in A \) değeri için,
\( a \le x \lt a + \delta \Longrightarrow \abs{f(x) - f(a)} \lt \varepsilon \)
Soldan Süreklilik
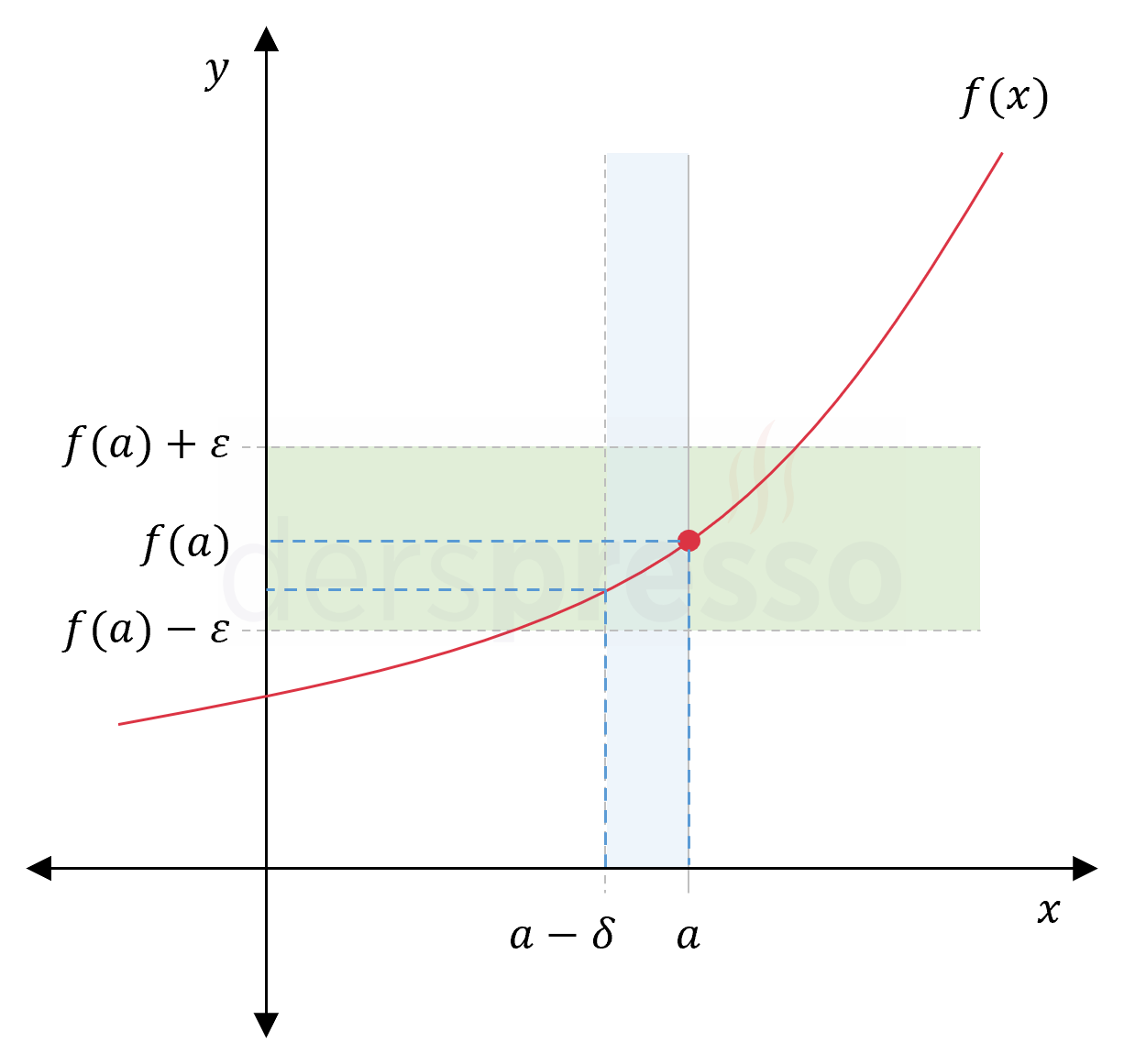
Soldan sürekliliğin epsilon-delta tanımında, \( x \) \( a \)'ya soldan yaklaştığı için \( \abs{x - a} \lt \delta \) eşitsizliği yerine \( a - \delta \lt x \le a \) kullanılır.
Yukarıda tanımını yaptığımız \( f \) fonksiyonu için,
her \( \varepsilon \gt 0 \) değeri için aşağıdaki koşullu önermeyi sağlayan bir \( \delta \gt 0 \) değeri bulunabiliyorsa \( f \) fonksiyonu \( a \) noktasında soldan süreklidir.
Her \( x \in A \) değeri için,
\( a - \delta \lt x \le a \Longrightarrow \abs{f(x) - f(a)} \lt \varepsilon \)