Ara Değer Teoremi
Ara değer teoremine göre, bir \( f \) fonksiyonu tanım kümesi içindeki bir \( [a, b] \) kapalı aralığında sürekli ise fonksiyon bu aralıkta \( f(a) \) ve \( f(b) \) arasındaki bir \( s \) değerini en az bir kez alır.
\( I = [a, b] \) reel sayılar kümesinde kapalı bir aralık,
\( f: I \to \mathbb{R} \) sürekli bir fonksiyon olmak üzere,
\( I \) aralığında \( f(a) \le s \le f(b) \) ya da \( f(a) \ge s \ge f(b) \) koşulunu sağlayan en az bir \( f(c) = s \) noktası bulunabilir.
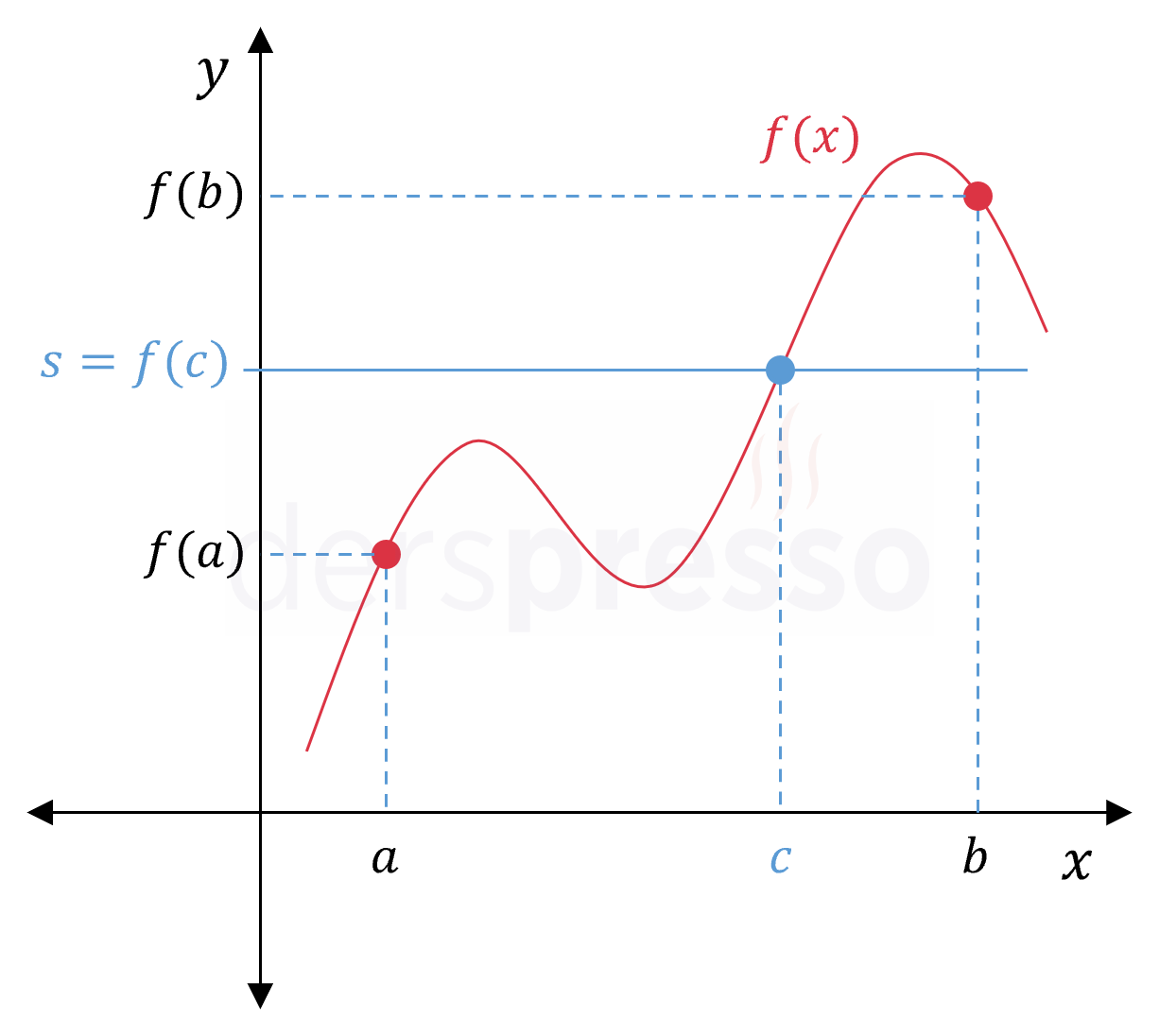
Ara değer teoremini şu şekilde de ifade edebiliriz: Sürekli bir fonksiyon \( f(a) \) ve \( f(b) \) değerlerini alıyorsa \( [a, b] \) aralığında bu iki değer arasındaki tüm değerleri de en az bir kez alır.
Ara değer teoreminin uygulamalarından biri de bir fonksiyonun belirli bir aralıkta kökünün olup olmadığını bulmaktır. Eğer bir \( f \) fonksiyonunun \( [a, b] \) aralığında sürekli olduğunu biliyorsak ve \( f(a) \) ve \( f(b) \) değerleri ters işaretli ise fonksiyon \( [a, b] \) aralığında en azından bir noktada \( f(x) = 0 \) değerini almak zorundadır, dolayısıyla fonksiyonun bu aralıkta en az bir kökü vardır. Dikkat edilirse, ara değer teoremi bize bir kök değerlerini vermemekte, sadece bir aralıkta fonksiyonun kökünün olup olmadığını söylemektedir.
Aşağıdaki fonksiyonun \( [-2, 2] \) aralığında hangi tam sayı aralıklarında kökü olduğunu bulalım.
\( f(x) = x^5 - 5x^2 - x + 3 \)
Tanımı verilen fonksiyonun verilen aralıktaki her tam sayı için fonksiyon değerini bulalım.
\( f(-2) = (-2)^5 - 5 \cdot (-2)^2 - (-2) + 3 = -47 \)
\( f(-1) = (-1)^5 - 5 \cdot (-1)^2 - (-1) + 3 = -2 \)
\( f(0) = 0^5 - 5 \cdot 0^2 - 0 + 3 = 3 \)
\( f(1) = 1^5 - 5 \cdot 1^2 - 1 + 3 = -2 \)
\( f(2) = 2^5 - 5 \cdot 2^2 - 2 + 3 = 13 \)
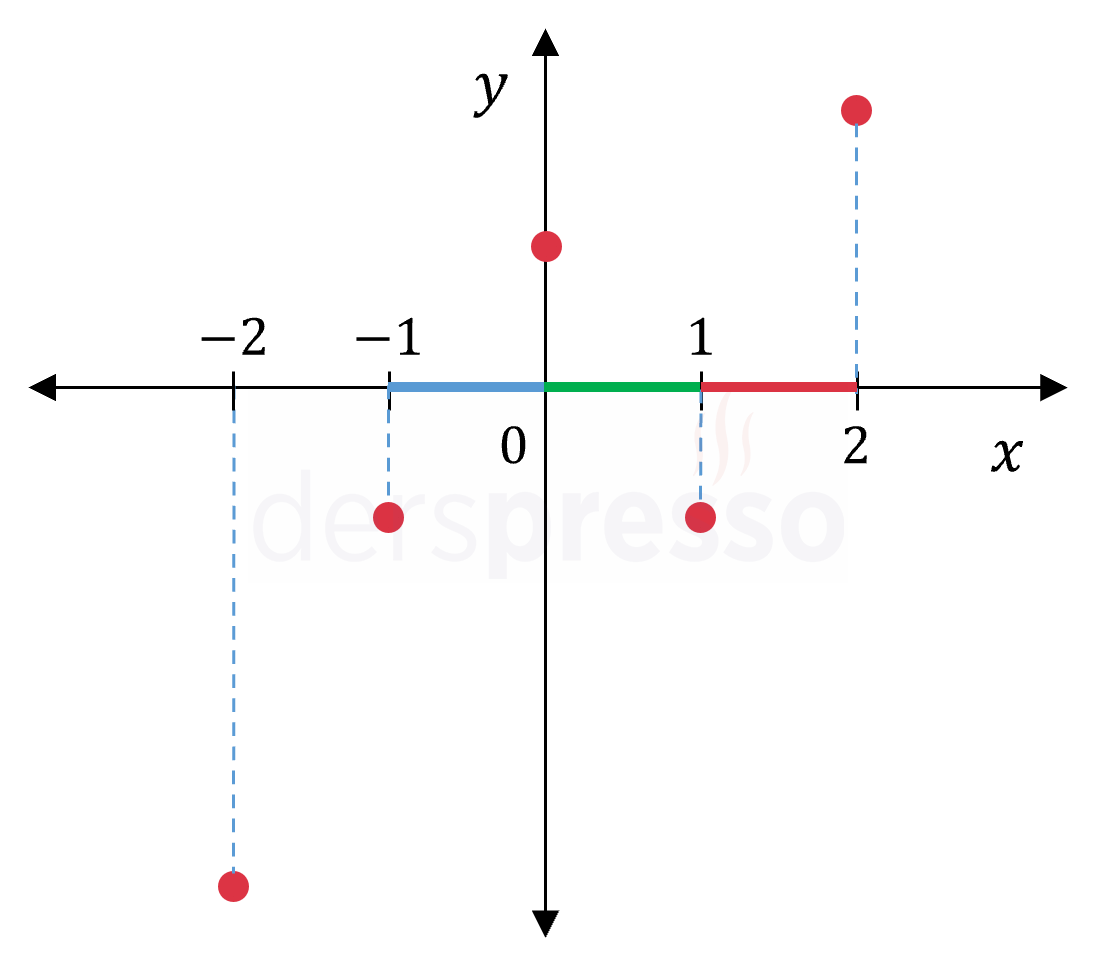
Bu değerleri yukarıdaki gibi analitik düzlemde işaretlediğimizde aşağıdaki yorumları yapabiliriz. Fonksiyonun \( x \) eksenini kestiğinden emin olduğumuz aralıklar \( x \) ekseni üzerinde renkli işaretlenmiştir.
\( (-2, -1) \) aralığı: Bu aralığın iki ucunda fonksiyonun işareti negatif olduğu için bu aralıkta bir kök olduğunu kesinlikle söyleyemeyiz. Grafik bu aralıkta \( x \) eksenini kesmeyebilir ya da kesip tekrar \( x \) ekseninin altına inebilir.
\( (-1, 0) \) aralığı: Bu aralıkta fonksiyon işaret değiştirdiği için bu aralıkta en azından bir kök olduğunu söyleyebiliriz.
\( (0, 1) \) aralığı: Bu aralıkta fonksiyon işaret değiştirdiği için bu aralıkta en azından bir kök olduğunu söyleyebiliriz.
\( (1, 2) \) aralığı: Bu aralıkta fonksiyon işaret değiştirdiği için, bu aralıkta en azından bir kök olduğunu söyleyebiliriz.
Aşağıda \( f(x) \) fonksiyonunun gerçek grafiği verilmiştir. Bu grafikte fonksiyonun \( x \) eksenini ara değer teoremi ile belirlediğimiz ve renkli işaretlediğimiz aralıklarda kestiğini görebiliriz.
\( x \in \mathbb{R} - \{ 0 \} \) olmak üzere,
\( f(x) = 3^x - \dfrac{12}{x} \) fonksiyonunun reel kökü olup olmadığını bulunuz.
Çözümü Göster\( f \) fonksiyonu tüm tanım kümesinde süreklidir.
Fonksiyonun tanım kümesini iki alt aralığa bölelim.
\( \mathbb{R} - \{ 0 \} = (-\infty, 0) \cup (0, \infty) \)
Durum 1: \( x \in (-\infty, 0) \)
Bu aralıkta \( \frac{12}{x} \lt 0 \) olduğu için her \( x \) değeri için \( f(x) \gt 0 \) olur.
Fonksiyon bu aralıkta daima pozitif değerler alır. Dolayısıyla \( x \) eksenini kesmez, yani bu aralıkta \( f \) fonksiyonunun reel kökü yoktur.
Durum 2: \( x \in (0, \infty) \)
Fonksiyonun bu aralığın iki ucunda yaklaştığı değerleri bulalım.
\( \lim\limits_{x \to 0^+} f(x) = \lim\limits_{x \to 0^+} (3^x - \dfrac{12}{x}) \)
\( x \to 0^+ \) iken \( \frac{12}{x} \to +\infty \) olur.
\( = -\infty \)
\( \lim\limits_{x \to \infty} f(x) = \lim\limits_{x \to \infty} (3^x - \dfrac{12}{x}) \)
\( x \to \infty \) iken \( 3^x \to +\infty \) olur.
\( x \to \infty \) iken \( \frac{12}{x} \to 0 \) olur.
\( = +\infty \)
Fonksiyon bu aralıkta işaret değiştirdiği için ara değer teoremine göre bu aralıkta en azından bir kez \( x \) eksenini kestiğini, yani bir kökü olduğunu söyleyebiliriz.