Rasyonel Sayı Tanımı
Paydası sıfır olmamak şartıyla, iki tam sayının oranı şeklinde yazılabilen sayılara rasyonel sayılar denir. Rasyonel sayılar kümesi \( \mathbb{Q} \) sembolü ile gösterilir.
\( \mathbb{Q} = \left\{ \dfrac{a}{b} \mid a, b \in \mathbb{Z}, b \ne 0 \right\} \)
Bu tanıma göre aşağıdaki sayılar birer rasyonel sayıdır.
\( \dfrac{1}{2}, -\dfrac{4}{3} \)
\( 2\dfrac{4}{5} = \dfrac{14}{5} \)
Kesirli şekilde ifade edilebilen ondalık ve yüzdeli ifadeler de birer rasyonel sayıdır.
\( 2,5 = \dfrac{5}{2} \)
\( \%75 = \dfrac{3}{4} \)
Tam sayılar kesirli şekilde yazılabildikleri için birer rasyonel sayıdır.
\( 0 = \dfrac{0}{1} = \dfrac{0}{5} \)
\( 1 = \dfrac{1}{1} = \dfrac{5}{5} \)
\( -2 = -\dfrac{2}{1} = -\dfrac{4}{2} \)
Virgülden sonra sonlu sayıda basamağı olan ondalık sayılar, kesirli şekilde yazılabildikleri için birer rasyonel sayıdır.
\( 0,123456 = \dfrac{123456}{1000000} \)
Devirli ondalık sayılar virgülden sonraki basamakları tekrar ederek sonsuza gitse de, kesirli şekilde yazılabildikleri için birer rasyonel sayıdır.
\( 0,333\ldots = 0,\overline{3} = \dfrac{1}{3} \)
\( 2,272727\ldots = 2,\overline{27} = \dfrac{25}{11} \)
Özetle, ondalık gösterimdeki bir rasyonel sayının ya virgülden sonra sonlu sayıda basamağı vardır ya da bu basamaklar sonsuza gidiyorsa bir basamaktan sonra kendini tekrar eder.
\( \pi \) ve \( e \) sayıları, virgülden sonraki basamakları tekrar etmeden sonsuza gittiği için rasyonel sayı değildir. Bazı sorularda \( \pi \) sayısı için verilen \( 3,14 \) ve \( \frac{22}{7} \) değerleri \( \pi \) sayısının gerçek değeri olmayıp hesaplama kolaylığı açısından verilen yaklaşık değerlerdir.
Kökten tamamen kurtulmayan köklü ifadelerin virgülden sonraki basamakları tekrar etmeden sonsuza gider, dolayısıyla bu sayılar rasyonel sayı değildir.
Rasyonel sayı değil:
\( \sqrt{2} = 1,414213\ldots \)
\( \sqrt[3]{5} = 1,709975\ldots \)
Rasyonel sayı:
\( \sqrt{16} = 4 \)
\( \sqrt{\frac{9}{16}} = \frac{3}{4} \)
\( \sqrt[3]{-27} = -3 \)
Sayı doğrusu üzerinde işaretlenecek birbirinden farklı iki rasyonel sayı arasında sonsuz sayıda rasyonel sayı vardır.
\( a, b, c, d \in \mathbb{Z}, \quad b \ne 0, \quad d \ne 0 \),
\( \dfrac{a}{b} \lt \dfrac{c}{d} \) olmak üzere,
\( \frac{a}{b} \) ve \( \frac{c}{d} \) rasyonel sayılarının ortalamasını, yani sayı doğrusu üzerindeki orta noktalarını bulalım.
Ortalama: \( \dfrac{\frac{a}{b} + \frac{c}{d}}{2} = \dfrac{ad + bc}{2bd} \)
\( a, b, c, d \) birer tam sayı olduğu için \( ad + bc \) ve \( 2bd \) ifadeleri de birer tam sayıdır, dolayısıyla bu orta noktanın karşılık geldiği sayı da bir rasyonel sayıdır.
Bu orta nokta ile işleme başladığımız rasyonel sayılardan herhangi biri ile bu işlemi ne kadar tekrarlarsak tekrarlayalım, elde edeceğimiz sayı yine bir rasyonel sayı olur.
Rasyonel Sayıların Gösterim Şekilleri
Rasyonel sayılar kesirli, ondalık sayı ve yüzde şeklinde ifade edilebilirler. Bu üç gösterim birbirinden farklı sayılar olmayıp herhangi bir rasyonel sayı için bu gösterimlerin üçü de kullanılabilir.
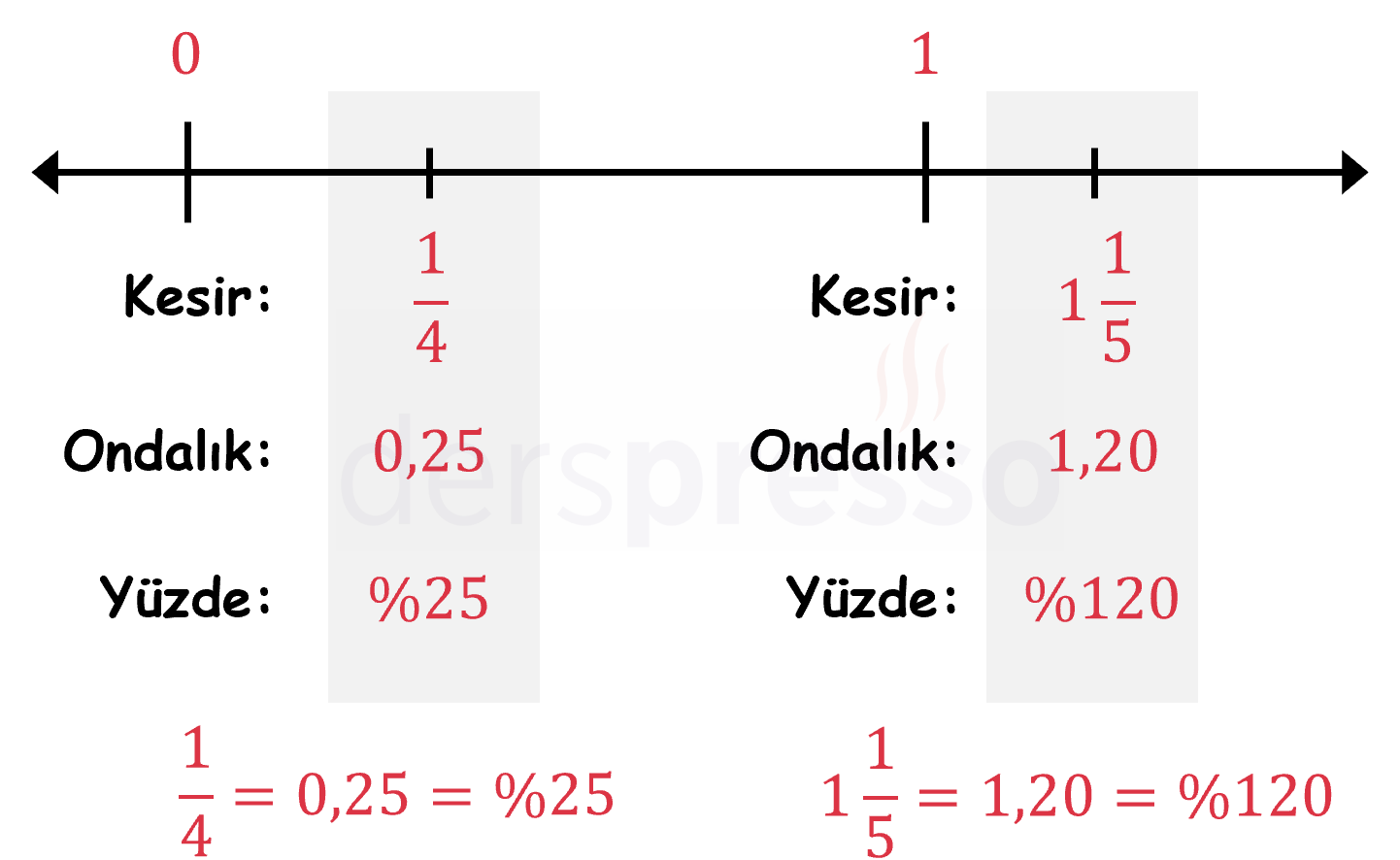
Aşağıdaki ifadelerden kaç tanesi rasyonel sayıdır?
\( \dfrac{14}{3}; \quad 1,3\overline{2}; \quad -29; \quad 9,999... \)
\( \dfrac{45}{0}; \quad \dfrac{3\sqrt{5}}{11}; \quad 0; \quad \pi \)
Çözümü Göster\( \frac{14}{3} \) iki tam sayının oranı şeklinde yazılabildiği için rasyonel sayıdır.
Devirli ondalık sayılar iki tam sayının oranı şeklinde yazılabildiği için rasyonel sayılardır (\( 1,3\overline{2} = \frac{119}{90} \)).
\( -29 \) bir tam sayıdır ve aynı zamanda rasyonel sayıdır.
\( 9,999... \) devirli ondalık sayısı 10'a eşit olduğu için bir tam sayıdır ve aynı zamanda rasyonel sayıdır.
\( \frac{45}{0} \) paydası sıfır olduğundan tanımsızdır ve rasyonel sayı değildir.
\( \sqrt{5} \) ifadesi kökten kurtarılamadığı için \( \frac{3\sqrt{5}}{11} \) rasyonel sayı değildir.
0 bir tam sayıdır ve aynı zamanda rasyonel sayıdır.
\( \pi \) sayısı rasyonel sayı değildir.
Buna göre verilen ifadelerden 5 tanesi rasyonel sayıdır.