Ondalık Sayılarla İşlemler
Bu bölümde ondalık sayılarla dört işlem kurallarını inceleyeceğiz.
Ondalık Sayılarla Toplama
Ondalık sayılarla toplama işlemi aşağıdaki şekilde yapılır.
- Sayılar ondalık işaretleri birbiriyle hizalanacak şekilde alt alta yazılır.
- Daha az sayıda ondalık basamağa sahip olan sayının sonuna sayıların ondalık basamak sayıları aynı olacak şekilde sıfır eklenir.
- Sayılar ondalık işaretini dikkate almadan normal toplama işlemi ile alt alta toplanır.
- Elde edilen sonuçta ondalık işareti üstteki sayılarla aynı basamağa konur.
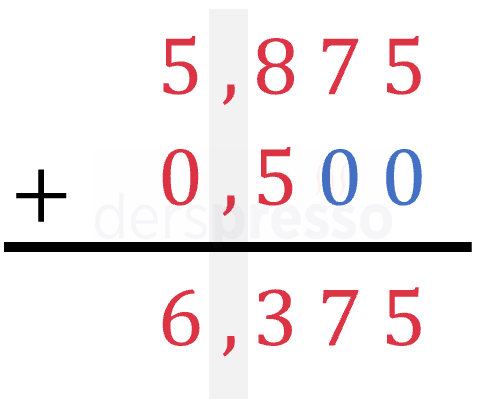
Ondalık Sayılarla Çıkarma
Ondalık sayılarla çıkarma işlemi aşağıdaki şekilde yapılır.
- Sayılar ondalık işaretleri birbiriyle hizalanacak şekilde alt alta yazılır.
- Daha az sayıda ondalık basamağa sahip olan sayının sonuna sayıların ondalık basamak sayıları aynı olacak şekilde sıfır eklenir.
- Sayılar ondalık işaretini dikkate almadan normal çıkarma işlemi ile alt alta çıkarılır.
- Elde edilen sonuçta ondalık işareti üstteki sayılarla aynı basamağa konur.
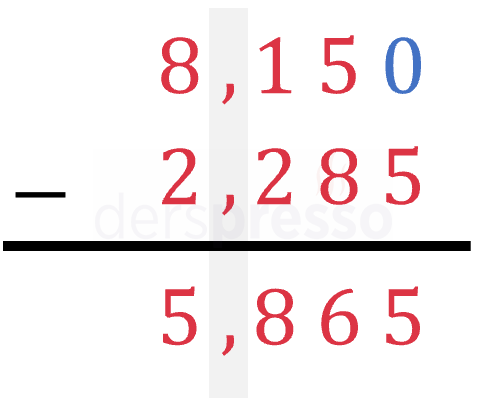
Ondalık Sayılarla Çarpma
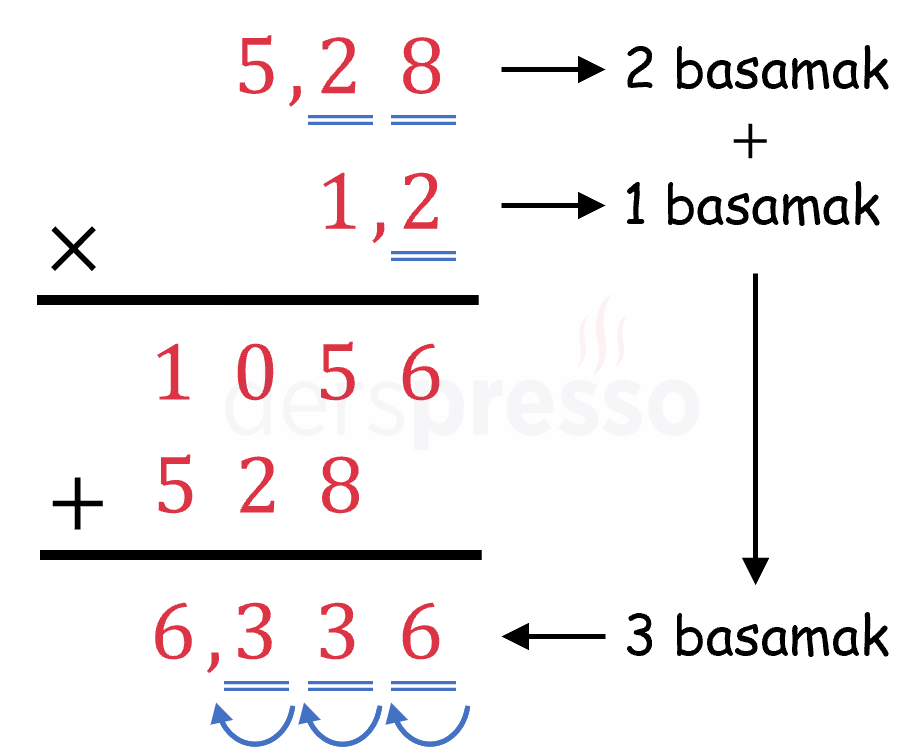
Ondalık sayılarla çarpma işlemi aşağıdaki şekilde yapılır.
- Sayılar alt alta yazılır, sonlarına eksik basamaklar için sıfır eklenmez, sayılar ondalık işaretlerine göre hizalanmaz, tam sayılarla çarpmada olduğu gibi en sağdaki basamakları hizalanacak şekilde dizilir.
- Sayılar ondalık işaretini dikkate almadan normal çarpma işlemi ile alt alta çarpılır.
- Çarpılan sayıların virgülden sonraki basamak sayıları toplanır, çarpma işleminin sonucunda sağdan o kadar basamak sayılarak ondalık işareti yerine konur.
Bu çarpma işleminde arka planda yaptığımız işlem, çarpanları 10'un kuvvetleri biçiminde yazıp çarpma işlemini tam sayı ve 10'un kuvveti bileşenleri için ayrı ayrı yapmaktır. Aşağıda aynı işlem bu detayla birlikte gösterilmiştir.
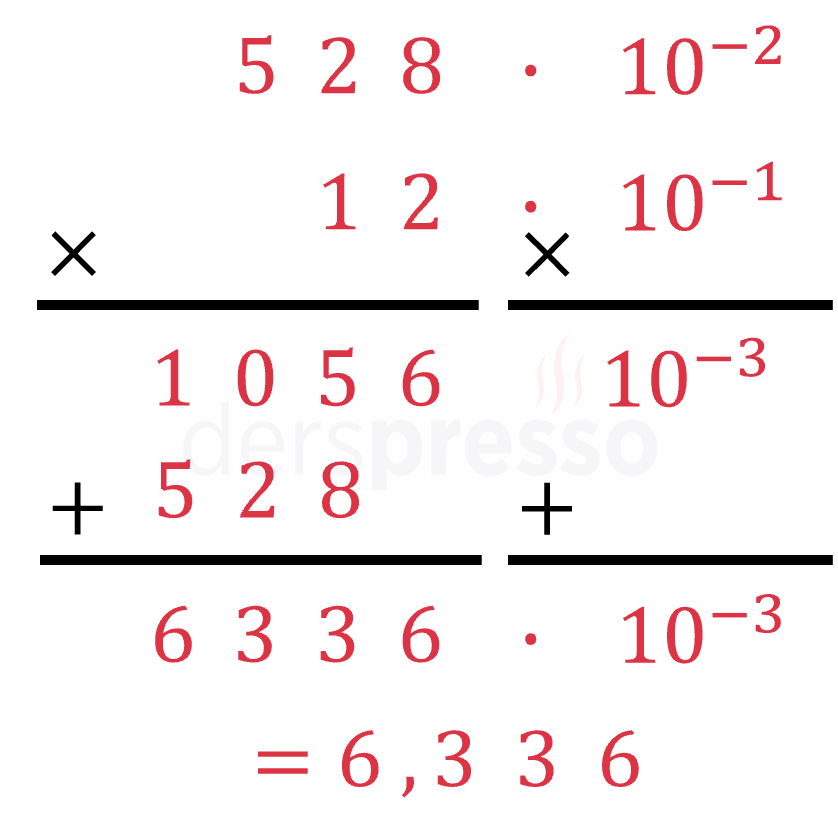
Ondalık Sayılarla Bölme
Ondalık sayılarla bölme işlemi aşağıdaki şekilde yapılır.
- Kesir işlemi bölme işlemi ile özdeş olduğu için, bölünen ve bölen sayılar bir kesrin payı ve paydası olarak düşünülür.
- Pay ve payda tam sayı olana kadar kesir 10 ile genişletilir. Her genişletme işlemi sonucunda, payda ya da paydada ondalık basamak varsa virgül bir basamak sağa kaydırılır. Ondalık basamak kalmadıysa sayının sonuna bir sıfır eklenir.
- Pay ve paydanın ikisi de tam sayı olduğunda bu iki sayı arasında normal bölme işlemi yapılır. Elde edilen sonuç iki ondalık sayının bölümüne eşittir.
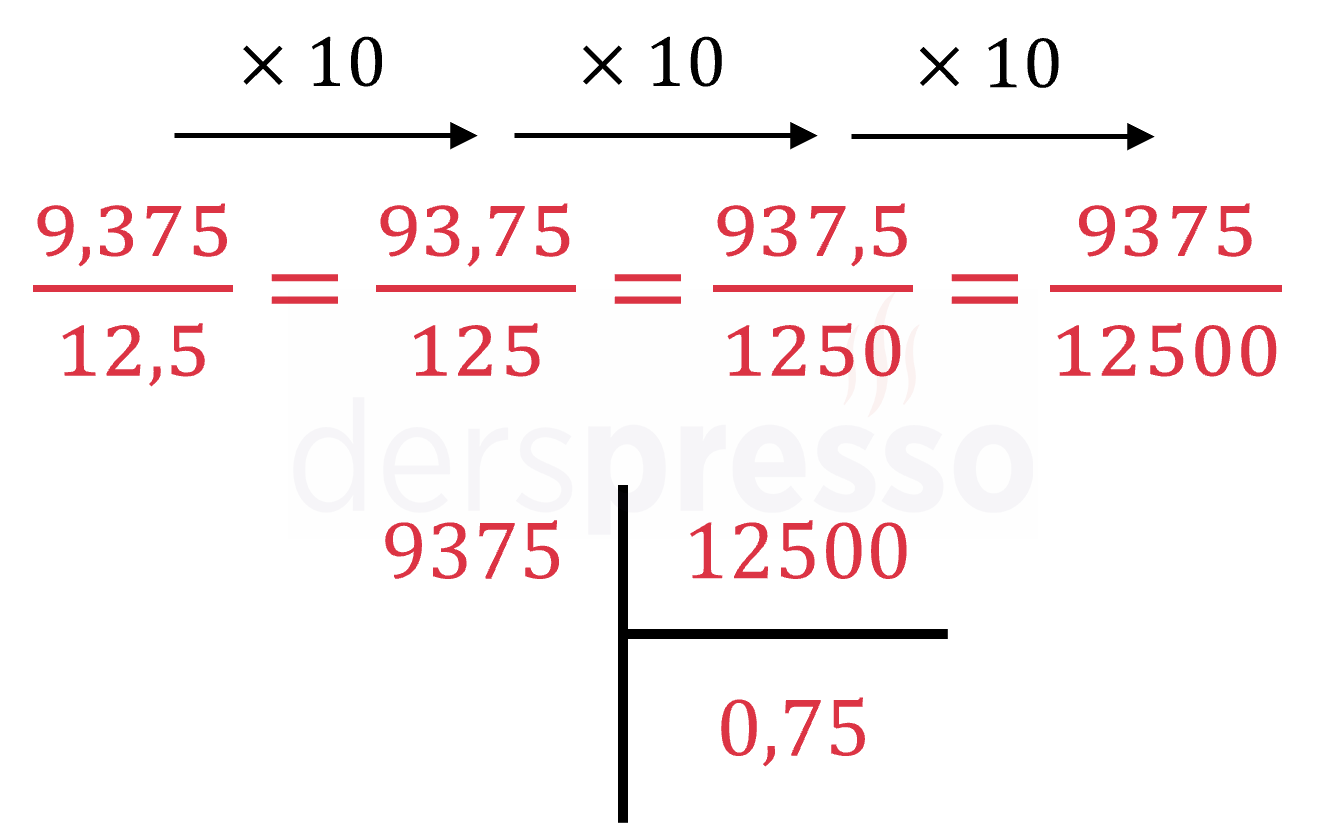
Aşağıdaki işlemlerin sonucunu bulunuz.
(a) \( 3,6 \cdot 0,5 + 3,2 \)
(b) \( (\dfrac{5,5}{1,1} - \dfrac{0,9}{3}) \cdot \dfrac{1}{47} \)
(c) \( \dfrac{0,07 - 0,045}{0,01} - \dfrac{1}{2} \)
Çözümü Göster(a) seçeneği:
\( 3,6 \cdot 0,5 + 3,2 \)
Ondalık sayıları kesirli gösterimde yazalım.
\( = \dfrac{36}{10} \cdot \dfrac{5}{10} + \dfrac{32}{10} \)
Gerekli sadeleştirmeleri yapalım.
\( = \dfrac{9}{5} + \dfrac{16}{5} \)
Paydaları eşit iki kesrin toplamında paylar toplanır.
\( = \dfrac{25}{5} = 5 \)
(b) seçeneği:
\( (\dfrac{5,5}{1,1} - \dfrac{0,9}{3}) \cdot \dfrac{1}{47} \)
Kesirleri pay ve payda tam sayı olana kadar 10 ile genişletelim.
\( = (\dfrac{55}{11} - \dfrac{9}{30}) \cdot \dfrac{1}{47} \)
\( = (5 - \dfrac{3}{10}) \cdot \dfrac{1}{47} \)
\( = \dfrac{5 \cdot 10 - 3}{10} \cdot \dfrac{1}{47} \)
\( = \dfrac{47}{10} \cdot \dfrac{1}{47} \)
\( = \dfrac{1}{10} = 0,1 \)
(c) seçeneği:
\( \dfrac{0,07 - 0,045}{0,01} - \dfrac{1}{2} \)
\( = \dfrac{0,070 - 0,045}{0,01} - \dfrac{1}{2} \)
\( = \dfrac{0,025}{0,01} - \dfrac{1}{2} \)
Kesirleri pay ve payda tam sayı olana kadar 10 ile genişletelim.
\( = \dfrac{25}{10} - \dfrac{1}{2} \)
\( = \dfrac{25}{10} - \dfrac{5}{10} \)
\( = \dfrac{20}{10} = 2 \)
Aşağıdaki işlemlerin sonucunu bulunuz.
(a) \( \dfrac{0,8}{0,16} + \dfrac{0,54}{0,09} - \dfrac{5,5}{0,10} \)
(b) \( (\dfrac{4}{0,08} + \dfrac{3}{0,5} - \dfrac{2}{0,25}) \cdot \dfrac{1}{1,92} \)
(c) \( \dfrac{4,05}{0,45} + \dfrac{3,5}{0,56} \)
Çözümü Göster(a) seçeneği:
\( \dfrac{0,8}{0,16} + \dfrac{0,54}{0,09} - \dfrac{5,5}{0,10} \)
Kesirleri pay ve payda tam sayı olana kadar 10 ile genişletelim.
\( \dfrac{80}{16} + \dfrac{54}{9} - \dfrac{550}{10} \)
\( = 5 + 6 - 55 \)
\( = -44 \) bulunur.
(b) seçeneği:
\( (\dfrac{4}{0,08} + \dfrac{3}{0,5} - \dfrac{2}{0,25}) \cdot \dfrac{1}{1,92} \)
Kesirleri pay ve payda tam sayı olana kadar 10 ile genişletelim.
\( = (\dfrac{400}{8} + \dfrac{30}{5} - \dfrac{200}{25}) \cdot \dfrac{100}{192} \)
\( = (50 + 6 - 8) \cdot \dfrac{100}{192} \)
\( = 48 \cdot \dfrac{100}{192} \)
\( = \dfrac{100}{4} = 25 \)
(c) seçeneği:
\( \dfrac{4,05}{0,45} + \dfrac{3,5}{0,56} \)
Kesirleri pay ve payda tam sayı olana kadar 10 ile genişletelim.
\( = \dfrac{405}{45} + \dfrac{350}{56} \)
\( = 9 + \dfrac{25}{4} \)
\( = \dfrac{9 \cdot 4 + 25}{4} \)
\( = \dfrac{61}{4} = 15,25 \)
Aşağıdaki işlemlerin sonucunu bulunuz.
(a) \( \sqrt{0,0009} \)
(b) \( \sqrt{10,24} \)
(c) \( \sqrt[3]{0,064} \)
Çözümü Göster(a) seçeneği:
\( \sqrt{0,0009} = \sqrt{\dfrac{9}{10000}} \)
\( = \sqrt{\dfrac{3^2}{100^2}} \)
\( = \dfrac{3}{100} = 0,03 \)
(b) seçeneği:
\( \sqrt{10,24} = \sqrt{\dfrac{1024}{100}} \)
\(= \sqrt{\dfrac{32^2}{10^2}} \)
\( = \dfrac{32}{10} = 3,2 \)
(c) seçeneği:
\( \sqrt[3]{0,064} = \sqrt[3]{\dfrac{64}{1000}} \)
\( = \sqrt[3]{\dfrac{4^3}{10^3}} \)
\( = \dfrac{4}{10} = 0,4 \)
\( \dfrac{3}{3,41} + \dfrac{14}{84} + 3 + \dfrac{7}{8,4} + \dfrac{41}{341} \)
ifadesinin değeri kaçtır?
Çözümü GösterKesirleri pay ve payda tam sayı olana kadar 10 ile genişletelim.
\( = \dfrac{300}{341} + \dfrac{14}{84} + 3 + \dfrac{70}{84} + \dfrac{41}{341} \)
Paydaları eşit olan terimleri kendi aralarında toplayalım.
\( = \dfrac{300 + 41}{341} + \dfrac{14 + 70}{84} + 3 \)
\( = \dfrac{341}{341} + \dfrac{84}{84} + 3 \)
\( = 1 + 1 + 3 = 5 \) bulunur.
\( a + \dfrac{9}{40} = b \)
\( b \) bir tam sayı olduğuna göre, \( a \) ondalık sayısının virgülden sonraki kısmı nedir?
Çözümü GösterKesri ondalık gösterimde yazalım.
\( a + \dfrac{9 \cdot 25}{40 \cdot 25} = b \)
\( a + \dfrac{225}{1000} = b \)
\( a + 0,225 = b \)
\( b \)'nin tam sayı olabilmesi için \( a \)'nın virgülden sonraki kısmı 775 olmalıdır.
\( a = \ldots,775 \)
\( \dfrac{1}{4} \), \( \sqrt{6,25} \), \( (0,16)^2 \), \( 0,05 \) reel sayılarını küçükten büyüğe doğru sıralayın.
Çözümü GösterTüm sayıları ondalık gösterimde yazalım.
\( \dfrac{1}{4} = 0,25 \)
\( \sqrt{6,25} = \sqrt{\dfrac{625}{100}} = \dfrac{25}{10} = 2,5 \)
\( (0,16)^2 = 0,0256 \)
\( 0,05 \)
Sayıların küçükten büyüğe sıralaması aşağıdaki gibi olur.
\( 0,0256 \lt 0,05 \lt 0,25 \lt 2,5 \)
\( (0,16)^2 \lt 0,05 \lt \frac{1}{4} \lt \sqrt{6,25} \)
\( 0,04(4a - 8) + 0,02a - 0,4 = 0,15 \)
Yukarıdaki eşitliği sağlayan \( a \) değeri kaçtır?
Çözümü GösterOndalık sayıları kesirli gösterimde yazalım.
\( \dfrac{4}{100}(4a - 8) + \dfrac{2}{100}a - \dfrac{4}{10} = \dfrac{15}{100} \)
Kesirli ifadelerin paydalarını eşitleyelim.
\( \dfrac{4}{100}(4a - 8) + \dfrac{2}{100}a - \dfrac{40}{100} = \dfrac{15}{100} \)
Eşitliğin taraflarını 100 ile çarptığımızda tüm terimlerin paydalarındaki 100'ler sadeleşir.
\( 4(4a - 8) + 2a - 40 = 15 \)
\( 16a - 32 + 2a - 40 = 15 \)
\( 18a = 87 \)
\( a = \dfrac{29}{6} \) bulunur.