Kesirler
Bir bütünün bölündüğü eşit parçalardan birinin ya da birkaçının bütüne oranına kesir denir.
Aşağıdaki şekiller eşit parçalara bölündükleri için birer kesir ifade ederler. Her parçanın ayrı ayrı ve boyalı alanın toplamda karşılık geldiği kesir değerleri şekillerin üzerinde belirtilmiştir.
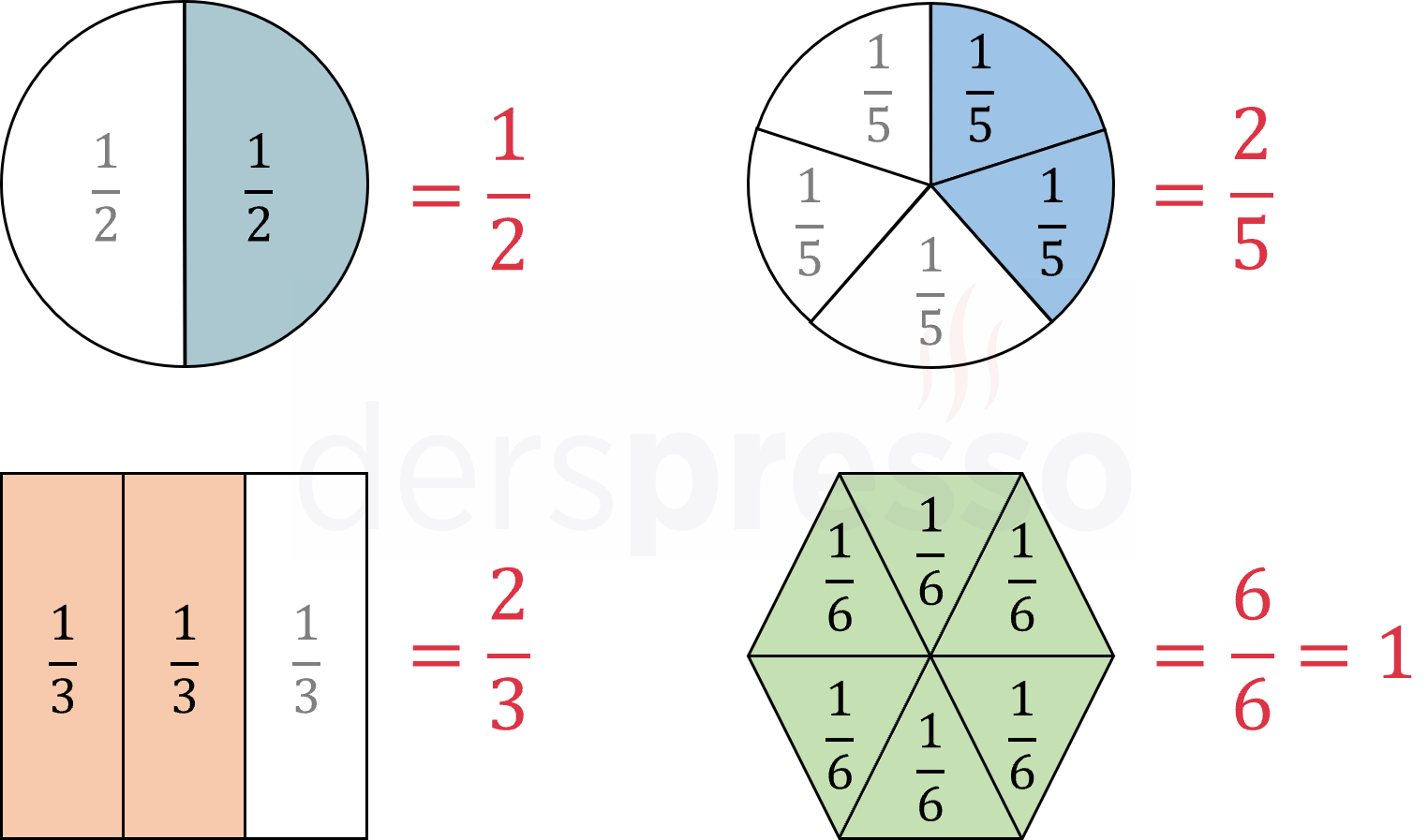
Aşağıdaki şekiller eşit parçalara bölünmedikleri için kesir ifade etmezler.
Kesir gösteriminde çizginin altındaki değere payda denir ve bütünün kaç eşit parçaya bölündüğünü gösterir. Çizginin üstündeki değere pay denir ve bu eşit parçalardan kaçının seçildiğini gösterir. Payı ve paydayı ayıran çizgiye kesir çizgisi denir.
Yukarıdaki \( \frac{2}{5} \) kesrini örnek olarak alırsak, kesirler "2 bölü 5" ya da "5'te 2" şeklinde okunurlar.
Kesirler sadece bir şekil ya da kavram değil, aynı zamanda 1, 2, 3 gibi birer sayıdır, bir büyüklük ifade ederler, sayı doğrusu üzerinde gösterilebilirler, matematiksel işlemlerde ve pratik hayatta diğer sayılar gibi kullanılırlar (\( \frac{1}{2} \) ekmek, \( \frac{1}{4} \) altın gibi).
Günlük hayatta kullanılan "tam/bütün" ifadeleri 1 sayısına, "yarım" ifadesi \( \frac{1}{2} \) kesrine, "çeyrek" ifadesi de \( \frac{1}{4} \) kesrine karşılık gelir.
2 yarım: \( 2 \cdot \dfrac{1}{2} = \dfrac{2}{2} = 1 \)
3 çeyrek: \( 3 \cdot \dfrac{1}{4} = \dfrac{3}{4} \)
Kesir Tipleri
Birim Kesir
Payı 1 ve paydası bir pozitif tam sayı olan kesirlere birim kesir denir. Birim kesir bir bütünün bölündüğü eşit parçalardan her birine karşılık gelir.
\( \dfrac{1}{2}, \dfrac{1}{3}, \dfrac{1}{4}, \dfrac{1}{5}, \ldots \)
Basit Kesir
Payı paydasından mutlak değer olarak küçük olan kesirlere basit kesir denir.
\( 0 \le \abs{a} \lt \abs{b} \) ise,
\( \dfrac{a}{b} \) bir bileşik kesirdir.
Pozitif basit kesirler:
\( \dfrac{1}{3}, \dfrac{7}{9}, \dfrac{99}{100} \)
Negatif basit kesirler:
\( -\dfrac{1}{3}, \dfrac{-7}{9}, \dfrac{99}{-100} \)
Basit kesirler sayısal değer olarak 1'den küçük, -1'den büyüktür.
Bileşik Kesir
Payı paydasından mutlak değer olarak büyük ya da ona eşit olan kesirlere bileşik kesir denir.
\( 0 \lt \abs{b} \le \abs{a} \) ise,
\( \dfrac{a}{b} \) bir bileşik kesirdir.
Pozitif bileşik kesirler:
\( \dfrac{5}{3}, \dfrac{20}{19} , \dfrac{7}{7} \)
Negatif bileşik kesirler:
\( -\dfrac{5}{3}, \dfrac{-20}{19} , \dfrac{7}{-7} \)
Tam Sayılı Kesir
Bir tam sayı ve bir basit kesirden oluşan kesirlere tam sayılı kesir denir.
\( 1\dfrac{2}{3}, 3\dfrac{2}{5}, -2\dfrac{4}{9} \)
Tam sayılı kesirlerde tam sayı ve kesir kısımları arasında bir işaret bulunmasa da matematiksel olarak toplama işlemi vardır, dolayısıyla iki sayı arasında çarpma işlemi olduğu varsayılmamalıdır.
\( 2\dfrac{2}{3} = 2 + \dfrac{2}{3} \)
Kesir Gösterimleri Arası Çevrimler
Bileşik Kesri Tam Sayılı Kesre Çevirme
Bir bileşik kesir tam sayılı kesre aşağıdaki şekilde çevrilir.
- Bileşik kesir içinde kaç bütün olduğunu bulmak için paydaki sayı paydadaki sayıya bölünür.
- Bölme işleminin bölümü kesrin tam sayı kısmına, kalanı payına yazılır.
- Bileşik kesrin paydası tam sayılı kesrin paydasına aynen taşınır.
Bu işlemin daha iyi anlaşılması adına, yukarıdaki kesir aşağıdaki şekilde uzun yoldan tam sayılı kesre çevrilebilir.
\( \dfrac{23}{5} = \dfrac{5 + 5 + 5 + 5 + 3}{5} \)
\( = \dfrac{5}{5} + \dfrac{5}{5} + \dfrac{5}{5} + \dfrac{5}{5} + \dfrac{3}{5} \)
\( = 1 + 1 + 1 + 1 + \dfrac{3}{5} = 4\dfrac{3}{5} \)
Tam Sayılı Kesri Bileşik Kesre Çevirme
Bir tam sayılı kesir bileşik kesre aşağıdaki şekilde çevrilir.
- Kesrin paydasındaki sayı kesrin tam sayı kısmı ile çarpılır ve paydaki sayı ile toplanır.
- Elde edilen toplam bileşik kesrin payına yazılır.
- Tam sayılı kesrin paydası bileşik kesrin paydasına aynen taşınır.
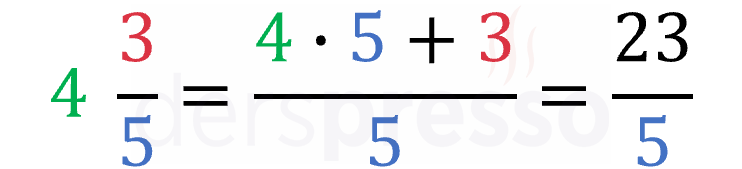
Bu işlemin daha iyi anlaşılması adına, yukarıdaki kesir aşağıdaki şekilde uzun yoldan bileşik kesre çevrilebilir.
\( 4\dfrac{3}{5} = 4 + \dfrac{3}{5} \)
\( = 1 + 1 + 1 + 1 + \dfrac{3}{5} \)
\( = \dfrac{5}{5} + \dfrac{5}{5} + \dfrac{5}{5} + \dfrac{5}{5} + \dfrac{3}{5} \)
\( = \dfrac{5 + 5 + 5 + 5 + 3}{5} = \dfrac{23}{5} \)
Kesirlerin Sayı Doğrusu Üzerinde Gösterimi
Kesirler de birer reel sayı oldukları için sayı doğrusu üzerinde gösterilebilirler. Bir kesir, bulunduğu tam sayı aralığı kesrin paydası kadar eşit parçaya bölünerek sayı doğrusu üzerinde işaretlenebilir.
Aşağıdaki örnekte 0-1 sayıları arası iki eşit parçaya, 1-2 sayıları arası üç eşit parçaya, 2-3 sayıları arası dört eşit parçaya bölünerek işaretli her noktanın karşılık geldiği kesirler belirtilmiştir.
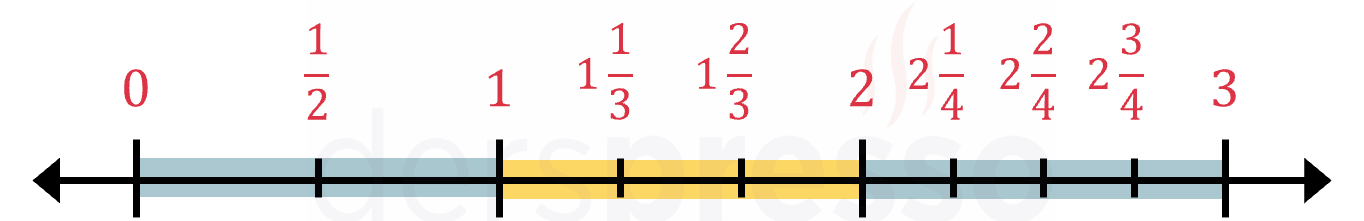
Negatif Kesirler
Kesirli ifadeler, diğer sayılar gibi pozitif olabildikleri gibi negatif de olabilirler. Aşağıdaki gösterimler birbirine eşit olup birer negatif kesir ifade etmektedir.
\( \dfrac{-2}{3} = \dfrac{2}{-3} = -\dfrac{-2}{-3} = -\dfrac{2}{3} \)
Payın ve paydanın negatif olduğu durumlarda negatif işaretleri birbirini götürür ve kesir pozitif değer alır.
\( \dfrac{-2}{-3} = -\dfrac{2}{-3} = -\dfrac{-2}{3} = \dfrac{2}{3} \)
Kesirlerin Bölme Anlamı
Kesir işareti anlam olarak bölme işareti ile özdeştir, bu yüzden kesir işlemi paydaki sayının paydadaki sayıya bölümü olarak da düşünülebilir.
\( \dfrac{a}{b} = a \div b \)
\( \dfrac{3}{4} = 3 \div 4 = 0,75 \)
\( \dfrac{12}{5} = 12 \div 5 = 2,4 \)
Aşağıdaki kesirli ifadeleri sayı doğrusu üzerinde gösterin.
\( \dfrac{3}{4}, \quad -1\dfrac{2}{3}, \quad 2\dfrac{1}{5} \)
Çözümü Göster\( \dfrac{3}{4} \) sayı doğrusu üzerinde \( 0 \) ve \( 1 \) sayıları arasındadır.
\( -1\dfrac{2}{3} \) sayı doğrusu üzerinde \( -2 \) ve \( -1 \) sayıları arasındadır.
\( 2\dfrac{1}{5} \) sayı doğrusu üzerinde \( 2 \) ve \( 3 \) sayıları arasındadır.
Bu sayıları sayı doğrusu üzerinde gösterelim.
Aşağıdaki bileşik kesirleri tam sayılı kesre çevirerek sayı doğrusu üzerinde gösterin.
(a) \( \dfrac{7}{2} \)
(b) \( \dfrac{33}{15} \)
(c) \( -\dfrac{11}{6} \)
Çözümü GösterVerilen bileşik kesirleri tam sayılı kesre çevirelim.
(a) seçeneği:
Pay içindeki paydanın tam sayı katlarını kesrin dışına alalım.
\( \dfrac{7}{2} = \dfrac{3 \cdot 2 + 1}{2} \)
\( = 3\dfrac{1}{2} \)
(b) seçeneği:
Kesrin payını ve paydasını 3 ile sadeleştirelim.
\( \dfrac{33}{15} = \dfrac{11}{5} \)
Pay içindeki paydanın tam sayı katlarını kesrin dışına alalım.
\( = \dfrac{2 \cdot 5 + 1}{5} = 2\dfrac{1}{5} \)
(c) seçeneği:
Pay içindeki paydanın tam sayı katlarını kesrin dışına alalım.
\( -\dfrac{11}{6} = -\dfrac{1 \cdot 6 + 5}{6} \)
\( = -1\dfrac{5}{6} \)
Bu sayıları sayı doğrusu üzerinde gösterelim.
\( \dfrac{7}{4 - 3a} \) ifadesinin bileşik kesir olması için \( a \)'nın alabileceği tam sayı değerlerin toplamı kaçtır?
Çözümü Gösterİfadenin bileşik kesir olması için pay paydaya eşit ya da mutlak değerce ondan büyük olmalıdır.
\( \abs{4 - 3a} \le 7 \)
\( -7 \le 4 - 3a \le 7 \)
Eşitsizliğin taraflarından 4 çıkaralım.
\( -11 \le -3a \le 3 \)
Tarafları -1 ile çarpalım. Bir eşitsizliğin tarafları negatif bir sayı ile çarpıldığında eşitsizlik yön değiştirir.
\( 11 \ge 3a \ge -3 \)
Tarafları 3'e bölelim.
\( \dfrac{11}{3} \ge a \ge -1 \)
\( a \)'nın alabileceği tam sayı değerlerin toplamını bulalım.
\( -1 + 0 + 1 + 2 + 3 = 5 \) bulunur.
\( a \in \mathbb{Z^+} \) olmak üzere,
\( \frac{7}{a} \) basit kesir ve \( \frac{45}{2a} \) bileşik kesir olduğuna göre, \( a \) sayısının alabileceği kaç değer vardır?
Çözümü GösterPayı paydasından mutlak değer olarak küçük olan kesirlere basit kesir denir.
\( \frac{7}{a} \) basit kesirdir.
\( 7 \lt a \)
Payı paydasından mutlak değer olarak büyük ya da ona eşit olan kesirlere bileşik kesir denir.
\( \frac{45}{2a} \) bileşik kesirdir.
\( 2a \le 45 \)
\( a \le 22,5 \)
Buna göre \( a \) değer aralığı aşağıdaki gibidir.
\( 7 \lt a \le 22,5 \)
\( a \in \{ 8, 9, 10, 11, \ldots, 22 \} \)
Buna göre \( a \) sayısının alabileceği \( 22 - 8 + 1 = 15 \) değer vardır.
\( (999 \dfrac{999}{1000}) \cdot 3 \) ifadesini tam sayılı kesir olarak yazın.
Çözümü GösterTam sayılı kesrin tam sayı ve kesir kısımları toplama işlemi ile ayrılabilir.
\( (999 + \dfrac{999}{1000}) \cdot 3 \)
3'ü parantez içine dağıtalım.
\( = 3 \cdot 999 + \dfrac{3 \cdot 999}{1000} \)
\( = 2997 + \dfrac{2997}{1000} \)
Kesrin payı içindeki 1000'in katlarını ayıralım.
\( = 2997 + \dfrac{2 \cdot 1000 + 997}{1000} \)
\( = 2997 + 2 + \dfrac{997}{1000} \)
\( = 2999 + \dfrac{997}{1000} \)
\( = 2999 \dfrac{997}{1000} \) bulunur.
\( a, b \in \mathbb{R} \) olmak üzere,
\( 3 \lt a \lt b \lt 22 \)
olduğuna göre, \( \frac{b}{a} \) kesrinin alabileceği tam sayı değerlerin toplamı kaçtır?
Çözümü Göster\( a \) ve \( b \) birbirine en yakın sayılar seçildiğinde \( \frac{b}{a} \) en küçük, birbirine en uzak sayılar seçildiğinde ise en büyük değerini alır.
Sayıların birbirine en yakın oldukları durumda \( a = b \) ve \( \frac{b}{a} = 1 \) olur.
Sayıların birbirine en uzak oldukları durumda \( a = 3 \), \( b = 22 \) ve \( \frac{b}{a} = \frac{22}{3} \) olur.
Verilen eşitsizlikte \( \lt \) sembolü kullanıldığı için bu değerler \( \frac{b}{a} \) değer aralığına dahil olmazlar.
\( 1 \lt \dfrac{b}{a} \lt \dfrac{22}{3} \)
\( \frac{b}{a} \)'nın alabileceği tam sayı değerleri toplayalım.
\( 2 + 3 + 4 + 5 + 6 + 7 = 27 \) bulunur.
Aşağıdaki kesirlerden hangisi yarıma (\( 0,5 \)) daha yakındır?
\( \dfrac{31}{59}, \quad \dfrac{37}{67}, \quad \dfrac{43}{89}, \quad \dfrac{47}{97} \)
Çözümü GösterVerilen rasyonel sayıların payını paydasına bölerek ondalık sayı şeklinde yazalım.
\( \dfrac{31}{59} = 31 \div 59 = 0,5254... \)
\( \dfrac{37}{67} = 37 \div 67 = 0,5522... \)
\( \dfrac{43}{89} = 43 \div 89 = 0,4831... \)
\( \dfrac{47}{97} = 47 \div 97 = 0,4845... \)
Bu sayılardan yarıma en yakın olan \( \frac{47}{97} = 0,4845... \)'dir.
\( x, y \in \mathbb{Z} \) olmak üzere,
\( \dfrac{1}{2x - y + 3} + \dfrac{1}{y - 4x - 3} = 1 \)
olduğuna göre, \( x \cdot y \) çarpımının sonucu kaçtır?
Çözümü GösterPaydalar birer tam sayı olduğu için, iki birim kesrin toplamı 1 ise bu kesirler ayrı ayrı \( \frac{1}{2} \) olmalıdır.
Birinci kesrin paydasını 2'ye eşitleyelim.
\( 2x - y + 3 = 2 \)
\( 2x - y = -1 \)
İkinci kesrin paydasını 2'ye eşitleyelim.
\( y - 4x - 3 = 2 \)
\( y - 4x = 5 \)
Bulduğumuz iki eşitliği taraf tarafa toplayalım.
\( (2x - y) + (y - 4x) = -1 + 5 \)
\( x = -2 \)
Bulduğumuz değeri birinci eşitlikte yerine yazalım.
\( 2(-2) - y = -1 \)
\( y = -3 \)
\( x \cdot y \) çarpımının sonucu \( -2 \cdot (-3) = 6 \) olarak bulunur.
\( \dfrac{4 - 3y}{13x - y} \) kesri tanımsız olduğuna göre, \( \dfrac{2x - 3y}{16x + 9y} \) kesrinin değeri kaçtır?
Çözümü GösterBir kesrin paydası sıfır olamaz.
Verilen kesir tanımsız olduğuna göre paydası sıfıra eşittir.
\( 13x - y = 0 \)
\( y = 13x \)
İstenen kesrin değerini bulmak için \( y = 13x \) yazalım.
\( \dfrac{2x - 3y}{16x + 9y} = \dfrac{2x - 3(13x)}{16x + 9(13x)} \)
\( = \dfrac{-37x}{133x} = -\dfrac{37}{133} \) bulunur.
Aşağıdaki kesirler belirli bir örüntüye göre sıralanmıştır.
\( \dfrac{12}{132}, \dfrac{17}{125}, \dfrac{22}{118}, \ldots , \dfrac{102}{6} \)
Bu kesirlerden kaç tanesi bileşik kesirdir?
Çözümü GösterÖrüntünün genel terimini bulalım.
\( n \in \mathbb{N} \) olmak üzere,
\( \dfrac{12 + 5n}{132 - 7n} \)
\( 0 \le n \le 18 \)
Payı paydasından mutlak değer olarak büyük ya da ona eşit olan kesirler bileşik kesirdir.
\( 12 + 5n \ge 132 - 7n \)
\( 12n \ge 120 \)
\( n \ge 10 \)
Buna göre aşağıdaki \( n \) değerleri için örüntünün terimleri bileşik kesirdir.
\( 10 \le n \le 18 \)
Buna göre örüntüdeki \( 18 - 10 + 1 = 9 \) terim bileşik kesirdir.
\( \dfrac{8x + 4y}{28 - 7x} = 0 \)
ifadesinde \( x \) ve \( y \)'nin alamayacağı değerlerinin çarpımı kaçtır?
Çözümü GösterBir kesrin paydası sıfır olamaz.
\( 28 - 7x \ne 0 \)
\( x \ne 4 \)
Sonucun sıfır olması için pay sıfır, payda sıfırdan farklı olmalıdır.
\( x \)'in alamayacağı değer için payı sıfır yapan \( y \) değeri, \( y \)'nin alamayacağı değeri verir.
\( 8(4) + 4y \ne 0 \)
\( y \ne -8 \)
\( x \) ve \( y \)'nin alamayacağı değerleri çarpalım.
\( 4 \cdot (-8) = 32 \) bulunur.