Ondalık Sayılar
Paydası 10, 100, 1000 gibi 10'un bir tam sayı kuvveti olan kesirlere ondalık kesir denir.
\( \dfrac{7}{10}, \quad \dfrac{137}{100}, \quad \dfrac{143}{1000} \)
Ondalık kesirlerin birden büyük ve küçük kısımlarının virgülle ayrılarak ve paydasız şekilde yazılışına ondalık sayı denir. Yukarıdaki ondalık kesirlerin ondalık sayı yazılışları aşağıdaki gibidir.
\( 0,7; \quad 1,37; \quad 0,143 \)
Ondalık sayıların virgülden önceki kısmına tam sayı kısmı, virgülden sonraki kısmına ondalık kısım denir. Ondalık sayıların tam ve ondalık kısımlarını birbirinden ayıran virgül işaretine ondalık işareti denir. Ondalık sayılarda virgülün solunda sayının birden büyük olan kısmı, sağında birden küçük olan kısmı bulunur.
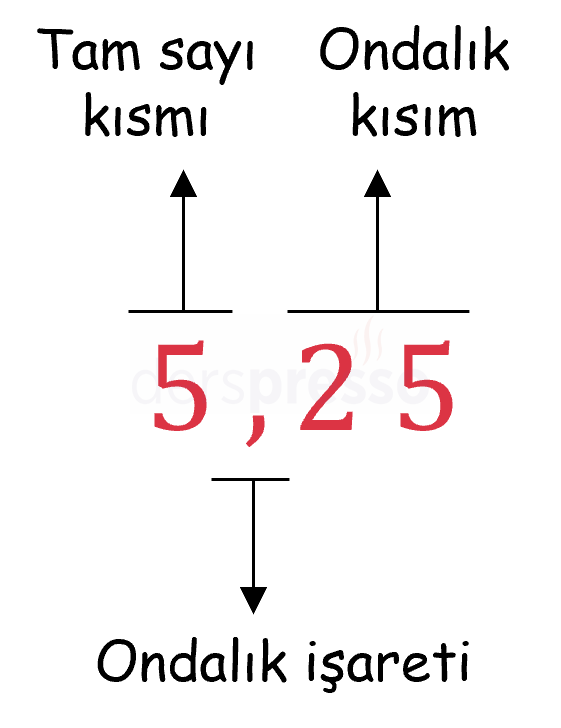
Ondalık sayılar tam sayı ve ondalık kısımlarının toplamına eşittir.
\( 5,25 = 5 + 0,25 \)
Ondalık sayıların ondalık kısmının sonuna sıfır eklemek sayının değerini değiştirmez.
\( 1,45 = 1,450 = 1,4500000 \)
\( 0,01 = 0,010 = 0,0100000 \)
Ondalık basamağa sahip sayılar üç grup altında incelenebilir.
Sonlu Ondalık Sayılar
Bu sayılar sonlu sayıda ondalık basamağa sahip sayılardır.
\( 1,75 = \dfrac{7}{4} \)
\( 0,12345 = \dfrac{12345}{100000} \)
Bu sayılar iki tam sayının oranı şeklinde yazılabildikleri için rasyonel sayılar kümesine dahildirler.
Devirli (Tekrarlı Sonsuza Giden) Ondalık Sayılar
Ondalık kısmı bir basamaktan sonra kendini tekrarlayarak sonsuza giden ondalık sayılara devirli ondalık sayı denir.
\( 0,333\ldots = 0,\overline{3} = \dfrac{1}{3} \)
\( 0,818181\ldots = 0,\overline{81} = \dfrac{9}{11} \)
Tüm devirli ondalık sayılar kesirli şekilde yazılabilirler, dolayısıyla rasyonel sayıdırlar.
Devirli ondalık sayıları daha detaylı şekilde önümüzdeki bölümlerde inceleyeceğiz.
Tekrarsız Sonsuza Giden Sayılar
Bu sayıların ondalık kısımları devirli ondalık sayılar gibi sonsuza gider, ancak basamaklar kendini tekrarlamaz. Bu sayılara örnek olarak \( \pi \) sayısı, \( e \) sayısı ve kökten tamamen kurtulmayan köklü sayılar (\( \sqrt{2}, \sqrt{3}, \sqrt[3]{5} \) vb.) verilebilir.
\( \pi = 3,1415926535\ldots \)
\( e = 2,7182818284\ldots \)
\( \sqrt{2} = 1,4142135623\ldots \)
Bu sayılar iki tam sayının oranı şeklinde yazılamadıkları için rasyonel sayılar kümesine dahil değildirler, dolayısıyla irrasyonel sayılardır.