Ondalık Sayılarda Basamak Değerleri
Konu tekrarı için: Basamak Kavramı
Basamak Değerleri
Ondalık sayılarda virgülden sonraki basamakların da birer basamak değeri vardır. Basamak değerleri, virgülden sonra sağa doğru ilerledikçe her basamağın birim değeri solundaki basamağın 10'da biri olacak şekilde azalır.
Aşağıda virgülden önce üç, virgülden sonra altı basamaklı bir ondalık sayının basamak isimleri ve birim basamak değerleri verilmiştir.

Aşağıdaki şekilde gösterildiği gibi, ondalık sayıların virgülden önceki tam sayı kısmında her basamak kendisinden sonraki basamaklarda sıfır olan ama bu sıfırların gösterilmediği daha büyük bir sayının değerini taşır. Virgülden sonraki basamaklarda da her basamak kendisinden önceki basamaklarda sıfır olan ama bu sıfırların gösterilmediği daha küçük bir sayının değerini taşır.
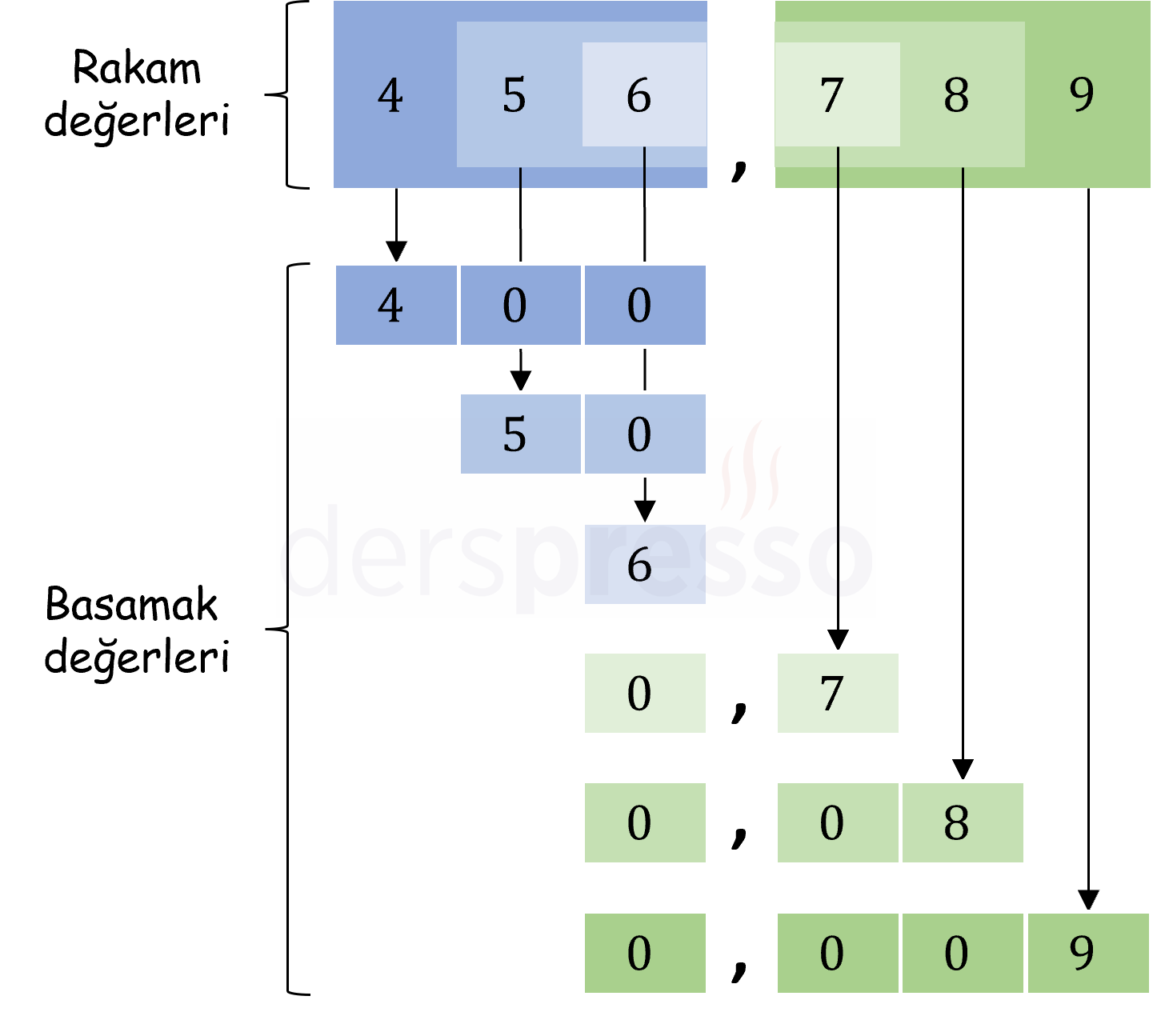
Yukarıda şekildeki \( 456,789 \) sayısının basamaklarının basamak değerlerinin hesaplaması aşağıdaki tabloda verilmiştir:
| Basamak Adı | Rakam Değeri | Hesaplama | Basamak Değeri |
|---|---|---|---|
| Yüzler basamağı | \( 4 \) | \( 4 \times 100 \) | \( 400 \) |
| Onlar basamağı | \( 5 \) | \( 5 \times 10 \) | \( 50 \) |
| Birler basamağı | \( 6 \) | \( 6 \times 1 \) | \( 6 \) |
| Onda birler basamağı | \( 7 \) | \( 7 \times 0,1 \) | \( 0,7 \) |
| Yüzde birler basamağı | \( 8 \) | \( 8 \times 0,01 \) | \( 0,08 \) |
| Binde birler basamağı | \( 9 \) | \( 9 \times 0,001 \) | \( 0,009 \) |
Bu basamak değerleri toplandığında aşağıdaki gibi sayının gerçek sayısal değerine ulaşılır.
\( 400 + 50 + 6 + 0,7 + 0,08 + 0,009 = 456,789 \)
Bir Sayının Çözümlenmesi
Bir sayının basamaklarının basamak değerlerinin toplamı şeklinde yazılışına o sayının çözümlenmesi denir.
Yukarıdaki örnekte kullandığımız \( (456,789) \) sayısının çözümlenmiş hali aşağıdaki gibidir.
\( (456,789) = 4 \times 100 + 5 \times 10 + 6 \times 1 + 7 \times 0,1 + 8 \times 0,01 + 9 \times 0,001 \)
6 basamaklı bir \( (abc,def) \) sayısının çözümlenmiş hali aşağıdaki gibidir.
\( (abc,def) = a \times 100 + b \times 10 + c \times 1 + d \times 0,1 + e \times 0,01 + f \times 0,001 \)
\( a \) ve \( b \) birer rakam olmak üzere,
\( (a,b) - (b,a) = 3,6 \) olduğuna göre, \( a - b \) farkı kaçtır?
Çözümü GösterVerilen ondalıklı sayıları tam sayıya çevirelim.
\( \dfrac{(ab)}{10} - \dfrac{(ba)}{10} = \dfrac{36}{10} \)
\( (ab) - (ba) = 36 \)
Sayıların çözümlemesini yapalım.
\( 10a + b - 10b - a = 36 \)
\( 9a - 9b = 36 \)
\( 9(a - b) = 36 \)
\( a - b = 4 \) bulunur.
\( a \) ve \( b \) birer rakam olmak üzere,
\( \dfrac{9a + b}{(a,b) - (ab,b)} \) ifadesinin sonucu kaçtır?
Çözümü GösterVerilen ondalıklı sayıları tam sayıya çevirelim.
\( \dfrac{9a + b}{(a,b) - (ab,b)} = \dfrac{9a + b}{\frac{(ab)}{10} - \frac{(abb)}{10}} \)
\( = \dfrac{9a + b}{\frac{(ab) - (abb)}{10}} \)
\( = \dfrac{10(9a + b)}{(ab) - (abb)} \)
Sayıların çözümlemesini yapalım.
\( = \dfrac{10(9a + b)}{10a + b - (100a + 10b + b)} \)
\( = \dfrac{10(9a + b)}{-90a - 10b} \)
\( = \dfrac{10(9a + b)}{-10(9a + b)} \)
\( = -1 \) bulunur.
\( a \) ve \( b \) birer rakam olmak üzere,
\( a = b - 1 \) olduğuna göre, \( (ac,b) - (bc,a) \) farkı kaçtır?
Çözümü GösterVerilen ondalıklı sayıları tam sayıya çevirelim.
\( (ac,b) - (bc,a) = \dfrac{(acb)}{10} - \dfrac{(bca)}{10} \)
Sayıların çözümlemesini yapalım.
\( = \dfrac{100a + 10c + b}{10} - \dfrac{100b + 10c + a}{10} \)
\( = \dfrac{99a - 99b}{10} \)
Verilen \( a \) değerini ifadede yerine koyalım.
\( = \dfrac{99(b - 1) - 99b}{10} \)
\( = \dfrac{99b - 99 - 99b}{10} \)
\( = -\dfrac{99}{10} = -9,9 \) bulunur.
\( a \) ve \( b \) birer rakam olmak üzere,
\( 2a + b = 14 \)
\( (a,b) = b - 4,2 \)
olduğuna göre, \( (a,b) \) sayısı kaçtır?
Çözümü Göster\( (a,b) = b - \dfrac{42}{10} \)
\( (a,b) = \dfrac{10b - 42}{10} \)
\( 10(a,b) = 10b - 42 \)
\( (ab) = 10b - 42 \)
Sayının çözümlemesini yapalım.
\( 10a + b = 10b - 42 \)
\( 10a - 9b = -42 \)
Bu ve soruda verilen denklemi ortak çözelim.
\( 2a + b = 14 \)
Bu eşitliğin taraflarını \( -5 \) ile çarpıp birinci denklemle ortak çözelim.
\( 10a - 9b = -42 \)
\( -10a - 5b = -70 \)
İki denklemi taraf tarafa toplayalım.
\( -14b = -112 \)
\( b = 8 \)
Bu değeri soruda verilen denklemde yerine koyarak \( a \) değerini bulalım.
\( 2a + 8 = 14 \)
\( a = 3 \)
\( (a,b) = 3,8 \) bulunur.
On adet sayının her birinin onda birler basamağı 3 azaltılıp yüzde birler basamağı 5 artırılıyor.
İlk durumdaki sayıların toplamı ile oluşan yeni sayıların toplamı arasındaki fark kaçtır?
Çözümü GösterBir sayının bir basamağını azaltmak (artırmak), sayıyı basamak değeri kadar azaltır (artırır).
Bir sayının onda birler basamağını 3 azaltmak sayının değerini \( 3 \cdot 0,1 = 0,3 \) azaltır.
Bir sayının yüzde birler basamağını 5 artırmak sayının değerini \( 5 \cdot 0,01 = 0,05 \) artırır.
Bir sayının onda birler basamağı 3 azaltılıp yüzde birler basamağı 5 artırıldığında sayının değerindeki değişimi bulalım.
\( -0,3 + 0,05 = -0,25 \)
Buna göre 10 adet sayının her birinin değeri \( 0,25 \) azalır.
\( 10 \cdot (-0,25) = -2,5 \)
Dolayısıyla, yeni sayıların toplamı ilk sayıların toplamından \( 2,5 \) daha azdır.
\( a \) ve \( b \) birer rakam olmak üzere,
\( (ab) \) sayısının rakamlarının toplamı 8'dir. Sayının rakamları yer değiştirdiğinde sayının değeri 18 azaldığına göre, bu sayı kaçtır?
Çözümü GösterSayının rakamlarının toplamı 8'dir.
\( a + b = 8 \)
Sayının rakamları yer değiştirdiğinde sayının değeri 18 azalıyor.
\( (ab) = (ba) + 18 \)
Sayıların çözümlemesini yapalım.
\( 10a + b = 10b + a + 18\)
\( 9a - 9b = 18 \)
\( 9(a - b) = 18 \)
\( a - b = 2 \)
Bulduğumuz iki denklemi ortak çözelim.
\( a + b = 8 \)
\( a - b = 2 \)
İki denklemi taraf tarafa toplayalım.
\( 2a = 10 \)
\( a = 5 \)
\( a \) değerini ilk denklemde yerine koyalım.
\( 5 + b = 8 \)
\( b = 3 \)
\( (ab) = 53 \) bulunur.
\( a \) ve \( b \) birer rakam olmak üzere,
\( (2,ab) \) sayısının birler basamağı ile onda birler basamağının yer değiştirmesiyle elde edilen sayı \( (2,ab) \) sayısının 3 katından \( 3,8 \) eksiktir.
Buna göre, \( (2,ab) \) sayısı kaçtır?
Çözümü Göster\( (2,ab) \) sayısının birler basamağı ile onda birler basamağını yer değiştirelim.
\( (a,2b) \)
Soruda verilen eşitliği yazalım.
\( (a,2b) = 3(2,ab) - 3,8 \)
Verilen ondalıklı sayıları tam sayıya çevirelim.
\( \dfrac{(a2b)}{100} = \dfrac{3(2ab)}{100} - \dfrac{38}{10} \)
\( (a2b) = 3(2ab) - 380 \)
Sayıların çözümlemesini yapalım.
\( 100a + 20 + b = 3(200 + 10a + b) - 380 \)
\( 100a + 20 + b = 600 + 30a + 3b - 380 \)
\( 70a - 2b = 200 \)
\( 35a - b = 100 \)
\( a \) ve \( b \) rakamlarının alabileceği değerleri bulalım.
\( a \lt 3 \) olduğunda \( b \) negatif olacağı için bu \( a \) değerleri için geçerli bir çözüm yoktur.
\( a = 3 \) verirsek \( b = 5 \) olur.
\( a \gt 3 \) olduğunda \( b \) bir rakam olmayacağı için bu \( a \) değerleri için geçerli bir çözüm yoktur.
Buna göre tek geçerli çözüm vardır.
\( a = 3, \quad b = 5 \)
\( (2,ab) = (2,35) \) bulunur.
\( a \) ve \( b \) birer rakam olmak üzere,
\( a^2 = b^2 + 39 \) olduğuna göre, \( (ab) - (ba) \) farkı kaçtır?
Çözümü GösterVerilen eşitliği düzenleyelim.
\( a^2 - b^2 = 39 \)
İki kare farkı özdeşliğini kullanalım.
\( (a - b)(a + b) = 39 \)
\( a \) ve \( b \) rakam olduğu için farkları ve toplamları tam sayıdır.
39'u çarpanlarına ayıralım.
\( (a - b)(a + b) = 3 \cdot 13 \)
İki rakamın toplamı ve farkı sırasıyla 39 ve 1 olamayacağı için 13 ve 3 olmalıdır.
\( a + b = 13 \)
\( a - b = 3 \)
Bulduğumuz iki denklemi ortak çözelim.
İki denklemi taraf tarafa toplayalım.
\( 2a = 16 \)
\( a = 8 \)
\( a \) değerini ilk denklemde yerine koyalım.
\( 8 + b = 13 \)
\( b = 5 \)
\( (ab) - (ba) = 85 - 58 = 27 \) bulunur.
\( x \cdot 1,5 - 8,96 = 1,04 \)
Yukarıdaki işlemi yapan Ferhat soruyu tekrar incelediğinde çarpma işlemi yerine toplama işlemi yaptığını fark ediyor ve işlemi tekrar yapıyor.
Ferhat'ın 2. bulduğu sonuç doğru olduğuna göre, bu sonuç kaçtır?
Çözümü Gösterİşlemi önce hatalı şekliyle yapalım.
\( x + 1,5 - 8,96 = 1,04 \)
\( x + 1,5 = 10 \)
\( x = 8,5 \)
İşlemi şimdi doğru şekliyle yapalım.
\( 8,5 \cdot 1,5 - 8,96 = \dfrac{85}{10} \cdot \dfrac{15}{10} - \dfrac{896}{100} \)
\( = \dfrac{1275}{100} - \dfrac{896}{100} \)
\( = \dfrac{379}{100} = 3,79 \) bulunur.
\( a \) ve \( b \) asal sayı rakamlar olmak üzere,
\( (a,aa) - (b,bb) = 4,44 \) olduğuna göre, \( a + b \) toplamı kaçtır?
Çözümü GösterVerilen ondalıklı sayıları tam sayıya çevirelim.
\( \dfrac{(aaa)}{100} - \dfrac{(bbb)}{100} = \dfrac{(444)}{100} \)
\( (aaa) - (bbb) = 444 \)
Sayıların çözümlemesini yapalım.
\( 100a + 10a + a - 100b - 10b - b = 444 \)
\( 111a - 111b = 444 \)
\( 111(a - b) = 444 \)
\( a - b = 4 \)
\( a \) ve \( b \) rakamlarının alabileceği değerleri bulalım.
\( a = 9, \quad b = 5 \)
\( a = 8, \quad b = 4 \)
\( a = 7, \quad b = 3 \)
\( a = 6, \quad b = 2 \)
\( a = 5, \quad b = 1 \)
\( a = 4, \quad b = 0 \)
\( a \) ve \( b \) rakamlarının ikisinin de asal olduğu bir durum vardır.
\( a + b = 7 + 3 = 10 \) bulunur.
\( a, b, c \) birer rakam olmak üzere,
\( (a,bc) + (b,c) = 9,76 \)
olduğuna göre, \( abc \) çarpımı kaçtır?
Çözümü GösterVerilen ondalıklı sayıları tam sayıya çevirelim.
\( \dfrac{(abc)}{100} + \dfrac{(bc)}{10} = \dfrac{976}{100} \)
Sayıların çözümlemesini yapalım.
\( \dfrac{100a + 10b + c}{100} + \dfrac{10b + c}{10} = \dfrac{976}{100} \)
\( \dfrac{100a + 10b + c}{100} + \dfrac{10(10b + c)}{100} = \dfrac{976}{100} \)
\( 100a + 10b + c + 100b + 10c = 976 \)
\( 100a + 110b + 11c = 976 \)
\( a, b, c \) rakamlarının alabileceği değerleri bulalım.
\( a = 9 \) verirsek \( b = 0 \) olur.
\( 900 + 0 + 11c = 976 \)
\( 11c = 76 \)
Bu durumda geçerli bir \( c \) değeri yoktur.
\( a = 8 \) verirsek \( b = 1 \) olur.
\( 800 + 110 + 11c = 976 \)
\( 11c = 66 \)
\( c = 6 \)
\( a = 7 \) verirsek \( b = 2 \) olur.
\( 700 + 220 + 11c = 976 \)
\( 11c = 56 \)
Bu durumda geçerli bir \( c \) değeri yoktur.
\( a \) için 0 - 6 aralığındaki diğer değerler denendiğinde başka geçerli çözüm bulunmadığı görülecektir.
Buna göre tek geçerli çözüm vardır.
\( a = 8, \quad b = 1, \quad c = 6 \)
\( (abc) = 816 \)
\( abc = 8 \cdot 1 \cdot 6 = 48 \) bulunur.