Polinom Tanımı
Katsayıların, değişkenlerin ve bu değişkenlerin doğal sayı kuvvetlerinin çarpımından oluşan tek terimli cebirsel ifadelere monom denir.
\( 3x^2, \quad 5x^3y \)
\( -2xy^2z^5, \quad 4 \)
Yukarıdaki tanıma göre bir monom ifadede değişkenler;
- Sadece doğal sayı kuvvetleri ile bulunabilir (\( x, x^2, x^3, \ldots \)).
- Köklü ya da mutlak değerli ifadelerin içinde yer alamaz.
- Kesirli bir ifadenin paydasında bulunamaz.
- Trigonometrik ya da logaritmik fonksiyonların içinde yer alamaz.
Aşağıdaki ifadelerin neden birer monom olmadığını belirtin.
\( 3x^2 - y, \quad \frac{x}{y^2}, \quad 2^x \)
\( 5x^2\sqrt{y^3}, \quad 4\abs{y} \)
\( 3\sin{x}, \quad 2x^2\log(y) \)
Çözümü Göster\( 3x^2 - y \): Bir monom ifade tek bir terimden oluşabilir.
\( \frac{x}{y^2} = xy^{-2} \): Bir monom ifadede değişkenler sadece doğal sayı kuvvetleri ile bulunabilir, dolayısıyla değişkenlerin üsleri negatif olamaz.
\( 2^x \): Bir monom ifadede değişkenler üslü bir ifadenin tabanında bulunabilir, üssünde bulunamaz.
\( 5x^2\sqrt{y^3} = 5x^2y^{\frac{3}{2}} \): Bir monom ifadede değişkenler sadece doğal sayı kuvvetleri ile bulunabilir, dolayısıyla köklü ifade içinde yer alamaz.
\( 4\abs{y} \): Bir monom ifadede değişkenler mutlak değer içinde yer alamaz.
\( 3\sin{x} \): Bir monom ifadede değişkenler trigonometrik fonksiyonların içinde yer alamaz.
\( 2x^2\log(y) \): Bir monom ifadede değişkenler logaritmik fonksiyonların içinde yer alamaz.
Yukarıdaki kısıtlamalar ifadenin katsayısı için geçerli değildir, buna göre aşağıdaki ifadeler birer monomdur.
\( -\frac{1}{3}x^2y, \quad \sqrt{3}x, \quad \abs{-3}xy^3 \)
\( \sin{\frac{\pi}{3}} \cdot xy^2z^3, \quad -\log{5} \cdot x^2y \)
Sonlu sayıda monomun toplamından oluşan çok terimli ifadelere polinom denir. Polinomlar genellikle \( P(x) \), \( Q(x) \), \( R(x) \) şeklinde büyük harflerle gösterilir.
\( P(x) = 3xy^2 - x^2y + 2xy \)
\( Q(x) = 5x^6y^2z - 3xz^3 + yz + 6 \)
Reel Katsayılı, Bir Değişkenli Polinomlar
Yukarıda yaptığımız tanıma göre polinomlar birden fazla değişken içerebilir ve katsayıları reel ya da karmaşık sayı olabilir. Biz bu bölümde reel katsayılı ve bir değişkenli polinomları inceleyeceğiz.
\( n \in \mathbb{N} \) ve \( a_0, a_1, \ldots, a_n \in \mathbb{R} \) olmak üzere,
\( P(x) = a_nx^n + a_{n - 1}x^{n - 1} + a_{n - 2}x^{n - 2} + \ldots + a_2x^2 + a_1x + a_0 \)
formundaki polinomlara reel katsayılı ve bir değişkenli polinom denir.
\( P(x) = 3x^2 - 5 \)
\( Q(x) = x^5 - 2x^4 + x^2 - 3x + 7 \)
\( R(x) = x^{99} - x \)
Polinomun Bileşenleri
Bir polinomun toplama ve çıkarma işlemleriyle ayrılmış kısımlarına polinomun terimleri denir.
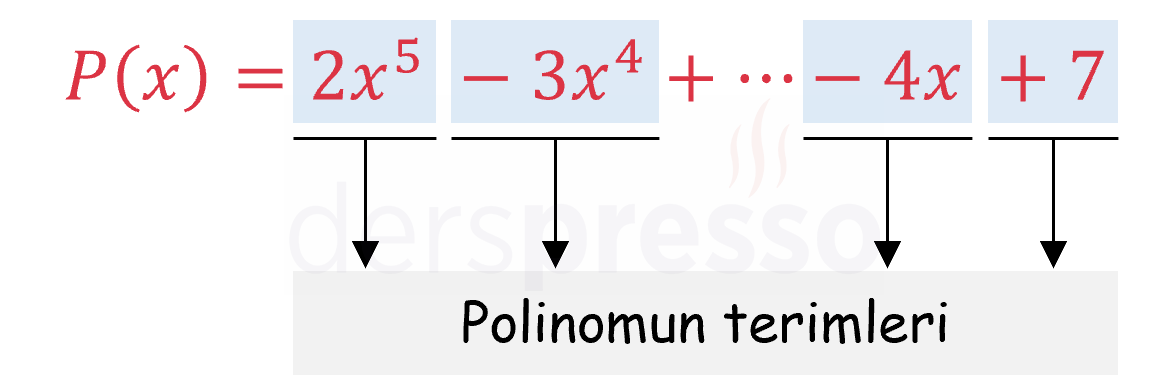
Bir değişkenin doğal sayı üssü o değişkenin derecesidir. Her polinom terimi bir değişkenden, değişkenin derecesinden ve önündeki reel katsayıdan oluşur.

Bir terimin önündeki \( + \) ya da \( - \) işareti o terimin katsayısının bir parçasıdır, dolayısıyla önündeki işaret \( - \) olan bir terimin katsayısı negatiftir.
Bir polinomun değişken içermeyen terimine polinomun sabit terimi denir. Sabit terim derecesi sıfır olan terimin katsayısı olarak da düşünülebilir.
\( P(x) = 2x^2 + 3x - \textcolor{red}{4} = 2x^2 + 3x^1 - \textcolor{red}{4x^0} \)
Bir polinomda belirli bir dereceden terim bulunmuyorsa o terimin katsayısı sıfır kabul edilir.
\( P(x) = 5x^3 - 3x = 5x^3 + \textcolor{red}{0}x^2 - 3x + \textcolor{red}{0}x^0 \)
Tek değişkenli polinomlarda değişkenin derecesi aynı zamanda o terimin derecesini belirler. Bir terimin derecesi çift sayı ise o terime çift dereceli terim, tek sayı ise tek dereceli terim denir. Sabit terim derecesi sıfır olduğu için çift dereceli bir terimdir.

Polinomun en yüksek dereceli teriminin katsayısına polinomun başkatsayısı denir.

Polinomların terimleri standart yazılışta en yüksek dereceden en düşük dereceye doğru sıralanır.
Polinomun Derecesi
Bir polinomun en yüksek dereceli teriminin derecesi o polinomun derecesi olur ve \( der[P(x)] \) ile gösterilir.
Bir polinomun (en yüksek dereceli teriminin) derecesi çift sayı ise o polinoma çift dereceli polinom, tek sayı ise tek dereceli polinom denir.
Aşağıda bazı örnek polinomlar ve dereceleri verilmiştir.
| Örnek Polinom | Derece | Polinomun Adı |
|---|---|---|
| \( P(x) = \textcolor{red}{3} \) | \( 0 \) | Sabit polinom |
| \( P(x) = \textcolor{red}{2x} + 1 \) | \( 1 \) | Birinci dereceden (doğrusal) polinom |
| \( P(x) = \textcolor{red}{x^2} - 5x + 6 \) | \( 2 \) | İkinci dereceden polinom |
| \( P(x) = \textcolor{red}{-2x^3} - x^2 + 4x - 3 \) | \( 3 \) | Üçüncü dereceden polinom |
| \( P(x) = \textcolor{red}{x^n} - 2x^{n - 1} + x - 1 \) | \( n \) | \( n \). dereceden polinom |
\( P(x) = (m - 4)x^6 + 3x^{n - 2} + 2x^4 + 5 \)
polinomunun derecesi 5 ise, \( m + n \) toplamı kaçtır?
Çözümü GösterPolinomun derecesi 5 ise, derecesi 6 olan terimin katsayısı 0 olmalıdır ve polinomda derecesi 5 olan bir terim olmalıdır.
Buna göre,
\( m - 4 = 0 \Longrightarrow m = 4 \)
\( n - 2 = 5 \Longrightarrow n = 7 \)
\( m + n = 4 + 7 = 11 \) bulunur.
Örnek Bir Polinom
Aşağıdaki \( P(x) \) polinomu üzerinden polinomların bileşenlerini gösterelim.
\( P(x) = 2x^5 - 3x^4 + 5x^3 - x^2 - 4x + 8 \)
| Özellik | Değer |
|---|---|
| Polinomun derecesi | \( 5 \) |
| Polinomun başkatsayısı | \( 2 \) |
| Terim sayısı | \( 6 \) |
| Polinomun terimleri | \( 2x^5, -3x^4, 5x^3, -x^2, -4x, 8 \) |
| Polinomun katsayıları | \( 2, -3, 5, -1, -4, 8 \) |
| Polinomun sabit terimi | \( 8 \) |
Polinomların Sınıflandırması
Polinomlar terim sayılarına göre aşağıdaki şekilde sınıflandırılır.
Monom (tek terimli): \( x^2 \)
Binom (iki terimli): \( x^3 + 5 \)
Trinom (üç terimli): \( x^5 - 3x + 5 \)
Polinom (çok terimli) \( x^7 - 4x^5 + 2x^3 - 5x - 8 \)
Polinom Fonksiyonu
Tanım ve değer kümesi arasındaki eşleme kuralı bir polinom olarak tanımlanmış fonksiyonlara polinom fonksiyonu denir.
\( f: \mathbb{R} \to \mathbb{R} \)
\( f(x) = 3x^4 - x^3 + 2x^2 - 7x + 5 \)
Aşağıdaki özellikleri polinomları temel matematik konularının öğretimi açısından oldukça faydalı kılmaktadır.
- Birbiriyle toplamları, farkları ve çarpımları yine birer polinomdur.
- Polinom fonksiyonları tüm reel sayılar kümesinde tanımlıdır.
- Polinom fonksiyonları tüm reel sayılar kümesinde süreklidir.
- Polinom fonksiyonları tüm reel sayılar kümesinde türevlenebilirdir.
- Limit bulma, türev ve integral alma gibi işlemler üzerlerinde kolaylıkla yapılabilir.
- Grafikleri ve davranışları derece ve başkatsayılarına göre tahmin edilebilirdir.
Polinom fonksiyonlarını daha detaylı şekilde polinom fonksiyonları bölümünde inceleyeceğiz.
Aşağıdaki ifadelerden hangileri reel katsayılı polinomdur?
I. \( 3x^4 - 7x + \dfrac{3}{2x} \)
II. \( 2x^3 - x^2 + x - \sqrt{x + 1} \)
III. \( \sqrt{-2}x^2 - 3x + 1 \)
IV. \( 4i \cdot x^2 + 2x - 3 \)
Çözümü GösterTanım gereği bir polinomda değişkenler sadece doğal sayı kuvvetleri ile bulunabilir.
I. öncül: \( \frac{3}{2x} = \frac{3x^{-1}}{2} \) teriminde değişkenin kuvveti negatif olduğu için ifade polinom değildir.
II. öncül: \( \sqrt{x + 1} \) teriminde değişken kök içinde olduğu için ifade polinom değildir.
III. öncül: İfade polinomdur, ancak \( \sqrt{-2} \) reel sayı olmadığı için reel katsayılı polinom değildir.
IV. öncül: İfade polinomdur, ancak \( 4i \) sanal sayı olduğu için reel katsayılı polinom değildir.
Buna göre ifadelerin hiçbiri reel katsayılı polinom değildir.
\( P(x) = 3x^{2a + 1} + x^{8 - 3a} + \frac{a}{2}x + 1 \)
\( P(x) \) bir polinom olduğuna göre, \( a \)'nın alabileceği kaç farklı tam sayı değeri vardır?
Çözümü GösterTanım gereği bir polinomda değişkenler sadece doğal sayı kuvvetleri ile bulunabilir.
\( 2a + 1 \ge 0 \Longrightarrow a \ge -\frac{1}{2} \)
\( 8 - 3a \ge 0 \Longrightarrow a \le \frac{8}{3} \)
Bu iki aralığın kesişim kümesi aşağıdaki gibidir.
\( -\frac{1}{2} \le a \le \frac{8}{3} \)
Bu aralıkta \( a \)'nın alabileceği tam sayı değerleri aşağıdaki gibidir.
\( a \in \{ 0, 1, 2 \} \)
Polinomların katsayıları reel sayı oldukları için \( \frac{a}{2}x \) teriminde \( x \)'in katsayısının tam sayı olmaması \( P(x) \)'in polinom olmasına engel değildir.
\( P(x) = (a - 2)\dfrac{1}{x} + (b + 3)\sqrt{x} + 4x \) ifadesi bir polinom olduğuna göre, \( a \cdot b \) kaçtır?
Çözümü GösterTanım gereği bir polinomda değişkenler sadece doğal sayı kuvvetleri ile bulunabilir.
Buna göre polinomda \( \frac{1}{x} \) ve \( \sqrt{x} \) terimleri bulunamayacağı için katsayıları 0 olmalıdır.
\( a - 2 = 0 \Longrightarrow a = 2 \)
\( b + 3 = 0 \Longrightarrow b = -3 \)
\( a \cdot b = 2 \cdot (-3) = -6 \) bulunur.
\( P(x) = x^4 - 2x^3 + 2x + 1 \)
\( Q(x) = x^3 + x^2 - 3x - 2 \)
olduğuna göre, \( 3P(1) + 2Q(-1) \) toplamı kaçtır?
Çözümü Göster\( P(1) = 1^4 - 2(1)^3 + 2(1) + 1 = 2 \)
\( Q(-1) = (-1)^3 + (-1)^2 - 3(-1) - 2 = 1 \)
\( 3P(1) + 2Q(-1) = 3 \cdot 2 + 2 \cdot 1 \)
\( = 8 \) bulunur.
Aşağıdaki ifadelerden hangileri polinomdur?
I. \( x^4 - \sqrt{2x} + 1 \)
II. \( \sqrt{x^2} + 10 \)
III. \( 4x^6 - 2\sqrt[3]{x^3} + 1 \)
IV. \( 3 + \sqrt{5} \)
Çözümü GösterTanım gereği bir polinomda değişkenler sadece doğal sayı kuvvetleri ile bulunabilir.
I. öncül: \( \sqrt{2x} \) teriminde değişken kök içinde olduğu için ifade polinom değildir.
II. öncül: \( \sqrt{x^2} = \abs{x} \) terimi dışarıya mutlak değer içinde çıktığı için ifade polinom değildir.
III. öncül: \( \sqrt[3]{x^3} = x \) terimi dışarıya mutlak değersiz çıktığı için ifade polinom olma koşulunu sağlar.
IV. öncül: Kök içinde bir değişken bulunmadığı için ifade polinom olma koşulunu sağlar.
Buna göre III. ve IV. öncüllerdeki ifadeler birer polinomdur.
\( P(x) = x^{\frac{n + 10}{n + 1}} + x^{n - 2} + 1 \) ifadesi bir polinom belirttiğine göre,
\( n \) sayısının alabileceği değerler toplamı kaçtır?
Çözümü Göster\( P(x) \) ifadesi bir polinom olduğuna göre, birinci terimin kuvveti doğal sayı olmalıdır.
\( \dfrac{n + 10}{n + 1} = \dfrac{n + 1}{n + 1} + \dfrac{9}{n + 1} \)
\( = 1 + \dfrac{9}{n + 1} \)
Bu ifadeyi doğal sayı yapan \( n \) değerleri aşağıdaki gibi olur. \( n = -2 \) ve \( n = -4 \) değerleri ifadeyi tam sayı yapsa da doğal sayı yapmaz.
\( n \in \{-10, 0, 2, 8\} \)
Ayrıca ikinci terimin kuvveti de doğal sayı olmalıdır.
\( n - 2 \ge 0 \Longrightarrow n \ge 2 \)
Her iki koşulu sağlayan \( n \) değerleri aşağıdaki gibi olur.
\( n \in \{2, 8\} \)
\( n \) sayısının alabileceği değerler toplamı \( 2 + 8 = 10 \) olarak bulunur.
\( P(x) \) bir polinom ve \( P(x) = 2x^{\frac{3n + 1}{n - 2}} + x^2 - 7 \) olduğuna göre, \( n \)'nin alabileceği tam sayı değerlerin toplamı kaçtır?
Çözümü GösterTanım gereği bir polinomda değişkenler sadece doğal sayı kuvvetleri ile bulunabilir.
Buna göre birinci terimin kuvveti doğal sayı olmalıdır.
\( \dfrac{3n + 1}{n - 2} = \dfrac{3(n - 2) + 7}{n - 2} \)
\( = \dfrac{3(n - 2)}{n - 2} + \dfrac{7}{n - 2} \)
\( = 3 + \dfrac{7}{n - 2} \)
\( \frac{7}{n - 2} \) ifadesini tam sayı yapan \( n \) değerlerinden hangileri için \( 3 + \frac{7}{n - 2} \) ifadesinin doğal sayı olduğunu kontrol edelim.
7'nin tam bölenleri \( \{\pm 1, \pm 7\} \) olmak üzere dört tanedir.
Paydayı bu dört değer yapan tam sayı \( n \) değerleri \( \{3, 9, 1, -5\} \) olur.
Bu \( n \) değerleri için \( 3 + \frac{7}{n - 2} \) ifadesi sırasıyla \( \{10, 4, -4, 2\} \) olur.
Bu değerlerden \( -4 \) dışındakiler doğal sayıdır.
Buna göre \( n \)'nin alabileceği değerler toplamı \( 3 + 9 + (-5) = 7 \) olur.
\( P(x + 3) + Q(x - 4) = 4x^2 - 3x + 1 \)
\( Q(-2) = 6 \)
olduğuna göre, \( P(5) \) değeri kaçtır?
Çözümü GösterVerilen eşitlikte \( x = 2 \) yazdığımızda polinom ifadelerinin \( P(5) \) ve \( Q(-2) \) olduğunu görebiliriz.
\( P(2 + 3) + Q(2 - 4) = 4(2)^2 - 3(2) + 1 \)
\( P(5) + Q(-2) = 11 \)
\( P(5) + 6 = 11 \)
\( P(5) = 5 \) olarak bulunur.
\( P(3x - 2) = x^3 - 6x + 3 \)
olduğuna göre, \( P(4) \) kaçtır?
Çözümü GösterPolinom tanımında parantez içini 4 yapacak \( x \) değerini bulalım.
\( 3x - 2 = 4 \Longrightarrow x = 2 \)
Polinom tanımında \( x = 2 \) yazalım.
\( P(3(2) - 2) = 2^3 - 6(2) + 3 \)
\( P(4) = -1 \) bulunur.
\( P(3x - 2) = x^3 - ax^2 + 2x + 3 \) polinomu veriliyor.
\( P(4) = -P(-5) \) olduğuna göre, \( a \) kaçtır?
Çözümü GösterVerilen polinomda parantez içlerini \( P(4) \) ve \( P(-5) \) yapmak için \( x \) yerine önce 2, sonra -1 yazalım.
\( x = 2 \) yazalım.
\( P(3(2) - 2) = 2^3 - a \cdot 2^2 + 2(2) + 3 \)
\( P(4) = 15 - 4a \)
\( x = -1 \) yazalım.
\( P(3(-1) - 2) = (-1)^3 - a(-1)^2 + (-1)2 + 3 \)
\( P(-5) = -a \)
Bu değerleri soruda verilen eşitlikte yerine koyalım.
\( P(4) = -P(-5) \)
\( 15 - 4a = -(-a) \)
\( a = 3 \) bulunur.
\( P(x) = 2x^3 + x^{4 - n} - 3x^n + n \) polinomunun sabit teriminin alabileceği değerler toplamı kaçtır?
Çözümü GösterTanım gereği bir polinomda değişkenler sadece doğal sayı kuvvetleri ile bulunabilir.
Buna göre değişken içeren ifadelerin üsleri doğal sayı olmalıdır.
\( 4 - n \ge 0 \)
\( n \ge 0 \)
Buna göre \( n \)'nin alabileceği değerler aşağıdaki gibidir.
\( n \in \{0, 1, 2, 3, 4\} \)
\( n \in \{1, 2, 3\} \) için sabit terim \( n \) değerine eşittir.
\( n = 0 \) için sabit terim \( x^n \)'li terimin katsayısını da içerir.
\( P(x) = 2x^3 + x^{4 - 0} - 3x^0 + 0 \)
\( = 2x^3 + x^4 - 3 + 0 \)
\( = 2x^3 + x^4 - 3 \)
\( n = 4 \) için sabit terim \( x^{4 - n} \)'li terimin katsayısını da içerir.
\( P(x) = 2x^3 + x^{4 - 4} - 3x^4 + 4 \)
\( = 2x^3 + 1 - 3x^4 + 4 \)
\( = 2x^3 - 3x^4 + 5 \)
Buna göre sabit terimin alabileceği değerler toplamı \( -3 + 1 + 2 + 3 + 5 = 8 \) olarak bulunur.
\( P(x) = x^4 - 4x^3 + 6x^2 - 4x + 4 \)
olduğuna göre, \( P(\sqrt[4]{6} + 1) \) değeri kaçtır?
Çözümü GösterVerilen ifadeyi \( (x - 1)^4 \) binom ifadesinin açılımına benzetmek için ifadeden 3 çıkarıp 3 ekleyelim.
\( P(x) = x^4 - 4x^3 + 6x^2 - 4x + 4 - 3 + 3 \)
\( = x^4 - 4x^3 + 6x^2 - 4x + 1 + 3 \)
\( = (x - 1)^4 + 3 \)
\( P(x) \) polinomunda \( x = \sqrt[4]{6} + 1 \) yazalım.
\( P(\sqrt[4]{6} + 1) = (\sqrt[4]{6} + 1 - 1)^4 + 3 \)
\( = (\sqrt[4]{6})^4 + 3 \)
\( = 6 + 3 = 9 \) bulunur.
\( P(x^4 - x^3 + 3) = 2x^3- 2x^4 + 2 \)
olduğuna göre, \( P(x) \) nedir?
Çözümü GösterPolinom tanımını parantez içindeki ifade cinsinden yazmaya çalışalım.
\( x^4 - x^3 + 3 = t \) şeklinde değişken değiştirelim.
\( x^4 - x^3 = t - 3 \)
\( x^3 - x^4 = 3 - t \)
Bu değerleri verilen polinomda yerine koyalım.
\( P(x^4 - x^3 + 3) = 2(x^3 - x^4) + 2 \)
\( P(t) = 2(3 - t) + 2 \)
\( P(t) = 8 - 2t \)
\( t \) yerine \( x \) yazabiliriz.
\( P(x) = 8 - 2x \) bulunur.
\( P(x - 1) = 2x^2 + 3x - 4 \)
olduğuna göre, \( P(2x + 1) \) polinomu nedir?
Çözümü Göster\( P(x - 1) \) ifadesinde parantez içini \( 2x + 1 \) yapmak için polinomda \( x \) gördüğümüz yere \( 2x + 2 \) yazalım.
\( P((2x + 2) - 1) = 2(2x + 2)^2 + 3(2x + 2) - 4 \)
\( P(2x + 1) = 2(4x^2 + 8x + 4) + 6x + 6 - 4 \)
\( P(2x + 1) = 8x^2 + 22x + 10 \)