Descartes'ın İşaret Kuralı
Descartes'ın işaret kuralı, tek değişkenli ve reel katsayılı bir polinomun pozitif ve negatif reel köklerinin maksimum sayısını ayrı ayrı belirlememizi sağlayan bir yöntemdir. Bu yöntem gerçek kök değerlerini vermez, pozitif ve negatif reel köklerin sayısı hakkında bilgi verir.
Bu yöntemi örnek bir polinom üzerinden detaylandıralım.
Adım 1: Polinom terimleri dereceleri büyükten küçüğe olacak şekilde sıralanır.
\( P(x) = 2x^4 - x^3 - 3x^2 + 4x + 2 \)
Adım 2: Terimlerin katsayılarındaki işaret değişimleri (pozitiften negatife ya da negatiften pozitife) sayılır. Katsayısı sıfır olan terimler dikkate alınmaz.
\( +2 \to \textcolor{red}{-1} \to -3 \to \textcolor{red}{+4} \to +2 \)
\( P(x) \) için işaret değişim sayısı 2'dir.
Adım 3: Polinomun pozitif reel köklerinin ve karmaşık sayı köklerinin toplam sayısı bulduğumuz işaret değişimi sayısı kadar olur. Bir polinomun karmaşık sayı kökleri varsa bu kökler ikişerli ve birbirinin eşleniği şeklinde olacağı için, pozitif reel kök sayısı bulduğumuz bu sayıya eşit olabilir ya da bu sayıdan iki ya da ikinin katları şeklinde daha az olabilir. Buna göre, işaret değişim sayısı 5 ise pozitif reel kök sayısı 5, 3 ya da 1 olabilir, işaret değişim sayısı 4 ise pozitif reel kök sayısı 4, 2 ya da 0 olabilir.
\( P(x) \) için işaret değişim sayısı 2 olduğu için pozitif reel kök sayısı 2 ya da 0 olabilir.
Adım 4: Polinomun negatif reel köklerinin sayısını bulmak için \( P(-x) \) polinomu yazılır ve aynı yöntem uygulanır. Polinomun negatif reel köklerinin ve karmaşık sayı köklerinin toplam sayısı bulduğumuz işaret değişimi sayısı kadar olur. Adım 3'te olduğu gibi, negatif reel kök sayısı bulduğumuz bu sayıya eşit olabilir ya da bu sayıdan iki ya da ikinin katları şeklinde daha az olabilir.
\( P(-x) = 2(-x)^4 - (-x)^3 - 3(-x)^2 + 4(-x) + 2 \)
\( = 2x^4 + x^3 - 3x^2 - 4x + 2 \)
\( +2 \to +1 \to \textcolor{red}{-3} \to -4 \to \textcolor{red}{+2} \)
\( P(-x) \) için de işaret değişim sayısı 2 olduğu için negatif reel kök sayısı 2 ya da 0 olabilir.
Bu yöntemle ilgili diğer bazı önemli noktalar şunlardır.
- Çok katlı kökler katları adedince sayılır, buna göre \( (x - 3)^2 \) çarpanı için \( x = 3 \) iki pozitif reel kök olarak sayılır.
- Pozitif ya da negatif reel kök sayısını 0 ya da 1 olarak bulursak bu kökler içinde karmaşık kök bulunamayacağı için gerçek pozitif ya da negatif kök sayısını bulmuş oluruz.
- Eğer bir polinomun sabit terimi yoksa polinom sabit terim olacak şekilde \( x \)'in bir kuvveti parantezine alınır ve yukarıda bahsettiğimiz yöntem sabit terim içeren polinoma uygulanır. Bu durumda paranteze aldığımız \( x \) çarpanının katı adedince \( x = 0 \) polinomun bir kökü olur.
Önceki bölümde bahsettiğimiz cebirin temel teoremine göre, reel katsayılı ve \( n \). dereceden bir polinom denkleminin (tekrar eden kökler katları adedince sayıldığında) reel ya da karmaşık sayı toplam \( n \) kökü vardır.
\( P(x) = 2x^5 - 3x^4 - 2x^3 + 4x^2 - x - 1 \) polinomunun pozitif ve negatif reel köklerinin sayısını bulalım.
Polinomun sabit terimi vardır, dolayısıyla \( x = 0 \) polinomun bir kökü değildir.
Önce \( P(x) \) polinomunun katsayılarını yazalım ve katsayıların işaretlerindeki değişim sayısını bulalım.
\( +2 \to \textcolor{red}{-3} \to -2 \to \textcolor{red}{+4} \to \textcolor{red}{-1} \to -1 \)
Katsayılar \( -3 \), \( +4 \) ve \( -1 \)'de olmak üzere 3 kez işaret değiştirmiştir, dolayısıyla polinomun pozitif reel köklerinin ve karmaşık sayı köklerinin toplam sayısı 3 olur. Bu kökler içinde iki ya da ikinin katları adedince karmaşık sayı kök olabileceği için pozitif reel kök sayısı 3 ya da 1 olabilir.
Şimdi \( P(-x) \) polinomunu yazalım ve katsayıların işaretlerindeki değişim sayısını bulalım.
\( P(-x) = 2(-x)^5 - 3(-x)^4 - 2(-x)^3 + 4(-x)^2 - (-x) - 1 \)
\( = -2x^5 - 3x^4 + 2x^3 + 4x^2 + x - 1 \)
\( -2 \to -3 \to \textcolor{red}{+2} \to +4 \to +1 \to \textcolor{red}{-1} \)
Katsayılar \( +2 \) ve \( -1 \)'de olmak üzere 2 kez işaret değiştirmiştir, dolayısıyla polinomun negatif reel köklerinin ve karmaşık sayı köklerinin toplam sayısı 2 olur. Bu kökler içinde iki ya da ikinin katları adedince karmaşık kök olabileceği için negatif reel kök sayısı 2 ya da 0 olabilir.
Özetle, \( P(x) \) polinomunun 3 ya da 1 pozitif reel kökü, 2 ya da 0 negatif reel kökü vardır. Cebirin temel teoremine göre, 5. dereceden bir polinomun reel ya da karmaşık toplam 5 kökü olacağı için, \( P(x) \) polinomunun kökleri ile ilgili aşağıdaki olasılıklar vardır.
- 3 pozitif, 2 negatif reel kök
- 3 pozitif, 0 negatif reel kök, 2 karmaşık kök
- 1 pozitif, 2 negatif reel kök, 2 karmaşık kök
- 1 pozitif, 0 negatif reel kök, 4 karmaşık kök
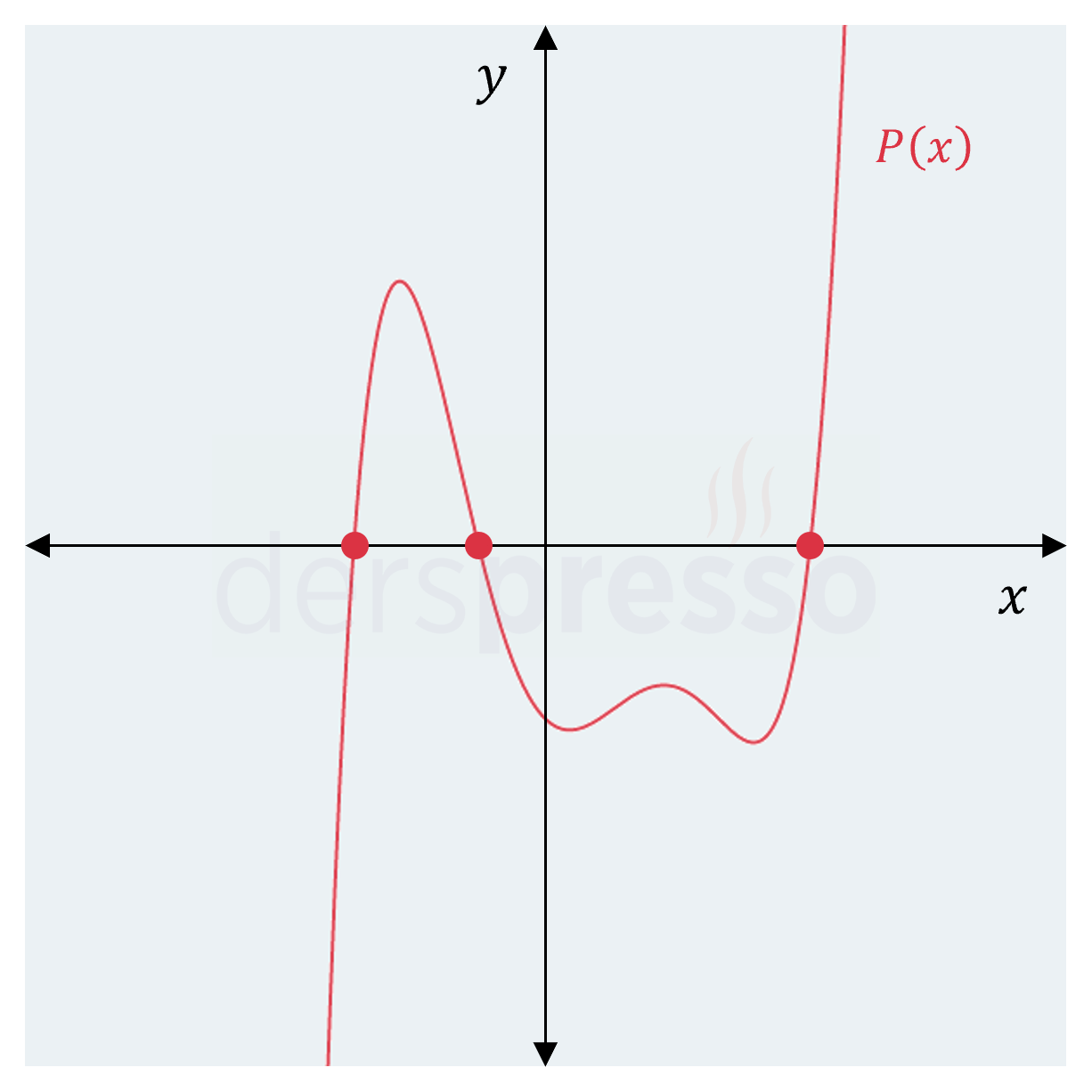
\( P(x) \) polinomunun grafiğini çizdiğimizde, aşağıda görülebileceği gibi 1 pozitif, 2 negatif reel kök olduğunu görürüz, dolayısıyla polinomun 2 de karmaşık sayı kökü vardır.
\( Q(x) = x^7 - 3x^6 + 3x^4 + 3x^3 - 4x \) polinomunun pozitif ve negatif reel köklerinin sayısını bulalım.
Polinomun sabit terimi olmadığı için polinomu \( x \) parantezine alalım.
\( Q(x) = x(x^6 - 3x^5 + 3x^3 + 3x^2 - 4) \)
Yöntemi sabit terim içeren parantez içindeki polinoma uygulayalım.
\( P(x) = x^6 - 3x^5 + 3x^3 + 3x^2 - 4 \)
Önce \( P(x) \) polinomunun katsayılarını yazalım ve katsayıların işaretlerindeki değişim sayısını bulalım.
\( +1 \to \textcolor{red}{-3} \to \textcolor{red}{+3} \to +3 \to \textcolor{red}{-4} \)
Katsayılar \( -3 \), \( +3 \) ve \( -4 \)'te olmak üzere 3 kez işaret değiştirmiştir, dolayısıyla polinomun pozitif reel köklerinin ve karmaşık sayı köklerinin toplam sayısı 3 olur. Bu kökler içinde iki ya da ikinin katları adedince karmaşık kök olabileceği için pozitif reel kök sayısı 3 ya da 1 olabilir.
Şimdi \( P(-x) \) polinomunu yazalım ve katsayıların işaretlerindeki değişim sayısını bulalım.
\( P(-x) = (-x)^6 - 3(-x)^5 + 3(-x)^3 + 3(-x)^2 - 4 \)
\( = x^6 + 3x^5 - 3x^3 + 3x^2 - 4 \)
\( +1 \to +3 \to \textcolor{red}{-3} \to \textcolor{red}{+3} \to \textcolor{red}{-4} \)
Katsayılar \( -3 \), \( +3 \) ve \( -4 \)'te olmak üzere 3 kez işaret değiştirmiştir, dolayısıyla polinomun negatif reel köklerinin ve karmaşık sayı köklerinin toplam sayısı 3 olur. Bu kökler içinde iki ya da ikinin katları adedince karmaşık kök olabileceği için negatif reel kök sayısı 3 ya da 1 olabilir.
Özetle, \( P(x) \) polinomunun 3 ya da 1 pozitif reel kökü, 3 ya da 1 negatif reel kökü vardır. Cebirin temel teoremine göre, 6. dereceden bir polinomun reel ya da karmaşık toplam 6 kökü olması gerektiği için, \( P(x) \) polinomunun kökleri ile ilgili aşağıdaki olasılıklar vardır.
- 3 pozitif, 3 negatif reel kök
- 3 pozitif, 1 negatif reel kök, 2 karmaşık kök
- 1 pozitif, 3 negatif reel kök, 2 karmaşık kök
- 1 pozitif, 1 negatif reel kök, 4 karmaşık kök
\( P(x) \) polinomunun grafiğini çizdiğimizde, aşağıda görülebileceği gibi biri iki katlı olmak üzere 3 pozitif, 1 negatif reel kök olduğunu görürüz, dolayısıyla polinomun 2 de karmaşık sayı kökü vardır.
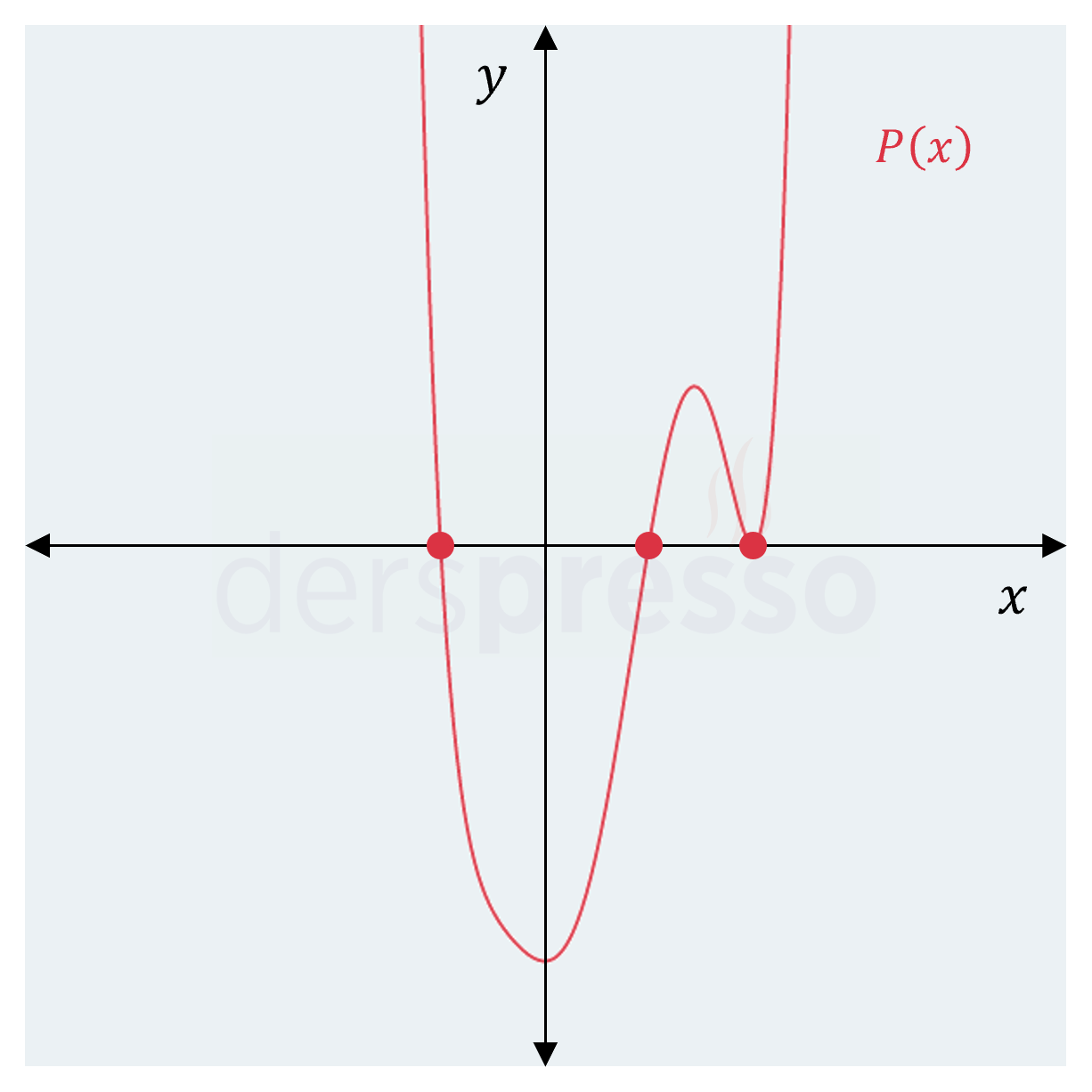
Son olarak, örnekte verilen \( Q(x) \) polinomunun \( x \) çarpanı da olduğu için, yukarıdakilere ek olarak \( x = 0 \) da bu polinomun bir köküdür.
\( P(x) = 3x^6 - 5x^2 + 2x \)
polinomunun pozitif olmayan kaç reel kökü vardır?
Çözümü GösterPolinomun sabit terimi olmadığından ifadeyi \( x \) parantezine alalım.
\( P(x) = x(3x^5 - 5x + 2) \)
Buna göre \( x = 0 \) polinomun bir köküdür. Descartes'ın işaret kuralını diğer çarpana uygulayarak negatif reel köklerin sayısını bulalım.
\( Q(x) = 3x^5 - 5x + 2 \)
Negatif reel köklerin sayısı bulmak için \( Q(-x) \) polinomunu yazalım ve katsayıların işaretlerindeki değişim sayısını bulalım.
\( Q(-x) = 3(-x)^5 - 5(-x) + 2 \)
\( = -3x^5 + 5x + 2 \)
\( -3 \to \textcolor{red}{+5} \to +2 \)
Katsayılar 1 kez işaret değiştirmiştir, dolayısıyla polinomun negatif reel köklerinin ve karmaşık sayı köklerinin toplam sayısı 1 olur. Bu kökler içinde iki ya da ikinin katları adedince karmaşık kök olabileceği için negatif reel kök sayısı 1 olur.
Buna göre \( x = 0 \) kökü ile birlikte polinomun pozitif olmayan 2 reel kökü vardır.
\( x^{10}(4x^8 + 5x^6 + 6x^4 + 7x^2 + 8) = 1 - x^2(9x^6 + 10x^4 + 11x^2 + 12) \)
denkleminin kaç karmaşık sayı kökü vardır?
Çözümü GösterParantez içindeki ifadeleri genişletelim ve tüm terimleri eşitliğin sol tarafında toplayalım.
\( 4x^{18} + 5x^{16} + 6x^{14} + 7x^{12} + 8x^{10} = 1 - 9x^8 - 10x^6 - 11x^4 - 12x^2 \)
\( 4x^{18} + 5x^{16} + 6x^{14} + 7x^{12} + 8x^{10} + 9x^8 + 10x^6 + 11x^4 + 12x^2 - 1 = 0 \)
Eşitliğin sol tarafını bir polinom olarak düşünerek Descartes'ın işaret kuralını uygulayalım.
\( P(x) = 4x^{18} + 5x^{16} + 6x^{14} + 7x^{12} + 8x^{10} + 9x^8 + 10x^6 + 11x^4 + 12x^2 - 1 \)
\( 4 \to 5 \to 6 \to 7 \to 8 \to 9 \to 10 \to 11 \to 12 \to \textcolor{red}{-1} \)
Katsayılar 1 kez işaret değiştirmiştir, dolayısıyla polinomun pozitif reel köklerinin ve karmaşık sayı köklerinin toplam sayısı 1 olur. Bu kökler içinde iki ya da ikinin katları adedince karmaşık sayı kök olabileceği için pozitif reel kök sayısı 1 olur.
Şimdi \( P(-x) \) polinomunu yazalım ve katsayıların işaretlerindeki değişim sayısını bulalım.
\( P(-x) = 4(-x)^{18} + 5(-x)^{16} + 6(-x)^{14} + 7(-x)^{12} + 8(-x)^{10} + 9(-x)^8 + 10(-x)^6 + 11(-x)^4 + 12(-x)^2 - 1 \)
\( = 4x^{18} + 5x^{16} + 6x^{14} + 7x^{12} + 8x^{10} + 9x^8 + 10x^6 + 11x^4 + 12x^2 - 1 \)
\( 4 \to 5 \to 6 \to 7 \to 8 \to 9 \to 10 \to 11 \to 12 \to \textcolor{red}{-1} \)
Katsayılar yine 1 kez işaret değiştirmiştir, dolayısıyla polinomun negatif reel köklerinin ve karmaşık sayı köklerinin toplam sayısı 1 olur. Bu kökler içinde iki ya da ikinin katları adedince karmaşık sayı kök olabileceği için negatif reel kök sayısı 1 olur.
Buna göre verilen denklemin bir pozitif ve bir negatif olmak üzere 2 reel kökü vardır.
Cebirin temel teoremine göre, 18. dereceden bir polinomun reel ya da karmaşık toplam 18 kökü olacağı için, geri kalan \( 18 - 2 = 16 \) kök karmaşık köklerdir.
\( P(x) = x^6 + 5x^5 + 3x^4 + 4x^3 + 7x^2 + 2x + 1 \)
polinomunun reel köklerinin sayısı bir asal sayı olduğuna göre, polinomun pozitif ve negatif reel köklerinin sayısı kaçtır?
Çözümü GösterÖnce \( P(x) \) polinomunun katsayılarını yazalım ve katsayıların işaretlerindeki değişim sayısını bulalım.
\( 1 \to 5 \to 3 \to 4 \to 7 \to 2 \to 1 \)
Katsayılar 0 kez işaret değiştirmiştir, dolayısıyla polinomun pozitif reel kökü yoktur.
Şimdi \( P(-x) \) polinomunu yazalım ve katsayıların işaretlerindeki değişim sayısını bulalım.
\( P(-x) = (-x)^6 + 5(-x)^5 + 3(-x)^4 + 4(-x)^3 + 7(-x)^2 + 2(-x) + 1 \)
\( = x^6 - 5x^5 + 3x^4 - 4x^3 + 7x^2 - 2x + 1 \)
\( 1 \to \textcolor{red}{-5} \to \textcolor{red}{3} \to \textcolor{red}{-4} \to \textcolor{red}{7} \to \textcolor{red}{-2} \to \textcolor{red}{1} \)
Katsayılar 6 kez işaret değiştirmiştir, dolayısıyla polinomun negatif reel köklerinin ve karmaşık sayı köklerinin toplam sayısı 6 olur. Bu kökler içinde iki ya da ikinin katları adedince karmaşık sayı kök olabileceği için negatif reel kök sayısı 6, 4, 2 ya da 0 olabilir.
Reel köklerin sayısı bir asal sayı olduğuna göre negatif reel kök sayısı sadece 2 olabilir.
Buna göre verilen polinomun 0 pozitif ve 2 negatif olmak üzere toplam 2 reel kökü vardır.
\( Q(x) = x^5 - 6x^4 + x^3 + x^2 + 6 \)
\( Q(x) = 0 \) denkleminin reel köklerinin sayısını \( Q(1) \) ve \( Q(2) \) değerlerini kıyaslayarak bulunuz.
Çözümü GösterÖnce \( Q(x) \) polinomunun katsayılarını yazalım ve katsayıların işaretlerindeki değişim sayısını bulalım.
\( 1 \to \textcolor{red}{-6} \to \textcolor{red}{1} \to 1 \to 6 \)
Katsayılar 2 kez işaret değiştirmiştir, dolayısıyla polinomun pozitif reel köklerinin ve karmaşık sayı köklerinin toplam sayısı 2 olur. Bu kökler içinde iki ya da ikinin katları adedince karmaşık sayı kök olabileceği için pozitif reel kök sayısı 2 ya da 0 olabilir.
Şimdi \( Q(-x) \) polinomunu yazalım ve katsayıların işaretlerindeki değişim sayısını bulalım.
\( Q(-x) = (-x)^5 - 6(-x)^4 + (-x)^3 + (-x)^2 + 6 \)
\( = -x^5 - 6x^4 - x^3 + x^2 + 6 \)
\( -1 \to -6 \to -1 \to \textcolor{red}{1} \to 6 \)
Katsayılar yine 1 kez işaret değiştirmiştir, dolayısıyla polinomun negatif reel köklerinin ve karmaşık sayı köklerinin toplam sayısı 1 olur. Bu kökler içinde iki ya da ikinin katları adedince karmaşık sayı kök olabileceği için negatif reel kök sayısı 1 olur.
Soruda belirtildiği üzere \( Q(1) \) ve \( Q(2) \) değerlerini bulup kıyaslayalım.
\( Q(1) = 1^5 - 6 \cdot 1^4 + 1^3 + 1^2 + 6 \)
\( = 3 \gt 0 \)
\( Q(2) = 2^5 - 6 \cdot 2^4 + 2^3 + 2^2 + 6 \)
\( = -46 \lt 0 \)
\( Q(2) \lt 0 \lt Q(1) \)
Ara değer teoremine göre, tüm reel sayılarda sürekli olan polinomun \( (1, 2) \) aralığında \( Q(x) = 0 \) değerini en az bir kez alacağını, yani polinomun bu aralıkta en azından bir kökü olduğunu söyleyebiliriz, dolayısıyla polinomun 0 değil 2 pozitif reel kökü olduğu sonucuna varabiliriz.
Buna göre verilen polinomun 2 pozitif ve 1 negatif olmak üzere toplam 3 reel kökü vardır.
\( P(x) = -x^4 + x^3 + x^2 + 1 \)
polinomunun kaç irrasyonel kökü vardır?
Çözümü GösterÖnce \( P(x) \) polinomunun katsayılarını yazalım ve katsayıların işaretlerindeki değişim sayısını bulalım.
\( -1 \to \textcolor{red}{+1} \to +1 \to +1 \)
Katsayılar 1 kez işaret değiştirmiştir, dolayısıyla polinomun pozitif reel köklerinin ve karmaşık sayı köklerinin toplam sayısı 1 olur. Bu kökler içinde iki ya da ikinin katları adedince karmaşık kök olabileceği için pozitif reel kök sayısı 1 olur.
Şimdi \( P(-x) \) polinomunu yazalım ve katsayıların işaretlerindeki değişim sayısını bulalım.
\( P(-x) = -(-x)^4 + (-x)^3 + (-x)^2 + 1 \)
\( = -x^4 - x^3 + x^2 + 1 \)
\( -1 \to -1 \to \textcolor{red}{+1} \to +1 \)
Katsayılar 1 kez işaret değiştirmiştir, dolayısıyla polinomun negatif reel köklerinin ve karmaşık sayı köklerinin toplam sayısı 1 olur. Bu kökler içinde iki ya da ikinin katları adedince karmaşık kök olabileceği için negatif reel kök sayısı 1 olur.
Özetle, \( P(x) \) polinomunun 1 pozitif reel kökü, 1 negatif reel kökü vardır.
Rasyonel kök teoremini kullanarak polinomun rasyonel kök değerlerini bulalım.
Rasyonel kök teoremine göre, bir polinom denkleminin tüm rasyonel kökleri (\( p \) polinomun sabit teriminin bir tam böleni ve \( q \) polinomun başkatsayısının bir tam böleni olmak üzere) \( \frac{p}{q} \) şeklinde yazılabilir.
Polinomun sabit teriminin tam bölenleri:
\( p: \{\pm 1\} \)
Polinomun başkatsayısının tam bölenleri:
\( q: \{\pm 1\} \)
Tüm \(\frac{p}{q}\) değerleri:
\( \dfrac{p}{q}: \{\pm 1\} \)
Bu 2 değerin ikisi de denklemin birer kökü olmayabilir, ancak denklemin tüm rasyonel kökleri bu listededir.
Bu 2 olası kök değerinden hangilerinin polinomu sıfır yaptığını kontrol edelim.
\( P(1) = -(1)^4 + (1)^3 + (1)^2 + 1 = 2 \)
\( P(-1) = -(-1)^4 + (-1)^3 + (-1)^2 + 1 = 0 \)
Bu değerlerden \( x = -1 \) polinomu sıfır yapmaktadır, dolayısıyla denklemin bir köküdür.
Özetlemek gerekirse, Descartes'ın işaret kuralına göre verilen polinomun 2 reel kökü vardır (4. dereceden polinomun diğer 2 kökü karmaşık sayı köklerdir).
Rasyonel kök teoremine göre polinomun bir rasyonel kökü vardır (\( x = -1 \)).
Rasyonel ve irrasyonel sayıların birleşimi reel sayıları oluşturduğu için, polinomun \( 2 - 1 = 1 \) irrasyonel kökü vardır.