Tam Bölen Sayısı
Tam Bölen Sayısı
Asal Bölen Sayısı
Bir \( A \) pozitif tam sayısının asal çarpanlarının kuvvetleri biçiminde yazılışı aşağıdaki gibi olsun.
\( A = x^a \cdot y^b \cdot z^c \)
Asal bölenler (çarpanlar): \( x, y, z \)
Asal bölenlerin (çarpanların) sayısı (ABS) \( = 3 \)
\( 360 = 2^3 \cdot 3^2 \cdot 5^1 \)
Asal bölenler: 2, 3, 5
Asal bölenlerin sayısı \( = 3 \)
Bölen Sayısı
\( A \) sayısının pozitif bölenlerinin sayısı asal çarpanlarının kuvvetlerinin birer fazlasının çarpımına eşittir. Bir bölenin negatif işaretlisi de aynı sayının böleni olduğu için pozitif ve negatif tüm bölenlerin sayısı pozitif bölenlerin sayısının iki katına eşittir.
Pozitif bölenlerin sayısı (PBS) \( = (a + 1)(b + 1)(c + 1) \)
Tüm (pozitif ve negatif) bölenlerin sayısı (TBS) \( = 2 \cdot (\text{PBS}) \)
360 sayısı için,
\( \text{PBS} = (3 + 1)(2 + 1)(1 + 1) = 24 \)
Pozitif bölenler: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120, 180, 360
\( \text{TBS} = 2 \cdot \text{PBS} = 48 \)
Tüm bölenler: Yukarıdaki pozitif bölenler ve negatif işaretlileri
İSPATI GÖSTER
\( A \) pozitif tam sayısının asal çarpanlarına ayrılmış şekli aşağıdaki gibi olsun.
\( A = x^a \cdot y^b \cdot z^c \)
Bir \( X \) pozitif tam sayısının \( A \) sayısının bir böleni olabilmesi için aşağıdaki iki koşulu sağlaması gerekir.
- Asal çarpanları sadece \( A \) sayısının asal çarpanlarını içerebilir.
- Her asal çarpanın kuvveti en fazla \( A \) sayısında bulunduğu kuvvette olabilir.
Dolayısıyla \( X \) sayısını asal çarpanlarına ayrılmış şekilde aşağıdaki gibi yazabiliriz.
\( X = x^p \cdot y^q \cdot z^r \)
\( 0 \le p \le a \)
\( 0 \le q \le b \)
\( 0 \le r \le c \)

Bu koşulları yukarıdaki gibi bir bölme işlemiyle de gösterebiliriz. Bir \( X \) sayısının \( A \) sayısını tam bölebilmesi için tüm çarpanları \( A \) sayısının çarpanları ile sadeleşmelidir. Bunun için \( X \) sayısı \( A \) sayısında bulunmayan bir asal çarpan içeremez ve bir asal çarpan \( X \) sayısında \( A \) sayısında bulunduğu kuvvetten daha fazla bir kuvvette bulunamaz. Aksi durumlarda sadeleşmeler sonucunda paydada çarpan(lar) kalacak ve işlem sonucu bir tam sayı olmayacaktır.
Bu doğrultuda oluşturabileceğimiz farklı \( X \) sayıları yukarıdaki üç eşitsizliği sağlayan \( p \), \( q \) ve \( r \) tam sayılarının sayısı kadar olacaktır. Buna göre \( p \) sayısı için \( a + 1 \), \( q \) sayısı için \( b + 1 \), \( r \) sayısı için de \( c + 1 \) farklı değer seçeneği oluşmaktadır.
\( p = \{ 0, 1, \ldots, a \} \)
\( q = \{ 0, 1, \ldots, b \} \)
\( r = \{ 0, 1, \ldots, c \} \)
Sayma konusunda göreceğimiz çarpma yoluyla sayma kuralına göre, \( p \), \( q \) ve \( r \) sayılarının her biri sırasıyla \( a + 1 \), \( b + 1 \) ve \( c + 1 \) farklı şekilde seçilebiliyorsa bu üç sayı birlikte \( (a + 1)(b + 1)(c + 1) \) farklı şekilde seçilebilir.
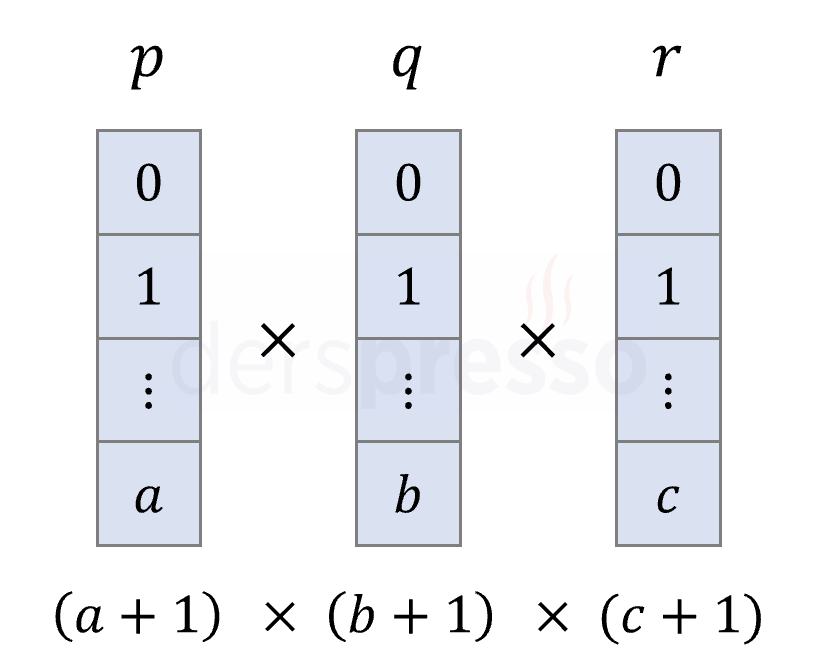
Buna göre \( A \) pozitif tam sayısını tam bölen \( (a + 1)(b + 1)(c + 1) \) farklı pozitif tam sayı yazılabilir.
Asal Olmayan Bölen Sayısı
Bir sayının asal olmayan pozitif bölenlerinin sayısı pozitif bölen ve asal bölen sayılarının farkına eşittir. Bir sayının asal olmayan tüm bölenlerinin sayısını da benzer şekilde hesaplayabiliriz. Asal sayılar negatif olamayacağı için asal bölenlerin negatif işaretlilerini birer asal bölen olarak düşünemeyiz.
Asal olmayan pozitif bölenlerin sayısı \( = (\text{PBS}) - (\text{ABS}) \)
Asal olmayan bölenlerin sayısı \( = (\text{TBS}) - (\text{ABS}) \)
360 sayısı için,
Asal olmayan pozitif bölenlerin sayısı \( = 24 - 3 = 21 \)
Asal olmayan pozitif bölenler: 2, 3 ve 5 hariç pozitif bölenler
Asal olmayan bölenlerin sayısı \( = 48 - 3 = 45 \)
Asal olmayan bölenler: 2, 3 ve 5 hariç tüm bölenler (-2, -3 ve -5 dahil)
Tek/Çift Pozitif Bölen Sayısı
\( A \) sayısının asal çarpanlarından \( x \)'in çift sayı, \( y \) ve \( z \)'nin tek sayı olduğunu varsayalım. Bu durumda \( A \)'nın pozitif bölenlerinden tek sayı olanların sayısını bulmak için sadece tek asal çarpanları dikkate alarak pozitif bölen sayısını hesaplarız. Çift sayı pozitif bölen sayısı toplam pozitif bölen sayısının tek sayı pozitif bölen sayısından farkına eşittir.
\( x \) çift sayı, \( y \) ve \( z \) tek sayı olmak üzere,
Tek sayı pozitif bölenlerin sayısı (TPBS) \( = (b + 1)(c + 1) \)
Çift sayı pozitif bölenlerin sayısı (ÇPBS) \( = (\text{PBS}) - (\text{TPBS}) \)
360 sayısı için,
\( \text{TPBS} = (2 + 1)(1 + 1) = 6 \)
Tek sayı pozitif bölenler: 1, 3, 5, 9, 15, 45
\( \text{ÇPBS} = 24 - 6 = 18 \)
Çift sayı pozitif bölenler: Yukarıdaki tek sayı pozitif bölenler hariç tüm pozitif bölenler
İSPATI GÖSTER
\( A \) pozitif tam sayısının asal çarpanlarına ayrılmış şekli aşağıdaki gibi olsun.
\( A = x^a \cdot y^b \cdot z^c \)
\( A \) sayısının asal çarpanlarından \( x \)'in çift sayı, \( y \) ve \( z \)'nin tek sayı olduğunu varsayalım.
\( n \) tane tam sayının çarpımında sayılardan en az biri çift ise sonuç çift olur, bir diğer deyişle bir tam sayı tek ise asal çarpanlarının tümü tektir. Buna göre \( A \)'nın tek sayı bölenleri çift asal çarpan içermeyen bölenler olur ve bu bölenlerin sayısını bulmak için \( A \)'nın sadece tek asal çarpanlarını dikkate alarak pozitif bölen sayısını hesaplarız.
Tek sayı pozitif bölenlerin sayısı (TPBS) \( = (b + 1)(c + 1) \)
Çift sayı bölen sayısını toplam pozitif bölen sayısından tek sayı bölen sayısını çıkararak bulabiliriz. Bir bölenin çift sayı olması için içinde en az bir çift asal çarpan olması yeterlidir, bir diğer ifadeyle çarpanlarının tümünün tek sayı olmaması gerekir.
Çift sayı pozitif bölenlerin sayısı (ÇPBS) \( = (\text{PBS}) - (\text{TPBS}) \)
Tüm asal sayılar içinde sadece 2'nin çift sayı olduğunu burada tekrar hatırlatalım, dolayısıyla asal çarpan olarak 2 içermeyen sayıların hem kendileri hem de tüm bölenleri tek sayıdır.
Bölenlerin Toplamı
Bir sayının pozitif bölenlerinin toplamı aşağıdaki iki formülle bulunabilir.
\( A = x^a \cdot y^b \cdot z^c \)
Asal bölenlerin toplamı \( = x + y + z \)
Pozitif bölenlerin toplamı \( = \dfrac{x^{a + 1} - 1}{x - 1} \cdot \dfrac{y^{b + 1} - 1}{y - 1} \cdot \dfrac{z^{c + 1} - 1}{z - 1} \)
Pozitif bölenlerin toplamı \( = (x^0 + x^1 + x^2 + \ldots + x^a)(y^0 + y^1 + y^2 + \ldots + y^b)(z^0 + z^1 + z^2 + \ldots + z^c) \)
200 sayısının 12 pozitif böleninin toplamını her iki formülle hesaplayalım.
\( 200 = 2^3 \cdot 5^2 \)
Pozitif bölenlerin toplamı \( = \dfrac{2^{3 + 1} - 1}{2 - 1} \cdot \dfrac{5^{2 + 1} - 1}{5 - 1} \)
\( = \dfrac{15}{1} \cdot \dfrac{124}{4} = 465 \)
Pozitif bölenlerin toplamı \( = (2^0 + 2^1 + 2^2 + 2^3)(5^0 + 5^1 + 5^2) \)
\( = (1 + 2 + 4 + 8)(1 + 5 + 25) \)
\( = 15 \cdot 31 = 465 \)
Yukarıda listelediğimiz 200 sayısının 12 pozitif bölenini toplarsak da 465 sayısını elde ederiz.
İSPATI GÖSTER
\( A \) sayısının asal çarpanlarının kuvvetleri biçiminde yazılışı aşağıdaki gibi olsun:
\( A = x^a \cdot y^b \cdot z^c \)
Bir sayının \( A \) sayısının pozitif böleni olabilmesi için \( A \) sayısı ile aynı asal çarpanlara en fazla \( A \) sayısında bulunduğu sayıda sahip olması gerekir. Dolayısıyla \( A \) sayısının bir pozitif böleni \( x \) asal çarpanını \( 0 \) ile \( a \) adet arası bir sayıda içerebilir (diğer asal çarpanlar için de aynı şekilde).
\( A \) sayısının asal çarpanları arasından bu şekilde seçilerek oluşturulabilecek tüm pozitif bölenlerin aşağıdaki ifadenin açılımındaki terimlerle birebir eşleşeceğini söyleyebiliriz.
\( (x^0 + x^1 + x^2 + ... + x^a) \cdot (y^0 + y^1 + y^2 + ... + y^b) \cdot (z^0 + z^1 + z^2 + ... + z^c) \)
Buna göre, bu ifadenin kendisi bize \( A \) sayısının pozitif bölenlerinin toplamını verecektir.
Pozitif bölenlerinin toplamı \( = (x^0 + x^1 + x^2 + ... + x^a) \cdot (y^0 + y^1 + y^2 + ... + y^b) \cdot (z^0 + z^1 + z^2 + ... + z^c) \)
Bu ifadedeki her bir çarpan bir geometrik dizi ifade etmektedir. \( x \) asal çarpanının karşılık geldiği ilk çarpanı örnek olarak alırsak:
Geometrik dizinin terimleri: \( x^0, x^1, x^2, ..., x^a \)
İlk terim (\( a_1 \)): \( x^0 = 1 \)
Terim sayısı (n): \( a + 1 \)
Ortak çarpan (r): \( x \)
Geometrik diziler konusunda göreceğimiz terimler toplamı formülüne göre bu dizinin terimler toplamını aşağıdaki formülle hesaplayabiliriz (bu formülün ispatı verilen linkte bulunabilir):
Terimler toplamı \( = a_1 \cdot \dfrac{r^n - 1}{r - 1} \)
Terimler toplamı \( = x^0 \cdot \dfrac{x^{a + 1} - 1}{x - 1} = \dfrac{x^{a + 1} - 1}{x - 1} \)
Bu formülü yukarıdaki formüldeki tüm asal çarpanlara yansıtırsak \( A \) sayısının pozitif bölenlerinin toplamı formülünü aşağıdaki şekilde elde ederiz:
Pozitif bölenlerinin toplamı \( = \dfrac{x^{a + 1} - 1}{x - 1} \cdot \dfrac{y^{b + 1} - 1}{y - 1} \cdot \dfrac{z^{c + 1} - 1}{z - 1} \)
Bölenlerin Çarpımı
Bir \( A \) sayısının bölenlerinin çarpımını aşağıdaki formülle bulabiliriz.
Pozitif bölenlerin çarpımı \( = \sqrt{A^\text{PBS}} \)
PBS: \( A \) sayısının pozitif bölenlerinin sayısı
200 sayısının 12 pozitif böleninin çarpımını hesaplayalım.
\( 200 = 2^3 \cdot 5^2 \)
Pozitif bölenlerin çarpımı \( = \sqrt{200^{(3 + 1)(2 + 1)}} = 200^6 \)
İSPATI GÖSTER
\( A \) sayısının asal çarpanlarının kuvvetleri biçiminde yazılışı aşağıdaki gibi olsun:
\( A = x^a \cdot y^b \cdot z^c \)
Daha önce bahsettiğimiz gibi, \( A \) sayısının pozitif bölenleri aşağıdaki ifadenin açılımındaki terimlerle birebir eşleşir. Dolayısıyla bu açılımdaki terimlerin çarpımını bulmamız gerekmektedir.
\( (x^0 + x^1 + x^2 + ... + x^a) \cdot (y^0 + y^1 + y^2 + ... + y^b) \cdot (z^0 + z^1 + z^2 + ... + z^c) \)
\( A \) sayısının pozitif bölenlerinin çarpımını aşağıdaki şekilde yazabiliriz.
\( \underbrace{x^0y^0z^0}_\text{1. bölen} \cdot \underbrace{x^0y^0z^1}_\text{2. bölen} \cdots \underbrace{x^1y^1z^1}_\text{k. bölen} \cdots \underbrace{x^a y^b z^c}_\text{PBS. bölen} \)
Bu çarpımda sadece \( x \) asal çarpanını dikkate alırsak, \( x \)'in her farklı kuvvetinin \( (b + 1)(c + 1) \) kez tekrarladığını görebiliriz. Buna göre yukarıdaki ifadedeki \( x \) içeren çarpanları aşağıdaki şekilde yazabiliriz.
\( \underbrace{x^0 \cdot x^1 \cdot x^2 \cdots x^a}_\text{(b + 1)(c + 1) adet} \)
\( x \)'in kuvvetlerini toplayarak tek tabanda birleştirelim.
\( = \underbrace{x^{0 + 1 + 2 + \cdots + a}}_\text{(b + 1)(c + 1) adet} \)
Ardışık sayıların toplam formülünü kullanarak kuvveti tekrar yazalım.
\( = \underbrace{x^\frac{a(a + 1)}{2}}_\text{(b + 1)(c + 1) adet} \)
Son olarak bu çarpan \( (b + 1)(c + 1) \) kez tekrarladığı için yanyana yazmamız durumunda \( x \)'in kuvvetini bu sayı ile çarpabiliriz.
\( = x^\frac{a(a + 1)(b + 1)(c + 1)}{2} \)
\( PBS = (a + 1)(b + 1)(c + 1) \) olduğu için formülde bu ifade yerine PBS yazalım.
\( = x^\frac{a \cdot PBS}{2} \)
Bu ifade sadece tabanın \( x \) olduğu çarpanları içeriyordu, diğer asal çarpanları da eklersek tüm pozitif bölenlerin çarpımını aşağıdaki şekilde buluruz.
Pozitif bölenlerinin çarpımı \( = x^\frac{a \cdot PBS}{2} \cdot y^\frac{b \cdot PBS}{2} \cdot z^\frac{c \cdot PBS}{2} \)
Asal çarpanların ortak kuvvetlerini sabit tutarak tabanları birleştirelim.
\( = (x^a \cdot y^b \cdot z^c)^\frac{PBS}{2} \)
Taban \( A \) sayısına eşit olduğu için yerine koyduğumuzda pozitif bölenlerin çarpımı formülünü elde ederiz.
Pozitif bölenlerinin çarpımı \( = A^\frac{PBS}{2} = \sqrt{A^{PBS}} \)
360 sayısını asal çarpanlarının kuvvetleri biçiminde yazıp yukarıda listelenen bölen sayılarını hesaplayın.
Çözümü Göster360'ın asal çarpanlarının kuvvetleri biçiminde yazalım.
\( 360 = 2^3 \cdot 3^2 \cdot 5^1 \)
Asal bölenler: 2, 3, 5
Asal bölenlerin sayısı \( = 3 \)
Pozitif bölenlerin sayısı \( = (3 + 1)(2 + 1)(1 + 1) = 24 \)
Pozitif bölenler: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120, 180, 360
Tüm (pozitif ve negatif) bölenlerin sayısı \( = 2 \cdot 24 = 48 \)
Tüm bölenler: Yukarıdaki pozitif bölenler ve negatif işaretlileri
Asal olmayan pozitif bölenlerin sayısı \( = 24 - 3 = 21 \)
Asal olmayan pozitif bölenler: 2, 3 ve 5 hariç pozitif bölenler
Asal olmayan bölenlerin sayısı \( = 48 - 3 = 45 \)
Asal olmayan bölenler: 2, 3 ve 5 hariç tüm bölenler
Tek sayı pozitif bölenlerin sayısı \( = (2 + 1)(1 + 1) = 6 \)
Tek sayı pozitif bölenler: 1, 3, 5, 9, 15, 45
Çift sayı pozitif bölenlerin sayısı \( = 24 - 6 = 18 \)
Çift sayı pozitif bölenler: Yukarıdaki tek sayı pozitif bölenler hariç tüm pozitif bölenler
Asal bölenlerin toplamı \( = 2 + 3 + 5 = 10 \)
Pozitif bölenlerin toplamı \( = (2^0 + 2^1 + 2^2 + 2^3) \cdot (3^0 + 3^1 + 3^2) \cdot (5^0 + 5^1) \)
\( = 15 \cdot 13 \cdot 6 = 1170 \)
Pozitif bölenlerin çarpımı \( = \sqrt{360^{24}} = 360^{12} \)
\( 70^{n - 4} \) sayısının pozitif tam bölenlerinin sayısı 27 olduğuna göre, \( n \) kaçtır?
Çözümü GösterSayıyı asal çarpanlarına ayıralım.
\( 70^{n - 4} = (2 \cdot 5 \cdot 7)^{n - 4} \)
\( = 2^{n - 4} \cdot 5^{n - 4} \cdot 7^{n - 4} \)
Bir sayının pozitif bölenlerinin sayısı (PBS) asal çarpanlarının kuvvetlerinin birer fazlasının çarpımına eşittir.
PBS \( = (n - 3)(n - 3)(n - 3) \)
\( (n - 3)^3 = 27 \)
\( n = 6 \) bulunur.
\( 16! \) sayısının asal bölenlerinin toplamı kaçtır?
Çözümü Göster\( 16! = 16 \cdot 15 \cdot \ldots \cdot 2 \cdot 1 \)
Sayıyı asal çarpanlarına ayırmadan \( 16! \) içindeki asal çarpanları yazalım.
\( \{ 2, 3, 5, 7, 11, 13 \} \)
\( 16! \) sayısının asal bölenlerinin toplamı \( 2 + 3 + 5 + 7 + 11 + 13 = 41 \) olarak bulunur.
\( 4^4 \cdot 3^{n + 1} \) sayısının 36 pozitif tam sayı böleni olduğuna göre, \( n \) kaçtır?
Çözümü Göster\( 4^4 \cdot 3^{n + 1} = 2^8 \cdot 3^{n + 1} \)
Bir sayının pozitif bölenlerinin sayısı (PBS) asal çarpanlarının kuvvetlerinin birer fazlasının çarpımına eşittir.
PBS \( = (8 + 1)(n + 2) = 36 \)
\( = 9(n + 2) = 36 \)
\( n = 2 \) bulunur.
359999 sayısının pozitif bölenlerini bulunuz.
Çözümü Göster359999 sayısını iki kare farkı şeklinde yazalım.
\( 359999 = 360000 - 1 = 600^2 - 1 \)
\( = (600 - 1)(600 + 1) = 599 \cdot 601 \)
599 ve 601 asal sayılardır.
Dolayısıyla, 359999 sayısının pozitif bölenleri 1, 599, 601, 359999 olarak bulunur.
200 sayısını asal çarpanlarının kuvvetleri biçiminde yazıp yukarıda listelenen bölen sayılarını hesaplayın.
Çözümü Göster200'ün asal çarpanlarının kuvvetleri biçiminde yazalım.
\( 200 = 2^3 \cdot 5^2 \)
Asal bölenler: 2, 5
Asal bölenlerin sayısı \( = 2 \)
Pozitif bölenlerin sayısı \( = (3 + 1)(2 + 1) = 12 \)
Pozitif bölenler: 1, 2, 4, 5, 8, 10, 20, 25, 40, 50, 100, 200
Tüm (pozitif ve negatif) bölenlerin sayısı \( = 2 \cdot 12 = 24 \)
Tüm bölenler: Yukarıdaki pozitif bölenler ve negatif işaretlileri
Asal olmayan pozitif bölenlerin sayısı \( = 12 - 2 = 10 \)
Asal olmayan pozitif bölenler: 2 ve 5 hariç pozitif bölenler
Asal olmayan bölenlerin sayısı \( = 24 - 2 = 22 \)
Asal olmayan bölenler: 2 ve 5 hariç tüm bölenler
Tek sayı pozitif bölenlerin sayısı \( = (2 + 1) = 3 \)
Tek sayı pozitif bölenler: 1, 5, 25
Çift sayı pozitif bölenlerin sayısı \( = 12 - 3 = 9 \)
Çift sayı pozitif bölenler: Yukarıdaki tek sayı pozitif bölenler hariç tüm pozitif bölenler
\( A = 111^2 + 333^2 + 555^2 \) olduğuna göre, \( A \) sayısının kaç tane pozitif böleni vardır?
Çözümü Göster\( A \) sayısını asal çarpanlarına ayıralım.
\( A = 111^2 + 333^2 + 555^2 \)
\( = 111^2 + (3 \cdot 111)^2 + (5 \cdot 111)^2 \)
\( = 111^2 + 3^2 \cdot 111^2 + 5^2 \cdot 111^2 \)
\( = 111^2 \cdot (1 + 3^2 + 5^2) \)
\( = 111^2 \cdot 35 \)
\( = 3^2 \cdot 5 \cdot 7 \cdot 37^2 \)
Bir sayının pozitif bölenlerinin sayısı (PBS) asal çarpanlarının kuvvetlerinin birer fazlasının çarpımına eşittir.
PBS \( = (2 + 1)(1 + 1)(1 + 1)(2 + 1) \)
\( = 36 \) bulunur.
\( \dfrac{2x + 180}{x} \) kesrini tam sayı yapan kaç farklı \( x \) tam sayısı vardır?
Çözümü Göster\( \dfrac{2x + 180}{x} = \dfrac{2x}{x} + \dfrac{180}{x} = 2 + \dfrac{180}{x} \)
İlk terim bir tam sayı olduğu için ikinci terimi tam sayı yapan \( x \) değerleri tüm ifadeyi de tam sayı yapar.
180'in her böleni için bu kesirli ifadenin sonucu tam sayı olur.
\( 180 = 2^2 \cdot 3^2 \cdot 5 \)
Bir sayının pozitif bölenlerinin sayısı (PBS) asal çarpanlarının kuvvetlerinin birer fazlasının çarpımına eşittir.
PBS \( = (2 + 1)(2 + 1)(1 + 1) = 18 \)
Bir sayının pozitif ve negatif tüm bölenlerinin sayısı (TBS) pozitif bölenlerinin sayısının iki katına eşittir.
TBS \( = 2 \cdot 18 = 36 \) bulunur.
\( a \in \mathbb{Z^+} \) olmak üzere,
\( 6^{a + 9} \cdot 7^2 \cdot 8^{\frac{2 - 3a}{3}} \) sayısının 90 tane pozitif tam böleni olduğuna göre, \( a \) kaçtır?
Çözümü Gösterİfadeyi asal çarpanlarının kuvvetleri biçiminde yazalım.
\( 3^{a + 9} \cdot 2^{a + 9} \cdot 7^2 \cdot 2^{3 \cdot \frac{2 - 3a}{3}} \)
\( = 3^{a + 9} \cdot 2^{a + 9} \cdot 7^2 \cdot 2^{2 - 3a} \)
\( = 2^{11 - 2a} \cdot 3^{a + 9} \cdot 7^2 \)
Bir sayının pozitif bölenlerinin sayısı (PBS) asal çarpanlarının kuvvetlerinin birer fazlasının çarpımına eşittir.
PBS \( = (11 - 2a + 1)(a + 9 + 1)(2 + 1) = 90 \)
\( (12 - 2a)(a + 10) = 30 \)
\( -2a^2 - 8a + 120 = 30 \)
\( a^2 + 4a - 45 = 0 \)
\( (a + 9)(a - 5) = 0 \)
\( a = -9 \) ya da \( a = 5 \)
\( a \) pozitif tam sayı olduğu için \( a = 5 \) olur.
\( A = 9^{24} + 9^{25} + 9^{26} + 9^{27} \) olduğuna göre, \( A \)'nın pozitif tam sayı bölenlerinin sayısı kaçtır?
Çözümü GösterTam sayı bölen sayısını bulmak için \( A \)'yı asal çarpanlarına ayıralım.
İfadeyi \( 9^{24} \) parantezine alalım.
\( A = 9^{24}(1 + 9 + 9^2 + 9^3) \)
\( = 3^{48}(1 + 9 + 81 + 729) \)
\( = 3^{48} \cdot 820 \)
\( = 2^2 \cdot 3^{48} \cdot 5 \cdot 41 \)
Bir sayının pozitif bölenlerinin sayısı (PBS) asal çarpanlarının kuvvetlerinin birer fazlasının çarpımına eşittir.
PBS \( = (2 + 1)(48 + 1)(1 + 1)(1 + 1) = 588 \) bulunur.
\( \{ 1, 2, 6, 9, a, b \} \) kümesinin elemanları bir doğal sayının tüm pozitif bölenleri olduğuna göre, \( a + b \) kaçtır?
Çözümü GösterVerilen kümenin elemanlarını asal çarpanları cinsinden yazalım.
\( \{ 1, 2, 2 \cdot 3, 3^2, a, b \} \)
Listede 3 çarpanı içeren bölen bulunduğu için 3 de bu sayının bir pozitif böleni olmalıdır.
\( a = 3 \)
Listede \( 2 \) ve \( 3^2 \) çarpanları içeren bölen bulunduğu için bunların çarpımı da bu sayının bir pozitif böleni olmalıdır.
\( b = 2 \cdot 3^2 = 18 \)
\( a + b = 3 + 18 = 21 \) bulunur.
2500 sayısının kaç tane tam kare böleni vardır?
Çözümü Göster2500'ü asal çarpanlarına ayıralım.
\( 2500 = 2^2 \cdot 5^4 \)
İfadeyi tam kare çarpanlar cinsinden yazalım.
\( 2500 = (2^2)^1 \cdot (5^2)^2 \)
Tam kare bölenlerin içinde tüm çarpanların tam kare şeklinde bulunması gerektiği için parantez içindeki çarpanları bölünmez birer asal çarpan gibi düşünerek pozitif bölen sayısını bulalım.
Tam kare bölen sayısı \( = (1 + 1)(2 + 1) = 6 \)
2500'ün 6 tam kare böleni aşağıdaki sayılardır.
\( \{ 1, 4, 25, 100, 625, 2500 \} \)
4860'a tam bölünen en küçük tam kare sayı kaçtır?
Çözümü Gösterİstenen sayıya \( A \) diyelim.
4860 sayısını asal çarpanlarına ayıralım.
\( 4860 = 2^2 \cdot 3^5 \cdot 5 \)
4860'a tam bölünmesi için, \( A \) sayısı 4860 sayısının tüm asal çarpanlarını içermelidir.
Ayrıca tam kare bir sayı olması için, \( A \) sayısının tüm asal çarpanlarının kuvvetleri çift sayı olmalıdır.
Bu koşulları sağlayan en küçük \( A \) sayısını yazalım.
\( A = 2^2 \cdot 3^6 \cdot 5^2 = 72900 \) bulunur.
\( A = 2^5 \cdot 5^4 \cdot 6^3 \) olduğuna göre, \( A \) sayısının 1'den büyük kaç tane tam kare böleni vardır?
Çözümü Göster\( A \) sayısını asal çarpanlarına ayıralım.
\( A = 2^5 \cdot 5^4 \cdot 2^3 \cdot 3^3 \)
\( = 2^8 \cdot 3^3 \cdot 5^4 \)
İfadeyi tam kare çarpanlar cinsinden yazalım.
\( A = (2^2)^4 \cdot (3^2)^1 \cdot 3 \cdot (5^2)^2 \)
Tam kare bölenlerin içinde tüm çarpanların tam kare şeklinde bulunması gerektiği için parantez içindeki çarpanları bölünmez birer asal çarpan gibi düşünerek pozitif bölen sayısını bulalım.
Tam kare bölen sayısı \( = (4 + 1)(1 + 1)(2 + 1) = 30 \)
Bulduğumuz tam kare bölen sayısına 1 de dahil olduğu için sonuçtan 1 çıkaralım.
\( 30 - 1 = 29 \) bulunur.
\( \dfrac{300}{x} \) ve \( \dfrac{x}{15} \) birer pozitif tam sayı olduğuna göre, \( x \)'in alabileceği kaç farklı tam sayı değeri vardır?
Çözümü Göster15 ve 300'ü asal çarpanlarına ayıralım.
\( 15 = 3 \cdot 5 \)
\( 300 = 2^2 \cdot 3 \cdot 5^2 \)
Verilen iki ifadenin tam sayı olması için \( x \) en az \( 3 \cdot 5 \), en fazla \( 2^2 \cdot 3 \cdot 5^2 \) çarpanlarını içermelidir.
300 içinde olup 15 içinde olmayan çarpanlar \( 2^2 \cdot 5 \) olur ve bu çarpanlar ile yazılabilecek sayı kadar farklı \( x \) sayısı yazılabilir.
\( 2^2 \cdot 5 \) çarpanları ile \( (2 + 1)(1 + 1) = 6 \) farklı sayı yazılabilir. Bu sayıların her birini \( 15 = 3 \cdot 5 \) ile çarptığımızda istenen koşulu sağlayan \( x \) değerlerini buluruz.
\( x \)'in alabileceği bu 6 değer aşağıdaki gibidir.
\( 15 \cdot 2^0 \cdot 5^0 = 15 \)
\( 15 \cdot 2^1 \cdot 5^0 = 30 \)
\( 15 \cdot 2^2 \cdot 5^0 = 60 \)
\( 15 \cdot 2^0 \cdot 5^1 = 75 \)
\( 15 \cdot 2^1 \cdot 5^1 = 150 \)
\( 15 \cdot 2^2 \cdot 5^1 = 300 \)
\( 2^{16} - 1 \) sayısının 2 basamaklı kaç tane pozitif böleni vardır?
Çözümü GösterKare farkı özdeşliğini kullanarak ifadeyi çarpanlarına ayıralım.
\( 2^{16} - 1^2 = (2^8 + 1)(2^8 - 1) \)
\( = (2^8 + 1)(2^4 + 1)(2^4 - 1) \)
\( = (2^8 + 1)(2^4 + 1)(2^2 + 1)(2^2 - 1) \)
\( = (2^8 + 1)(2^4 + 1)(2^2 + 1)(2^1 + 1)(2^1 - 1) \)
\( = 257 \cdot 17 \cdot 5 \cdot 3 \)
Bu ifadedeki çarpanların tümü asal sayı olduğu için sayıyı daha fazla çarpanlarına ayıramayız.
Bu asal çarpanların oluşturduğu pozitif bölenler arasından 2 basamaklı olanları bulalım.
257 asal çarpanı 3 basamaklı olduğundan sadece 17, 5 ve 3 çarpanlarını dikkate almamız yeterlidir.
\( 17 = 17 \)
\( 3 \cdot 5 = 15 \)
\( 3 \cdot 17 = 51 \)
\( 5 \cdot 17 = 85 \)
Buna göre \( 2^{16} - 1 \) sayısının 15, 17, 51 ve 85 olmak üzere dört tane 2 basamaklı pozitif böleni vardır.
\( x, y \in \mathbb{Z^+} \) olmak üzere,
\( (x - 2)(y + 8) = 210 \) eşitliğini sağlayan kaç farklı \( x \) sayısı vardır?
Çözümü Göster210 sayısını asal çarpanlarının kuvvetleri biçiminde yazalım.
\( 210 = 2 \cdot 3 \cdot 5 \cdot 7 \)
Buna göre 210'un \( 2 \cdot 2 \cdot 2 \cdot 2 = 16 \) pozitif tam sayı böleni vardır ve her biri için çarpımları 210 olan bir sıralı ikili yazılabilir.
\( (x - 2, y + 8) \in \{(1, 210), (2, 105), (3, 70), \ldots\} \)
\( y \in \mathbb{Z^+} \) olduğu için \( y + 8 \gt 8 \) olur.
\( y + 8 \notin \{ 1, 2, 3, 5, 6, 7 \} \)
Buna göre \( x \)'in alabileceği değerlerin sayısı \( 16 - 6 = 10 \) olarak bulunur.
2514'ü böldüğünde 98 kalanını veren en küçük sayı kaçtır?
Çözümü Göster\( 2514 - 98 = 2416 \)
İstenen sayı 2416'yı tam bölmelidir.
2416'yı çarpanlarına ayıralım.
\( 2416 = 2^4 \cdot 151 \)
2416'nın asal çarpanlarının (2, 2, 2, 2, 151) herhangi bir alt kümesindeki elemanların çarpımı 2416'yı tam böler.
Bu sayı ayrıca 2514'ü böldüğünde 98 kalanını verdiği için 98'den büyük olmalıdır.
2416'ın 98'den büyük olan en küçük böleni 151'dir.
\( \dfrac{8820}{n} \) kesrinin sonucunu tam kare sayı yapan kaç farklı \( n \) tam sayısı vardır?
Çözümü GösterBir tam sayının karesi olan sayılara tam kare sayı denir.
\( 8820 \) sayısını asal çarpanlarına ayıralım.
\( 8820 = 2^2 \cdot 3^2 \cdot 5 \cdot 7^2 \)
Bir sayının tam kare olması için sayının tüm asal çarpanlarının kuvveti çift sayı olmalıdır.
8820 sayısında 5 çarpanı bir kez bulunduğu için kesrin sonucunda 5 çarpanı bulunmamalıdır, dolayısıyla \( n \) sayısı mutlaka 5 çarpanı içermelidir.
\( n \) sayısının içinde 5 dışındaki diğer asal çarpanlar tam kare şeklinde bulunduğunda ifadenin sonucu yine tam kare olur.
\( 2^2, 3^2, 5^2 \) çarpanları ile \( 2^3 = 8 \) farklı sayı oluşturulabilir.
\( (1 + 1)(1 + 1)(1 + 1) = 8 \)
5 çarpanının bu 8 farklı sayı ile çarpılmasıyla elde edilen 8 farklı \( n \) sayısı verilen kesrin sonucunu tam sayı yapar.
\( n \in \{5, 5 \cdot 2^2, 5 \cdot 3^2, 5 \cdot 7^2, 5 \cdot 2^2 \cdot 3^2, 5 \cdot 2^2 \cdot 7^2, 5 \cdot 3^2 \cdot 7^2, 5 \cdot 2^2 \cdot 3^2 \cdot 7^2\} \)
\( 2^5 \cdot 3^3 \cdot 5^2 \cdot 7 \) sayısının pozitif bölenlerinden kaç tanesi 4'e tam bölünür ancak 7'ye tam bölünmez?
Çözümü GösterVerilen sayıya \( A \) diyelim.
\( A = 2^5 \cdot 3^3 \cdot 5^2 \cdot 7 \)
Bir sayının pozitif bölenlerinin sayısı (PBS) asal çarpanlarının kuvvetlerinin birer fazlasının çarpımına eşittir.
Önce pozitif bölenlerden 4'e tam bölünenleri bulalım.
\( A \) sayısının içindeki 4 çarpanını ayıralım.
\( 2^2 \cdot (2^3 \cdot 3^3 \cdot 5^2 \cdot 7) \)
Buna göre \( A \) sayısının \( 2^3 \cdot 3^3 \cdot 5^2 \cdot 7 \) sayısının pozitif bölen sayısı kadar 4'e tam bölünen pozitif böleni vardır.
\( (3 + 1)(3 + 1)(2 + 1)(1 + 1) = 96 \) pozitif bölen
Şimdi de pozitif bölenlerden 4 ve 7'ye tam bölünenleri bulalım. Bunun için \( A \) sayısının içindeki 4 ve 7 çarpanlarını ayıralım.
\( 2^2 \cdot 7 \cdot (2^3 \cdot 3^3 \cdot 5^2) \)
\( A \) sayısının \( 2^3 \cdot 3^3 \cdot 5^2 \) sayısının pozitif bölen sayısı kadar 4 ve 7'ye tam bölünen pozitif böleni vardır.
\( (3 + 1)(3 + 1)(2 + 1) = 48 \) pozitif bölen
Tüm durumdan istenmeyen durumu çıkardığımızda istenen durumu buluruz.
\( 96 - 48 = 48 \) pozitif bölen bulunur.
\( 2^{18} + 2^{10} + 1 \) sayısının kaç tane pozitif böleni vardır?
Çözümü Gösterİfadeyi düzenleyelim.
\( (2^9)^2 + 2 \cdot 2^9 + 1 \)
İfadeyi parantez karesi formunda yazalım.
\( = (2^9 + 1)^2 \)
\( = (512 + 1)^2 = 513^2 \)
513 sayısını asal çarpanlarının kuvvetleri biçiminde yazalım.
\( = (3^3 \cdot 19)^2 \)
\( = 3^6 \cdot 19^2 \)
Bir sayının pozitif bölenlerinin sayısı (PBS) asal çarpanlarının kuvvetlerinin birer fazlasının çarpımına eşittir.
PBS \( = (6 + 1)(2 + 1) = 21 \) bulunur.
Pozitif \( N \) tam sayısının pozitif bölenlerinin sayısı 6'dır.
Bu bölenlerden beşinin çarpımı 28125 olduğuna göre, altıncı bölen kaçtır?
Çözümü GösterBir sayının pozitif bölenlerinin sayısı (PBS) asal çarpanlarının kuvvetlerinin birer fazlasının çarpımına eşittir.
Dolayısıyla, \( N \) tam sayısının asal çarpanlarına ayrılmış hali \( a^5 \) ya da \( a^2 \cdot b \) formunda olmalıdır.
28125 sayısını çarpanlarına ayıralım.
\( 28125 = 3^2 \cdot 5^5 \)
\( N \) sayısı iki asal çarpan içerdiği için \( a^5 \) formunda değil, \( a^2 \cdot b \) formunda olmalıdır.
\( N = a^2 \cdot b = 5^2 \cdot 3 = 75 \)
PBS \( N \) sayısının pozitif bölenlerinin sayısı olmak üzere, pozitif bölenlerin çarpımı aşağıdaki formülle bulunur.
\( \sqrt{N^\text{PBS}} = \sqrt{75^6} = 75^3 \)
Tüm bölenlerin çarpımını beş bölenin çarpımına böldüğümüzde altıncı böleni buluruz.
\( \dfrac{75^3}{28125} = \dfrac{3^3 \cdot 5^6}{3^2 \cdot 5^5} \)
\( = 3 \cdot 5 = 15 \) bulunur.
\( a, b \in \mathbb{Z^+} \) olmak üzere,
\( 27^{2024} = a^b \) eşitliğini sağlayan kaç farklı \( (a, b) \) ikilisi yazılabilir?
Çözümü Göster\( 27^{2024} = a^b \)
\( (3^3)^{2024} = a^b \)
\( 3^{6072} = a^b \)
\( a \) ve \( b \) pozitif tam sayılar olduğu için, verilen eşitlik gereği \( a \) sayısı 3'ün bir pozitif tam sayı kuvveti olmalıdır.
\( k \in \mathbb{Z^+} \) olmak üzere,
\( a = 3^k \)
\( 3^{6072} = (3^k)^b = 3^{kb} \)
\( 6072 = kb \)
\( k \) sayısı 6072 sayısının herhangi bir pozitif böleni olabilir.
6072 sayısını asal çarpanlarına ayıralım.
\( 6072 = 2^3 \cdot 3 \cdot 11 \cdot 23 \)
Bir sayının pozitif bölenlerinin sayısı (PBS) asal çarpanlarının kuvvetlerinin birer fazlasının çarpımına eşittir.
PBS \( = (3 + 1)(1 + 1)(1 + 1)(1 + 1) = 32 \)
Buna göre 32 farklı \( k \) sayısı vardır.
\( k \) sayısını oluşturan asal çarpanlar dışındaki çarpanlar \( b \) sayısını oluşturur, 3'ün \( k \). kuvveti de \( a \) sayısını belirler.
Buna göre verilen eşitliği sağlayan 32 farklı \( (a, b) \) ikilisi yazılabilir.
44 ve 77 dahil olmak üzere toplam 16 pozitif böleni olan pozitif tam sayı nedir?
Çözümü Gösterİstenen sayıya \( A \) diyelim.
\( 44 = 2^2 \cdot 11 \)
\( 77 = 7 \cdot 11 \)
Buna göre \( A \) sayısı \( 2^2 \), \( 7 \) ve \( 11 \) asal çarpanlarını içerir.
\( A = 2^2 \cdot 7 \cdot 11 \cdot k \)
Bir sayının pozitif bölenlerinin sayısı (PBS) asal çarpanlarının kuvvetlerinin birer fazlasının çarpımına eşittir.
\( A \) sayısının \( k = 1 \) olduğu durumdaki pozitif bölen sayısını bulalım.
PBS \( = (2 + 1)(1 + 1)(1 + 1) = 12 \)
PBS değeri sadece 2'nin üssü 3 olduğunda (yani \( k = 2 \) olduğunda) 16 olur.
PBS \( = (3 + 1)(1 + 1)(1 + 1) = 16 \)
Buna göre \( A \) sayısı aşağıdaki gibi olur.
\( A = 2^3 \cdot 7 \cdot 11 = 616 \) bulunur.
9360 sayısının pozitif bölenlerinden kaçının 3'ten fazla pozitif böleni vardır?
Çözümü Göster9360 sayısını asal çarpanlarına ayıralım.
\( 9360 = 2^4 \cdot 3^2 \cdot 5 \cdot 13 \)
Bir sayının pozitif bölenlerinin sayısı (PBS) asal çarpanlarının kuvvetlerinin birer fazlasının çarpımına eşittir.
PBS \( = (4 + 1)(2 + 1)(1 + 1)(1 + 1) = 5 \cdot 3 \cdot 2 \cdot 2 = 60 \)
9360 sayısının pozitif bölenleri içinde 1, 2 ve 3 pozitif böleni olan sayıları bulalım.
9360'ın bölenleri içinde sadece bir pozitif böleni olan tek sayı 1'dir.
9360'ın bölenleri içinde sadece iki pozitif böleni olan sayılar asal çarpan listesindeki asal çarpanlardır. 2, 3, 5 ve 13'ün her birinin pozitif bölenleri 1 ve kendileridir.
Buna göre sadece iki pozitif böleni olan 4 sayı vardır.
9360'ın bölenleri içinde sadece üç pozitif böleni olan sayılar kuvveti 2 ve daha büyük olan asal çarpanların kareleridir.
Buna göre \( 2^2 = 4 \) ve \( 3^2 = 9 \) sayılarının 3'er pozitif böleni vardır. 4'ün bölenleri 1, 2 ve 4; 9'un bölenleri 1, 3 ve 9'dur.
3'ten fazla pozitif böleni olan sayıları bulmak için 60'tan bu sayıları çıkaralım.
\( 60 - 1 - 4 - 2 = 53 \) bulunur.
\( x, y, z \in \mathbb{Z} \) olmak üzere,
\( xy = 168 \)
\( yz = 420 \)
olduğuna göre, \( y \) sayısının alabileceği kaç farklı değer vardır?
Çözümü Göster\( xy = 168 \)
\( x = \dfrac{168}{y} \)
\( yz = 420 \)
\( z = \dfrac{420}{y} \)
\( x, y, z \) tam sayı oldukları için, \( y \) sayısı 168 ve 420 sayılarının ortak bir böleni, yani EBOB'u ya da EBOB'unun bir böleni olmalıdır.
\( EBOB(168, 420) = 84 \)
\( 84 \)'ü asal çarpanlarına ayıralım.
\( 84 = 2^2 \cdot 3^1 \cdot 7^1 \)
Bir sayının pozitif bölenlerinin sayısı (PBS) asal çarpanlarının kuvvetlerinin birer fazlasının çarpımına eşittir.
PBS \( = (2 + 1)(1 + 1)(1 + 1) = 12 \)
Bir sayının pozitif ve negatif tüm bölenlerinin sayısı (TBS) pozitif bölenlerinin sayısının iki katına eşittir.
TBS \( = 2 \cdot 12 = 24 \) bulunur.
\( X = 2^4 \cdot 5^2 \cdot 7^3 \cdot 13 \) sayısının tek sayı bölenlerinin toplamının, çift sayı bölenlerinin toplamına oranı kaçtır?
Çözümü GösterAşağıdaki şekilde tanımlı bir \( A \) sayısının pozitif bölenlerinin toplamı aşağıdaki formülle bulunur.
\( A = x^a \cdot y^b \cdot z^c \)
Pozitif bölenlerin toplamı \( = (x^0 + x^1 + x^2 + \ldots + x^a) (y^0 + y^1 + y^2 + \ldots + y^b) (z^0 + z^1 + z^2 + \ldots + z^c) \)
Bu bölenlerden en az bir tane 2 çarpanı içerenler çift sayı, hiç 2 çarpanı içermeyenler ise tek sayı olur.
\( X \) sayısının tek sayı pozitif bölenlerinin toplamına \( n \) diyelim.
Her ne kadar \( n \) değerine aşağıdaki çözümde ihtiyaç duymayacak olsak da bu değer 2 dışındaki asal çarpanlarla oluşturulabilecek tüm bölenlerin toplamına eşittir.
\( n = (2^0)(5^0 + 5^1 + 5^2)(7^0 + 7^1 + 7^2 + 7^3)(13^0 + 13^1) \)
\( X \) sayısının çift sayı pozitif bölenlerinin toplamına \( m \) diyelim.
\( X \) sayısının çift sayı pozitif bölenleri en az bir 2 çarpanı içeren bölenlerden oluşur.
\( m = (2^1 + 2^2 + 2^3 + 2^4) \cdot n = 30n \)
Bulduğumuz iki değerin oranını bulalım.
\( \dfrac{\text{Tek bölenlerin toplamı}}{\text{Çift bölenlerin toplamı}} = \dfrac{n}{30n} \)
\( = \dfrac{1}{30} \) bulunur.
\( a \) sayısının pozitif tam bölenlerinin kümesine \( B_a \) diyelim.
Buna göre aşağıdaki kümelerin eleman sayısı kaçtır?
(a) \( B_{168} \cap B_{1540} \)
(b) \( B_{168} \cup B_{1540} \)
Çözümü Göster(a) seçeneği:
168 ve 1540 sayılarını asal çarpanlarının kuvvetleri biçiminde yazalım.
\( 168 = 2^3 \cdot 3^1 \cdot 7^1 \)
\( 1540 = 2^2 \cdot 5^1 \cdot 7^1 \cdot 11^1 \)
\( B_{168} \cap B_{1540} \) kümesi, 168 ve 1540 sayılarının tüm ortak pozitif bölenlerinden, dolayısıyla EBOB'larının pozitif tam bölenlerinden oluşur.
\( EBOB(168, 1540) = 2^2 \cdot 7^1 = 28 \)
28 sayısının pozitif tam bölen sayısı \( (2 + 1)(1 + 1) = 6 \)'dır.
\( s(B_{168} \cap B_{1540}) = s(B_{28}) = 6 \)
(b) seçeneği:
168 ve 1540 sayılarının pozitif bölenlerinin sayısını bulalım.
\( B_{168} = (3 + 1)(1 + 1)(1 + 1) = 16 \)
\( B_{1540} = (2 + 1)(1 + 1)(1 + 1)(1 + 1) = 24 \)
İki kümenin birleşiminin eleman sayısı, kümelerin eleman sayıları toplamından kesişimlerinin eleman sayısı çıkarılarak bulunur.
\( s(A \cup B) = s(A) + s(B) - s(A \cap B) \)
\( s(B_{168} \cup B_{1540}) = s(B_{168}) + s(B_{168}) - s(B_{168} \cap B_{1540}) \)
\( = 16 + 24 - 6 = 34 \) bulunur.
\( 185^8 \) sayısının karekökü veya küpkökü tam sayı olan kaç tane pozitif böleni vardır?
Çözümü GösterBir sayı, karekökü tam sayı ise tam kare, küpkökü tam sayı ise tam küp bir sayıdır.
Aşağıdaki kümeleri tanımlayalım.
\( A \): \( 185^8 \) sayısının tüm pozitif bölenlerinin kümesi
\( A_2 \): \( 185^8 \) sayısının tam kare bölenlerinin kümesi
\( A_3 \): \( 185^8 \) sayısının tam küp pozitif bölenlerinin kümesi
Bu kümeleri bir Venn şemasında gösterelim.

\( 185^8 \) sayısının tam kare veya tam küp pozitif bölenlerinin sayısı, \( A_2 \cup A_3 \) birleşim kümesinin eleman sayısına eşittir.
\( 185^8 \) sayısını asal çarpanlarına ayıralım.
\( 185^8 = 5^8 \cdot 37^8 \)
Bir sayının tam kare olması için asal çarpanlarının tümünün üsleri çift sayı olmalıdır.
\( 185^8 = (5^2)^4 \cdot (37^2)^4 \)
Buna göre \( 185^8 \) sayısının \( (4 + 1)(4 + 1) = 25 \) tane tam kare böleni vardır.
\( s(A_2) = 25 \)
Bir sayının tam küp olması için asal çarpanlarının tümünün üsleri 3'ün birer tam sayı katı olmalıdır.
\( 185^8 = (5^3)^2 \cdot (37^3)^2 \cdot x \)
Buna göre \( 185^8 \) sayısının \( (2 + 1)(2 + 1) = 9 \) tane tam küp böleni vardır.
\( s(A_3) = 9 \)
6 hem 2'ye hem de 3'e bölündüğü için asal çarpanların 6 olduğu durumda oluşan bölenler hem tam kare hem de tam küptür ve yukarıda tanımladığımız iki kümenin de elemanıdır.
\( 185^8 = (5^6)^1 \cdot (37^6)^1 \cdot y \)
Buna göre \( 185^8 \) sayısının \( (1 + 1)(1 + 1) = 4 \) tane böleni hem tam kare hem de tam küptür.
\( s(A_2 \cap A_3) = 4 \)
Hem tam kare hem de tam küp olan bölenler: \( 5^0 \cdot 37^0, 5^0 \cdot 37^6, 5^6 \cdot 37^0, 5^6 \cdot 37^6 \)
\( A_2 \cup A_3 \) kümesinin eleman sayısını bulmak için iki kümenin birleşiminin eleman sayısı formülünü kullanalım.
\( s(A_2 \cup A_3) = s(A_2) + s(A_3) - s(A_2 \cap A_3) \)
\( = 25 + 9 - 4 = 30 \) bulunur.
\( 398^{10} \) sayısının \( 10^5 \) sayısından küçük olan kaç tane pozitif böleni vardır?
Çözümü Göster\( 398^{10} \) sayısını asal çarpanlarına ayıralım.
\( 398^{10} = (2 \cdot 199)^{10} \)
\( = 2^{10} \cdot 199^{10} \)
2'nin ve 199'un hangi kuvvetlerinin \( 10^5 \)'ten küçük olduğunu bulalım.
199'un sıfırdan başlayarak artan kuvvetleri için 2'nin hangi kuvvetlerinin istenen koşulu sağladığını bulalım.
Durum 1: \( 199^0 \)
2'nin tüm kuvvetleri \( 10^5 \)'ten küçüktür.
\( 2^{10} = 1024 \lt 10^5 \)
Aşağıdaki 11 sayı bu durumda istenen koşulu sağlar.
\( 2^0, 2^1, 2^2, \ldots, 2^{10} \)
Durum 2: \( 199^1 \)
\( 199^1 \) ile 2'nin ilk 8 kuvvetinin çarpımı \( 10^5 \)'ten küçüktür.
\( 199 \cdot 2^8 = 50944 \lt 10^5 \)
Aşağıdaki 9 sayı bu durumda istenen koşulu sağlar.
\( 199 \cdot 2^0, 199 \cdot 2^1, \ldots, 199 \cdot 2^8 \)
Durum 3: \( 199^2 \)
\( 199^2 \) ile 2'nin birinci kuvvetinin çarpımı \( 10^5 \)'ten küçüktür.
\( 199^2 \cdot 2 = 79202 \lt 10^5 \)
Aşağıdaki 2 sayı bu durumda istenen koşulu sağlar.
\( 199^2 \cdot 2^0, 199^2 \cdot 2^1 \)
Buna göre istenen koşulu sağlayan pozitif bölen sayısı \( 11 + 9 + 2 = 22 \) olarak bulunur.
10000'den küçük kaç tane pozitif tam sayının 21 tane pozitif böleni vardır?
Çözümü Göster\( 21 = 7 \cdot 3 \)
Bir sayının pozitif bölenlerinin sayısı asal çarpanlarının kuvvetlerinin birer fazlasının çarpımına eşittir.
İstenen koşulu sağlayan sayıların asal çarpanlarına \( x \) ve \( y \), kuvvetlerine \( a \) ve \( b \) diyelim.
\( A = x^a \cdot y^b \)
\( (a + 1)(b + 1) = 7 \cdot 3 \)
\( a = 6, \quad b = 2 \)
İki asal çarpanı olan, asal çarpanlarının kuvvetleri 6 ve 2 olan ve 10000'den küçük olan sayıları bulalım.
Durum 1:
Üssü 6 olan asal çarpanın 2 olduğunu varsayalım.
\( 2^6 \cdot 3^2 = 576 \lt 10^4 \)
\( 2^6 \cdot 5^2 = 1600 \lt 10^4 \)
\( 2^6 \cdot 7^2 = 3136 \lt 10^4 \)
\( 2^6 \cdot 11^2 = 7744 \lt 10^4 \)
\( 2^6 \cdot 13^2 = 10816 \gt 10^4 \)
Bu durumda istenen koşulu sağlayan 4 sayı vardır.
Durum 2:
Üssü 6 olan asal çarpanın 3 olduğunu varsayalım.
\( 3^6 \cdot 2^2 = 2916 \lt 10^4 \)
\( 3^6 \cdot 5^2 = 18225 \gt 10^4 \)
Bu durumda istenen koşulu sağlayan 1 sayı vardır.
Durum 3:
Üssü 6 olan asal çarpanın 5 olduğunu varsayalım.
\( 5^6 \cdot 2^2 = 62500 \gt 10^4 \)
Bu durumda istenen koşulu sağlayan sayı yoktur.
Buna göre istenen koşulu sağlayan 5 pozitif tam sayı vardır.