Asal Çarpanlara Ayırma
Bir pozitif tam sayıyı tam olarak bölen asal sayılara o sayının asal bölenleri ya da asal çarpanları denir.
\( x \), \( y \), \( z \) birbirinden farklı asal sayılar ve \( a \), \( b \), \( c \) birer pozitif tam sayı olmak üzere,
\( A = x^a \cdot y^b \cdot z^c \)
ifadesine \( A \) sayısının asal çarpanlarının kuvvetleri biçiminde yazılışı, yapılan bu işleme de asal çarpanlara ayırma denir.
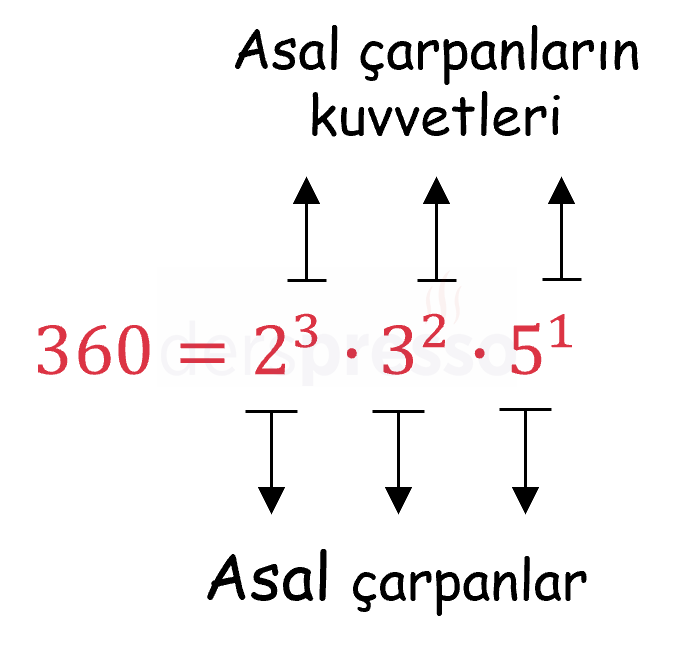
Bir asal sayı bir sayının içinde çarpan olarak birden fazla kez yer alıyorsa çarpan listesinde tekrarlanmaz ve üslü ifade şeklinde yazılır. Bir sayının asal çarpanlarının kuvvetleri biçiminde yazılışında çarpanlar genellikle tabanlara göre (kuvvetlere göre değil) küçükten büyüğe doğru sıralanır.
Aritmetiğin Temel Teoremi
Aritmetiğin temel teoremine göre, 1'den büyük tüm tam sayılar asal sayıların çarpımı biçiminde ve çarpanların sıralaması hariç tek bir şekilde yazılabilir.
Aşağıda birkaç sayının asal çarpanları cinsinden yazılışları verilmiştir.
\( 12 = 2^2 \cdot 3^1 \)
\( 13 = 13^1 \)
\( 300 = 2^2 \cdot 3^1 \cdot 5^2 \)
Bir sayıyı asal çarpanlarının kuvvetleri biçiminde yazarken iki noktaya dikkat edilmelidir, bu iki prensip sayesinde sayılar asal çarpanları cinsinden çarpanların sıralaması hariç tek bir şekilde yazılabilirler.
Birinci nokta: Çarpan listesinde sadece asal sayılar kullanılır, çünkü bileşik sayıların kullanılması bir sayının diğer sayıların çarpımı biçiminde birden fazla şekilde yazılabilmesi anlamına gelir.
Asal çarpanlar biçiminde doğru yazılış:
\( 72 = 2^3 \cdot 3^2 \)
Asal çarpanlar biçiminde yanlış yazılışlar:
\( 72 = 2 \cdot 36 \)
\( 72 = 4 \cdot 3 \cdot 6 \)
İkinci nokta: 1 bir asal sayı olmadığı için asal çarpan listesinde yer almaz. Her sayının asal çarpanları cinsinden tek bir şekilde yazılabilmesi 1 sayısının bir asal sayı olarak kabul edilmeme sebeplerinden biridir. 1 sayısı bir asal sayı olarak kabul edilmiş olsaydı sayılar asal çarpanları cinsinden birden fazla (hatta sonsuz farklı) biçimde yazılabilirdi.
Asal çarpanlar biçiminde doğru yazılış:
\( 12 = 2^2 \cdot 3^1 \)
Asal çarpanlar biçiminde yanlış yazılışlar:
\( 12 = 1^1 \cdot 2^2 \cdot 3^1 \)
\( 12 = 1^2 \cdot 2^2 \cdot 3^1 \)
Bu bilgiler ışığında, önümüzdeki bölenler, katlar, EKOK ve EBOB konularında karşımıza çıkacak sayıları bu sayıları oluşturan asal çarpanları cinsinden düşünüyor olmamız önem taşımaktadır.
Asal Çarpanlara Ayırma Yöntemleri
Bölen Listesi Yöntemi
Bir sayıyı asal çarpanlarına ayırmak için kullanabileceğimiz yöntemlerden biri bölen listesi yöntemidir. Bu yöntemde bir sayıyı asal çarpanlarına aşağıdaki adımlarla ayırabiliriz.
- Önce asal çarpanlarına ayırmak istediğimiz sayıyı ilk satırın ilk sütununa yazarak sağına dikey bir çizgi çizeriz.
- En küçük asal sayı olan 2'den başlayarak, bu asal sayının birinci sütundaki sayıyı kalansız bölüp bölmediğini kontrol ederiz.
- Eğer denediğimiz asal sayı birinci sütundaki sayıyı kalansız bölüyorsa bu asal sayıyı dikey çizginin sağındaki sütuna yazarız.
- Birinci sütundaki sayıyı ikinci sütuna yazdığımız bu asal sayıya böleriz ve bölümü birinci sütundaki sayının hemen altına yazarız.
- Her yeni satırda 2., 3. ve 4. adımları tekrarlarız. Her yeni satırda denemeye bir önceki satırda kullandığımız asal sayı ile devam ederiz. Eğer son satırda kullandığımız asal sayı bu satırdaki sayıyı kalansız bölmüyorsa bu asal sayıdan büyük bir sonraki asal sayıyı deneriz.
- Birinci sütunda 1 sayısına ulaştığımızda asal çarpanlara ayırma işlemi tamamlanmıştır. İkinci sütundaki asal sayıları küçükten büyüğe ve her asal sayının tekrar sayısı o sayının kuvveti olacak şekilde çarpan listesi olarak yazarız.
Bu yöntemi kullanarak 504 sayısını asal çarpanlarına aşağıdaki şekilde ayırabiliriz.
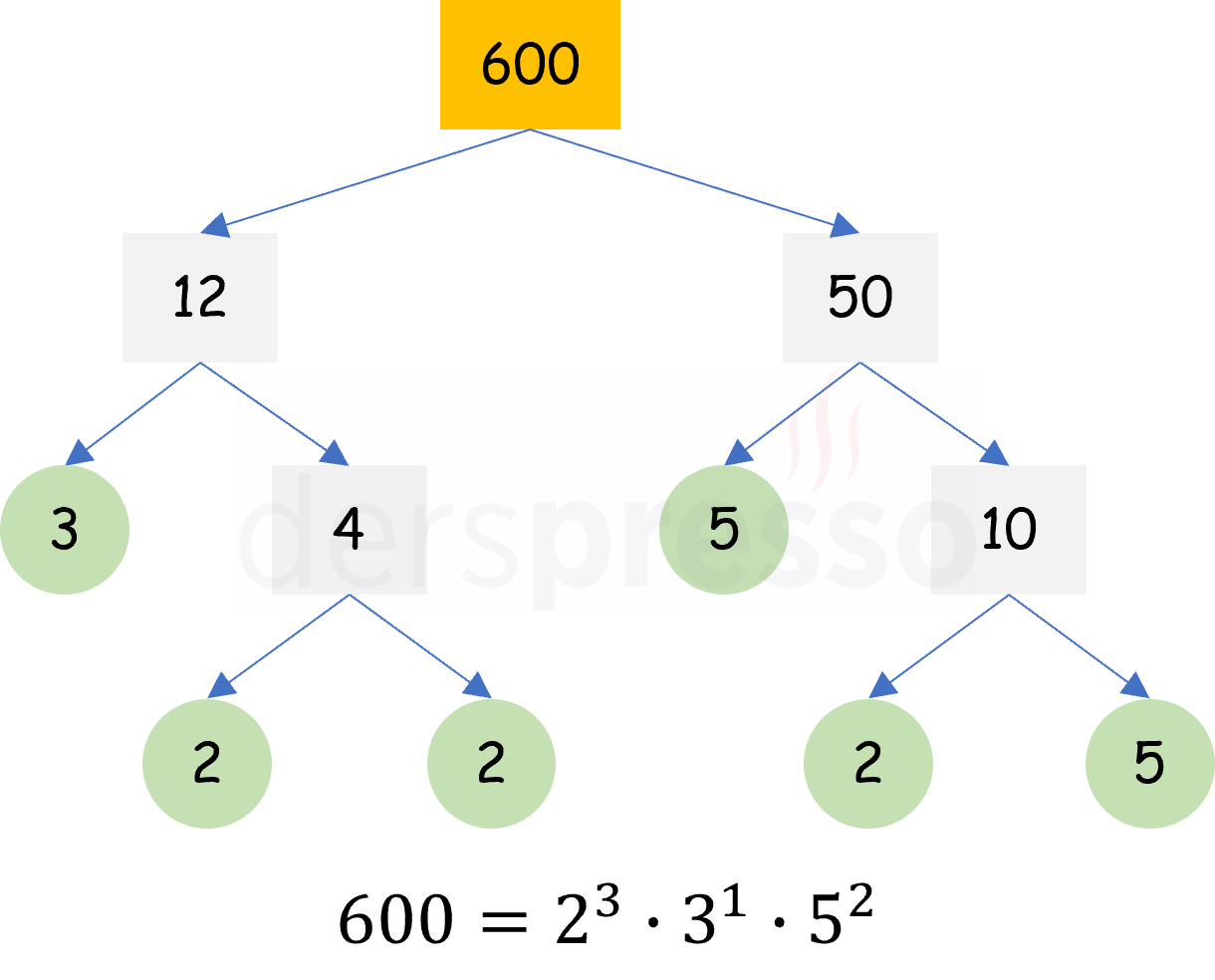
Çarpan Ağacı Yöntemi
Bir sayıyı asal çarpanlarına ayırmada kullanabileceğimiz diğer bir yöntem çarpan ağacı yöntemidir. Bu yöntemde bir sayıyı asal çarpanlarına aşağıdaki adımlarla ayırabiliriz.
- Önce asal çarpanlarına ayırmak istediğimiz sayıyı en üstte bir kutuya yazarız (şekildeki turuncu kutu).
- Bu sayıyı asal ya da bileşik sayı herhangi iki çarpanına ayırırız ve bu çarpanları sayıdan çıkan iki okun bağlandığı yeni kutulara yazarız. Bir sayıyı çarpanlarına ayırırken sayının kendisini ve 1'i çarpan olarak kullanmayız.
- Eklediğimiz bir kutunun içindeki çarpan bir asal sayı ise sayıyı bir daire içine alırız (şekildeki yeşil kutular). Asal sayı elde ettiğimiz bir kolda çarpanlara ayırma işlemi tamamlanmıştır.
- Eklediğimiz bir kutunun içindeki çarpan bir bileşik sayı ise (şekildeki gri kutular) bu kolda çarpanlara ayırma işlemine 2. adımdaki şekilde devam ederiz.
- Tüm kollarda birer asal sayı elde ettiğimizde çarpanlara ayırma işlemi tamamlanmıştır. Daire içine aldığımız asal sayıları küçükten büyüğe ve her asal sayının tekrar sayısı o sayının kuvveti olacak şekilde çarpan listesi olarak yazarız.
Bu yöntemi kullanarak 600 sayısını asal çarpanlarına aşağıdaki şekilde ayırabiliriz.
Emre'nin yeğenlerinin yaşları asal sayı olup yaşlarının çarpımı 280'dir. Buna göre Emre'nin yeğenlerinin yaşlarının ortalaması kaçtır?
Çözümü Göster280'i asal çarpanlarına ayıralım.
\( 280 = 2^3 \cdot 5 \cdot 7 \)
Buna göre yaşları asal sayı olan yeğenlerin sayısı 5 ve yaşları 2, 2, 2, 5 ve 7 olabilir.
Yeğenlerin yaşlarının ortalamasını bulalım.
\( \dfrac{2 + 2 + 2 + 5 + 7}{5} = 3,6 \) bulunur.
\( a \) asal sayı, \( b \) ve \( c \) pozitif tam sayılardır.
\( a \cdot b = 540 \) ve \( a \cdot c = 315 \) olduğuna göre, \( a \)'nın alabileceği değerler toplamı kaçtır?
Çözümü Göster\( a \cdot b = 540 = 2^2 \cdot 3^3 \cdot 5 \)
\( a \cdot c = 315 = 3^2 \cdot 5 \cdot 7 \)
\( a \) iki ifadede de ortak olduğu için, hem 540'ta hem de 315'te ortak olan çarpanlardan oluşmalıdır.
\( 3^2 \cdot 5 \)
\( a \) asal sayı olduğu için sadece 3 ve 5 değerlerini alabilir.
\( 3 + 5 = 8 \) bulunur.
\( a \in \mathbb{N} \) olmak üzere,
\( \dfrac{a^5}{x} = 400 \) eşitliğini sağlayan en küçük \( x \) doğal sayısının rakamları toplamı kaçtır?
Çözümü Göster\( \dfrac{a^5}{x} = 400 \)
\( a^5 = 400x \)
\( a^5 = 2^4 \cdot 5^2 \cdot x \)
\( a \) doğal sayısının 5. kuvvetinin asal çarpanlarına ayrılmış halinde tüm asal çarpanların kuvvetleri 5'in bir tam sayı katı olmalıdır.
2'nin kuvvetini 5'e tamamlamak için gerekli en küçük sayı \( 2^1 = 2 \), 5'in kuvvetini 5'e tamamlamak için gerekli en küçük sayı \( 5^3 = 125 \) olur.
\( a^5 = 2^4 \cdot 2^1 \cdot 5^2 \cdot 5^3 \)
\( a^5 = 2^5 \cdot 5^5 \)
\( x = 2^1 \cdot 5^3 = 250 \)
\( x \) sayısının rakamları toplamı \( 2 + 5 + 0 = 7 \) olur.
\( A \cdot 10! \) çarpımı bir pozitif tam sayının karesi olduğuna göre, \( A \)'nın alabileceği en küçük değer kaçtır?
Çözümü Göster\( A \cdot 10! \) sayısının bir pozitif tam sayının karesi olması için, asal çarpanlarına ayrıldığında tüm asal çarpanların üsleri 2'nin katı olmalıdır (çift sayı olmalıdır).
\( 10! = 10 \cdot 9 \cdot 8 \cdot \ldots \cdot 2 \cdot 1 \)
Her çarpanı ayrı ayrı asal çarpanlarına ayıralım.
\( = 2^8 \cdot 3^4 \cdot 5^2 \cdot 7 \)
Bu ifadede üssü çift sayı olmayan tek asal çarpan 7 olduğu için \( A \)'nın en küçük değeri 7 olur.
\( A = 7 \) olduğunda oluşan sayının tam kare sayı olduğunu gösterelim.
\( A \cdot 10! = 7 \cdot 10! \)
\( = 2^8 \cdot 3^4 \cdot 5^2 \cdot 7^2 \)
\( = (2^4 \cdot 3^2 \cdot 5 \cdot 7)^2 \)
1000'den küçük asal sayıların çarpımının sondan kaç basamağı sıfırdır?
Çözümü GösterBir sayının içerdiği 10 çarpanı kadar sonunda sıfır bulunur.
10'un asal çarpanları 2 ve 5'tir.
1000'den küçük asal sayılar içinde 2 ve 5 dışında 2 ve 5 asal çarpanlarını içeren sayı yoktur.
Bu durumda 1000'den küçük tüm asal sayıların çarpımı sadece birer tane 2 ve 5 çarpanı, dolayısıyla 1 tane 10 çarpanı içerir. Dolayısıyla bu sayıların çarpımının sondan 1 basamağı sıfır olur.
\( a, b, c, d \in \mathbb{Z} \) olmak üzere,
\( (5 - a)(5 - b)(5 - c)(5 - d) = 9 \)
\( a, b, c, d \) sayıları birbirinden farklı sayılar olduğuna göre, bu sayıların toplamı kaça eşittir?
Çözümü GösterSayılar birbirinden farklı olduğu için verilen eşitlikteki dört çarpanın da değeri birbirinden farklı olmalıdır.
Çarpımları 9 olan dört tam sayı değer -3, -1, 1 ve 3 olabilir.
\( 9 = -3 \cdot (-1) \cdot 1 \cdot 3 \)
Soruda \( a, b, c, d \) sayılarının toplamı sorulduğu için bu değişkenleri bu dört değere herhangi bir sırada atayabiliriz.
\( 5 - a = -3 \Longrightarrow a = 8 \)
\( 5 - b = -1 \Longrightarrow b = 6 \)
\( 5 - c = 1 \Longrightarrow c = 4 \)
\( 5 - d = 3 \Longrightarrow d = 2 \)
\( a + b + c + d = 8 + 6 + 4 + 2 \)
\( = 20 \) bulunur.
99.999.744 sayısının en büyük asal çarpanı nedir?
Çözümü GösterVerilen sayıyı düzenleyelim.
\( 99.999.744 = 100.000.000 - 256 \)
\( = 10^8 - 2^8 \)
\( = 2^8(5^8 - 1) \)
İki kare farkı özdeşliğini kullanalım.
\( = 2^8(5^4 - 1)(5^4 + 1) \)
Tekrar iki kare farkı özdeşliğini kullanalım.
\( = 2^8(5^2 - 1)(5^2 + 1)(5^4 + 1) \)
\( = 2^8 \cdot 24 \cdot 26 \cdot 626 \)
\( = 2^8 \cdot (2^3 \cdot 3) \cdot (2 \cdot 13) \cdot (2 \cdot 313) \)
Buna göre 99.999.744 sayısının asal çarpanlarının kuvvetleri biçiminde yazılışı aşağıdaki gibidir.
\( = 2^{13} \cdot 3 \cdot 13 \cdot 313 \)
99.999.744 sayısının en büyük asal çarpanı 313 olarak bulunur.
1 ile 800 arasındaki tam sayılardan kaçı 4 farklı asal sayının çarpımına eşittir?
Çözümü GösterÇözümde kolaylık olması açısından 30'a kadarki asal sayıları listeleyelim.
2, 3, 5, 7, 11, 13, 17, 19, 23, 29
En küçük üç asal sayıyı seçip dördüncü asal sayıyı deneme yanılma yoluyla belirleyelim.
Durum 1:
En küçük üç asal sayıyı 2, 3 ve 5 olarak seçelim ve dördüncü asal sayıya \( a \) diyelim.
\( 2 \cdot 3 \cdot 5 \cdot a \le 800 \)
\( 30 \cdot a \le 800 \)
Bu durumda \( a \) aşağıdaki 6 değeri alabilir.
\( a \in \{7, 11, 13, 17, 19, 23\} \)
Durum 2:
En küçük üç asal sayıyı 2, 3 ve 7 olarak seçelim ve dördüncü asal sayıya \( a \) diyelim.
\( 2 \cdot 3 \cdot 7 \cdot a \le 800 \)
\( 42 \cdot a \le 800 \)
Bu durumda \( a \) aşağıdaki 4 değeri alabilir.
\( a \in \{11, 13, 17, 19\} \)
Durum 3:
En küçük üç asal sayıyı 2, 5 ve 7 olarak seçelim ve dördüncü asal sayıya \( a \) diyelim.
\( 2 \cdot 5 \cdot 7 \cdot a \le 800 \)
\( 70 \cdot a \le 800 \)
Bu durumda \( a \) aşağıdaki 1 değeri alabilir.
\( a \in \{11\} \)
Durum 4:
En küçük üç asal sayıyı 3, 5 ve 7 olarak seçelim ve dördüncü asal sayıya \( a \) diyelim.
\( 3 \cdot 5 \cdot 7 \cdot a \le 800 \)
\( 105 \cdot a \le 800 \)
Bu durumda \( a \) için geçerli bir değer yoktur.
\( a \in \{\} \)
Durum 5:
En küçük üç asal sayıyı 2, 3 ve 11 olarak seçelim ve dördüncü asal sayıya \( a \) diyelim.
\( 2 \cdot 3 \cdot 11 \cdot a \le 800 \)
\( 66 \cdot a \le 800 \)
Bu durumda \( a \) için geçerli bir değer yoktur.
Seçeceğimiz daha büyük asal sayı üçlülerinde, çarpımları 800'den küçük olan dördüncü bir asal sayı bulunamaz.
Buna göre, verilen aralıkta \( 6 + 4 + 1 = 11 \) tane sayı 4 farklı asal sayının çarpımına eşittir.
\( n \in \mathbb{Z} \) olmak üzere,
\( 3969 \cdot (\dfrac{3}{7})^n \) ifadesinin sonucunu tam sayı yapan kaç tane \( n \) sayısı vardır?
Çözümü Göster3969 sayısını asal çarpanlarına ayıralım.
\( 3969 = 3^4 \cdot 7^2 \)
\( 3969 \cdot (\dfrac{3}{7})^n = 3^4 \cdot 7^2 \cdot \dfrac{3^n}{7^n} \)
\( = 3^{4 + n} \cdot 7^{2 - n} \)
İfadenin sonucunun tam sayı olması için 3'ün ve 7'nin üsleri negatif olmamalıdır.
\( 4 + n \ge 0 \Longrightarrow n \ge -4 \)
\( 2 - n \ge 0 \Longrightarrow n \le 2 \)
İki eşitsizliği tek eşitsizlik şeklinde yazalım.
\( -4 \le n \le 2 \)
Bu eşitsizliği sağlayan \( 2 - (-4) + 1 = 7 \) tam sayı \( n \) değeri vardır.
6500'den küçük olmak koşuluyla, 5'e tam bölünen kaç tane çift tam kare sayı vardır?
Çözümü GösterTam kare sayılarda her asal çarpanın üssü 2'nin bir tam sayı katıdır (çift sayıdır).
5'e tam bölünen çift sayılar hem 5 hem de 2 çarpanını içerir.
Buna göre istenen tam kare sayıyı aşağıdaki şekilde yazabiliriz.
\( a \in \mathbb{Z^+} \) olmak üzere,
\( A = 5^2 \cdot 2^2 \cdot a^2 \)
Bu sayının 6500'den küçük olması isteniyor.
\( 5^2 \cdot 2^2 \cdot a^2 \lt 6500 \)
\( 100 \cdot a^2 \lt 6500 \)
\( a^2 \lt 65 \)
\( a \in \{ 0, 1, 2, 3, 4, 5, 6, 7, 8 \} \)
Buna göre verilen koşulları sağlayan 9 tam kare sayı vardır.
\( A \in \{ 0, 100, 400, 900, 1600, 2500, 3600, 4900, 6400 \} \)