Kuvvet Fonksiyonları
Bir değişkenin bir reel sayı kuvveti şeklindeki fonksiyonlara kuvvet fonksiyonu denir.

Kuvvet fonksiyonunda \( x \) fonksiyonun değişkeni, \( n \) fonksiyonun derecesi, \( k \) fonksiyonun katsayısıdır.
\( k, n \in \mathbb{R}, \quad k \ne 0 \) olmak üzere,
\( f: \mathbb{R} \to \mathbb{R} \)
\( f(x) = k \cdot x^n \)
Kuvvet fonksiyonları derecelerine göre farklı formlarda ve isimlerle karşımıza çıkabilir. Aşağıdaki fonksiyonların tümü birer kuvvet fonksiyonudur.
| Derece | Fonksiyon | Fonksiyon Adı |
|---|---|---|
| \( 0 \) | \( f(x) = x^0 = 1 \) | Sabit fonksiyon |
| \( 1 \) | \( f(x) = x^1 = x \) | Birim fonksiyon |
| \( 2 \) | \( f(x) = x^2 \) | İkinci dereceden fonksiyon |
| \( -1 \) | \( f(x) = x^{-1} = \dfrac{1}{x} \) | Ters fonksiyon |
| \( \dfrac{1}{2} \) | \( f(x) = x^\frac{1}{2} = \sqrt{x} \) | Karekök fonksiyonu |
| \( \dfrac{1}{3} \) | \( f(x) = x^\frac{1}{3} = \sqrt[3]{x} \) | Küpkök fonksiyonu |
Her ne kadar kuvvet fonksiyonlarının üssü herhangi bir reel sayı olabilse de, bu konu anlatımında üs değerlerini pozitif tam sayı değerleri ile sınırlı tutacağız.
Değer Tablosu ve Grafiği
\( f(x) = x^2 \) ve \( g(x) = x^3 \) fonksiyonlarının bazı değerleri için değer tablosu aşağıdaki gibidir.
| \( x \) | \( f(x) = x^2 \) | \( g(x) = x^3 \) |
|---|---|---|
| \( -3 \) | \( f(-3) = (-3)^2 = 9 \) | \( g(-3) = (-3)^3 = -27 \) |
| \( -2 \) | \( f(-2) = (-2)^2 = 4 \) | \( g(-2) = (-2)^3 = -8 \) |
| \( -1 \) | \( f(-1) = (-1)^2 = 1 \) | \( g(-1) = (-1)^3 = -1 \) |
| \( 0 \) | \( f(0) = 0^2 = 0 \) | \( g(0) = 0^3 = 0 \) |
| \( 1 \) | \( f(1) = 1^2 = 1 \) | \( g(1) = 1^3 = 1 \) |
| \( 2 \) | \( f(2) = 2^2 = 4 \) | \( g(2) = 2^3 = 8 \) |
| \( 3 \) | \( f(3) = 3^2 = 9 \) | \( g(3) = 3^3 = 27 \) |
| \( 4 \) | \( f(4) = 4^2 = 16 \) | \( g(4) = 4^3 = 64 \) |
Her iki fonksiyon için bulunan bu noktalar analitik düzlemde işaretlendiğinde aşağıdaki grafikler elde edilir.
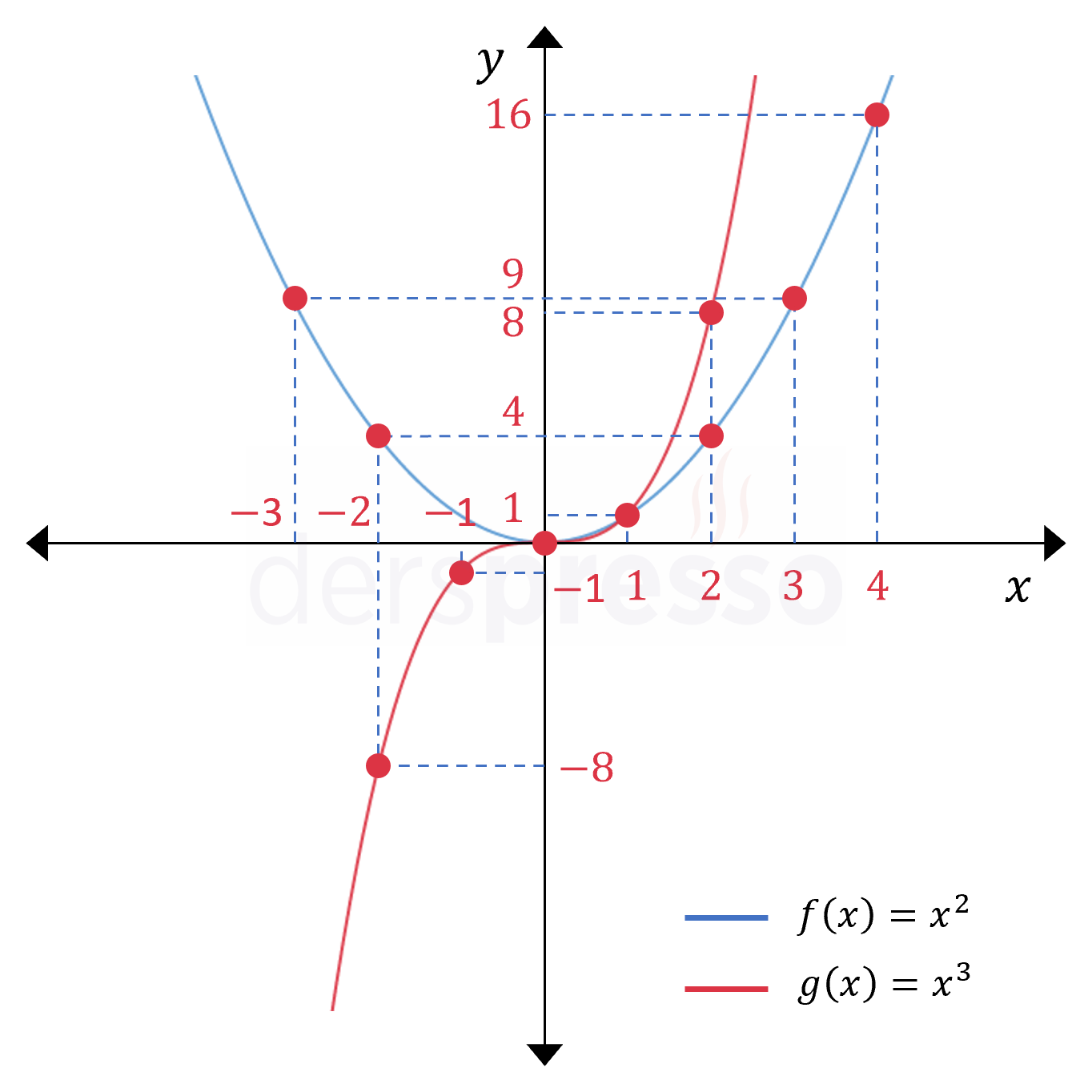
Bu grafiklerde görülebileceği gibi, çift dereceli bir fonksiyon olan \( f(x) \) ve tek dereceli bir fonksiyon olan \( g(x) \)'in grafikleri arasındaki en önemli fark, \( f(x) \)'in sadece pozitif değer alması, \( g(x) \)'in ise pozitif ve negatif değer alabilmesidir. Bunun sebebi çift dereceli üslü ifadelerin sonucunun her zaman pozitif olmasıdır.
Hiçbir dönüşüme uğramamış haliyle çift dereceli kuvvet fonksiyonları (\( x^2, x^4, \ldots \)) birer çift fonksiyondur ve \( y \) eksenine göre simetriktir. Benzer şekilde, hiçbir dönüşüme uğramamış haliyle tek dereceli kuvvet fonksiyonları (\( x, x^3, \ldots \)) birer tek fonksiyondur ve orijine göre simetriktir.
Kuvvet Fonksiyonu Dönüşümleri
Fonksiyonların dönüşümü konusunda gördüğümüz tüm dönüşümler kuvvet fonksiyonlarına uygulanarak fonksiyonun denkleminde, grafiğinin konumunda ve şeklinde değişiklikler meydana getirilebilir.
Bu dönüşümlere aşağıdaki gibi birkaç örnek verilebilir.
\( f(x) = 2x^3 + 3 \)
\( g(x) = -(x - 2)^2 - 1 \)
\( h(x) = 3(-2x + 1)^4 + 2 \)