Yükseklik
Bir üçgende herhangi bir köşeden karşısındaki kenara ya da kenarın uzantısına indirilen dikmeye yükseklik denir. \( A \), \( B \) ve \( C \) köşelerine ait yükseklikler sırasıyla \( h_a \), \( h_b \) ve \( h_c \) ile gösterilir.
Bir kenara ait yükseklik aynı zamanda üçgenin bir köşesi ile karşısındaki kenar arasındaki en kısa uzaklıktır.
Bir üçgenin yükseklikleri her zaman tek bir noktada kesişir. Bu noktaya üçgenin diklik merkezi denir. İki yüksekliğin kesiştiği nokta biliniyorsa bu nokta üçgenin diklik merkezidir ve üçüncü yükseklik de bu noktadan geçmek zorundadır.
Aşağıda dar açılı bir üçgenin yükseklikleri ve diklik merkezi (\( D \) noktası) gösterilmiştir. Dar açılı üçgenlerde diklik merkezi üçgenin iç bölgesindedir.
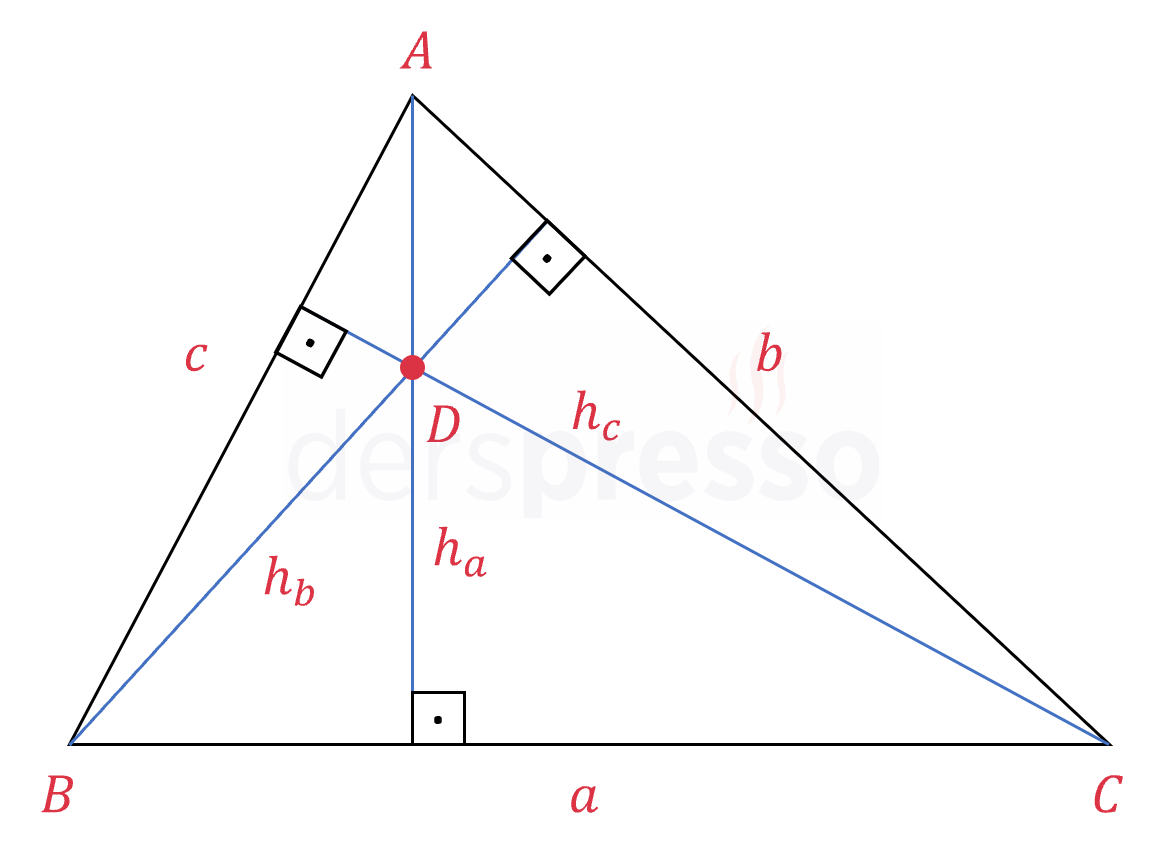
Aşağıda dik açılı bir üçgenin yükseklikleri ve diklik merkezi (\( B \) noktası) gösterilmiştir. Dik üçgenlerde dik kenarlar aynı zamanda birer yüksekliktir ve diklik merkezi dik kenarların kesiştiği köşededir.

Aşağıda geniş açılı bir üçgenin yükseklikleri ve diklik merkezi (\( D \) noktası) gösterilmiştir. Geniş açılı üçgenlerde diklik merkezi üçgenin dış bölgesindedir.
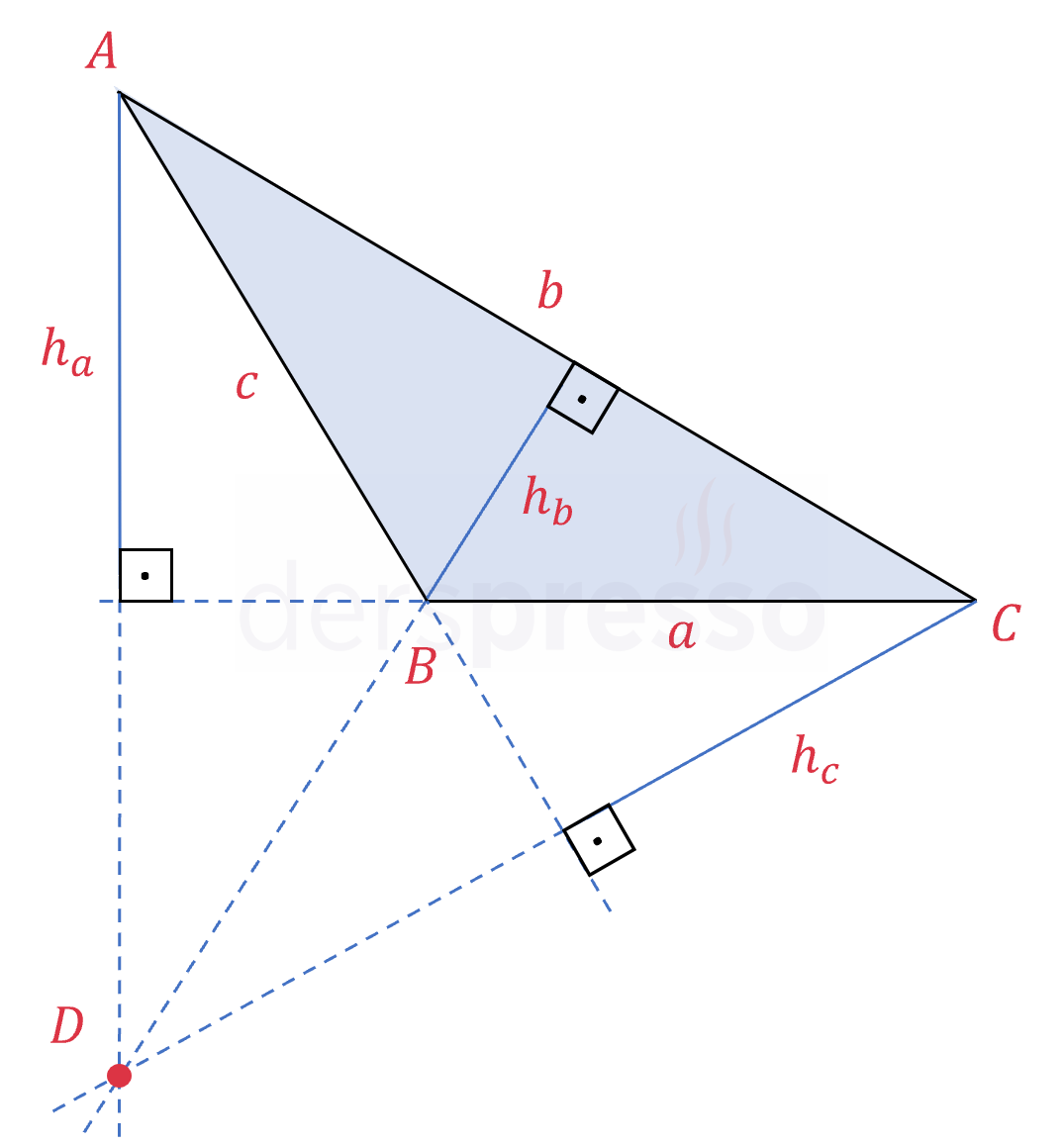
Üç kenar uzunluğu da bilinen bir üçgenin belirli bir kenarına ait yükseklik aşağıdaki formülle bulunur.
\( u \) üçgenin yarı çevresi olmak üzere,
\( u = \frac{1}{2}(a + b + c) \)
\( h_a = \dfrac{2\sqrt{u(u - a)(u - b)(u - c)}}{a} \)
\( h_b = \dfrac{2\sqrt{u(u - a)(u - b)(u - c)}}{b} \)
\( h_c = \dfrac{2\sqrt{u(u - a)(u - b)(u - c)}}{c} \)
Kenar uzunlukları \( a = 5 \), \( b = 6 \) ve \( c = 7 \) br olan üçgenin \( a \) kenarına ait yükseklik:
\( u = \frac{1}{2}(5 + 6 + 7) = 9 \)
\( h_a = \dfrac{2\sqrt{9(9 - 5)(9 - 6)(9 - 7)}}{5} \)
\( = \dfrac{12\sqrt{6}}{5} \)
İSPATI GÖSTER
Bir \( ABC \) üçgeninde \( a \) kenarını taban kabul ederek alan formülünü yazalım.
\( A(ABC) = \dfrac{a \cdot h_a}{2} \)
Aynı üçgen için Heron alan formülünü yazalım.
\( u \) üçgenin yarı çevresi olmak üzere,
\( u = \frac{1}{2}(a + b + c) \)
\( A(ABC) = \sqrt{u(u - a)(u - b)(u - c)} \)
İki alan formülünü birbirine eşitleyelim.
\( \dfrac{a \cdot h_a}{2} = \sqrt{u(u - a)(u - b)(u - c)} \)
\( a \) kenarına ait yüksekliği yalnız bırakalım.
\( h_a = \dfrac{2\sqrt{u(u - a)(u - b)(u - c)}}{a} \)
Bir üçgenin en uzun yüksekliği üçgenin en kısa kenarına aittir.
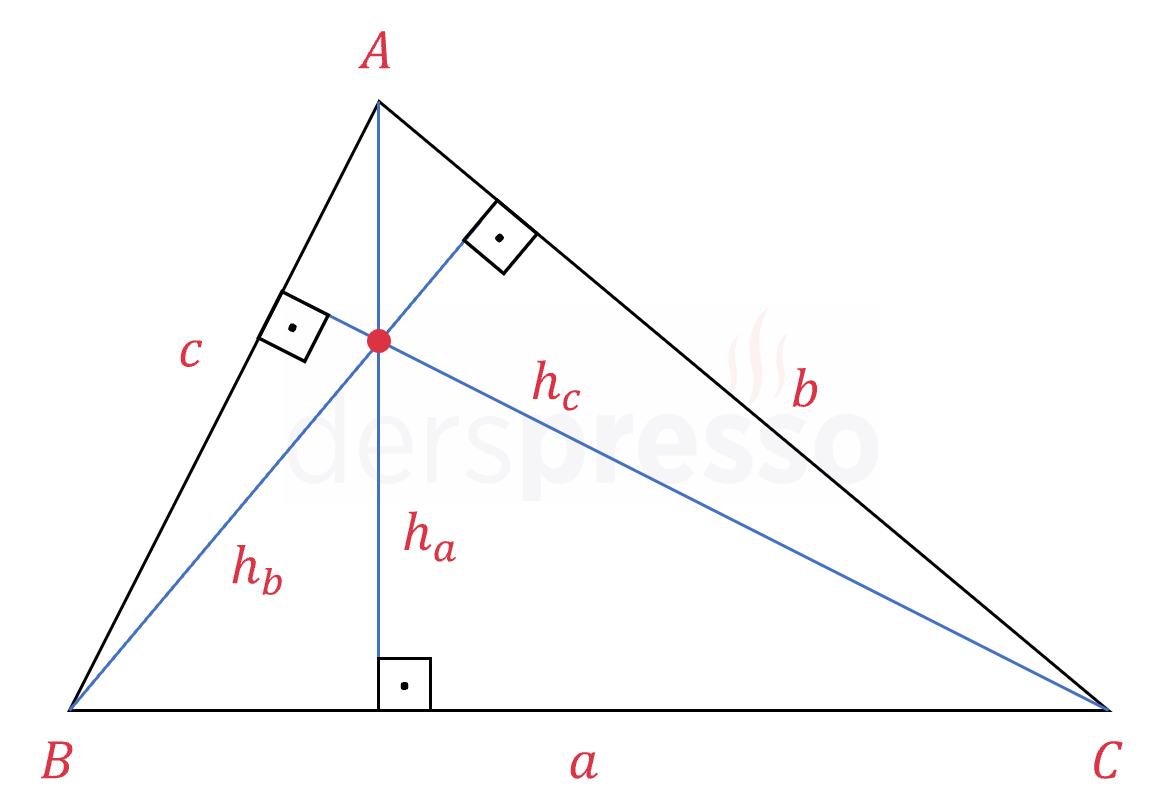
\( a \ge b \ge c \) ise,
\( h_a \le h_b \le h_c \)

\( ABC \) dik üçgeninde \( \abs{AB} = 12, \abs{BC} = 20 \)
olduğuna göre, \( [BC] \) kenarına ait yükseklik kaçtır?
Çözümü Göster\( ABC \) üçgeninin kenar uzunlukları 3-4-5 özel üçgeninin 4 katıdır, buna göre \( [AC] \) kenar uzunluğu 16 olur.

\( [BC] \) kenarına ait yüksekliğe \( h \) diyelim.
Üçgenin alanını iki farklı kenarı taban olarak kullanarak iki şekilde hesaplayarak birbirine eşitleyelim.
\( A(ABC) = A(ABC) \)
\( \dfrac{12 \cdot 16}{2} = \dfrac{20 \cdot h}{2} \)
\( 12 \cdot 16 = 20 \cdot h \)
\( h = \dfrac{48}{5} \) bulunur.