Üçgende Açı - Kenar Bağıntıları
Bir üçgende ölçüsü daha geniş olan açının gördüğü kenar daha uzundur. Benzer şekilde daha uzun kenarın karşısındaki açı daha geniştir. Buna göre, bir üçgenin köşe açılarının ölçüleri ve bu açıların gördüğü kenarların uzunlukları arasındaki sıralama aynıdır.
\( m(\widehat{A}) \ge m(\widehat{B}) \ge m(\widehat{C}) \Longleftrightarrow a \ge b \ge c \)
İSPATI GÖSTER
\( [AC] \) kenarının \( [AB] \) kenarından uzun olduğunu varsayalım ve bunun sonucu olarak \( \hat{B} \) açısının \( \hat{C} \) açısından daha geniş olduğunu göstermeye çalışalım.
\( b \gt c \) olduğunu bildiğimiz için, \( [AC] \) kenarında \( A \) noktasından \( c \) birim uzaklıktaki noktayı \( D \) noktası olarak işaretleyelim ve \( B \) noktası ile bu noktayı birleştirelim.
Oluşan \( \overset{\triangle}{ABD} \) üçgeni bir ikizkenar üçgen olmaktadır.
\( \abs{AB} = \abs{AD} = c \)
\( m(\widehat{ABD}) = m(\widehat{ADB}) = x \)
\( \hat{C} \) açısının ölçüsüne \( z \) diyelim. \( \overset{\triangle}{BCD} \) üçgeninin bir dış açısı olan \( \widehat{BDA} \) açısı iki iç açının toplamına eşit olur.
\( x = y + z \)
\( \hat{B} \) açısının ölçüsünü aşağıdaki şekilde yazabiliriz.
\( m(\hat{B}) = x + y \)
\( \hat{C} \) açısının ölçüsünü yukarıda elde ettiğimiz eşitliği kullanarak aşağıdaki şekilde yazabiliriz.
\( m(\hat{C}) = z = x - y \)
Bu iki eşitlikten, \( \hat{B} \) açısının ölçüsünün \( x \)'ten büyük, \( \hat{C} \) açısının ise \( x \)'ten küçük olduğunu, bunun bir sonucu olarak da \( \hat{B} \) açısının \( \hat{C} \) açısından daha geniş olduğunu söyleyebiliriz.
\( m(\hat{B}) = m(\hat{C}) + 2y \)
Dolayısıyla, iki kenarın arasında daha uzun olan kenarı gören açının ölçüsünün daha geniş olduğunu göstermiş olduk.
Bir üçgende bir köşe açısı 90°'den küçükse karşı kenar uzunluğu Pisagor teoremi ile hesaplanan hipotenüs uzunluğundan küçük olur. Benzer şekilde, bir köşe açısı 90°'den büyükse karşı kenar uzunluğu Pisagor teoremi ile hesaplanan hipotenüs uzunluğundan büyük olur.
\( m(\widehat{A}) \lt 90° \Longrightarrow a^2 \lt b^2 + c^2 \)
\( m(\widehat{A}) = 90° \Longrightarrow a^2 = b^2 + c^2 \quad \) (Pisagor teoremi)
\( m(\widehat{A}) \gt 90° \Longrightarrow a^2 \gt b^2 + c^2 \)
Yukarıda bahsettiğimiz açı - kenar bağıntıları belirli bir üçgen için geçerli olup üçgenler arasında böyle bir kıyaslama yapılamaz. Buna göre örneğin bir üçgende 30°'lik açının gördüğü kenar başka bir üçgende 60°'lik açının gördüğü kenardan uzun olabilir.
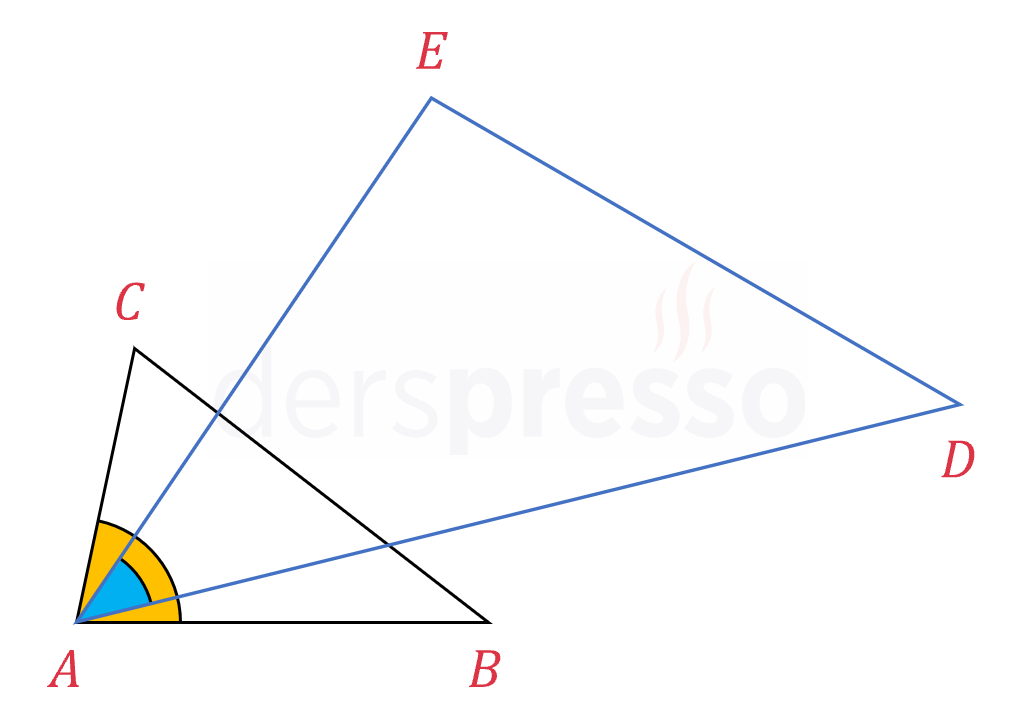
Hinge Teoremi
Bu teoreme göre, iki üçgenin ikişer kenar uzunluğu eşitse bu iki kenarın arasındaki açısı daha büyük olan üçgenin üçüncü kenar uzunluğu diğer üçgenin üçüncü kenar uzunluğundan büyüktür.
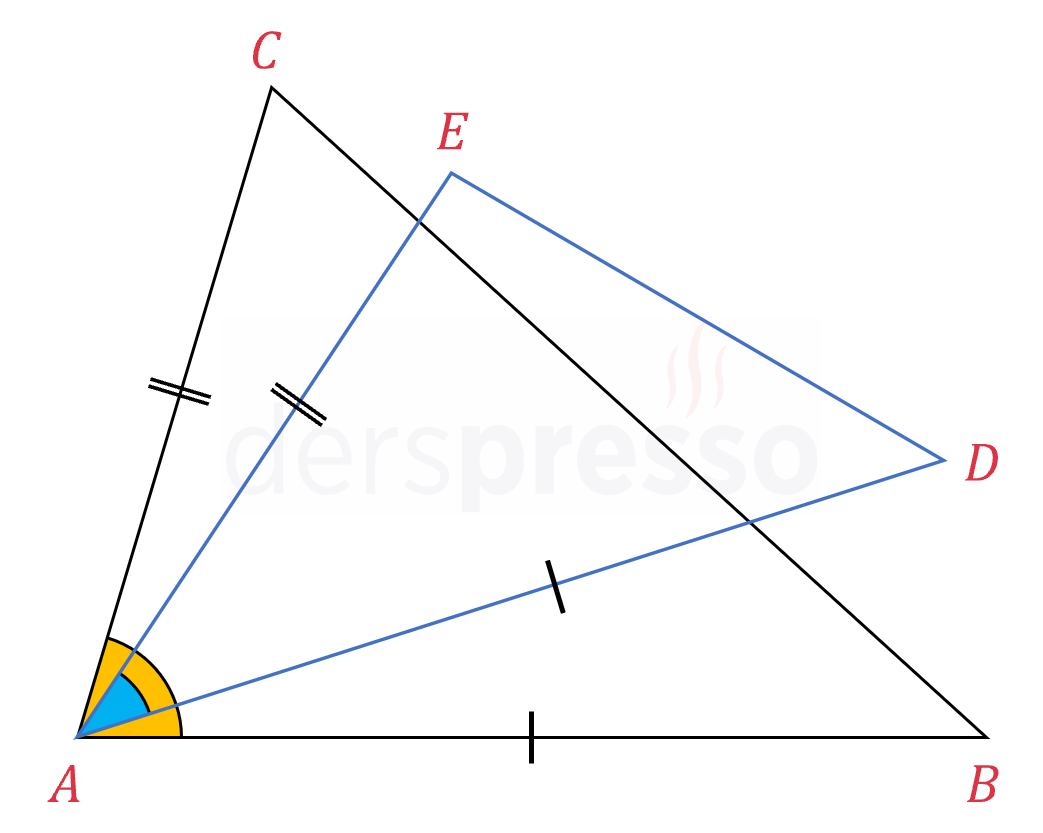
\( \abs{AB} = \abs{AD} \) ve \( \abs{AC} = \abs{AE} \) olmak üzere,
\( m(\widehat{BAC}) \gt m(\widehat{DAE}) \) ise,
\( \abs{BC} \gt \abs{DE} \)
İSPATI GÖSTER
Teoremin ispatını kosinüs teoremini kullanarak yapalım
\( ABC \) üçgeni için kosinüs teoremi formülünü yazalım.
\( \abs{BC}^2 = \abs{AB}^2 + \abs{AC}^2 - 2\abs{AB}\abs{AC}\cos(\widehat{BAC}) \)
\( ADE \) üçgeni için kosinüs teoremi formülünü yazalım.
\( \abs{DE}^2 = \abs{AD}^2 + \abs{AE}^2 - 2\abs{AD}\abs{AE}\cos(\widehat{DAE}) \)
Aşağıdaki iki eşitliği kullanarak ikinci denklemi düzenleyelim.
\( \abs{AB} = \abs{AD}, \quad \abs{AC} = \abs{AE} \)
\( \abs{DE}^2 = \abs{AB}^2 + \abs{AC}^2 - 2\abs{AB}\abs{AC}\cos(\widehat{DAE}) \)
İkinci denklemi birinci denklemden taraf tarafa çıkaralım.
\( \abs{BC}^2 - \abs{DE}^2 = -(2\abs{AB}\abs{AC}\cos(\widehat{BAC}) - 2\abs{AB}\abs{AC}\cos(\widehat{DAE})) \)
\( = -2\abs{AB}\abs{AC}(\cos(\widehat{BAC}) - \cos(\widehat{DAE})) \)
\( m(\widehat{BAC}) \gt m(\widehat{DAE}) \) olduğu biliniyor.
Kosinüs fonksiyonu \( [0, 2\pi] \) aralığında azalan bir fonksiyondur, dolayısıyla bu aralıkta daha büyük olan açının kosinüs değeri daha küçük olur.
Buna göre \( \cos(\widehat{BAC}) - \cos(\widehat{DAE}) \) ifadesi negatif, eşitliğin sağ tarafı negatif katsayıdan dolayı pozitif olur.
\( \abs{BC}^2 - \abs{DE}^2 \gt 0 \)
\( \abs{BC}^2 \gt \abs{DE}^2 \)
Dolayısıyla \( ABC \) kenarının üçüncü kenarı \( ADE \) üçgeninin üçüncü kenarından daha uzundur.
\( \abs{BC} \gt \abs{DE} \)
Bu kuralın karşıtı da doğrudur, yani üçüncü kenar uzunluğu daha büyük olan üçgende iki kenar arasındaki açı daha büyüktür.
Üçgen Eşitsizliği
Bir üçgenin herhangi bir kenarının uzunluğu diğer iki kenarının uzunlukları toplamından küçük, farkının mutlak değerinden ise büyüktür.
\( \abs{b - c} \lt a \lt b + c \)
\( \abs{a - c} \lt b \lt a + c \)
\( \abs{a - b} \lt c \lt a + b \)
İki kenar uzunluğu 5 ve 7 br olan bir üçgenin üçüncü kenar uzunluğunun alabileceği değerler:
\( \abs{5 - 7} \lt a \lt 5 + 7 \)
\( 2 \lt a \lt 12 \)
İSPATI GÖSTER
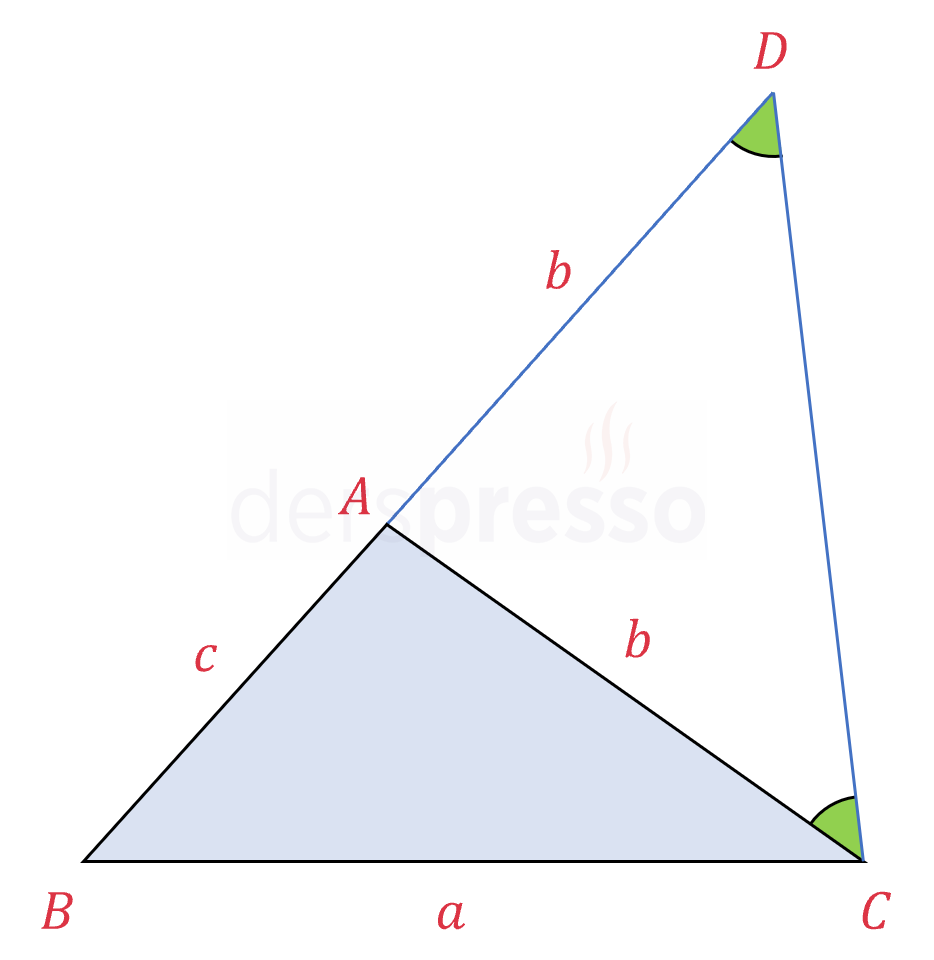
Şekildeki \( \overset{\triangle}{ABC} \) üçgeninin \( [BA] \) kenarını \( [AC] \) kenarı uzunluğunda \( b \) birim uzatalım (mavi çizgi). Bu doğru parçasının sonlandığı \( D \) noktası ile üçgenin \( C \) köşesini birleştirelim.
Oluşan \( \overset{\triangle}{ADC} \) üçgeni iki kenar uzunluğu eşit olduğu için bir ikizkenar üçgendir, dolayısıyla iki açısı da eşittir.
\( \abs{AD} = \abs{AC} = b \)
\( m(\widehat{ADC}) = m(\widehat{ACD}) \)
Bir üçgende daha geniş olan açının gördüğü kenar daha uzundur. Buna göre büyük üçgende \( \widehat{BCD} \) açısı \( \widehat{ACD} \) açısından büyük olduğu için bu açıya eşit \( \widehat{BDC} \) açısından da büyüktür, dolayısıyla \( [BD] \) kenarı \( [BC] \) kenarından uzun olur.
\( m(\widehat{ACD}) \lt m(\widehat{BCD}) \) olduğu için,
\( m(\widehat{BDC}) \lt m(\widehat{BCD}) \)
\( \abs{BC} \lt \abs{BD} \)
\( \abs{BC} \lt \abs{BA} + \abs{AD} \)
\( \abs{AD} = \abs{AC} = b \) olduğu için,
\( \abs{BC} \lt \abs{BA} + \abs{AC} \)
\( a \lt b + c \)
Buna göre \( [BC] \) kenarı için üçgen eşitsizliğinin sağ tarafını bulmuş oluruz. Aynı ispat diğer kenarlar için de tekrarlanabilir.
Üçgen eşitsizliğinin sol tarafını elde etmek için diğer iki kenara ait eşitsizliklerin sağ tarafını yazalım.
\( b \lt a + c \)
\( c \lt a + b \)
Bu eşitsizliklerde \( a \)'yı yalnız bırakalım.
\( b - c \lt a \)
\( c - b \lt a \Longrightarrow -(b - c) \lt a \)
\( a \) sayısı bir ifadenin hem pozitif hem de negatif işaretlisinden büyükse bu iki ifadenin daha büyüğüne eşit olan mutlak değerinden de büyüktür.
\( \abs{b - c} \lt a \)
Buna göre \( [BC] \) kenarı için üçgen eşitsizliğinin sol tarafını da bulmuş oluruz. Buna göre bu kenar için tüm eşitsizlik aşağıdaki şekilde olur.
\( \abs{b - c} \lt a \lt b + c \)
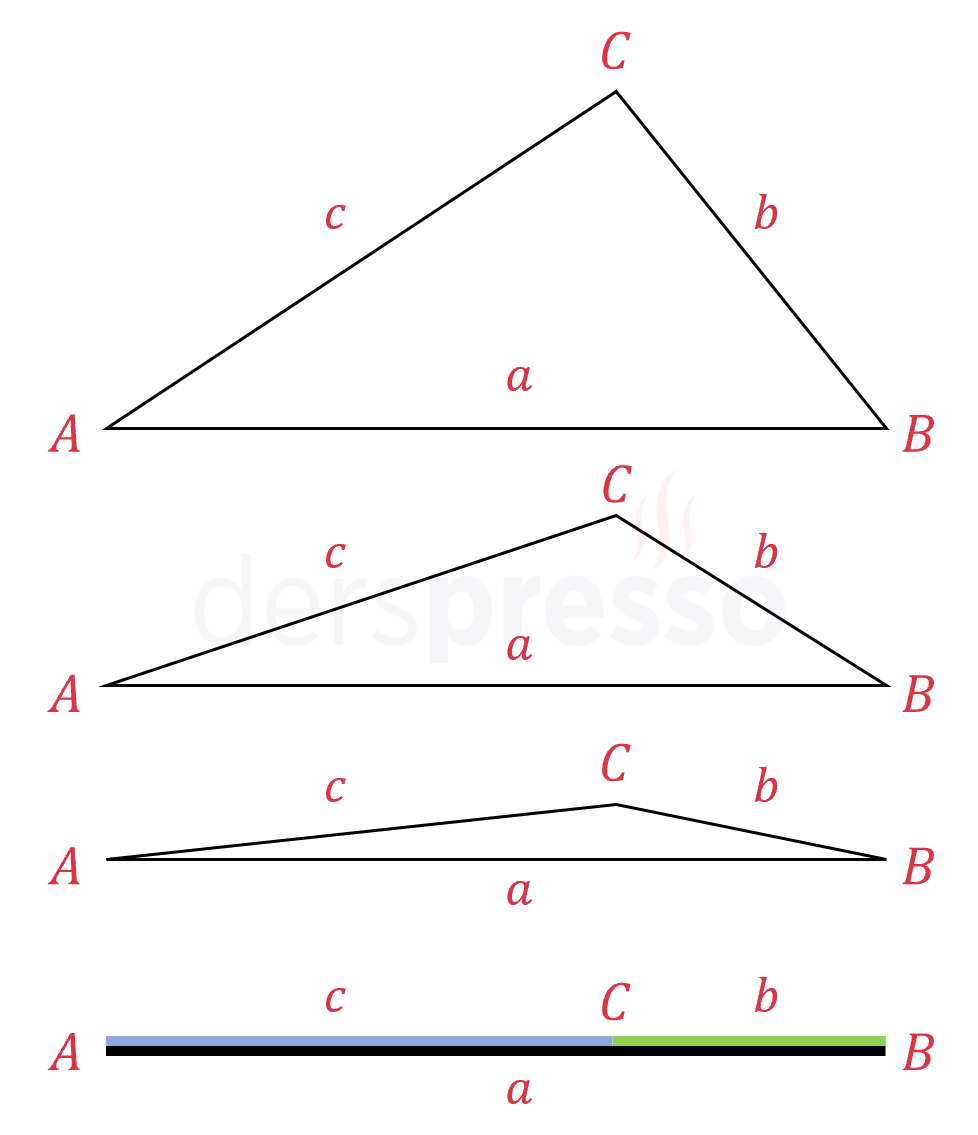
Üçgen eşitsizliğini aşağıdaki şekildeki üçgen üzerinden anlatmaya çalışalım. Bu eşitsizliğe göre \( a \) uzunluğu \( b \) ve \( c \) uzunlukları toplamından küçüktür. Üçgenin \( C \) köşesini gitgide \( [AB] \) kenarına yaklaştırırsak \( b + c \) uzunluğu gitgide küçülerek \( a \) uzunluğuna yaklaşır. \( a = b + c \) olduğu nokta \( C \) köşesinin \( [AB] \) doğru parçası üzerine geldiği noktadır, ancak bu durumda üç köşe noktası üçgen değil bir doğru oluştururlar, dolayısıyla \( C \) köşesi \( [AB] \) kenarına ne kadar yaklaşırsa yaklaşsın \( a \lt b + c \) eşitsizliği sağlanır.
Benzer şekilde \( b \) uzunluğu \( a \) ve \( c \) uzunlukları farkından büyüktür. Üçgenin \( C \) köşesini gitgide \( [AB] \) kenarına yaklaştırırsak (\( c \) uzunluğu kısaldığı için) \( a - c \) uzunluğu gitgide büyüyerek gitgide küçülen \( b \) uzunluğuna yaklaşır. \( b = a - c \) olduğu nokta \( C \) köşesinin \( [AB] \) doğru parçası üzerine geldiği noktadır, ancak bu durumda üç köşe noktası üçgen değil bir doğru oluştururlar, dolayısıyla \( C \) köşesi \( [AB] \) kenarına ne kadar yaklaşırsa yaklaşsın \( \abs{a - c} \lt b \) eşitsizliği sağlanır.
Üçgen eşitsizliği iç içe iki üçgene aşağıdaki şekilde uygulabilir.
\( \abs{BC} \lt \abs{DB} + \abs{DC} \lt \abs{AB} + \abs{AC} \)
İSPATI GÖSTER
\( [BD] \) kenarını \( [AC] \) kenarını kesecek şekilde uzatalım ve doğru parçasının ( [AC] \) kenarını kestiği noktaya \( E \) diyelim.
\( ABE \) üçgeninde üçgen eşitsizliği yazalım.
\( \abs{DB} + \abs{DE} \lt \abs{AB} + \abs{AE} \)
\( EDC \) üçgeninde üçgen eşitsizliği yazalım.
\( \abs{DC} \lt \abs{DE} + \abs{EC} \)
İki eşitsizliği taraf tarafa toplayalım.
\( \abs{DB} + \abs{DE} + \abs{DC} \lt \abs{AB} + \abs{AE} + \abs{DE} + \abs{EC} \)
\( \abs{DB} + \abs{DC} \lt \abs{AB} + \abs{AE} + \abs{EC} \)
\( \abs{AE} + \abs{EC} = \abs{AC} \) yazalım.
\( \abs{DB} + \abs{DC} \lt \abs{AB} + \abs{AC} \)
\( BDC \) üçgeninde üçgen eşitsizliği yazalım.
\( \abs{BC} \lt \abs{DB} + \abs{DC} \)
İki eşitsizliği birleştirelim.
\( \abs{BC} \lt \abs{DB} + \abs{DC} \lt \abs{AB} + \abs{AC} \)
Yardımcı Eleman Bağıntıları
Bir üçgenin iç açı ölçülerinin sıralaması ile; yükseklik, açıortay ve kenarortay uzunluk sıralamaları arasındaki ilişki aşağıdaki gibidir.
\( m(\widehat{A}) \gt m(\widehat{B}) \gt m(\widehat{C}) \) ise,
Yükseklikler: \( h_a \lt h_b \lt h_c \)
Açıortaylar: \( n_a \lt n_b \lt n_c \)
Kenarortaylar: \( V_a \lt V_b \lt V_c \)
Herhangi iki (ikizkenar üçgen) ya da üç (eşkenar üçgen) köşeye ait açıların eşit olması durumunda bu köşelere ait yükseklik, açıortay ve kenarortay uzunlukları da eşit olur.
Herhangi bir çeşitkenar üçgende, bir \( \widehat{A} \) açısına ait yükseklik (\( h_a \)), açıortay (\( n_a \)) ve kenarortayın (\( V_a \)) uzunluk sıralaması aşağıdaki gibidir.
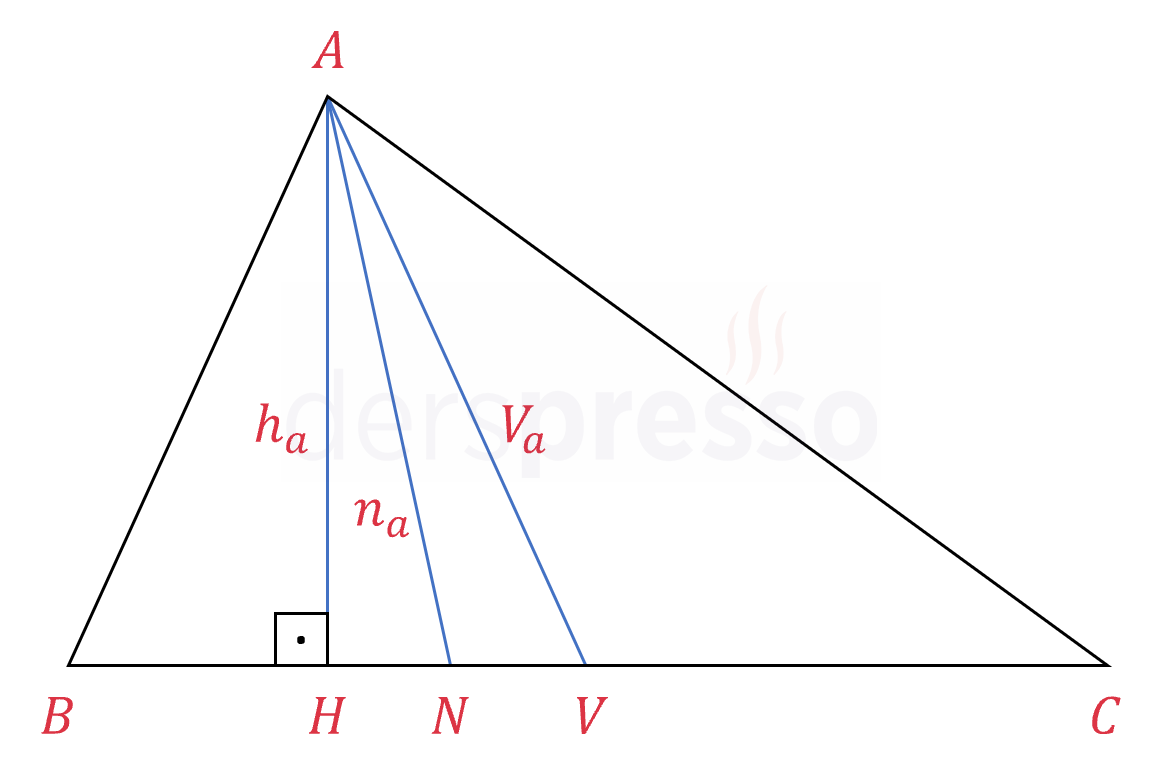
\( h_a \lt n_a \lt V_a \)
Kenar uzunlukları tam sayı ve birbirinden farklı ve çevresi 14 cm'den küçük olan kaç farklı üçgen çizilebilir?
Çözümü GösterBir üçgenin herhangi bir kenarının uzunluğu diğer iki kenarının uzunlukları toplamından küçük olur.
Verilen şartları sağlayan farklı üçgenler aşağıdaki gibidir.
Buna göre toplam 5 farklı üçgen yazılabilir.
\( x, y \in \mathbb{Z} \) olmak üzere,
Bir üçgenin kenar uzunlukları \( 16 \), \( x \), \( y \) birimdir.
\( xy = 45 \) olduğuna göre, bu üçgenin çevresi kaç birimdir?
Çözümü Göster\( x \ge y \) olduğunu varsayalım.
\( xy = 45 \) denkleminin sağlayan \( (x, y) \) sıralı ikililerini bulalım.
\( (x, y) = \{ (45, 1), (15, 3), (9, 5) \} \)
Verilen üçgen için üçgen eşitsizliğini yazalım.
\( x - y \lt 16 \lt x + y \)
Bulduğumuz sıralı ikililerden üçgen eşitsizliğini sadece \( (15, 3) \) sağlar, buna göre üçgenin bilinmeyen kenarlarının uzunluğu 15 ve 3 birimdir.
Üçgenin çevresi \( 16 + 15 + 3 = 34 \) birim bulunur.
\( ABC \) bir çeşitkenar üçgendir.
\( \abs{AC} \gt \abs{BC}, \quad m(\widehat{ACB}) = 80° \)
olduğuna göre, \( m(\widehat{ABC}) \)'nin alabileceği en küçük tam sayı değeri nedir?
Çözümü GösterBir üçgende daha uzun kenarın karşısındaki açı daha geniştir.
\( \widehat{ABC} \) ve \( \widehat{BAC} \) açılarını eşit varsayarak ölçülerine \( x \) diyelim.
\( 2x + 80° = 180° \)
\( x = 50° \)
\( \abs{AC} \gt \abs{BC} \) olduğundan \( m(\widehat{ABC}) \gt m(\widehat{BAC}) \) olmalıdır.
\( m(\widehat{ABC}) \)'nin en küçük değeri 50°'den büyük en küçük tam sayı olan 51° olabilir.
\( m(\widehat{ABC}) = 51° \) bulunur.
\( \abs{BC} = a, \abs{AC} = b, \abs{AB} = c \)
\( b \lt a \lt c \)
\( m(\widehat{BAC}) = 52° \)
olduğuna göre, \( m(\widehat{ACB}) \)'nin alabileceği en küçük tam sayı değeri kaçtır?
Çözümü GösterBir üçgende daha uzun kenarın karşısındaki açı daha geniştir.
Buna göre üçgenin açı ölçüleri arasındaki sıralama aşağıdaki şekilde olur.
\( m(\widehat{ABC}) \lt m(\widehat{BAC}) \lt m(\widehat{ACB}) \)
\( m(\widehat{ACB}) \)'nin en küçük tam sayı değerini alması için \( m(\widehat{ABC}) \lt m(\widehat{BAC}) \) olmak koşuluyla \( m(\widehat{ABC}) \) en büyük tam sayı değerini almalıdır.
\( m(\widehat{ABC}) = 51° \)
\( m(\widehat{ACB}) = 180° - 52° - 51° \)
\( = 77° \) bulunur.
\( 51° \lt 52° \lt 77° \)
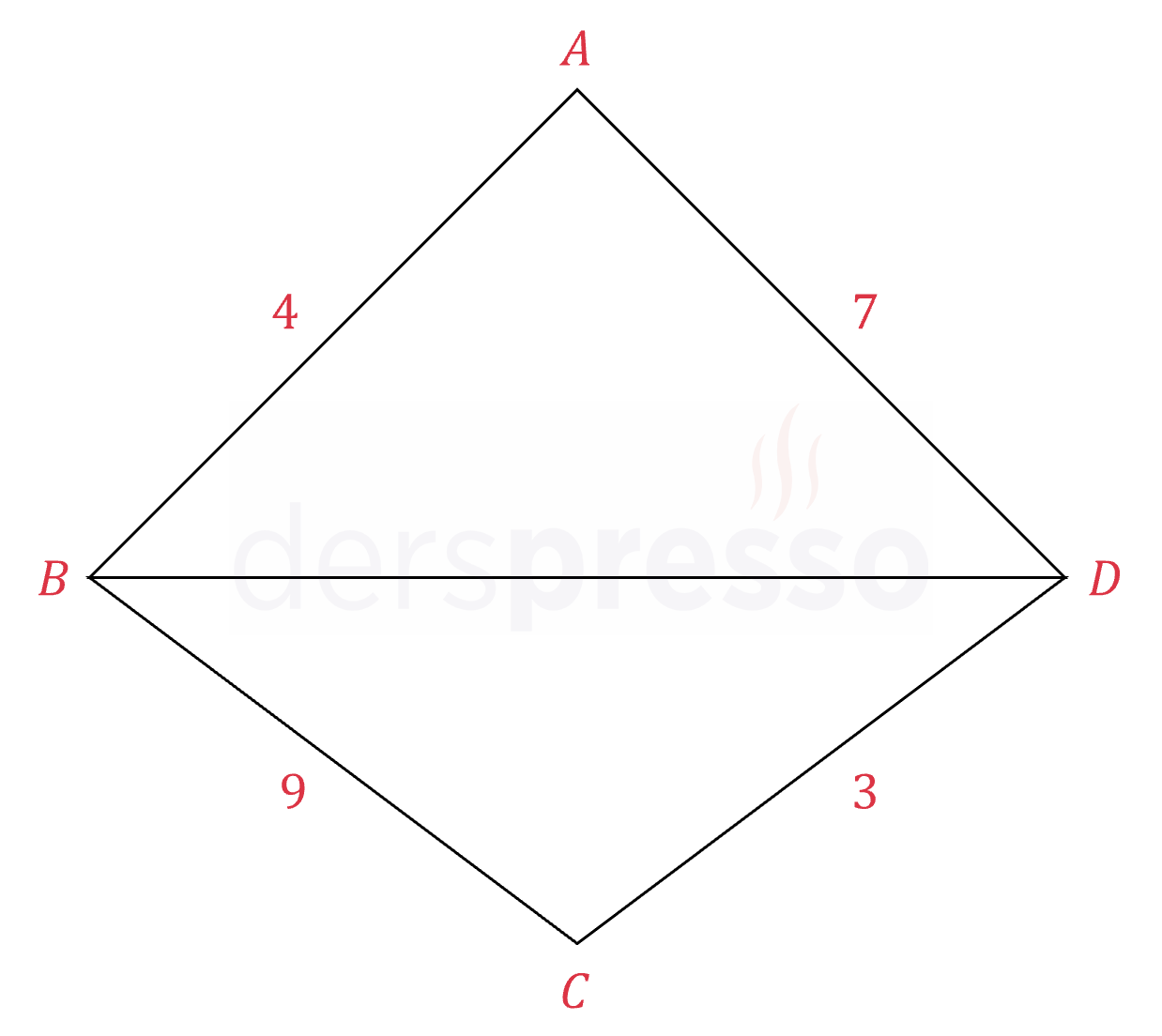
\( \abs{AB} = 4, \quad \abs{BC} = 9 \)
\( \abs{CD} = 3, \quad \abs{AD} = 7 \)
olduğuna göre, \( \abs{BD} \) hangi tam sayı değerlerini alabilir?
Çözümü Göster\( \abs{BD} = x \) diyelim.
Bu durumda \( ABD \) ve \( BCD \) üçgenleri için üçgen eşitsizlikleri aşağıdaki gibi olur.
\( ABD \) üçgeni için:
\( \abs{7 - 4} \lt x \lt \abs{7 + 4} \)
\( 3 \lt x \lt 11 \)
\( BCD \) üçgeni için:
\( \abs{9 - 3} \lt x \lt \abs{9 + 3} \)
\( 6 \lt x \lt 12 \)
\( x \) uzunluğunun her iki üçgen için de üçgen eşitsizliğini sağlanması gerektiği için bulduğumuz eşitsizliklerin alt sınır değerlerinden büyük olanı, üst sınır değerlerinden de küçük olanı seçmeliyiz.
\( 6 \lt x \lt 11 \)
Buna göre \( x \) aşağıdaki 4 tam sayı değeri alabilir.
\( x \in \{7, 8, 9, 10\} \) bulunur.
\( \abs{AB} = 6, \abs{BC} = 11, \abs{AC} = 3x - 1 \)
olduğuna göre, \( x \)' in alabileceği tam sayı değerlerin toplamı kaçtır?
Çözümü Göster\( ABC \) üçgeni için üçgen eşitsizliğini yazalım.
\( \abs{6 - 11} \lt 3x - 1 \lt \abs{6 + 11} \)
\( 5 \lt 3x - 1 \lt 17 \)
\( x \)'i eşitsizlikte yalnız bırakalım.
\( 6 \lt 3x \lt 18 \)
\( 2 \lt x \lt 6 \)
Buna göre \( x \) aşağıdaki 3 tam sayı değeri alabilir.
\( x \in \{3, 4, 5\} \)
\( x \)'in alabileceği tam sayı değerlerin toplamı \( 3 + 4 + 5 = 12 \) olur.
\( \abs{AB} = 5, \quad \abs{BC} = 12 \)
\( m(\widehat{BAC}) \lt m(\widehat{ABC}) \)
olduğuna göre, \( \abs{AC} = x \)'in alabileceği değerler nedir?
Çözümü Göster\( ABC \) üçgeni için üçgen eşitsizliğini yazalım.
\( \abs{5 - 12} \lt x \lt \abs{5 + 12} \)
\( 7 \lt x \lt 17 \)
Bir üçgende ölçüsü daha geniş olan açının gördüğü kenar daha uzundur.
\( m(\widehat{BAC}) \lt m(\widehat{ABC}) \) olduğu için \( x \gt 12 \) olmalıdır.
Yukarıdaki iki eşitsizliği birlikte sağlayan eşitsizlik aşağıdaki gibi olur.
\( 12 \lt x \lt 17 \)
Buna göre \( x \) aşağıdaki 4 tam sayı değeri alabilir.
\( x \in \{13, 14, 15, 16\} \) bulunur.
\( \abs{AB} = 5, \abs{AD} = 9, \abs{DC} = 4 \)
olduğuna göre, \( \abs{BC} = x \)'in alabileceği en büyük tam sayı değeri kaçtır?
Çözümü Göster\( \abs{BD} = y \) diyelim.
\( x \) en büyük değerini \( y \) en büyük değerini aldığında alır.
\( ABD \) üçgeni için üçgen eşitsizliğini yazalım.
\( \abs{9 - 5} \lt y \lt \abs{9 + 5} \)
\( 4 \lt y \lt 14 \)
\( y = 14 \) değerini alamasa da bu değeri \( BCD \) üçgeni için üçgen eşitsizliğinde üst sınır değeri olarak kullanabiliriz.
\( BCD \) üçgeni için üçgen eşitsizliğini yazalım.
\( \abs{14 - 4} \lt x \lt \abs{14 + 4} \)
\( 10 \lt x \lt 18 \)
Buna göre \( x \)'in en büyük tam sayı değeri 17 olur.
\( [AB] \perp [DB] \)
\( m(\widehat{BAC}) = 55°, m(\widehat{ACB}) = 50°, m(\widehat{ADB}) = 65° \)
\( \abs{BC} = a, \abs{AC} = b, \abs{AB} = c \)
\( \abs{AD} = d, \abs{DB} = e \)
olduğuna göre, şekildeki en kısa kenar hangisidir?
Çözümü Göster\( m(\widehat{ABC}) = 180° - (55° + 50°) = 75° \)
Bir üçgende ölçüsü daha geniş olan açının gördüğü kenar daha uzundur.
Buna göre \( ABC \) üçgeninde kenar uzunluklarının sıralaması aşağıdaki gibi olur.
\( c \lt a \lt b \)
\( m(\widehat{DAB}) = 180° - (90° + 65°) = 25° \)
\( ADB \) üçgeninde kenar uzunluklarının sıralaması aşağıdaki gibi olur.
\( e \lt c \lt d \)
Birinci eşitsizlikte en kısa kenar \( c \), \( c \) kenarını da içeren ikinci eşitsizlikte ise \( e \)'dir.
Buna göre verilen iki üçgende en kısa kenar \( e \) olur.
\( [BD] \), \( [AC] \) kenarının kenarortayıdır.
\( \abs{AB} = 6, \quad \abs{BC} = 8 \)
\( ABC \) üçgeninin çevresi 20 birimdir.
Buna göre \( \abs{BD} = x \)'in alabileceği kaç tam sayı değeri vardır?
Çözümü GösterÜçgeninin çevresi 20 birimdir.
\( 6 + 8 + \abs{AC} = 20 \)
\( \abs{AD} = \abs{DC} = 3 \)
Bu durumda \( ABD \) ve \( BCD \) üçgenleri için üçgen eşitsizlikleri aşağıdaki gibi olur.
\( ABD \) üçgeni için:
\( \abs{6 - 3} \lt x \lt \abs{6 + 3} \)
\( 3 \lt x \lt 9 \)
\( BCD \) üçgeni için:
\( \abs{8 - 3} \lt x \lt \abs{8 + 3} \)
\( 5 \lt x \lt 11 \)
Ayrıca \( D \) noktasından tabana paralel bir doğru çizelim ve bu doğru parçasının \( [AB] \) kenarını kestiği noktaya \( E \) diyelim.
\( [ED] \parallel [BC] \) olduğu için bu doğru parçası üçgenin bir orta tabanıdır, dolayısıyla \( [AB] \) kenarını ortalar ve uzunluğu tabanın yarısıdır.
\( \abs{AE} = \abs{EB} = 3 \)
\( \abs{ED} = 4 \)
Oluşan \( BED \) üçgeninde de üçgen eşitsizliği sağlanmalıdır.
\( \abs{4 - 3} \lt x \lt 4 + 3 \)
\( 1 \lt x \lt 7 \)
Bulduğumuz üç eşitsizliği de sağlayan tam sayı \( x \) değeri sadece 6 olur.
\( x \in \{6\} \) bulunur.
\( [ED] \perp [AB], \quad \abs{AD} = \abs{BD} \)
\( \abs{EC} = 4, \quad \abs{AC} = 7 \)
olduğuna göre, \( \abs{BE} = x \)'in alabileceği tam sayı değerleri nelerdir?
Çözümü Göster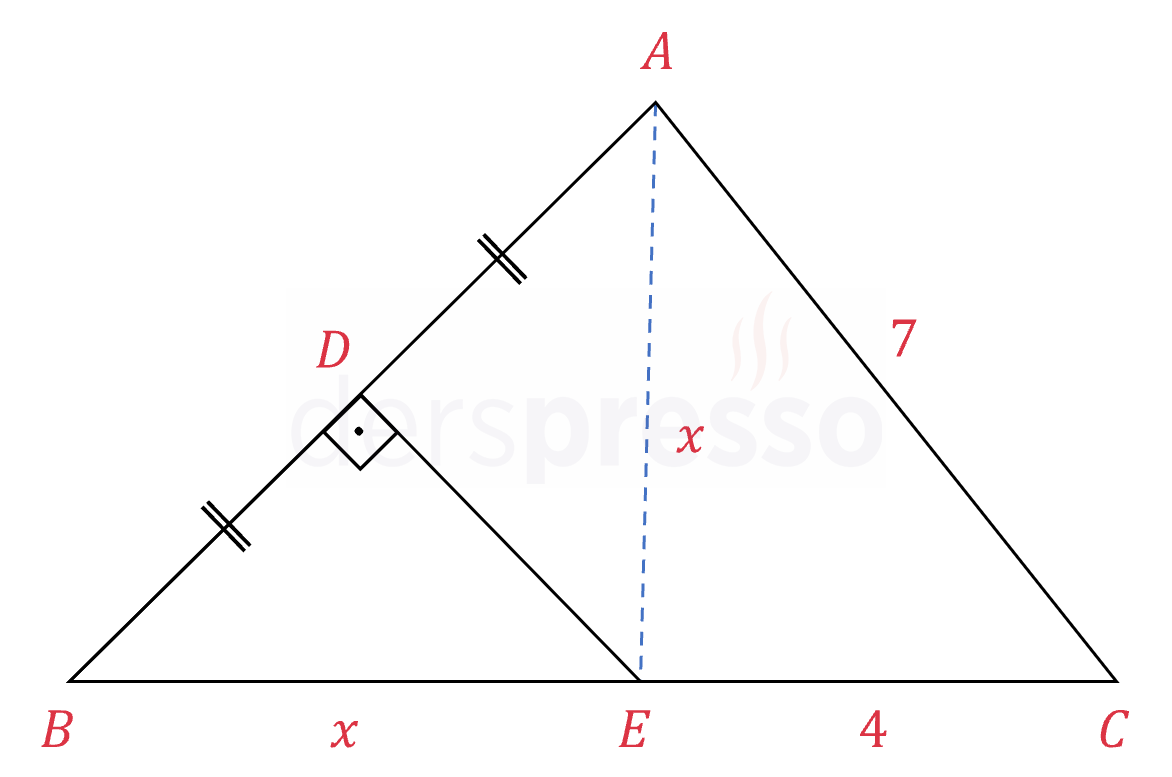
\( A \) ve \( E \) noktalarını birleştirelim.
\( [ED] \) doğru parçası \( [AB] \) kenarının hem yüksekliği hem de kenarortayı olduğu için \( ABE \) bir ikizkenar üçgendir.
\( \abs{AE} = \abs{BE} = x \)
\( AEC \) üçgeni için üçgen eşitsizliğini yazalım.
\( \abs{7 - 4} \lt x \lt \abs{7 + 4} \)
\( 3 \lt x \lt 11 \)
\( x \in [4, 10] \) aralığındaki tam sayı değerlerini alabilir.
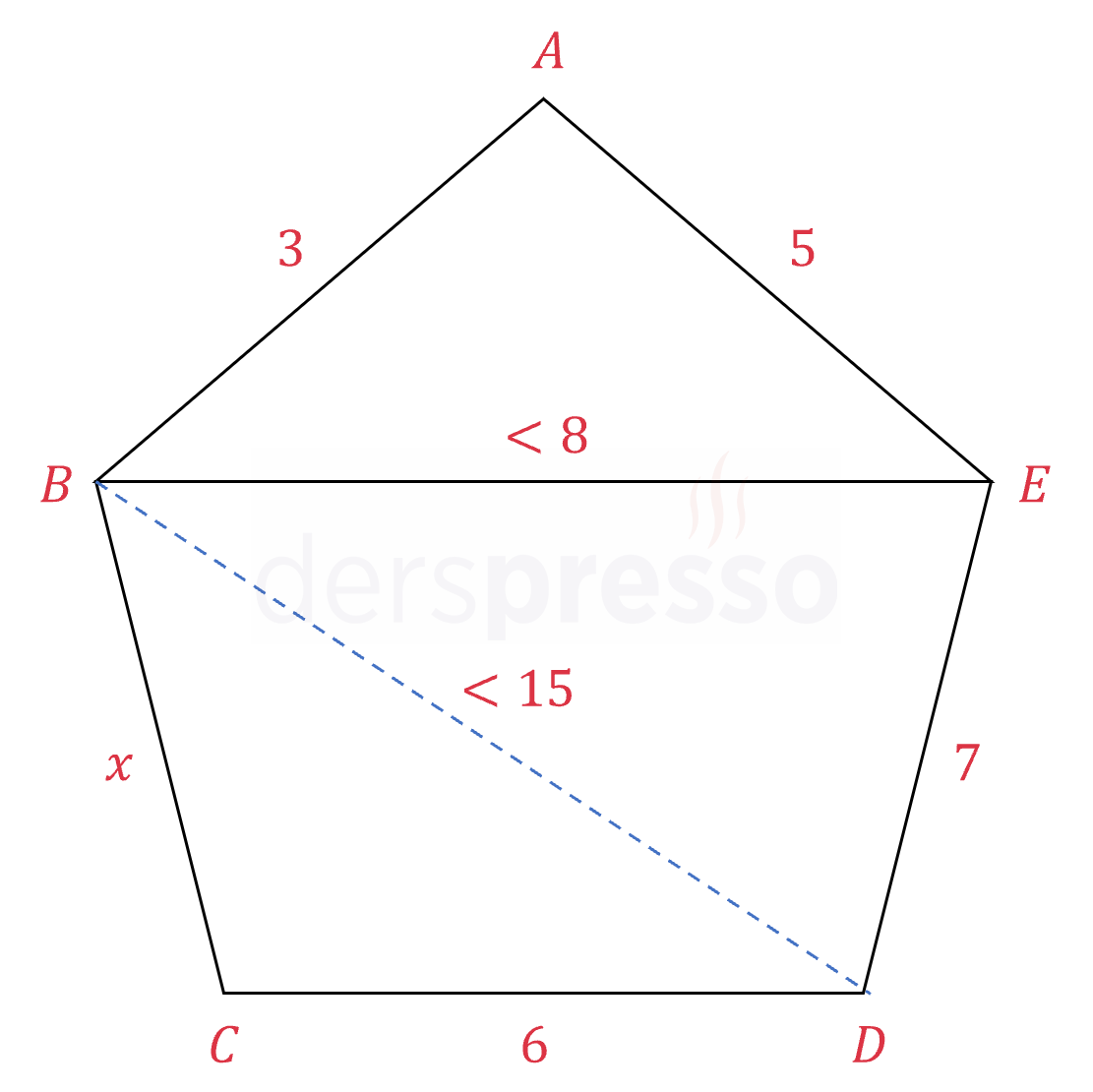
Bir yamuk ve bir üçgenden oluşan şekildeki uzunluk değerleri aşağıda verilmiştir.
\( \abs{AB} = 3, \quad \abs{AE} = 5 \)
\( \abs{CD} = 6, \quad \abs{DE} = 7 \)
olduğuna göre, \( \abs{BC} = x \)'in alabileceği en büyük tam sayı değeri kaçtır?
Çözümü Göster\( B \) ve \( D \) noktalarını birleştirelim.
Birden fazla adımda uygulayacağımız üçgen eşitsizliklerinde \( x \)'in en büyük değerini bulmak için diğer üçgenlerdeki bilinmeyen kenar uzunluklarının da en büyük değerlerini almalıyız.
\( ABE \) üçgeni için üçgen eşitsizliğini yazalım.
\( \abs{5 - 3} \lt \abs{BE} \lt \abs{5 + 3} \)
\( 2 \lt \abs{BE} \lt 8 \)
\( \abs{BE} \) uzunluğu için üst sınır 8 birimdir.
\( BED \) üçgeni için üçgen eşitsizliğini yazalım.
\( \abs{8 - 7} \lt \abs{BD} \lt \abs{8 + 7} \)
\( 1 \lt \abs{BD} \lt 15 \)
\( \abs{BD} \) uzunluğu için üst sınır 15 birimdir.
\( BCD \) üçgeni için üçgen eşitsizliğini yazalım.
\( \abs{15 - 6} \lt x \lt \abs{15 + 6} \)
\( 9 \lt x \lt 21 \)
\( x = 21 \) olamayacağı için \( x \)'in en büyük değeri 20 olur.
\( [AB] \perp [AC] \) ve \( D \) noktası \( ABC \) üçgeninin iç bölgesinde bir noktadır.
\( \abs{BD} = 12, \quad \abs{DC} = 5 \)
olduğuna göre, \( \abs{BC} = x \)'in alabileceği tam sayı değerleri nelerdir?
Çözümü Göster
\( m(\widehat{BDC}) \) açısının 90°'den büyük ya da küçük olduğunu bulmaya çalışalım.
\( m(\widehat{ABD}) = a, m(\widehat{DBC}) = b \)
\( m(\widehat{ACD}) = c, m(\widehat{DCB}) = d \) diyelim.
\( a + b + c + d + 90° = 180° \)
\( a + b + c + d = 90° \)
\( b + c \lt 90° \)
Buna göre \( BDC \) üçgeninde \( m(\widehat{BDC}) \gt 90° \) olur.
\( \widehat{BDC} \) açısı geniş açı olduğu için \( BDC \) üçgeninde en uzun kenarı görür.
\( x \gt 12 \)
\( BDC \) üçgeni için üçgen eşitsizliğini yazalım.
\( \abs{12 - 5} \lt x \lt \abs{12 + 5} \)
\( 7 \lt x \lt 17 \)
Ayrıca \( \widehat{BDC} \) açısı geniş açı olduğu için, \( x \) uzunluğu \( m(\widehat{BDC}) = 90° \) olduğu durumda oluşacak hipotenüs uzunluğundan büyük olmalı.
\( x^2 \gt 12^2 + 5^2 \)
\( x \gt 13 \)
Bulduğumuz üç eşitsizliği de sağlayan en geniş aralık aşağıdaki gibidir.
\( 13 \lt x \lt 17 \)
Buna göre \( x \) aşağıdaki 3 tam sayı değeri alabilir.
\( x \in \{14, 15, 16\} \)
\( \abs{AB} = 5, \abs{DE} = 3, \abs{BE} = 12 \)
olduğuna göre, \( \abs{AC} + \abs{CD} \)'nin alabileceği en büyük tam sayı değeri kaçtır?
Çözümü Göster
\( \abs{AC} = a, \abs{CD} = b \)
\( \abs{BC} = x, \abs{CE} = y \) diyelim.
İki üçgen için üçgen eşitsizliklerini yazalım.
\( \abs{5 - x} \lt a \lt \abs{5 + x} \)
\( \abs{3 - y} \lt b \lt \abs{3 + y} \)
Eşitsizlikleri alt alta toplayalım.
\( \abs{5 - x} + \abs{3 - y} \lt a + b \lt \abs{5 + x} + \abs{3 + y} \)
\( x \) ve \( y \) pozitif değerler olduğu için eşitsizliğin sağındaki ifadeler mutlak değerden oldukları gibi çıkarlar.
\( \abs{5 - x} + \abs{3 - y} \lt a + b \lt 5 + x + 3 + y \)
\( x + y = 12 \)
\( \abs{5 - x} + \abs{3 - y} \lt a + b \lt 20 \)
Buna göre \( \abs{AC} + \abs{CD} \)'nin alabileceği en büyük tam sayı değeri 19'dur.
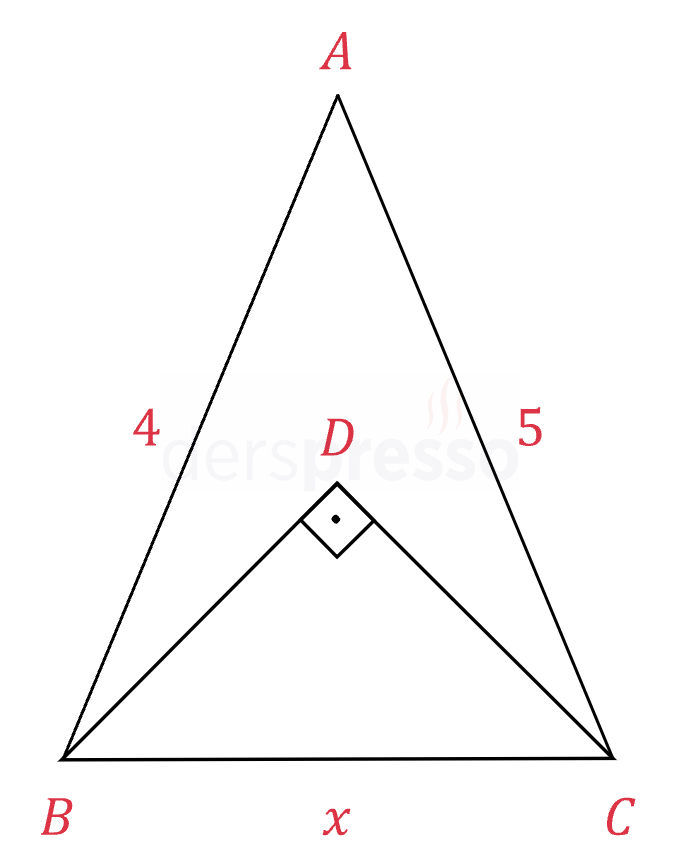
\( [BD] \perp [DC]\)
\( \abs{AB} = 4, \quad \abs{AC} = 5 \)
olduğuna göre, \( \abs{BC} = x \)'in alabileceği tam sayı değerleri nedir?
Çözümü Göster\( ABC \) üçgeni için üçgen eşitsizliğini yazalım.
\( \abs{4 - 5} \lt x \lt \abs{4 + 5} \)
\( 1 \lt x \lt 9 \)
Ayrıca \( ABC \) üçgeni içinde bir dik üçgen oluştuğu için \( m(\widehat{BAC}) \) açısı 90°'den küçük olmalıdır, dolayısıyla \( \abs{BC} \) uzunluğu \( m(\widehat{BAC}) = 90° \) olduğu durumundaki hipotenüs uzunluğundan kısa olmalıdır.
\( x^2 \lt 4^2 + 5^2 \)
\( x \lt \sqrt{41} \)
Bulduğumuz iki eşitsizliği de sağlayan en geniş aralık aşağıdaki gibidir.
\( 1 \lt x \lt \sqrt{41} \)
Buna göre \( x \) aşağıdaki 5 tam sayı değeri alabilir.
\( x \in \{2, 3, 4, 5, 6\} \)
Kenar uzunlukları tam sayı ve çevresi 22 cm olan kaç üçgen çizilebilir?
Çözümü GösterÜçgenin kenar uzunluklarına sırasıyla \( a \), \( b \) ve \( c \) diyelim.
\( a + b + c = 22 \)
Bir üçgende herhangi 2 kenar uzunluğu toplamı üçüncü kenar uzunluğundan büyüktür.
Bu durumda herhangi 2 kenar uzunluğu toplamı \( \frac{22}{2} = 11 \)'den büyük ve herhangi bir kenar uzunluğu 11'den küçük olur.
\( a + b \gt 11, b + c \gt 11, a + c \gt 11 \)
\( a \lt 11, b \lt 11, c \lt 11 \)
Bu koşulları sağlayan aşağıdaki üçgenler çizilebilir.
1) \( 10, 10, 2 \)
2) \( 10, 9, 3 \)
3) \( 10, 8, 4 \)
4) \( 10, 7, 5 \)
5) \( 10, 6, 6 \)
6) \( 9, 9, 4 \)
7) \( 9, 8, 5 \)
8) \( 9, 7, 6 \)
9) \( 8, 8, 6 \)
10) \( 8, 7, 7 \)
Buna göre istenen koşulları sağlayan 10 üçgen çizilebilir.
Kenar uzunlukları birer rakam olan ve eşkenar olmayıp ikizkenar olan kaç farklı üçgen çizilebilir?
Çözümü GösterÜçgenin eşit kenarlarının uzunluğuna \( a \), üçüncü kenar uzunluğuna \( b \) diyelim.
Üçgen eşitsizliğine göre, bir üçgenin iki kenar uzunluğunun toplamı üçüncü kenar uzunluğundan büyük, farkı üçüncü kenar uzunluğundan küçüktür.
Farklı \( a \) değerleri için bu koşulu sağlayan \( b \) değerleri aşağıdaki gibidir.
\( a = 1 \Rightarrow b \in \emptyset \)
\( a = 2 \Rightarrow b \in \{ 1, 3 \} \)
\( a = 3 \Rightarrow b \in \{ 1, 2, 4, 5 \} \)
\( a = 4 \Rightarrow b \in \{ 1, 2, 3, 5, 6, 7 \} \)
\( a = 5 \Rightarrow b \in \{ 1, 2, 3, 4, 6, 7, 8, 9 \} \)
\( a = 6 \Rightarrow b \in \{ 1, 2, 3, 4, 5, 7, 8, 9 \} \)
\( a = 7 \Rightarrow b \in \{ 1, 2, 3, 4, 5, 6, 8, 9 \} \)
\( a = 8 \Rightarrow b \in \{ 1, 2, 3, 4, 5, 6, 7, 9 \} \)
\( a = 9 \Rightarrow b \in \{ 1, 2, 3, 4, 5, 6, 7, 8 \} \)
Buna göre istenen koşulu sağlayan \( 2 + 4 + 6 + 8 + 8 + 8 + 8 + 8 = 52 \) farklı üçgen çizilebilir.
Bir üçgenin iki kenar uzunluğu 7 cm'dir. Bu üçgenin alanının en büyük olması için üçüncü kenar uzunluğu kaç cm olmalıdır?
Çözümü GösterVerilen üçgenin alanını bulmak için sinüs teoremini kullanalım.
Uzunlukları verilen kenarlara \( a \) ve \( b \), bu kenarların arasında kalan açıya \( \alpha \) diyelim.
\( A = \dfrac{1}{2}ab\sin{\alpha} \)
Üçgenin alanının en büyük olması için \( \sin{\alpha} \) en büyük değerini almalıdır, dolayısıyla \( \alpha \) açısı 90° olmalıdır.
Üçgenin üçüncü kenarına \( c \) diyelim.
Üçüncü kenar (hipotenüs) uzunluğunu bulmak için Pisagor teoremini kullanalım.
\( c^2 = 7^2 + 7^2 \)
\( c = 7\sqrt{2} \) olarak bulunur.
\( k \in \mathbb{Z^+} \) olmak üzere,
Bir üçgenin kenarları sırasıyla 8, 13 ve \( k \) cm uzunluğundadır.
Kaç tane \( k \) değeri için bu üçgen geniş açılı üçgen olur?
Çözümü GösterKosinüs teoremine göre, geniş açılı bir üçgende en uzun kenarın karesi diğer iki kenarın karesinden büyük olur.
Kosinüs teoremini kullanarak \( k \) değerinin sınırlarını bulalım.
İlk önce \( k \) değerinin en uzun kenar olmadığı durumu inceleyelim.
\( 13^2 \gt 8^2 + k^2 \)
\( 169 \gt 64 + k^2 \)
\( 105 \gt k^2 \)
\( k \le 10 \)
Üçgen eşitsizliğine göre, \( k \) diğer iki kenar uzunlukları farkından büyük olmak zorundadır.
\( 5 \lt k \le 10 \)
Şimdi \( k \) değerinin en uzun kenar olduğu durumu inceleyelim.
\( k^2 \gt 13^2 + 8^2 \)
\( k^2 \gt 233 \)
\( k \ge 16 \)
Üçgen eşitsizliğine göre, \( k \) diğer iki kenar uzunlukları toplamından küçük olmak zorundadır.
\( 16 \le k \lt 21 \)
Her iki durumda bulduğumuz aralıkların birleşimi \( k \) değer aralığını verir.
\( k \in (5, 10] \cup [16, 21) \)
Bu aralıkta 10 tane tam sayı \( k \) değeri bulunur.
Kenar uzunlukları birer tam sayı ve çevre uzunluğu 30 cm olacak şekilde oluşturulabilecek ikizkenar üçgenlerin, farklı uzunluktaki kenarının uzunluğunun alabileceği en büyük ve en küçük değerler arasındaki fark en çok kaç olabilir?
Çözümü Gösterİkizkenar üçgenin eşit uzunluktaki kenarlarının uzunluğuna \( a \) cm, diğer kenarının uzunluğuna \( b \) cm diyelim.
Üçgen eşitsizliğine göre; bir üçgenin herhangi bir kenarının uzunluğu, diğer iki kenarının uzunlukları toplamından küçük, farkının mutlak değerinden büyük olmalıdır.
Bu kuralı uzunluğu \( b \) olan kenara uygulayalım.
\( \abs{a - a} \lt b \lt a + a \)
\( 0 \lt b \lt 2a \)
İkizkenar üçgenin çevre uzunluğu 30 cm'dir.
\( 2a + b = 30 \)
\( b = 30 - 2a \)
Bu değeri yukarıda elde ettiğimiz eşitsizlikte yerine yazalım.
\( 0 \lt 30 - 2a \lt 2a \)
\( 2a \lt 30 \lt 4a \)
\( a \lt 15 \lt 2a \)
Bu eşitsizliği iki ayrı eşitsizlik olarak inceleyelim ve \( a \) değer aralığını bulalım.
\( a \lt 15 \)
\( 15 \lt 2a\Longrightarrow 7,5 \lt a \)
Buna göre \( a \) değer aralığı aşağıdaki gibi bulunur.
\( 7,5 \lt a \lt 15 \)
\( a \)'nın bu aralıkta alabileceği tam sayı değerleri 8, 9, 10, 11, 12, 13 ve 14'tür.
\( a \) bu değerleri alırken, \( 2a + b = 30 \) denklemine göre \( b \) sırasıyla 14, 12, 10, 8, 6, 4, 2 değerlerini alır.
\( b \) değerinin alabileceği en büyük ve en küçük değerler arasındaki fark \( 14 - 2 = 12 \) olarak bulunur.