İkizkenar Üçgen
İki kenar uzunluğu birbirine eşit, üçüncü kenar uzunluğu farklı olan üçgene ikizkenar üçgen denir.
Bir ikizkenar üçgende uzunlukları eşit olan kenarlara yan kenar, uzunluğu farklı olan üçüncü kenara taban, yan kenarlarla taban arasında kalan eşit açılara taban açısı, yan kenarlar arasındaki üçüncü açıya tepe açısı denir.
İkizkenar üçgenin taban açıları eşittir. Bunun karşıtı da doğrudur, yani taban açıları eşit olan bir üçgenin yan kenar uzunlukları eşittir, dolayısıyla bu üçgen ikizkenardır.
\( \abs{AB} = \abs{AC} \Longleftrightarrow m(\widehat{B}) = m(\widehat{C}) \)
İSPATI GÖSTER
İkizkenar üçgenin taban açıları eşittir.
Tabana ait yüksekliği çizelim.
\( \abs{AD} = h \)
\( ADB \) ve \( ADC \) birer dik üçgendir. Bu iki üçgenin yükseklikleri (\( h \)) ve hipotenüsleri eşittir.
\( \abs{AB} = \abs{AC} \)
Buna göre Pisagor teoreminden iki üçgenin taban uzunluklarının da eşit olduğunu bulabiliriz.
\( \abs{BD} = \abs{DC} \)
Üç kenarı da eş olan üçgenler eş üçgenlerdir.
\( \overset{\triangle}{ADB} \cong \overset{\triangle}{ADC} \)
Eş üçgenlerin iç açıları eşittir.
\( m(\widehat{B}) = m(\widehat{C}) \)
Buna göre ikizkenar üçgenlerin taban açıları eşittir.
Taban açıları eşit olan üçgen ikizkenardır.
\( ABC \) üçgeninde iki taban açısının ölçülerinin eşit olduğunu varsayalım.
\( m(\widehat{B}) = m(\widehat{C}) \)
Bu durumda \( ADB \) ve \( ADC \) üçgenlerinin ikişer açısı eşit olduğu için üçüncü açıları da eşit olur.
\( m(\widehat{BAD}) = m(\widehat{CAD}) \)
Üç açısı eşit olan üçgenler benzerdir.
\( \overset{\triangle}{ADB} \sim \overset{\triangle}{ADC} \)
Bu iki üçgenin yükseklikleri ortak olduğu için Açı-Kenar-Açı eşliğinden üçgenlerin aynı zamanda eş üçgenler olduğu sonucuna varabiliriz.
\( \overset{\triangle}{ADB} \cong \overset{\triangle}{ADC} \)
İki üçgen eş olduğu için hipotenüs uzunlukları eşit olur.
\( \abs{AB} = \abs{AC} \)
Buna göre taban açıları eşit olan bir üçgen ikizkenardır.
Yukarıdaki ispata göre bir ikizkenar üçgende tabana ait yükseklik üçgeni \( ADB \) ve \( ADC \) olmak üzere iki eş üçgene böler. Bunun sonuçlarını aşağıdaki şekilde listeleyebiliriz.
- Tabana ait yükseklik tabanı ortalar, dolayısıyla aynı zamanda tabana ait kenarortaydır.
- Tabana ait yükseklik tepe açısını iki eşit açıya böler, dolayısıyla aynı zamanda tabana ait açıortaydır.
- Tabana ait yükseklik tabanı ortaladığı için aynı zamanda tabana ait orta dikmedir.
- Üçgen tabana ait yüksekliğe göre simetriktir.
\( \abs{BD} = \abs{DC} \)
\( h_a = n_a = V_a \)
Bir üçgende bir kenara ait yükseklik, açıortay, kenarortay ve orta dikmeden herhangi ikisinin eşit olduğunu biliyorsak diğerlerinin de eşit olduğunu ve diğer iki kenar uzunluğunun eşit olduğunu söyleyebiliriz. Örneğin bir üçgende aynı doğru parçası hem yükseklik hem kenarortay ise bu üçgen ikizkenar üçgendir.
İkizkenar üçgende tabana ait yüksekliği kenar uzunlukları cinsinden aşağıdaki şekilde ifade edebiliriz.
\( a \) taban uzunluğu,
\( b \) yan kenarlardan birinin uzunluğu olmak üzere,
\( h_a = \sqrt{b^2 - \frac{a^2}{4}} \)
İSPATI GÖSTER
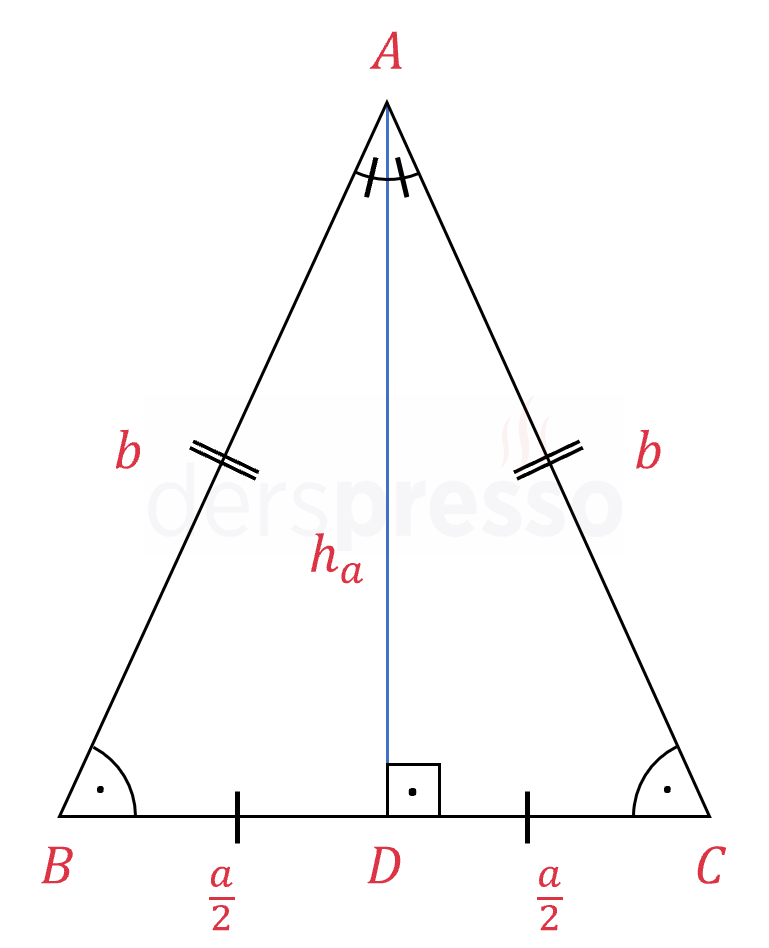
Yukarıda ispatını verdiğimiz üzere, ikizkenar üçgende taban yüksekliği aynı zamanda kenarortaydır.
\( \abs{BD} = \abs{DC} = \dfrac{a}{2} \)
Taban yüksekliğini Pisagor teoremini kullanarak aşağıdaki şekilde hesaplayabiliriz.
\( b^2 = h_a^2 + (\frac{a}{2})^2 \)
\( h_a^2 = b^2 - \frac{a^2}{4} \)
\( h_a = \sqrt{b^2 - \frac{a^2}{4}} \)
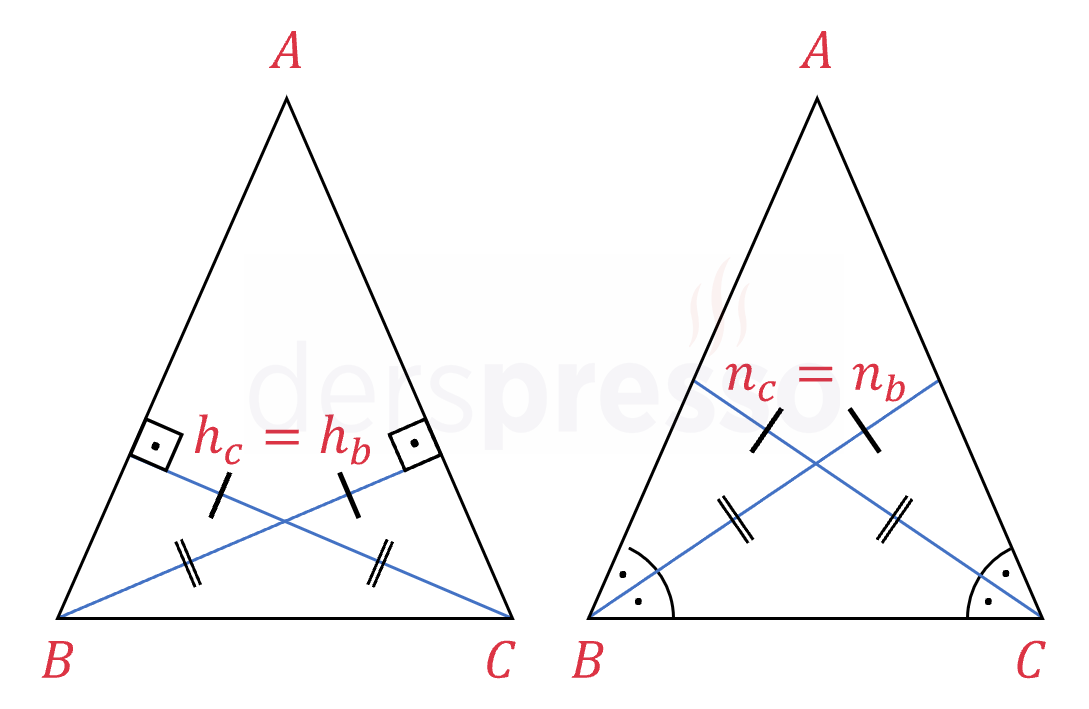
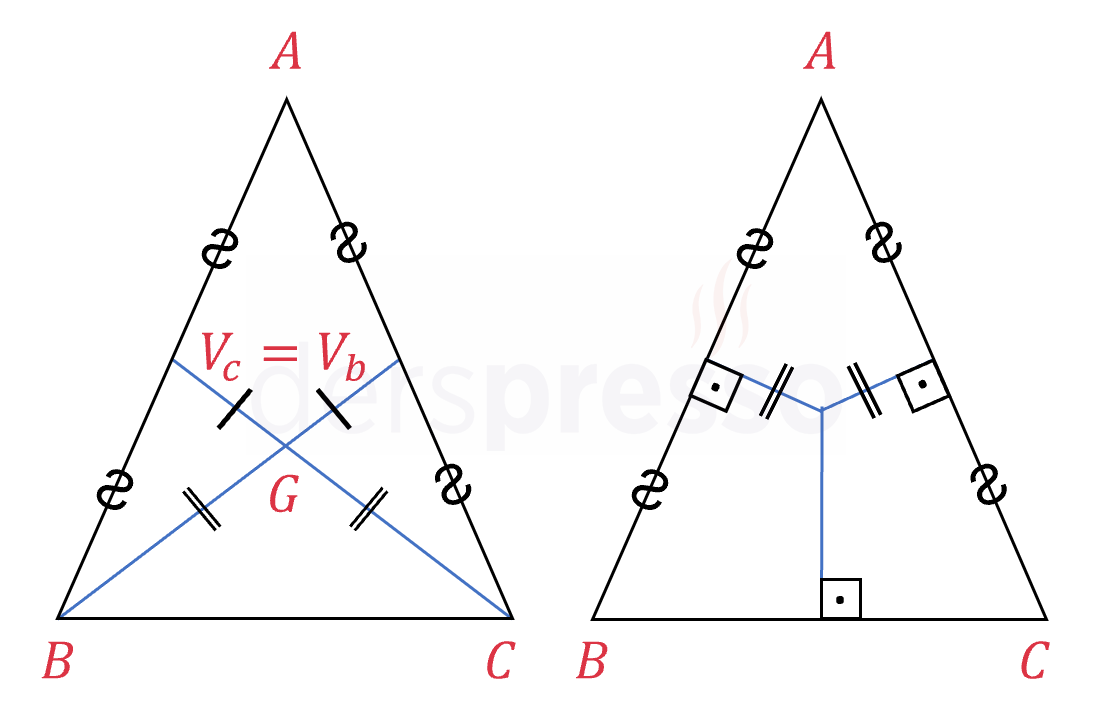
İkizkenar üçgende eşit kenarlara/açılara ait yükseklik, açıortay, kenarortay ve orta dikmelerin uzunlukları birbirine eşittir. Ayrıca bu yükseklik, açıortay ve kenarortayların kesişimleri birbirine eş parçalar oluşturur.
\( h_b = h_c \)
\( n_b = n_c \)
\( V_b = V_c \)
İkizkenar üçgende tabanın üzerindeki herhangi bir noktadan yan kenarlara çizilen paralel doğru parçalarının uzunluklarının toplamı, yan kenarlardan birinin uzunluğuna eşittir.
\( P \) taban üzerinde herhangi bir nokta,
\( [PR] \parallel [AB] \) ve \( [PS] \parallel [AC] \) olmak üzere,
\( \abs{PR} + \abs{PS} = \abs{AR} + \abs{AS} \) \( = \abs{AB} = \abs{AC} \)
İSPATI GÖSTER
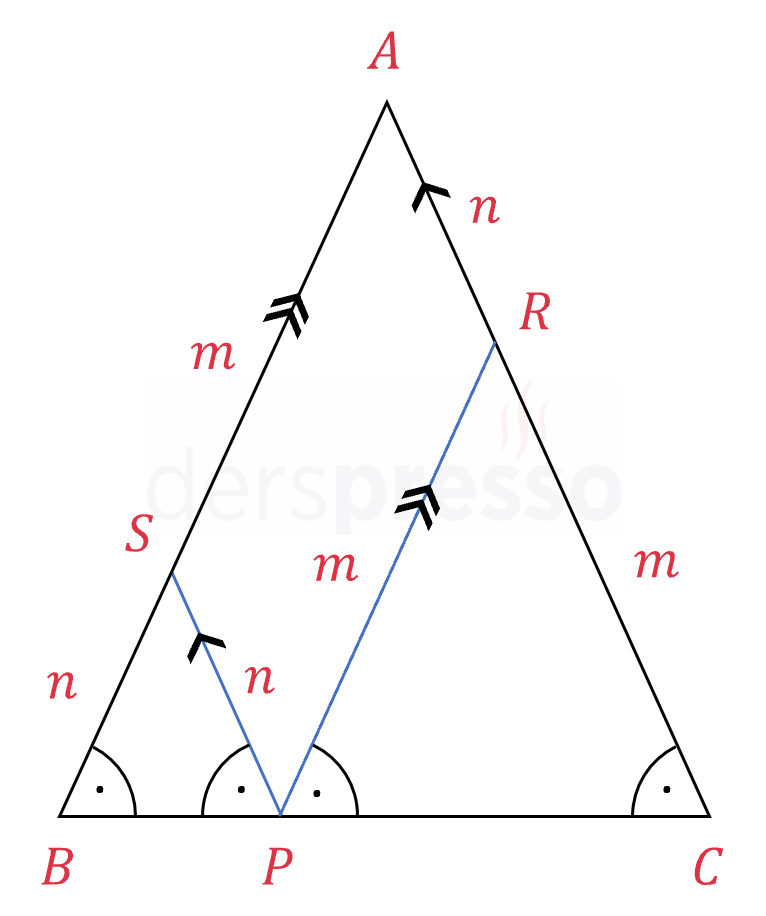
\( [AB] \parallel [RP] \) olduğu için \( \widehat{ABC} \) ve \( \widehat{RPC} \) yöndeş açılardır ve ölçüleri eşittir.
Dolayısıyla \( RPC \) ikizkenar bir üçgendir.
\( \abs{RP} = \abs{RC} = m \)
\( [AC] \parallel [SP] \) olduğu için \( \widehat{ACB} \) ve \( \widehat{SPB} \) yöndeş açılardır ve ölçüleri eşittir.
Dolayısıyla \( SBP \) ikizkenar bir üçgendir.
\( \abs{SB} = \abs{SP} = n \)
\( ASPR \) bir paralelkenar olduğu için karşılıklı kenar uzunlukları birbirine eşittir.
\( \abs{AS} = \abs{RP} = m \)
\( \abs{AR} = \abs{SP} = n \)
İkizkenar üçgende tabanın üzerindeki herhangi bir noktadan yan kenarlara çizilen dikmelerin uzunluklarının toplamı, yan kenarlardan birine ait yüksekliğe eşittir.
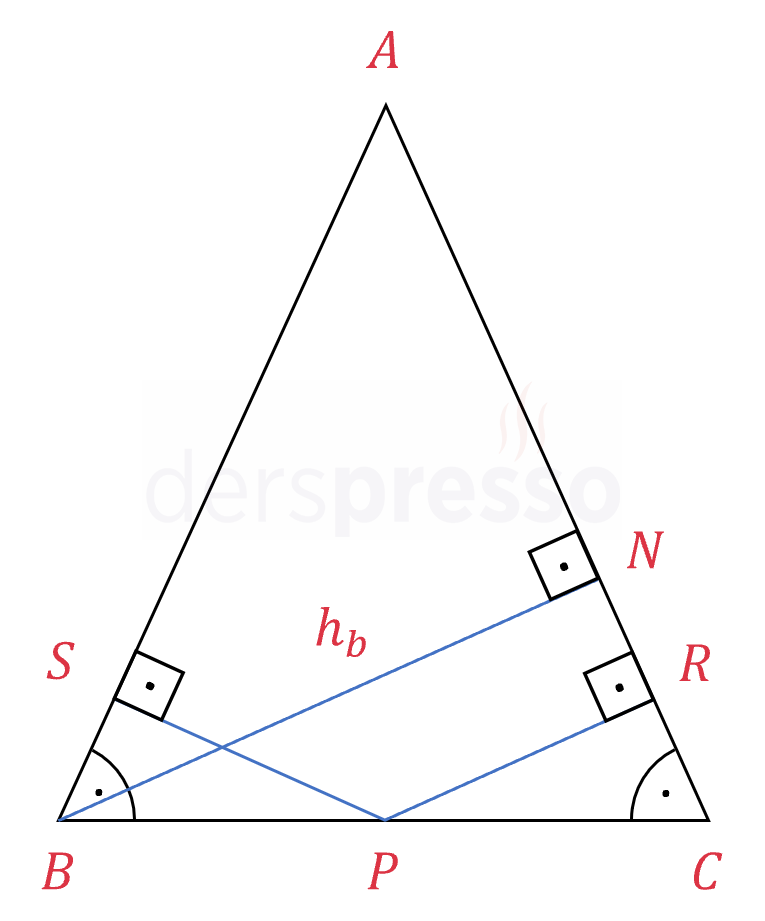
\( P \) taban üzerinde herhangi bir nokta,
\( [PR] \perp [AC] \) ve \( [PS] \perp [AB] \) olmak üzere,
\( \abs{PR} + \abs{PS} = \abs{BN} = h_b = h_c \)
İSPATI GÖSTER
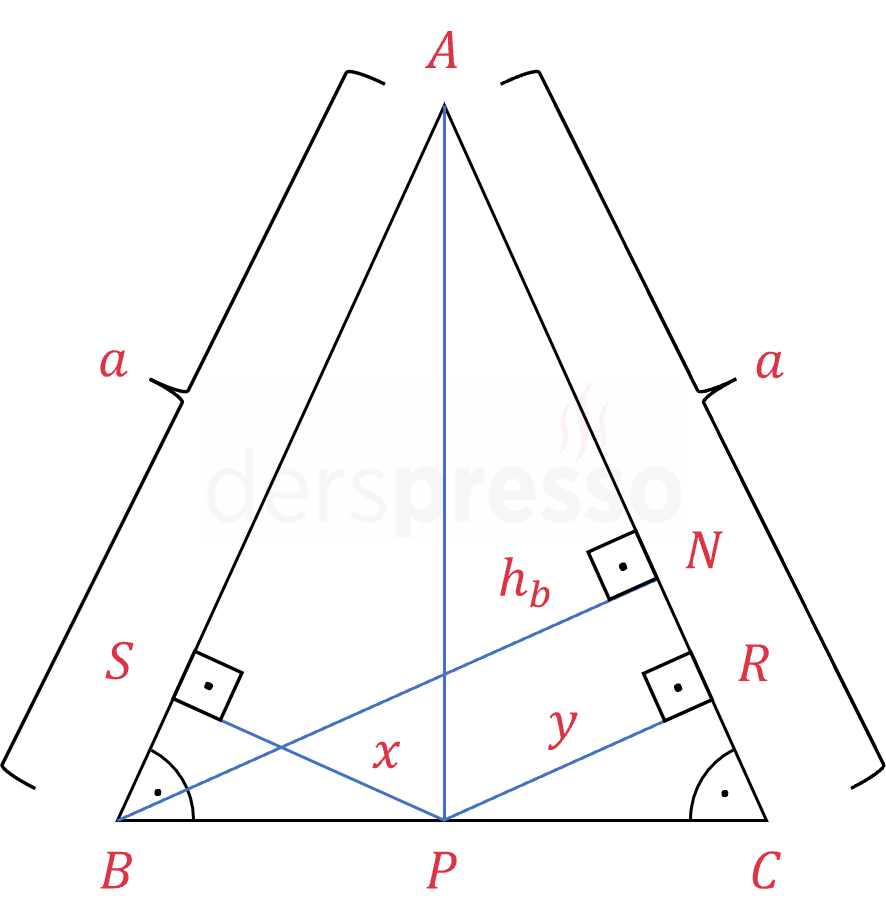
\( A \) köşesinden \( P \) noktasına bir doğru parçası çizelim.
\( \abs{AB} = \abs{AC} = a \)
\( \abs{SP} = x \)
\( \abs{RP} = y \) diyelim.
\( ABC \) üçgeninin alanı \( ABP \) ve \( APC \) üçgenlerinin alanları toplamına eşittir.
\( A(ABC) = \dfrac{a \cdot h_b}{2} \)
\( A(ABP) = \dfrac{a \cdot x}{2} \)
\( A(APC) = \dfrac{a \cdot y}{2} \)
\( A(ABC) = A(ABP) + A(APC) \)
\( \dfrac{a \cdot h_b}{2} = \dfrac{a \cdot x}{2} + \dfrac{a \cdot y}{2} \)
\( a \cdot h_b = a \cdot (x + y) \)
\( h_b = x + y \)
\( \abs{PR} + \abs{PS} = \abs{BN} = h_b = h_c \)
İkizkenar dik üçgende taban açıları 45° olur ve Pisagor teoreminden hipotenüs uzunluğu bir dik kenar uzunluğunun \( \sqrt{2} \) katıdır.
Bir ikizkenar üçgenin herhangi bir açısı 60° ise bu üçgen aynı zamanda eşkenar üçgendir.
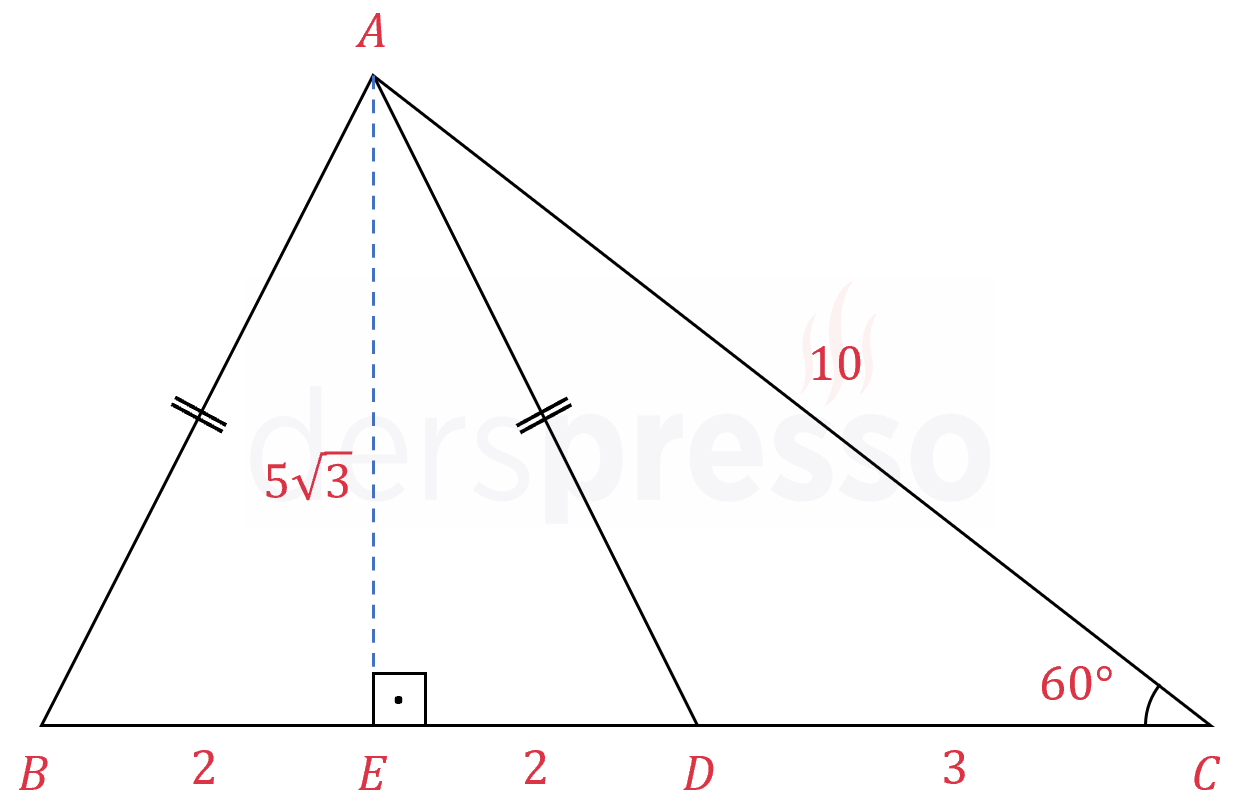
Şekilde \( ABD \) ve \( ADC \) üçgenleri verilmiştir.
\( \abs{AB} = \abs{AD}, \quad \abs{BD} = 4 \)
\( \abs{AC} = 10, \quad \abs{DC} = 3 \)
\( m(\widehat{ACB}) = 60° \)
olduğuna göre, \( \abs{AB} \) kaçtır?
Çözümü Göster\( \abs{AB} = \abs{AD} \) olduğuna göre \( ABD \) üçgeni ikizkenardır.
\( ABD \) üçgeninde tabana ait yüksekliği çizelim.
İkizkenar üçgende tabana ait yükseklik tabanı ortalar.
\( \abs{BE} = \abs{ED} = 2 \)
\( AEC \) üçgeni 30-60-90° üçgeni olur. 30-60-90° üçgeninde kenar uzunlukları arasındaki orantı sırasıyla \( 1:\sqrt{3}:2 \) şeklinde olur.
\( \abs{EC} = 2 + 3 = 5 \)
\( \abs{AE} = 5\sqrt{3} \)
\( AEB\) dik üçgeninde Pisagor teoremini kullanalım.
\( \abs{AB}^2 = \abs{AE}^2 + \abs{BE}^2 \)
\( = (5\sqrt{3})^2 + 2^2 \)
\( \abs{AB} = \sqrt{79} \) bulunur.
Şekilde \( ABC \) ikizkenar üçgeni verilmiştir.
\( \abs{AB} = \abs{AC} \)
\( [DF] \parallel [AC], \quad [EF] \parallel [AB] \)
\( \abs{DF} = 5, \quad \abs{EF} = 3 \)
olduğuna göre, \( \abs{AB} \) kaçtır?
Çözümü Göster\( ABC \) ikizkenar üçgenini ve paralellikleri kullanarak aşağıdaki eşitlikleri yazabiliriz.
\( m(\widehat{ABC}) = m(\widehat{ACB}) \)
\( m(\widehat{DFB}) = m(\widehat{ACB}) = m(\widehat{DBF}) \)
\( m(\widehat{EFC}) = m(\widehat{ABC}) = m(\widehat{ECF}) \)
Buna göre \( DBF \) ve \( EFC \) üçgenleri de ikizkenardır.
\( \abs{DB} = \abs{DF} = 5 \)
\( \abs{EF} = \abs{EC} = 3 \)
\( ADFE \) bir paralelkenar olduğu için karşılıklı kenar uzunlukları birbirine eşittir.
\( \abs{AD} = 3, \quad \abs{AE} = 5 \)
\( \abs{AB} = 5 + 3 = 8 \) bulunur.
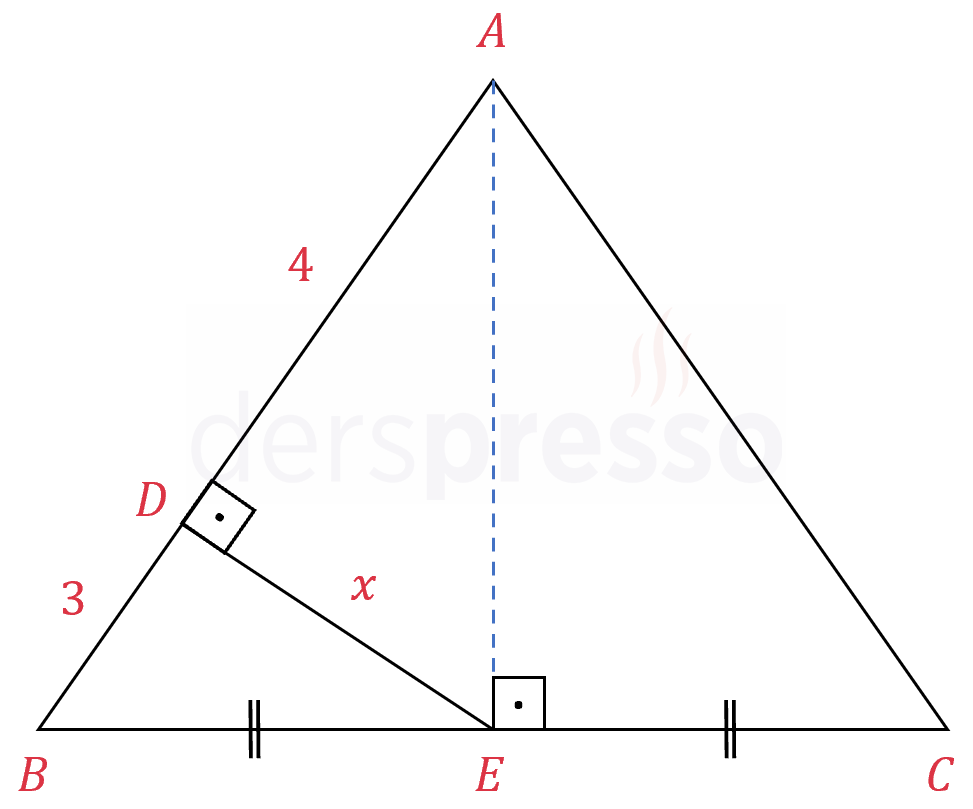
Şekilde \( ABC \) ikizkenar üçgeni verilmiştir.
\( \abs{AB} = \abs{AC} \)
\( [DE] \perp [AB] \)
\( \abs{AD} = 4, \quad \abs{DB} = 3 \)
\( \abs{BE} = \abs{EC} \)
olduğuna göre \( \abs{DE} = x \) kaçtır?
Çözümü Göster\( ABC \) üçgeninde \( A \) köşesinden tabana ait yüksekliği çizelim.
\( ABC \) üçgeni ikizkenar olduğundan tabana ait yükseklik tabanı ortalar.
\( E \) noktası tabanın orta noktası olduğu için aynı zamanda tabana ait yüksekliğin tabanı kestiği noktadır.
\( AEB \) üçgeninde Öklid bağıntısını kullanalım.
\( \abs{DE}^2 = \abs{AD} \cdot \abs{DB} \)
\( = 4 \cdot 3 \)
\( \abs{DE} = x = 2\sqrt{3} \) bulunur.
Şekilde \( ABD \) ve \( ADC \) üçgenleri verilmiştir.
\( \abs{AB} = \abs{AD} \)
\( \abs{BD} = 6\sqrt{2}, \quad \abs{DC} = \sqrt{2} \)
\( m(\widehat{ACB}) = 45° \)
olduğuna göre, \( \abs{AC} = x \) kaçtır?
Çözümü Göster\( ABD \) üçgeninde \( A \) köşesinden tabana ait yüksekliği çizelim.
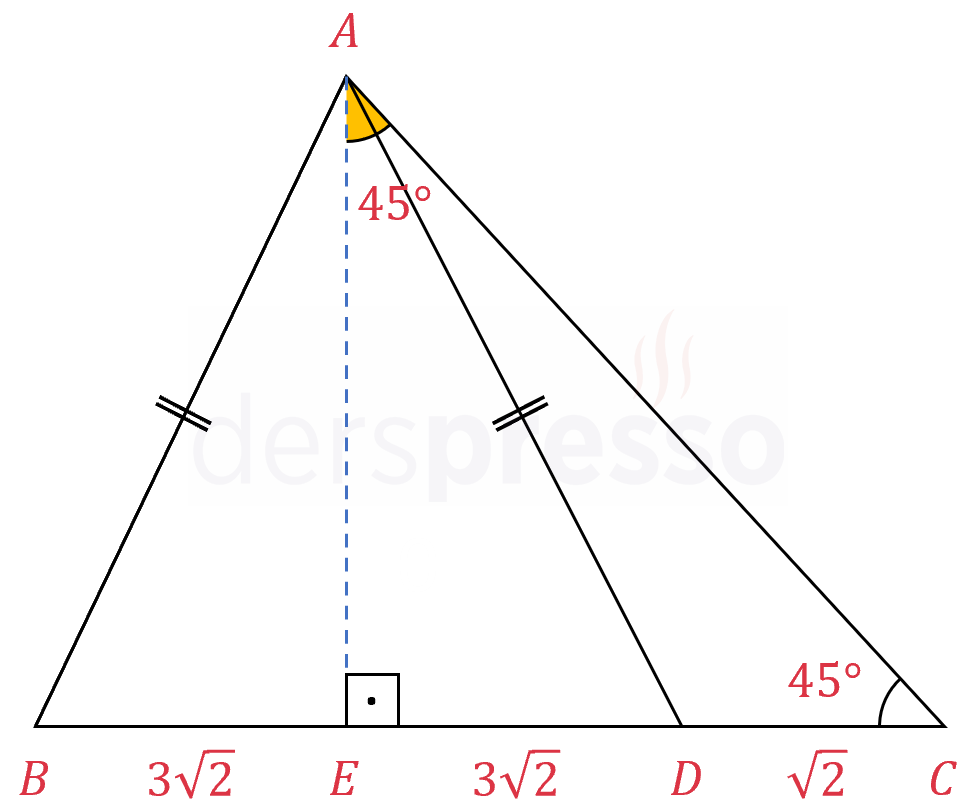
\( ABD \) üçgeni ikizkenar olduğundan tabana ait yükseklik tabanı ortalar.
\( \abs{BE} = \abs{ED} = 3\sqrt{2} \)
\( \abs{EC} = 3\sqrt{2} + \sqrt{2} = 4\sqrt{2} \)
\( AEC \) üçgeni 45-45-90° üçgeni olur. 45-45-90° üçgeninde kenar uzunlukları arasındaki orantı sırasıyla \( 1:1:\sqrt{2} \) şeklinde olur.
Bu orantıyı kullanarak \( x \) uzunluğunu bulalım.
\( \abs{AC} = 4\sqrt{2} \cdot \sqrt{2} = 8 \) bulunur.
Eşit kenarları \( a \), diğer kenarı \( b \) ve eşit olmayan kenara ait yüksekliği \( h \) olan ikizkenar üçgenin belirtilen uzunluk değerleri arasında üçer birim fark vardır.
\( b \gt a \gt h \) olduğu bilindiğine göre üçgenin alanı kaç br\( ^2 \)'dir?
Çözümü Göster\( h = 2n \) diyelim.
Bu durumda \( a = 2n + 3 \) ve \( b = 2n + 6 \) olur.
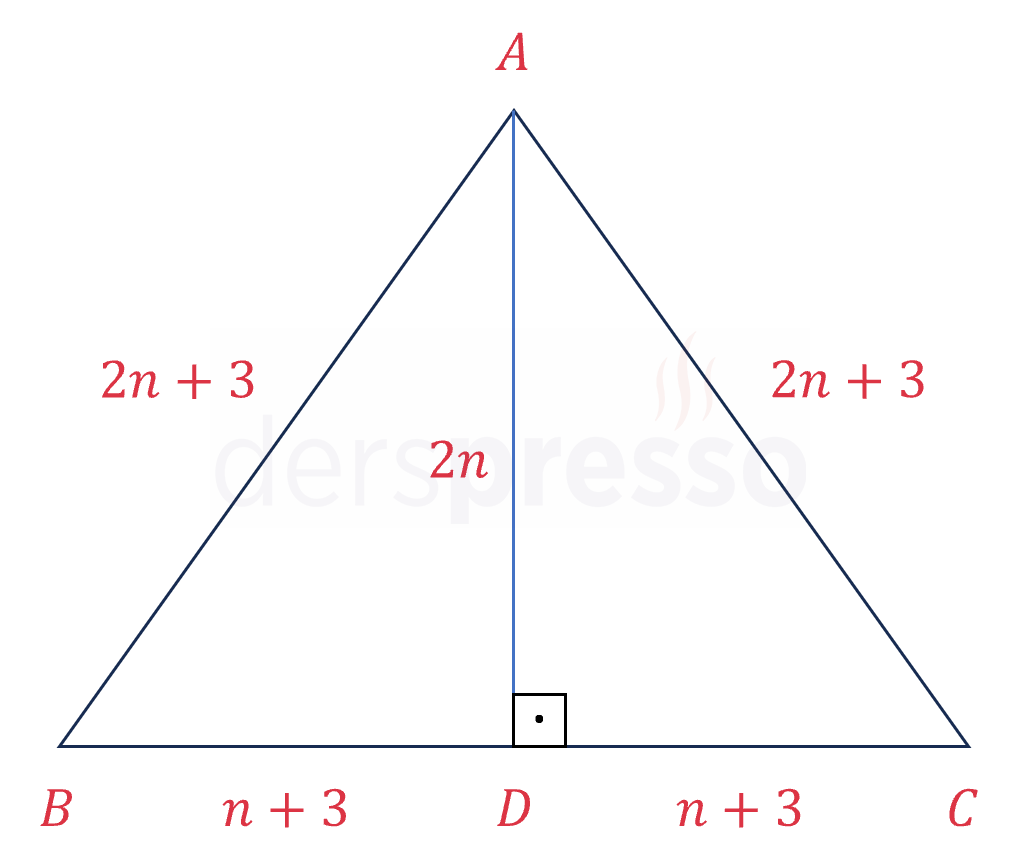
Bir ikizkenar üçgende yükseklik tabanı iki eşit parçaya ayırır ve iki eş dik üçgen oluşturur.
Oluşan dik üçgenlerin dik kenarları \( 2n \), \( n + 3 \) ve hipotenüsü \( 2n + 3 \) olur.
\( n \)'yi bulmak için Pisagor teoremini kullanalım.
\( (n + 3)^2 + (2n)^2 = (2n + 3)^2 \)
\( n^2 + 6n + 9 + 4n^2 = 4n^2 + 12n + 9 \)
\( n^2 - 6n = 0 \)
\( n(n - 6) = 0 \)
Bu denklemin kökleri \( n = 0 \) ve \( n = 6 \) olarak bulunur.
Uzunluk sıfır olamayacağı için \( n = 0 \) geçerli bir çözüm değildir.
Büyük üçgenin alanını bulalım.
\( A = \dfrac{(2 \cdot 6 + 6)(2 \cdot 6)}{2} = 108 \) olarak bulunur.
Bir ikizkenar üçgenin iç açılarından ikisi \( 58° \) ve \( x° \) olduğuna göre, \( x \)'in alabileceği değerlerin toplamı kaçtır?
Çözümü GösterBir ikizkenar üçgenin bir tepe açısı ve ölçüleri eşit iki taban açısı vardır.
\( x \) açısı için üç farklı durum vardır.
Durum 1: Taban açıları \( 58° \) ve \( x° \)
\( x = 58° \)
Bu durumda üçgenin açıları \( 64 - 58 - 58° \) olur.
Durum 2: Tepe açısı \( 58° \), taban açıları \( x° \)
\( 58 + x + x = 180 \)
\( x = 61° \)
Bu durumda üçgenin açıları \( 58 - 61 - 61° \) olur.
Durum 3: Tepe açısı \( x° \), taban açıları \( 58° \)
\( x + 58 + 58 = 180 \)
\( x = 64° \)
Bu durumda üçgenin açıları \( 64 - 58 - 58° \) olur.
\( x \)'in alabileceği değerlerin toplamı \( 58 + 61 + 64 = 183° \) olarak bulunur.
Şekilde \( ABC \) ikizkenar üçgeni verilmiştir.
\( \abs{AB} = \abs{AC} \)
\( \abs{BD} = 7, \quad \abs{DC} = 3 \)
\( \abs{AD} = 6 \)
olduğuna göre, \( \abs{AC} \) kaçtır?
Çözümü Göster\( ABC \) üçgeninde \( A \) köşesinden tabana ait yüksekliği çizelim.
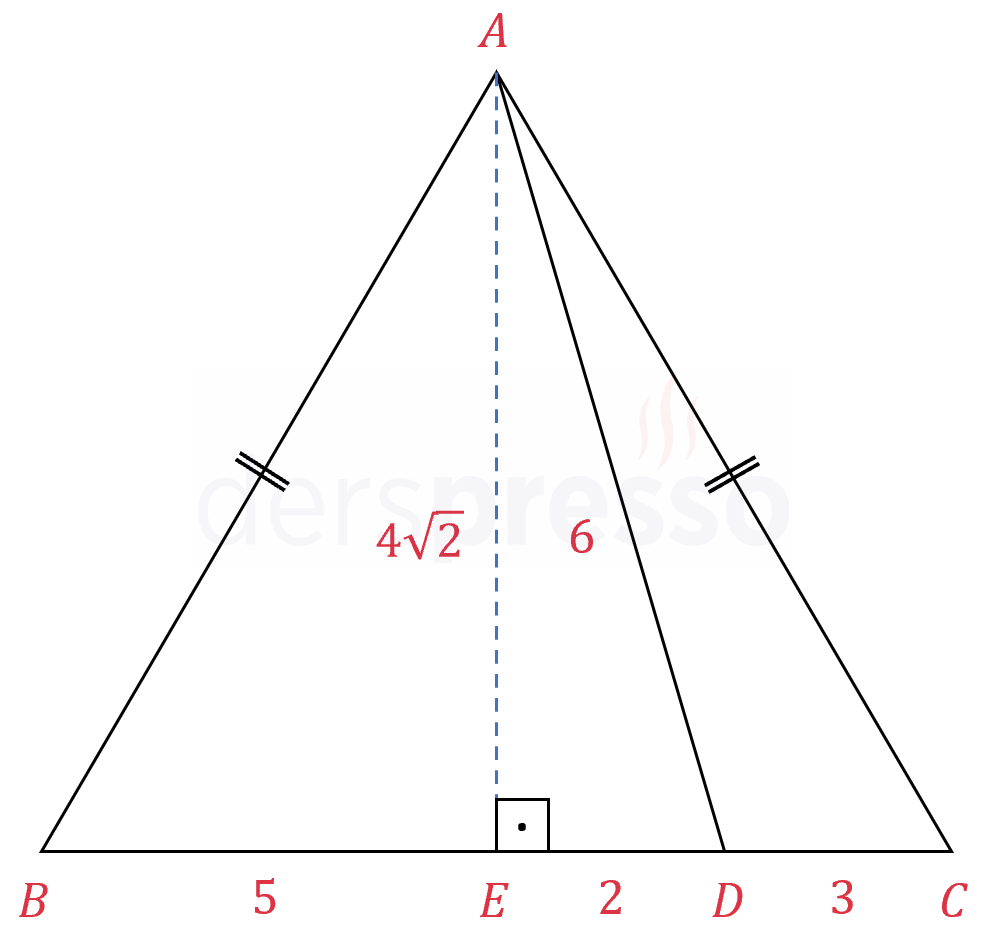
\( ABC \) üçgeni ikizkenar olduğundan tabana ait yükseklik tabanı ortalar.
Buna göre tabanda oluşan doğru parçalarının uzunlukları aşağıdaki gibi olur.
\( \abs{BE} = 5, \abs{ED} = 2, \abs{DC} = 3 \)
\( AED \) dik üçgeninde Pisagor teoremini kullanalım.
\( \abs{AD}^2 = \abs{AE}^2 + \abs{ED}^2 \)
\( 6^2 = \abs{AE}^2 + 2^2 \)
\( \abs{AE} = 4\sqrt{2} \)
\( AEC \) dik üçgeninde Pisagor teoremini kullanalım.
\( \abs{AC}^2 = \abs{AE}^2 + \abs{EC}^2 \)
\( = (4\sqrt{2})^2 + (2 + 3)^2 \)
\( = 32 + 25 \)
\( \abs{AC} = \sqrt{57} \) bulunur.
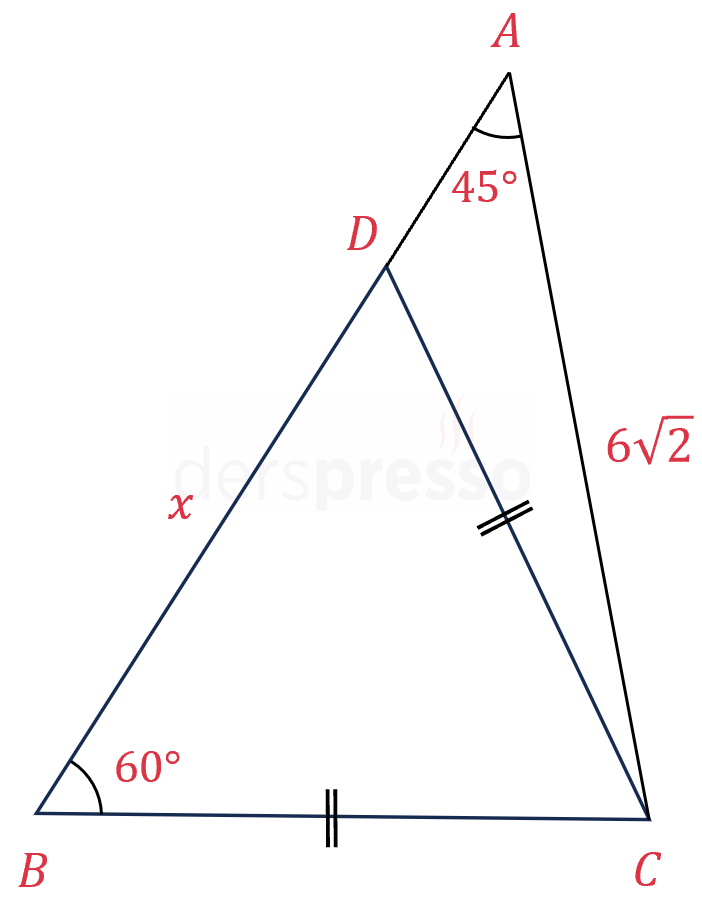
Şekilde \( DBC \) ve \( ABC \) üçgenleri verilmiştir.
\( \abs{CB} = \abs{CD} \)
\( \abs{AC} = 6\sqrt{2} \)
\( m(\widehat{DBC}) = 60° \)
\( m(\widehat{DAC}) = 45° \)
olduğuna göre, \( \abs{BD} = x \) kaçtır?
Çözümü GösterBir ikizkenar üçgenin herhangi bir açısı 60° ise bu üçgen aynı zamanda eşkenar üçgendir.
\( m(\widehat{DBC}) = m(\widehat{BDC}) = m(\widehat{DCB}) = 60° \)
\( DBC \) eşkenar üçgeninde \( C \) köşesinden \( [DB] \) kenarına ait yüksekliği çizelim.
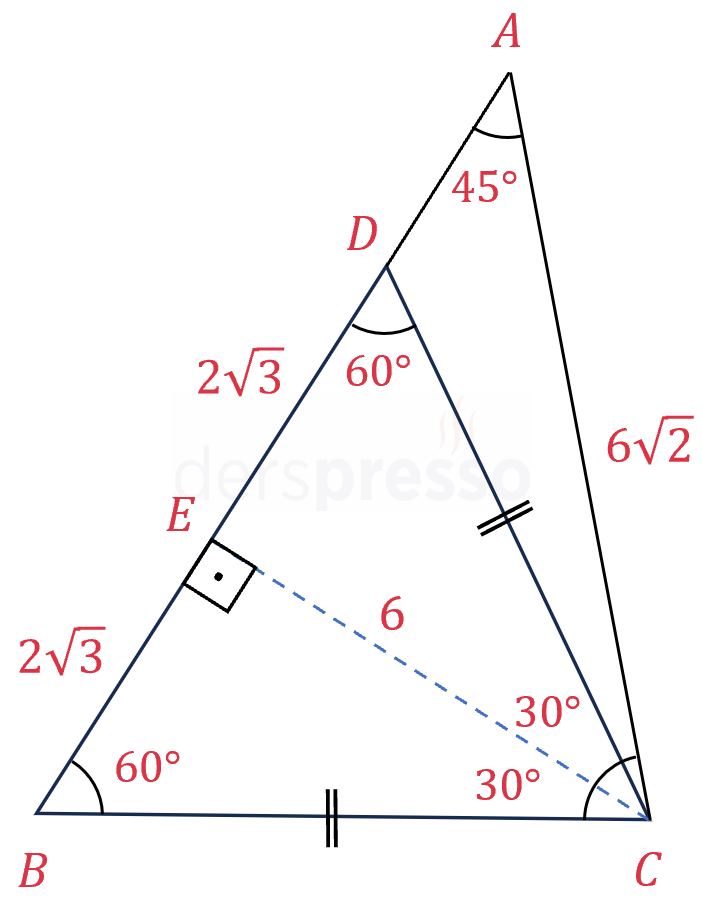
\( [CE] \) doğrusu aynı zamanda kenarortay ve açıortay olur.
\( m(\widehat{DCE}) = m(\widehat{BCE}) = 30° \)
\( CEA \) üçgeni 45-45-90° üçgeni olur. 45-45-90° üçgeninde kenar uzunlukları arasındaki orantı sırasıyla \( 1:1:\sqrt{2} \) şeklinde olur.
\( \abs{CE} = \abs{AE} = 6 \)
\( CED \) üçgeni 30-60-90° üçgeni olur. 30-60-90° üçgeninde kenar uzunlukları arasındaki orantı sırasıyla \( 1:\sqrt{3}:2 \) şeklinde olur.
\( \abs{ED} \cdot \sqrt{3} = 6 \)
\( \abs{ED} = \dfrac{6}{\sqrt{3}} = 2\sqrt{3} \)
\( [CE] \) doğrusu \( [BD] \) kenarının kenarortayıdır.
\( \abs{BE} = \abs{ED} = 2\sqrt{3} \)
\( \abs{BD} = x = 4\sqrt{3} \) bulunur.
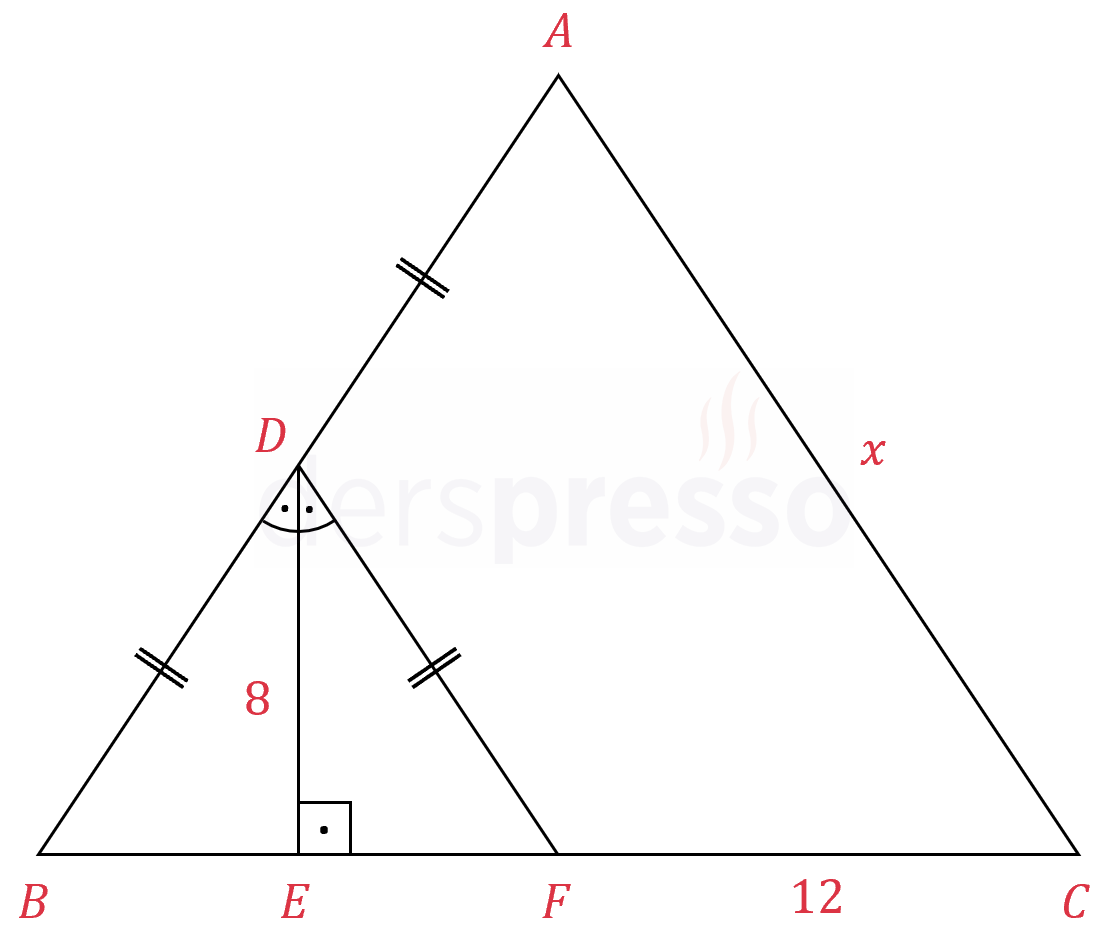
Şekilde \( ABC \) üçgeni verilmiştir.
\( \abs{DB} = \abs{DF} \)
\( [DE] \perp [BF] \)
\( m(\widehat{BDE}) = m(\widehat{EDF}) \)
\( \abs{AD} = \abs{DB} = \abs{DF} \)
\( \abs{FC} = 12, \quad \abs{DE} = 8 \)
olduğuna göre, \( \abs{AC} = x \) kaçtır?
Çözümü Göster\( A \) köşesi ile \( F \) noktasını birleştirelim (mavi kesikli çizgi).
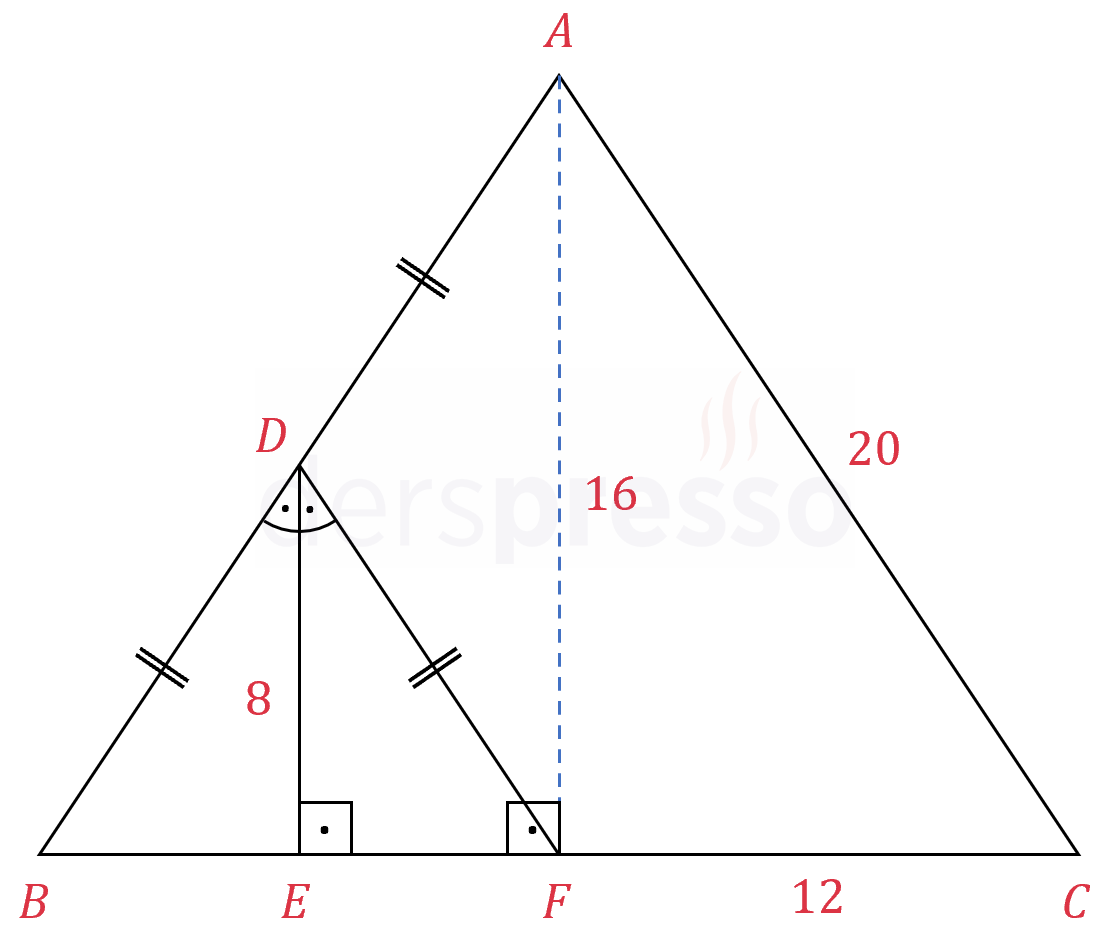
\( \abs{AD} = \abs{BD} = \abs{DF} \) eşitliği \( AFB \) üçgeninde muhteşem üçlü oluşturduğu için \( [AF] \) doğru parçası \( [BC] \) kenarını dik keser, dolayısıyla bu kenarın yüksekliğidir.
\( [DE] \perp [BF] \) ve \( [AF] \perp [BC] \) olduğu için \( [DE] \parallel [AF] \) olur.
\( \abs{AD} = \abs{DB} \) ve \( [DE] \parallel [AF] \) olduğu için \( [DE] \) doğru parçası \( DBF \) üçgeninin bir orta tabanıdır.
Bir üçgende orta taban uzunluğu taban uzunluğunun yarısıdır.
\( 2\abs{DE} = \abs{AF} \)
\( \abs{AF} = 16 \)
\( AFC \) üçgeni 3-4-5 özel üçgeni ile \( k = 4 \) benzerlik oranına sahip 12-16-20 üçgenidir.
\( \abs{AC} = x = 20 \) bulunur.
Şekilde \( ABD \) üçgeni ve \( ADC \) ikizkenar üçgeni verilmiştir.
\( \abs{AD} = \abs{AC} \)
\( \abs{BD} = 6 \)
\( m(\widehat{DAC}) = 120° \)
\( m(\widehat{ABD}) = 15° \)
olduğuna göre, \( \abs{DC} = x \) kaçtır?
Çözümü Göster\( ADC \) üçgeninde \( A \) köşesinden \( [DC] \) kenarına ait yüksekliği çizelim.
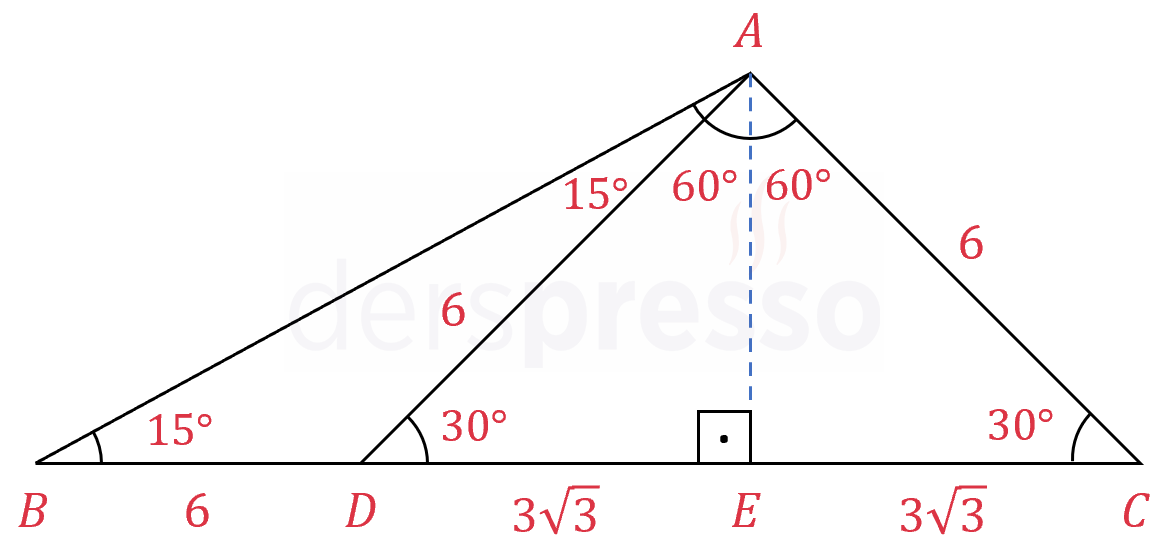
\( ADC \) ikizkenar üçgen olduğu için \( [AE] \) aynı zamanda kenarortay ve açıortay olur.
\( ADC \) üçgeninde açı değerleri aşağıdaki gibi olur.
\( m(\widehat{ADE}) = m(\widehat{ACE}) = 30° \)
\( m(\widehat{DAE}) = m(\widehat{CAE}) = 60° \)
\( ABD \) üçgeni için, bir dış açı iki iç açının toplamına eşittir.
\( m(\widehat{ADC}) = m(\widehat{ABD}) + m(\widehat{BAD}) \)
\( m(\widehat{BAD}) = 30 - 15 = 15° \)
\( m(\widehat{ABD}) = m(\widehat{BAD}) \) olduğuna göre \( ABD \) üçgeni de ikizkenardır.
\( \abs{BD} = \abs{AD} = 6 \)
\( ADE \) üçgeni 30-60-90° üçgeni olur. 30-60-90° üçgeninde kenar uzunlukları arasındaki orantı sırasıyla \( 1:\sqrt{3}:2 \) şeklinde olur.
\( \dfrac{\abs{DE}}{\abs{AD}} = \dfrac{\sqrt{3}}{2} \)
\( \abs{DE} = \dfrac{6\sqrt{3}}{2} = 3\sqrt{3} \)
\( \abs{DC} = x = 6\sqrt{3} \) bulunur.
\( ABC \) bir dik üçgendir.
\( \abs{AD} = 4, \quad \abs{DC} = 12 \)
\( [DE] \perp [BC] \)
\( \abs{BE} = \abs{CE} \)
olduğuna göre, \( \abs{AB} = x \) kaçtır?
Çözümü Göster\( B \) ve \( D \) noktalarını birleştirelim.
\( [BC] \) kenarının orta dikmesi üçgenin \( D \) köşesinden geçtiği için \( BCD \) üçgeni bir ikizkenar üçgendir.
\( \abs{BD} = \abs{DC} = 12 \)
\( ADB \) dik üçgeninde Pisagor bağıntısını kullanabiliriz.
\( \abs{BD}^2 = \abs{AD}^2 + \abs{AB}^2 \)
\( 12^2 = 4^2 + x^2 \)
\( x = \sqrt{128} = 8\sqrt{2} \) bulunur.
\( ABC \) bir ikizkenar üçgendir.
\( \abs{AB} = \abs{AC} \)
\( \abs{BE} = 3, \abs{EC} = 1, \abs{DC} = 3 \)
\( [DE] \perp [BC] \)
olduğuna göre, \( \abs{AD} = x \) kaçtır?
Çözümü Göster\( ABC \) üçgeninde \( A \) köşesinden tabana ait yüksekliği çizelim.
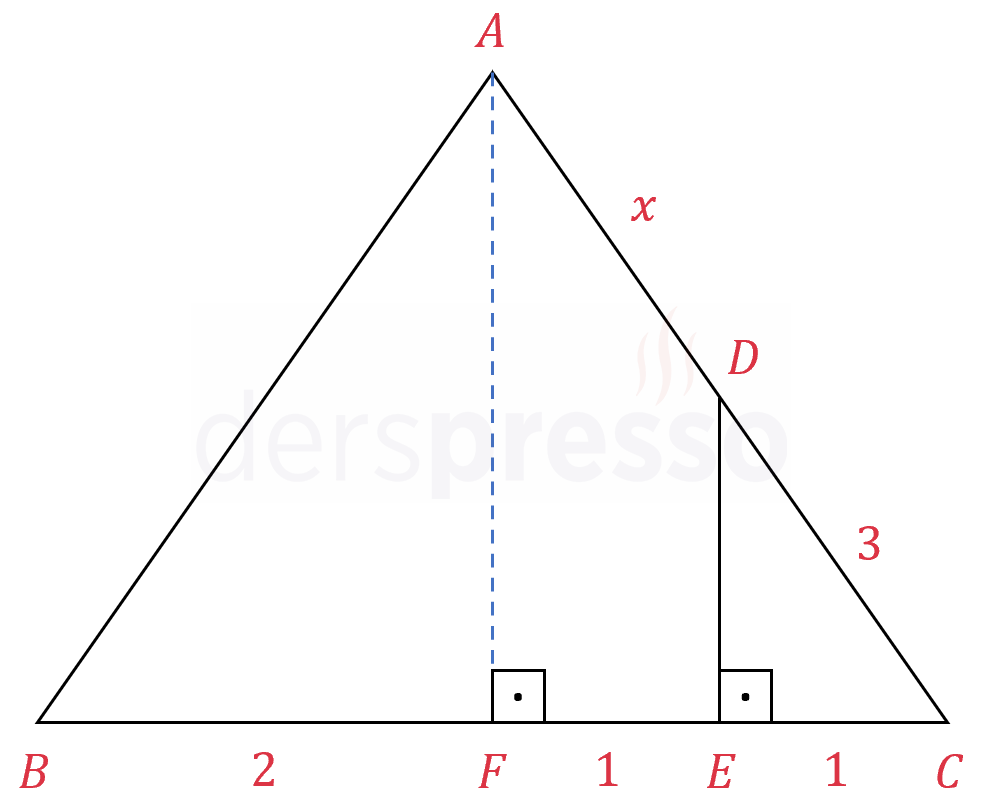
\( ABC \) ikizkenar üçgen olduğu için \( [AF] \) yüksekliği tabanı ortalar.
Buna göre tabandaki doğru parçası uzunlukları aşağıdaki gibi olur.
\( \abs{BF} = 2, \abs{FE} = 1, \abs{EC} = 1 \)
\( [DE] \) doğrusu \( AFC \) üçgeninin \( [FC] \) kenarını ortaladığı ve \( [DE] \parallel [AF] \) olduğu için \( AFC \) üçgeninin bir orta tabanıdır.
Bir üçgende orta taban her iki yan kenarı ortalar.
\( \abs{AD} = x = \abs{DC} = 3 \) bulunur.
Şekilde \( ABC \) ve \( AEF \) üçgenleri verilmiştir.
\( [BC] \perp [AF] \)
\( \abs{EB} = \abs{ED} = 4 \)
\( \abs{EA} = 11 \)
olduğuna göre, \( \abs{DF} = x \) kaçtır?
Çözümü Göster\( BED \) ikizkenar üçgeninin taban açı ölçülerine \( a \) diyelim.
\( m(\widehat{EBD}) = m(\widehat{EDB}) = a \)
Ters açıların ölçüleri eşittir.
\( m(\widehat{FDC}) = a \)
\( \widehat{DFC} \) açısının ölçüsüne \( b \) diyelim.
\( m(\widehat{DFC}) = b \)
\( DCF \) üçgeninin iç açıları toplamını yazalım.
\( a + b + 90° = 180° \)
\( a + b = 90° \)
\( ABC \) üçgeninde iç açılar toplamı 180° olması için \( m(\widehat{BAC}) = b \) olmalıdır.
Buna göre \( AEF \) üçgeni ikizkenardır.
\( m(\widehat{EAF}) = m(\widehat{EFA}) = b \)
\( \abs{EA} = \abs{EF} = 11 \)
\( \abs{ED} + \abs{DF} = \abs{EF} \)
\( 4 + x = 11 \)
\( \abs{DF} = x = 7 \) bulunur.
Şekilde \( ABC \) dik üçgeni verilmiştir.
\( [BA] \perp [CA], \quad [DF] \perp [AE] \)
\( \abs{BE} = \abs{EC} = 5 \)
\( \abs{FE} = 1 \)
\( m(\widehat{BED}) = m(\widehat{DEA}) \)
olduğuna göre, \( \abs{DF} = x \) kaçtır?
Çözümü Göster
\( ABC \) üçgeninin dik açılı köşesinden tabana inen doğru parçası tabanı eşit iki parçaya böldüğü için muhteşem üçlü oluşur.
\( \abs{BE} = \abs{EC} = \abs{AE} = 5 \)
\( \abs{AF} = 5 - 1 = 4 \)
\( m(\widehat{BED}) = m(\widehat{DEA}) = a \) diyelim.
\( ABE \) ikizkenar üçgendir.
\( m(\widehat{ABE}) = m(\widehat{BAE}) = b \)
\( ABE \) üçgeninde iç açıların toplamını bulalım.
\( m(\widehat{ABE}) + m(\widehat{BAE}) + m(\widehat{BEA}) = 180° \)
\( b + b + 2a = 180° \)
\( a + b = 90° \)
Bu durumda \( m(\widehat{BDE}) = m(\widehat{ADE}) = 90° \) olarak bulunur.
\( ADE \) üçgeninde \( [DF] \) doğru parçası dik açılı köşeden inen dikme olduğu için Öklid bağıntısını kullanabiliriz.
\( \abs{DF}^2 = \abs{EF} \cdot \abs{FA} \)
\( x^2 = 1 \cdot 4 \)
\( \abs{DF} = x = 2 \) olarak bulunur.
\( ABCD \) dörtgeni için uzunluk ve açı değerleri aşağıdaki gibidir.
\( \abs{AB} = 10, \quad \abs{DC} = 8 \)
\( \abs{BC} = 16\sqrt{2} \)
\( m(\widehat{ABC}) = m(\widehat{DCB}) = 45° \)
olduğuna göre, \( \abs{AD} = x \) kaçtır?
Çözümü Göster\( [BA] \) ve \( [CD] \) kenarlarını bir üçgen oluşturacak şekilde uzatalım ve kesişim noktalarına \( E \) diyelim.
\( EBC \) üçgeni 45-45-90° üçgeni olur. 45-45-90° üçgeninde kenar uzunlukları arasındaki orantı sırasıyla \( 1:1:\sqrt{2} \) şeklinde olur.
\( \abs{EB} = \abs{EC} = \dfrac{16\sqrt{2}}{\sqrt{2}} = 16 \)
\( \abs{EA} = 16 - 10 = 6 \)
\( \abs{ED} = 16 - 8 = 8 \)
\( EAD \) üçgeni 3-4-5 özel üçgeni ile \( k = 2 \) benzerlik oranına sahip 6-8-10 üçgenidir.
\( \abs{AD} = x = 10 \) olarak bulunur.
Şekilde \( ABC \) ikizkenar üçgeni ve \( ADC \) dik üçgeni verilmiştir.
\( \abs{AB} = \abs{AC} \)
\( [DA] \perp [AC] \)
\( \abs{BD} = 2, \quad \abs{DC} = 10 \)
olduğuna göre, \( \abs{AD} = x \) kaçtır?
Çözümü Göster\( ABC \) üçgeninde \( A \) köşesinden tabana ait yüksekliği çizelim.
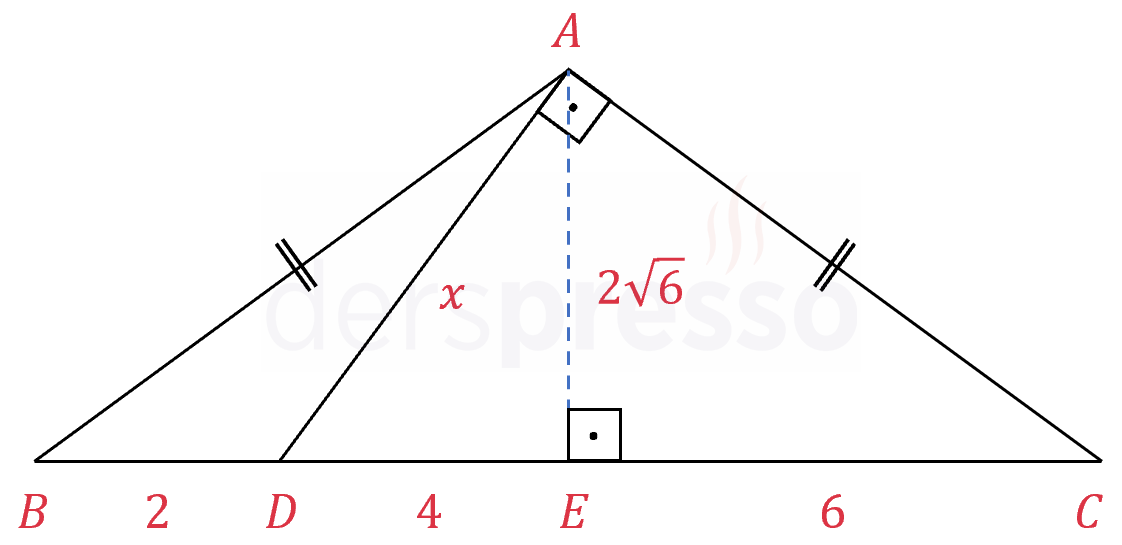
\( ABC \) üçgeni ikizkenar olduğundan tabana ait yükseklik tabanı ortalar.
\( \abs{BC} = 2 + 10 = 12 \)
\( \abs{BE} = \abs{EC} = 6 \)
\( \abs{DE} = 6 - 2 = 4 \)
\( DAC \) dik üçgeninde Öklid bağıntısını kullanarak tabana ait yüksekliği bulalım.
\( \abs{AE}^2 = \abs{DE} \cdot \abs{EC} \)
\( = 4 \cdot 6 \)
\( \abs{AE} = 2\sqrt{6} \)
\( ADE \) üçgeninde Pisagor teoremini kullanalım.
\( \abs{AD}^2 = \abs{AE}^2 + \abs{DE}^2 \)
\( = (2\sqrt{6})^2 + 4^2 \)
\( \abs{AD} = x = 2\sqrt{10} \) bulunur.
Şekilde \( ABC \) üçgeni verilmiştir.
\( \abs{CB} = \abs{CD} \)
\( [DE] \perp [BC] \)
\( m(\widehat{BAD}) = 30° \)
olduğuna göre, \( \abs{AB} = x \) kaçtır?
Çözümü Göster\( BCD \) üçgeninde \( B \) köşesinden \( [CD] \) kenarına ait yüksekliği çizelim.
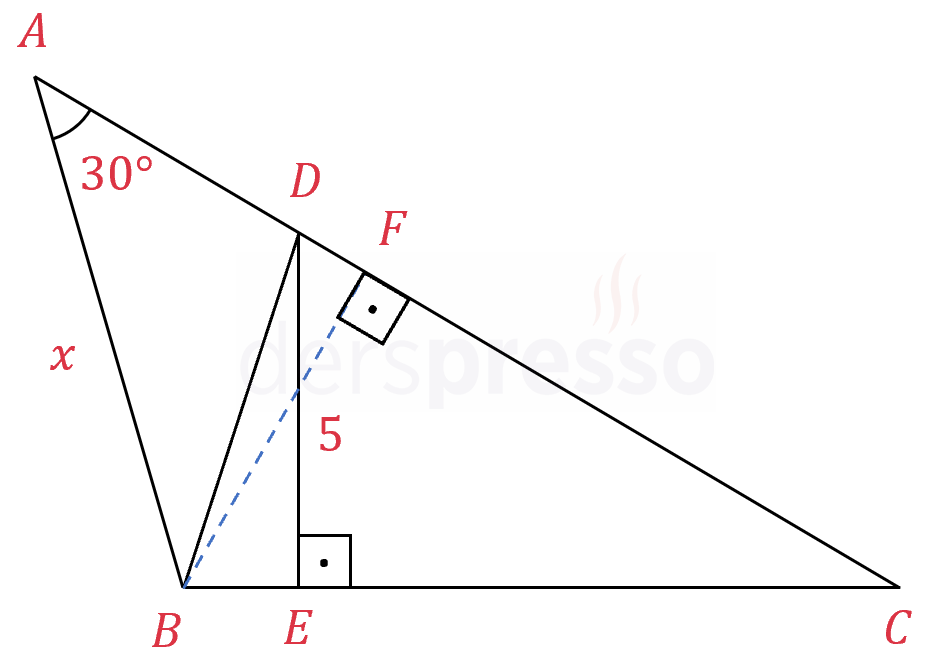
İkizkenar üçgende eşit kenarlara ait yüksekliklerin uzunlukları birbirine eşittir.
\( \abs{DE} = \abs{BF} = 5 \)
\( AFB \) üçgeni 30-60-90° üçgeni olur. 30-60-90° üçgeninde kenar uzunlukları arasındaki orantı sırasıyla \( 1:\sqrt{3}:2 \) şeklinde olur.
\( \abs{AB} = 2\abs{BF} \)
\( \abs{AB} = x = 10 \) bulunur.
Şekilde \( ABC \) ikizkenar üçgeni verilmiştir.
\( \abs{AB} = \abs{AC} = 10 \)
\( m(\widehat{BAC}) = 60° \)
\( [FD] \perp [AB], \quad [FE] \perp [AC] \)
\( \abs{FD} = 3\sqrt{3}\)
olduğuna göre, \( \abs{FE} = x \) kaçtır?
Çözümü Gösterİkizkenar üçgende taban üzerindeki herhangi bir noktadan yan kenarlara çizilen dikmelerin uzunluklarının toplamı, yan kenarlardan birine ait yüksekliğe eşittir.
\( B \) köşesinden \( [AC] \) kenarına ait yüksekliği çizelim.
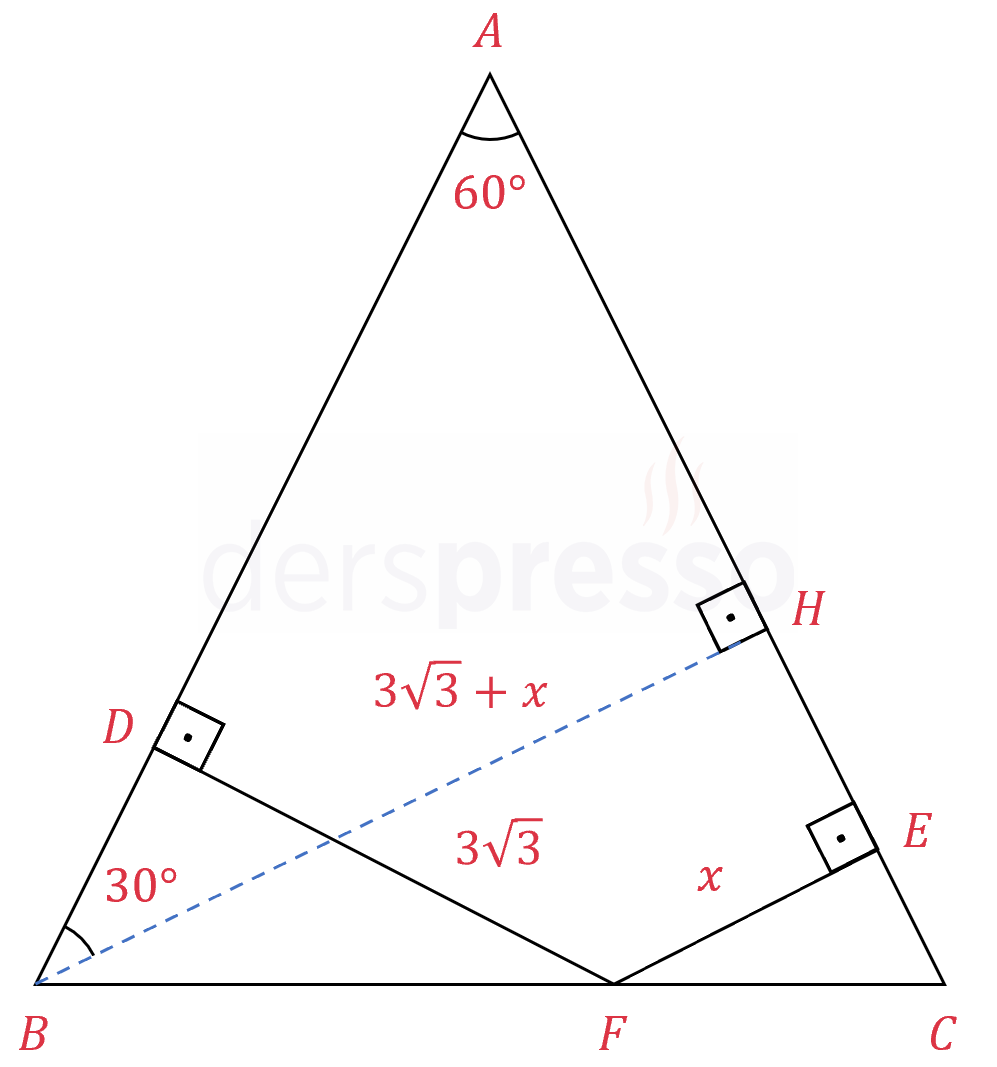
\( \abs{BH} = 3\sqrt{3} + x \)
\( BAH \) üçgeni 30-60-90° üçgeni olur. 30-60-90° üçgeninde kenar uzunlukları arasındaki orantı sırasıyla \( 1:\sqrt{3}:2 \) şeklinde olur.
\( \dfrac{\abs{BH}}{\abs{AB}} = \dfrac{\sqrt{3}}{2} \)
\( 3\sqrt{3} + x = 10 \cdot \dfrac{\sqrt{3}}{2} \)
\( 3\sqrt{3} + x = 5\sqrt{3} \)
\( x = 2\sqrt{3} \) bulunur.
Şekilde \( ADB \) dik üçgeni ve \( DBC \) ikizkenar üçgeni verilmiştir.
\( [AB] \perp [BC], \quad [AD] \perp [BD] \)
\( \abs{DB} = \abs{DC} \)
\( \abs{BC} = 12, \quad \abs{AD} = 2\sqrt{13} \)
olduğuna göre, \( DBC \) üçgeninin alanı kaçtır?
Çözümü Göster\( DBC \) üçgeninde \( [BC] \) kenarına ve \( ADB \) üçgeninde \( [AB] \) kenarına ait yükseklikleri çizelim.
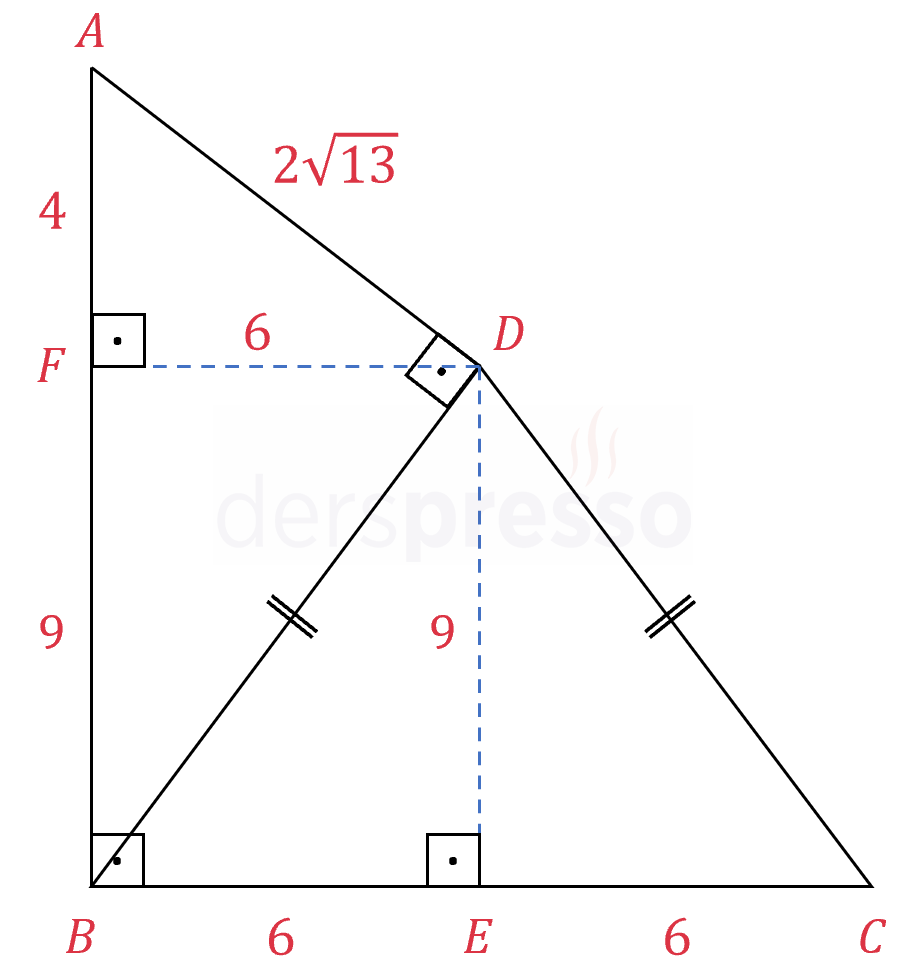
İkizkenar üçgende tabana ait yükseklik tabanı ortalar.
\( \abs{BE} = \abs{EC} = 6 \)
Oluşan \( BEDF \) dörtgeni bir dikdörtgendir. Dikdörtgende karşılıklı kenar uzunlukları birbirine eşittir.
\( \abs{FD} = \abs{BE} = 6 \)
\( \abs{AF} \) uzunluğunu bulmak için \( AFD \) dik üçgeninde Pisagor teoremini kullanalım.
\( \abs{AF}^2 + \abs{FD}^2 = \abs{AD}^2 \)
\( \abs{AF}^2 + 6^2 = (2\sqrt{13})^2 \)
\( \abs{AF} = 4 \)
\( \abs{FB} \) uzunluğunu bulmak için \( ADB \) üçgeninde Öklid bağıntısını kullanalım.
\( \abs{AD}^2 = \abs{AF} \cdot \abs{AB} \)
\( (2\sqrt{13})^2 = 4 \cdot (4 + \abs{FB}) \)
\( \abs{FB} = 9 \)
Dikdörtgende karşılıklı kenar uzunlukları birbirine eşittir.
\( \abs{DE} = \abs{FB} = 9 \)
\( DBC \) üçgeninin alanını bulalım.
\( A(DBC) = \dfrac{\abs{BC} \cdot \abs{DE}}{2} \)
\( = \dfrac{12 \cdot 9}{2} = 54 \) bulunur.
Şekilde \( AEB \) dik üçgeni ve \( ABC \) üçgeni verilmiştir.
\( \abs{AD} = \abs{AC} = 15 \)
\( m(\widehat{ABD}) = m(\widehat{DBE}) \)
\( \abs{DC} = 18 \)
olduğuna göre, \( \abs{BD} = x \) kaçtır?
Çözümü Göster\( \abs{AD} = \abs{AC} \) olduğu için \( ADC \) üçgeni ikizkenardır.
\( ADC \) üçgeninde \( A \) köşesinden tabana ait yüksekliği çizelim.
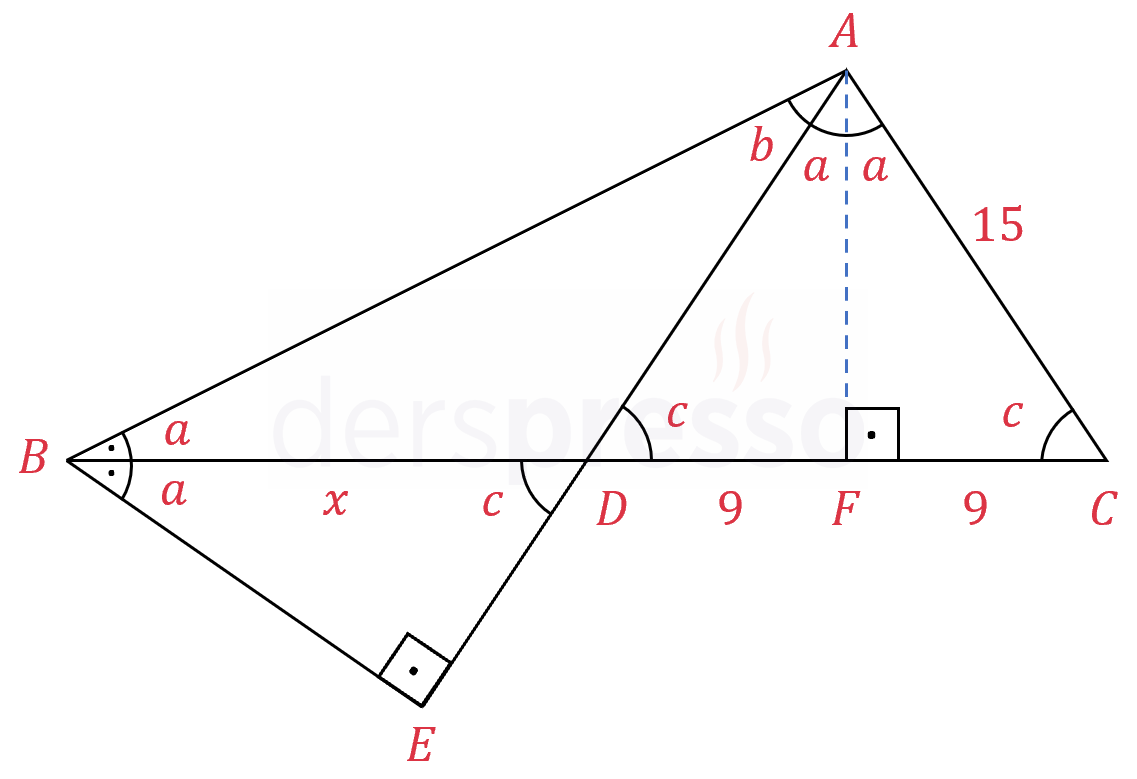
\( ADC \) üçgeni ikizkenar olduğundan tabana ait yükseklik tabanı ortalar.
\( \abs{DF} = \abs{FC} = 9 \)
\( BED \) üçgeninin iç açıları aşağıdaki gibi olsun.
\( m(\widehat{DBE}) = m(\widehat{ABD}) = a \)
\( m(\widehat{BAE}) = b \)
\( m(\widehat{BDE}) = c \)
\( BED \) üçgeninin iç açıları toplamı 180°'dir.
\( a + c + 90° = 180° \)
\( a + c = 90° \)
Ters açılar birbirine eşittir.
\( m(\widehat{ADC}) = m(\widehat{BDE}) = c \)
İkizkenar üçgende taban açıları eşittir.
\( m(\widehat{ACD}) = m(\widehat{ADC}) = c \)
\( AFD \) ve \( AFC \) dik üçgendir.
\( m(\widehat{DAF}) = m(\widehat{CAF}) = a \)
\( ABC \) üçgeninin iç açıları toplamını yazalım.
\( a + b + a + a + c = 180° \)
\( 3a + b + c = 180° \)
\( a + c = 90° \) olduğunu biliyoruz.
\( 2a + b = 90° \)
Buna göre \( m(\widehat{BAC}) = 90° \) olarak bulunur.
\( ABC \) üçgeninde Öklid bağıntısını kullanarak \( \abs{BD} \) uzunluğunu bulalım.
\( \abs{AC}^2 = \abs{CF} \cdot \abs{CB} \)
\( 15^2 = 9 \cdot (9 + 9 + \abs{BD} ) \)
\( 25 = 18 + x \)
\( \abs{BD} = x = 7 \) bulunur.
Şekilde \( ACB \) ve \( DBC \) ikizkenar üçgenleri ile \( ACD \) dik üçgeni verilmiştir.
\( [AC] \perp [CD] \)
\( \abs{AC} = \abs{BC} \)
\( \abs{DB} = \abs{DC} \)
\( \abs{AD} = 10 \)
olduğuna göre, \( \abs{DB} \) kaçtır?
Çözümü Göster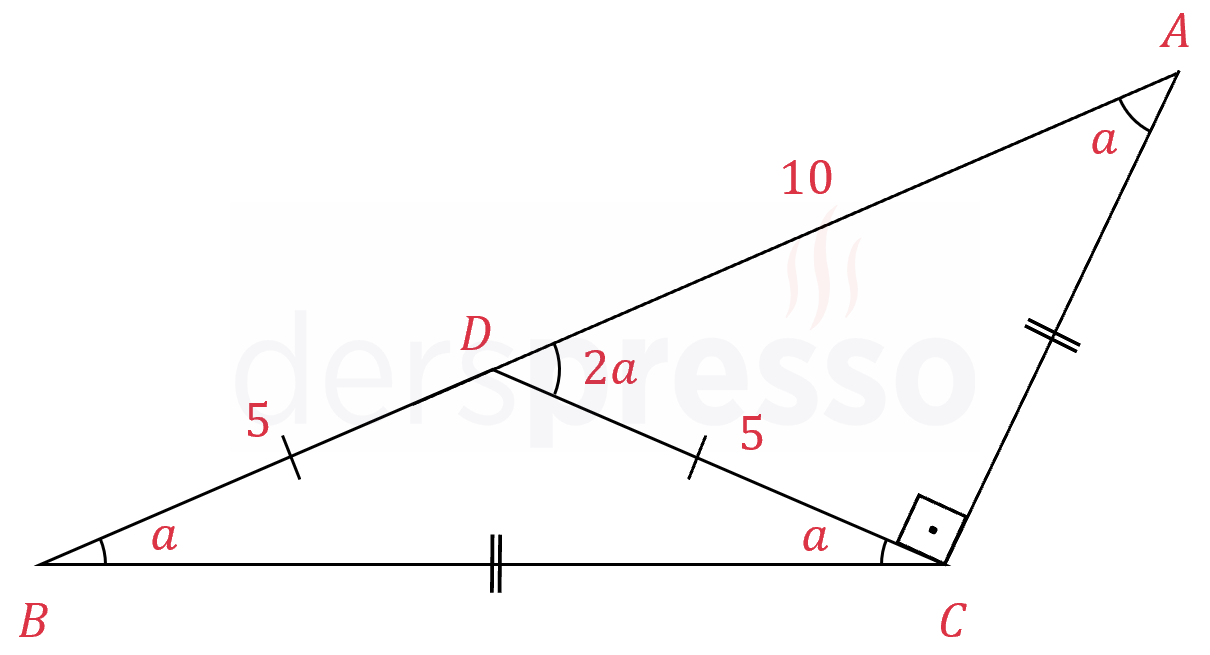
\( DBC \) üçgeni ikizkenardır.
\( m(\widehat{DBC}) = m(\widehat{DCB}) = a \) diyelim.
\( ACB \) üçgeni ikizkenardır.
\( m(\widehat{CAB}) = m(\widehat{CBA}) = a \)
\( DBC \) üçgeninde bir dış açı iki iç açının toplamına eşittir.
\( m(\widehat{ADC}) = 2a \)
\( ACD \) üçgeninde iç açıların toplamını alalım.
\( 2a + a + 90° = 180° \)
\( a = 30° \)
\( ACD \) üçgeni 30-60-90° üçgeni olur. 30-60-90° üçgeninde kenar uzunlukları arasındaki orantı sırasıyla \( 1:\sqrt{3}:2 \) şeklinde olur.
\( \abs{AD} = 10 \) ise \( \abs{DC} = 5 \)
\( \abs{DB} = \abs{DC} = 5 \) bulunur.
Şekilde \( ABC \) ve \( DFC \) dik üçgenleri ile \( DEC \) ikizkenar üçgeni verilmiştir.
\( [AB] \perp [EC], \quad [DF] \perp [EC] \)
\( \abs{DE} = \abs{DC} \)
\( \abs{GB} = 2, \quad \abs{DF} = 5 \)
olduğuna göre, \( \abs{AG} = x \) kaçtır?
Çözümü Göster\( m(\widehat{GEB}) = a, m(\widehat{EGB}) = b \) diyelim.
\( GEB \) üçgeninde iç açıların toplamını bulalım.
\( a + b + 90° = 180° \)
\( a + b = 90° \)
\( DEC \) üçgeni ikizkenardır.
\( m(\widehat{DCE}) = m(\widehat{DEC}) = a \)
\( a + b = 90° \) olduğuna göre \( 2a + 2b = 180° \) olur.
\( DEC \) üçgeninde iç açılar toplamı 180° olduğundan \( m(\widehat{EDC}) = 2b \) olur.
\( DEC \) üçgeni ikizkenar olduğundan \( [DF] \) yüksekliği aynı anda açıortaydır.
\( m(\widehat{EDF}) = m(\widehat{CDF}) = b \)
\( [DH] \parallel [EC] \) olacak şekilde \( D \) noktasından \( [AB] \) kenarına bir dikme çizelim.
\( [GK] \parallel [HD] \) olacak şekilde \( G \) noktasından \( [DF] \) kenarına bir dikme çizelim.
Oluşan yeni kenar uzunlukları aşağıdaki gibidir.
\( \abs{KF} = \abs{GB} = 2 \)
\( \abs{DK} = \abs{HG} = 5 - 2 = 3 \)
\( DEC \) üçgeninde bir dış açı iki iç açının toplamına eşittir.
\( m(\widehat{ADG}) = 2a \)
Ters açılar birbirine eşittir.
\( m(\widehat{AGD}) = m(\widehat{EGB}) = b \)
Tümler açıların toplamı 90° olur.
\( m(\widehat{HDG}) = a \)
\( m(\widehat{HDA}) = 2a - a = a \)
Tümler açıların toplamı 90° olur.
\( m(\widehat{GAD}) = b \)
Buna göre \( ADG \) üçgeni ikizkenardır.
\( ADG \) ikizkenar üçgeninde tabana inen dikme aynı zamanda kenarortay, açıortay ve yükseklik olur.
\( \abs{AH} = \abs{HG} = 3 \)
\( \abs{AG} = x = 3 + 3 = 6 \) bulunur.
Şekildeki üçgen bir ikizkenar üçgen olduğuna göre, \( n \) sayısının alabileceği değerler toplamı kaçtır?
Çözümü GösterKenar uzunluklarını sırasıyla ikili olarak birbirine eşitleyerek denklemleri çözelim.
Durum 1:
\( n^2 + 2n = 4n + 15 \)
\( n^2 - 2n - 15 = 0 \)
\( (n + 3)(n - 5) = 0 \)
\( n = -3 \) ya da \( n = 5 \)
\( x = -3 \) için kenar uzunlukları aşağıdaki gibi olur.
\( n^2 + 2n, 4n + 15, 4n + 8 \)
\( (-3)^2 + 2(-3), 4(-3) + 15, 4(-3) + 8 \)
\( 3, 3, -4 \)
\( -4 \) bir üçgenin kenar uzunluğu olamayacağı için \( n = -3 \) geçerli bir çözüm değildir.
\( n = 5 \) için kenar uzunlukları aşağıdaki gibi olur.
\( n^2 + 2n, 4n + 15, 4n + 8 \)
\( 5^2 + 2(5), 4(5) + 15, 4(5) + 8 \)
\( 35, 35, 28 \)
Durum 2:
\( n^2 + 2n = 4n + 8 \)
\( n^2 - 2n - 8 = 0 \)
\( (n + 2)(n - 4) = 0 \)
\( n = -2 \) ya da \( n = 4 \)
\( n = -2 \) için kenar uzunlukları aşağıdaki gibi olur.
\( n^2 + 2n, 4n + 15, 4n + 8 \)
\( (-2)^2 + 2(-2), 4(-2) + 15, 4(-2) + 8 \)
\( 0, 7, 0 \)
\( 0 \) bir üçgenin kenar uzunluğu olamayacağı için \( n = -2 \) geçerli bir çözüm değildir.
\( n = 4 \) için kenar uzunlukları aşağıdaki gibi olur.
\( n^2 + 2n, 4n + 15, 4n + 8 \)
\( 4^2 + 2(4), 4(4) + 15, 4(4) + 8 \)
\( 24, 31, 24 \)
Durum 3:
\( 4n + 15 = 4n + 8 \)
\( 15 = 8 \)
Bu durumda geçerli bir çözüm yoktur.
İstenen koşulu sağlayan farklı \( n \) değerleri aşağıdaki gibi bulunur.
\( n \in \{ 4, 5 \} \)
\( n \)'nin alabileceği değerlerin toplamı \( 4 + 5 = 9 \) bulunur.